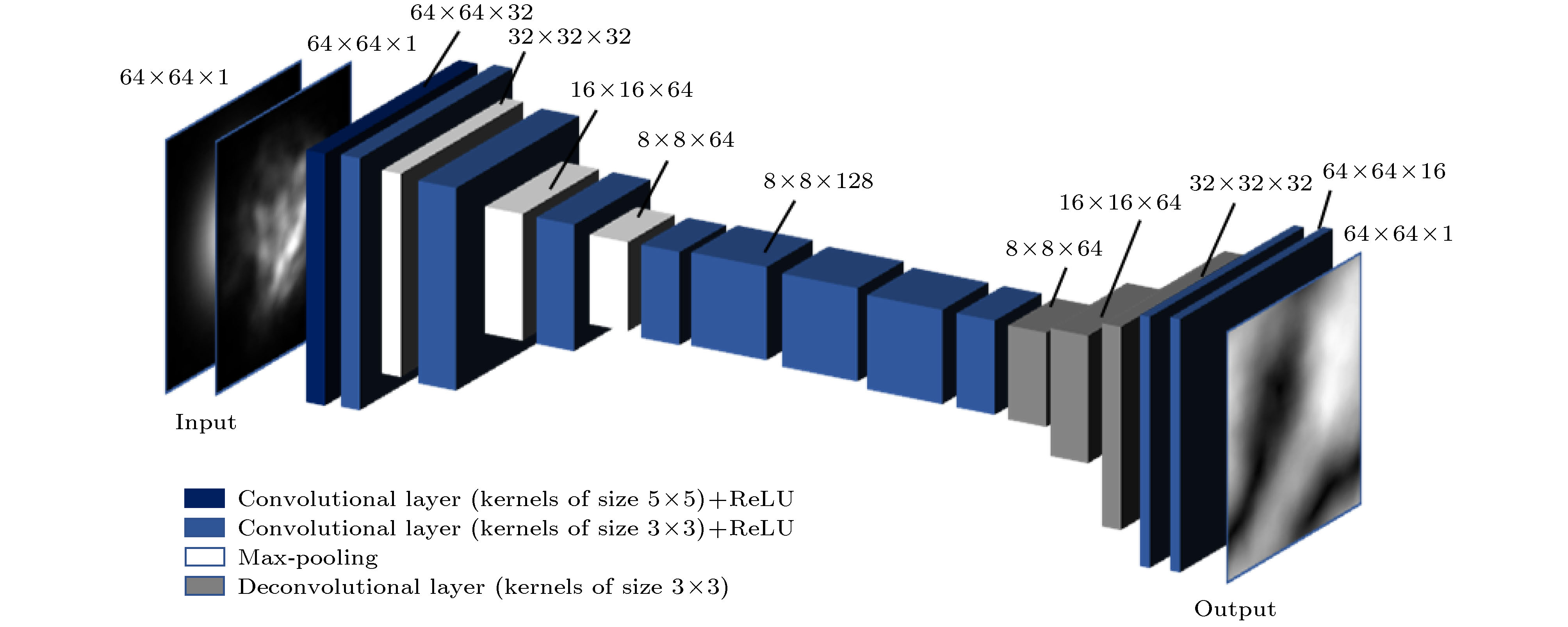
-
When a light beam transmits in free space, it is easily affected by atmospheric turbulence. The effect on transmitted light is equivalent to adding a random noise phase to it, which leads its transmission quality to deteriorate. The method of improving the quality of transmitted beams is usually to compensate for the phase distortion at the receiver by adding reverse turbulence phase, and the premise of this method is to obtain the turbulence phase carried by the distorted beam. The adaptive optics system is the most common way to extract the phase information. However, it is inefficient to be applied to varying turbulence environments due to the fact that a wave-front sensor and complex optical system are usually contained. Deep convolutional neural network (CNN) that can directly capture feature information from images is widely used in computer vision, language processing, optical information processing, etc. Therefore, in this paper proposed is a turbulence phase information extraction scheme based on the CNN, which can quickly and accurately extract the turbulence phase from the intensity patterns affected by atmosphere turbulence. The CNN model in this paper consists of 17 layers, including convolutional layers, pooling layers and deconvolutional layers. The convolutional layers and pooling layers are used to extract the turbulent phase from the feature image, which is the core structure of the network. The function of the deconvolutional layers is to visualize the extracted turbulence information and output the final predicted turbulence phase. After learning a huge number of samples, the loss function value of CNN converges to about 0.02, and the average loss function value on the test set is lower than 0.03. The trained CNN model has a good generalization capability and can directly extract the turbulent phase according to the input light intensity pattern. Using an I5-8500 CPU, the average time to predict the turbulent phase is as low as s under the condition of
$C_{{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}}^{ - 2/3}}$ ,$ 5 \times {10^{ - 14}}\;{{\rm{m}}^{ - 2/3}}$ , and$1 \times {10^{ - 13}}\;{{\rm{m}}^{ - 2/3}}$ . In addition, the turbulence phase extraction capability of CNN can be further enhanced by improving computing power or optimizing model structure. These results indicate that the CNN-based turbulence phase extraction method can effectively extract the turbulence phase, which has important application value in turbulence compensation, atmospheric turbulence characteristics research and image reconstruction.-
Keywords:
- atmospheric turbulence /
- phase extraction /
- deep convolutional neural network /
- Gerchberg-Saxton algorithm
[1] Zheng G, Wang L, Wang J, Zhou M C, Song M M 2018 J. Mod. Opt. 65 1616
Google Scholar
[2] Yuan Y S, Liu D, Zhou Z X, Xu H F, Qu J, Cai Y J 2018 Opt. Express 26 21861
Google Scholar
[3] Li Y Q, Wang L G, Wu Z S 2018 Optik 158 1349
Google Scholar
[4] Wang Y K, Xu H Y, Li D Y, Wang R, Jin C B, Yin X H, Gao S J, Mu Q Q, Xuan L, Cao Z L 2018 Sci. Rep. 8 1124
Google Scholar
[5] Gerçekcioğlu H 2019 Opt. Commun. 439 233
Google Scholar
[6] Usenko V C, Peuntinger C, Heim B, Günthner K, Derkach I, Elser D, Marquardt C, Filip R, Leuchs G 2018 Opt. Express 26 31106
Google Scholar
[7] Hope D A, Jefferies S M, Hart M, Nagy J G 2016 Opt. Express 24 12116
Google Scholar
[8] Wen W, Jin Y, Hu M J, Liu X L, Cai Y J, Zou C J, Luo M, Zhou L W, Chu X X 2018 Opt. Commun. 415 48
Google Scholar
[9] Ren Y X, Xie G D, Huang H, Ahmed N, Yan Y, Li L, Bao C J, Lavery M P, Tur M, Neifeld M A, Boyd R W, Shapiro J H, Willner A E 2014 Optica 1 376
Google Scholar
[10] Yin X L, Chang H, Cui X Z, Ma J X, Wang Y J, Wu G H, Zhang L J, Xin X J 2018 Appl. Opt. 57 7644
Google Scholar
[11] Neo R, Goodwin M, Zheng J, Lawrence J, Leon-Saval S, Bland-Hawthorn J, Molina-Terriza G 2016 Opt. Express 24 2919
Google Scholar
[12] Gerchberg R W 1972 Optik 35 237
[13] Fu S Y, Zhang S K, Wang T L, Gao C Q 2016 Opt. Lett. 41 3185
Google Scholar
[14] Nelson W, Palastro J P, Wu C, Davis C C 2016 Opt. Lett. 41 1301
Google Scholar
[15] Hinton G E, Salakhutdinov R R 2006 Science 313 504
Google Scholar
[16] Lecun Y, Bengio Y, Hinton G 2015 Nature 521 436
Google Scholar
[17] Li J, Zhang M, Wang D S, Wu S J, Zhan Y Y 2018 Opt. Express 26 10494
Google Scholar
[18] Roddier N A 1990 Opt. Eng. 29 1174
Google Scholar
[19] Mcglamery B L 1967 J. Opt. Soc. Am. 57 293
Google Scholar
[20] Zhao S M, Leach J, Gong L Y, Ding J, Zheng B Y 2012 Opt. Express 20 452
Google Scholar
[21] Rumerlhar D E 1986 Nature 323 533
Google Scholar
[22] Lecun Y, Bottou L, Bengio Y, Haffner P 1998 Proc. IEEE 86 2278
Google Scholar
[23] Barakat R, Newsam G 1985 J. Opt. Soc. Am. A 2 2027
Google Scholar
[24] Guo Y M, Liu Y, Oerlemans A, Lao S Y, Wu S, Lew M S 2016 Neurocomputing 187 27
Google Scholar
[25] Hinton G E, Osindero S, Teh Y 2006 Neural Comput. 18 1527
Google Scholar
[26] Qian Y M, Bi M X, Tan T, Yu K 2016 IEEE Trans. Audio Speech Lang. Process. 24 2263
Google Scholar
[27] Sheridan P M, Cai F X, Du C, Ma W, Zhang Z Y, Lu W D 2017 Nat. Nanotech. 12 784
Google Scholar
-
图 1 各湍流强度下的随机相位屏 (a), (b)
$C_{{n}}^2 \!=\! 1 \!\!\times\!\! {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (c), (d)$C_{{n}}^2 \!=\! 5 \!\!\times\!\!{10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (e), (f)$C_{\rm{n}}^2 \!=\! 1 \!\!\times\!\! {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ Figure 1. Random phase screen at each turbulence intensity: (a), (b)
$C_{{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (c), (d)$C_{\rm{n}}^2 = 5 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (e), (f)$C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ .
图 2 各湍流强度影响下传输光束截面光斑 (a)初始高斯光束; (b), (c)
$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}}^{ - 2/3}}$ ; (d), (e)$C_{\rm{n}}^2 = 5 \times $ ${10^{ - 14}}\;{{\rm{m}}^{ - 2/3}} $ ; (f), (g)$C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}}^{ - 2/3}}$ Figure 2. The cross-section spot of transmission beam at each turbulence intensity: (a) Initial Gaussian beam; (b), (c)
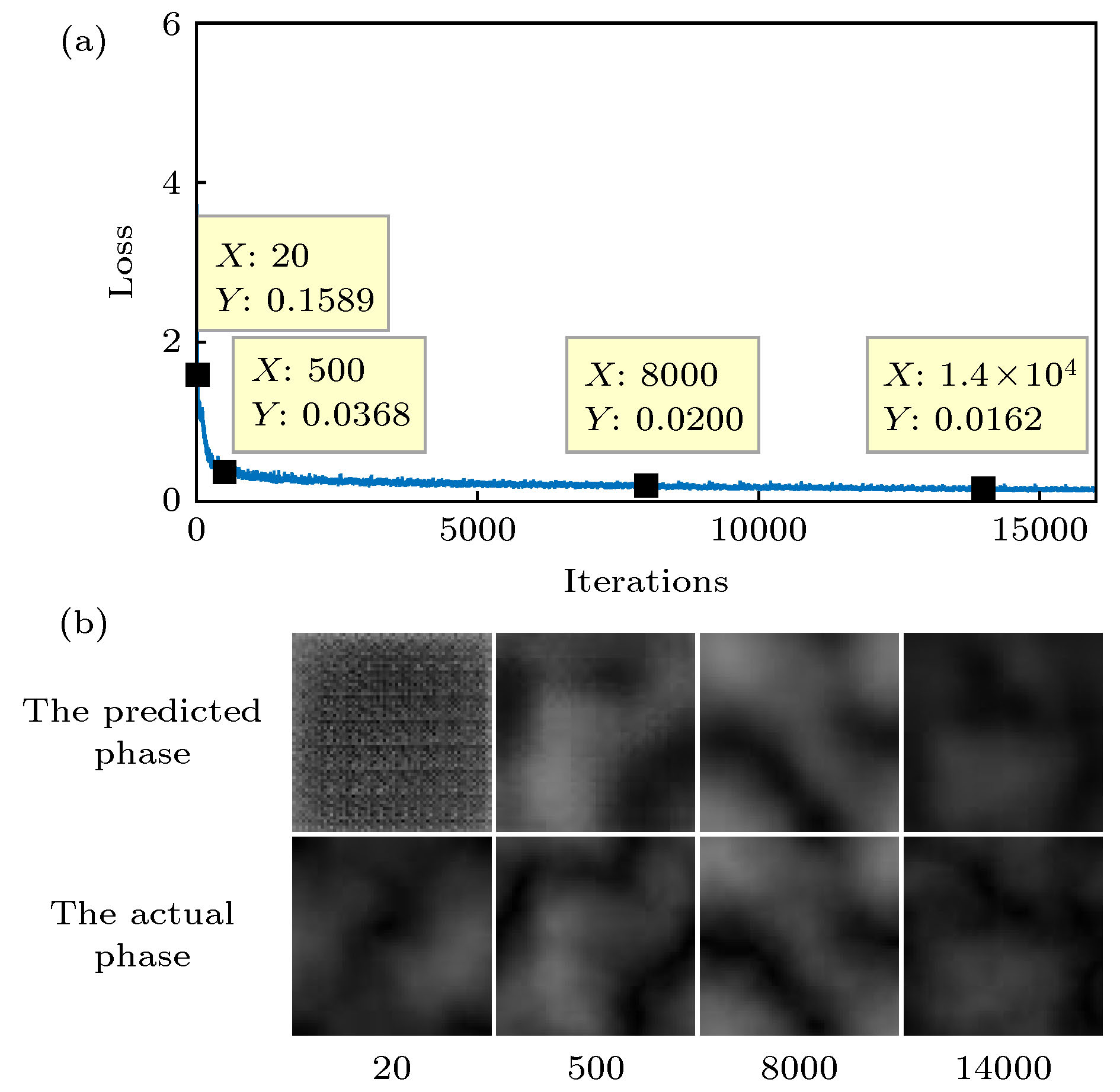
$C_{\rm{n}}^2 = $ $1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (d), (e)$C_{\rm{n}}^2 = 5 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (f), (g)$C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ .
图 3 提取湍流相位的CNN结构
Figure 3. The CNN structure of extracting the turbulent phase.
图 4 训练过程损失函数曲线
Figure 4. The loss function curve of training process.
图 5 训练过程提取到的湍流相 (a)与(b), (c)与(d), (e)与(f), (g)与(h), (i)与(j)和(k)与(l)的迭代次数分别为1, 100, 500, 4000, 8000, 14000
Figure 5. The turbulent phase during the training process: The number of iterations of (a) and (b), (c) and (d), (e) and (f), (g) and (h), (i) and (j), and (k) and (l) is 1, 100, 500, 4000, 8000, 14000.
图 6 各湍流强度损失函数曲线
Figure 6. The loss function curve at each turbulence intensity.
图 7 不同湍流强度下, 经过CNN提取到的湍流相位 (a), (b), (c)初始高斯光束; (d), (e), (f) 受大气湍流影响的高斯光束; (g), (h), (i)实际的大气湍流相位; (j), (k), (l) CNN输出的预测湍流相位
Figure 7. The predicted turbulent phase based on CNN at each turbulence intensity: (a), (b), (c) Initial Gaussian beam; (d), (e), (f) Gaussian beam affected by atmospheric turbulence; (g), (h), (i) the actual turbulence phase; (j), (k), (l) the output phase of CNN.
图 8 CNN与GS算法提取湍流相位效果对比 (a), (b), (c)受湍流强度为
$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 影响的高斯光束; (d), (e), (f)实际湍流相位; (g), (h), (i)基于CNN模型提取的湍流相位; (j), (k), (l) GS算法提取的湍流相位Figure 8. The comparison of CNN and GS algorithm for extracting turbulence phase: (a), (b), (c) Gaussian beam affected by atmospheric turbulence with
$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (d), (e), (f) the actual turbulence phase; (g), (h), (i) the predicted turbulent phase based on CNN; (j), (k), (l) the predicted turbulent phase based on GS algorithm.
图 9 训练及验证测试结果 (a)训练过程损失函数曲线; (b)训练过程中利用验证集测试得到的预测湍流相位
Figure 9. Training and validation set test results: (a) The loss function curve of training process; (b) the predicted turbulence phase obtained by testing the validation set during training.
表 1 仿真参数
Table 1. Parameter of simulation.
Parameter Simulation Value Number of Grid Elements N 128 Grid spacing ${{\varDelta x} / {\rm{cm}}}$ About 0.047 Laser wavelength ${\lambda / {\rm{nm}}}$ 1550 Initial ${1 / {\rm{e}}}$ amplitude radius ${{{\omega _0}} / {\rm{cm}}}$ 2 Total path length ${L / {\rm{m}}}$ 20 Inner scale of Turbulence ${{{l_0}} / {\rm{m}}}$ $2 \times {10^{ - 4}}$ Outer scale of Turbulence ${{{L_0}} / {\rm{m}}}$ 50 Number of phase screens n 1 
DownLoad: CSV
表 2 两方法预测时间对比
Table 2. The predicted time comparison of two methods.
Data Set Average time/s GS algorithm (70 iterations) CNN model $C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 0.39 0.0049 $C_{\rm{n}}^2 = 5 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 0.39 0.0048 $C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 0.41 0.0051
DownLoad: CSV
-
[1] Zheng G, Wang L, Wang J, Zhou M C, Song M M 2018 J. Mod. Opt. 65 1616
Google Scholar
[2] Yuan Y S, Liu D, Zhou Z X, Xu H F, Qu J, Cai Y J 2018 Opt. Express 26 21861
Google Scholar
[3] Li Y Q, Wang L G, Wu Z S 2018 Optik 158 1349
Google Scholar
[4] Wang Y K, Xu H Y, Li D Y, Wang R, Jin C B, Yin X H, Gao S J, Mu Q Q, Xuan L, Cao Z L 2018 Sci. Rep. 8 1124
Google Scholar
[5] Gerçekcioğlu H 2019 Opt. Commun. 439 233
Google Scholar
[6] Usenko V C, Peuntinger C, Heim B, Günthner K, Derkach I, Elser D, Marquardt C, Filip R, Leuchs G 2018 Opt. Express 26 31106
Google Scholar
[7] Hope D A, Jefferies S M, Hart M, Nagy J G 2016 Opt. Express 24 12116
Google Scholar
[8] Wen W, Jin Y, Hu M J, Liu X L, Cai Y J, Zou C J, Luo M, Zhou L W, Chu X X 2018 Opt. Commun. 415 48
Google Scholar
[9] Ren Y X, Xie G D, Huang H, Ahmed N, Yan Y, Li L, Bao C J, Lavery M P, Tur M, Neifeld M A, Boyd R W, Shapiro J H, Willner A E 2014 Optica 1 376
Google Scholar
[10] Yin X L, Chang H, Cui X Z, Ma J X, Wang Y J, Wu G H, Zhang L J, Xin X J 2018 Appl. Opt. 57 7644
Google Scholar
[11] Neo R, Goodwin M, Zheng J, Lawrence J, Leon-Saval S, Bland-Hawthorn J, Molina-Terriza G 2016 Opt. Express 24 2919
Google Scholar
[12] Gerchberg R W 1972 Optik 35 237
[13] Fu S Y, Zhang S K, Wang T L, Gao C Q 2016 Opt. Lett. 41 3185
Google Scholar
[14] Nelson W, Palastro J P, Wu C, Davis C C 2016 Opt. Lett. 41 1301
Google Scholar
[15] Hinton G E, Salakhutdinov R R 2006 Science 313 504
Google Scholar
[16] Lecun Y, Bengio Y, Hinton G 2015 Nature 521 436
Google Scholar
[17] Li J, Zhang M, Wang D S, Wu S J, Zhan Y Y 2018 Opt. Express 26 10494
Google Scholar
[18] Roddier N A 1990 Opt. Eng. 29 1174
Google Scholar
[19] Mcglamery B L 1967 J. Opt. Soc. Am. 57 293
Google Scholar
[20] Zhao S M, Leach J, Gong L Y, Ding J, Zheng B Y 2012 Opt. Express 20 452
Google Scholar
[21] Rumerlhar D E 1986 Nature 323 533
Google Scholar
[22] Lecun Y, Bottou L, Bengio Y, Haffner P 1998 Proc. IEEE 86 2278
Google Scholar
[23] Barakat R, Newsam G 1985 J. Opt. Soc. Am. A 2 2027
Google Scholar
[24] Guo Y M, Liu Y, Oerlemans A, Lao S Y, Wu S, Lew M S 2016 Neurocomputing 187 27
Google Scholar
[25] Hinton G E, Osindero S, Teh Y 2006 Neural Comput. 18 1527
Google Scholar
[26] Qian Y M, Bi M X, Tan T, Yu K 2016 IEEE Trans. Audio Speech Lang. Process. 24 2263
Google Scholar
[27] Sheridan P M, Cai F X, Du C, Ma W, Zhang Z Y, Lu W D 2017 Nat. Nanotech. 12 784
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 14386
- PDF Downloads: 374
- Cited By: 0
