-
We consider a two-mode entangled coherent light field, in which one mode of the light field is injected into the cavity and interacts with a two-level atom. According to the theory of cavity electrodynamics, the evolution state of atomic system is deduced. Aiming at the dynamic process from the initial state of an atomic system to the target evolution state, the quantum speed limit time is used to characterize the maximum evolution rate of the quantum state of an atomic system. The maximum evolution rate of an atomic system can be controlled by adjusting the coherent parameters of the two-mode entangled coherent light field. But up to now, which kind of quantum speed limit time can be better, universal and strict applicable to the quantum dynamics process of any system is still an unresolved important issue. Based on different methods of measuring the distance between two quantum states and different dynamic evolution channels, many definitions of the quantum speed limit time have been given. The quantum speed limit time proposed by Deffner and Lutz (Deffner S, Lutz E 2013 Phys. Rev. Lett. 111 010402) and the other deduced by Campaioli et al. (Campaioli F, Pollock F A, Binder F C, Modi K 2018 Phys. Rev. Lett. 120 060409; Campaioli F, Pollock F A, Modi K 2018 arXiv:1806.08742) have attracted extensive attention. In this paper, we first compare the advantages of two quantum speed limit times to characterize the maximum evolution rate of quantum states. We find that the quantum speed limit time expression given by Campaioli et al. (Campaioli F, Pollock F A, Modi K 2018 arXiv:1806.08742) in 2018 is a tighter bound when describing the boundary of the shortest time required for the quantum state evolution of a two-level atomic system. Therefore, this paper is mainly based on the quantum speed limit time given by Campaioli et al. to analyze how to achieve the maximum evolution rate of the quantum state of the atomic system by manipulating the parameters of a two-level entangled coherent light field. The results show that the maximum evolution speed of the quantum state of the atomic system can be significantly affected by the coherent parameters of the light field interacting with the atom under certain conditions. Furthermore, when the interacting light field parameters cannot well control the maximum evolution speed of the quantum state, the quantum correlation with the two-mode entangled coherent light field can realize the remote control of the maximum evolution speed of quantum state of atomic system by the light field parameters that are not involved in the atom-light interaction.
-
Keywords:
- quantum speed limit time /
- entangled coherent state /
- two-level atom
[1] Mandelstam L, Tamm I 1945 J. Phys. (USSR)
9 249 [2] Anandan J, Aharonov Y 1990 Phys. Rev. Lett. 65 1697
Google Scholar
[3] Margolus N, Levitin L B 1998 Physica D 120 188
Google Scholar
[4] Levitin L B, Toffoli T 2009 Phys. Rev. Lett. 103 160502
Google Scholar
[5] Giovannetti V, Lloyd S, Maccone L 2003 Phys. Rev. A 67 052109
Google Scholar
[6] Pfeifer P, Frohlich J 1995 Rev. Mod. Phys. 67 759
Google Scholar
[7] Deffner S, Lutz E 2013 Phys. Rev. Lett. 111 010402
Google Scholar
[8] Campaioli F, Pollock F A, Binder F C, Modi K 2018 Phys. Rev. Lett. 120 060409
Google Scholar
[9] Campaioli F, Pollock F A, Modi K 2018 arXiv: 1806.08742
[10] Georgescu I M, Ashhab S, Nori F 2014 Rev. Mod. Phys. 86 153
Google Scholar
[11] Nielsen M A, Chuang I L 2000 Quantum Computation and Quantum Communication (Cambridge: Cambridge University Press) p546
[12] Lloyd S 2002 Phys. Rev. Lett. 88 237901
Google Scholar
[13] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photon. 5 222
Google Scholar
[14] Hegerfeldt G C 2013 Phys. Rev. Lett. 111 260501
Google Scholar
[15] Xu Z Y, Luo S L, Yang W L, Liu C, Zhu S Q 2014 Phys. Rev. A 89 012307
Google Scholar
[16] Xu Z Y 2016 New J. Phys. 18 073005
Google Scholar
[17] Zhang Y J, Xia Y J, Fan H 2016 Europhys. Lett. 116 30001
Google Scholar
[18] Liu H B, Yang W L, An J H, Xu Z Y 2016 Phys. Rev. A 93 020105(R)
Google Scholar
[19] Baksic A, Ribeiro H, Clerk A A 2016 Phys. Rev. Lett. 116 230503
Google Scholar
[20] Xu K, Zhang Y J, Xia Y J, Wang Z D, Fan H 2018 Phys. Rev. A 98 022114
Google Scholar
[21] Zhang Y J, Han W, Xia Y J, Cao J P, Fan H 2015 Phys. Rev. A 91 032112
Google Scholar
[22] Cimmarusti A D, Yan Z, Patterson B D, Corcos L P, Orozco L A, Deffner S 2015 Phys. Rev. Lett. 114 233602
Google Scholar
[23] Sanders B C 1992 Phys. Rev. A 45 6811
Google Scholar
[24] An B N, Kim J 2009 Phys. Rev. A 80 042316
Google Scholar
[25] 夏云杰, 高德营 2007 56 3703
Google Scholar
Xia Y J, Gao D Y 2007 Acta Phys. Sin. 56 3703
Google Scholar
[26] 张英杰, 夏云杰, 任延琦, 杜秀梅, 刘玉玲 2009 58 722
Google Scholar
Zhang Y J, Xia Y J, Ren Y Q, Du X M, Liu Y L 2009 Acta Phys. Sin. 58 722
Google Scholar
-
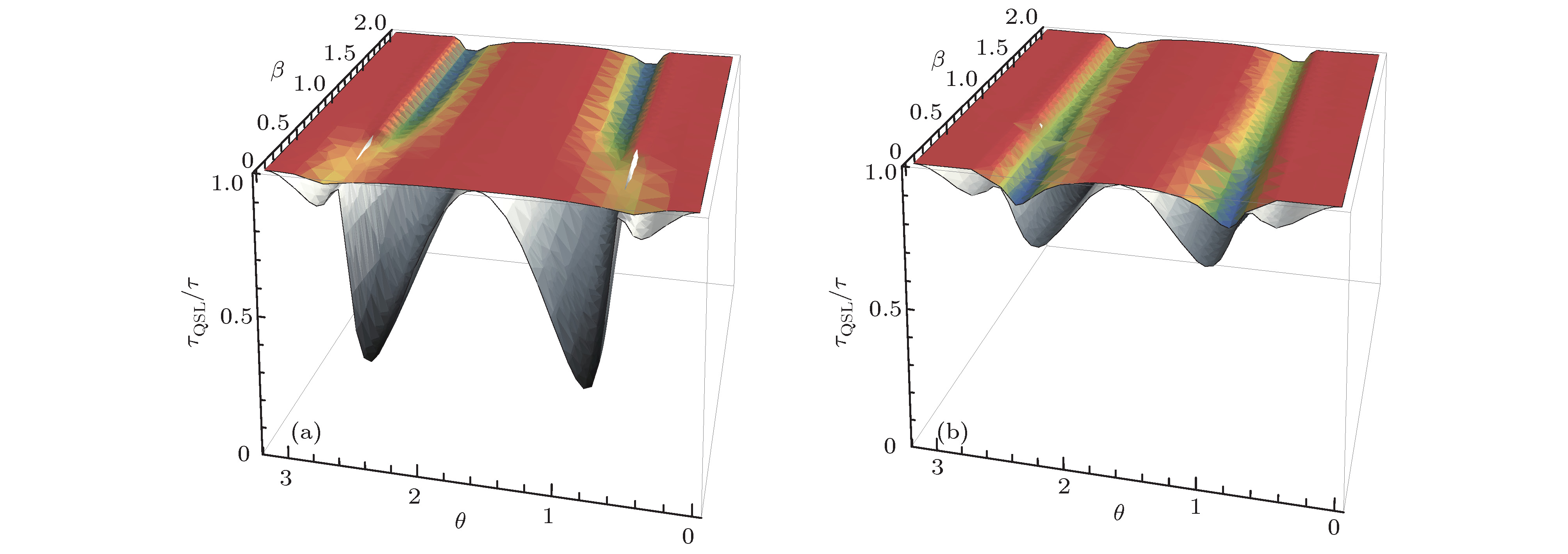
图 1 二能级原子系统量子态的两种量子速率极限时间
${\tau _{{\rm{QSL}}}}$ 与实际演化时间τ的比值随未参加相互作用光场b的相干参数β和初始量子态参数θ的变化, 这里$g = 1$ , 彩虹图形描述Campaioli表达式(8), 灰色图形描述Deffner表达式(7) (a)$\alpha = 1$ 和$\tau = 1$ 时, 初始纠缠相干光场状态为${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b)$\alpha = 1$ 和$\tau = 1$ 时, 初始纠缠相干光场状态为${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ Figure 1. Ratio of the quantum speed limit time
${\tau _{{\rm{QSL}}}}$ to the actual evolution time τ for the two-level atomic system quantum state as a function of the dimensionless initial state parameter θ and the coherent parameter β of the non-interaction light field b, and$g = 1$ , the rainbow graph describes Campaioli’s expression (8) and the gray graph describes Deffner’s expression (7). (a) When$\alpha = 1$ and$\tau = 1$ , the initial entangled coherent state is${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b) when$\alpha = 1$ and$\tau = 1$ , the initial entangled coherent state is${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ .
图 2 原子系统量子态的量子速率极限时间与实际演化时间的比值
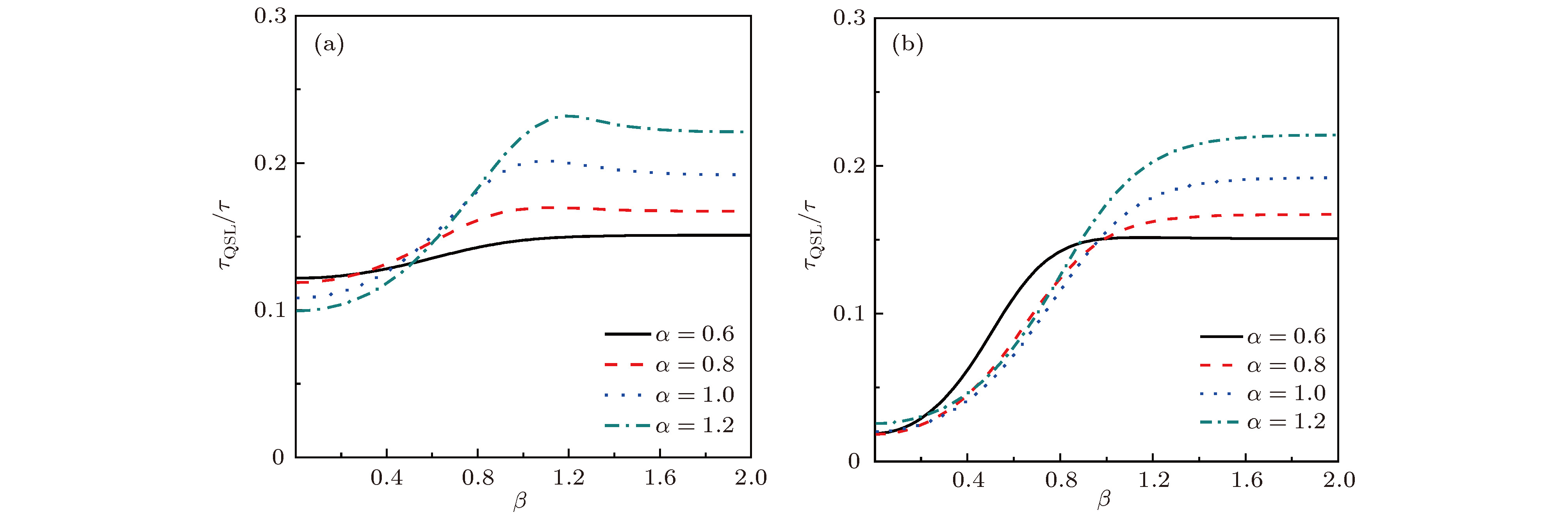
${\tau _{{\rm{QSL}}}}/\tau $ 随双模纠缠相干光场参数α和β的变化规律, 这里$g = 1$ ,$\theta = 3{\text{π}}/4$ , 彩虹图形描述Campaioli表达式(8), 灰色图形描述Deffner表达式(7) (a)和(c)分别为$\tau = 1$ 和$\tau = 5$ 时, 初始时刻双模纠缠相干光场为${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b)和(d)分别为$\tau = 1$ 和$\tau = 5$ 时, 初始时刻双模纠缠相干光场为${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ Figure 2. Ratio
${\tau _{{\rm{QSL}}}}/\tau $ of the quantum speed limit time to the actual evolution time for the two-level atomic system quantum state as a function of the two-mode entangled coherent light field parameters α and β, and$g = 1$ ,$\theta = 3{\text{π}} /4$ , the rainbow graph describes Campaioli’s expression (8) and the gray graph describes Deffner’s expression (7). Here, in (a) and (c) the initial entangled coherent state is${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ , for$\tau = 1$ and$\tau = 5$ respectively; in (b) and (d) the initial entangled coherent state is${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ , for$\tau = 1$ and$\tau = 5$ respectively.
图 3 考虑不同的实际演化时间τ时, 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值
${\tau _{{\rm{QSL}}}}/\tau $ 随参加相互作用光场a的相干参数α的变化规律, 这里$\beta = 0$ ,$g = 1$ ,$\theta = 3{\text{π}} /4$ (a)初始光场a为$\left( {{\left| \alpha \right\rangle _a} + {\left| { - \alpha } \right\rangle _a}} \right)/{\left( {2 + 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ ; (b)初始光场a为$\left( {{\left| \alpha \right\rangle _a} - {\left| { - \alpha } \right\rangle _a}} \right)/{\left( {2 - 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ Figure 3. By considering different actual evolution times, the ratio
${\tau _{{\rm{QSL}}}}/\tau $ of the quantum speed limit time to the actual evolution time for the two-level atomic system quantum state as a function of the coherent parameter α of the interaction light field a, and$\beta = 0$ ,$g = 1$ ,$\theta = 3{\text{π}}/4$ : (a) The initial state of the light field a is$\left( {{\left| \alpha \right\rangle _a} + {\left| { - \alpha } \right\rangle _a}} \right)/{\left( {2 + 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ ; (b) the initial state of the light field a is$\left( {{\left| \alpha \right\rangle _a} - {\left| { - \alpha } \right\rangle _a}} \right)/{\left( {2 - 2{{\rm{e}}^{ - 2{{\left| \alpha \right|}^2}}}} \right)^{ - 1/2}}$ .
图 4 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值
${\tau _{{\rm{QSL}}}}/\tau $ 随双模纠缠光场相干参数α, β的变化规律, 这里$\tau = 1$ ,$g = 1$ ,$\theta = 3{\text{π}}/4$ (a)初始双模纠缠相干光场${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b)初始双模纠缠相干光场${N_ - }\left( { {\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ Figure 4. Ratio
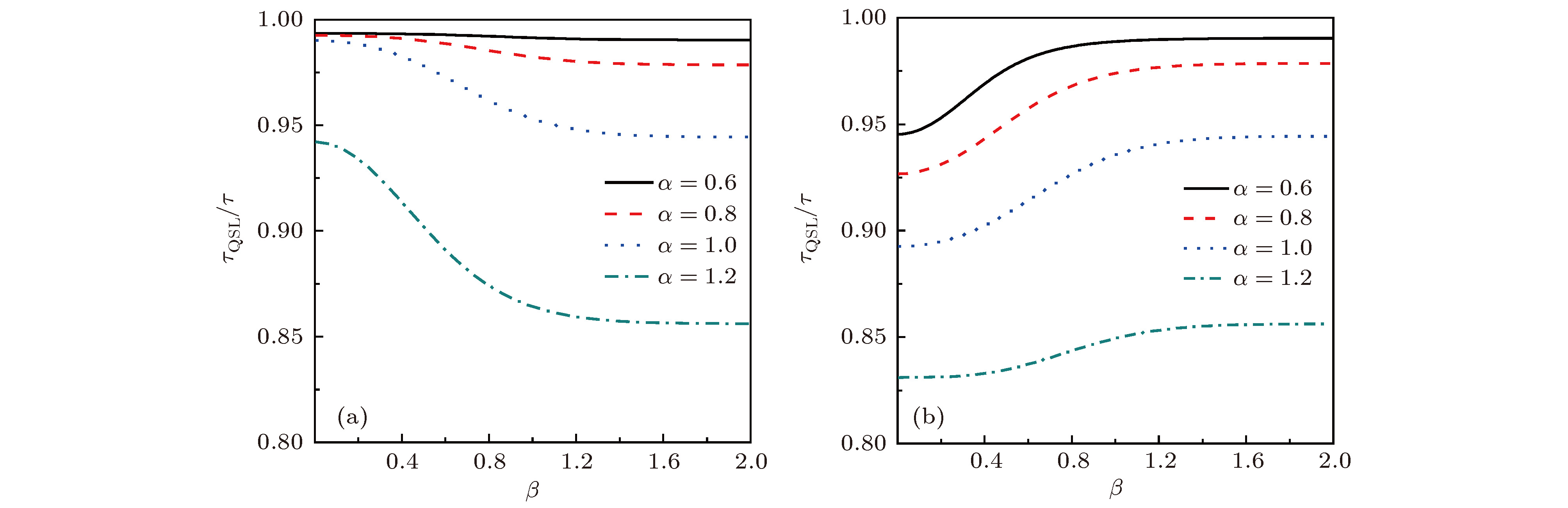
${\tau _{{\rm{QSL}}}}/\tau $ of the quantum speed limit time to the actual evolution time for the two-level atomic system quantum state as a function of the two-mode entangled coherent light field parameters α and β, and$\tau = 1$ ,$g = 1$ ,$\theta = 3{\text{π}}/4$ : (a) The initial entangled coherent state is${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b) the initial entangled coherent state is${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ .
图 5 二能级原子系统量子态的量子速率极限时间与实际演化时间的比值
${\tau _{{\rm{QSL}}}}/\tau $ 随双模纠缠相干光场参数α, β的变化规律, 这里$\tau = 15$ ,$g = 1$ ,$\theta = 3{\text{π}}/4$ (a)初始双模纠缠相干光场为${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b)初始双模纠缠相干光场为${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ Figure 5. Ratio
${\tau _{{\rm{QSL}}}}/\tau $ of the two quantum speed limit time to the actual evolution time for the two-level atomic system quantum state as a function of the two-mode entangled coherent light field parameters α and β, here parameters$\tau = 15$ ,$g = 1$ ,$\theta = 3{\text{π}}/4$ : (a) The initial entangled coherent state is${N_ + }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} + {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ ; (b) the initial entangled coherent state${N_ - }\left( {{\left| \alpha \right\rangle _a}{\left| \beta \right\rangle _b} - {\left| { - \alpha } \right\rangle _a}{\left| { - \beta } \right\rangle _b}} \right)$ . -
[1] Mandelstam L, Tamm I 1945 J. Phys. (USSR)
9 249 [2] Anandan J, Aharonov Y 1990 Phys. Rev. Lett. 65 1697
Google Scholar
[3] Margolus N, Levitin L B 1998 Physica D 120 188
Google Scholar
[4] Levitin L B, Toffoli T 2009 Phys. Rev. Lett. 103 160502
Google Scholar
[5] Giovannetti V, Lloyd S, Maccone L 2003 Phys. Rev. A 67 052109
Google Scholar
[6] Pfeifer P, Frohlich J 1995 Rev. Mod. Phys. 67 759
Google Scholar
[7] Deffner S, Lutz E 2013 Phys. Rev. Lett. 111 010402
Google Scholar
[8] Campaioli F, Pollock F A, Binder F C, Modi K 2018 Phys. Rev. Lett. 120 060409
Google Scholar
[9] Campaioli F, Pollock F A, Modi K 2018 arXiv: 1806.08742
[10] Georgescu I M, Ashhab S, Nori F 2014 Rev. Mod. Phys. 86 153
Google Scholar
[11] Nielsen M A, Chuang I L 2000 Quantum Computation and Quantum Communication (Cambridge: Cambridge University Press) p546
[12] Lloyd S 2002 Phys. Rev. Lett. 88 237901
Google Scholar
[13] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photon. 5 222
Google Scholar
[14] Hegerfeldt G C 2013 Phys. Rev. Lett. 111 260501
Google Scholar
[15] Xu Z Y, Luo S L, Yang W L, Liu C, Zhu S Q 2014 Phys. Rev. A 89 012307
Google Scholar
[16] Xu Z Y 2016 New J. Phys. 18 073005
Google Scholar
[17] Zhang Y J, Xia Y J, Fan H 2016 Europhys. Lett. 116 30001
Google Scholar
[18] Liu H B, Yang W L, An J H, Xu Z Y 2016 Phys. Rev. A 93 020105(R)
Google Scholar
[19] Baksic A, Ribeiro H, Clerk A A 2016 Phys. Rev. Lett. 116 230503
Google Scholar
[20] Xu K, Zhang Y J, Xia Y J, Wang Z D, Fan H 2018 Phys. Rev. A 98 022114
Google Scholar
[21] Zhang Y J, Han W, Xia Y J, Cao J P, Fan H 2015 Phys. Rev. A 91 032112
Google Scholar
[22] Cimmarusti A D, Yan Z, Patterson B D, Corcos L P, Orozco L A, Deffner S 2015 Phys. Rev. Lett. 114 233602
Google Scholar
[23] Sanders B C 1992 Phys. Rev. A 45 6811
Google Scholar
[24] An B N, Kim J 2009 Phys. Rev. A 80 042316
Google Scholar
[25] 夏云杰, 高德营 2007 56 3703
Google Scholar
Xia Y J, Gao D Y 2007 Acta Phys. Sin. 56 3703
Google Scholar
[26] 张英杰, 夏云杰, 任延琦, 杜秀梅, 刘玉玲 2009 58 722
Google Scholar
Zhang Y J, Xia Y J, Ren Y Q, Du X M, Liu Y L 2009 Acta Phys. Sin. 58 722
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7414
- PDF Downloads: 84
- Cited By: 0
