明亮压缩态光场的操控及量子层析

李庆回; 姚文秀; 李番; 田龙; 王雅君; 郑耀辉

doi:10.7498/aps.70.20210318

摘要

连续变量量子态的制备与操控是进行量子通信、量子密钥分发以及量子网络构建的重要基础. 本文基于二阶非线性过程, 利用周期极化磷酸氧钛钾晶体构成的简并光学参量放大腔, 在实验上实现了1064 nm波段明亮压缩态光场的制备, 所制备的明亮压缩态光场在泵浦光功率为310 mW、分析频率为3 MHz处的压缩度为–11.6 dB. 当注入50 mW泵浦光时, 实现了压缩度为–6 dB, 纯度为98.5%的压缩态光场; 在此基础上, 利用光电调制器进行明亮压缩态光场的线性光学操控, 并基于平衡零拍探测系统的直流信号准确判断压缩态光场时域信号对应的相位, 之后结合极大似然估计算法实现压缩态的量子层析, 得到量子态的密度矩阵及相空间的Wigner函数, 从而获得量子态的光子数分布等全部信息.

关键词:

Abstract

Generation and manipulation of continuous variable quantum states are the building blocks of quantum communication, quantum key distribution and quantum networks. According to the second-order nonlinear process of the periodically-poled potassium titanyl phosphate (PPKTP) crystal, we design a semi-monolithic optical parametric amplifier (OPA) cavity to generate the bright squeezed light at a wavelength of 1064 nm. With the injection of a seed beam, the squeezed state generated by the OPA has a coherent amplitude, so called bright squeezed state. The squeezing level is directly observed to be –11.6 dB when the pump power is 310 mW at an analysis frequency of 3 MHz. However, with the increase of the pump power, the purity of the squeezed state gets lower and lower due to the increased influence of the anti-squeezing quadrature component on the squeezed quadrature component in the detection process. To obtain a higher purity of the squeezed state for achieving linear optical manipulation and quantum tomography, we choose the pump power of 50 mW, the squeezing level decreases to –6 dB, and the purity of the squeezed state is 98.5% in this case. An electro-optic modulator is adopted to realize the liner manipulation of the squeezed light in the phase space. During the measurement of the bright squeezed state, all the data are taken on condition that the length of the OPA cavity and relative phase between the seed beam and the pump beam are locked by a locking loop. The direct current (DC) signal of the balanced homodyne detection (BHD) is used to accurately determine the phase corresponding to the time domain signal of the squeezed state, while the alternate current (AC) signal of the BHD is mixed with the signal generated by the function generator, after passing through a low-pass filter and a high-pass filter, the signal is then amplified by using a low-noise amplifier. A high-performance oscilloscope is finally used to simultaneously collect the signals, thus obtaining the quantum noise signal of the bright squeezed light after linear manipulation. Together with the maximum likelihood estimation algorithm, the quantum tomography, the density matrix and the Wigner function of the bright squeezed light are obtained, that is, all the information such as the photon number distribution of the quantum state is determined. Multiple iterations are taken in the maximum likelihood estimation algorithm process to eliminate the influence of the low quantum efficiency on the detection system, so that the density matrix is fitted well with the theoretical results.

Keywords:

作者及机构信息

1.
山西大学光电研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

2.
山西大学, 极端光学协同创新中心, 太原　030006

通信作者: 田龙, tianlong@sxu.edu.cn

基金项目: 国家自然科学基金(批准号: 62027821, 11654002, 11874250, 11804207, 11804206, 62035015)、国家重点研发计划(批准号: 2020YFC2200402)、山西省重点研发计划(批准号: 201903D111001)、陕西省自然科学基础研究计划(批准号: 2019JQ-943)、山西省三晋学者特聘教授项目、山西省“1331”重点建设学科和山西省高等学校中青年拔尖创新人才计划资助的课题

Authors and contacts

1.
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China

2.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Tian Long, tianlong@sxu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grants Nos. 62027821, 11654002, 11874250, 11804207, 11804206, 62035015), the National Key R&D Program of China (Grant No. 2020YFC2200402), the Key R&D Program of Shanxi Province, China (Grant No. 201903D111001), the Natural Science Basic Research Program of Shaanxi Province, China (Grant No. 2019JQ-943), the Program for Sanjin Scholar of Shanxi Province, China, the Fund for Shanxi 1331 Project Key Subjects Construction, China, and the Program for the Top Young and Middle-aged Innovative Talents of Higher Learning Institutions of Shanxi Province, China

文章全文 : translate this paragraph

参考文献

[1]	Schrödinger E 1926 Sci. Nat. 14 664 Google Scholar
[2]	Kennard E H 1927 J. Z. Phys. 44 326 Google Scholar
[3]	Darwin C G 1927 Proc. R. Soc. London, Ser. A 117 258 Google Scholar
[4]	Slusher R E, Hollberg L W, Yurke B, Mertz J C, Valley J F 1985 Phys. Rev. Lett. 55 2409 Google Scholar
[5]	Walls D F 1983 Nature 306 141 Google Scholar
[6]	Caves C M 1981 Phys. Rev. D 23 1693 Google Scholar
[7]	Acernese F, et al. (Virgo Collaboration). 2019 Phys. Rev. Lett. 123 231108 Google Scholar
[8]	Acernese F, et al. (Virgo Collaboration). 2020 Phys. Rev. Lett. 125 131101 Google Scholar
[9]	Eberle T, Händchen V, Schnabel R 2013 Opt. Express 21 11546 Google Scholar
[10]	Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706 Google Scholar
[11]	Asavanant W, Nakashima K, Shiozawa Y, Yoshikawa J I, Furusawa A 2017 Opt. Express 25 32227 Google Scholar
[12]	Polzik E S, Carri J, Kimble H J 1992 Phys. Rev. Lett. 68 3020 Google Scholar
[13]	Yang W, Shi S, Wang Y, Ma W, Zheng Y, Peng K 2017 Opt. Lett. 42 4553 Google Scholar
[14]	Madsen L S, Usenko V C, Lassen M, Filip R, Andersen U L 2012 Nat. Commun. 3 1083 Google Scholar
[15]	Shi S, Tian L, Wang Y, Zheng Y, Xie C, Peng K 2020 Phys. Rev. Lett. 125 070502 Google Scholar
[16]	Li Y Q, Guzun D, Xiao M 1999 Phys. Rev. Lett. 82 5225 Google Scholar
[17]	Xu C, Zhang L, Huang S, Ma T, Liu F, Yonezawa H, Zhang Y, Xiao M 2019 Photonics Res. 7 A14 Google Scholar
[18]	Schönbeck A, Thies F, Schnabel R 2018 Opt. Lett. 43 110 Google Scholar
[19]	Sun X, Wang Y, Tian L, Zheng Y, Peng K 2019 Chin. Opt. Lett. 17 072701 Google Scholar
[20]	Zhao J, Liu K, Jeng H, Gu M, Thompson J, Lam P K, Assad S M 2020 Nat. Photonics 14 306 Google Scholar
[21]	仲银银, 潘晓州, 荆杰泰 2020 69 130301 Google Scholar Zhong Y Y, Pan X Z, Jing J T 2020 Acta Phys. Sin. 69 130301 Google Scholar
[22]	Wang W, Zhang K, Jing J T 2020 Phys. Rev. Lett. 125 140501 Google Scholar
[23]	Shi S, Wang Y, Yang W, Zheng Y, Peng K 2018 Opt. Lett 43 5411 Google Scholar
[24]	Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801 Google Scholar
[25]	Sun X C, Wang Y J, Tian L, Shi S P, Zheng Y H, Peng K C 2019 Opt. Lett. 44 1789 Google Scholar
[26]	Chelkowski S, Vahlbruch H, Danzmann K, Schnabel R 2007 Phys. Rev. A 75 043814 Google Scholar
[27]	Vogel K, Risken H 1989 Phys. Rev. A 40 2847 Google Scholar
[28]	Schiller S, Breitenbach G, Pereira S F, Müller T, Mlynek J 1996 Phys. Rev. Lett. 77 2933 Google Scholar
[29]	Beck M, Smithey D T, Raymer M G 1993 Phys. Rev. A 48 R890 Google Scholar
[30]	Smithey D T, Beck M, Cooper J, Raymer M G 1993 Phys. Rev. A 48 3159 Google Scholar
[31]	Lvovsky A I, Raymer M G 2009 Rev. Mod. Phys. 81 299 Google Scholar
[32]	Lvovsky A I 2004 J. Opt. B: Quantum Semiclassical Opt. 6 S556 Google Scholar
[33]	李淑静, 张娜娜, 闫红梅, 徐忠孝, 王海 2018 67 094204 Google Scholar Li S J, Zhang N N, Yan H M, Xu Z X, Wang H 2018 Acta Phys. Sin. 67 094204 Google Scholar
[34]	叶晨光, 张靖 2008 57 6962 Google Scholar Ye C G, Zhang J 2008 Acta Phys. Sin. 57 6962 Google Scholar
[35]	Breitenbach G, Schiller S, Mlynek J 1997 Nature 387 471 Google Scholar
[36]	Smithey D T, Beck M, Cooper J, Raymer M G, Faridani A 1993 Phys. Scr. 1993 35 Google Scholar
[37]	Neergaard-Nielsen J S, Nielsen B M, Takahashi H, Vistnes A I, Polzik E S 2007 Opt. Express 15 7940 Google Scholar
[38]	Zavatta A, Parigi V, Bellini M 2007 Phys. Rev. A 75 052106 Google Scholar
[39]	Ourjoumtsev A, Tualle-Brouri R, Laurat J, Grangier P J S 2006 Science 312 83 Google Scholar
[40]	Yao W, Wang Q, Tian L, Li R, Shi S, Wang J, Wang Y, Zheng Y 2020 Laser Phys. Lett. 18 015001 Google Scholar
[41]	Yang W, Wang Y, Zheng Y, Lu H 2015 Opt. Express 23 19624 Google Scholar
[42]	Wang J R, Wang Q W, Tian L, Su J, Zheng Y H 2020 Chin. Phys. B 29 034205 Google Scholar
[43]	Wang J R, Zhang H Y, Zhao Z L, Zheng Y H 2020 Chin. Phys. B 29 124207 Google Scholar
[44]	Li Z, Tian Y, Wang Y, Ma W, Zheng Y 2019 Opt. Express 27 7064 Google Scholar
[45]	张宏宇, 王锦荣, 李庆回, 吉宇杰, 贺子洋, 杨荣草, 田龙 2019 量子光学学报 25 456 Google Scholar Zhang H Y, Wang J R, Li Q H, Ji Y J, He Z Y, Yang R C, Tian L 2019 Acta Sin. Quantum Opt. 25 456 Google Scholar
[46]	Schneider K, Bruckmeier R, Hansen H, Schiller S, Mlynek J 1996 Opt. Lett. 21 1396 Google Scholar
[47]	Morgan P H 2011 Ph. D. Dissertation (Canberra: Australian National University)

施引文献

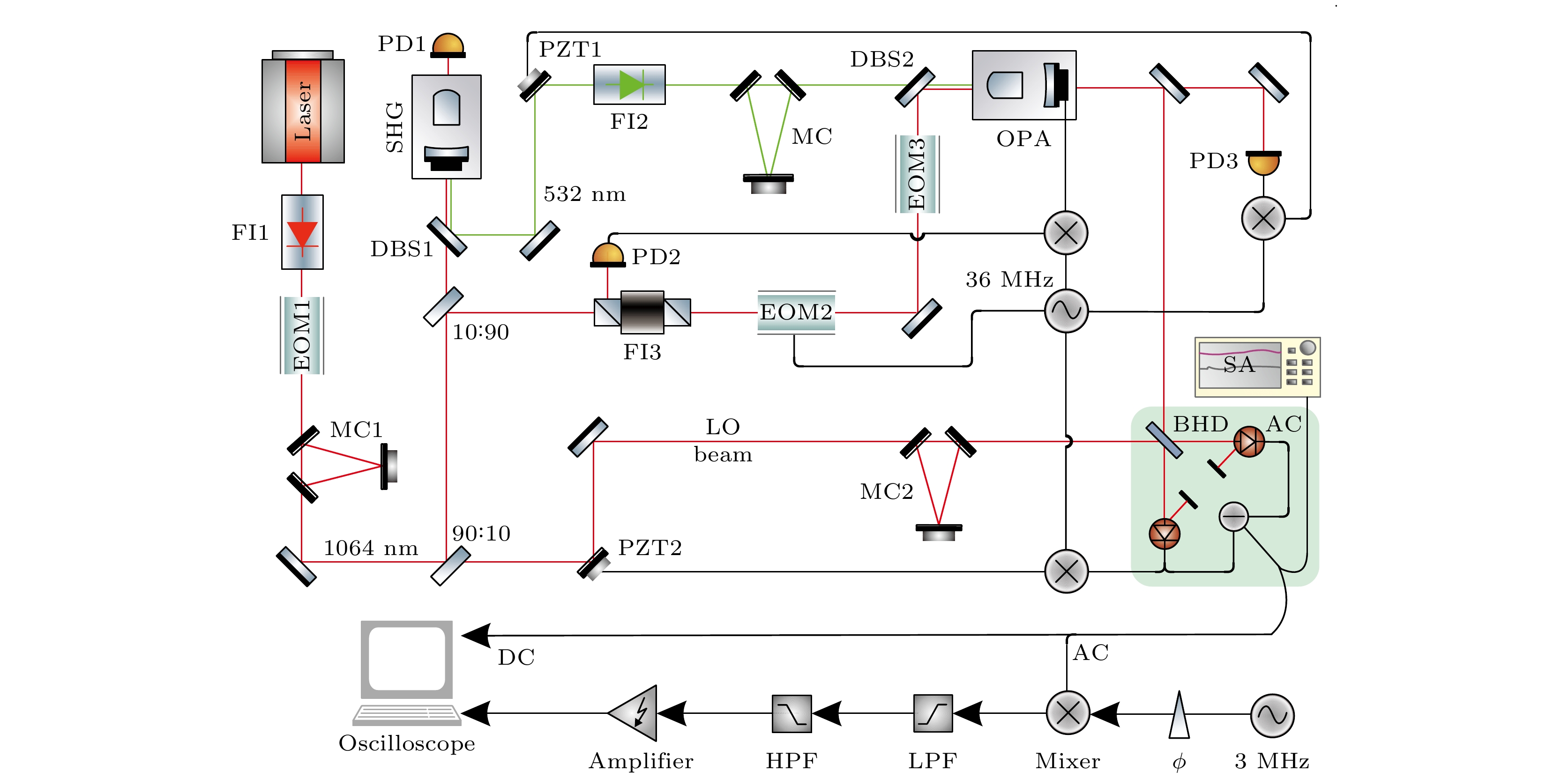
图 1 实验装置图(SHG, 倍频腔; OPA, 光学参量放大腔; EOM, 光电调制器; MC, 模式清洁器; DBS, 双色镜; FI, 隔离器; PZT, 压电驱动器; PD, 光电探测器; BHD, 平衡零拍探测器; SA, 频谱分析仪; LPF, 低通滤波器; HPF, 高通滤波器)

Fig. 1. Experimental setup. SHG, second harmonic generation; OPA, optical parameter amplifier; EOM, electric-optic modular; MC, mode cleaner; DBS, dichroic beam splitter; FI, Faraday isolator; PZT, piezoe-lectric transducer; PD, photodetector; BHD, balance homodyne detector; SA, spectrum analyzer; LPF, low-pass filter; HPF, high-pass filter.

下载: 全尺寸图片幻灯片

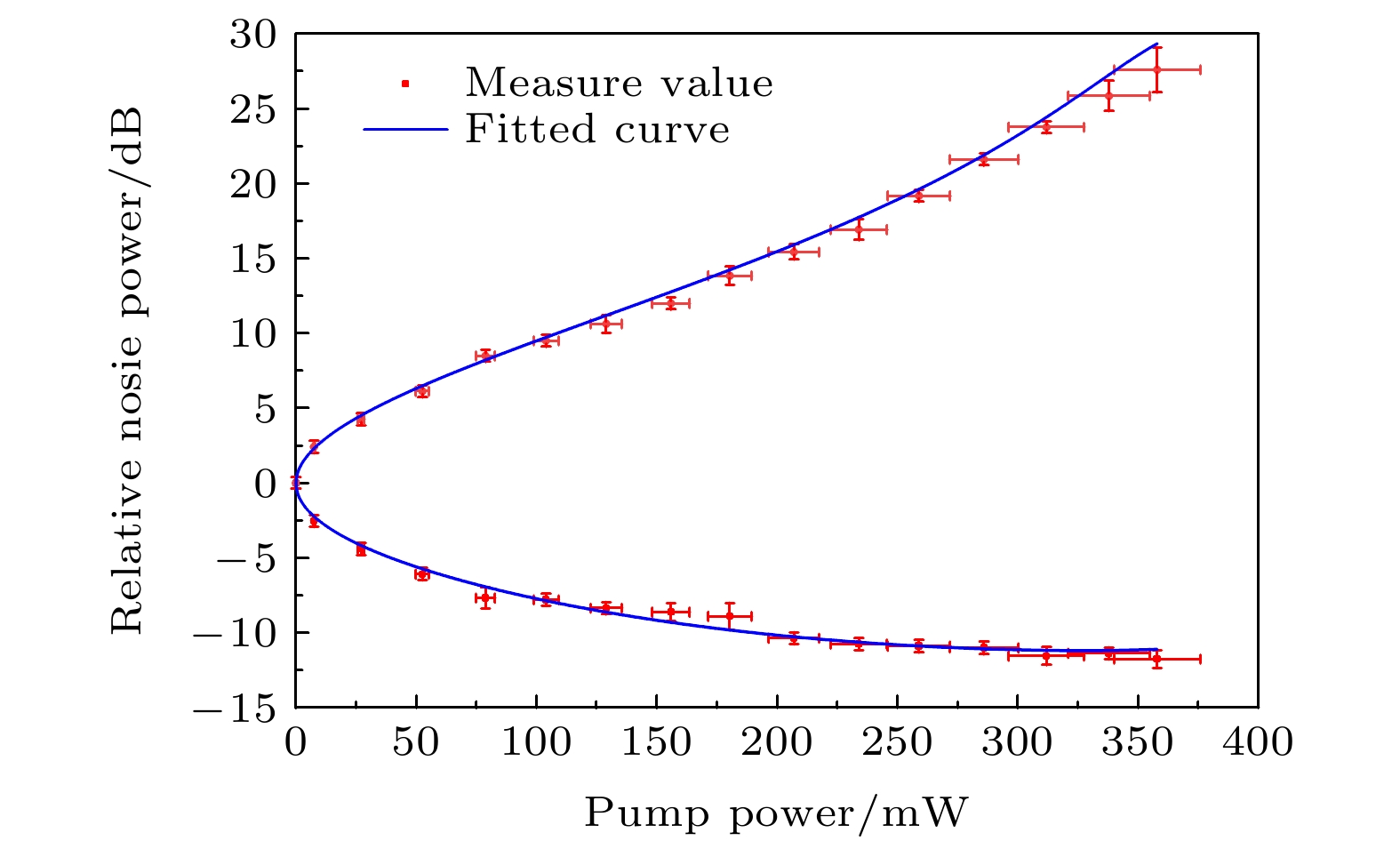
图 2 压缩和反压缩随泵浦功率的变化趋势图, 分析频率为3 MHz, 分辨率带宽(RBW)为300 kHz, 视频带宽(VBW) 200 Hz. 所有的数据点均包括探测器的电子学噪声的影响, 为直接测量结果

Fig. 2. Pump power dependence of anti-squeezed and squeezed quadrature variances. These measurements are recorded at a Fourier frequency of 3 MHz, with a resolution bandwidth (RBW) of 300 kHz and a video bandwidth (VBW) of 200 Hz. The data still include electronic noise, and represent direct observations.

下载: 全尺寸图片幻灯片

图 3 (a), (b)未进行线性操控的明亮压缩态噪声时域测量结果及量子层析后对应的密度矩阵; (c), (d)进行线性操控后的明亮压缩态噪声时域测量结果及量子层析后对应的密度矩阵

Fig. 3. (a), (b) Time domain signal and corresponding density matrix of bright squeezed state before linearly manipulating, respectively; (c), (d) time domain signal and corresponding density matrix of linearly manipulated bright squeezed state, respectively.

下载: 全尺寸图片幻灯片

图 4 明亮压缩态光场在3 MHz分析边带的光子数分布概率　(a)线性操控光学前; (b)线性操控光学后

Fig. 4. Photon number distribution of the bright squeezed state at 3 MHz: (a) Before linearly manipulating optics; (b) after linearly manipulating optics.

下载: 全尺寸图片幻灯片

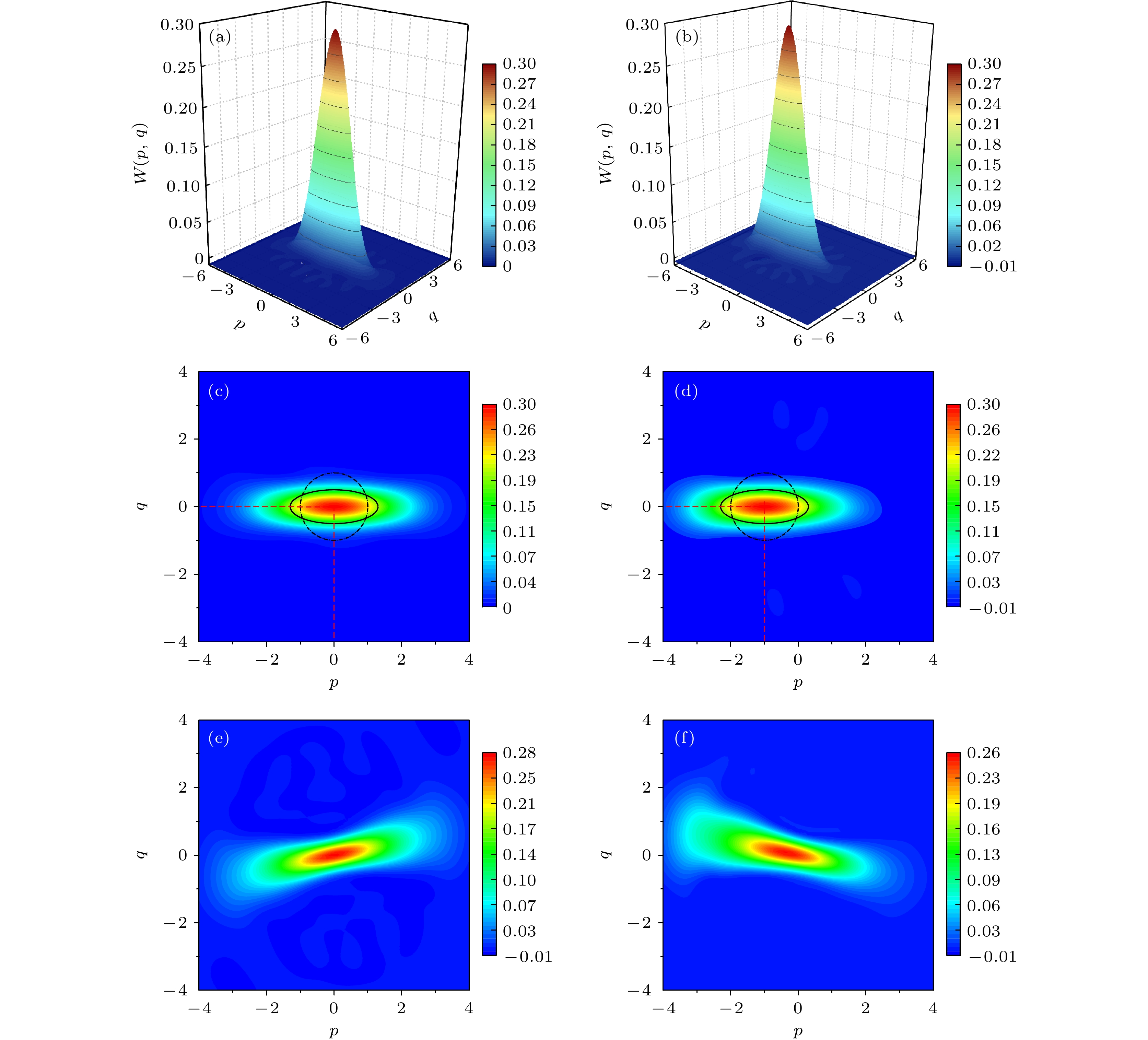
图 5 (a), (c)从极大似然估计重构得到的无调制时的明亮压缩态Wigner函数和等高线图; (b), (d)从极大似然估计重构得到的光电相位调制器操控后的明亮压缩态Wigner 函数和等高线图; (e), (f)利用均匀相位分配法重构得到的无操控时以及操控后的明亮压缩态Wigner函数的等高线图

Fig. 5. (a), (c) Wigner function and the contour plot of the bright squeezed state obtained by maximum likelihood estimation without linearly manipulating optics, respectively; (b), (d) Wigner function and the contour plot of the squeezed state obtained by maximum likelihood estimation with linearly manipulating optics, respectively; (e), (f) Wigner functions of the bright squeezed state obtained by the method of artificially homogeneous phase distribution without or with linearly manipulating optics, respectively.

下载: 全尺寸图片幻灯片

map

[1]	Schrödinger E 1926 Sci. Nat. 14 664 Google Scholar
[2]	Kennard E H 1927 J. Z. Phys. 44 326 Google Scholar
[3]	Darwin C G 1927 Proc. R. Soc. London, Ser. A 117 258 Google Scholar
[4]	Slusher R E, Hollberg L W, Yurke B, Mertz J C, Valley J F 1985 Phys. Rev. Lett. 55 2409 Google Scholar
[5]	Walls D F 1983 Nature 306 141 Google Scholar
[6]	Caves C M 1981 Phys. Rev. D 23 1693 Google Scholar
[7]	Acernese F, et al. (Virgo Collaboration). 2019 Phys. Rev. Lett. 123 231108 Google Scholar
[8]	Acernese F, et al. (Virgo Collaboration). 2020 Phys. Rev. Lett. 125 131101 Google Scholar
[9]	Eberle T, Händchen V, Schnabel R 2013 Opt. Express 21 11546 Google Scholar
[10]	Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706 Google Scholar
[11]	Asavanant W, Nakashima K, Shiozawa Y, Yoshikawa J I, Furusawa A 2017 Opt. Express 25 32227 Google Scholar
[12]	Polzik E S, Carri J, Kimble H J 1992 Phys. Rev. Lett. 68 3020 Google Scholar
[13]	Yang W, Shi S, Wang Y, Ma W, Zheng Y, Peng K 2017 Opt. Lett. 42 4553 Google Scholar
[14]	Madsen L S, Usenko V C, Lassen M, Filip R, Andersen U L 2012 Nat. Commun. 3 1083 Google Scholar
[15]	Shi S, Tian L, Wang Y, Zheng Y, Xie C, Peng K 2020 Phys. Rev. Lett. 125 070502 Google Scholar
[16]	Li Y Q, Guzun D, Xiao M 1999 Phys. Rev. Lett. 82 5225 Google Scholar
[17]	Xu C, Zhang L, Huang S, Ma T, Liu F, Yonezawa H, Zhang Y, Xiao M 2019 Photonics Res. 7 A14 Google Scholar
[18]	Schönbeck A, Thies F, Schnabel R 2018 Opt. Lett. 43 110 Google Scholar
[19]	Sun X, Wang Y, Tian L, Zheng Y, Peng K 2019 Chin. Opt. Lett. 17 072701 Google Scholar
[20]	Zhao J, Liu K, Jeng H, Gu M, Thompson J, Lam P K, Assad S M 2020 Nat. Photonics 14 306 Google Scholar
[21]	仲银银, 潘晓州, 荆杰泰 2020 69 130301 Google Scholar Zhong Y Y, Pan X Z, Jing J T 2020 Acta Phys. Sin. 69 130301 Google Scholar
[22]	Wang W, Zhang K, Jing J T 2020 Phys. Rev. Lett. 125 140501 Google Scholar
[23]	Shi S, Wang Y, Yang W, Zheng Y, Peng K 2018 Opt. Lett 43 5411 Google Scholar
[24]	Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801 Google Scholar
[25]	Sun X C, Wang Y J, Tian L, Shi S P, Zheng Y H, Peng K C 2019 Opt. Lett. 44 1789 Google Scholar
[26]	Chelkowski S, Vahlbruch H, Danzmann K, Schnabel R 2007 Phys. Rev. A 75 043814 Google Scholar
[27]	Vogel K, Risken H 1989 Phys. Rev. A 40 2847 Google Scholar
[28]	Schiller S, Breitenbach G, Pereira S F, Müller T, Mlynek J 1996 Phys. Rev. Lett. 77 2933 Google Scholar
[29]	Beck M, Smithey D T, Raymer M G 1993 Phys. Rev. A 48 R890 Google Scholar
[30]	Smithey D T, Beck M, Cooper J, Raymer M G 1993 Phys. Rev. A 48 3159 Google Scholar
[31]	Lvovsky A I, Raymer M G 2009 Rev. Mod. Phys. 81 299 Google Scholar
[32]	Lvovsky A I 2004 J. Opt. B: Quantum Semiclassical Opt. 6 S556 Google Scholar
[33]	李淑静, 张娜娜, 闫红梅, 徐忠孝, 王海 2018 67 094204 Google Scholar Li S J, Zhang N N, Yan H M, Xu Z X, Wang H 2018 Acta Phys. Sin. 67 094204 Google Scholar
[34]	叶晨光, 张靖 2008 57 6962 Google Scholar Ye C G, Zhang J 2008 Acta Phys. Sin. 57 6962 Google Scholar
[35]	Breitenbach G, Schiller S, Mlynek J 1997 Nature 387 471 Google Scholar
[36]	Smithey D T, Beck M, Cooper J, Raymer M G, Faridani A 1993 Phys. Scr. 1993 35 Google Scholar
[37]	Neergaard-Nielsen J S, Nielsen B M, Takahashi H, Vistnes A I, Polzik E S 2007 Opt. Express 15 7940 Google Scholar
[38]	Zavatta A, Parigi V, Bellini M 2007 Phys. Rev. A 75 052106 Google Scholar
[39]	Ourjoumtsev A, Tualle-Brouri R, Laurat J, Grangier P J S 2006 Science 312 83 Google Scholar
[40]	Yao W, Wang Q, Tian L, Li R, Shi S, Wang J, Wang Y, Zheng Y 2020 Laser Phys. Lett. 18 015001 Google Scholar
[41]	Yang W, Wang Y, Zheng Y, Lu H 2015 Opt. Express 23 19624 Google Scholar
[42]	Wang J R, Wang Q W, Tian L, Su J, Zheng Y H 2020 Chin. Phys. B 29 034205 Google Scholar
[43]	Wang J R, Zhang H Y, Zhao Z L, Zheng Y H 2020 Chin. Phys. B 29 124207 Google Scholar
[44]	Li Z, Tian Y, Wang Y, Ma W, Zheng Y 2019 Opt. Express 27 7064 Google Scholar
[45]	张宏宇, 王锦荣, 李庆回, 吉宇杰, 贺子洋, 杨荣草, 田龙 2019 量子光学学报 25 456 Google Scholar Zhang H Y, Wang J R, Li Q H, Ji Y J, He Z Y, Yang R C, Tian L 2019 Acta Sin. Quantum Opt. 25 456 Google Scholar
[46]	Schneider K, Bruckmeier R, Hansen H, Schiller S, Mlynek J 1996 Opt. Lett. 21 1396 Google Scholar
[47]	Morgan P H 2011 Ph. D. Dissertation (Canberra: Australian National University)

[1]	张科, 李兰兰, 任刚, 杜建明, 范洪义. 量子扩散通道中Wigner算符的演化规律. , 2020, 69(9): 090301. doi: 10.7498/aps.69.20200106
[2]	张娜娜, 李淑静, 闫红梅, 何亚亚, 王海. 实验条件不完美对薛定谔猫态制备的影响. , 2018, 67(23): 234203. doi: 10.7498/aps.67.20180381
[3]	李淑静, 张娜娜, 闫红梅, 徐忠孝, 王海. 铷原子D1线真空压缩光场的产生及态重构. , 2018, 67(9): 094204. doi: 10.7498/aps.67.20172396
[4]	林惇庆, 朱泽群, 王祖俭, 徐学翔. 相位型三头薛定谔猫态的量子统计属性. , 2017, 66(10): 104201. doi: 10.7498/aps.66.104201
[5]	宋佳凝, 徐国栋, 李鹏飞. 多谐波脉冲星信号时延估计方法. , 2015, 64(21): 219702. doi: 10.7498/aps.64.219702
[6]	范洪义, 梁祖峰. 相空间中对应量子力学基本对易关系的积分变换及求Wigner函数的新途径. , 2015, 64(5): 050301. doi: 10.7498/aps.64.050301
[7]	梁修东, 台运娇, 程建民, 翟龙华, 许业军. 量子相空间分布函数与压缩相干态表示间的变换关系. , 2015, 64(2): 024207. doi: 10.7498/aps.64.024207
[8]	刘世右, 郑凯敏, 贾芳, 胡利云, 谢芳森. 单-双模组合压缩热态的纠缠性质及在量子隐形传态中的应用. , 2014, 63(14): 140302. doi: 10.7498/aps.63.140302
[9]	张浩亮, 贾芳, 徐学翔, 郭琴, 陶向阳, 胡利云. 光子增减叠加相干态在热环境中的退相干. , 2013, 62(1): 014208. doi: 10.7498/aps.62.014208
[10]	徐学翔, 张英孔, 张浩亮, 陈媛媛. N00N态的Wigner函数及N00N态作为输入的量子干涉. , 2013, 62(11): 114204. doi: 10.7498/aps.62.114204
[11]	文洪燕, 杨杨, 韦联福. 光学微腔中少光子数叠加态的耗散动力学. , 2012, 61(18): 184206. doi: 10.7498/aps.61.184206
[12]	袁洪春, 徐学翔. 单双模连续压缩真空态及其量子统计性质. , 2012, 61(6): 064205. doi: 10.7498/aps.61.064205
[13]	宋军, 范洪义, 周军. 双模压缩数态光场的Wigner函数及其特性. , 2011, 60(11): 110302. doi: 10.7498/aps.60.110302
[14]	余海军, 杜建明, 张秀兰. 一类特殊单模压缩态的Wigner函数. , 2011, 60(9): 090305. doi: 10.7498/aps.60.090305
[15]	徐学翔, 袁洪春, 胡利云. 广义压缩粒子数态的非经典性质及其退相干. , 2010, 59(7): 4661-4671. doi: 10.7498/aps.59.4661
[16]	宋军, 范洪义. Schwinger Bose实现下自旋相干态Wigner函数的特性分析. , 2010, 59(10): 6806-6813. doi: 10.7498/aps.59.6806
[17]	蓝海江, 庞华锋, 韦联福. 多光子激发相干态的Wigner函数. , 2009, 58(12): 8281-8288. doi: 10.7498/aps.58.8281
[18]	叶晨光, 张靖. 利用PPKTP晶体产生真空压缩态及其Wigner准概率分布函数的量子重构. , 2008, 57(11): 6962-6967. doi: 10.7498/aps.57.6962
[19]	孟祥国, 王继锁, 梁宝龙. 增光子奇偶相干态的Wigner函数. , 2007, 56(4): 2160-2167. doi: 10.7498/aps.56.2160
[20]	杨庆怡, 孙敬文, 韦联福, 丁良恩. 增、减光子奇偶相干态的Wigner函数. , 2005, 54(6): 2704-2709. doi: 10.7498/aps.54.2704

计量

文章访问数: 5875
PDF下载量: 191
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

明亮压缩态光场的操控及量子层析