-
When laser beam propagates through the turbulent atmosphere, there are branch points in wavefront, which are caused by deep turbulence or long propagation distance. Conventional least-square reconstruction algorithms cannot restore the discontinuous wavefront, which severely limits correction performance of an adaptive optics system. If the incoming wavefront contains a branch cut, there is
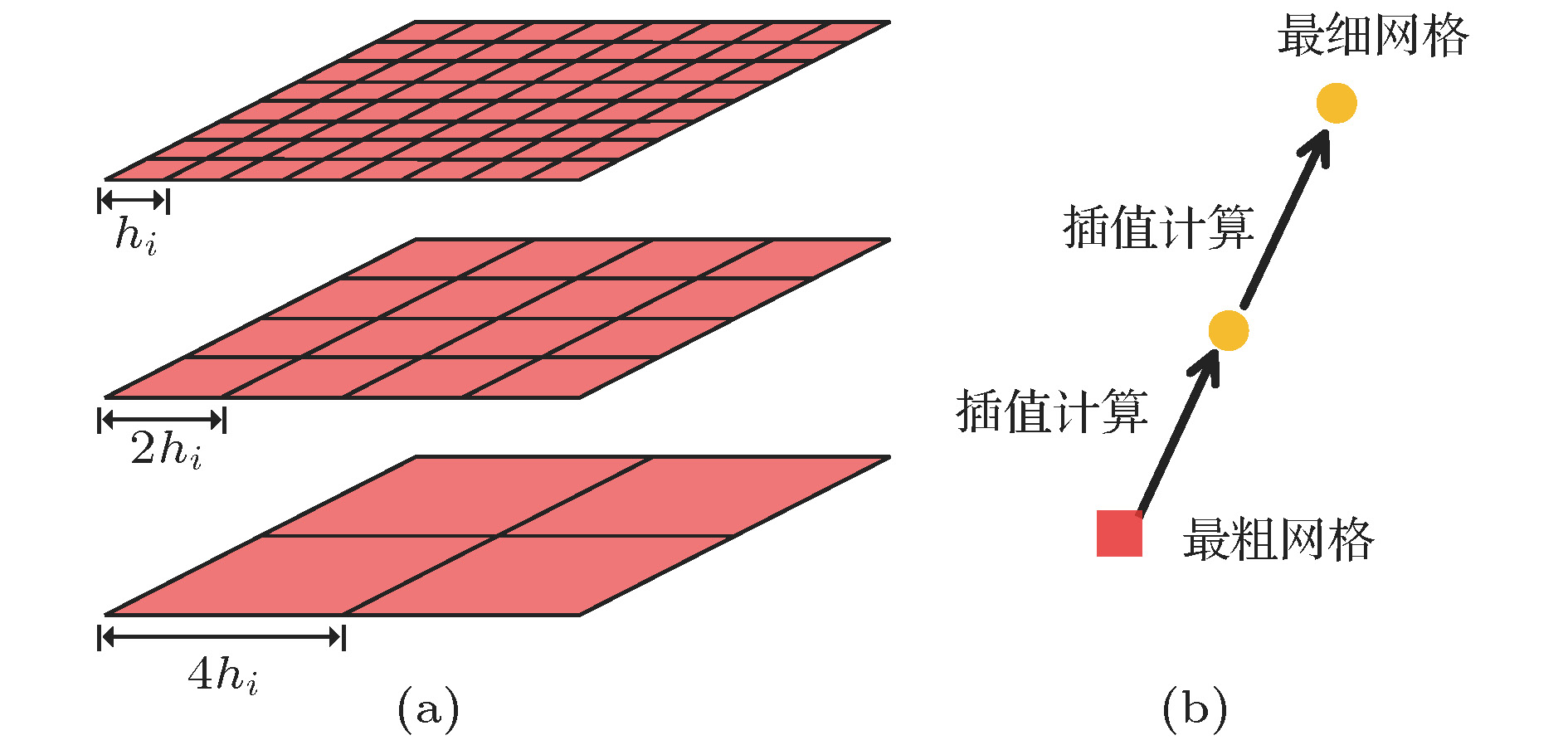
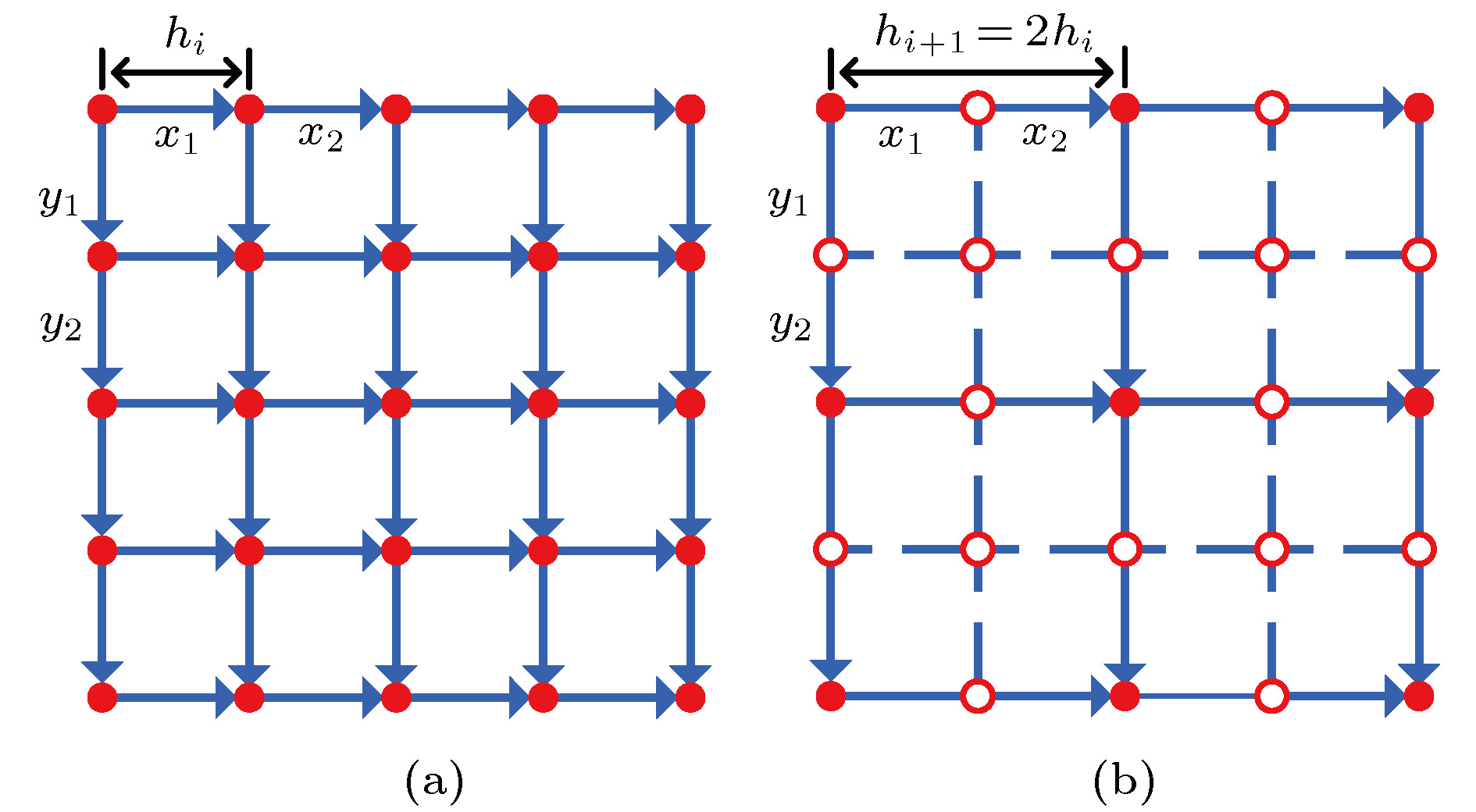
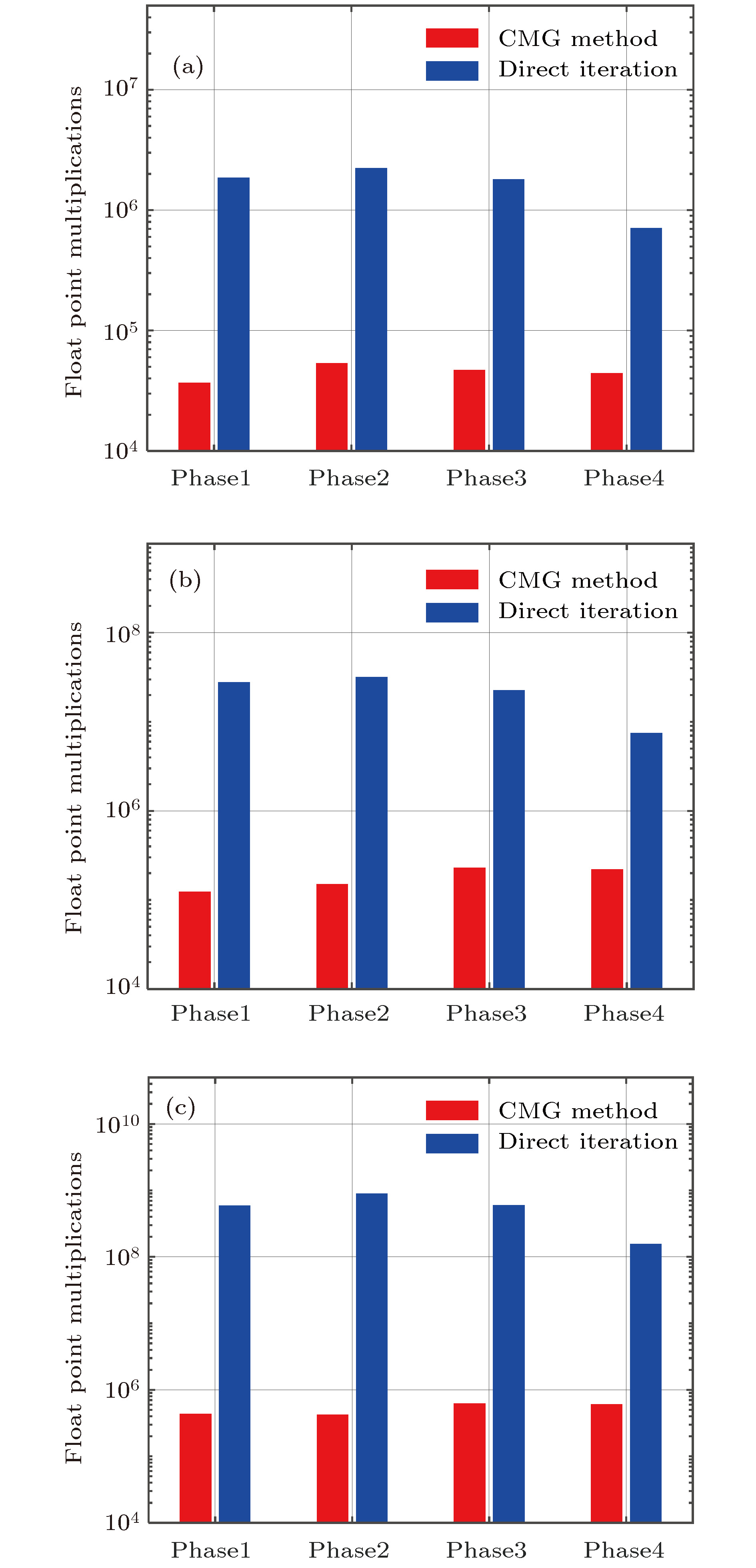
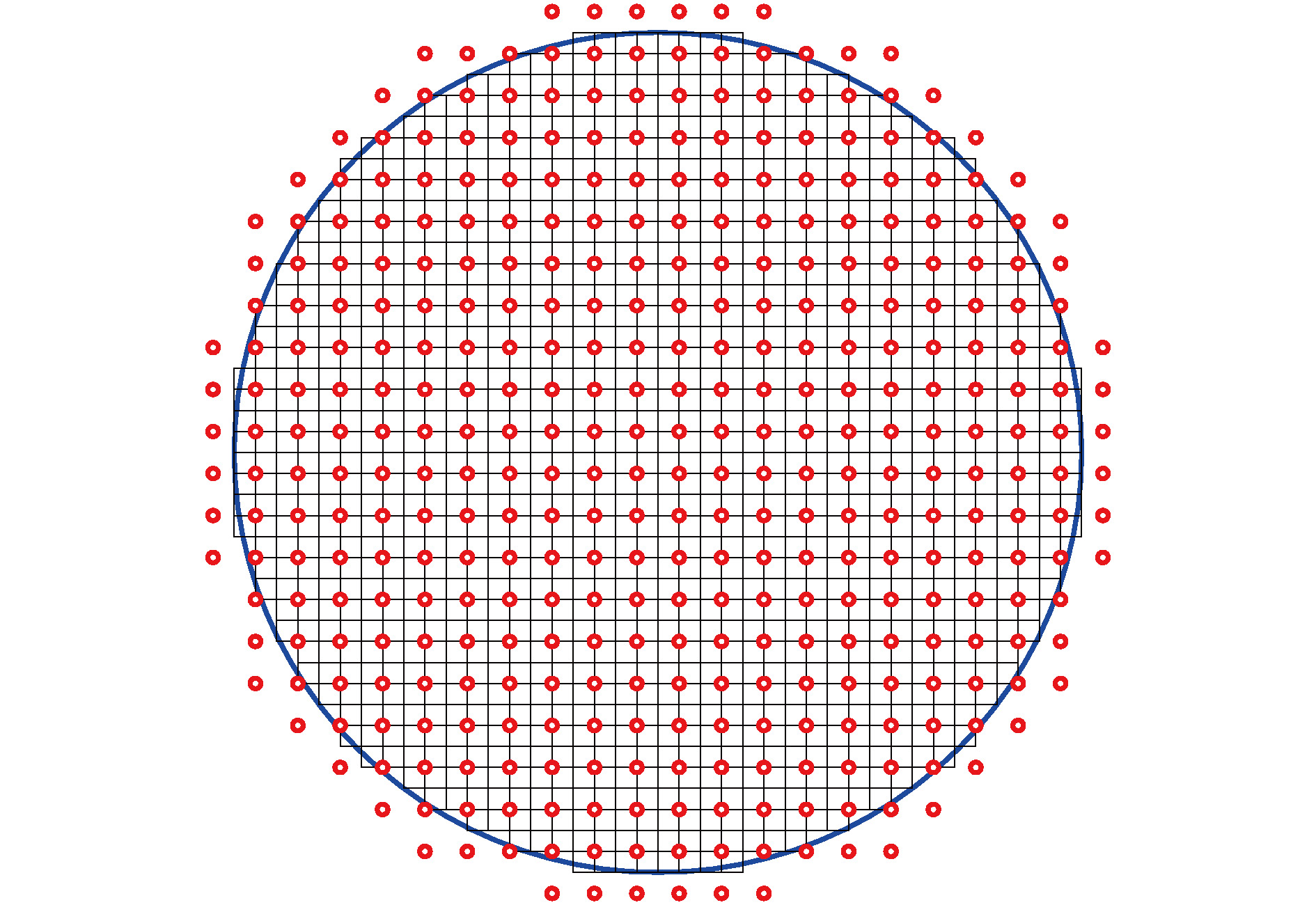
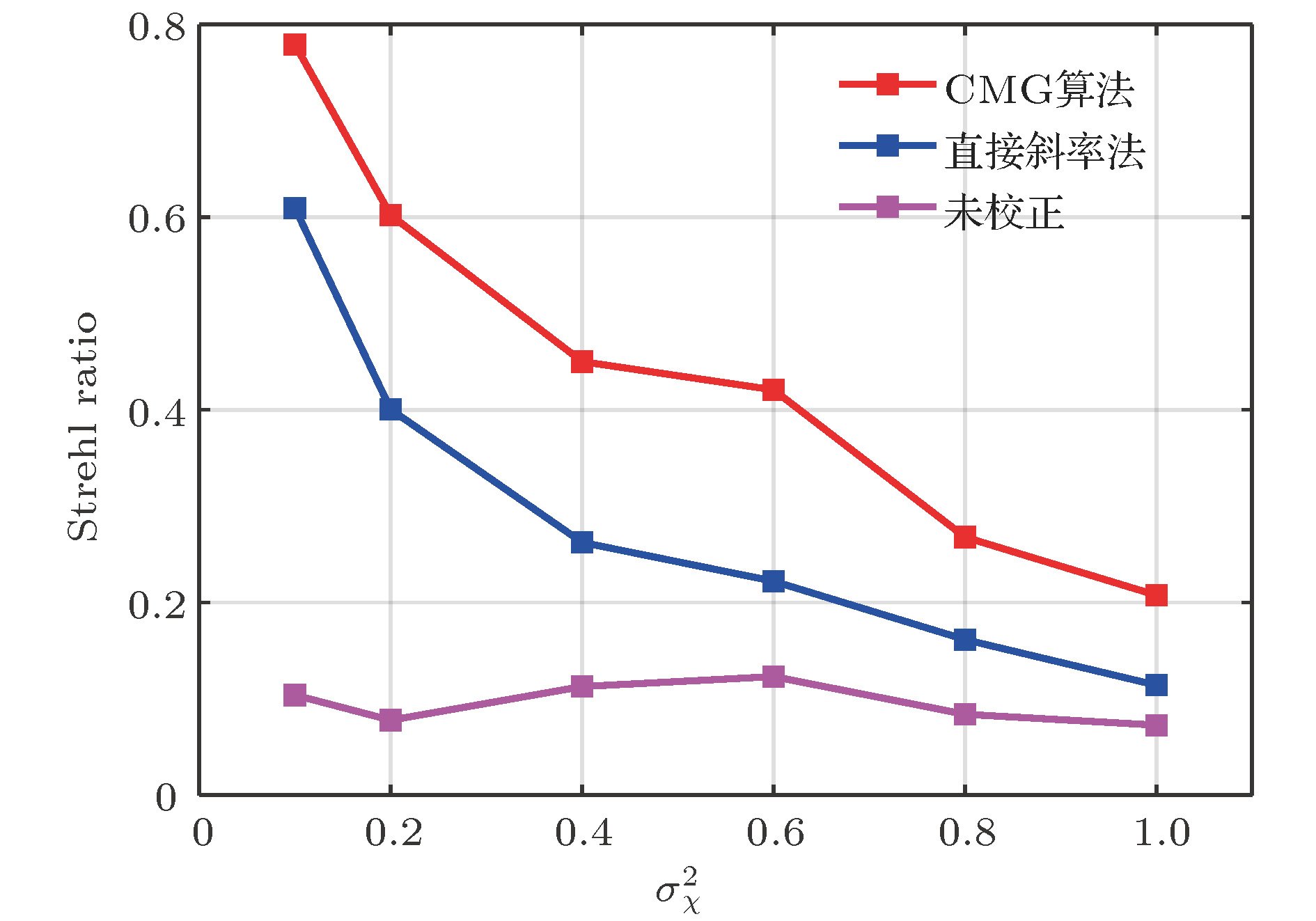
$ {\rm{2}}n{\text{π}} $ difference between the measured phase difference and the principle phase difference, which is the reason why conventional least-square reconstruction algorithms cannot reconstruct wavefront with branch points. The complex exponential reconstructor is developed to restore the discontinuous wavefront with phase difference replaced by complex exponents. However, thousands of iterations are required by the complex exponential reconstructor before converging to an acceptable solution. In order to speed up the iterative calculation, the cascadic multigrid method (CMG) is introduced in the process of wavefront reconstruction. The proposed method can be used to restore discontinuous wavefront with lower residual error similar to those reconstructed by the direct iteration. The number of float point multiplications required by the CMG method is nearly 2 orders of magnitude lower than that required by the direct iteration. The acceleration of the CMG method increases with the number of subapertures increasing. The performance of CMG method to recover continuous wavefront is also investigated and compared with conventional wavefront reconstruction algorithm based on successive over-relaxation. It is shown that the CMG method has good capability for wavefront reconstruction with high precision and low computation cost no matter whether it is applied to discontinuous or continuous wavefront. Furthermore, the CMG method is used in the adaptive optics for correcting the turbulence aberration. The direct slope wavefront reconstruction algorithm based on the assumption that the measured slope and the control voltage satisfy the linear relationship cannot restore the wavefront with branch points. As a result, the adaptive optics system with the CMG method doubles the correction quality evaluated by the Strehl ratio compared with that with the direct slope wavefront reconstruction algorithm.-
Keywords:
- adaptive optics /
- wavefront reconstruction /
- cascadic multigrid method /
- branch point
[1] Fried D L, Vaughn J L 1992 Appl. Opt. 31 2865
Google Scholar
[2] Fried D L 1998 JOSA A 15 2759
Google Scholar
[3] Primmerman C A, Price T R, Humphreys R A, et al. 1995 Appl. Opt. 34 2081
Google Scholar
[4] Lukin V P, Fortes B V 2002 Appl. Opt. 41 5616
Google Scholar
[5] Steinbock M J, Hyde M W, Schmidt J D 2014 Appl. Opt. 53 3821
Google Scholar
[6] Le B E, Wild W J, Kibblewhite E J 1998 Opt. Lett. 23 10
Google Scholar
[7] Fried D L 2001 Opt. Commun. 200 43
Google Scholar
[8] Barchers J D, Fried D L, Link D J 2002 Appl. Opt. 41 1012
Google Scholar
[9] Aubailly M, Vorontsov M A 2012 JOSA A 29 1707
[10] Yazdani R, Fallah H 2017 Appl. Opt. 56 1358
Google Scholar
[11] Goodman J W ( translated by Qin K C, L P S, Chen J B, Cao Q Z) 2013 Introduction to Fourier Optics (3rd Ed.) (Beijing: Publishing House of Electronics Industry) p77
[12] Hudgin R H 1977 JOSA 67 378
Google Scholar
[13] Hudgin R H 1977 JOSA 67 375
Google Scholar
[14] Bornemann F A, Deuflhard P 1996 Numerische Mathematik 75 135
Google Scholar
[15] Venema T M, Schmidt J D 2008 Opt. Express 16 6985
Google Scholar
[16] Steinbock M J, Schmidt J D, Hyde M W 2012 Aerospace Conference Big Sky, MT, USA, 3-10 March, 2012, pp1-13
[17] Roddier N A 1990 Opt. Eng. 29 1174
Google Scholar
[18] Southwell W H 1980 JOSA 70 998
Google Scholar
[19] Jr J A F, Morris J R, Feit M D 1976 Appl. Phys. 10 129
[20] 蔡冬梅, 王昆, 贾鹏, 王东, 刘建霞 2014 63 104217
Google Scholar
Cai D M, Wang K, Jia P, Wang D, Liu J X 2014 Acta Phys. Sin. 63 104217
Google Scholar
[21] 程生毅, 陈善球, 董理治, 王帅, 杨平, 敖明武, 许冰 2015 64 094207
Google Scholar
Cheng Y C, Shan Q C, Dong L Z, Wang S, Yang P, Ao M W, Xu B 2015 Acta Phys. Sin. 64 094207
Google Scholar
[22] Fan C, Wang Y, Gong Z 2004 Appl. Opt. 43 4334
Google Scholar
-
图 1 测量相位差和重建相位点的关系
Figure 1. The relationship between phase differences and phase.
图 2 瀑布型多重网格法示意图 (a)网格结构; (b)CMG算法计算流程
Figure 2. Schematic of the CMG method: (a) Structure of network layers; (b) calculation process.
图 3 CMG算法降采样过程 (a)细网格上光场; (b)粗网格上光场
Figure 3. Downsampling process of the CMG method: (a) Data on the fine network; (b) data on the coarse network.
图 4 CMG算法插值过程 (a)细网格光场和粗网格光场的关系; (b)待插值数据位于正方形中心; (c), (d)待插值数据位于正方形四边上
Figure 4. Interpolation process of the CMG method: (a) The relationship between grid points on coarse network and fine network; (b) the new grid point located at the center of the unit square; (c), (d) the new grid point located on the edge of the unit square.
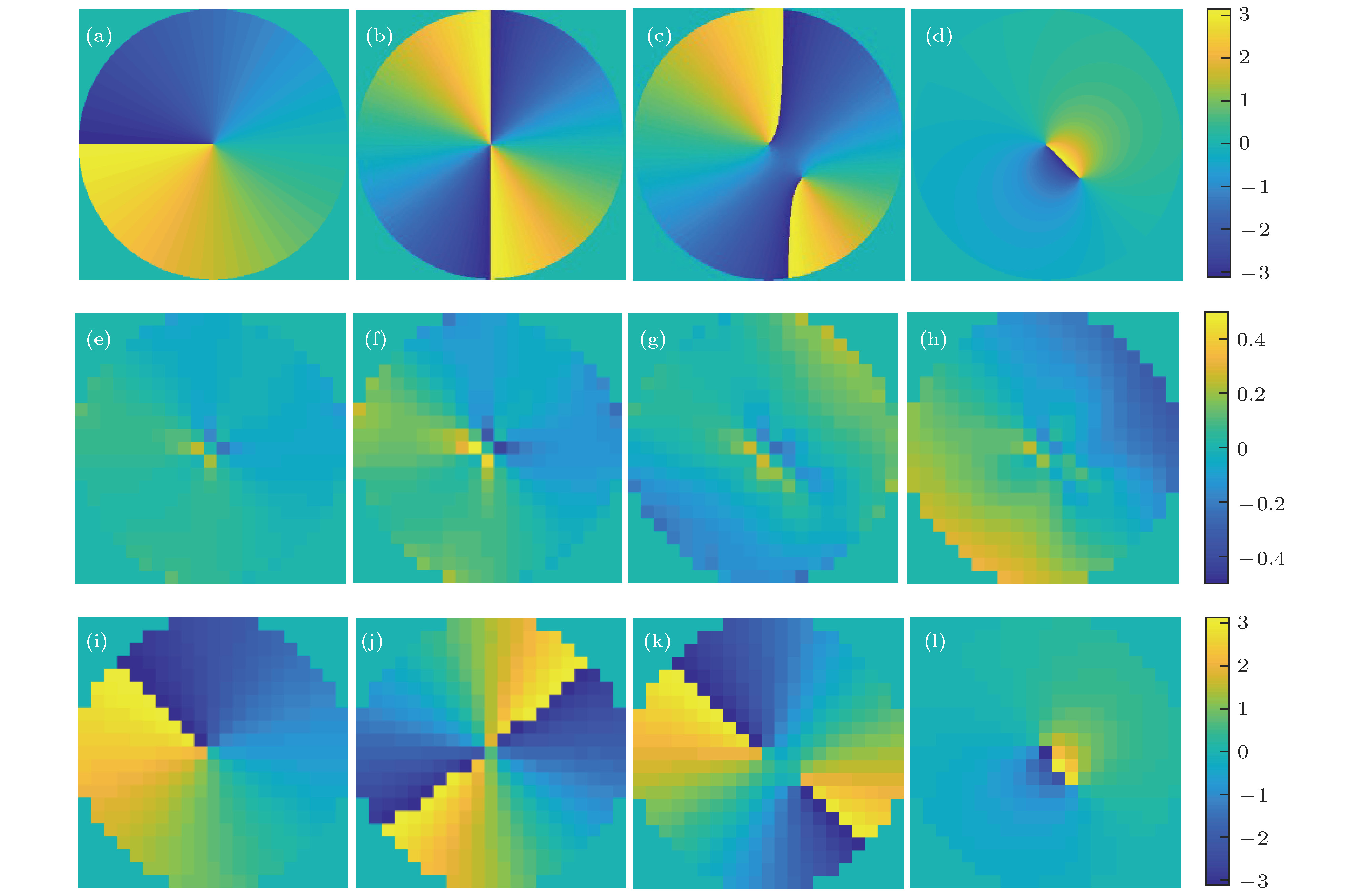
图 5 (a)−(d) Phase1, Phase2, Phase3和Phase4二维分布; (e)−(h)最小二乘法波前复原结果; (i)−(l)复指数波前复原算法结果
Figure 5. (a)−(d) Two-dimensional distribution of Phase1, Phase2, Phase3 and Phase4; (e)−(h) wavefront reconstructed by the least-squares reconstruction algorithm; (i)−(l) wavefront reconstructed by the CER algorithm.
图 6 直接迭代和CMG算法波前复原残差 (a)子孔径数目为20 × 20; (b)子孔径数目为40 × 40; (c)子孔径数目为80 × 80
Figure 6. Wavefront residual error of the direct iteration method and the CMG method, the number of subapertures is (a) 20 × 20; (b) 40 × 40; (c) 80 × 80.
图 7 CMG算法和直接迭代过程所需浮点乘运算数目(a)子孔径数目为20 × 20; (b)子孔径数目为40 × 40; (c)子孔径数目为80 × 80
Figure 7. Float point multiplications required by the CMG method and the process of the direct iteration the number of subapertures is (a) 20 × 20; (b) 40 × 40; (c) 80 × 80.
图 8 CMG算法和SOR算法波前复原残差统计结果
Figure 8. Wavefront residual statistics of the CMG method and SOR method.
图 9 变形镜驱动器和哈特曼波前传感器子孔径匹配关系
Figure 9. Matching relation between actuators of deformable mirror and subapertures of Shack-Hartmann sensor.
图 10 不同Rytov方差时, 自适应光学系统校正前后远场光强分布及其峰值Strehl比
Figure 10. Far field intensity and Strehl ratio of laser beam before and after corrected by the adaptive optics system.
图 11 不同Rytov方差时, 自适应光学系统校正光束Strehl比
Figure 11. Strehl ratio of laser beam after corrected by the adaptive optics system in different Rytov number.
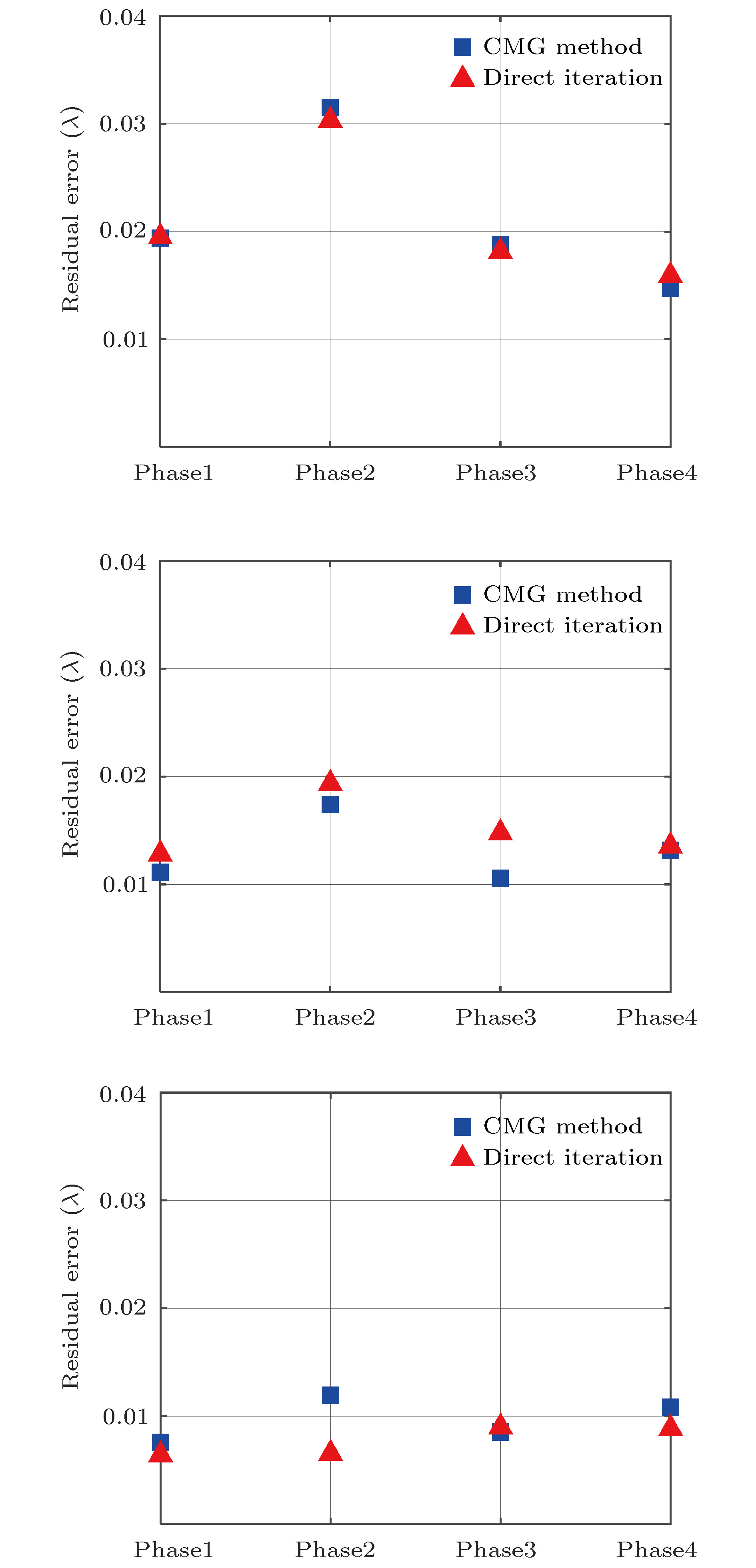
表 1 直接迭代和CMG算法波前复原时间(单位: s)
Table 1. Time required by the direct iteration and CMG method (in s).
子孔径数目20 × 20 子孔径数目40 × 40 子孔径数目80 × 80 直接迭代 CMG算法 直接迭代 CMG算法 直接迭代 CMG算法 Phase1 4.261 0.081 67.39 0.271 1400 0.920 Phase2 5.112 0.119 77.61 0.319 2134 0.852 Phase3 4.184 0.103 54.56 0.519 1424 1.339 Phase4 1.891 0.097 18.43 0.494 370.8 1.308 
DownLoad: CSV
-
[1] Fried D L, Vaughn J L 1992 Appl. Opt. 31 2865
Google Scholar
[2] Fried D L 1998 JOSA A 15 2759
Google Scholar
[3] Primmerman C A, Price T R, Humphreys R A, et al. 1995 Appl. Opt. 34 2081
Google Scholar
[4] Lukin V P, Fortes B V 2002 Appl. Opt. 41 5616
Google Scholar
[5] Steinbock M J, Hyde M W, Schmidt J D 2014 Appl. Opt. 53 3821
Google Scholar
[6] Le B E, Wild W J, Kibblewhite E J 1998 Opt. Lett. 23 10
Google Scholar
[7] Fried D L 2001 Opt. Commun. 200 43
Google Scholar
[8] Barchers J D, Fried D L, Link D J 2002 Appl. Opt. 41 1012
Google Scholar
[9] Aubailly M, Vorontsov M A 2012 JOSA A 29 1707
[10] Yazdani R, Fallah H 2017 Appl. Opt. 56 1358
Google Scholar
[11] Goodman J W ( translated by Qin K C, L P S, Chen J B, Cao Q Z) 2013 Introduction to Fourier Optics (3rd Ed.) (Beijing: Publishing House of Electronics Industry) p77
[12] Hudgin R H 1977 JOSA 67 378
Google Scholar
[13] Hudgin R H 1977 JOSA 67 375
Google Scholar
[14] Bornemann F A, Deuflhard P 1996 Numerische Mathematik 75 135
Google Scholar
[15] Venema T M, Schmidt J D 2008 Opt. Express 16 6985
Google Scholar
[16] Steinbock M J, Schmidt J D, Hyde M W 2012 Aerospace Conference Big Sky, MT, USA, 3-10 March, 2012, pp1-13
[17] Roddier N A 1990 Opt. Eng. 29 1174
Google Scholar
[18] Southwell W H 1980 JOSA 70 998
Google Scholar
[19] Jr J A F, Morris J R, Feit M D 1976 Appl. Phys. 10 129
[20] 蔡冬梅, 王昆, 贾鹏, 王东, 刘建霞 2014 63 104217
Google Scholar
Cai D M, Wang K, Jia P, Wang D, Liu J X 2014 Acta Phys. Sin. 63 104217
Google Scholar
[21] 程生毅, 陈善球, 董理治, 王帅, 杨平, 敖明武, 许冰 2015 64 094207
Google Scholar
Cheng Y C, Shan Q C, Dong L Z, Wang S, Yang P, Ao M W, Xu B 2015 Acta Phys. Sin. 64 094207
Google Scholar
[22] Fan C, Wang Y, Gong Z 2004 Appl. Opt. 43 4334
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7123
- PDF Downloads: 39
- Cited By: 0
