拓扑选择性非厄米趋肤效应

杨星; 刘梦蛟; 侯佳浩; 李添悦; 王漱明

doi:10.7498/aps.74.20250526

摘要

拓扑边界态因在带隙中的鲁棒性和无损耗的传输特性备受关注, 但在复杂系统中实现其稳定激发仍是一个挑战. 本文提出了一种利用亚对称性保护的边界态与长程非互易耦合系数, 实现具有拓扑选择性的非厄米趋肤效应 (non-Hermitian skin effect, NHSE) 的方法. 该方法能够选择性地对平庸体态施加非厄米趋肤效应, 同时保持拓扑边界态不受影响, 从而实现拓扑模式与体态模式在空间上的有效分离, 并在能带密集的系统中实现鲁棒的边界态激发. 此外, 本文将该模型扩展到二维体系, 实现了角态与体态模式的有效分离. 通过紧束缚模型进行理论预测, 分析了该模型中非厄米效应对能谱和趋肤性质的调控机制, 并利用有限元仿真在光学耦合环中验证了这一机制的可行性, 研究了非厄米趋肤效应的本征态特性, 并实现了拓扑态的鲁棒激发. 该机制将非厄米物理与拓扑光子学相结合, 为提升光子系统中信号的稳定性提供了新的思路与方向.

关键词:

Abstract

Topologically protected waveguides have aroused increasing interest due to their robustness against disorder and defects. In parallel, the advent of non-Hermitian physics with its inherent gain-and-loss mechanisms has introduced new tools for manipulating wave localization and transport. However, most attempts to combine non-Hermitian effects with topological systems uniformly impose the non-Hermitian skin effect (NHSE) on all modes, without selectivity targeting topological states. In this work, we propose a scheme thatachieves topologically selective NHSE by combining sub-symmetry-protected boundary modes with long-range non-reciprocal couplings. In an improved Su–Schrieffer–Heeger (SSH) chain, we analytically demonstrate that robust zero-energy edge modes can be preserved even in spectra filled with bulk states, while selectively applying the NHSE to the trivial bulk states to achieve the spatial separation between topological state and bulk state. By adjusting the long-range couplings a non-Hermitian phase transition can be observed in the complex energy spectrum: it transitions from a closed loop (circle) to an open arc, and ultimately to a reversely coiled loop. These transitions correspond respectively to a leftward NHSE, the disappearance of the NHSE, and a rightward NHSE. According to the calculations of the generalized Brillouin zone (GBZ), we confirm this transition by observing the GBZ passing through the unit circle, indicating a change in the direction of NHSE.We further extend our model to a two-dimensional higher-order SSH lattice, where selective non-Hermitian modulation enables clear spatial separation between topological corner states and bulk modes. To quantify this, we compute the local density of states (LDOS) in the complex energy plane for site 0 (a topologically localized corner) and site 288 (a region exhibiting NHSE). The comparison of LDOS between the two sites reveals that the topological states are primarily localized at site 0, while the bulk states affected by NHSE accumulate at site 288.To validate the theoretical predictions, we perform finite-element simulations of optical resonator arrays by using whispering-gallery modes. By adjusting the coupling distances and incorporating gain/loss through refractive index engineering, we replicate the modified SSH model and confirm the selective localization of topological and bulk modes.Our results provide a robust method for selectively exciting and spatially controlling the topological states in non-Hermitian systems, and also lay a foundation for future low-crosstalk high-stability topological photonic devices.

Keywords:

作者及机构信息

1.
南京大学物理学院, 固体微结构国家重点实验室, 南京　210093

2.
南京大学, 人工微结构科学与技术协同创新中心, 南京　210093

通信作者: 王漱明, wangshuming@nju.edu.cn

基金项目: 国家重点基础研究发展计划(批准号: 2022YFA1404300)、国家自然科学基金(批准号: 12325411, 62288101, 11774162)、江苏省自然科学基金(批准号: BK20233001)和江苏省重点研发计划(批准号: BG2024029)资助的课题.

Authors and contacts

1.
National Laboratory of Solid State Microstructures, School of Physics, College of Engineering and Applied Sciences, Nanjing University, Nanjing 210093, China

2.
Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China

Corresponding author: WANG Shuming, wangshuming@nju.edu.cn

Funds: Project supported by the National Basic Research Program of China (Grant No. 2022YFA1404300), the National Natural Science Foundation of China (Grant Nos. 12325411, 62288101, 11774162), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20233001), and the Jiangsu Provincial Key Research and Development Program, China (Grant No. BG2024029).

文章全文

参考文献

[1]	Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698 Google Scholar
[2]	Wang Z, Chong Y, Joannopoulos J D, Soljačić M 2009 Nature 461 772 Google Scholar
[3]	Hafezi M, Demler E A, Lukin M D, Taylor J M 2011 Nat. Phys. 7 907 Google Scholar
[4]	Fang K, Yu Z, Fan S 2012 Nat. Photonics 6 782 Google Scholar
[5]	Hafezi M, Mittal S, Fan J, Migdall A, Taylor J M 2013 Nat. Photonics 7 1001 Google Scholar
[6]	Khanikaev A B, Hossein Mousavi S, Tse W K, Kargarian M, MacDonald A H, Shvets G 2013 Nat. Mater. 12 233 Google Scholar
[7]	Wu L H, Hu X 2015 Phys. Rev. Lett. 114 223901 Google Scholar
[8]	Ma T, Shvets G 2016 New J. Phys. 18 025012 Google Scholar
[9]	王子尧, 陈福家, 郗翔, 高振, 杨怡豪 2024 73 064201 Google Scholar Wang Z Y, Chen F J, Xi X, Gao Z, Yang Y H 2024 Acta Phys. Sin. 73 064201 Google Scholar
[10]	王洪飞, 解碧野, 詹鹏, 卢明辉, 陈延峰 2019 68 224206 Google Scholar Wang H F, Xie B Y, Zhan P, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 224206 Google Scholar
[11]	孙晓晨, 何程, 卢明辉, 陈延峰 2017 66 224203 Google Scholar Sun X C, He C, Lu M H, Chen Y F 2017 Acta Phys. Sin. 66 224203 Google Scholar
[12]	Xie B, Wang H X, Zhang X, Zhan P, Jiang J H, Lu M, Chen Y 2021 Nat. Rev. Phys. 3 520 Google Scholar
[13]	Benalcazar W A, Noh J, Wang M, Huang S, Chen K P, Rechtsman M C 2022 Phys. Rev. B 105 195129 Google Scholar
[14]	Wang Q, Xue H, Zhang B, Chong Y 2020 Phys. Rev. Lett. 124 243602 Google Scholar
[15]	胡军容, 孔鹏, 毕仁贵, 邓科, 赵鹤平 2022 71 054301 Google Scholar Hu J R, Kong P, Bi R G, Deng K, Zhao H P 2022 Acta Phys. Sin. 71 054301 Google Scholar
[16]	严忠波 2019 68 226101 Google Scholar Yan Z B 2019 Acta Phys. Sin. 68 226101 Google Scholar
[17]	Wang Z, Wang X, Hu Z, et al. 2023 Nat. Phys. 19 992 Google Scholar
[18]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[19]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[20]	Bender C, Boettcher S, Meisinger P 1999 J. Math. Phys. 40 2201 Google Scholar
[21]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[22]	Lee T E 2016 Phys. Rev. Lett. 116 133903 Google Scholar
[23]	Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801 Google Scholar
[24]	Song W, Sun W, Chen C, Song Q, Xiao S, Zhu S, Li T 2019 Phys. Rev. Lett. 123 165701 Google Scholar
[25]	Li Y, Liang C, Wang C, Lu C, Liu Y C 2022 Phys. Rev. Lett. 128 223903 Google Scholar
[26]	Wang W, Wang X, Ma G 2022 Nature 608 50 Google Scholar
[27]	Zhu W, Gong J 2022 Phys. Rev. B 106 035425 Google Scholar
[28]	Liu G G, Mandal S, Zhou P, Xi X, Banerjee R, Hu Y H, Wei M, Wang M, Wang Q, Gao Z, Chen H, Yang Y, Chong Y, Zhang B 2024 Phys. Rev. Lett. 132 113802 Google Scholar
[29]	Song W, Lin Z, Ji J, Sun J, Chen C, Wu S, Huang C, Yuan L, Zhu S, Li T 2024 Phys. Rev. Lett. 132 143801 Google Scholar
[30]	Chen J, Shi A, Peng Y, Peng P, Liu J 2024 Chin. Phys. Lett. 41 037103 Google Scholar
[31]	Martinez Alvarez V M, Barrios Vargas J E, Foa Torres L E F 2018 Phys. Rev. B 97 121401 Google Scholar
[32]	Pan M, Zhao H, Miao P, Longhi S, Feng L 2018 Nat. Commun. 9 1308 Google Scholar
[33]	Huang Q K L, Liu Y K, Cao P C, Zhu X F, Li Y 2023 Chin. Phys. Lett. 40 106601 Google Scholar
[34]	Leykam D, Bliokh K Y, Huang C, Chong Y, Nori F 2017 Phys. Rev. Lett. 118 040401 Google Scholar
[35]	Liu X, Lin Z, Song W, Sun J, Huang C, Wu S, Xiao X, Xin H, Zhu S, Li T 2024 Phys. Rev. Lett. 132 016601 Google Scholar
[36]	Jackiw R, Rebbi C 1976 Phys. Rev. D 13 3398 Google Scholar
[37]	Qi X L, Wu Y S, Zhang S C 2006 Phys. Rev. B 74 045125 Google Scholar
[38]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[39]	Yang Z, Zhang K, Fang C, Hu J 2020 Phys. Rev. Lett. 125 226402 Google Scholar
[40]	Wang Z, Wang X, Li A, Zhang K, Ji Y, Zhong M 2023 Chin. Phys. B 32 064207 Google Scholar
[41]	陈云天, 王经纬, 陈伟锦, 徐竞 2020 69 154206 Google Scholar Chen Y T, Wang J W, Chen W J, Xu J 2020 Acta Phys. Sin. 69 154206 Google Scholar
[42]	Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006 Google Scholar
[43]	Yan Q C, Ma R, Hu X Y, Gong Q H 2023 Chin. Phys. B 33 010301 Google Scholar
[44]	Xu Y X, Tang W J, Jiang L W, Wu D X, Wang H, Xu B C, Chen L 2024 Chin. Phys. B 33 060306 Google Scholar
[45]	Wu D, Chen J, Su W, Wang R, Wang B, Xing D Y 2023 Commun. Phys. 6 1 Google Scholar
[46]	Xu X W, Li Y Z, Liu Z F, Chen A X 2020 Phys. Rev. A 101 063839 Google Scholar

施引文献

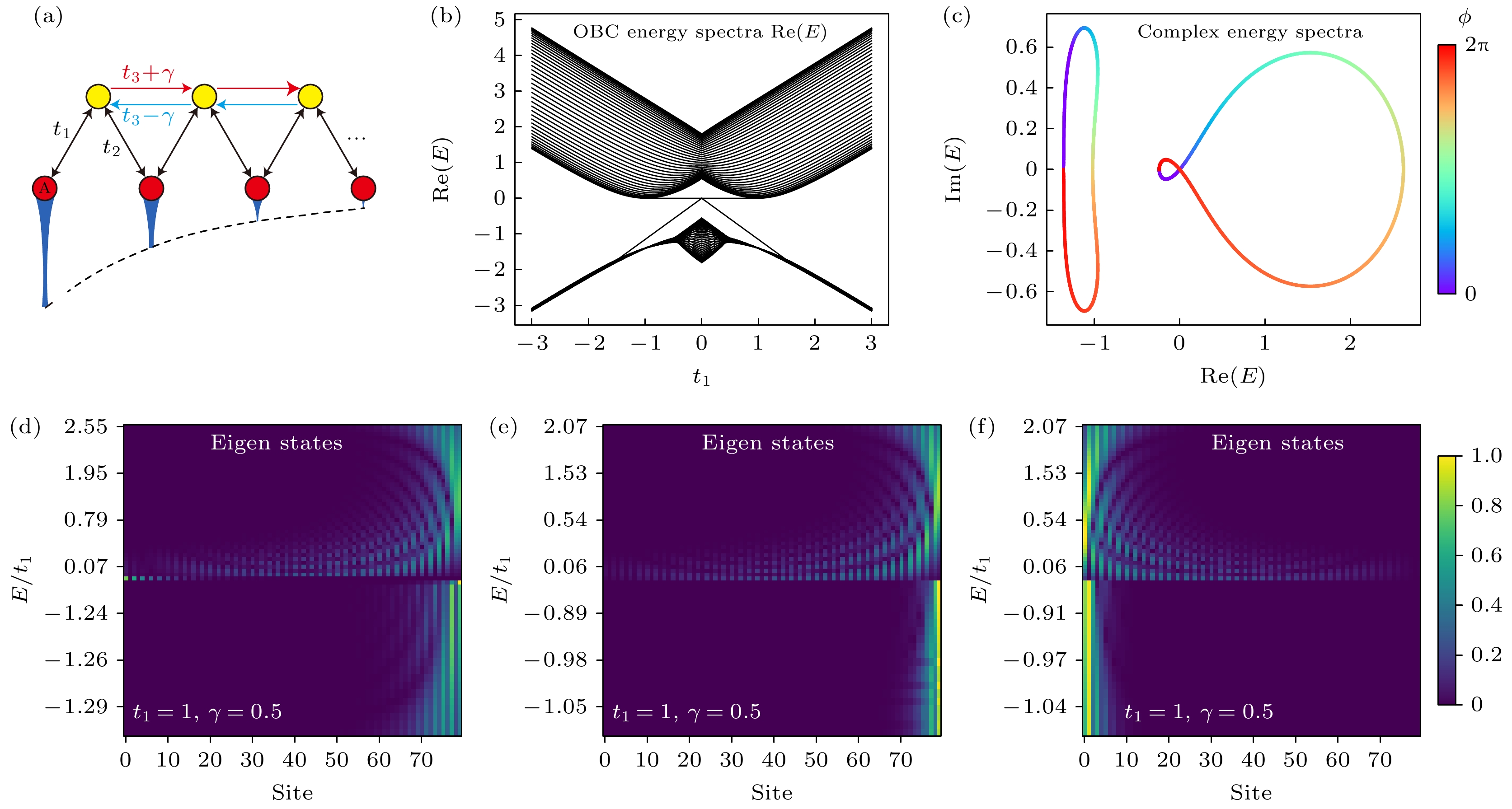
图 1 (a) 系统的紧束缚耦合示意图, 红色/黄色为A/B位点, 耦合系数为$ t_1, t_2, t_3, \gamma $, 箭头表示具有方向的耦合系数; (b) 系统的实能量分布随$ t_1 $的变化图; (c) 系统的复能量分布, 颜色的变化代表Bloch动量相位(ϕ)的变化; (d) 具有选择性非厄米趋肤效应的模式图, 横坐标为位点, 纵坐标为实能量, 白字标示了耦合参数大小; (e) 无拓扑模式非厄米趋肤效应的模式图, 横坐标为位点, 纵坐标为实能量, 白字标示了耦合参数大小; (f) 具有反方向非厄米趋肤效应的模式图, 横坐标为位点, 纵坐标为实能量, 白字表示了耦合参数大小

Fig. 1. (a) Schematic diagram of the system's tight-binding couplings. Red/yellow dots represent A/B sites, and the coupling coefficients are $ t_1 $, $ t_2 $, $ t_3 $, and γ. Arrows indicate direction-dependent coupling. (b) Plot of the system’s real energy spectrum as $ t_1 $ changes from $ -3 $ to $ 3 $. (c) System’s complex energy spectrum. The color gradient indicates the variation of the Bloch momentum phase (ϕ). (d) Mode distribution exhibiting topological selective non-Hermitian skin effect, white text denotes coupling coefficients. The horizontal axis represents site index, and the vertical axis represents real energy. (e) Mode distribution under non-Hermitian skin effect without topological modes. The horizontal axis represents site index, and the vertical axis represents real energy, white text denotes coupling coefficients. (f) Mode distribution exhibiting reverse non-Hermitian skin effect. The horizontal axis represents site index, and the vertical axis represents real energy, white text denotes coupling coefficients.

下载: 全尺寸图片幻灯片

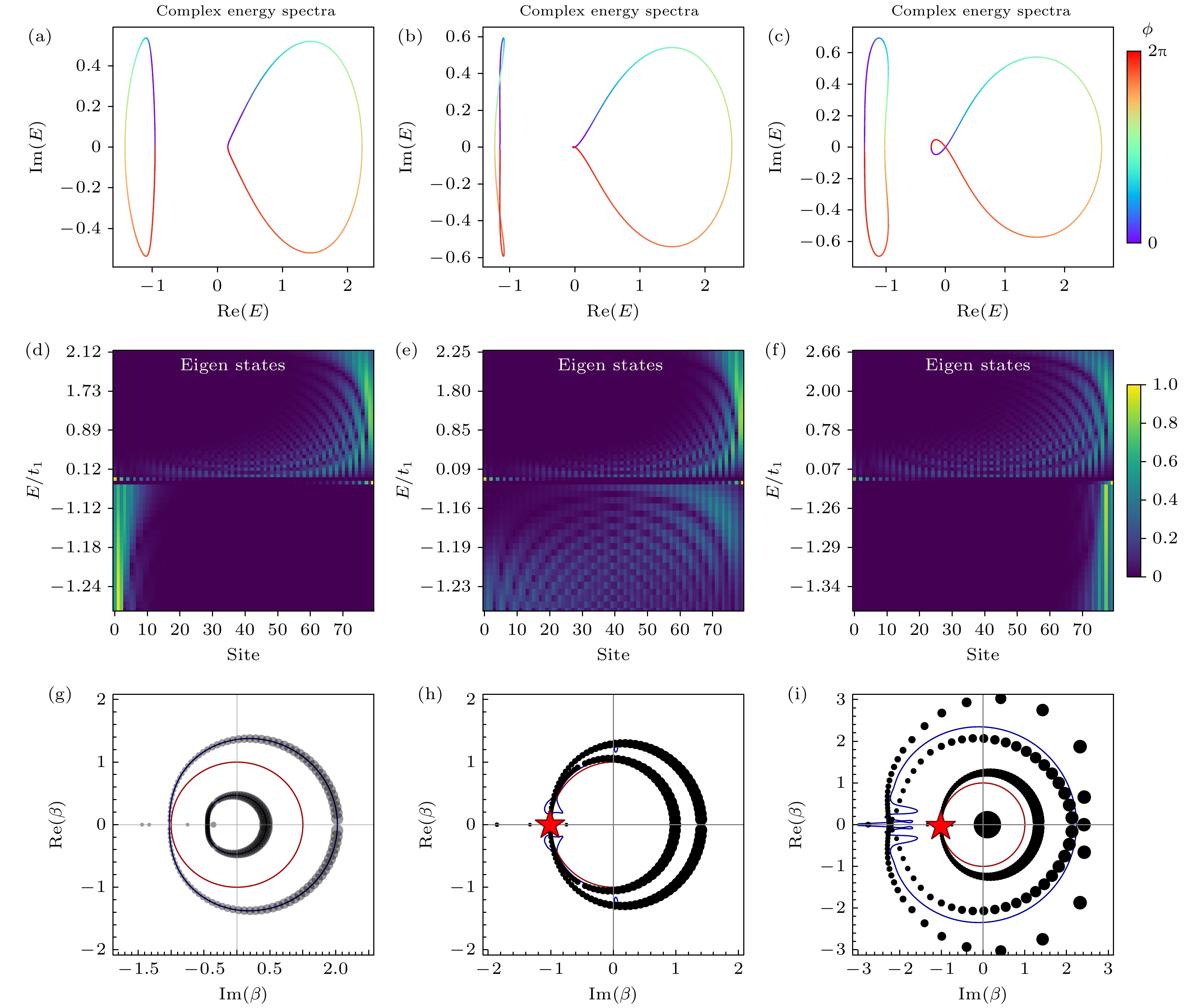
图 2 (a), (d), (g) $ t_3=0.4 $时的能带, 本征态分布和GBZ, (a)横坐标/纵坐标分别为实/虚能量, 颜色图标代表Bloch动量的相位ϕ, (d)横坐标/纵坐标为位点/能量, 颜色图标代表模式振幅, (g)横坐标/纵坐标为虚/实β, 灰色小球代表有限模型$ (n=100) $计算出的GBZ, 红星处$ \beta =1 $; (b), (e), (h) $ t_3=0.59 $时的能带, 本征态分布和GBZ; (c), (f), (i) $ t_3=0.8 $时的能带, 本征态分布和GBZ

Fig. 2. (a), (d), (g) Energy bands, eigenstate and GBZ at $ t_3 = 0.4 $. In (a), the horizontal(vertical) axes is real (imaginary) parts of eigen energy, color bar indicates the phase of the Bloch momentum. In (d), the horizontal axis is the site index, the vertical axis is the energy, and the color bar represents the mode amplitude. In (g), the horizontal (vertical) axes is real (imaginary) parts of β, gray dots means GBZ calculated from finite model ($ n=100 $), the red star means where $ \beta=1 $. (b), (e), (h) Energy bands, eigenstate distribution and GBZ at $ t_3 = 0.59 $. (c), (f), (i) Energy bands, eigenstate distribution and GBZ at $ t_3 = 0.8 $.

下载: 全尺寸图片幻灯片

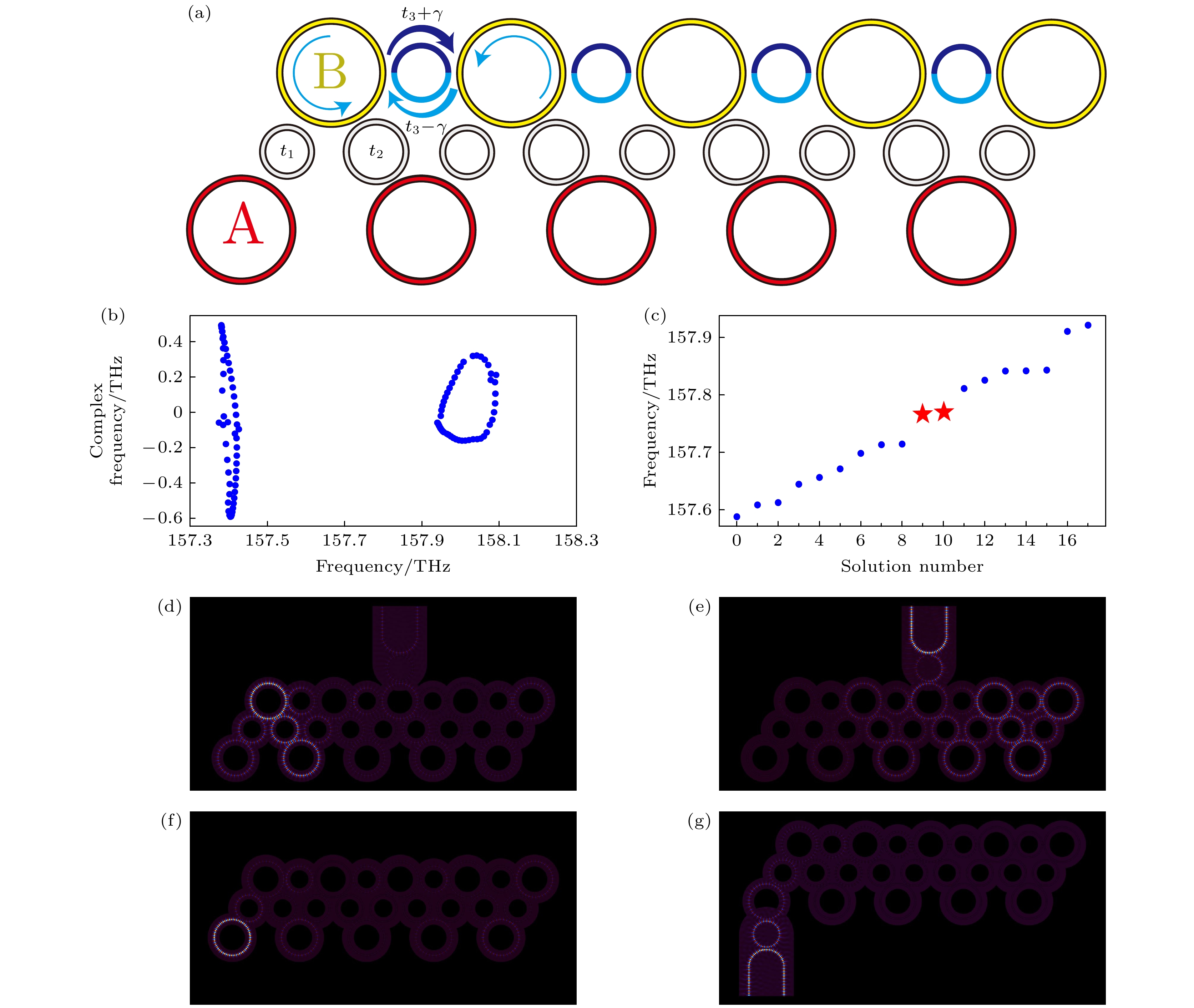
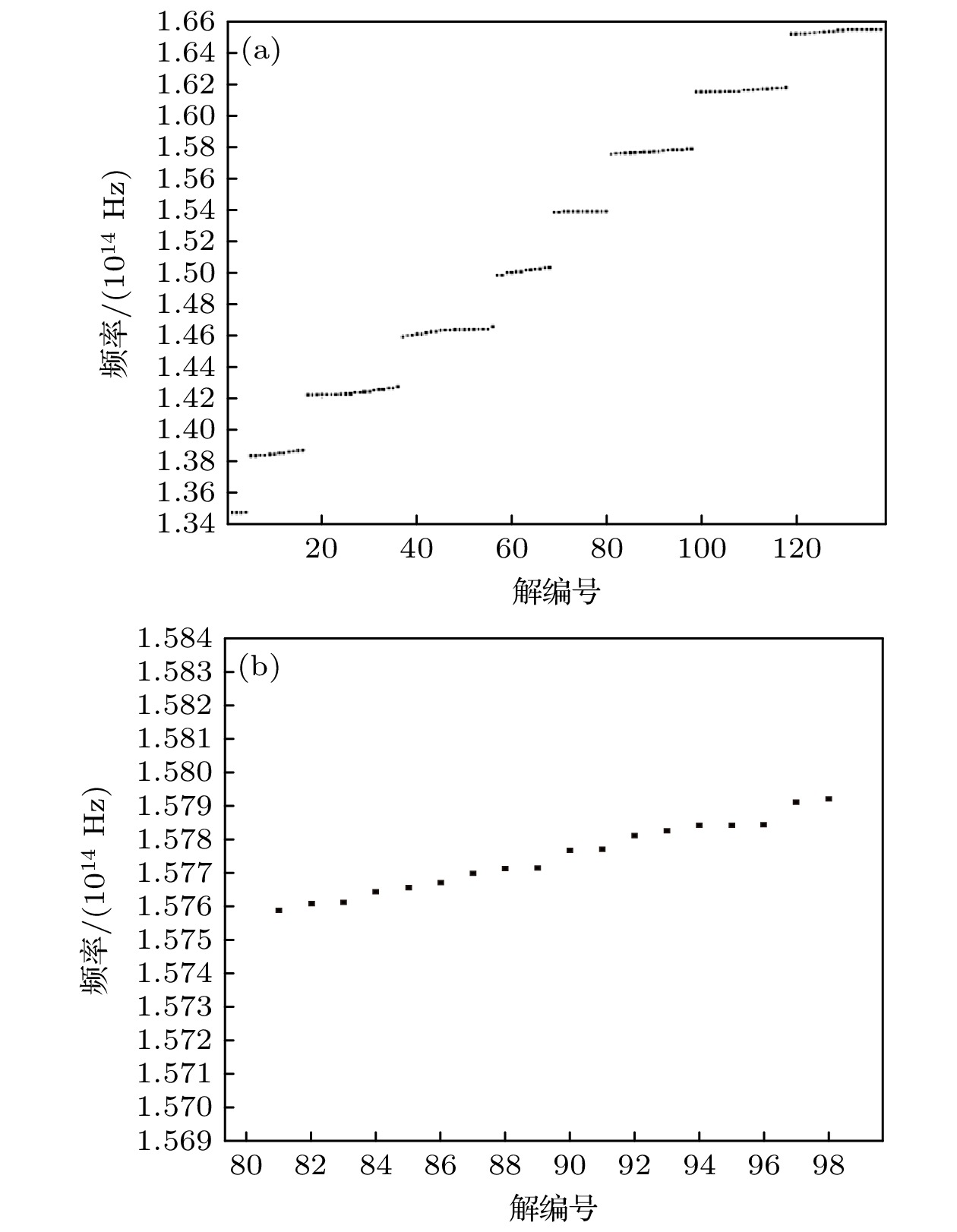
图 3 (a) 耦合环示意图; (b) 有限元仿真的周期行边界复能带, x轴为实频率, y轴为复频率; (c) 有限元仿真的开放边界能带$ (n=10) $, x轴为解数, y轴为实频率, 红色五角星代表拓扑态; (d) 有限元仿真的向左的NHSE; (e) 有限元仿真的向右的NHSE; (f) 有限元仿真中的拓扑模式; (g) 在特定位点上激发的拓扑模式

Fig. 3. (a) Schematic diagram of the coupling rings; (b) complex energy band of finite element simulation under periodic boundary condition; (c) real energy band of finite element simulation under open boundary condition$ (n=10) $, the red star denotes topological states; (d) leftward non-Hermitian skin effect (NHSE) from finite element simulation; (e) rightward non-Hermitian skin effect (NHSE) from finite element simulation; (f) topological mode in the finite element simulation; (g) excited topological mode.

下载: 全尺寸图片幻灯片

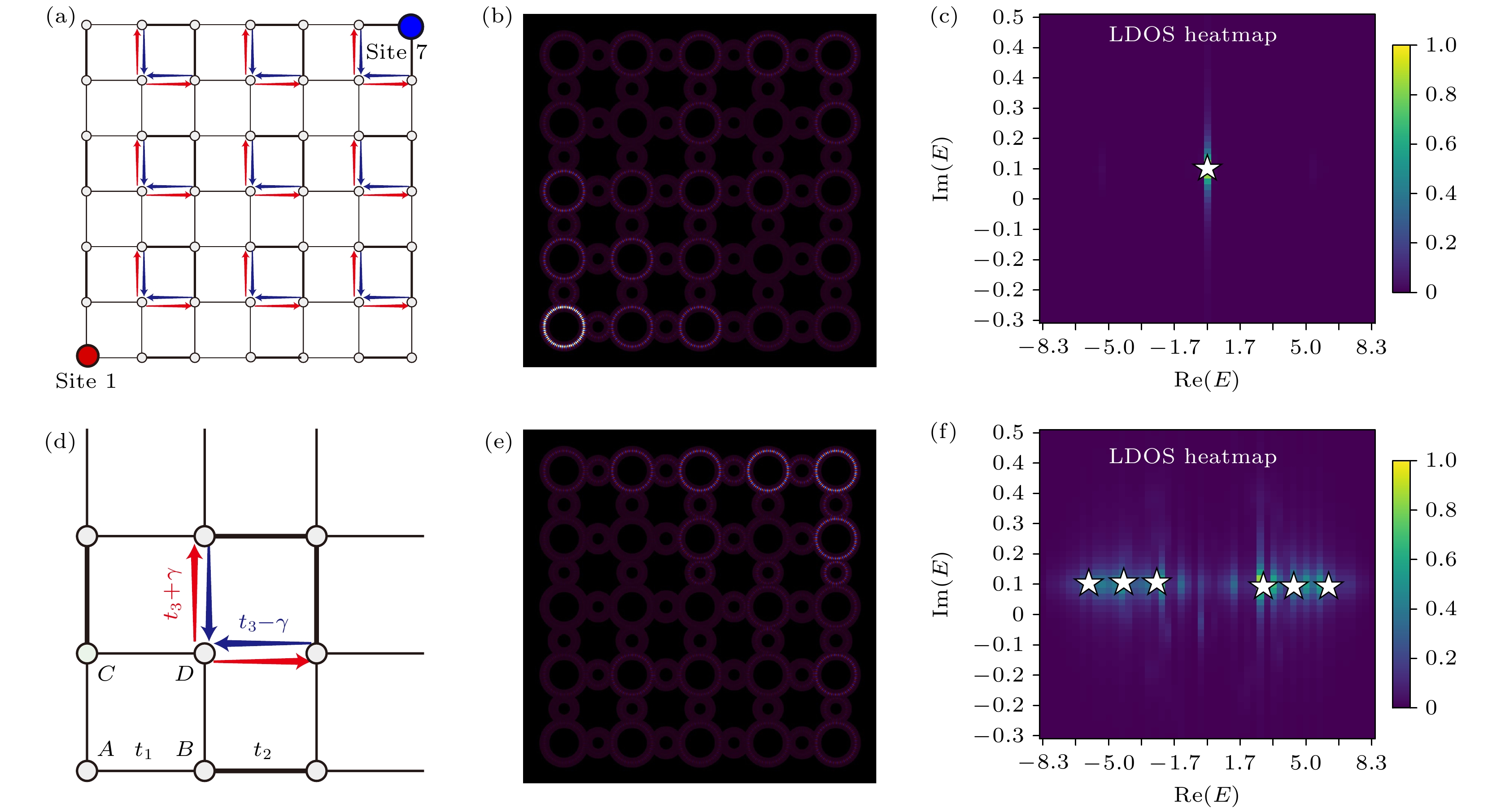
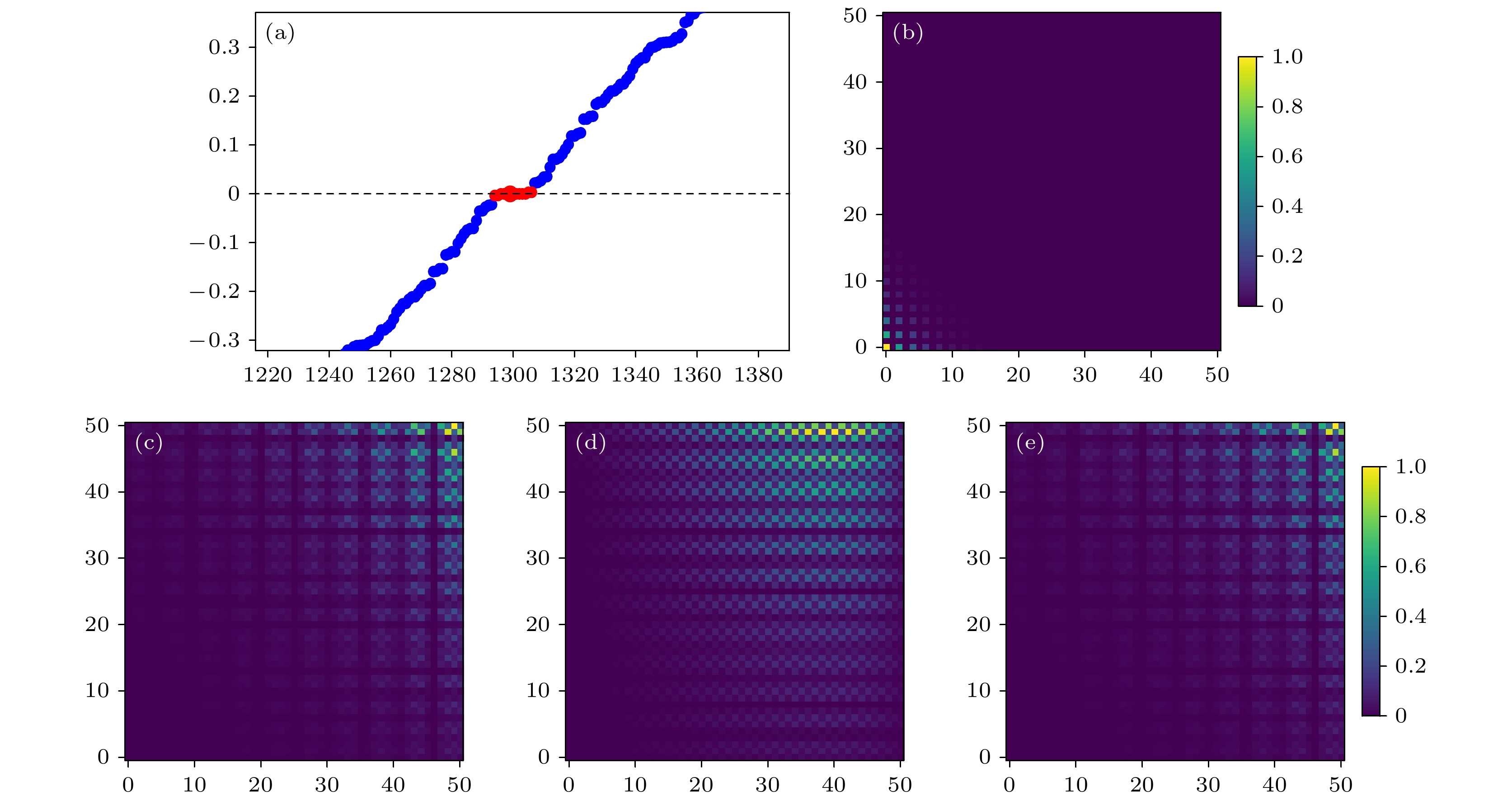
图 4 (a) 2维高阶SSH模型示意图; (b) 非互易耦合环中的二维高阶拓扑态; (c) 位点0处的复平面LDOS; (d) 二维模型的放大示意图; (e) $ B, C, D $三个位点非互易耦合导致的体态非厄米效应; (f) 位点288处的复平面LDOS

Fig. 4. (a) schematic diagram of the 2D higher-order SSH model. (b) 2D higher-order topological state in the presence of non-reciprocal coupling rings. (c) complex plane LDOS at finite slab site 0. (d) enlarged unit cell schematic of the 2D model. (e) non-Hermitian skin effect on bulk states induced by non-reciprocal coupling among sites B, C, and D. (f) complex plane LDOS at site 288.

下载: 全尺寸图片幻灯片

图 A1 (a) 光学耦合环系统的本征能带; (b) 本文选取光学耦合环系统的本征能带

Fig. A1. (a) Eigenenergy band of the optical coupling ring system; (b) enlarged chosen eigenenergy band of the optical coupling ring system.

下载: 全尺寸图片幻灯片

图 A2 (a) 2D选择性非互易趋肤效应SSH模型的本征能带, 红色表示零能模式; (b) 2D选择性模式中不受到影响的零能模式; (c) 2D选择性非互易趋肤效应SSH模型的代表本征态之一; (d) 2D选择性非互易趋肤效应SSH模型的代表本征态之二; (e) 2D选择性非互易趋肤效应SSH模型的代表本征态之三

Fig. A2. (a) Eigenenergy band of the 2D selective non-reciprocal skin effect SSH model, red denote zero energy mode; (b) 2D topological mode not affected by the selective skin effect; (c) representative eigenstate 1 of the 2D selective non-reciprocal skin; (d) representative eigenstate 2 of the 2D selective non-reciprocal skin; (e) representative eigenstate 3 of the 2D selective non-reciprocal skin.

下载: 全尺寸图片幻灯片

map

[1]	Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698 Google Scholar
[2]	Wang Z, Chong Y, Joannopoulos J D, Soljačić M 2009 Nature 461 772 Google Scholar
[3]	Hafezi M, Demler E A, Lukin M D, Taylor J M 2011 Nat. Phys. 7 907 Google Scholar
[4]	Fang K, Yu Z, Fan S 2012 Nat. Photonics 6 782 Google Scholar
[5]	Hafezi M, Mittal S, Fan J, Migdall A, Taylor J M 2013 Nat. Photonics 7 1001 Google Scholar
[6]	Khanikaev A B, Hossein Mousavi S, Tse W K, Kargarian M, MacDonald A H, Shvets G 2013 Nat. Mater. 12 233 Google Scholar
[7]	Wu L H, Hu X 2015 Phys. Rev. Lett. 114 223901 Google Scholar
[8]	Ma T, Shvets G 2016 New J. Phys. 18 025012 Google Scholar
[9]	王子尧, 陈福家, 郗翔, 高振, 杨怡豪 2024 73 064201 Google Scholar Wang Z Y, Chen F J, Xi X, Gao Z, Yang Y H 2024 Acta Phys. Sin. 73 064201 Google Scholar
[10]	王洪飞, 解碧野, 詹鹏, 卢明辉, 陈延峰 2019 68 224206 Google Scholar Wang H F, Xie B Y, Zhan P, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 224206 Google Scholar
[11]	孙晓晨, 何程, 卢明辉, 陈延峰 2017 66 224203 Google Scholar Sun X C, He C, Lu M H, Chen Y F 2017 Acta Phys. Sin. 66 224203 Google Scholar
[12]	Xie B, Wang H X, Zhang X, Zhan P, Jiang J H, Lu M, Chen Y 2021 Nat. Rev. Phys. 3 520 Google Scholar
[13]	Benalcazar W A, Noh J, Wang M, Huang S, Chen K P, Rechtsman M C 2022 Phys. Rev. B 105 195129 Google Scholar
[14]	Wang Q, Xue H, Zhang B, Chong Y 2020 Phys. Rev. Lett. 124 243602 Google Scholar
[15]	胡军容, 孔鹏, 毕仁贵, 邓科, 赵鹤平 2022 71 054301 Google Scholar Hu J R, Kong P, Bi R G, Deng K, Zhao H P 2022 Acta Phys. Sin. 71 054301 Google Scholar
[16]	严忠波 2019 68 226101 Google Scholar Yan Z B 2019 Acta Phys. Sin. 68 226101 Google Scholar
[17]	Wang Z, Wang X, Hu Z, et al. 2023 Nat. Phys. 19 992 Google Scholar
[18]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[19]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[20]	Bender C, Boettcher S, Meisinger P 1999 J. Math. Phys. 40 2201 Google Scholar
[21]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[22]	Lee T E 2016 Phys. Rev. Lett. 116 133903 Google Scholar
[23]	Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801 Google Scholar
[24]	Song W, Sun W, Chen C, Song Q, Xiao S, Zhu S, Li T 2019 Phys. Rev. Lett. 123 165701 Google Scholar
[25]	Li Y, Liang C, Wang C, Lu C, Liu Y C 2022 Phys. Rev. Lett. 128 223903 Google Scholar
[26]	Wang W, Wang X, Ma G 2022 Nature 608 50 Google Scholar
[27]	Zhu W, Gong J 2022 Phys. Rev. B 106 035425 Google Scholar
[28]	Liu G G, Mandal S, Zhou P, Xi X, Banerjee R, Hu Y H, Wei M, Wang M, Wang Q, Gao Z, Chen H, Yang Y, Chong Y, Zhang B 2024 Phys. Rev. Lett. 132 113802 Google Scholar
[29]	Song W, Lin Z, Ji J, Sun J, Chen C, Wu S, Huang C, Yuan L, Zhu S, Li T 2024 Phys. Rev. Lett. 132 143801 Google Scholar
[30]	Chen J, Shi A, Peng Y, Peng P, Liu J 2024 Chin. Phys. Lett. 41 037103 Google Scholar
[31]	Martinez Alvarez V M, Barrios Vargas J E, Foa Torres L E F 2018 Phys. Rev. B 97 121401 Google Scholar
[32]	Pan M, Zhao H, Miao P, Longhi S, Feng L 2018 Nat. Commun. 9 1308 Google Scholar
[33]	Huang Q K L, Liu Y K, Cao P C, Zhu X F, Li Y 2023 Chin. Phys. Lett. 40 106601 Google Scholar
[34]	Leykam D, Bliokh K Y, Huang C, Chong Y, Nori F 2017 Phys. Rev. Lett. 118 040401 Google Scholar
[35]	Liu X, Lin Z, Song W, Sun J, Huang C, Wu S, Xiao X, Xin H, Zhu S, Li T 2024 Phys. Rev. Lett. 132 016601 Google Scholar
[36]	Jackiw R, Rebbi C 1976 Phys. Rev. D 13 3398 Google Scholar
[37]	Qi X L, Wu Y S, Zhang S C 2006 Phys. Rev. B 74 045125 Google Scholar
[38]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[39]	Yang Z, Zhang K, Fang C, Hu J 2020 Phys. Rev. Lett. 125 226402 Google Scholar
[40]	Wang Z, Wang X, Li A, Zhang K, Ji Y, Zhong M 2023 Chin. Phys. B 32 064207 Google Scholar
[41]	陈云天, 王经纬, 陈伟锦, 徐竞 2020 69 154206 Google Scholar Chen Y T, Wang J W, Chen W J, Xu J 2020 Acta Phys. Sin. 69 154206 Google Scholar
[42]	Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006 Google Scholar
[43]	Yan Q C, Ma R, Hu X Y, Gong Q H 2023 Chin. Phys. B 33 010301 Google Scholar
[44]	Xu Y X, Tang W J, Jiang L W, Wu D X, Wang H, Xu B C, Chen L 2024 Chin. Phys. B 33 060306 Google Scholar
[45]	Wu D, Chen J, Su W, Wang R, Wang B, Xing D Y 2023 Commun. Phys. 6 1 Google Scholar
[46]	Xu X W, Li Y Z, Liu Z F, Chen A X 2020 Phys. Rev. A 101 063839 Google Scholar

[1]	包茜茜, 郭刚峰, 谭磊, 刘伍明. 周期驱动系统中由次近邻跃迁诱导的非厄米拓扑相. , 2025, 74(17): . doi: 10.7498/aps.74.20250599
[2]	刘恩克. 磁序与拓扑的耦合: 从基础物理到拓扑磁电子学. , 2024, 73(1): 017103. doi: 10.7498/aps.73.20231711
[3]	古燕, 陆展鹏. 非厄米耦合链中的局域化转变. , 2024, 73(19): 197101. doi: 10.7498/aps.73.20240976
[4]	黄泽鑫, 圣宗强, 程乐乐, 曹三祝, 陈华俊, 吴宏伟. 一维非互易声学晶体的非厄米趋肤态操控. , 2024, 73(21): 214301. doi: 10.7498/aps.73.20241087
[5]	王子尧, 陈福家, 郗翔, 高振, 杨怡豪. 非互易拓扑光子学. , 2024, 73(6): 064201. doi: 10.7498/aps.73.20231850
[6]	王振宇, 李志雄, 袁怀洋, 张知之, 曹云姗, 严鹏. 磁子学中的拓扑物态与量子效应. , 2023, 72(5): 057503. doi: 10.7498/aps.72.20221997
[7]	徐灿鸿, 许志聪, 周子榆, 成恩宏, 郎利君. 非厄米格点模型的经典电路模拟. , 2023, 72(20): 200301. doi: 10.7498/aps.72.20230914
[8]	杨艳丽, 段志磊, 薛海斌. 非厄米Su-Schrieffer-Heeger链边缘态和趋肤效应依赖的电子输运特性. , 2023, 72(24): 247301. doi: 10.7498/aps.72.20231286
[9]	李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江. 一维${\cal {PT}}$对称非厄米自旋轨道耦合Su-Schrieffer-Heeger模型的拓扑性质. , 2022, 71(17): 177302. doi: 10.7498/aps.71.20220796
[10]	成恩宏, 郎利君. 非互易Aubry-André 模型的经典电路模拟. , 2022, 71(16): 160301. doi: 10.7498/aps.71.20220219
[11]	侯博, 曾琦波. 非厄米镶嵌型二聚化晶格. , 2022, 71(13): 130302. doi: 10.7498/aps.71.20220890
[12]	刘佳琳, 庞婷方, 杨孝森, 王正岭. 无序非厄米Su-Schrieffer-Heeger中的趋肤效应. , 2022, 71(22): 227402. doi: 10.7498/aps.71.20221151
[13]	陈舒越, 蒋闯, 柯少林, 王兵, 陆培祥. 基于Aharonov-Bohm笼的非厄米趋肤效应抑制现象. , 2022, 71(17): 174201. doi: 10.7498/aps.71.20220978
[14]	邓天舒. 畴壁系统中的非厄米趋肤效应. , 2022, 71(17): 170306. doi: 10.7498/aps.71.20221087
[15]	孙孔浩, 易为. 非厄米局域拓扑指标的动力学特性. , 2021, 70(23): 230309. doi: 10.7498/aps.70.20211576
[16]	胡渝民, 宋飞, 汪忠. 广义布里渊区与非厄米能带理论. , 2021, 70(23): 230307. doi: 10.7498/aps.70.20211908
[17]	廖庆洪, 邓伟灿, 文健, 周南润, 刘念华. 纳米机械谐振器耦合量子比特非厄米哈密顿量诱导的声子阻塞. , 2019, 68(11): 114203. doi: 10.7498/aps.68.20182263
[18]	许楠, 张岩. 三聚化非厄密晶格中具有趋肤效应的拓扑边缘态. , 2019, 68(10): 104206. doi: 10.7498/aps.68.20190112
[19]	梅宇涵, 邵越, 杭志宏. 基于紧束缚模型的拓扑物理微波实验验证平台的开发. , 2019, 68(22): 227803. doi: 10.7498/aps.68.20191452
[20]	王洪飞, 解碧野, 詹鹏, 卢明辉, 陈延峰. 拓扑光子学研究进展. , 2019, 68(22): 224206. doi: 10.7498/aps.68.20191437

计量

文章访问数: 1183
PDF下载量: 126
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

拓扑选择性非厄米趋肤效应