纳米机械谐振器耦合量子比特非厄米哈密顿量诱导的声子阻塞

廖庆洪; 邓伟灿; 文健; 周南润; 刘念华

doi:10.7498/aps.68.20182263

摘要

研究了纳米机械谐振器耦合量子比特系统中的声子阻塞现象. 发现在弱驱动的条件下, 非厄米哈密顿量的所有本征值都等于零时, 出现了强声子反聚束现象. 于是提出了零本征值方法来诱导声子阻塞. 本文详细分析了此方法对声子阻塞的影响, 给出了最佳条件并解释了背后的物理机理. 不同于传统的声子阻塞和非传统的声子阻塞, 不管是强非线性还是弱非线性, 都可以实现声子的反聚束效应.

关键词:

Nanomechanical resonator has important applications in the field of high-precision detection because it has a high-Q factor, high vibration frequency, small size, and other excellent characteristics. Superconducting qubit has very large magnetic dipole moments, so it can be easily combined with nanomechanical resonator. Furthermore, the system parameters including frequency and coupling strength can be designed according to requirements beforehand, which makes a superconducting qubit an ideal artificial atom. Compared with natural atom, superconducting qubit has abundant energy levels. For these reasons, nanomechanical system has aroused wide interest in the engineering, electron, physical and other fields of science and technology. According to the recent research, a new approach to the zero eigenvalues of non-Hermitian Hamiltonian is applied to the optomechanical system. It was found that the scheme is superior to conventional photon blockade (CPB) and unconventional photon blockade (UPB) in the cavity quantum electrodynamics (QED) system. So we propose a scheme to induce phonon blockade in order to explore a new avenue to the research about phonon blockades in the quantum open system. We study the phonon blockade in an optomechanical system that a qubit is coupled with nanomechanical resonator (NAMR) driven by two external weakly driving fields respectively in this way. In this paper, the Hamiltonian of such a system can be treated by the non-Hermitian Hamiltonian and it can be described in the form of matrix. Then the phenomenon of phonon blockade occurs when all the eigenvalues in the form of matrix are equal to zero. It is found that strong phonon antibunching can be triggered in both strong and weak nonlinearity when we use the method which has been already used in a gain optical cavity system. The distinct result reflects the advantage of our approach which possesses some outstanding characters between the ordinary methods (conventional phonon blockade and unconventional phonon blockade). In addition, the effect of our avenue on phonon blockade is analyzed and also the distinction between the conventional phonon blockade (CPNB) and unconventional phonon blockade (UPNB) is compared with each other in detail. By analytical calculation, the optimal conditions are given and the underlying physical mechanism is explained. In the comparison between CPNB and UPNB, we show the superiority of our scheme through some graphs. Finally, we describe briefly the measurements of phonon blockade in the NAMR-qubit system via a superconducting cavity. The proposal may provide a theoretical way to guide the manufacture of phonon devices in the future. The results obtained here may have a great significance and application in the field of quantum information processing and precision measurement.

Keywords:

作者及机构信息

1.
南昌大学电子信息工程系, 南昌　330031

2.
清华大学物理系, 低维量子物理国家重点实验室, 北京　100084

3.
南昌大学高等研究院, 南昌　330031

通信作者: 廖庆洪, nculqh@163.com

Authors and contacts

1.
Department of Electronic Information Engineering, Nanchang University, Nanchang 330031, China

2.
State Key Laboratory of Low-Dimensional Quantum Physics, Department of Physics, Tsinghua Universtiy, Beijing 100084, China

3.
Institute for Advanced Study, Nanchang University, Nanchang 330031, China

Corresponding author: Liao Qing-Hong, nculqh@163.com

文章全文 : translate this paragraph

参考文献

[1]	You J Q, Nori F 2011 Nature 474 589 Google Scholar
[2]	Armour A D, Blencowe M P, Schwab K C 2002 Phys. Rev. Lett. 88 148301 Google Scholar
[3]	Blencowe M 2004 Phys. Rep. 395 159 Google Scholar
[4]	Cleland A N, Geller M R 2004 Phys. Rev. Lett. 93 070501 Google Scholar
[5]	O'Connell A D, Hofheinz M, Ansmann M, Bialczak R C, Lenander M, Lucero E, Neeley M, Sank D, Wang H, Weides M, Wenner J, Martinis J M, Cleland A N 2010 Nature 464 697 Google Scholar
[6]	Liu Y X, Miranowicz A, Gao Y B, Bajer J, Sun C P, Nori F 2010 Phys. Rev. A 82 032101 Google Scholar
[7]	Imamoglu A, Schmidt H, Woods G, Deutsch M 1997 Phys. Rev. Lett. 79 1467 Google Scholar
[8]	Barzanjeh S, Vitali D 2016 Phys. Rev. A 93 033846 Google Scholar
[9]	Zhou Y H, Shen H Z, Yi X X 2015 Phys. Rev. A 92 023838 Google Scholar
[10]	Zhou Y H, Shen H Z, Shao X Q, Yi X X 2016 Opt. Express 24 17332 Google Scholar
[11]	石海泉, 谢智强, 徐勋卫, 刘念华 2018 67 044203 Google Scholar Shi H Q, Xie Z Q, Xu X W, Liu N H 2018 Acta Phys. Sin. 67 044203 Google Scholar
[12]	Cai K, Pan Z W, Wang R X, Ruan D, Yin Z Q, Long G L 2018 Opt. Lett. 43 1163 Google Scholar
[13]	Miranowicz A, Bajer J, Lambert N, Liu Y X, Nori F 2016 Phys. Rev. A 93 013808 Google Scholar
[14]	Wang X, Miranowicz A, Li H R, Nori F 2016 Phys. Rev. A 93 063861 Google Scholar
[15]	Ramos T, Sudhir V, Stannigel K, Zoller P, Kippenberg T J 2013 Phys. Rev. Lett. 110 193602 Google Scholar
[16]	Xu X W, Chen A X, Liu Y X 2016 Phys. Rev. A 94 063853 Google Scholar
[17]	Gerace D, Savona V 2014 Phys. Rev. A 89 031803 Google Scholar
[18]	Lemonde M A, Didier N, Clerk A A 2014 Phys. Rev. A 90 063824 Google Scholar
[19]	Bamba M, Imamoğlu A, Carusotto I, Ciuti C 2011 Phys. Rev. A 83 021802 Google Scholar
[20]	Qian Z, Zhao M M, Hou B P, Zhao Y H 2017 Opt. Express 25 33097 Google Scholar
[21]	Shi H Q, Zhou X T, Xu X W, Liu N H 2018 Sci. Rep. 2018 2212
[22]	Kong C, Li S, You C, Xiong H, Wu Y 2018 Sci. Rep. 8 1060 Google Scholar
[23]	Li G, Xiao X, Li Y, Wang X 2018 Phys. Rev. A 97 023801 Google Scholar
[24]	Guan S, Bowen W P, Liu C, Duan Z 2017 EPL 119 58001 Google Scholar
[25]	Xie H, Liao C G, Shang X, Ye M Y, Lin X M 2017 Phys. Rev. A 96 013861 Google Scholar
[26]	Yin T S, Lu X Y, Wan L L, Bin S W, Wu Y 2018 Opt. Lett. 43 2050 Google Scholar
[27]	Debnath S, Linke N M, Wang S T, Figgatt C, Landsman K A, Duan L M, Monroe C 2018 Phys. Rev. Lett. 120 073001 Google Scholar
[28]	Li S S 2018 Int. J. Theor. Phys. 57 2359 Google Scholar
[29]	Shen H, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402 Google Scholar
[30]	Longhi S 2017 J. Phys. A: Math. Theor. 50 505201 Google Scholar
[31]	Park K W, Kim J, Jeong K 2016 Opt. Commun. 368 190 Google Scholar
[32]	Khantoul B, Bounames A, Maamache M 2017 Eur. Phys. J. Plus 132 258 Google Scholar
[33]	Baradaran M, Panahi H 2017 Chin. Phys. B 26 060301 Google Scholar
[34]	Maamache M, Lamri S, Cherbal O 2017 Ann. Phys. 378 150 Google Scholar
[35]	Sergi A, Giaquinta P 2016 Entropy 18 451 Google Scholar
[36]	Miao Y G, Xu Z M 2016 Phys. Lett. A 380 1805 Google Scholar
[37]	Ferry D K, Akis R, Burke A M, Knezevic I, Brunner R, Bird J P, Meisels R, Kuchar F, Bird J P 2013 Fortschr. Phys. 61 291 Google Scholar
[38]	Sergi A, Zloshchastiev K G 2016 J. Stat. Mech: Theory Exp. 2016 033102 Google Scholar
[39]	Chen J H, Fan H Y 2012 Front. Phys. 7 632 Google Scholar
[40]	Greenberg Y S, Shtygashev A A 2015 Phys. Rev. A 92 063835 Google Scholar
[41]	Zloshchastiev K G 2015 Eur. Phys. J. D 69 253 Google Scholar
[42]	Bagarello F, Lattuca M, Passante R, Rizzuto L, Spagnolo S 2015 Phys. Rev. A 91 042134 Google Scholar
[43]	Giusteri G G, Mattiotti F, Celardo G L 2015 Phys. Rev. B 91 094301 Google Scholar
[44]	Zhou Y H, Shen H Z, Zhang X Y, Yi X X 2018 Phys. Rev. A 97 043819 Google Scholar
[45]	Li J, Yu R, Wu Y 2015 Phys. Rev. A 92 053837 Google Scholar
[46]	Xing Y, Qi L, Cao J, Wang D Y, Bai C H, Wang H F, Zhu A D, Zhang S 2017 Phys. Rev. A 96 043810 Google Scholar
[47]	Peng B, Ozdemir S K, Rotter S, Yilmaz H, Liertzer M, Monifi F, Bender C M, Nori F, Yang L 2014 Science 346 328 Google Scholar
[48]	Chang L, Jiang X, Hua S, Yang C, Wen J, Jiang L, Li G, Wang G, Xiao M 2014 Nat. Photonics 8 524 Google Scholar
[49]	Hodaei H, Miri M A, Heinrich M, Christodoulides D N, Khajavikhan M 2014 Science 346 975 Google Scholar
[50]	Peng B, Özdemir Ş K, Lei F, Monifi F, Gianfreda M, Long G L, Fan S, Nori F, Bender C M, Yang L 2014 Nat. Phys. 10 394 Google Scholar
[51]	Feng L, Wong Z J, Ma R M, Wang Y, Zhang X 2014 Science 346 972 Google Scholar
[52]	Fan L R, Fong K Y, Poot M, Tang H X 2015 Nat. Commun. 6 5850
[53]	Xiong C, Fan L R, Sun X K, Tang H X 2013 Appl. Phys. Lett 102 021110
[54]	Winger M, Blasius T D, Alegre T P M, Safavi Naeini A H, Meenehan S, Cohen J, Stobbe S, Painter O 2011 Opt. Express 19 24905 Google Scholar
[55]	Zhang J, Peng B, Ozdemir S K, Liu Y X, Jing H, Lu X Y, Liu Y L, Yang L, Nori F 2015 Phys. Rev. B 92 115407
[56]	Bahl G, Tomes M, Marquardt F, Carmon T 2012 Nat. Phys. 8 203 Google Scholar
[57]	Dong C H, Shen Z, Zou C L, Zhang Y L, Fu W, Guo G C 2015 Nat. Commun. 6 6193
[58]	Kepesidis K V, Milburn T J, Huber J, Makris K G, Rotter S, Rabl P 2016 New J. Phys. 18 095003
[59]	Xu X W, Liu Y X, Sun C P, Li Y 2015 Phys. Rev. A 92 013852
[60]	刘玉龙2017 博士学位论文 (北京: 清华大学) Liu Y L 2017 Ph. D. Dissertation (Beijing: Tsinghua University) (in Chinese)
[61]	Didier N, Pugnetti S, Blanter Y M, Fazio R 2011 Phys. Rev. B 84 054503 Google Scholar

施引文献

图 1 NAMR-量子比特系统的物理模型图

Fig. 1. Schematic diagram of the nanomechanical resonator coupled with a qubit.

下载: 全尺寸图片幻灯片

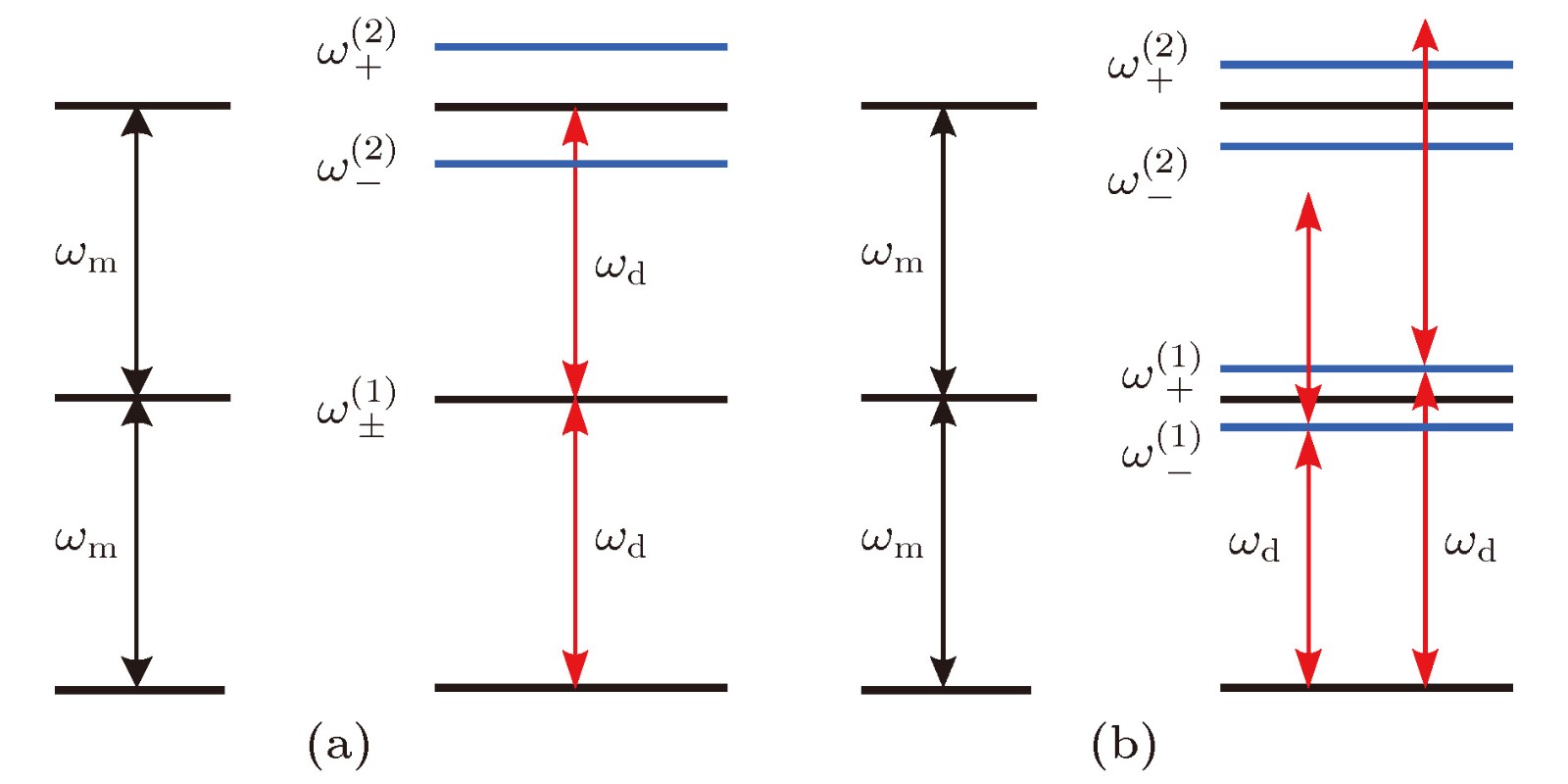
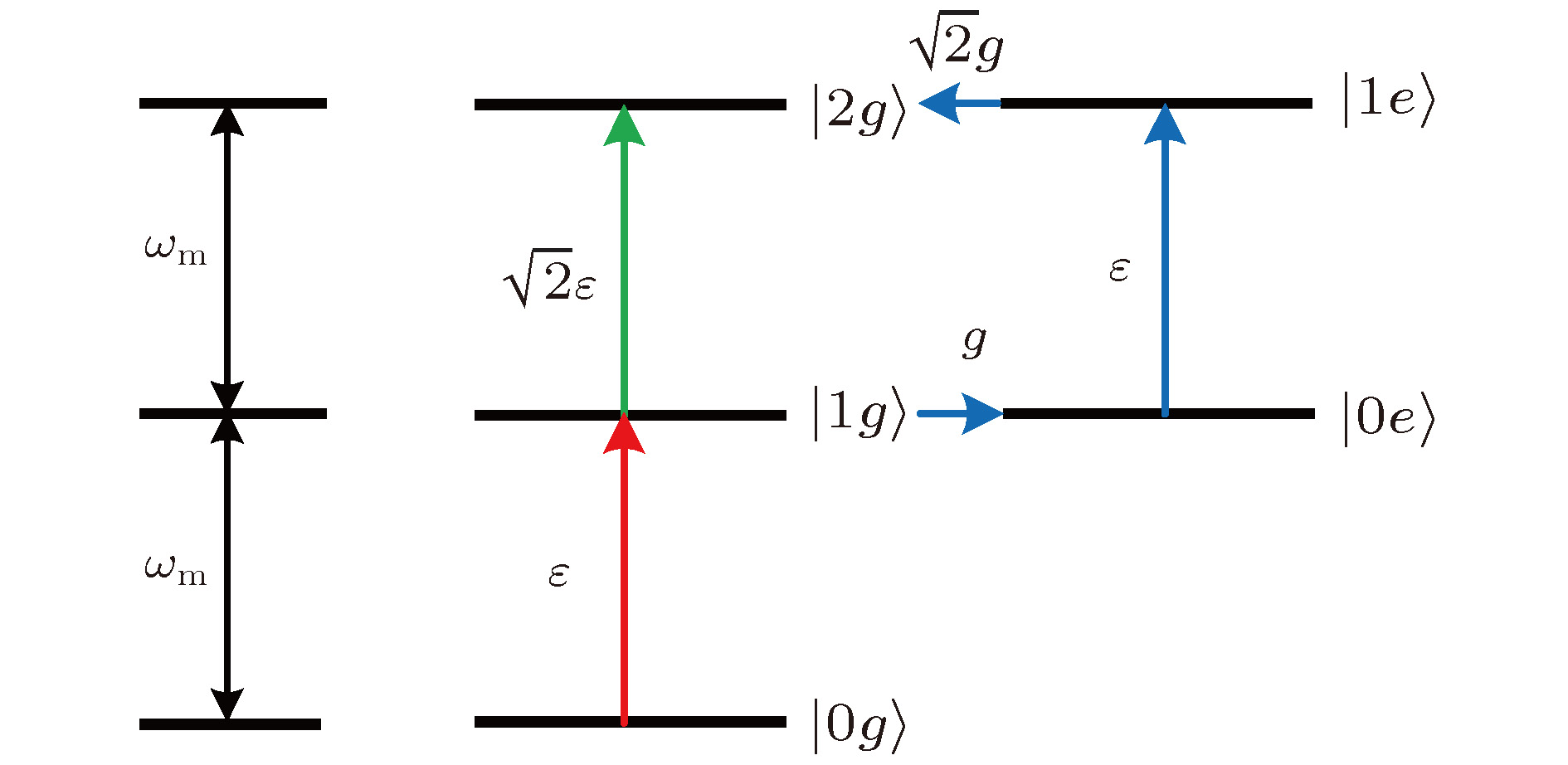
图 2 外加驱动场共振的情况下声子阻塞现象的能级图 (a)满足(8)式时的能级图, 其中$\omega _ \pm ^{\left( 1 \right)} = {\omega _{\rm{m}}}$和$\omega _ \pm ^{\left( 2 \right)} = 2{\omega _{\rm{m}}} \pm $ $2g + {\rm{i}}\dfrac{\gamma }{2}$; (b)满足(9)式时的能级图, 其中$\omega _ \pm ^{\left( 1 \right)} = {\omega _{\rm{m}}} \pm g$和$\omega _ \pm ^{\left( 2 \right)} = 2{\omega _{\rm{m}}} \pm \sqrt 2 g + {\rm{i}}\dfrac{\gamma }{2}$

Fig. 2. Schematic energy-level diagram explaining the occurrence of the phonon blockade by the driving field satisfying the resonance condition: (a) Energy-level diagram when Eqs. (8) are satisfied, where $\omega _ \pm ^{\left( 1 \right)} = {\omega _{\rm{m}}}$ and $\omega _ \pm ^{\left( 2 \right)} = 2{\omega _{\rm{m}}} \pm$ $ 2g + {\rm{i}}\dfrac{\gamma }{2}$; (b) energy-level diagram when Eqs. (9) are satisfied, where $\omega _ \pm ^{\left( 1 \right)} = {\omega _{\rm{m}}} \pm g$ and $\omega _ \pm ^{\left( 2 \right)} = 2{\omega _{\rm{m}}} \pm \sqrt 2 g + {\rm{i}}\dfrac{\gamma }{2}$.

下载: 全尺寸图片幻灯片

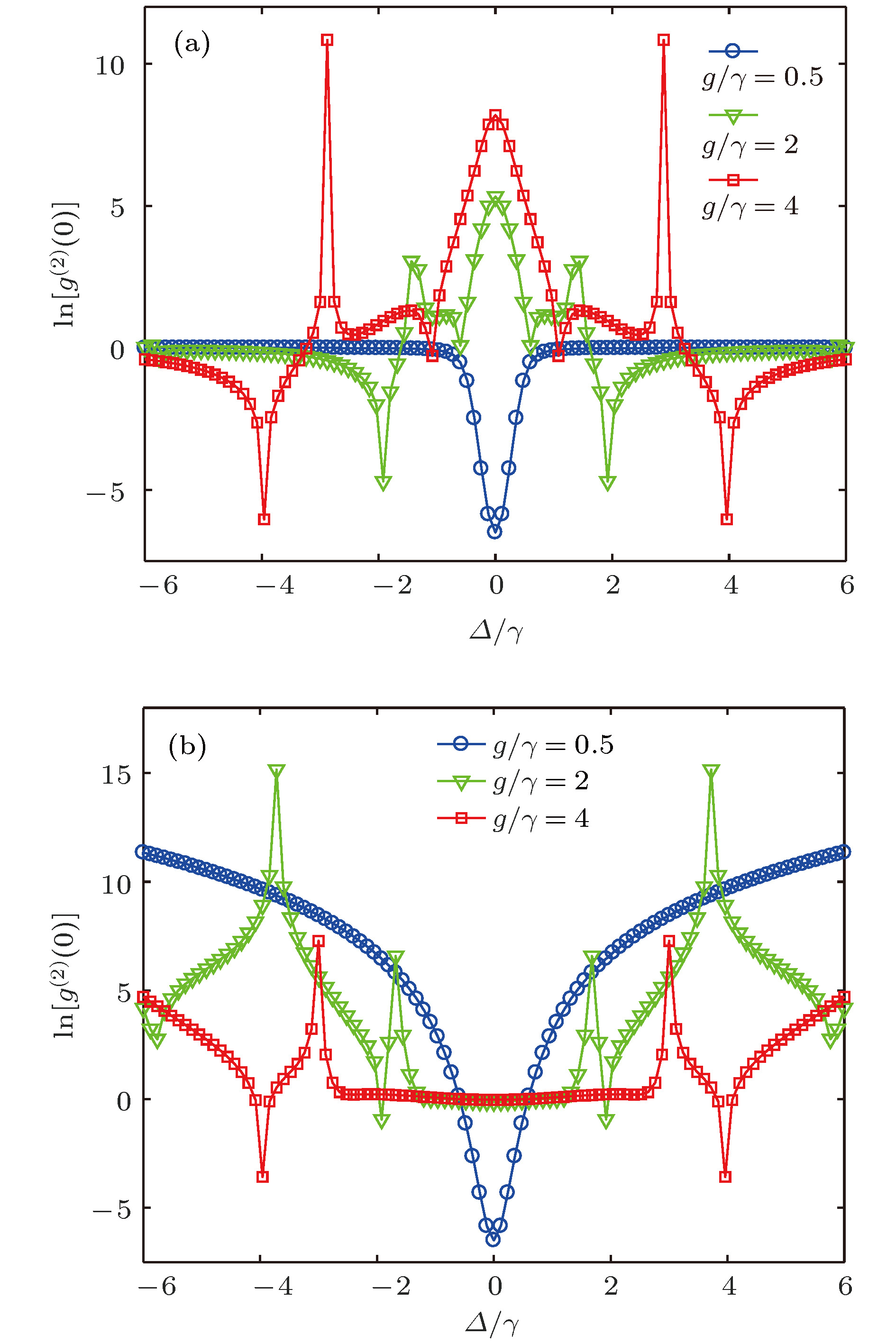
图 3 在不同的$g/\gamma $关系下, 二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right)$与$\varDelta /\gamma $的关系图　(a) $\kappa /\gamma = - 1$, $\varepsilon /\gamma = 0.1$, $\varOmega = 0$, $\varepsilon \ne 0$; (b) $\kappa /\gamma = - 1$, $\varOmega /\gamma = 0.1$, $\varepsilon = 0$, $\phi = 0$

Fig. 3. Logarithmic plot (of base e) of the zero-delay-time second-order correlation functions ${g^{\left( 2 \right)}}\left( 0 \right)$ as a function of $\varDelta /\gamma $ for different $g/\gamma $ with $\kappa /\gamma = - 1$: (a) $\varepsilon /\gamma = 0.1$, $\varOmega = 0$, $\varepsilon \ne 0$; (b) $\varOmega /\gamma = 0.1$, $\varepsilon = 0$, $\phi = 0$.

下载: 全尺寸图片幻灯片

图 4 UPNB能级图

Fig. 4. Schematic energy-level diagram of unconventional phonon blockade.

下载: 全尺寸图片幻灯片

图 5 本文方案与CPNB和UPNB的区别

Fig. 5. Different parameter range for the CPNB, the UPNB, and the present scheme.

下载: 全尺寸图片幻灯片

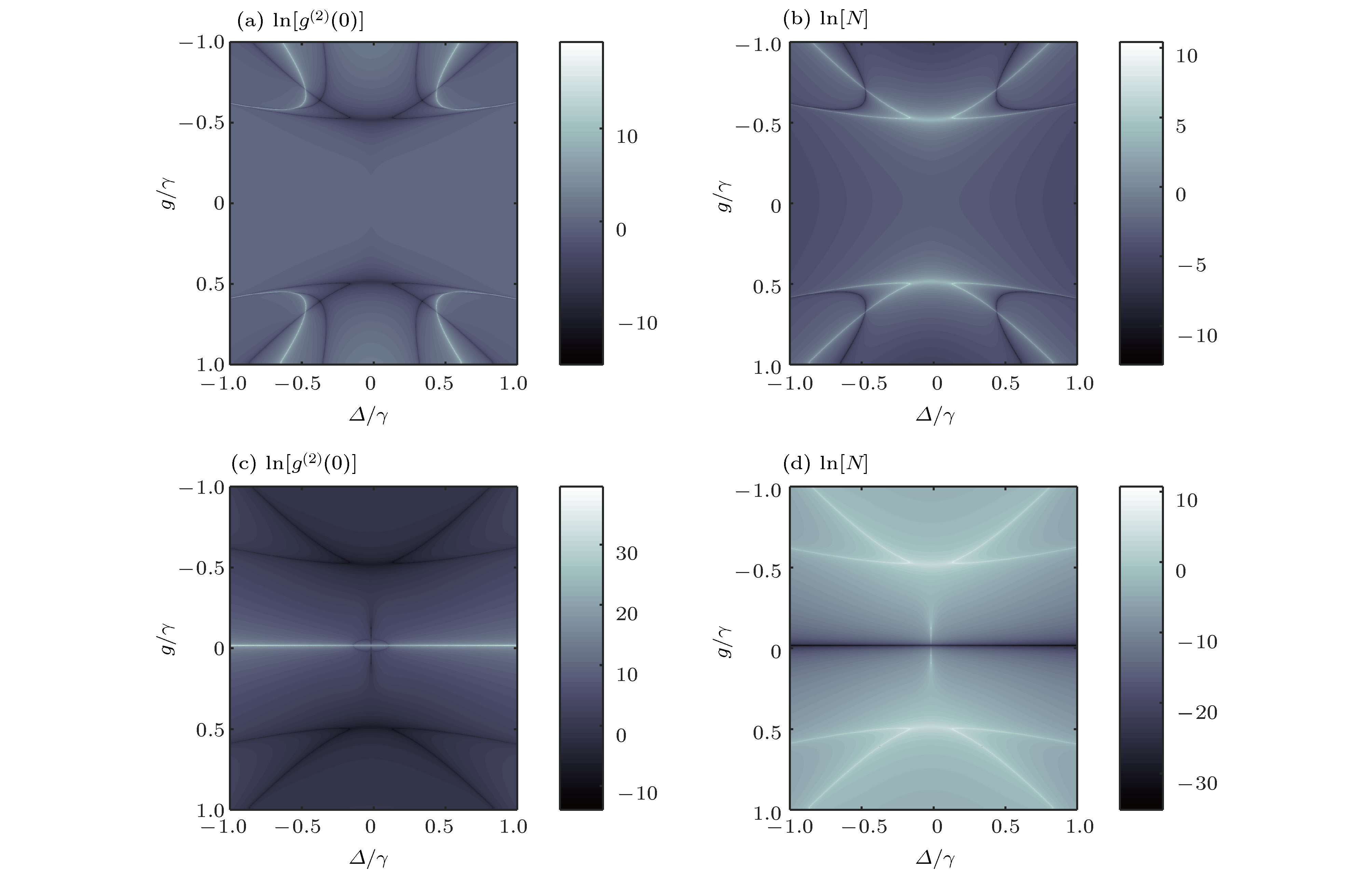
图 6 二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right)$ 和平均声子数$N = \left\langle {{a^ + }a} \right\rangle = \left[ {{\rm{Tr}}\left( {{\rho _s}{a^ + }a} \right)} \right]$的对数图像　(a), (b) $\varepsilon /\gamma = 0.1$, $\varOmega = 0$; (c), (d) $\varOmega /\gamma = 0.1$, $\varepsilon = 0$, $\phi = 0$. 其他参数为$\kappa /\gamma = - 1$.

Fig. 6. The logarithmic plot (of base e) of the zero-delay-time second-order correlation functions ${g^{\left( 2 \right)}}\left( 0 \right)$ and average photon numberN: (a) and (b) $\varepsilon /\gamma = 0.1$, $\varOmega = 0$; (c) and (d) $\varOmega /\gamma = 0.1$, $\varepsilon = 0$, $\phi = 0$. The shared parameters: $\kappa /\gamma = - 1$.

下载: 全尺寸图片幻灯片

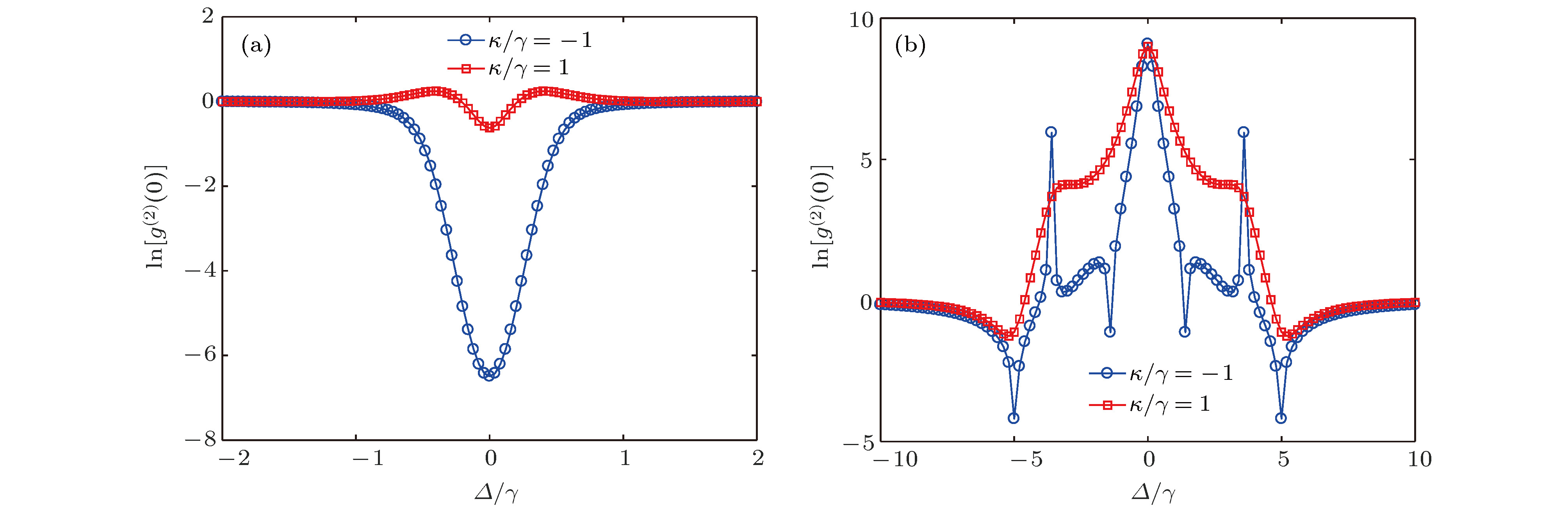
图 7 二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right)$(对数)与$\varDelta /\gamma $的关系图, 其中$\varepsilon /\gamma = 0.1$, $\varOmega = 0$ (a) $g/\gamma = 0.5$, $\kappa /\gamma = - 1$(本文方案), $\kappa /\gamma = 1$(UPNB); (b) $g/\gamma = 5$, $\kappa /\gamma = - 1$(本文方案), $\kappa /\gamma = 1$(CPNB)

Fig. 7. The logarithmic plot (of base e) of the zero-delay-time second-order correlation functions ${g^{\left( 2 \right)}}\left( 0 \right)$ as a function of $\varDelta /\gamma $. The shared parameters: $\varepsilon /\gamma = 0.1$, $\varOmega = 0$. Other parameters: (a) $g/\gamma = 0.5$, $\kappa /\gamma = - 1$(our scheme), $\kappa /\gamma = 1$ (UPNB); (b) $g/\gamma = 5$, $\kappa /\gamma = - 1$(our scheme), $\kappa /\gamma = 1$(CPNB).

下载: 全尺寸图片幻灯片

图 8 二阶关联函数${g^{\left( 2 \right)}}\left( 0 \right)$(对数)与$\varDelta /\gamma $的关系图, $\varOmega \ne 0$, $\varepsilon = 0$, $\phi = 0$ (a) $\varOmega /\gamma = 0.1$, $g/\gamma = 0.5$, $\kappa /\gamma = - 1$(本文方案), $\kappa /\gamma = 1$(UPNB); (b) $\varOmega /\gamma = 2$, $g/\gamma = 10$, $\kappa /\gamma = - 1$(本文方案), $\kappa /\gamma = 1$(CPNB)

Fig. 8. The logarithmic plot (of base e) of the zero-delay-time second-order correlation functions ${g^{\left( 2 \right)}}\left( 0 \right)$ as a function of $\varDelta /\gamma $: $\varOmega \ne 0$, $\varepsilon = 0$, $\phi = 0$. Other parameters: (a) $\varOmega /\gamma = 0.1$, $g/\gamma = 0.5$, $\kappa /\gamma = - 1$(our scheme), $\kappa /\gamma = 1$ (UPNB); (b) $\varOmega /\gamma = 2$, $g/\gamma = 10$, $\kappa /\gamma = - 1$(our scheme), $\kappa /\gamma = 1$(CPNB).

下载: 全尺寸图片幻灯片

图 9 声子统计特性探测模型

Fig. 9. The detecting model of the statistical properties of the phonons.

下载: 全尺寸图片幻灯片

map

[1]	You J Q, Nori F 2011 Nature 474 589 Google Scholar
[2]	Armour A D, Blencowe M P, Schwab K C 2002 Phys. Rev. Lett. 88 148301 Google Scholar
[3]	Blencowe M 2004 Phys. Rep. 395 159 Google Scholar
[4]	Cleland A N, Geller M R 2004 Phys. Rev. Lett. 93 070501 Google Scholar
[5]	O'Connell A D, Hofheinz M, Ansmann M, Bialczak R C, Lenander M, Lucero E, Neeley M, Sank D, Wang H, Weides M, Wenner J, Martinis J M, Cleland A N 2010 Nature 464 697 Google Scholar
[6]	Liu Y X, Miranowicz A, Gao Y B, Bajer J, Sun C P, Nori F 2010 Phys. Rev. A 82 032101 Google Scholar
[7]	Imamoglu A, Schmidt H, Woods G, Deutsch M 1997 Phys. Rev. Lett. 79 1467 Google Scholar
[8]	Barzanjeh S, Vitali D 2016 Phys. Rev. A 93 033846 Google Scholar
[9]	Zhou Y H, Shen H Z, Yi X X 2015 Phys. Rev. A 92 023838 Google Scholar
[10]	Zhou Y H, Shen H Z, Shao X Q, Yi X X 2016 Opt. Express 24 17332 Google Scholar
[11]	石海泉, 谢智强, 徐勋卫, 刘念华 2018 67 044203 Google Scholar Shi H Q, Xie Z Q, Xu X W, Liu N H 2018 Acta Phys. Sin. 67 044203 Google Scholar
[12]	Cai K, Pan Z W, Wang R X, Ruan D, Yin Z Q, Long G L 2018 Opt. Lett. 43 1163 Google Scholar
[13]	Miranowicz A, Bajer J, Lambert N, Liu Y X, Nori F 2016 Phys. Rev. A 93 013808 Google Scholar
[14]	Wang X, Miranowicz A, Li H R, Nori F 2016 Phys. Rev. A 93 063861 Google Scholar
[15]	Ramos T, Sudhir V, Stannigel K, Zoller P, Kippenberg T J 2013 Phys. Rev. Lett. 110 193602 Google Scholar
[16]	Xu X W, Chen A X, Liu Y X 2016 Phys. Rev. A 94 063853 Google Scholar
[17]	Gerace D, Savona V 2014 Phys. Rev. A 89 031803 Google Scholar
[18]	Lemonde M A, Didier N, Clerk A A 2014 Phys. Rev. A 90 063824 Google Scholar
[19]	Bamba M, Imamoğlu A, Carusotto I, Ciuti C 2011 Phys. Rev. A 83 021802 Google Scholar
[20]	Qian Z, Zhao M M, Hou B P, Zhao Y H 2017 Opt. Express 25 33097 Google Scholar
[21]	Shi H Q, Zhou X T, Xu X W, Liu N H 2018 Sci. Rep. 2018 2212
[22]	Kong C, Li S, You C, Xiong H, Wu Y 2018 Sci. Rep. 8 1060 Google Scholar
[23]	Li G, Xiao X, Li Y, Wang X 2018 Phys. Rev. A 97 023801 Google Scholar
[24]	Guan S, Bowen W P, Liu C, Duan Z 2017 EPL 119 58001 Google Scholar
[25]	Xie H, Liao C G, Shang X, Ye M Y, Lin X M 2017 Phys. Rev. A 96 013861 Google Scholar
[26]	Yin T S, Lu X Y, Wan L L, Bin S W, Wu Y 2018 Opt. Lett. 43 2050 Google Scholar
[27]	Debnath S, Linke N M, Wang S T, Figgatt C, Landsman K A, Duan L M, Monroe C 2018 Phys. Rev. Lett. 120 073001 Google Scholar
[28]	Li S S 2018 Int. J. Theor. Phys. 57 2359 Google Scholar
[29]	Shen H, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402 Google Scholar
[30]	Longhi S 2017 J. Phys. A: Math. Theor. 50 505201 Google Scholar
[31]	Park K W, Kim J, Jeong K 2016 Opt. Commun. 368 190 Google Scholar
[32]	Khantoul B, Bounames A, Maamache M 2017 Eur. Phys. J. Plus 132 258 Google Scholar
[33]	Baradaran M, Panahi H 2017 Chin. Phys. B 26 060301 Google Scholar
[34]	Maamache M, Lamri S, Cherbal O 2017 Ann. Phys. 378 150 Google Scholar
[35]	Sergi A, Giaquinta P 2016 Entropy 18 451 Google Scholar
[36]	Miao Y G, Xu Z M 2016 Phys. Lett. A 380 1805 Google Scholar
[37]	Ferry D K, Akis R, Burke A M, Knezevic I, Brunner R, Bird J P, Meisels R, Kuchar F, Bird J P 2013 Fortschr. Phys. 61 291 Google Scholar
[38]	Sergi A, Zloshchastiev K G 2016 J. Stat. Mech: Theory Exp. 2016 033102 Google Scholar
[39]	Chen J H, Fan H Y 2012 Front. Phys. 7 632 Google Scholar
[40]	Greenberg Y S, Shtygashev A A 2015 Phys. Rev. A 92 063835 Google Scholar
[41]	Zloshchastiev K G 2015 Eur. Phys. J. D 69 253 Google Scholar
[42]	Bagarello F, Lattuca M, Passante R, Rizzuto L, Spagnolo S 2015 Phys. Rev. A 91 042134 Google Scholar
[43]	Giusteri G G, Mattiotti F, Celardo G L 2015 Phys. Rev. B 91 094301 Google Scholar
[44]	Zhou Y H, Shen H Z, Zhang X Y, Yi X X 2018 Phys. Rev. A 97 043819 Google Scholar
[45]	Li J, Yu R, Wu Y 2015 Phys. Rev. A 92 053837 Google Scholar
[46]	Xing Y, Qi L, Cao J, Wang D Y, Bai C H, Wang H F, Zhu A D, Zhang S 2017 Phys. Rev. A 96 043810 Google Scholar
[47]	Peng B, Ozdemir S K, Rotter S, Yilmaz H, Liertzer M, Monifi F, Bender C M, Nori F, Yang L 2014 Science 346 328 Google Scholar
[48]	Chang L, Jiang X, Hua S, Yang C, Wen J, Jiang L, Li G, Wang G, Xiao M 2014 Nat. Photonics 8 524 Google Scholar
[49]	Hodaei H, Miri M A, Heinrich M, Christodoulides D N, Khajavikhan M 2014 Science 346 975 Google Scholar
[50]	Peng B, Özdemir Ş K, Lei F, Monifi F, Gianfreda M, Long G L, Fan S, Nori F, Bender C M, Yang L 2014 Nat. Phys. 10 394 Google Scholar
[51]	Feng L, Wong Z J, Ma R M, Wang Y, Zhang X 2014 Science 346 972 Google Scholar
[52]	Fan L R, Fong K Y, Poot M, Tang H X 2015 Nat. Commun. 6 5850
[53]	Xiong C, Fan L R, Sun X K, Tang H X 2013 Appl. Phys. Lett 102 021110
[54]	Winger M, Blasius T D, Alegre T P M, Safavi Naeini A H, Meenehan S, Cohen J, Stobbe S, Painter O 2011 Opt. Express 19 24905 Google Scholar
[55]	Zhang J, Peng B, Ozdemir S K, Liu Y X, Jing H, Lu X Y, Liu Y L, Yang L, Nori F 2015 Phys. Rev. B 92 115407
[56]	Bahl G, Tomes M, Marquardt F, Carmon T 2012 Nat. Phys. 8 203 Google Scholar
[57]	Dong C H, Shen Z, Zou C L, Zhang Y L, Fu W, Guo G C 2015 Nat. Commun. 6 6193
[58]	Kepesidis K V, Milburn T J, Huber J, Makris K G, Rotter S, Rabl P 2016 New J. Phys. 18 095003
[59]	Xu X W, Liu Y X, Sun C P, Li Y 2015 Phys. Rev. A 92 013852
[60]	刘玉龙2017 博士学位论文 (北京: 清华大学) Liu Y L 2017 Ph. D. Dissertation (Beijing: Tsinghua University) (in Chinese)
[61]	Didier N, Pugnetti S, Blanter Y M, Fazio R 2011 Phys. Rev. B 84 054503 Google Scholar

[1]	武博, 林沂, 吴逢川, 陈孝樟, 安强, 刘燚, 付云起. 基于平行板谐振器的量子微波电场测量技术. , 2023, 72(3): 034204. doi: 10.7498/aps.72.20221582
[2]	吴宇恺, 段路明. 离子阱量子计算规模化的研究进展. , 2023, 72(23): 230302. doi: 10.7498/aps.72.20231128
[3]	熊凡, 陈永聪, 敖平. 热噪声环境下偶极场驱动的量子比特动力学. , 2023, 72(17): 170302. doi: 10.7498/aps.72.20230625
[4]	徐达, 王逸璞, 李铁夫, 游建强. 微波驱动下超导量子比特与磁振子的相干耦合. , 2022, 71(15): 150302. doi: 10.7498/aps.71.20220260
[5]	高飞, 冯琦, 王霆, 张建军. 硅(001)图形衬底上锗硅纳米线的定位生长. , 2020, 69(2): 028102. doi: 10.7498/aps.69.20191407
[6]	乌云其木格, 韩超, 额尔敦朝鲁. 色散和杂质对双参量非对称高斯势量子点量子比特的影响. , 2019, 68(24): 247803. doi: 10.7498/aps.68.20190960
[7]	刘超, 邬云文. Λ型三能级原子与两个谐振器的量子相位门. , 2018, 67(17): 170302. doi: 10.7498/aps.67.20180830
[8]	赵虎, 李铁夫, 刘其春, 张颖珊, 刘建设, 陈炜. 三维传输子量子比特的退相干参数表征. , 2014, 63(22): 220305. doi: 10.7498/aps.63.220305
[9]	夏建平, 任学藻, 丛红璐, 王旭文, 贺树. 两量子比特与谐振子相耦合系统中的量子纠缠演化特性. , 2012, 61(1): 014208. doi: 10.7498/aps.61.014208
[10]	赵翠兰, 丛银川. 球壳量子点中极化子和量子比特的声子效应. , 2012, 61(18): 186301. doi: 10.7498/aps.61.186301
[11]	高吉, 杨涛, 马平, 戴远东. 用于高温射频超导量子干涉器的介质谐振器的性质研究. , 2010, 59(7): 5044-5048. doi: 10.7498/aps.59.5044
[12]	姜福仕, 赵翠兰. 量子环中量子比特的声子效应. , 2009, 58(10): 6786-6790. doi: 10.7498/aps.58.6786
[13]	陈英杰, 肖景林. 抛物线性限制势二能级系统量子点量子比特的温度效应. , 2008, 57(11): 6758-6762. doi: 10.7498/aps.57.6758
[14]	尹辑文, 肖景林, 于毅夫, 王子武. 库仑势对抛物量子点量子比特消相干的影响. , 2008, 57(5): 2695-2698. doi: 10.7498/aps.57.2695
[15]	刘云飞, 肖景林. LA声子对激子qubit纯退相干的影响. , 2008, 57(6): 3324-3327. doi: 10.7498/aps.57.3324
[16]	高宽云, 赵翠兰. 量子环中量子比特的性质. , 2008, 57(7): 4446-4449. doi: 10.7498/aps.57.4446
[17]	董庆瑞. 磁场方向调制的InAs量子点分子量子比特. , 2007, 56(9): 5436-5440. doi: 10.7498/aps.56.5436
[18]	李艳玲, 冯健, 孟祥国, 梁宝龙. 量子比特的普适远程翻转和克隆. , 2007, 56(10): 5591-5596. doi: 10.7498/aps.56.5591
[19]	王子武, 肖景林. 抛物线性限制势量子点量子比特及其光学声子效应. , 2007, 56(2): 678-682. doi: 10.7498/aps.56.678
[20]	胡学宁, 李新奇. 量子点接触对单电子量子态的量子测量. , 2006, 55(7): 3259-3264. doi: 10.7498/aps.55.3259

计量

文章访问数: 7806
PDF下载量: 101
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

纳米机械谐振器耦合量子比特非厄米哈密顿量诱导的声子阻塞