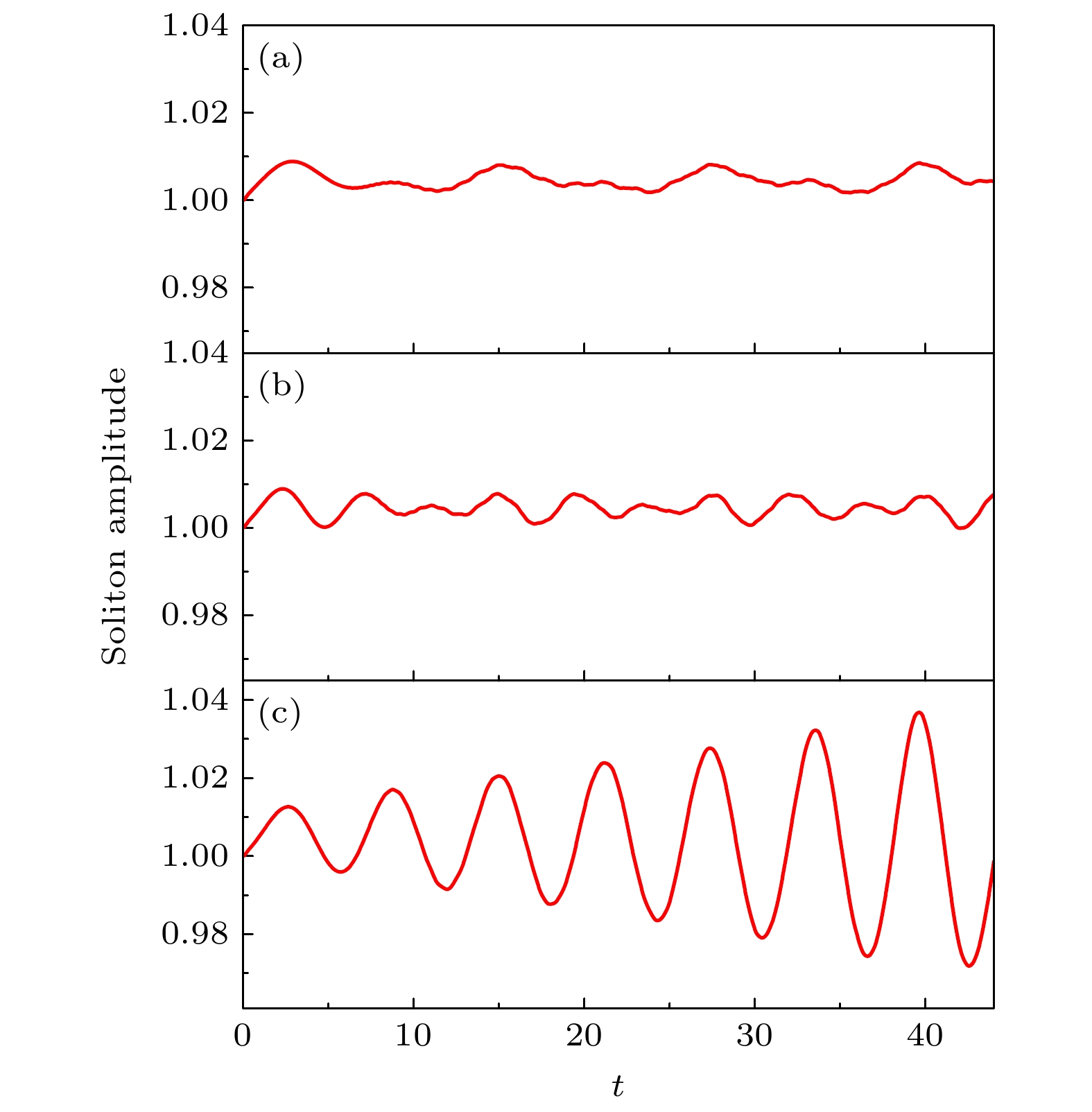
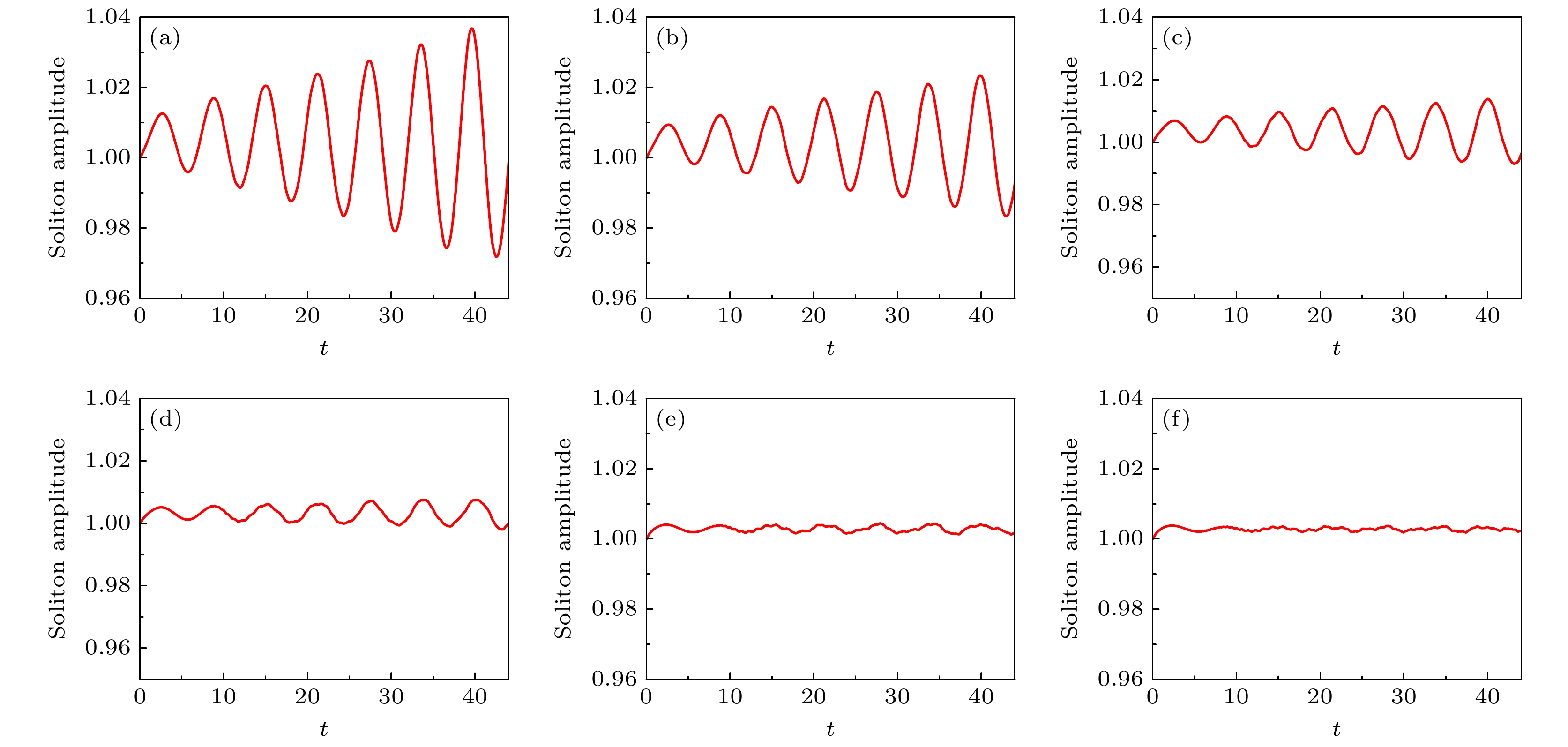
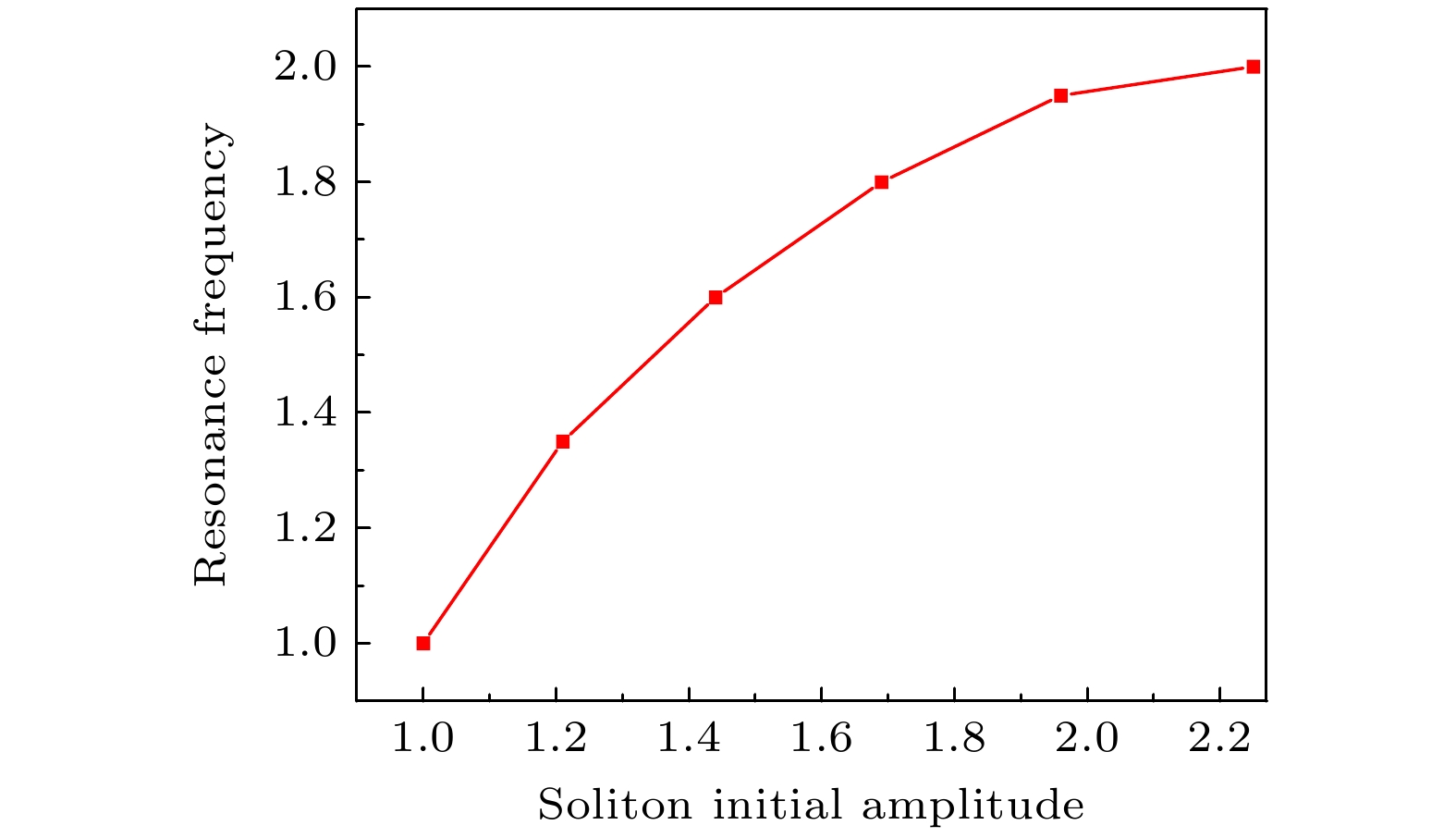
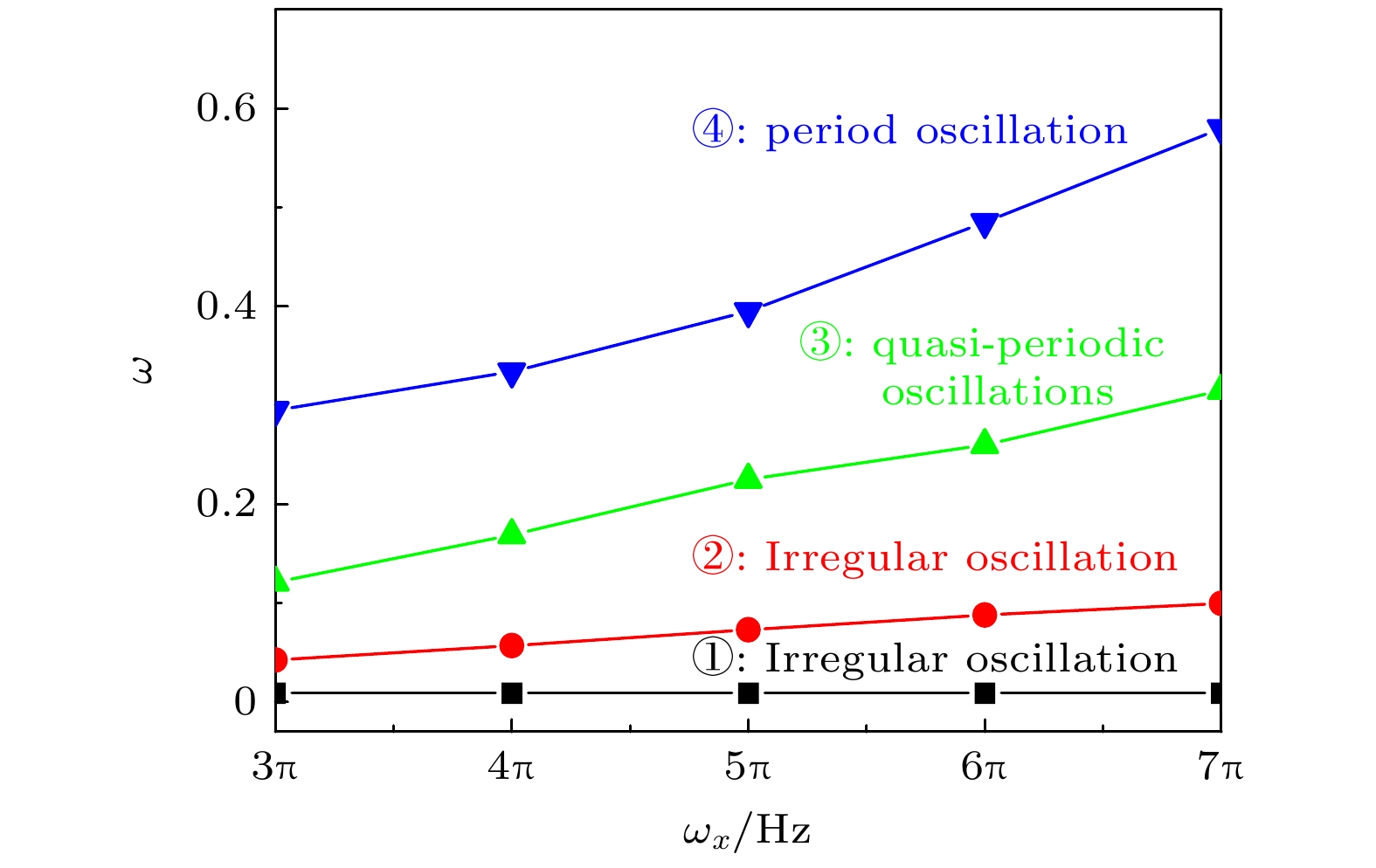
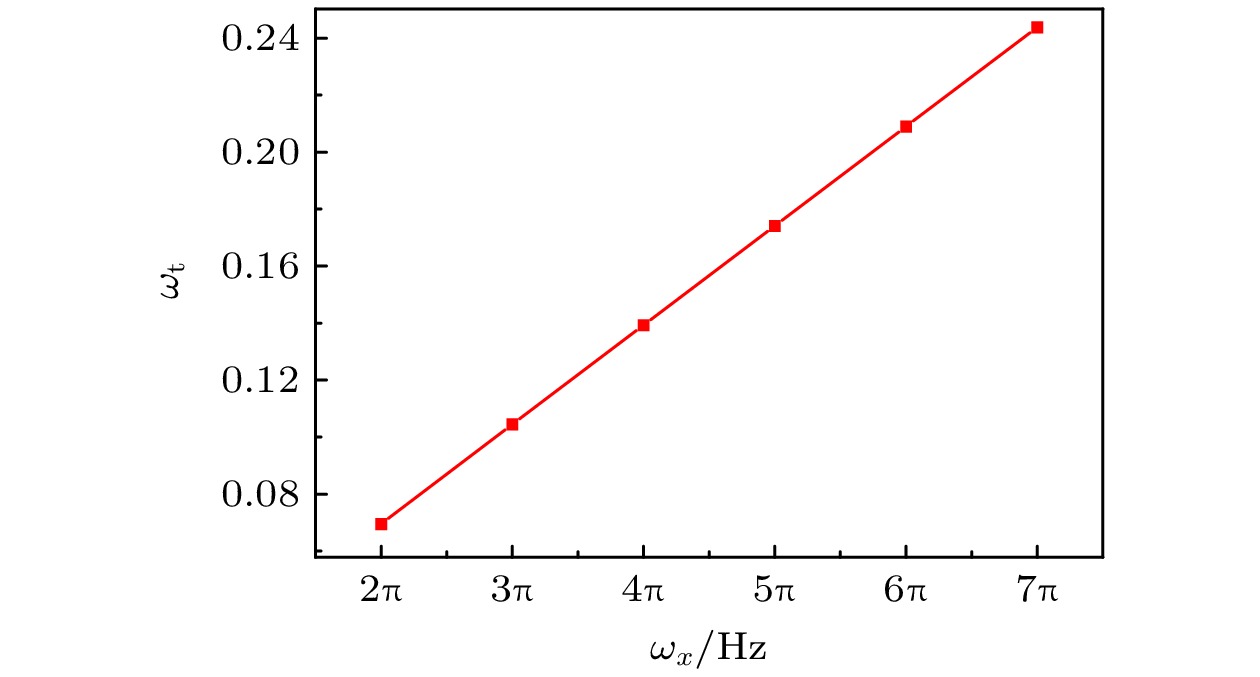
-
Kapitza’s pendulum is an inverted pendulum that is dynamically stabilized by rapidly driving its pivot point. Many applications of Kapitza stabilization in quantum systems have been proposed, such as optical molasses, the stability of optical resonators, preparation of molecular ions, the breaking of translation symmetry, the periodically driven sine-Gordon model, polariton Rabi oscillation, and the stabilization of bright solitons in a Bose-Einstein condensate. In particular, Kapitza stabilization can be used to trap particles. The most notable example of such an application is the Paul trap. Recently, the Kapitza trap was created by superimposing time-tuned focused laser beams to produce a periodically driven harmonic potential for ultracold atomic gases. This work opens up new possibilities to study Floquet systems of ultracold atomic gases. So we consider the periodically driven harmonic potential, and investigate the properties of soliton in ultracold atomic gases by numerical simulations. It is found interestingly that when a soliton is located at the center of the harmonic potential, a resonance phenomenon of soliton amplitude oscillation occurs at a specific driven frequency. In addition, the oscillation amplitude increases with the increase of the trapping frequency of the harmonic potential, and the resonance frequency increases with theaugment of soliton initial amplitude. The change of driven frequency and initial phase has a significant effect on soliton motion when the soliton is located at the edge of the harmonic potential. When the initial phase is zero, there is a characteristic driven frequency. For the case where the driven frequency is equal to the characteristic frequency, soliton motion exhibits periodic oscillations. For the case where the driven frequency is slightly lower than the characteristic frequency, the resonance of soliton oscillation can be found. When the driven frequency is slightly higher than the characteristic frequency, the anti-resonance of soliton oscillation can be found. In addition, it is found that the characteristic driven frequency increases linearly with the increase of the trapping frequency of the harmonic potential. When the initial phase is not equal to zero, the irregular oscillation, quasi-periodic oscillation, and periodic oscillation can be observed with the increase of driven frequency. When the driven frequency is equal to a specific value, the resonance of soliton oscillation can also obtained. Furthermore, the fast driving has no effect on the motion trajectory of solitons. These results can help to precisely control ultracold atomic gases. -
Keywords:
- ultracold atomic gases /
- soliton /
- periodic modulation
[1] Weitenberg C, Simonet J 2021 Nat. Phys. 17 1342
Google Scholar
[2] Bukov M, D’Alessio L, Polkovnikov A 2015 Adv. Phys. 64 139
Google Scholar
[3] Eckardt A 2017 Rev. Mod. Phys. 89 011004
Google Scholar
[4] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006
Google Scholar
[5] Oka T, Kitamura S 2019 Annu. Rev. Condens. Matter Phys. 10 387
Google Scholar
[6] 焦宸, 简粤, 张爱霞, 薛具奎 2023 72 060302
Google Scholar
Jiao C, Jian Y, Zhang A X, Xue J K 2023 Acta Phys. Sin. 72 060302
Google Scholar
[7] Zhao W L, Liu J 2024 Phys. Rev. A 109 052215
Google Scholar
[8] Zhang L, Ke Y G, Lin L, Lee C H 2024 Phys. Rev. B 109 184313
Google Scholar
[9] Chen L, Zhu F, Zhang Y B, Pu H 2025 Phys. Rev. A 111 L011303
Google Scholar
[10] Kamal H, Kemp J, He Y C, Fuji Y, Aidelsburger M, Zoller P, Yao N Y 2024 Phys. Rev. Lett. 133 163403
Google Scholar
[11] Zhou L W, Chen C, Gong J B 2016 Phys. Rev. B 94 075443
Google Scholar
[12] Kapitza P L 1951 Usp. Fiz. Nauk 44 7
Google Scholar
[13] Bagnato V S, Bigelow N P, Surdutovich G I, Zílio S C 1994 Opt. Lett. 19 1568
Google Scholar
[14] Torosov B T, Della Valle G, Longhi S 2013 Phys. Rev. A 88 052106
Google Scholar
[15] Gilary I, Moiseyev N, Rahav S, Fishman S 2003 J. Phys. A: Math. Gen. 36 L409
[16] Citro R, Dalla Torre E G, D’Alessio L, Polkovnikov A, Babadi M, Oka T, Demler E 2015 Ann. Phys. 360 694
Google Scholar
[17] Smirnova O, Spanner M, Ivanov M Y 2003 Phys. Rev. Lett. 90 243001
Google Scholar
[18] Rajagopal S V, Fujiwara K M, Senaratne R, Singh K, Geiger Z A, Weld D M 2017 Ann. Phys. 529 1700008
Google Scholar
[19] Voronova N S, Elistratov A A, Lozovik Y E 2016 Phys. Rev. B 94 045413
Google Scholar
[20] Martin J, Georgeot B, Guéry-Odelin D, Shepelyansky D L 2018 Phys. Rev. A 97 023607
Google Scholar
[21] Park S J, Andersen H K, Mai S, Arlt J, Sherson J F 2012 Phys. Rev. A 85 033626
Google Scholar
[22] Eckardt A, Weiss C, Holthaus M 2005 Phys. Rev. Lett. 95 260404
Google Scholar
[23] 何章明, 张志强 2016 65 110502
Google Scholar
He Z M, Zhang Z Q 2016 Acta Phys. Sin. 65 110502
Google Scholar
[24] Abdullaev F Kh, Caputo J G, Kraenkel R A, Malomed Boris A 2003 Phys. Rev. A 67 013605
Google Scholar
[25] Goldman N, Dalibard J 2014 Phys. Rev. X 4 031027
[26] Jiang J, Bernhart E, Röhrle M, Benary J, Beck M, Baals C, Ott H 2023 Phys. Rev. Lett. 131 033401
Google Scholar
[27] Zhang X F, Yang Q, Zhang J F, Chen X Z, Liu W M 2008 Phys. Rev. A 77 023613
Google Scholar
[28] Kengne E, Liu W M 2018 Phys. Rev. E 98 012204
Google Scholar
-
图 1 超冷原子气体的概率密度演化图
Fig. 1. The evolution of the ultracold atom gases probability density.
图 2 不同驱动频率下孤子的幅度变化图 (a) $\omega = 0.5$; (b) $\omega = 1.5$; (c) $\omega = 1.0$
Fig. 2. The change of soliton amplitude under different driven frequency: (a) $\omega = 0.5$; (b) $\omega = 1.5$; (c) $\omega = 1.0$.
图 3 不同的囚禁频率下的孤子的幅度变化图 (a) ${\omega _x} = 5\pi \; {\text{Hz}}$; (b) ${\omega _x} = 4\pi \; {\text{Hz}}$; (c) ${\omega _x} = 3\pi \; {\text{Hz}}$; (d) ${\omega _x} = 2\pi \; {\text{Hz}}$; (e) ${\omega _x} = $$ 1\pi \; {\text{Hz}}$; (f) ${\omega _x} = 0.9\pi \; {\text{Hz}}$
Fig. 3. The change of soliton amplitude under different trapping frequency of harmonic potential: (a) ${\omega _x} = 5\pi \; {\text{Hz}}$; (b) ${\omega _x} = 4\pi \; {\text{Hz}}$; (c) ${\omega _x} = 3\pi \; {\text{Hz}}$; (d) ${\omega _x} = 2\pi \; {\text{Hz}}$; (e) ${\omega _x} = 1\pi \; {\text{Hz}}$; (f) ${\omega _x} = 0.9\pi \; {\text{Hz}}$.
图 4 共振频率随孤子的初始幅度变化图
Fig. 4. The resonance frequency varying with the soliton initial amplitude.
图 5 超冷原子气体中孤子运动的周期性振荡
Fig. 5. The periodic oscillation of soliton in the ultracold atom gases.
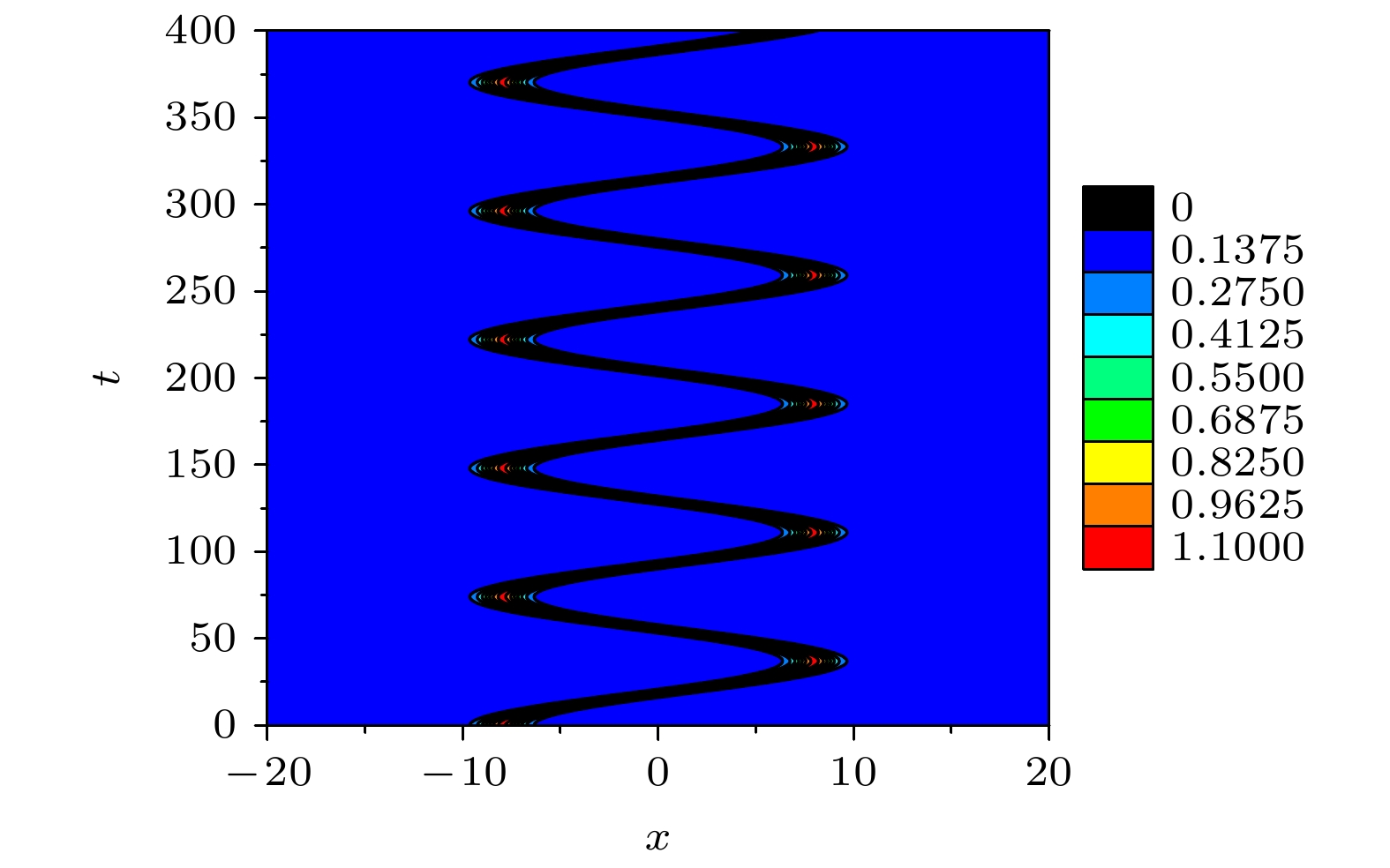
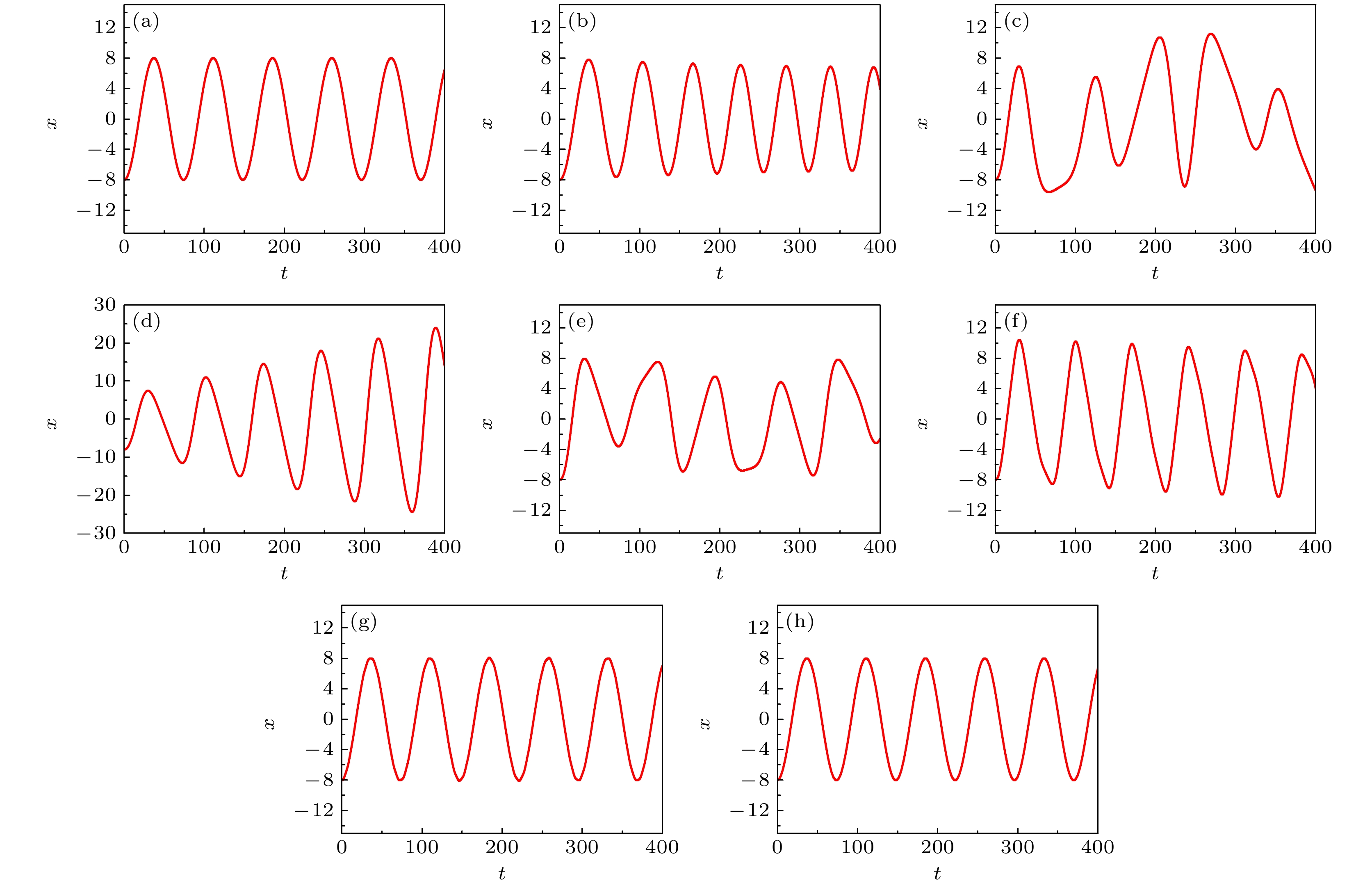
图 6 $\phi = 1.57$时不同驱动频率下孤子运动轨迹图 (a) $\omega = 0$; (b) $\omega = 0.003$; (c) $\omega = 0.06$; (d) $\omega = 0.088$; (e) $\omega = 0.1$; (f) $\omega = $$ 0.27$; (g) $\omega = 1.0$; (h) $\omega = 2.0$
Fig. 6. The trajectories of soliton with different driven frequencies at $\phi = 1.57$: (a) $\omega = 0$; (b) $\omega = 0.003$; (c) $\omega = 0.06$; (d) $\omega = $$ 0.088$; (e) $\omega = 0.1$; (f) $\omega = 0.27$; (g) $\omega = 1.0$; (h) $\omega = 2.0$.
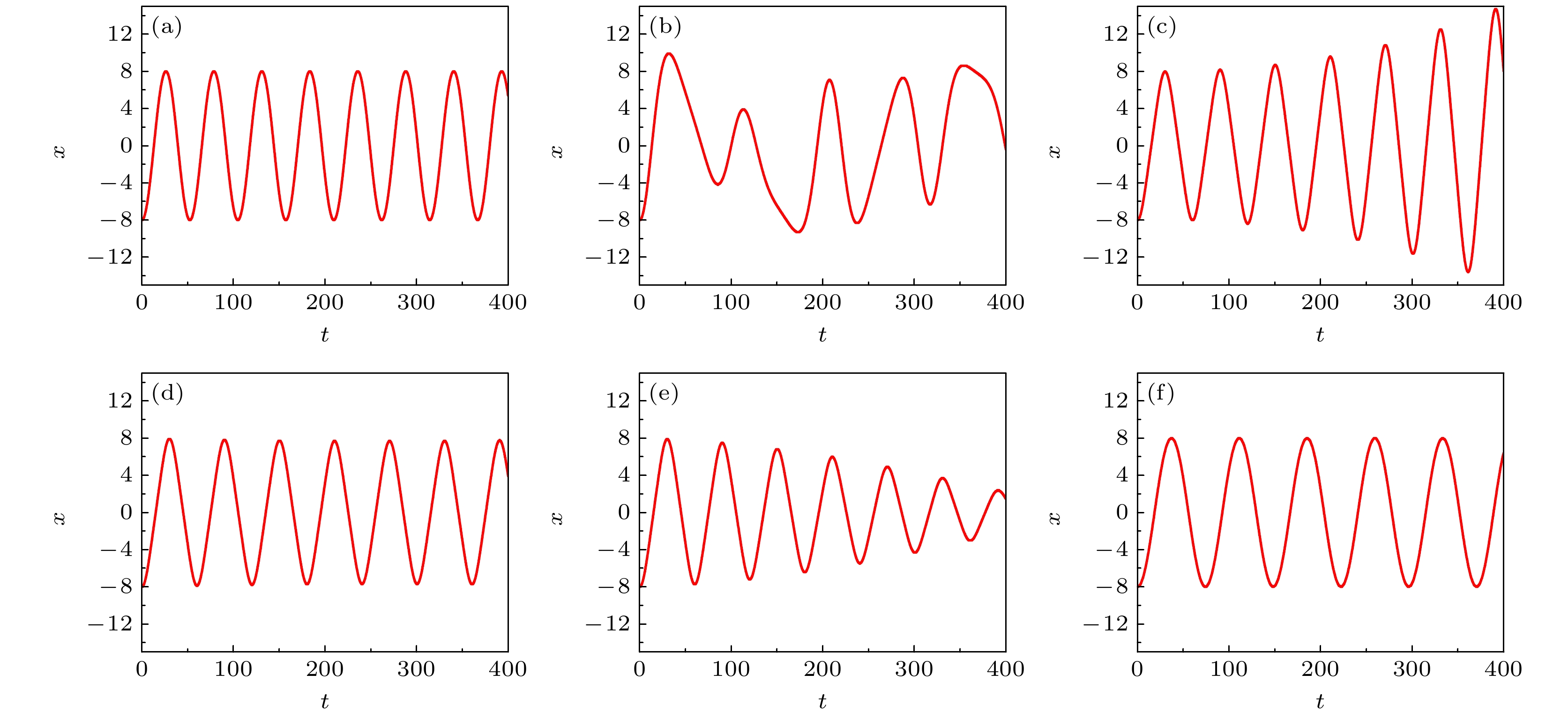
图 8 $\phi = 0$时不同驱动频率下孤子运动轨迹图 (a) $\omega = 0$; (b) $\omega = 0.06$; (c) $\omega = 0.208$; (d) $ \omega=0.209 $; (e) $\omega = 0.21$; (f)$\omega = 2.0$
Fig. 8. The trajectories of soliton with different driven frequencies at $\phi = 0$: (a) $\omega = 0$; (b) $\omega = 0.06$; (c) $\omega = 0.208$; (d) $ \omega=0.209 $; (e) $\omega = 0.21$; (f) $\omega = 2.0$.
图 9 特征驱动频率${\omega _t}$随谐振势阱的囚禁频率变化图
Fig. 9. The characteristic driven frequency ${\omega _t}$varying with the trapping frequency of harmonic potential.
-
[1] Weitenberg C, Simonet J 2021 Nat. Phys. 17 1342
Google Scholar
[2] Bukov M, D’Alessio L, Polkovnikov A 2015 Adv. Phys. 64 139
Google Scholar
[3] Eckardt A 2017 Rev. Mod. Phys. 89 011004
Google Scholar
[4] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006
Google Scholar
[5] Oka T, Kitamura S 2019 Annu. Rev. Condens. Matter Phys. 10 387
Google Scholar
[6] 焦宸, 简粤, 张爱霞, 薛具奎 2023 72 060302
Google Scholar
Jiao C, Jian Y, Zhang A X, Xue J K 2023 Acta Phys. Sin. 72 060302
Google Scholar
[7] Zhao W L, Liu J 2024 Phys. Rev. A 109 052215
Google Scholar
[8] Zhang L, Ke Y G, Lin L, Lee C H 2024 Phys. Rev. B 109 184313
Google Scholar
[9] Chen L, Zhu F, Zhang Y B, Pu H 2025 Phys. Rev. A 111 L011303
Google Scholar
[10] Kamal H, Kemp J, He Y C, Fuji Y, Aidelsburger M, Zoller P, Yao N Y 2024 Phys. Rev. Lett. 133 163403
Google Scholar
[11] Zhou L W, Chen C, Gong J B 2016 Phys. Rev. B 94 075443
Google Scholar
[12] Kapitza P L 1951 Usp. Fiz. Nauk 44 7
Google Scholar
[13] Bagnato V S, Bigelow N P, Surdutovich G I, Zílio S C 1994 Opt. Lett. 19 1568
Google Scholar
[14] Torosov B T, Della Valle G, Longhi S 2013 Phys. Rev. A 88 052106
Google Scholar
[15] Gilary I, Moiseyev N, Rahav S, Fishman S 2003 J. Phys. A: Math. Gen. 36 L409
[16] Citro R, Dalla Torre E G, D’Alessio L, Polkovnikov A, Babadi M, Oka T, Demler E 2015 Ann. Phys. 360 694
Google Scholar
[17] Smirnova O, Spanner M, Ivanov M Y 2003 Phys. Rev. Lett. 90 243001
Google Scholar
[18] Rajagopal S V, Fujiwara K M, Senaratne R, Singh K, Geiger Z A, Weld D M 2017 Ann. Phys. 529 1700008
Google Scholar
[19] Voronova N S, Elistratov A A, Lozovik Y E 2016 Phys. Rev. B 94 045413
Google Scholar
[20] Martin J, Georgeot B, Guéry-Odelin D, Shepelyansky D L 2018 Phys. Rev. A 97 023607
Google Scholar
[21] Park S J, Andersen H K, Mai S, Arlt J, Sherson J F 2012 Phys. Rev. A 85 033626
Google Scholar
[22] Eckardt A, Weiss C, Holthaus M 2005 Phys. Rev. Lett. 95 260404
Google Scholar
[23] 何章明, 张志强 2016 65 110502
Google Scholar
He Z M, Zhang Z Q 2016 Acta Phys. Sin. 65 110502
Google Scholar
[24] Abdullaev F Kh, Caputo J G, Kraenkel R A, Malomed Boris A 2003 Phys. Rev. A 67 013605
Google Scholar
[25] Goldman N, Dalibard J 2014 Phys. Rev. X 4 031027
[26] Jiang J, Bernhart E, Röhrle M, Benary J, Beck M, Baals C, Ott H 2023 Phys. Rev. Lett. 131 033401
Google Scholar
[27] Zhang X F, Yang Q, Zhang J F, Chen X Z, Liu W M 2008 Phys. Rev. A 77 023613
Google Scholar
[28] Kengne E, Liu W M 2018 Phys. Rev. E 98 012204
Google Scholar
-
[1] 王金玲, 张昆, 林机, 李慧军. 二维激子-极化子凝聚体中冲击波的产生与调控. , 2024, 73(11): 119601. doi: 10.7498/aps.73.20240229 [2] 李新月, 祁娟娟, 赵敦, 刘伍明. 自旋-轨道耦合二分量玻色-爱因斯坦凝聚系统的孤子解. , 2023, 72(10): 106701. doi: 10.7498/aps.72.20222319 [3] 孙斌, 赵立臣, 刘杰. 双孤子非线性干涉中的狄拉克磁单极势. , 2023, 72(10): 100501. doi: 10.7498/aps.72.20222416 [4] 陈礼元, 高超, 林机, 李慧军. $ {\cal{PT}}$ 对称极化子凝聚体系统中的稳定孤子及其调控. , 2022, 71(18): 181101. doi: 10.7498/aps.71.20220475[5] 贾瑞煜, 方乒乒, 高超, 林机. 玻色-爱因斯坦凝聚体中的淬火孤子与冲击波. , 2021, 70(18): 180303. doi: 10.7498/aps.70.20210564 [6] 文林, 梁毅, 周晶, 余鹏, 夏雷, 牛连斌, 张晓斐. 线性塞曼劈裂对自旋-轨道耦合玻色-爱因斯坦凝聚体中亮孤子动力学的影响. , 2019, 68(8): 080301. doi: 10.7498/aps.68.20182013 [7] 刘昊华, 王少华, 李波波, 李桦林. 缺陷致非线性电路孤子非对称传输. , 2017, 66(10): 100502. doi: 10.7498/aps.66.100502 [8] 朱坤占, 贾维国, 张魁, 于宇, 张俊萍, 门克内木乐. 在反常色散区艾里脉冲与光孤子相互作用规律的研究. , 2016, 65(2): 024208. doi: 10.7498/aps.65.024208 [9] 乔海龙, 贾维国, 王旭东, 刘宝林, 门克内木乐, 杨军, 张俊萍. 拉曼增益对双折射光纤中孤子传输特性的影响. , 2014, 63(9): 094208. doi: 10.7498/aps.63.094208 [10] 乔海龙, 贾维国, 刘宝林, 王旭东, 门克内木乐, 杨军, 张俊萍. 拉曼增益对孤子传输特性的影响. , 2013, 62(10): 104212. doi: 10.7498/aps.62.104212 [11] 庄彬先, 郭珺, 项元江, 戴小玉, 文双春. F-函数扩展法求解超介质中的亮孤子和暗孤子. , 2013, 62(5): 054207. doi: 10.7498/aps.62.054207 [12] 吴钦宽. 一类非线性扰动Burgers方程的孤子变分迭代解法. , 2012, 61(2): 020203. doi: 10.7498/aps.61.020203 [13] 陶锋, 陈伟中, 许文, 都思丹. 基于非线性超传导的能流不对称传输现象的研究. , 2012, 61(13): 134103. doi: 10.7498/aps.61.134103 [14] 石兰芳, 周先春. 一类扰动Burgers方程的孤子同伦映射解. , 2010, 59(5): 2915-2918. doi: 10.7498/aps.59.2915 [15] 何章明, 王登龙. 凝聚体中亮孤子和暗孤子的交替演化. , 2007, 56(6): 3088-3091. doi: 10.7498/aps.56.3088 [16] 翁紫梅, 陈 浩. 单离子各向异性影响下的一维铁磁链中的孤子. , 2007, 56(4): 1911-1918. doi: 10.7498/aps.56.1911 [17] 刘海兰, 文双春, 熊 敏, 戴小玉. 超常介质中暗孤子的形成和传输特性研究. , 2007, 56(11): 6473-6479. doi: 10.7498/aps.56.6473 [18] 沈守枫. (1+1)维广义的浅水波方程的变量分离解和孤子激发模式. , 2006, 55(3): 1016-1022. doi: 10.7498/aps.55.1016 [19] 洪学仁, 段文山, 孙建安, 石玉仁, 吕克璞. 非均匀尘埃等离子体中孤子的传播. , 2003, 52(11): 2671-2677. doi: 10.7498/aps.52.2671 [20] 卫青, 王奇, 施解龙, 陈园园. 孤子和辐射场的非线性相互作用. , 2002, 51(1): 99-103. doi: 10.7498/aps.51.99
下载:
计量
- 文章访问数: 342
- PDF下载量: 18
- 被引次数: 0
