一维高斯调制连续变量量子密钥分发现实源强度误差的影响

王普; 白增亮; 常利伟

doi:10.7498/aps.74.20250025

摘要

本文深入地研究了一维高斯调制连续变量量子密钥分发系统在源强度误差下的现实安全性和性能表现. 详细地分析了源强度误差对协议参数估计过程的影响机制, 并基于发送端的三种现实假设, 提出相应数据优化方案, 以减轻源强度误差的负面影响. 同时, 综合考虑了源强度误差及有限码长效应, 以保障系统的现实安全性. 研究结果表明, 源强度误差不可忽视, 对于显著的强度波动, 系统的最大传输距离将减少约20 km. 因此, 在协议的实际实施过程中, 必须充分考虑源强度误差的影响, 并采取相应的措施来减少或消除这些误差. 本研究为现实条件下实施一维高斯调制连续变量量子密钥分发提供了理论依据, 为构建高效、低成本、小型化的量子通信网络探索了新方向.

关键词:

Abstract

Unidimensional Gaussian modulation continuous-variable quantum key distribution (UD CV-QKD) uses only one modulator to encode information. The UD CV-QKD has the advantages of low implementation cost and low random number consumption, making it attractive for the construction of future miniaturized and low-cost large-scale quantum communication networks. However, in the actual application of the protocol, the intensity fluctuation of the source pulsed light, device defects, and external environmental interference maybe lead to the generation of source intensity errors, thereby affecting the realistic security and performance of the protocol. To solve these problems, the security and performance of UD CV-QKD are studied in depth under source intensity errors in this work. The mechanism of source intensity errors influencing the protocol parameter estimation process is analyzed. To make it possible that the protocol can operate stably under various realistic conditions and ensure communication security, three practical assumptions about the sender’s abilities are made in this work, and corresponding data optimization processing schemes for these assumptions are proposed to reduce the negative influence of source intensity errors. Additionally, both source errors and finite-size effect are comprehensively considered to ensure the realistic security of the system. The simulation results indicate that the source intensity errors cannot be neglected and the maximum transmission distance of the system will be reduced by approximately 20 km for significant intensity fluctuations. Therefore, in the practical implementation of the protocol, the influence of source intensity errors must be fully considered, and the corresponding countermeasures should be taken to reduce or even eliminate these errors. This study provides theoretical guidance for securely implementing the UD CV-QKD in real-world environments.

Keywords:

continuous-variable quantum key distribution /
unidimensional modulation /
source errors /
realistic security

作者及机构信息

山西财经大学信息学院, 太原　030006

通信作者: 王普, wangpu@sxufe.edu.cn

基金项目: 国家自然科学基金(批准号: 62305198)和山西省自然科学基金(批准号: 202303021212168, 202103021224290)资助的课题.

Authors and contacts

School of Information, Shanxi University of Finance and Economics, Taiyuan 030006, China

Corresponding author: WANG Pu, wangpu@sxufe.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 62305198) and the Natural Science Foundation of Shanxi Province, China (Grant Nos. 202303021212168, 202103021224290).

文章全文

参考文献

[1]	Bennett C H, Brassard G 1984 Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing (Bangalore: IEEE) p175
[2]	Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145 Google Scholar
[3]	Lo H K, Curty M, Tamaki K 2014 Nat. Photonics 8 595 Google Scholar
[4]	Bennett C H, Bessette F, Brassard G, Salvail L, Smolin J 1992 J. Cryptology 5 3 Google Scholar
[5]	Chen Y A, Zhang Q, Chen T Y, Cai W Q, Liao S K, Zhang J, Chen K, Yin J, Ren J G, Chen Z, Han S L, Yu Q, Liang K, Zhou F, Yuan X, Zhao M S, Wang T Y, Jiang X, Zhang L, Liu W Y, Li Y, Shen Q, Cao Y, Lu C Y, Shu R, Wang J Y, Li L, Liu N L, Xu F, Wang X B, Peng C Z, Pan J W 2021 Nature 589 214 Google Scholar
[6]	Xu F H, Ma X F, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002 Google Scholar
[7]	Pirandola S, Andersen U L, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C, Pereira J L, Razavi M, Shamsul Shaari J, Tomamichel M, Usenko V C, Vallone G, Villoresi P, Wallden P 2020 Adv. Opt. Photonics 12 1012 Google Scholar
[8]	Portmann C, Renner R 2022 Rev. Mod. Phys. 94 025008 Google Scholar
[9]	Diamanti E, Leverrier A 2015 Entropy 17 6072 Google Scholar
[10]	Li Y M, Wang X Y, Bai Z L, Liu W Y, Yang S S, Peng K C 2017 Chin. Phys. B 26 040303 Google Scholar
[11]	Guo H, Li Z Y, Yu S, Zhang Y C 2021 Fundam. Res. 1 96 Google Scholar
[12]	Zhang Y C, Bian Y M, Li Z Y, Yu S, Guo H 2024 Appl. Phys. Rev. 11 011318 Google Scholar
[13]	Lin J, Upadhyaya T, Lütkenhaus N 2019 Phys. Rev. X 9 041064 Google Scholar
[14]	Du S N, Tian Y, Li Y M 2020 Phys. Rev. Appl. 14 024013 Google Scholar
[15]	Li L, Huang P, Wang T, Zeng G H 2021 Phys. Rev. A 103 032611 Google Scholar
[16]	Liao Q, Wang Z, Liu H J, Mao Y Y, Fu X Q 2022 Phys. Rev. A 106 022607 Google Scholar
[17]	Liu J Q, Cao Y X, Wang P, Liu S S, Lu Z G, Wang X Y, Li Y M 2022 Opt. Express 30 27912 Google Scholar
[18]	吴晓东, 黄端, 黄鹏, 郭迎 2022 71 240304 Google Scholar Wu X D, Huang D, Huang P, Guo Y 2022 Acta Phys. Sin. 71 240304 Google Scholar
[19]	廖骎, 柳海杰, 王铮, 朱凌瑾 2023 72 040301 Google Scholar Liao Q, Liu H J, Wang Z, Zhu L J 2023 Acta Phys. Sin. 72 040301 Google Scholar
[20]	Huang L Y, Wang X Y, Chen Z Y, Sun Y H, Yu S, Guo H 2023 Phys. Rev. Appl. 19 014023 Google Scholar
[21]	Zapatero V, van Leent T, Arnon-Friedman R, Liu W Z, Zhang Q, Weinfurter H, Curty M 2023 npj Quantum Inf. 9 10 Google Scholar
[22]	Xu Y H, Wang T, Liao X J, Zhou Y M, Huang P, Zeng G H 2024 Photonics Res. 12 2549 Google Scholar
[23]	Fletcher A I, Harney C, Ghalaii M, Papanastasiou P, Mountogiannakis A, Spedalieri G, Hajomer A A E, Gehring T, Pirandola S 2025 arXiv: 2501.09818 [quant-ph]
[24]	Wang P, Wang X Y, Li Y M 2019 Phys. Rev. A 99 042309 Google Scholar
[25]	Zhang Y C, Chen Z Y, Pirandola S, Wang X Y, Zhou C, Chu B J, Zhao Y J, Xu B J, Yu S, Guo H 2020 Phys. Rev. Lett. 125 010502 Google Scholar
[26]	Dequal D, Trigo Vidarte L, Roman Rodriguez V, Vallone G, Villoresi P, Leverrier A, Diamanti E 2021 npj Quantum Inf. 7 3 Google Scholar
[27]	Jeong S, Jung H, Ha J 2022 npj Quantum Inf. 8 6 Google Scholar
[28]	Ma L, Yang J, Zhang T, Shao Y, Liu J L, Luo Y J, Wang H, Huang W, Fan F, Zhou C, Zhang L L, Zhang S, Zhang Y C, Li Y, Xu B J 2023 Sci. China Inf. Sci. 66 180507 Google Scholar
[29]	Pi Y D, Wang H, Pan Y, Shao Y, Li Y, Yang J, Zhang Y C, Huang W, Xu B J 2023 Opt. Lett. 48 1766 Google Scholar
[30]	Wang P, Zhang Y, Lu Z G, Wang X Y, Li Y M 2023 New J. Phys. 25 023019 Google Scholar
[31]	Yang S S, Yan Z L, Yang H Z, Lu Q, Lu Z G, Cheng L Y, Miao X Y, Li Y M 2023 EPJ Quantum Technol. 10 40 Google Scholar
[32]	Chen Z Y, Wang X Y, Yu S, Li Z Y, Guo H 2023 npj Quantum Inf. 9 28 Google Scholar
[33]	Hajomer A A E, Derkach I, Jain N, Chin H M, Andersen U L, Gehring T 2024 Sci. Adv. 10 eadi9474 Google Scholar
[34]	Zhang G, Haw J Y, Cai H, Xu F, Assad S M, Fitzsimons J F, Zhou X, Zhang Y, Yu S, Wu J, Ser W, Kwek L C, Liu A Q 2019 Nat. Photonics 13 839 Google Scholar
[35]	Qi B, Gunther H, Evans P G, Williams B P, Camacho R M, Peters N A 2020 Phys. Rev. Appl. 13 054065 Google Scholar
[36]	Milovančev D, Vokić N, Laudenbach F, Pacher C, Hübel H, Schrenk B 2021 J. Lightwave Technol. 39 3445 Google Scholar
[37]	Tian Y, Wang P, Liu J Q, Du S N, Liu W Y, Lu Z G, Wang X Y, Li Y M 2022 Optica 9 492 Google Scholar
[38]	Du S N, Wang P, Liu J Q, Tian Y, Li Y M 2023 Photonics Res. 11 463 Google Scholar
[39]	Wang X Y, Chen Z Y, Li Z H, Qi D K, Yu S, Guo H 2023 Opt. Lett. 48 3327 Google Scholar
[40]	Zhang M Q, Huang P, Wang P, Wei S R, Zeng G H 2023 Opt. Lett. 48 1184 Google Scholar
[41]	Hajomer A A E, Bruynsteen C, Derkach I, Jain N, Bomhals A, Bastiaens S, Andersen U L, Yin X, Gehring T 2024 Optica 11 1197 Google Scholar
[42]	Hajomer A A E, Derkach I, Filip R, Andersen U L, Usenko V C, Gehring T 2024 Light Sci. Appl. 13 291 Google Scholar
[43]	Ji F Y, Huang P, Wang T, Jiang X Q, Zeng G H 2024 Photonics Res. 12 1485 Google Scholar
[44]	Usenko V C, Grosshans F 2015 Phys. Rev. A 92 062337 Google Scholar
[45]	Wang P, Wang X Y, Li J Q, Li Y M 2017 Opt. Express 25 27995 Google Scholar
[46]	Wang X Y, Liu W Y, Wang P, Li Y M 2017 Phys. Rev. A 95 062330 Google Scholar
[47]	Jacobsen C S, Madsen L S, Usenko V C, Filip R, Andersen U L 2018 npj Quantum Inf. 4 32 Google Scholar
[48]	Liao Q, Guo Y, Xie C L, Huang D, Huang P, Zeng G H 2018 Quantum Inf. Process. 17 113 Google Scholar
[49]	Usenko V C 2018 Phys. Rev. A 98 032321 Google Scholar
[50]	Wang P, Wang X Y, Li Y M 2018 Entropy 20 157 Google Scholar
[51]	Wang X Y, Cao Y X, Wang P, Li Y M 2018 Quantum Inf. Process. 17 344 Google Scholar
[52]	Bai D Y, Huang P, Zhu Y Q, Ma H X, Xiao T L, Wang T, Zeng G H 2020 Quantum Inf. Process. 19 53 Google Scholar
[53]	Shen S Y, Dai M W, Zheng X T, Sun Q Y, Guo G C, Han Z F 2019 Phys. Rev. A 100 012325 Google Scholar
[54]	Zhang H, Ruan X C, Wu X D, Zhang L, Guo Y, Huang D 2019 Quantum Inf. Process. 18 128 Google Scholar
[55]	Zhao W, Shi R H, Feng Y Y, Huang D 2020 Phys. Lett. A 384 126061 Google Scholar
[56]	Zhou K L, Chen Z Y, Guo Y, Liao Q 2020 Phys. Lett. A 384 126074 Google Scholar
[57]	Bian Y M, Huang L Y, Zhang Y C 2021 Entropy 23 294 Google Scholar
[58]	Hu J K, Liao Q, Mao Y, Guo Y 2021 Quantum Inf. Process. 20 31 Google Scholar
[59]	Zhao W, Shi R H, Wu X M, Wang F Q, Ruan X C 2023 Opt. Express 31 17003 Google Scholar
[60]	Li Y Y, Wang T Y 2024 J. Phys. B: At. Mol. Opt. Phys. 57 145502 Google Scholar
[61]	Zhao R B, Zhou J, Shi R H, Shi J J 2024 Ann. Phys. 536 2300401 Google Scholar
[62]	Zheng Y, Huang P, Huang A Q, Peng J Y, Zeng G H 2019 Opt. Express 27 27369 Google Scholar
[63]	Zheng Y, Huang P, Huang A Q, Peng J Y, Zeng G H 2019 Phys. Rev. A 100 012313 Google Scholar
[64]	Wang P, Wang X Y, Li Y M 2020 Phys. Rev. A 102 022609 Google Scholar
[65]	Li C Y, Qian L, Lo H K 2021 npj Quantum Inf. 7 150 Google Scholar
[66]	Serafini A, Paris M G A, Illuminati F, Siena S D 2005 J. Opt. B: Quantum Semiclassical Opt. 7 R19 Google Scholar

施引文献

图 1 一维高斯调制连续变量量子密钥分发模型　(a)准备测量方案; (b)基于纠缠方案

Fig. 1. Unidimensional Gaussian modulation continuous-variable quantum key distribution models: (a) Preparation and measurement scheme; (b) entanglement-based scheme.

下载: 全尺寸图片幻灯片

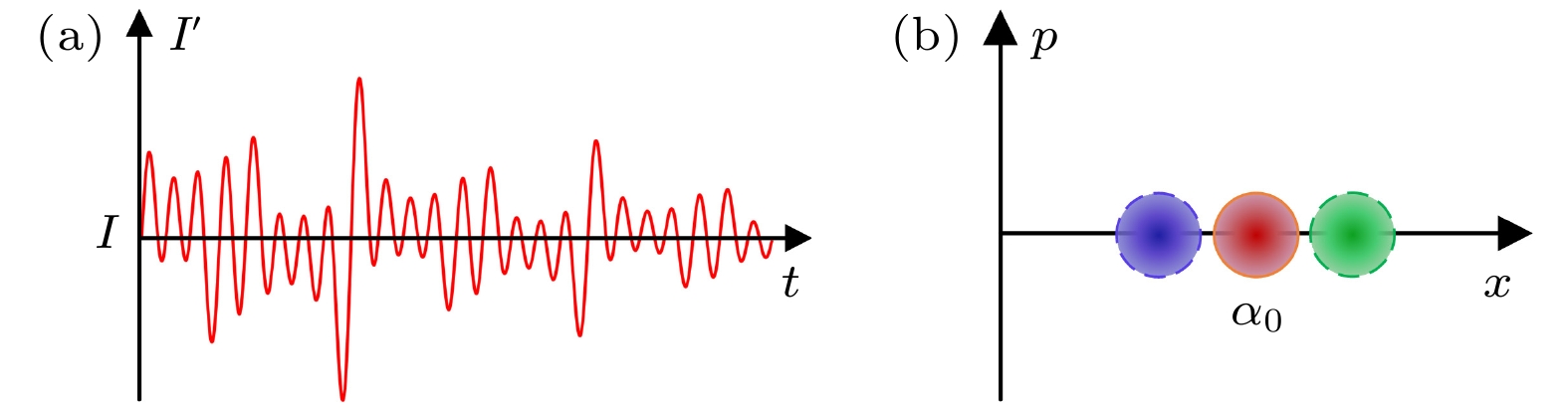
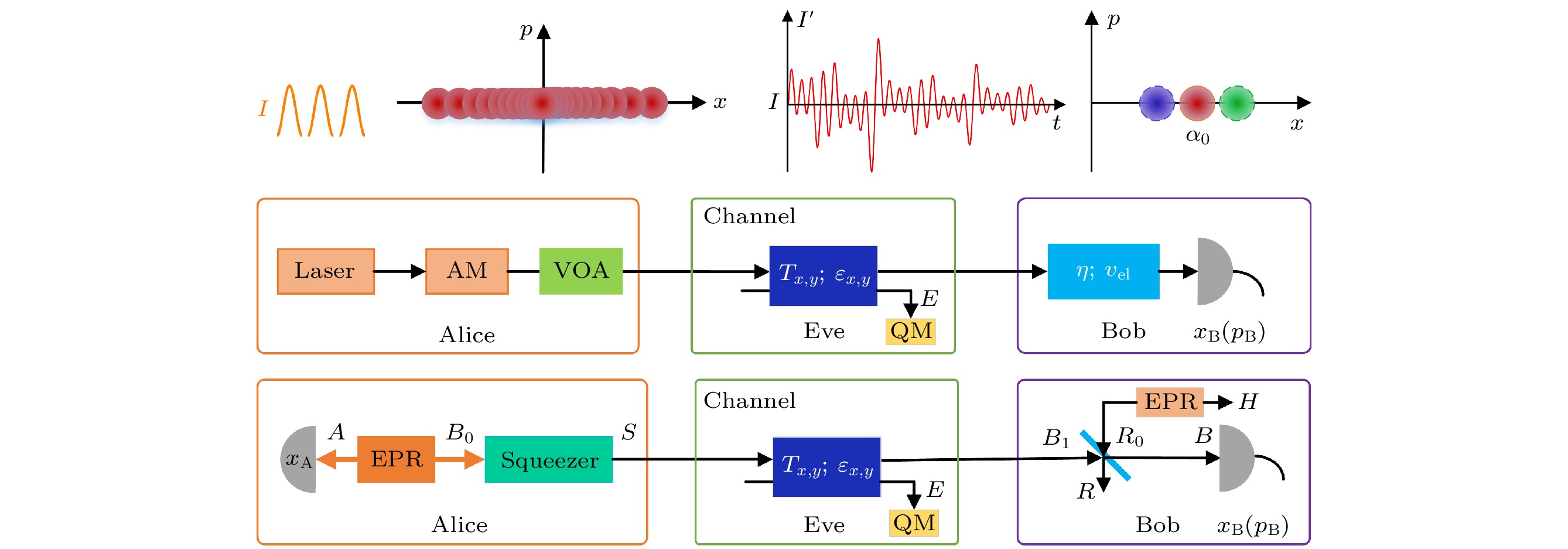
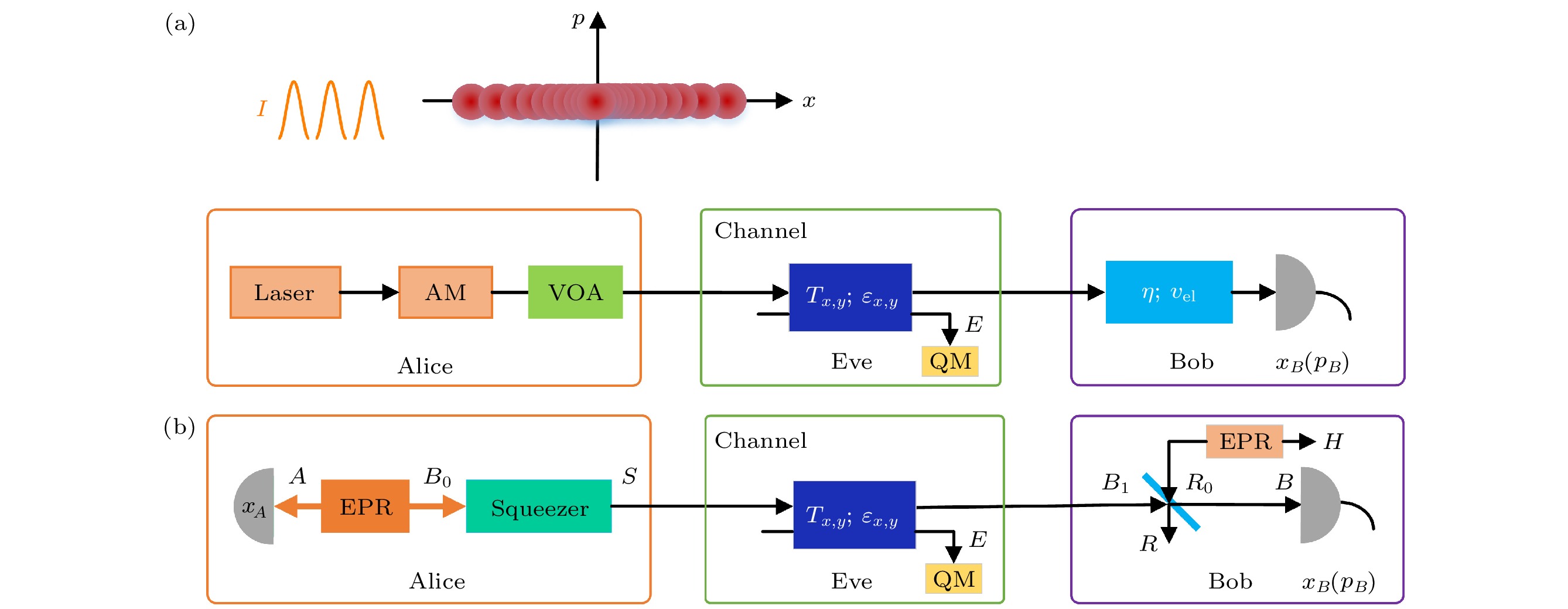
图 2 (a)实际的光脉冲强度$ I' $随时间$t$呈现出动态变化; (b)在相空间中, 由于源强度误差的影响, 实际制备的相干态可能会偏离目标相干态的位置

Fig. 2. (a) Actual optical pulse intensity dynamically changes over time; (b) the actual prepared coherent state may deviate from the target coherent state’s location in the phase space under the influence of source intensity errors.

下载: 全尺寸图片幻灯片

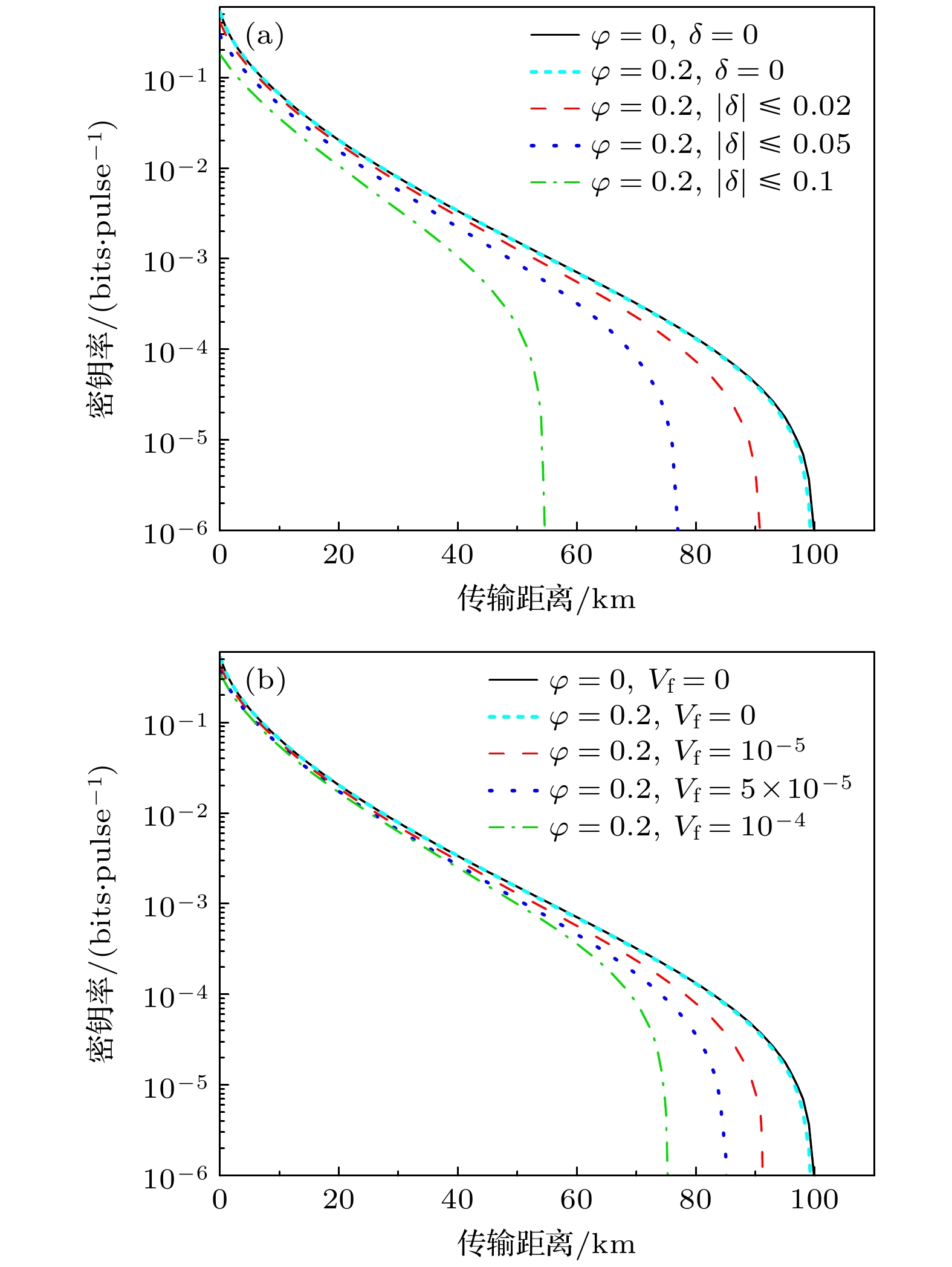
图 3 (a)不同均匀分布强度波动下密钥率随着传输距离的变化; (b)不同高斯分布强度波动下密钥率随着传输距离的变化

Fig. 3. (a) Comparison of secret key rates at various transmission distances for intensity fluctuation models following a uniform distribution; (b) comparison of secret key rates at various transmission distances for intensity fluctuation models adhering to a Gaussian distribution.

下载: 全尺寸图片幻灯片

图 4 不同源强度误差对协议性能的影响

Fig. 4. Influence of different source intensity errors on protocol performance.

下载: 全尺寸图片幻灯片

图 5 不同码长下协议性能比较　(a) 考虑第二种源误差模型; (b) 考虑第三种源误差模型

Fig. 5. Comparison of protocol performance under different total exchanged signals sizes: (a) Considering the second source error model; (b) considering the third source error model.

下载: 全尺寸图片幻灯片

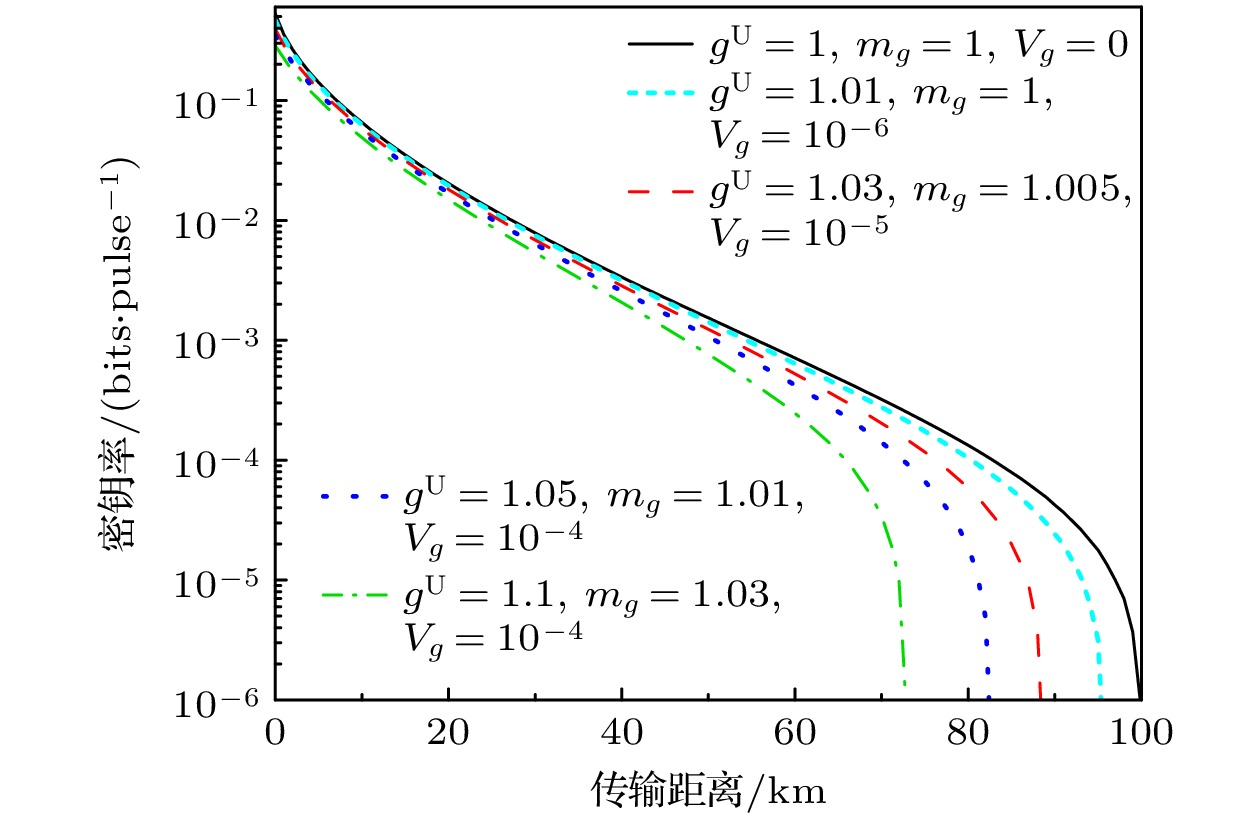
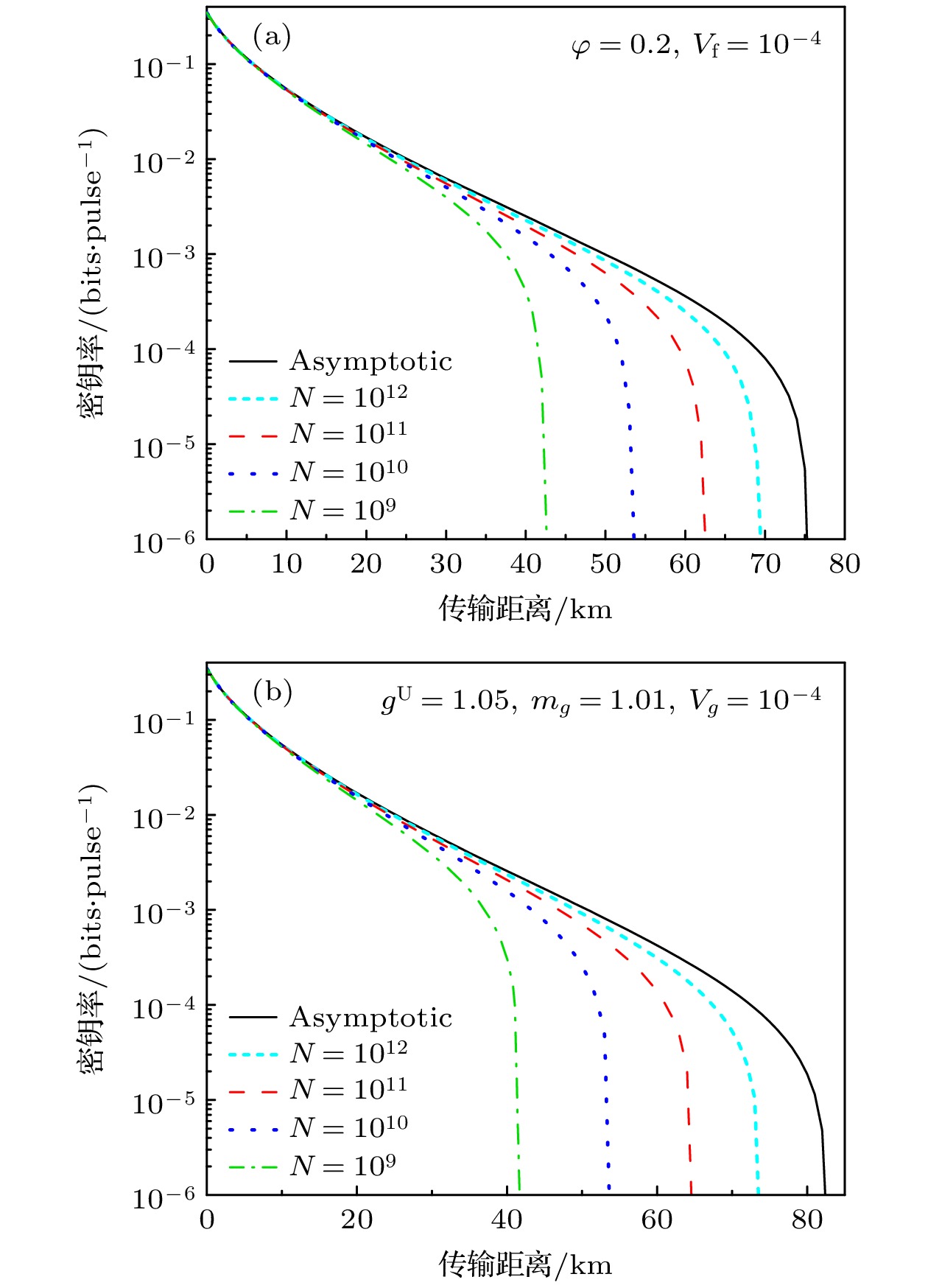
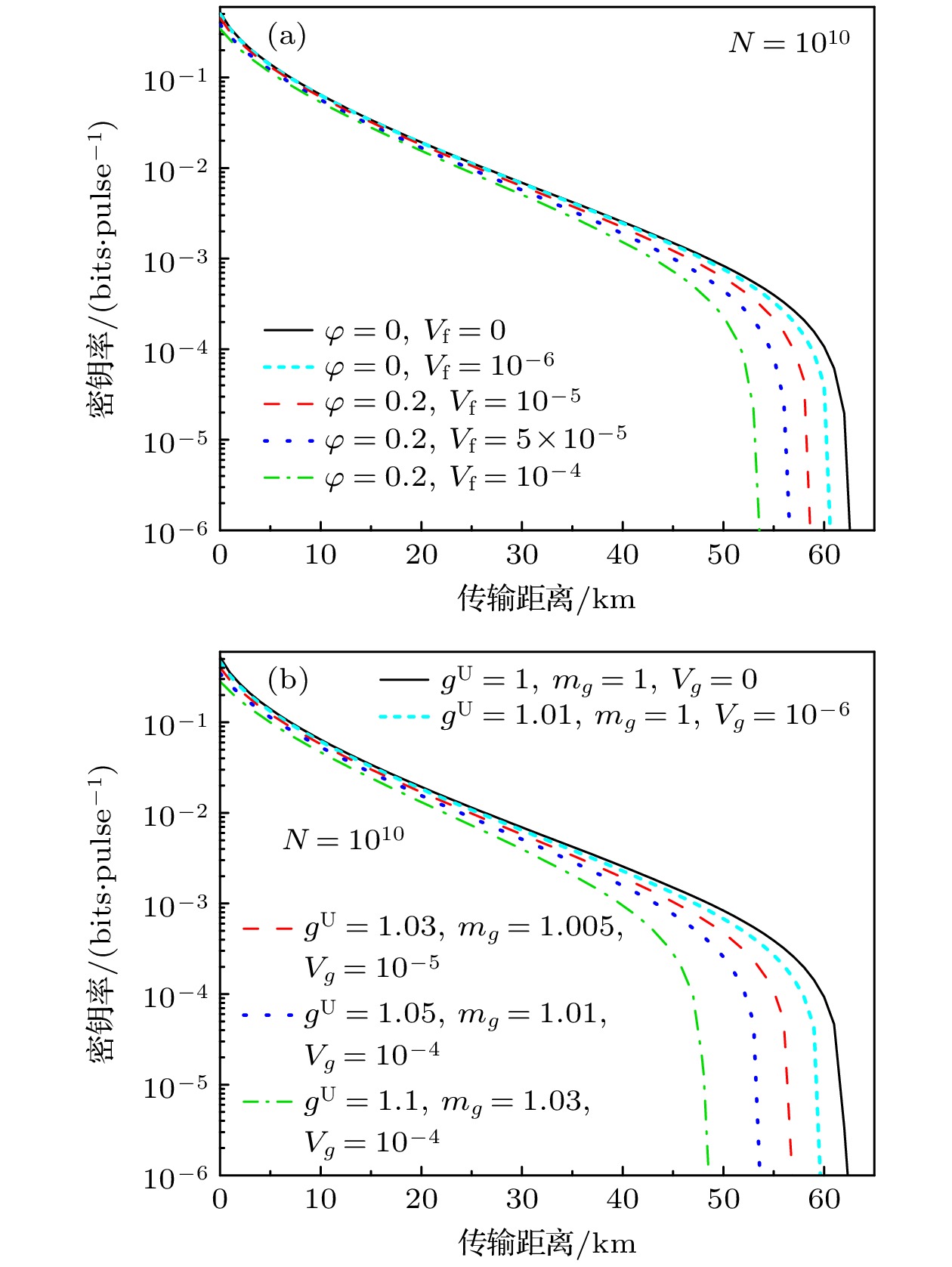
图 6 $N = {10^{10}}$码长下不同源误差对应的协议密钥率和传输距离　(a) 考虑第二种源误差模型; (b) 考虑第三种源误差模型

Fig. 6. Protocol key rate and transmission distance corresponding to different source errors under the total exchanged signals of $N = {10^{10}}$: (a) Considering the second source error model; (b) considering the third source error model.

下载: 全尺寸图片幻灯片

下载: 全尺寸图片幻灯片

map

[1]	Bennett C H, Brassard G 1984 Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing (Bangalore: IEEE) p175
[2]	Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145 Google Scholar
[3]	Lo H K, Curty M, Tamaki K 2014 Nat. Photonics 8 595 Google Scholar
[4]	Bennett C H, Bessette F, Brassard G, Salvail L, Smolin J 1992 J. Cryptology 5 3 Google Scholar
[5]	Chen Y A, Zhang Q, Chen T Y, Cai W Q, Liao S K, Zhang J, Chen K, Yin J, Ren J G, Chen Z, Han S L, Yu Q, Liang K, Zhou F, Yuan X, Zhao M S, Wang T Y, Jiang X, Zhang L, Liu W Y, Li Y, Shen Q, Cao Y, Lu C Y, Shu R, Wang J Y, Li L, Liu N L, Xu F, Wang X B, Peng C Z, Pan J W 2021 Nature 589 214 Google Scholar
[6]	Xu F H, Ma X F, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002 Google Scholar
[7]	Pirandola S, Andersen U L, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C, Pereira J L, Razavi M, Shamsul Shaari J, Tomamichel M, Usenko V C, Vallone G, Villoresi P, Wallden P 2020 Adv. Opt. Photonics 12 1012 Google Scholar
[8]	Portmann C, Renner R 2022 Rev. Mod. Phys. 94 025008 Google Scholar
[9]	Diamanti E, Leverrier A 2015 Entropy 17 6072 Google Scholar
[10]	Li Y M, Wang X Y, Bai Z L, Liu W Y, Yang S S, Peng K C 2017 Chin. Phys. B 26 040303 Google Scholar
[11]	Guo H, Li Z Y, Yu S, Zhang Y C 2021 Fundam. Res. 1 96 Google Scholar
[12]	Zhang Y C, Bian Y M, Li Z Y, Yu S, Guo H 2024 Appl. Phys. Rev. 11 011318 Google Scholar
[13]	Lin J, Upadhyaya T, Lütkenhaus N 2019 Phys. Rev. X 9 041064 Google Scholar
[14]	Du S N, Tian Y, Li Y M 2020 Phys. Rev. Appl. 14 024013 Google Scholar
[15]	Li L, Huang P, Wang T, Zeng G H 2021 Phys. Rev. A 103 032611 Google Scholar
[16]	Liao Q, Wang Z, Liu H J, Mao Y Y, Fu X Q 2022 Phys. Rev. A 106 022607 Google Scholar
[17]	Liu J Q, Cao Y X, Wang P, Liu S S, Lu Z G, Wang X Y, Li Y M 2022 Opt. Express 30 27912 Google Scholar
[18]	吴晓东, 黄端, 黄鹏, 郭迎 2022 71 240304 Google Scholar Wu X D, Huang D, Huang P, Guo Y 2022 Acta Phys. Sin. 71 240304 Google Scholar
[19]	廖骎, 柳海杰, 王铮, 朱凌瑾 2023 72 040301 Google Scholar Liao Q, Liu H J, Wang Z, Zhu L J 2023 Acta Phys. Sin. 72 040301 Google Scholar
[20]	Huang L Y, Wang X Y, Chen Z Y, Sun Y H, Yu S, Guo H 2023 Phys. Rev. Appl. 19 014023 Google Scholar
[21]	Zapatero V, van Leent T, Arnon-Friedman R, Liu W Z, Zhang Q, Weinfurter H, Curty M 2023 npj Quantum Inf. 9 10 Google Scholar
[22]	Xu Y H, Wang T, Liao X J, Zhou Y M, Huang P, Zeng G H 2024 Photonics Res. 12 2549 Google Scholar
[23]	Fletcher A I, Harney C, Ghalaii M, Papanastasiou P, Mountogiannakis A, Spedalieri G, Hajomer A A E, Gehring T, Pirandola S 2025 arXiv: 2501.09818 [quant-ph]
[24]	Wang P, Wang X Y, Li Y M 2019 Phys. Rev. A 99 042309 Google Scholar
[25]	Zhang Y C, Chen Z Y, Pirandola S, Wang X Y, Zhou C, Chu B J, Zhao Y J, Xu B J, Yu S, Guo H 2020 Phys. Rev. Lett. 125 010502 Google Scholar
[26]	Dequal D, Trigo Vidarte L, Roman Rodriguez V, Vallone G, Villoresi P, Leverrier A, Diamanti E 2021 npj Quantum Inf. 7 3 Google Scholar
[27]	Jeong S, Jung H, Ha J 2022 npj Quantum Inf. 8 6 Google Scholar
[28]	Ma L, Yang J, Zhang T, Shao Y, Liu J L, Luo Y J, Wang H, Huang W, Fan F, Zhou C, Zhang L L, Zhang S, Zhang Y C, Li Y, Xu B J 2023 Sci. China Inf. Sci. 66 180507 Google Scholar
[29]	Pi Y D, Wang H, Pan Y, Shao Y, Li Y, Yang J, Zhang Y C, Huang W, Xu B J 2023 Opt. Lett. 48 1766 Google Scholar
[30]	Wang P, Zhang Y, Lu Z G, Wang X Y, Li Y M 2023 New J. Phys. 25 023019 Google Scholar
[31]	Yang S S, Yan Z L, Yang H Z, Lu Q, Lu Z G, Cheng L Y, Miao X Y, Li Y M 2023 EPJ Quantum Technol. 10 40 Google Scholar
[32]	Chen Z Y, Wang X Y, Yu S, Li Z Y, Guo H 2023 npj Quantum Inf. 9 28 Google Scholar
[33]	Hajomer A A E, Derkach I, Jain N, Chin H M, Andersen U L, Gehring T 2024 Sci. Adv. 10 eadi9474 Google Scholar
[34]	Zhang G, Haw J Y, Cai H, Xu F, Assad S M, Fitzsimons J F, Zhou X, Zhang Y, Yu S, Wu J, Ser W, Kwek L C, Liu A Q 2019 Nat. Photonics 13 839 Google Scholar
[35]	Qi B, Gunther H, Evans P G, Williams B P, Camacho R M, Peters N A 2020 Phys. Rev. Appl. 13 054065 Google Scholar
[36]	Milovančev D, Vokić N, Laudenbach F, Pacher C, Hübel H, Schrenk B 2021 J. Lightwave Technol. 39 3445 Google Scholar
[37]	Tian Y, Wang P, Liu J Q, Du S N, Liu W Y, Lu Z G, Wang X Y, Li Y M 2022 Optica 9 492 Google Scholar
[38]	Du S N, Wang P, Liu J Q, Tian Y, Li Y M 2023 Photonics Res. 11 463 Google Scholar
[39]	Wang X Y, Chen Z Y, Li Z H, Qi D K, Yu S, Guo H 2023 Opt. Lett. 48 3327 Google Scholar
[40]	Zhang M Q, Huang P, Wang P, Wei S R, Zeng G H 2023 Opt. Lett. 48 1184 Google Scholar
[41]	Hajomer A A E, Bruynsteen C, Derkach I, Jain N, Bomhals A, Bastiaens S, Andersen U L, Yin X, Gehring T 2024 Optica 11 1197 Google Scholar
[42]	Hajomer A A E, Derkach I, Filip R, Andersen U L, Usenko V C, Gehring T 2024 Light Sci. Appl. 13 291 Google Scholar
[43]	Ji F Y, Huang P, Wang T, Jiang X Q, Zeng G H 2024 Photonics Res. 12 1485 Google Scholar
[44]	Usenko V C, Grosshans F 2015 Phys. Rev. A 92 062337 Google Scholar
[45]	Wang P, Wang X Y, Li J Q, Li Y M 2017 Opt. Express 25 27995 Google Scholar
[46]	Wang X Y, Liu W Y, Wang P, Li Y M 2017 Phys. Rev. A 95 062330 Google Scholar
[47]	Jacobsen C S, Madsen L S, Usenko V C, Filip R, Andersen U L 2018 npj Quantum Inf. 4 32 Google Scholar
[48]	Liao Q, Guo Y, Xie C L, Huang D, Huang P, Zeng G H 2018 Quantum Inf. Process. 17 113 Google Scholar
[49]	Usenko V C 2018 Phys. Rev. A 98 032321 Google Scholar
[50]	Wang P, Wang X Y, Li Y M 2018 Entropy 20 157 Google Scholar
[51]	Wang X Y, Cao Y X, Wang P, Li Y M 2018 Quantum Inf. Process. 17 344 Google Scholar
[52]	Bai D Y, Huang P, Zhu Y Q, Ma H X, Xiao T L, Wang T, Zeng G H 2020 Quantum Inf. Process. 19 53 Google Scholar
[53]	Shen S Y, Dai M W, Zheng X T, Sun Q Y, Guo G C, Han Z F 2019 Phys. Rev. A 100 012325 Google Scholar
[54]	Zhang H, Ruan X C, Wu X D, Zhang L, Guo Y, Huang D 2019 Quantum Inf. Process. 18 128 Google Scholar
[55]	Zhao W, Shi R H, Feng Y Y, Huang D 2020 Phys. Lett. A 384 126061 Google Scholar
[56]	Zhou K L, Chen Z Y, Guo Y, Liao Q 2020 Phys. Lett. A 384 126074 Google Scholar
[57]	Bian Y M, Huang L Y, Zhang Y C 2021 Entropy 23 294 Google Scholar
[58]	Hu J K, Liao Q, Mao Y, Guo Y 2021 Quantum Inf. Process. 20 31 Google Scholar
[59]	Zhao W, Shi R H, Wu X M, Wang F Q, Ruan X C 2023 Opt. Express 31 17003 Google Scholar
[60]	Li Y Y, Wang T Y 2024 J. Phys. B: At. Mol. Opt. Phys. 57 145502 Google Scholar
[61]	Zhao R B, Zhou J, Shi R H, Shi J J 2024 Ann. Phys. 536 2300401 Google Scholar
[62]	Zheng Y, Huang P, Huang A Q, Peng J Y, Zeng G H 2019 Opt. Express 27 27369 Google Scholar
[63]	Zheng Y, Huang P, Huang A Q, Peng J Y, Zeng G H 2019 Phys. Rev. A 100 012313 Google Scholar
[64]	Wang P, Wang X Y, Li Y M 2020 Phys. Rev. A 102 022609 Google Scholar
[65]	Li C Y, Qian L, Lo H K 2021 npj Quantum Inf. 7 150 Google Scholar
[66]	Serafini A, Paris M G A, Illuminati F, Siena S D 2005 J. Opt. B: Quantum Semiclassical Opt. 7 R19 Google Scholar

[1]	郭晓敏, 王岐岐, 罗越, 宋智杰, 李正雅, 瞿毅坤, 郭龑强, 肖连团. 实时熵源评估二重并行连续变量量子随机数发生器. , 2025, 74(11): . doi: 10.7498/aps.74.20250333
[2]	孙新, 郭俊杰, 陈宇杰, 程锦, 刘奥, 刘文博, 尹鹏, 陈兰剑, 吴田宜, 东晨. 空间信道离散调制连续变量量子密钥分发可行性分析. , 2025, 74(9): 090303. doi: 10.7498/aps.74.20241682
[3]	贺英, 王天一, 李莹莹. 线性光学克隆机改进的离散极化调制连续变量量子密钥分发可组合安全性分析. , 2024, 73(23): 230303. doi: 10.7498/aps.73.20241094
[4]	张光伟, 白建东, 颉琦, 靳晶晶, 张永梅, 刘文元. 连续变量量子密钥分发系统中动态偏振控制研究. , 2024, 73(6): 060301. doi: 10.7498/aps.73.20231890
[5]	吴晓东, 黄端. 基于非理想测量基选择的水下连续变量量子密钥分发方案. , 2024, 73(21): 210302. doi: 10.7498/aps.73.20240804
[6]	张云杰, 王旭阳, 张瑜, 王宁, 贾雁翔, 史玉琪, 卢振国, 邹俊, 李永民. 基于硬件同步的四态离散调制连续变量量子密钥分发. , 2024, 73(6): 060302. doi: 10.7498/aps.73.20231769
[7]	吴晓东, 黄端. 基于非高斯态区分探测的往返式离散调制连续变量量子密钥分发方案. , 2023, 72(5): 050303. doi: 10.7498/aps.72.20222253
[8]	廖骎, 柳海杰, 王铮, 朱凌瑾. 基于不可信纠缠源的高斯调制连续变量量子密钥分发. , 2023, 72(4): 040301. doi: 10.7498/aps.72.20221902
[9]	吴晓东, 黄端, 黄鹏, 郭迎. 基于实际探测器补偿的离散调制连续变量测量设备无关量子密钥分发方案. , 2022, 71(24): 240304. doi: 10.7498/aps.71.20221072
[10]	马啸, 孙铭烁, 刘靖阳, 丁华建, 王琴. 一种基于标记单光子源的态制备误差容忍量子密钥分发协议. , 2022, 71(3): 030301. doi: 10.7498/aps.71.20211456
[11]	毛宜钰, 王一军, 郭迎, 毛堉昊, 黄文体. 基于峰值补偿的连续变量量子密钥分发方案. , 2021, 70(11): 110302. doi: 10.7498/aps.70.20202073
[12]	叶炜, 郭迎, 夏莹, 钟海, 张欢, 丁建枝, 胡利云. 基于量子催化的离散调制连续变量量子密钥分发. , 2020, 69(6): 060301. doi: 10.7498/aps.69.20191689
[13]	曹正文, 张爽浩, 冯晓毅, 赵光, 柴庚, 李东伟. 基于散粒噪声方差实时监测的连续变量量子密钥分发系统的设计与实现. , 2017, 66(2): 020301. doi: 10.7498/aps.66.020301
[14]	刘建强, 王旭阳, 白增亮, 李永民. 时域脉冲平衡零拍探测器的高精度自动平衡. , 2016, 65(10): 100303. doi: 10.7498/aps.65.100303
[15]	徐兵杰, 唐春明, 陈晖, 张文政, 朱甫臣. 利用无噪线性光放大器增加连续变量量子密钥分发最远传输距离. , 2013, 62(7): 070301. doi: 10.7498/aps.62.070301
[16]	沈咏, 邹宏新. 离散调制连续变量量子密钥分发的安全边界. , 2010, 59(3): 1473-1480. doi: 10.7498/aps.59.1473
[17]	朱畅华, 陈南, 裴昌幸, 权东晓, 易运晖. 基于信道估计的自适应连续变量量子密钥分发方法. , 2009, 58(4): 2184-2188. doi: 10.7498/aps.58.2184
[18]	王开, 裴文江, 邹留华, 何振亚. 一种多混沌系统公钥密码算法的安全性分析. , 2006, 55(12): 6243-6247. doi: 10.7498/aps.55.6243
[19]	张权, 唐朝京, 张森强. B92量子密钥分配协议的变形及其无条件安全性证明. , 2002, 51(7): 1439-1447. doi: 10.7498/aps.51.1439
[20]	杨理, 吴令安, 刘颂豪. 复合量子密钥分发系统双速协议及其安全性分析. , 2002, 51(11): 2446-2451. doi: 10.7498/aps.51.2446

计量

文章访问数: 310
PDF下载量: 11
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

一维高斯调制连续变量量子密钥分发现实源强度误差的影响