基于不可信纠缠源的高斯调制连续变量量子密钥分发

廖骎; 柳海杰; 王铮; 朱凌瑾

doi:10.7498/aps.72.20221902

摘要

在实际的量子通信系统中, 连续变量量子密钥分发的信源安全可能会因为器件的缺陷或隐藏的攻击而受到威胁. 针对这个问题, 本文提出了基于不可信纠缠源的高斯调制连续变量量子密钥分发方案, 通过将高斯纠缠源置于不可信的量子信道来模拟纠缠源被攻击者所控制的场景, 从而验证实际复杂环境下高斯调制连续变量量子密钥分发的安全性. 本文详细分析不可信纠缠源对系统安全性的影响并引入了两种光学放大器来辅助提升所提方案的实际性能. 仿真实验结果表明, 本文所提方案即使在高斯纠缠源不可信的情况下仍然能够产生安全的量子密钥, 同时, 光学放大器也能够有效提升接收端探测器的量子效率. 该工作旨在推动高斯调制连续变量量子密钥分发系统的实用化进程, 为高斯调制连续变量量子密钥分发系统的实际部署和应用提供理论指导.

关键词:

Abstract

In a practical quantum communication system, the security of signal source of continuous-variable quantum key distribution may be jeopardized due to device flaws and hidden attacks. In this paper, an improved scheme for Gaussian-modulated continuous-variable quantum key distribution based on an untrusted entangled source is proposed. In particular, the entanglement source is placed in an untrusted quantum channel to simulate that it is controlled by an eavesdropper, thereby verifying the security of Gaussian-modulated continuous-variable quantum key distribution in a complex environment. This work in detail analyzes the influence of untrusted entanglement source on practical Gaussian-modulated continuous-variable quantum key distribution system, and the numerical simulation shows that the performance of Gaussian-modulated continuous-variable quantum key distribution will dramatically decrease once the entanglement source has moved out of the sender, and it will slightly rise as the untrusted entanglement source slowly moves away from the sender. This paper further introduces two kinds of optical amplifiers, which are phase-sensitive amplifier and phase-insensitive amplifier, to compensate for the imperfection of the coherent detector. These amplifiers are beneficial to enhancing the quantum efficiency of the receiver’s detector. Specifically, the security key rate of Gaussian-modulated continuous-variable quantum key distribution with homodyne detection can be well improved by phase-sensitive amplifier, and the security key rate of Gaussian-modulated continuous-variable quantum key distribution with heterodyne detection can be well improved by phase-insensitive amplifier. To summary, this paper proposes a scheme for Gaussian-modulated continuous-variable quantum key distribution with untrusted entanglement source, experimental results show that the proposed scheme can generate secure quantum keys even if the Gaussian entanglement source is untrusted, and the two optical amplifiers can effectively improve the quantum efficiency of the detector at the receiver. This work aims to promote the practical process of the Gaussian-modulated continuous-variable quantum key distribution system and provide theoretical guidance for the practical implementation and application of the Gaussian-modulated continuous-variable quantum key distribution system.

Keywords:

continuous-variable quantum key distribution /
untrusted entanglement source /
optical amplifier /
quantum communication

作者及机构信息

1.
湖南大学信息科学与工程学院, 长沙　410082

2.
湖南省计量检测研究院, 长沙　410014

通信作者: 朱凌瑾, zhulingjin1020@foxmail.com

基金项目: 国家自然科学基金项目(批准号: 62101180)、湖南省自然科学基金项目(批准号: 2022JJ30163)和国防科技大学高性能计算国家重点实验室(批准号: 202101-25)资助的课题.

Authors and contacts

1.
College of Computer Science and Electronic Engineering, Hunan University, Changsha 410082, China

2.
Hunan Institute of Metrology and Test, Changsha 410014, China

Corresponding author: Zhu Ling-Jin, zhulingjin1020@foxmail.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 62101180), the Natural Science Foundation of Hunan Province, China (Grant No. 2022JJ30163), and the State Key Laboratory of High Performance Computing, National University of Defense Technology (Grant No. 202101-25)

文章全文 : translate this paragraph

参考文献

[1]	Zhou N R, Li J F, Yu Z B, Gong L H, Farouk A 2016 Quantum Inf. Process 16 4
[2]	Scarani V, Bechmann-Pasquinucci H, Cerf N J, Dušek M, Lütkenhaus N, Peev M 2009 Rev. Mod. Phys. 81 1301 Google Scholar
[3]	Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145 Google Scholar
[4]	Gong L H, Li J F, Zhou N R 2018 Laser Phys. Lett. 15 105204 Google Scholar
[5]	Liao Q, Liu H J, Zhu L J, Guo Y 2021 Phys. Rev. A 103 032410 Google Scholar
[6]	Liao Q, Liu H J, Gong Y P, Wang Z, Peng Q Q, Guo Y 2022 Opt. Express 30 3876 Google Scholar
[7]	宋汉冲, 龚黎华, 周南润 2012 61 154206 Google Scholar Song H C, Gong L H, Zhou N R 2012 Acta Phys. Sin. 61 154206 Google Scholar
[8]	Zhou N R, Wang L J, Ding J, Gong L H, Zuo X W 2010 Int. J. Theor. Phys. 49 2035 Google Scholar
[9]	Guo Y, Liao Q, Wang Y J, Huang D, Huang P, Zeng G H 2017 Phys. Rev. A 95 032304 Google Scholar
[10]	钟海, 叶炜, 吴晓东, 郭迎 2021 70 020301 Google Scholar Zhong H, Ye W, Wu X D, Guo Y 2021 Acta Phys. Sin. 70 020301 Google Scholar
[11]	Lance A M, Symul T, Sharma V, Weedbrook C, Ralph T C, Lam P K 2005 Phys. Rev. Lett. 95 180503 Google Scholar
[12]	Ma X C, Sun S H, Jiang M S, Gui M, Liang L M 2014 Phys. Rev. A 89 042335 Google Scholar
[13]	Grosshans F, Grangier P 2002 Phys. Rev. Lett. 88 057902 Google Scholar
[14]	Leverrier A 2015 Phys. Rev. Lett. 114 070501 Google Scholar
[15]	Leverrier A, Grosshans F, Grangier P 2010 Phys. Rev. A 81 062343 Google Scholar
[16]	Jouguet P, Kunz-Jacques S, Diamanti E 2013 Phys. Rev. A 87 062313 Google Scholar
[17]	Ma X C, Sun S H, Jiang M S, Liang L M 2013 Phys. Rev. A 88 022339 Google Scholar
[18]	Qin H, Kumar R, Alléaume R 2016 Phys. Rev. A 94 012325 Google Scholar
[19]	Huang J Z, Weedbrook C, Yin Z Q, Wang S, Li H W, Chen W, Guo G C, Han Z F 2013 Phys. Rev. A 87 062329 Google Scholar
[20]	Ma X C, Sun S H, Jiang M S, Liang L M 2013 Phys. Rev. A 87 052309 Google Scholar
[21]	Qin H, Kumar R, Makarov V, Alléaume R 2018 Phys. Rev. A 98 012312 Google Scholar
[22]	Zhou N R, Zhang T F, Xie X W, Wu J Y 2023 Signal Process. Image Commun. 110 116891 Google Scholar
[23]	Liao Q, Xiao G, Zhong H, Guo Y 2020 New J. Phys. 22 083086 Google Scholar
[24]	Weedbrook C 2013 Phys. Rev. A 87 022308 Google Scholar
[25]	Liao Q, Xiao G, Xu C G, Xu Y, Guo Y 2020 Phys. Rev. A 102 032604 Google Scholar
[26]	Fossier S, Diamanti E, Debuisschert T, Tualle-Brouri R, Grangier P 2009 J. Phys. B: At., Mol. Opt. Phys. 42 114014 Google Scholar
[27]	Zhang H, Fang J, He G Q 2012 Phys. Rev. A 86 022338 Google Scholar
[28]	Wu X D, Wang Y J, Liao Q, Zhong H, Guo Y 2019 Entropy 21 333 Google Scholar
[29]	Pirandola S, Braunstein S L, Lloyd S 2008 Phys. Rev. Lett. 101 200504
[30]	García-Patrón R, Cerf N J 2006 Phys. Rev. Lett. 97 190503 Google Scholar
[31]	Navascués M, Grosshans F, Acín A 2006 Phys. Rev. Lett. 97 190502 Google Scholar
[32]	Huang D, Huang P, Lin D K, Zeng G H 2016 Sci. Rep. 6 19201 Google Scholar
[33]	Huang D, Lin D K, Wang C, Liu W Q, Fang S H, Peng J Y, Huang P, Zeng G H 2015 Opt. Express 23 017511 Google Scholar
[34]	Jouguet P, Kunz-Jacques S, Leverrier A, Grangier P, Diamanti E 2013 Nat. Photonics 7 378 Google Scholar
[35]	Huang L Y, Zhang Y C, Huang Y D, Jiang T W, Yu S 2019 Phys. B: At. Mol. Opt. Phys. 52 225502 Google Scholar
[36]	Zhang Y C, Li Z Y, Weedbrook C, Yu S, Gu W Y, Sun M Z, Peng X, Guo H 2014 J. Phys. B: At., Mol. Opt. Phys. 47 035501 Google Scholar
[37]	Guo Y, Li R J, Liao Q, Zhou J, Huang D 2018 Phys. Lett. A 382 372 Google Scholar
[38]	Blandino R, Leverrier A, Barbieri M, Etesse J, Grangier P, Tualle-Brouri R 2012 Phys. Rev. A 86 012327 Google Scholar
[39]	Bencheikh K, Lopez O, Abram I, Levenson J A 1995 Appl. Phys. Lett. 66 399 Google Scholar

施引文献

图 1 基于不可信纠缠源的GMCVQKD的方案图

Fig. 1. Scheme diagram of the GMCVQKD based on untrusted entanglement source.

下载: 全尺寸图片幻灯片

图 2 纠缠源可信的GMCVQKD的方案图

Fig. 2. Scheme diagram of the GMCVQKD with trusted entanglement source.

下载: 全尺寸图片幻灯片

图 3 零差探测下不可信纠缠源的GMCVQKD方案的与原始GMCVQKD方案的性能对比　(a) 两种方案的安全密钥率与传输距离的关系; (b)两种方案的互信量与传输距离的关系; (c)两种方案的Holevo界与传输距离的关系

Fig. 3. The performance comparison between the GMCVQKD scheme with an untrusted entanglement source and the original GMCVQKD scheme under homodyne detection: (a) The relationship between the security key rate and transmission distance of the two schemes; (b) the relationship between mutual information and transmission distance of the two schemes; (c) the relationship between Holevo bound and transmission distance of two schemes.

下载: 全尺寸图片幻灯片

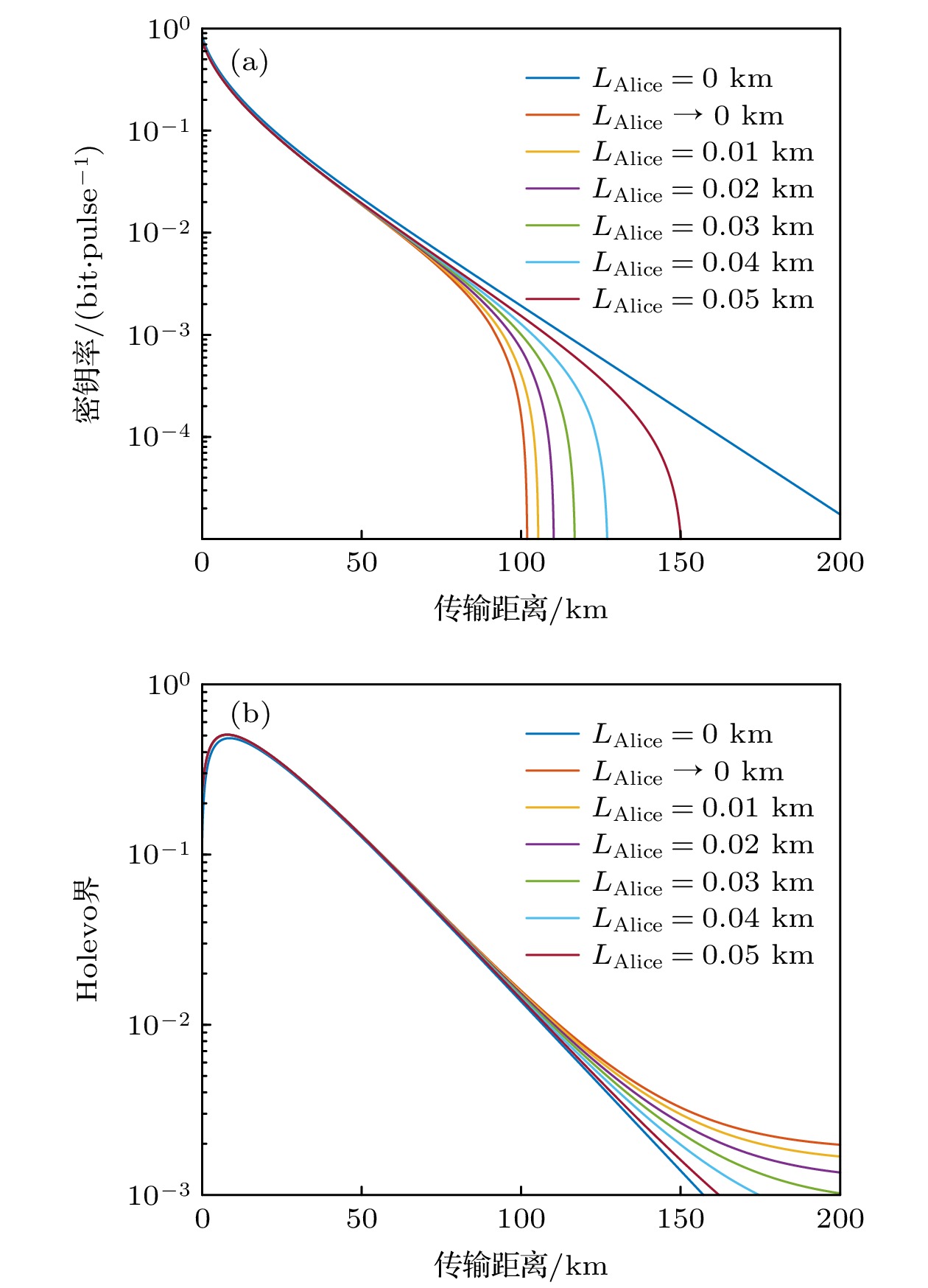
图 4 零差探测下基于不可信纠缠源的GMCVQKD方案在不同纠缠源距离下的性能　(a)所提方案的安全密钥率与传输距离的关系; (b)所提方案的Holevo界与传输距离的关系

Fig. 4. Performance of the GMCVQKD scheme based on an untrusted entanglement source with homodyne detection at different entanglement source distances: (a) Relationship between the security key rate of the proposed scheme and the transmission distance; (b) relationship between the Holevo bound of the proposed scheme and the transmission distance.

下载: 全尺寸图片幻灯片

图 5 零差探测下基于不可信纠缠源的GMCVQKD方案在不同过噪声下的性能

Fig. 5. The performance of the GMCVQKD scheme based on an untrusted entanglement source under different excess noise.

下载: 全尺寸图片幻灯片

图 6 外差探测下基于不可信纠缠源的GMCVQKD方案在不同纠缠源距离下的性能　(a) 所提方案的安全密钥率与传输距离的关系; (b)所提方案的Holevo界与传输距离的关系

Fig. 6. Performance of the GMCVQKD scheme based on an untrusted entanglement source with heterodyne detection at different entanglement source distances: (a) Relationship between the security key rate of the proposed scheme and the transmission distance; (b) relationship between the Holevo bound of the proposed scheme and the transmission distance.

下载: 全尺寸图片幻灯片

图 7 PSA的模型

Fig. 7. Model of PSA.

下载: 全尺寸图片幻灯片

图 8 零差探测与PSA组合后的安全密钥率

Fig. 8. Security key rate for the combination of homodyne detection and PSA.

下载: 全尺寸图片幻灯片

图 9 PIA的模型

Fig. 9. Model of PIA.

下载: 全尺寸图片幻灯片

图 10 外差探测与PIA组合后的安全密钥率

Fig. 10. Security key rate for the combination of heterodyne detection and PIA.

下载: 全尺寸图片幻灯片

map

[1]	Zhou N R, Li J F, Yu Z B, Gong L H, Farouk A 2016 Quantum Inf. Process 16 4
[2]	Scarani V, Bechmann-Pasquinucci H, Cerf N J, Dušek M, Lütkenhaus N, Peev M 2009 Rev. Mod. Phys. 81 1301 Google Scholar
[3]	Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145 Google Scholar
[4]	Gong L H, Li J F, Zhou N R 2018 Laser Phys. Lett. 15 105204 Google Scholar
[5]	Liao Q, Liu H J, Zhu L J, Guo Y 2021 Phys. Rev. A 103 032410 Google Scholar
[6]	Liao Q, Liu H J, Gong Y P, Wang Z, Peng Q Q, Guo Y 2022 Opt. Express 30 3876 Google Scholar
[7]	宋汉冲, 龚黎华, 周南润 2012 61 154206 Google Scholar Song H C, Gong L H, Zhou N R 2012 Acta Phys. Sin. 61 154206 Google Scholar
[8]	Zhou N R, Wang L J, Ding J, Gong L H, Zuo X W 2010 Int. J. Theor. Phys. 49 2035 Google Scholar
[9]	Guo Y, Liao Q, Wang Y J, Huang D, Huang P, Zeng G H 2017 Phys. Rev. A 95 032304 Google Scholar
[10]	钟海, 叶炜, 吴晓东, 郭迎 2021 70 020301 Google Scholar Zhong H, Ye W, Wu X D, Guo Y 2021 Acta Phys. Sin. 70 020301 Google Scholar
[11]	Lance A M, Symul T, Sharma V, Weedbrook C, Ralph T C, Lam P K 2005 Phys. Rev. Lett. 95 180503 Google Scholar
[12]	Ma X C, Sun S H, Jiang M S, Gui M, Liang L M 2014 Phys. Rev. A 89 042335 Google Scholar
[13]	Grosshans F, Grangier P 2002 Phys. Rev. Lett. 88 057902 Google Scholar
[14]	Leverrier A 2015 Phys. Rev. Lett. 114 070501 Google Scholar
[15]	Leverrier A, Grosshans F, Grangier P 2010 Phys. Rev. A 81 062343 Google Scholar
[16]	Jouguet P, Kunz-Jacques S, Diamanti E 2013 Phys. Rev. A 87 062313 Google Scholar
[17]	Ma X C, Sun S H, Jiang M S, Liang L M 2013 Phys. Rev. A 88 022339 Google Scholar
[18]	Qin H, Kumar R, Alléaume R 2016 Phys. Rev. A 94 012325 Google Scholar
[19]	Huang J Z, Weedbrook C, Yin Z Q, Wang S, Li H W, Chen W, Guo G C, Han Z F 2013 Phys. Rev. A 87 062329 Google Scholar
[20]	Ma X C, Sun S H, Jiang M S, Liang L M 2013 Phys. Rev. A 87 052309 Google Scholar
[21]	Qin H, Kumar R, Makarov V, Alléaume R 2018 Phys. Rev. A 98 012312 Google Scholar
[22]	Zhou N R, Zhang T F, Xie X W, Wu J Y 2023 Signal Process. Image Commun. 110 116891 Google Scholar
[23]	Liao Q, Xiao G, Zhong H, Guo Y 2020 New J. Phys. 22 083086 Google Scholar
[24]	Weedbrook C 2013 Phys. Rev. A 87 022308 Google Scholar
[25]	Liao Q, Xiao G, Xu C G, Xu Y, Guo Y 2020 Phys. Rev. A 102 032604 Google Scholar
[26]	Fossier S, Diamanti E, Debuisschert T, Tualle-Brouri R, Grangier P 2009 J. Phys. B: At., Mol. Opt. Phys. 42 114014 Google Scholar
[27]	Zhang H, Fang J, He G Q 2012 Phys. Rev. A 86 022338 Google Scholar
[28]	Wu X D, Wang Y J, Liao Q, Zhong H, Guo Y 2019 Entropy 21 333 Google Scholar
[29]	Pirandola S, Braunstein S L, Lloyd S 2008 Phys. Rev. Lett. 101 200504
[30]	García-Patrón R, Cerf N J 2006 Phys. Rev. Lett. 97 190503 Google Scholar
[31]	Navascués M, Grosshans F, Acín A 2006 Phys. Rev. Lett. 97 190502 Google Scholar
[32]	Huang D, Huang P, Lin D K, Zeng G H 2016 Sci. Rep. 6 19201 Google Scholar
[33]	Huang D, Lin D K, Wang C, Liu W Q, Fang S H, Peng J Y, Huang P, Zeng G H 2015 Opt. Express 23 017511 Google Scholar
[34]	Jouguet P, Kunz-Jacques S, Leverrier A, Grangier P, Diamanti E 2013 Nat. Photonics 7 378 Google Scholar
[35]	Huang L Y, Zhang Y C, Huang Y D, Jiang T W, Yu S 2019 Phys. B: At. Mol. Opt. Phys. 52 225502 Google Scholar
[36]	Zhang Y C, Li Z Y, Weedbrook C, Yu S, Gu W Y, Sun M Z, Peng X, Guo H 2014 J. Phys. B: At., Mol. Opt. Phys. 47 035501 Google Scholar
[37]	Guo Y, Li R J, Liao Q, Zhou J, Huang D 2018 Phys. Lett. A 382 372 Google Scholar
[38]	Blandino R, Leverrier A, Barbieri M, Etesse J, Grangier P, Tualle-Brouri R 2012 Phys. Rev. A 86 012327 Google Scholar
[39]	Bencheikh K, Lopez O, Abram I, Levenson J A 1995 Appl. Phys. Lett. 66 399 Google Scholar

[1]	张光伟, 白建东, 颉琦, 靳晶晶, 张永梅, 刘文元. 连续变量量子密钥分发系统中动态偏振控制研究. , 2024, 73(6): 060301. doi: 10.7498/aps.73.20231890
[2]	吴晓东, 黄端. 基于非理想测量基选择的水下连续变量量子密钥分发方案. , 2024, 73(21): 210302. doi: 10.7498/aps.73.20240804
[3]	张云杰, 王旭阳, 张瑜, 王宁, 贾雁翔, 史玉琪, 卢振国, 邹俊, 李永民. 基于硬件同步的四态离散调制连续变量量子密钥分发. , 2024, 73(6): 060302. doi: 10.7498/aps.73.20231769
[4]	吴晓东, 黄端. 基于非高斯态区分探测的往返式离散调制连续变量量子密钥分发方案. , 2023, 72(5): 050303. doi: 10.7498/aps.72.20222253
[5]	杨瑞科, 李福军, 武福平, 卢芳, 魏兵, 周晔. 沙尘湍流大气对自由空间量子通信性能影响研究. , 2022, 71(22): 220302. doi: 10.7498/aps.71.20221125
[6]	危语嫣, 高子凯, 王思颖, 朱雅静, 李涛. 基于单光子双量子态的确定性安全量子通信. , 2022, 71(5): 050302. doi: 10.7498/aps.71.20210907
[7]	刘瑞熙, 马磊. 海洋湍流对光子轨道角动量量子通信的影响. , 2022, 71(1): 010304. doi: 10.7498/aps.71.20211146
[8]	陈以鹏, 刘靖阳, 朱佳莉, 方伟, 王琴. 机器学习在量子通信资源优化配置中的应用. , 2022, 71(22): 220301. doi: 10.7498/aps.71.20220871
[9]	徐笑吟, 刘胜帅, 荆杰泰. 基于四波混频过程的纠缠光放大. , 2022, 71(5): 050301. doi: 10.7498/aps.71.20211324
[10]	Xiaoyin Xu, shengshuai liu, 荆杰泰. 基于四波混频过程的纠缠光放大. , 2021, (): . doi: 10.7498/aps.70.20211324
[11]	李熙涵. 量子直接通信. , 2015, 64(16): 160307. doi: 10.7498/aps.64.160307
[12]	张沛, 周小清, 李智伟. 基于量子隐形传态的无线通信网络身份认证方案. , 2014, 63(13): 130301. doi: 10.7498/aps.63.130301
[13]	聂敏, 张琳, 刘晓慧. 量子纠缠信令网Poisson生存模型及保真度分析. , 2013, 62(23): 230303. doi: 10.7498/aps.62.230303
[14]	何锐. 基于超导量子干涉仪与介观LC共振器耦合电路的量子通信. , 2012, 61(3): 030303. doi: 10.7498/aps.61.030303
[15]	宋汉冲, 龚黎华, 周南润. 基于量子远程通信的连续变量量子确定性密钥分配协议. , 2012, 61(15): 154206. doi: 10.7498/aps.61.154206
[16]	印娟, 钱勇, 李晓强, 包小辉, 彭承志, 杨涛, 潘阁生. 远距离量子通信实验中的高维纠缠源. , 2011, 60(6): 060308. doi: 10.7498/aps.60.060308
[17]	周南润, 曾宾阳, 王立军, 龚黎华. 基于纠缠的选择自动重传量子同步通信协议. , 2010, 59(4): 2193-2199. doi: 10.7498/aps.59.2193
[18]	沈咏, 邹宏新. 离散调制连续变量量子密钥分发的安全边界. , 2010, 59(3): 1473-1480. doi: 10.7498/aps.59.1473
[19]	周小清, 邬云文. 利用三粒子纠缠态建立量子隐形传态网络的探讨. , 2007, 56(4): 1881-1887. doi: 10.7498/aps.56.1881
[20]	周南润, 曾贵华, 龚黎华, 刘三秋. 基于纠缠的数据链路层量子通信协议. , 2007, 56(9): 5066-5070. doi: 10.7498/aps.56.5066

计量

文章访问数: 3744
PDF下载量: 98
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于不可信纠缠源的高斯调制连续变量量子密钥分发