-
离子回旋共振(ion cyclotron resonance, ICR)方法是一种通过选择性加热目标离子实现分离效应的先进同位素分离方法. 为确定各参数对ICR分离过程影响, 开展了ICR同位素分离理论研究, 基于单粒子模型方法对等离子体束流在稳恒磁场与交变电场组合场中的传输过程进行数值模拟, 对初始等离子体束流、共振加热区电磁场等影响分离效应的核心参数进行分析. 结果表明, 共振区交变电场强度、射频天线波长、共振区尺寸、等离子体初始轴向能量及其分布对等离子体束流整体加热效果均存在明显影响; 共振区磁感应强度、射频天线波长、等离子体初始轴向能量分布对加热过程的选择性存在直接影响. 所得结论对ICR分离装置参数的初步设计有一定借鉴价值.The ion cyclotron resonance (ICR) isotope separation method is an advanced electromagnetic separation method. The key process of this method is the transport of ions in an axial magnetic field. By injecting microwaves at the target ion cyclotron frequency, only the target ions can be heated so that the energy values of target ions can be distinguished. Due to its high separation coefficient, multiple types of isotopes that can be separated, and high flux, some countries have already built ICR isotope separation devices and conducted various isotope separation experiments since 1980. The main elements of an ICR separation device include three parts: a plasma source, a selective ion heating system, and an ion collector. The electron cyclotron resonance (ECR) ion source is the most popular plasma source, which generates the ions to be separated. The selective ion heating system is the key part of the separation device, mainly composed of a superconducting magnetic coil and a radio frequency (RF) antenna, which are used to provide a stable magnetic field and microwaves at a specific frequency to heat the target isotope ions, respectively. The ion collector is used to collect the separated ions. To clarify the key process of the ICR separation method, the transport process of ions in the electromagnetic field inside the selective ion heating system is simulated, and the influences on the selective heating effects of core parameters, such as parameters of initial plasma beam and electromagnetic field inside the selective ion heating system, are discussed in detail. The numerical simulation model used in this study is the single particle model, in which the interaction between ions and the induced electromagnetic field of the plasma beam is ignored. The simulation results show that the intensity of the alternating electric field in the selective ion heating system, the wavelength of the RF antenna, the size of the ion selective heating system, the initial axial energy of the plasma and its distribution all have a significant influence on the overall heating effect of the plasma beam. The magnetic induction intensity in the ion selective heating system, the wavelength of the RF antenna, and the initial axial energy distribution of the plasma have a direct influence on the selectivity of the heating process. Considering the limitations of the single particle model, a more accurate model will be used for further simulation. The design of the RF antenna and ECR ion source will also be considered in the further research.
-
Keywords:
- ion cyclotron resonance /
- isotope separation /
- selective heating /
- plasma flow
[1] 杜丹 2015 博士学位论文 (衡阳: 南华大学)
Du D 2015 Ph. D. Dissertation (Hengyang: University of South China
[2] Li J G, Wang B N 2011 Nucl. Fusion. 51 09007
Google Scholar
[3] Bering E A, Chang-Diaz F R, Squire J P, et al. 2008 Adv. Space Res. 42 192
Google Scholar
[4] 杨涓, 牟浩, 耿海, 吴先明 2023 推进技术 44 2208095
Google Scholar
Yang J, Mou H, Gen H, Wu X M 2023 J. Propul. Technol. 44 2208095
Google Scholar
[5] Schmitt J P M 1973 Phys. Rev. Lett. 31 982
Google Scholar
[6] Dolgolenko D A, Muromkin Y A 2009 Phys. -Usp. 52 345
Google Scholar
[7] Tracy J G, Aaron W S 1993 Nucl. Instrum. Methods Phys. Res. Sect. A. 334 45
Google Scholar
[8] Stevenson N R, Bigelow T S, Tarallo F J 2003 J. Radioanal. Nucl. Chem. 257 153
Google Scholar
[9] Louvet P, Compant A, Larousse B, Patris M 1994 Proceeding of 4th Workshop on Separation Phenomena in Liquids and Gases Beijing, China, August 21–25, 1994 p83
[10] Dolgolenko D A, Muromkin Y A, Pashkovsky V G 2019 Instrum. Exp. Tech. 62 798
Google Scholar
[11] Muromkin Y A 2013 J. Energy Power Eng. 7 306
[12] Takao I, Ohmi K, Akira T Ken-ichi T, Tatsuya S, Noriyosu H, Naoto H, Tokushi S 2017 J. Part. Accel. Soc. Jan. 14 15
Google Scholar
[13] Egle B, Asgari M, Bigelow T, et al. https://www.osti.gov/servlets/purl/1647749 [2020-6-30]
[14] Timofeev A V 2007 Plasma Phys. Rep. 33 890
Google Scholar
[15] Gueroult R, Rax J M, Fisch N J 2018 J. Cleaner Prod. 182 1060
Google Scholar
[16] Potanin E P, Ustinov A V 2013 Plasma Phys. Rep. 39 510
Google Scholar
[17] Potanin E P 2022 Instrum. Exp. Tech. 65 766
Google Scholar
[18] 李定, 陈银华, 马锦秀 杨维纮 2006 等离子体物理学 (北京: 高等教育出版社) 第14—19页
Li D, Chen Y H, Ma J X, Yang W H 2006 Plasma Physics (Beijing: Higher Education Press) pp14–19
[19] Berger J M, Newcomb W A, Dawson J M, Frieman E A, Kulsurd R M, Lenard A 1958 Phys. Fluids 1 301
Google Scholar
[20] Potanin E P 2005 Tech. Phys. 50 698
Google Scholar
[21] Ohmi K, Inagaki T, Kichimi H, Takagi A, Tanaka K, Suzuki T, Shibata T, Fujii Y 2013 Jan. J. Appl. Phys. 52 126401
Google Scholar
[22] Potanin E P 2006 Tech. Phys. 51 1586
Google Scholar
[23] 巴朗诺夫 V U著 (王立军译) 2004 同位素性质、制取与应用 (北京: 清华大学出版社) 第215页
Baranov V U (translated by Wang L J) 2004 Isotopes Property, Preparation and Application (Beijing: Tsinghua University Press) p215
-
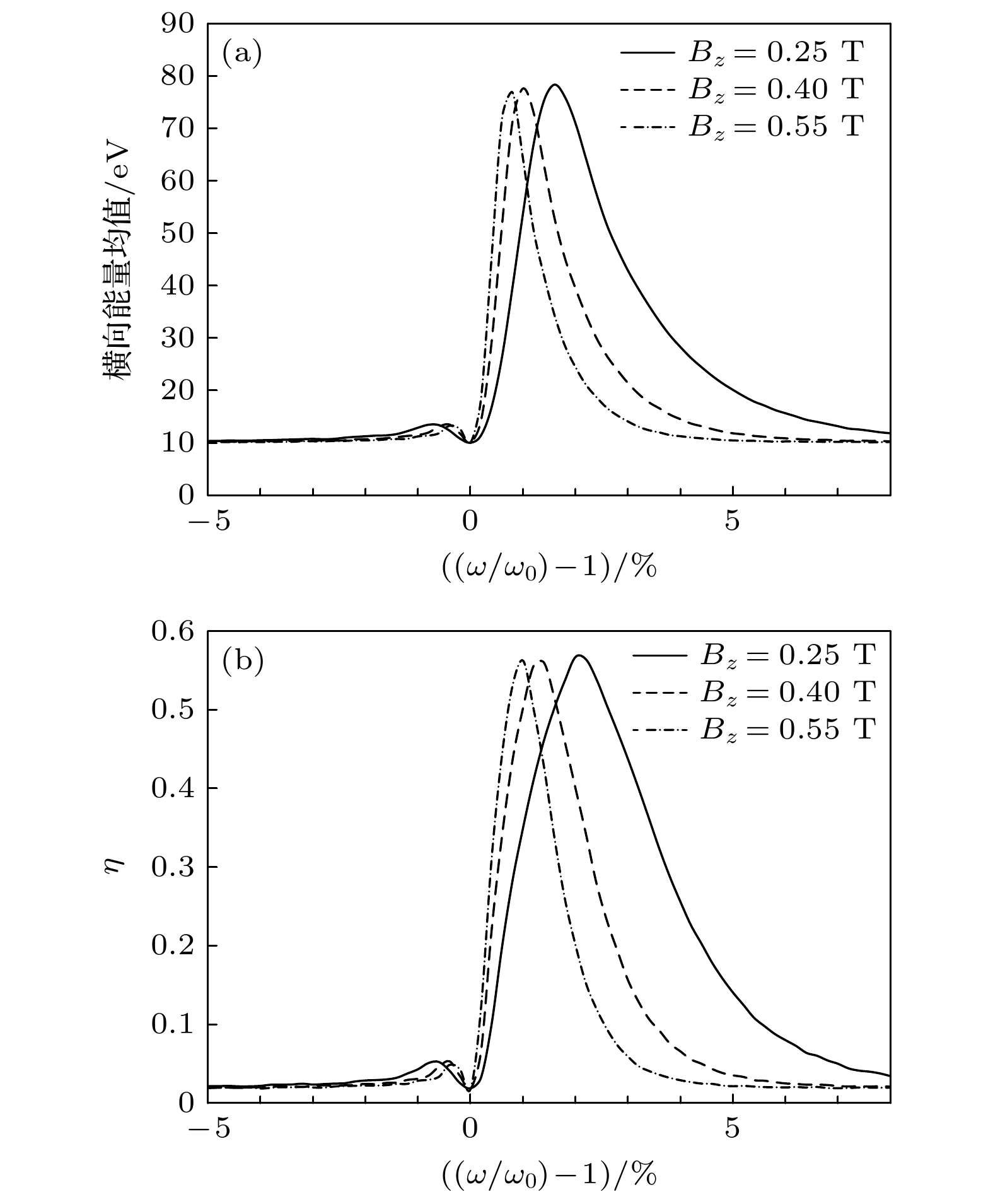
图 2 不同磁感应强度下, (a) 加热区出口离子横向能量均值和(b)加热系数 $ \eta ~(E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ 分布曲线
Fig. 2. Distribution of (a) ion average transverse energy in the exit of the heating field and (b) ion heating efficiency $ \eta ~(E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ for different magnetic induction intensity.
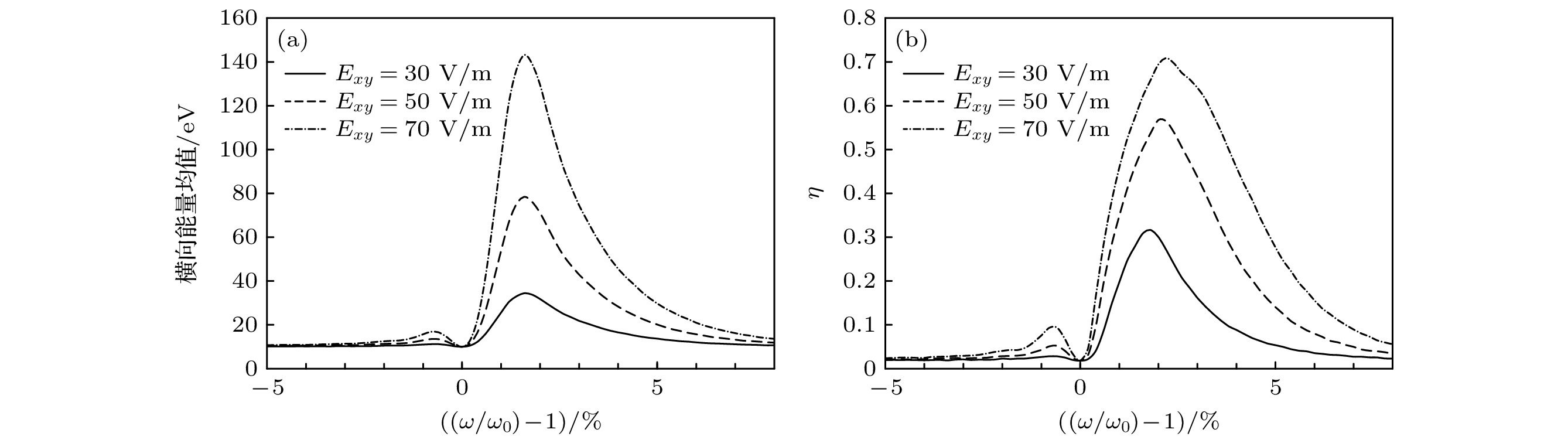
图 3 不同电场强度下, (a) 加热区出口离子横向能量均值和(b)加热系数 $ \eta ~(E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ 分布曲线
Fig. 3. Distribution of (a) ion average transverse energy in the exit of the heating field and (b) ion heating efficiency $ \eta ~(E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ for different electric field intensity.
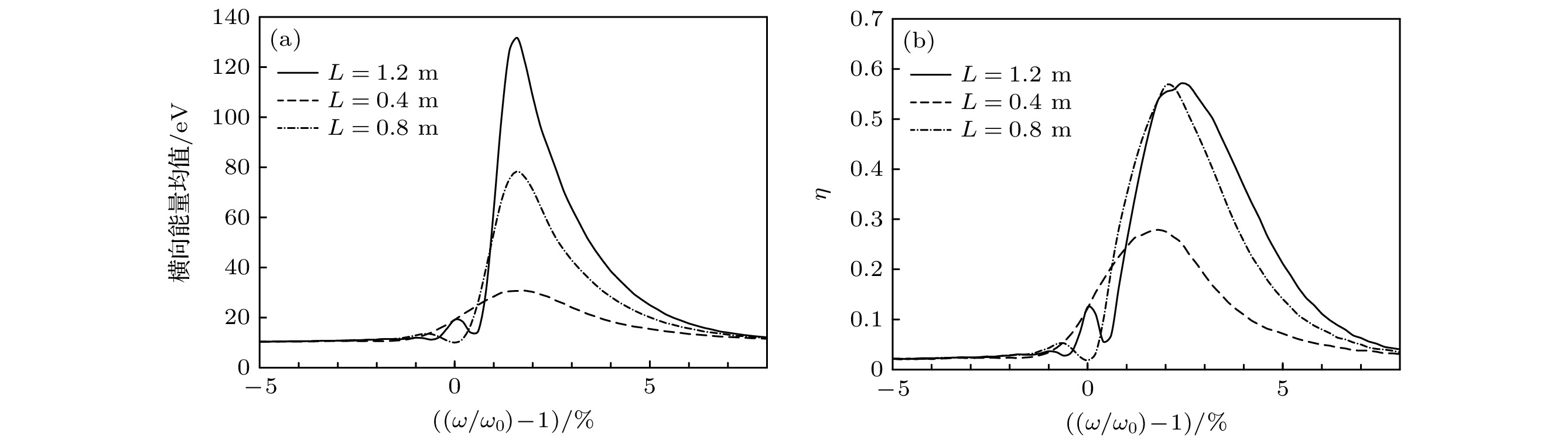
图 4 不同共振区长度下, (a) 加热区出口离子横向能量均值和(b)加热系数 $ \eta~ (E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ 分布曲线
Fig. 4. Distribution of (a) ion average transverse energy in the exit of the heating filed and (b) ion heating efficiency $ \eta~ (E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ for different length of the heating field.
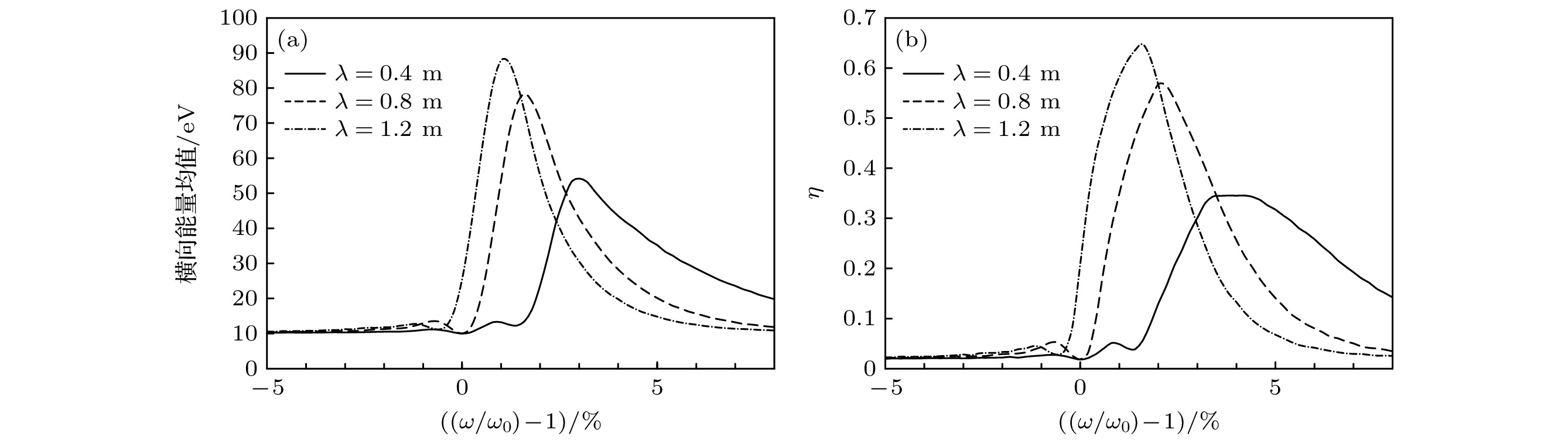
图 5 不同波长下, (a) 加热区出口离子横向能量均值和(b)加热系数 $ \eta~ (E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $分布曲线
Fig. 5. Distribution of (a) ion average transverse energy in the exit of the heating field and (b) ion heating efficiency $ \eta ~(E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ for different wave length.
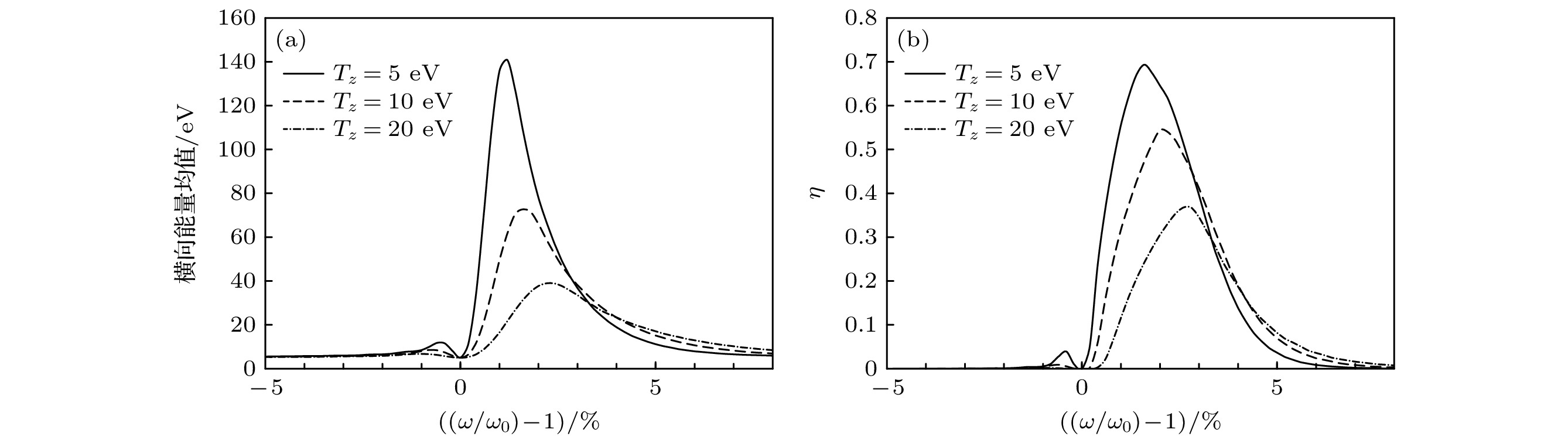
图 6 不同轴向能量下, (a)加热区出口离子横向能量均值和(b)加热系数 $ \eta ~(E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $分布曲线
Fig. 6. Distribution of (a) ion average transverse energy in the exit of the heating field and (b) ion heating efficiency $ \eta~ (E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ for different axial energy.
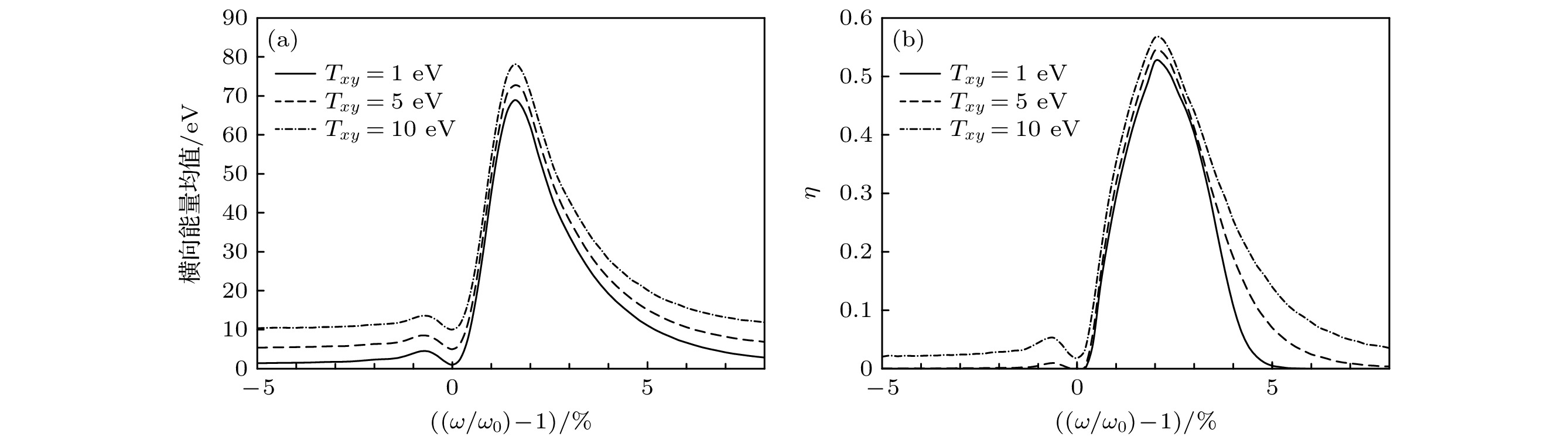
图 7 不同初始横向能量下, (a)加热区出口离子横向能量均值和(b)加热系数 $ \eta~ (E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ 分布曲线
Fig. 7. Distribution of (a) ion average transverse energy in the exit of the heating area and (b) ion heating efficiency $ \eta~ (E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ for different initial transverse energy.
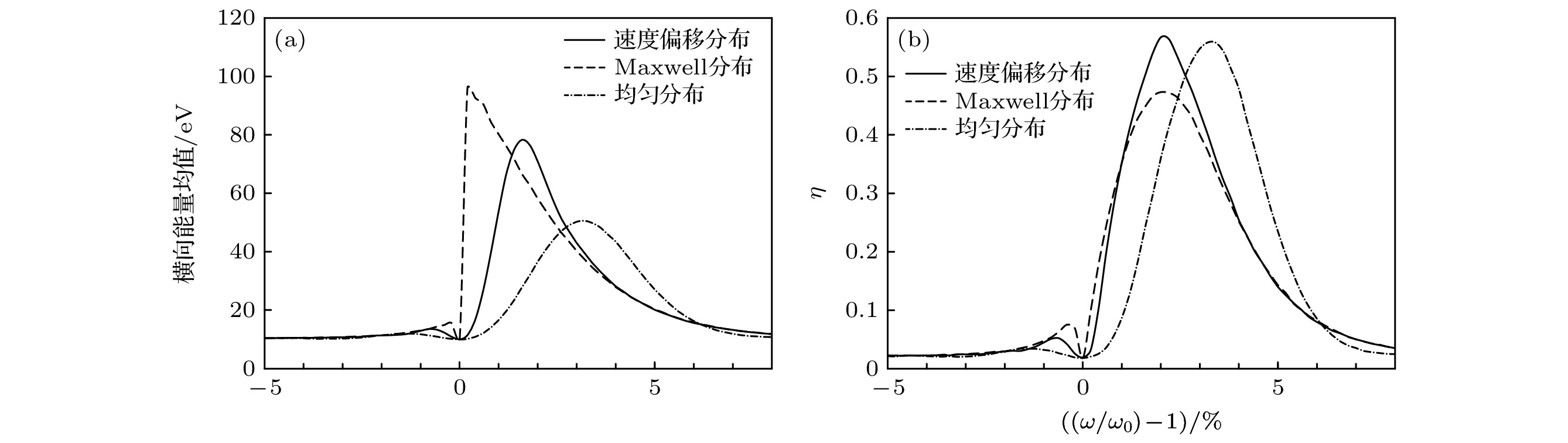
图 8 不同速度分布下, (a)加热区出口离子横向能量均值和(b) 加热系数$ \eta~ (E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $分布曲线(速度偏移分布服从(5)式, 均匀分布为能量范围5—15 eV内的均匀分布, 3种分布形式平均能量均为10 eV)
Fig. 8. Distribution of (a) ion average transverse energy in the exit of the heating area and (b) ion heating efficiency $ \eta~ (E > {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}) $ for different velocity distribution (the shifted velocity distribution follows Eq. (5) with the average energy 10 eV, the same as the Maxwell distribution, and uniform distribution is with the energy between 5 eV and 15 eV).
-
[1] 杜丹 2015 博士学位论文 (衡阳: 南华大学)
Du D 2015 Ph. D. Dissertation (Hengyang: University of South China
[2] Li J G, Wang B N 2011 Nucl. Fusion. 51 09007
Google Scholar
[3] Bering E A, Chang-Diaz F R, Squire J P, et al. 2008 Adv. Space Res. 42 192
Google Scholar
[4] 杨涓, 牟浩, 耿海, 吴先明 2023 推进技术 44 2208095
Google Scholar
Yang J, Mou H, Gen H, Wu X M 2023 J. Propul. Technol. 44 2208095
Google Scholar
[5] Schmitt J P M 1973 Phys. Rev. Lett. 31 982
Google Scholar
[6] Dolgolenko D A, Muromkin Y A 2009 Phys. -Usp. 52 345
Google Scholar
[7] Tracy J G, Aaron W S 1993 Nucl. Instrum. Methods Phys. Res. Sect. A. 334 45
Google Scholar
[8] Stevenson N R, Bigelow T S, Tarallo F J 2003 J. Radioanal. Nucl. Chem. 257 153
Google Scholar
[9] Louvet P, Compant A, Larousse B, Patris M 1994 Proceeding of 4th Workshop on Separation Phenomena in Liquids and Gases Beijing, China, August 21–25, 1994 p83
[10] Dolgolenko D A, Muromkin Y A, Pashkovsky V G 2019 Instrum. Exp. Tech. 62 798
Google Scholar
[11] Muromkin Y A 2013 J. Energy Power Eng. 7 306
[12] Takao I, Ohmi K, Akira T Ken-ichi T, Tatsuya S, Noriyosu H, Naoto H, Tokushi S 2017 J. Part. Accel. Soc. Jan. 14 15
Google Scholar
[13] Egle B, Asgari M, Bigelow T, et al. https://www.osti.gov/servlets/purl/1647749 [2020-6-30]
[14] Timofeev A V 2007 Plasma Phys. Rep. 33 890
Google Scholar
[15] Gueroult R, Rax J M, Fisch N J 2018 J. Cleaner Prod. 182 1060
Google Scholar
[16] Potanin E P, Ustinov A V 2013 Plasma Phys. Rep. 39 510
Google Scholar
[17] Potanin E P 2022 Instrum. Exp. Tech. 65 766
Google Scholar
[18] 李定, 陈银华, 马锦秀 杨维纮 2006 等离子体物理学 (北京: 高等教育出版社) 第14—19页
Li D, Chen Y H, Ma J X, Yang W H 2006 Plasma Physics (Beijing: Higher Education Press) pp14–19
[19] Berger J M, Newcomb W A, Dawson J M, Frieman E A, Kulsurd R M, Lenard A 1958 Phys. Fluids 1 301
Google Scholar
[20] Potanin E P 2005 Tech. Phys. 50 698
Google Scholar
[21] Ohmi K, Inagaki T, Kichimi H, Takagi A, Tanaka K, Suzuki T, Shibata T, Fujii Y 2013 Jan. J. Appl. Phys. 52 126401
Google Scholar
[22] Potanin E P 2006 Tech. Phys. 51 1586
Google Scholar
[23] 巴朗诺夫 V U著 (王立军译) 2004 同位素性质、制取与应用 (北京: 清华大学出版社) 第215页
Baranov V U (translated by Wang L J) 2004 Isotopes Property, Preparation and Application (Beijing: Tsinghua University Press) p215
下载:
计量
- 文章访问数: 380
- PDF下载量: 5
- 被引次数: 0
