-
富集钕-150同位素在核工业、科学研究等领域具有重要应用. 基于高效高选择性多步电离路径, 原子蒸气激光同位素分离法能够实现钕同位素分离, 但现用路径第2步跃迁的同位素位移(isotope shift, IS)几乎为零, 导致产品中Nd-150丰度偏低. 本文基于密度矩阵理论建立了通用的三步电离路径选择性光电离模型, 模型中综合考虑了同位素位移、超精细结构等原子参数和频率、功率、线宽、偏振等激光参数, 可在磁子能级级别计算原子与激光的相互作用过程. 基于上述模型, 通过与文献数据对比获得了现用路径分支比的最优拟合值, 评估了现用路径在不同线宽下的Nd-150丰度水平; 在仅改变第2步跃迁的前提下构造假定电离路径, 开展所有钕同位素的电离率计算, 评估不同同位素位移、超精细结构下的Nd-150丰度, 指导后续原子光谱实验. 数值计算发现第二激发态角动量J3 = 6, 同位素位移IS23,148 ≥ 300 MHz时, 在b12 ≤ 0.5 GHz, b23 ≤ 1.0 GHz, 平行线偏振的典型激光参数下可实现与电磁法相当的Nd-150丰度(> 95%). 在此基础上压窄激光线宽, 能够在保持电离率的同时获得超过电磁法的Nd-150产品. 后续原子光谱实验应着重寻找IS23,148 ≥ 300 MHz, J3 = 6的第2步跃迁, 第2步跃迁的约化电偶极矩达到现用路径的30%即可满足丰度要求.The enriched neodymium-150 (Nd-150) isotope has important applications in fields such as nuclear industry and basic scientific research. The Nd isotope separation can be conducted by atomic vapor laser isotope separation (AVLIS), where the target isotope is selectively ionized through the λ1 = 596 nm → λ2 = 579 nm → λ3 = 640 nm photoionization scheme, and non-target isotopes remain neutral due to the frequency-detuned excitation. Subsequently, an external electric field is applied to extract the ions from the laser-produced plasma. The Nd-150 abundance in the product cannot meet the requirement of the application, attributed to the nearly negligible isotope shift of the λ2 = 579 nm transition, thus resulting in the excess ionization of non-target isotopes. A new high-selectivity photoionization scheme is desirable to address this limitation, and its expected parameter values can be determined through numerical calculations prior to the time-consuming atomic spectroscopy experiments. In this study, a three-step selective photoionization model is established based on the density matrix theory, with the consideration of the hyperfine structures and magnetic sublevels. This model allows the flexible adjustments of atomic parameters (e.g. branching ratio, isotope shift, hyperfine constant) and laser parameters (e.g. frequency, power density, bandwidth, polarization), while the ionization probabilities of magnetic sublevel transitions can be quantitatively predicted. For the existing schemes, the branching ratios are determined by comparing literature data with numerical results, and the Nd-150 abundance values under different laser bandwidths are evaluated. Further, an alternative scheme is numerically explored on the assumption that the first transition remains unchanged and the second transition has a more significant isotope shift and a smaller branching ratio, and the Nd-150 abundance values under different combinations of isotope shifts, hyperfine structures, and laser bandwidths are evaluated, with all the natural Nd isotopes included. From the numerical results, a scheme with the angular momentum of the second excited state J3 = 6, the isotope shift between Nd-148 and Nd-150 IS23,148 ≥ 300 MHz, and a lower reduced dipole matrix element of the second transition reaching approximately 30% of that of λ2 = 579 nm, can produce the high-abundance Nd-150 (>95%, equivalent to that of the electromagnetic separation method) under the bandwidths: b12 ≤ 0.5 GHz and b23 ≤ 1.0 GHz, and parallel linear-polarized lasers. Using the lasers with narrower bandwidth can achieve higher abundance, which is superior to the electromagnetic separation method. The expected high-abundance Nd-150 can be attributed to the combined effects of multi-factors: the larger isotope shift between Nd-150 and Nd-148 than that between other adjacent isotope pairs, the insignificant hyperfine splitting of odd isotopes, and the match between narrow-bandwidth lasers and Nd I spectroscopic parameters. These parameter values can serve as benchmarks helpful for experimental parameter selection in the forthcoming high-precision spectroscopy experiments.
-
Keywords:
- Nd-150 /
- selective photoionization /
- isotope shift /
- hyperfine structure
[1] Akhmedzhanov R A, Gushchin L A, Nizov N A, Nizov V A, Sobgayda D A, Zelensky I V 2024 JETP Lett. 119 834
 Google Scholar
Google Scholar
[2] Liang P J, Liu X, Li P Y, Zhou Z Q, Li C F, Guo G C 2020 J. Opt. Soc. Am. B 37 1653
 Google Scholar
Google Scholar
[3] Broderick K, Lusk R, Hinderer J, Griswold J, Boll R, Garland M, Heilbronn L, Mirzadeh S 2019 Appl. Radiat. Isot. 144 54
 Google Scholar
Google Scholar
[4] Hu F, Cutler C S, Hoffman T, Sieckman G, Volkert W A, Jurisson S S 2002 Nucl. Med. Biol. 29 423
 Google Scholar
Google Scholar
[5] Committee A 2015 Standard Practice for Analysis of Spent Nuclear Fuel to Determine Selected Isotopes and Estimate Fuel Burnup
[6] Suryanarayana M V 2022 Sci. Rep. 12 11471
 Google Scholar
Google Scholar
[7] Barabash A S, Belli P, Bernabei R, Boiko R S, Cappella F, Caracciolo V, Cerulli R, Danevich F A, Fang D L, Ferella F, Incicchitti A, Kobychev V V, Konovalov S I, Laubenstein M, Leoncini A, Merlo V, Nisi S, Niţescu O, Poda D V, Polischuk O G, Shcherbakov I B K, Šimkovic F, Timonina A, Tinkova V S, Tretyak V I, Umatov V I 2025 Eur. Phys. J. C 85 174
 Google Scholar
Google Scholar
[8] https://www.isotopes.gov/products/neodymium
[9] Letokhov V, Ryabov E (Trigg G L ed) 2004 Encyclopedia of Applied Physics (New York: Wiley) pp1015–1028
[10] Babichev A P, Grigoriev I S, Grigoriev A I, Dorovskii A P, D'Yachkov A B, Kovalevich S K, Kochetov V A, Kuznetsov V A, Labozin V P, Matrakhov A V, Mironov S M, Nikulin S A, Pesnya A V, Timofeev N I, Firsov V A, Tsvetkov G O, Shatalova G G 2005 Quantum Electron. 35 879
 Google Scholar
Google Scholar
[11] Grigoriev I, Diachkov A, Kovalevich S, Labosin V, Mironov S, Nikulin S, Pesnia A, Firsov V, Shatalova G, Tsvetkov G 2003 Proc. SPIE Int. Soc. Opt. Eng. 5121 406
[12] D'Yachkov A B, Kovalevich S K, Labozin V P, Mironov S M, Panchenko V Y, Firsov V A, Tsvetkov G O, Shatalova G G 2012 Quantum Electron. 42 953
 Google Scholar
Google Scholar
[13] Kramida A, Ralchenko Y, Reader J, (NIST ASD Team) 2024 NIST Atomic Spectra Database (Gaithersburg, MD: National Institute of Standards and Technology
[14] Miyabe M, Iwata Y, Tomita H, Morita M, Sakamoto T 2024 Spectrochim. Acta Part B At. Spectrosc. 221 107036
 Google Scholar
Google Scholar
[15] van Leeuwen K A H, Eliel E R, Post B H, Hogervorst W 1981 Z. Phys. A 301 95
 Google Scholar
Google Scholar
[16] Zyuzikov A D, Mishin V I, Fedoseev V N 1988 Opt. Spectrosc. 64 287
[17] D'Yachkov A B, Gorkunov A A, Labozin A V, Mironov S M, Panchenko V Y, Firsov V A, Tsvetkov G O 2018 Quantum Electron. 48 75
 Google Scholar
Google Scholar
[18] 张钧尧, 熊静逸, 魏少强, 李云飞, 卢肖勇 2023 72 193203
 Google Scholar
Google Scholar
Zhang J Y, Xiong J Y, Wei S Q, Li Y F, Lu X Y 2023 Acta Phys. Sin. 72 193203
 Google Scholar
Google Scholar
[19] Campbell P, Moore I D, Pearson M R 2016 Prog. Part. Nucl. Phys. 86 127
 Google Scholar
Google Scholar
[20] Yang X F, Wang S J, Wilkins S G, Ruiz R F G 2023 Prog. Part. Nucl. Phys. 129 104005
 Google Scholar
Google Scholar
[21] Lu X Y, Wang L D 2023 Chin. Phys. B 32 53204
 Google Scholar
Google Scholar
[22] Lu X Y, Wang L D 2024 Appl. Radiat. Isot. 210 111334
 Google Scholar
Google Scholar
[23] Demtröder W 2008 Laser Spectroscopy: Vol. 1 Basic Principles (Berlin: Springer) pp5–60
[24] Greenland P T 1990 Contemp. Phys. 31 405
 Google Scholar
Google Scholar
[25] Axner O, Gustafsson J, Omenetto N, Winefordner J D 2004 Spectrochim. Acta Part B At. Spectrosc. 59 1
 Google Scholar
Google Scholar
[26] Agarwal G S 1970 Phys. Rev. A 1 1445
 Google Scholar
Google Scholar
[27] Lambropoulos P, Lyras A 1989 Phys. Rev. A 40 2199
 Google Scholar
Google Scholar
[28] Blagoev K B, Komarovskii V A 1994 At. Data Nucl. Data Tables 56 1
 Google Scholar
Google Scholar
[29] Childs W J, Goodman L S 1972 Phys. Rev. A 6 1772
 Google Scholar
Google Scholar
[30] Shen X P, Wang W L, Zhai L H, Deng H, Xu J, Yuan X L, Wei G Y, Wang W, Fang S, Su Y Y, Li Z M 2018 Spectrochim. Acta Part B At. Spectrosc. 145 96
 Google Scholar
Google Scholar
[31] Lu X Y, Wang L D 2025 J. Phys. B: At. Mol. Opt. Phys. 58 025001
 Google Scholar
Google Scholar
[32] Wakasugi M, Horiguchi T, Guo Jin W, Sakata H, Yoshizawa Y 1990 J. Phys. Soc. Jpn. 59 2700
 Google Scholar
Google Scholar
-
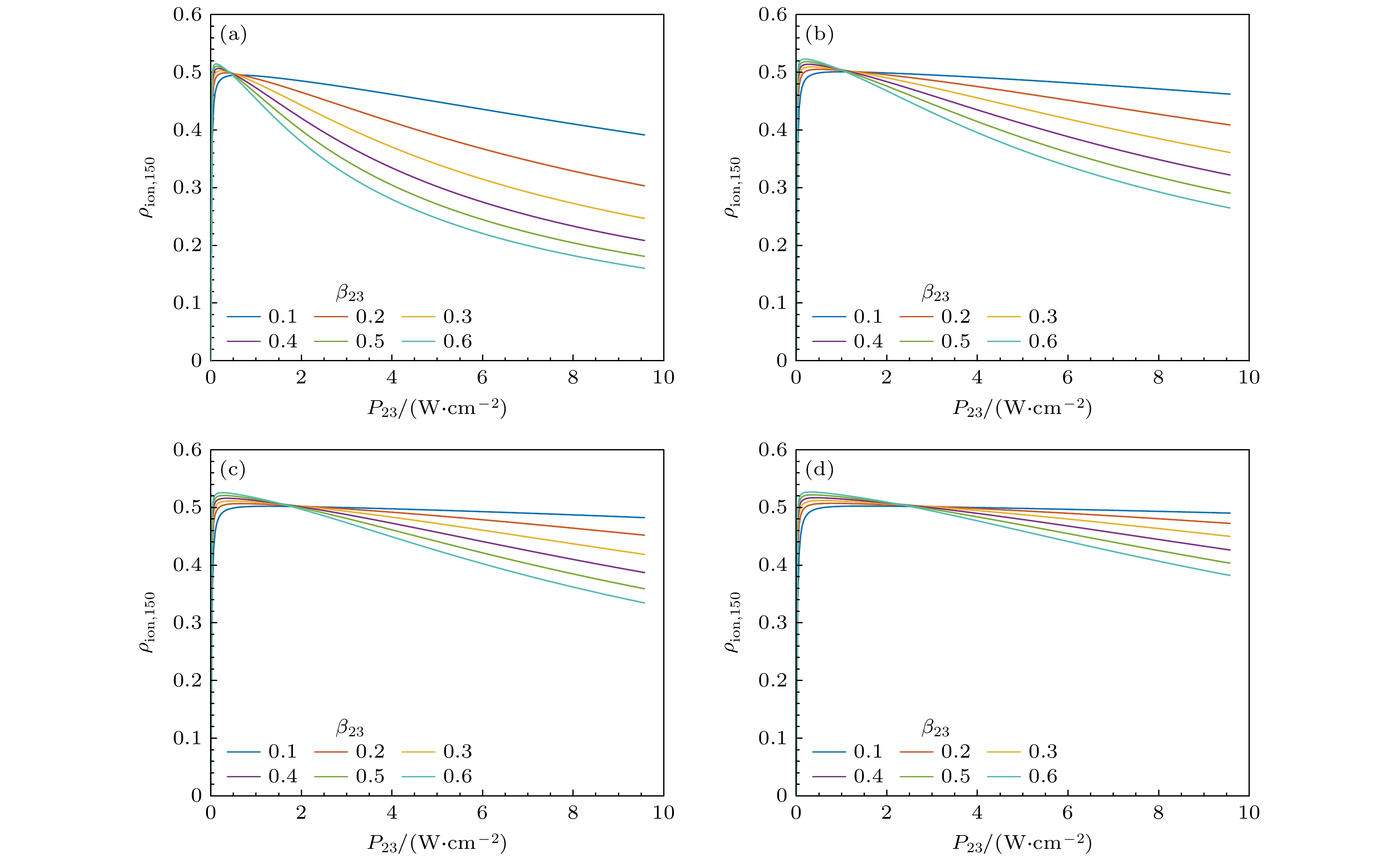
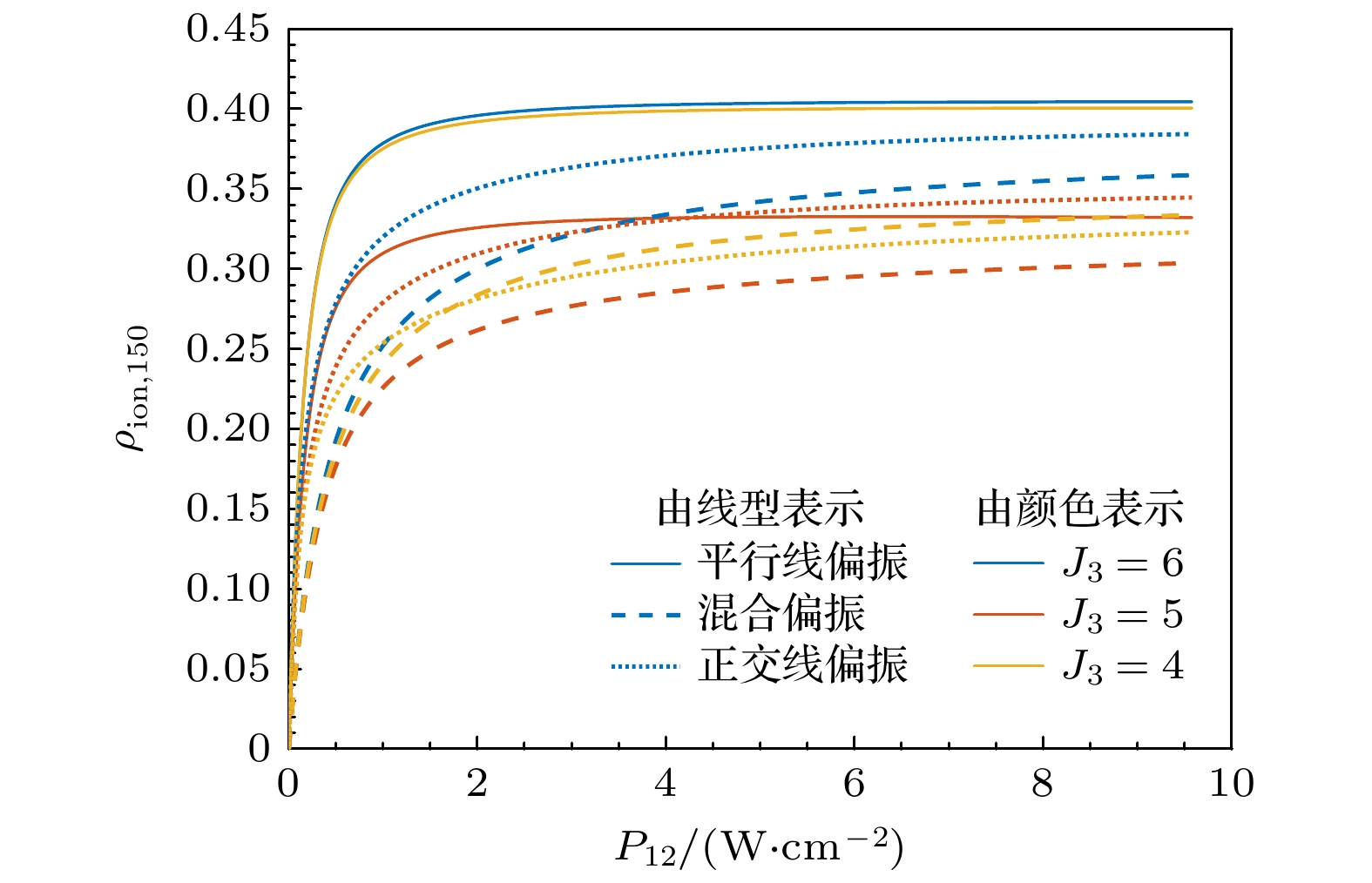
图 3 b23 = 0.1 GHz时, 不同β12, β23下的第2步饱和功率曲线计算值 (a) β12 = 0.05; (b) β12 = 0.1; (c) β12 = 0.15; (d) β12 = 0.2
Fig. 3. The numerical saturated power density curve of the second transition under b23 = 0.1 GHz and different combinations of β12, β23: (a) β12 = 0.05; (b) β12 = 0.1; (c) β12 = 0.15; (d) β12 = 0.2.
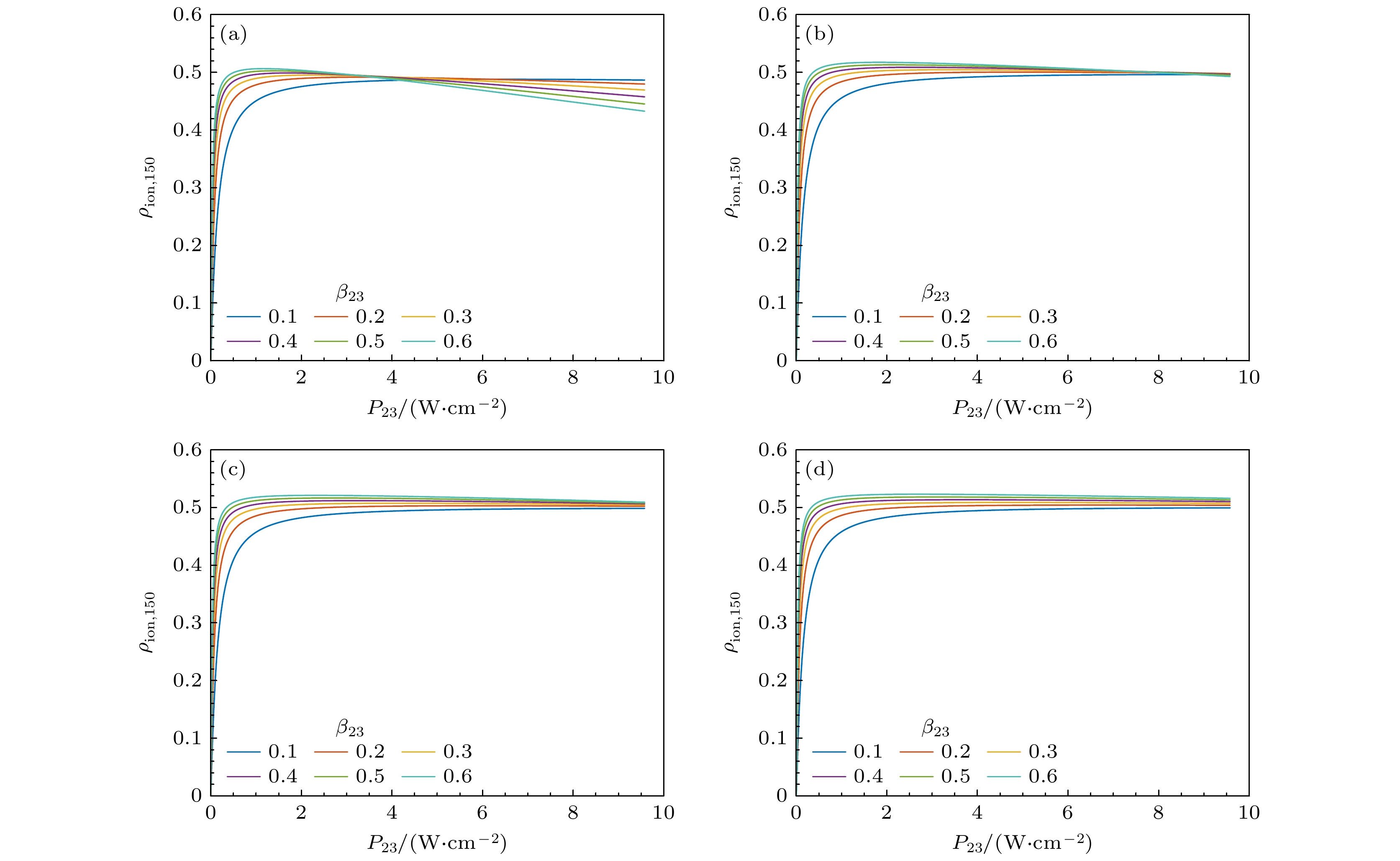
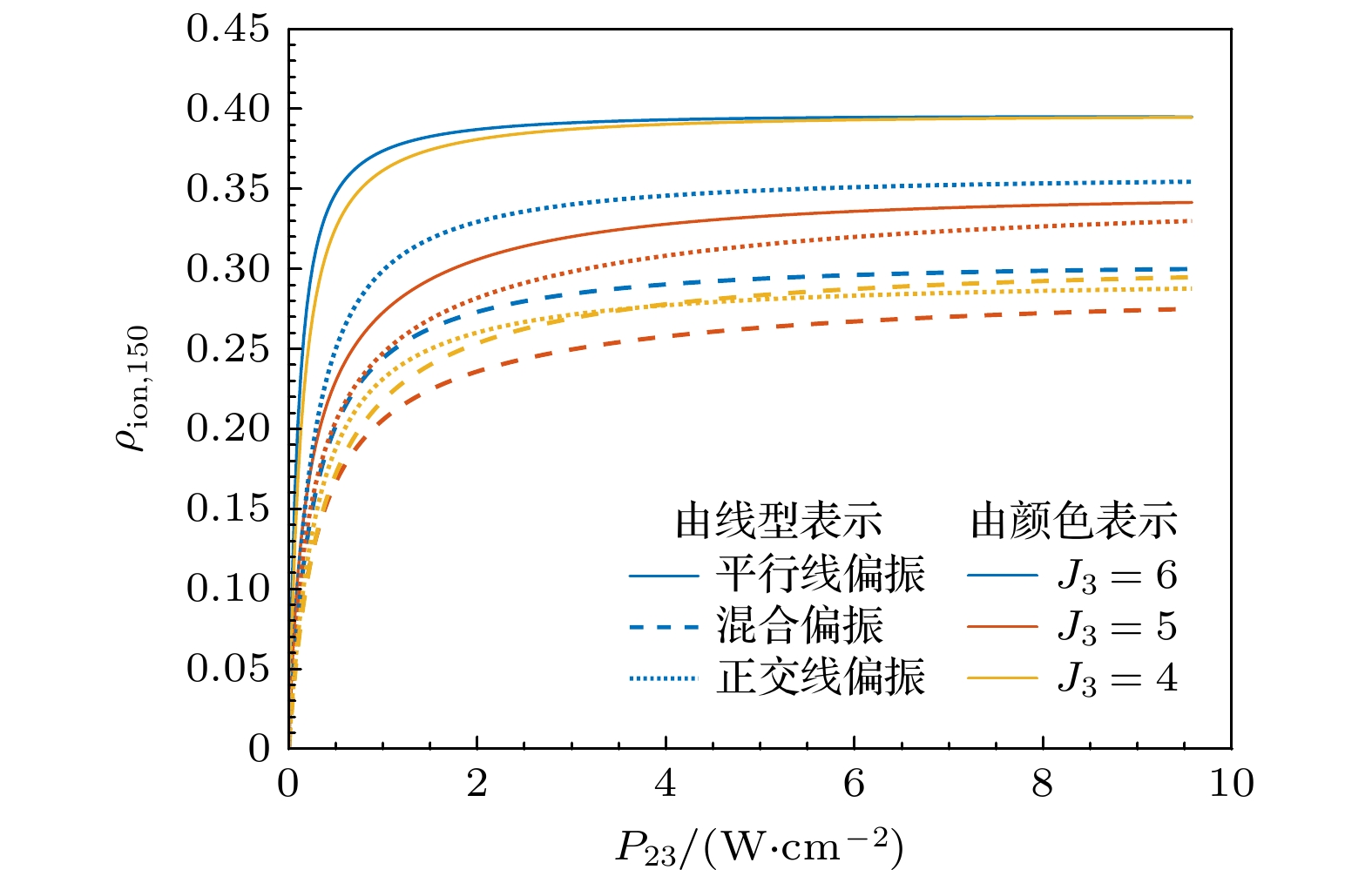
图 4 b23 = 1.5 GHz时, 不同β12, β23下的第2步饱和功率曲线计算值 (a) β12 = 0.05; (b) β12 = 0.1; (c) β12 = 0.15; (d) β12 = 0.2
Fig. 4. The numerical saturated power density curve of the second transition under b23 = 1.5 GHz and different combinations of β12, β23: (a) β12 = 0.05; (b) β12 = 0.1; (c) β12 = 0.15; (d) β12 = 0.2.
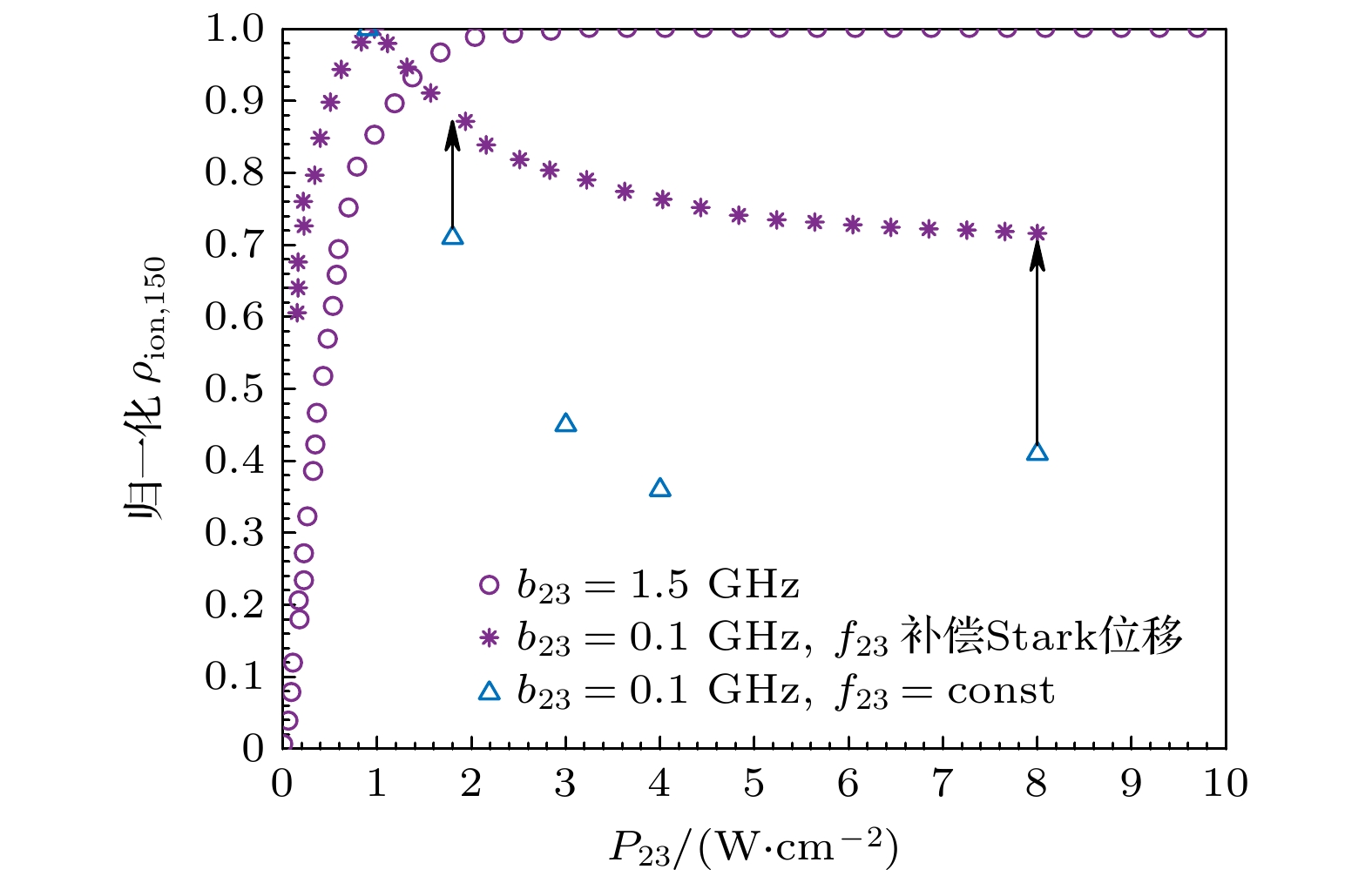
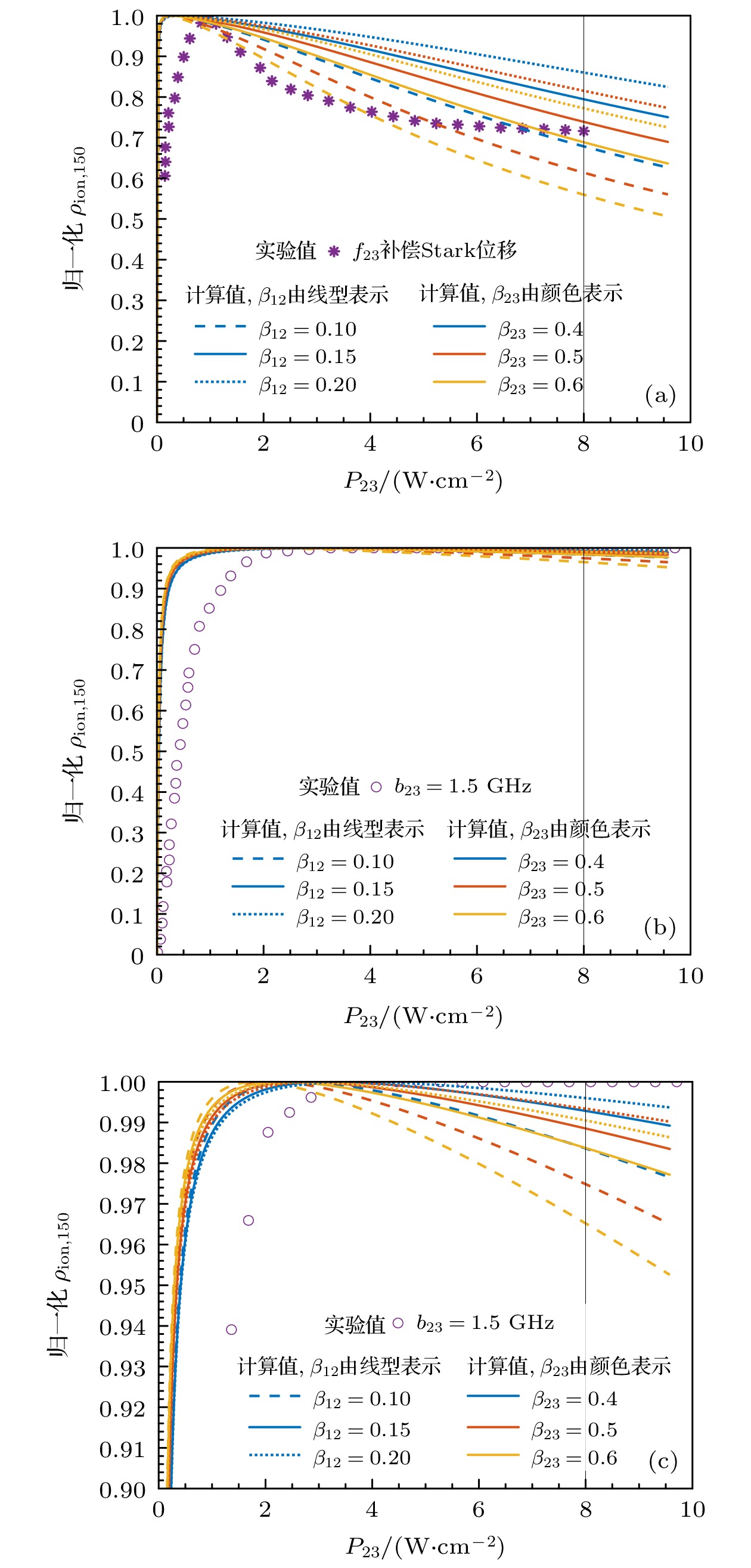
图 5 第2步饱和功率曲线的归一化Nd-150电离率计算值与实验值对比 (a) b23 = 0.1 GHz; (b) b23 = 1.5 GHz; (c) b23 = 1.5 GHz, 纵轴[0.9, 1]的局部放大图
Fig. 5. The numerical and experimental saturated power density curve of the second transition (shown as normalized ionization probability of Nd-150): (a) b23 = 0.1 GHz; (b) b23 = 1.5 GHz; (c) b23 = 1.5 GHz, the partial enlarged view of the vertical axis in the range of [0.9, 1].
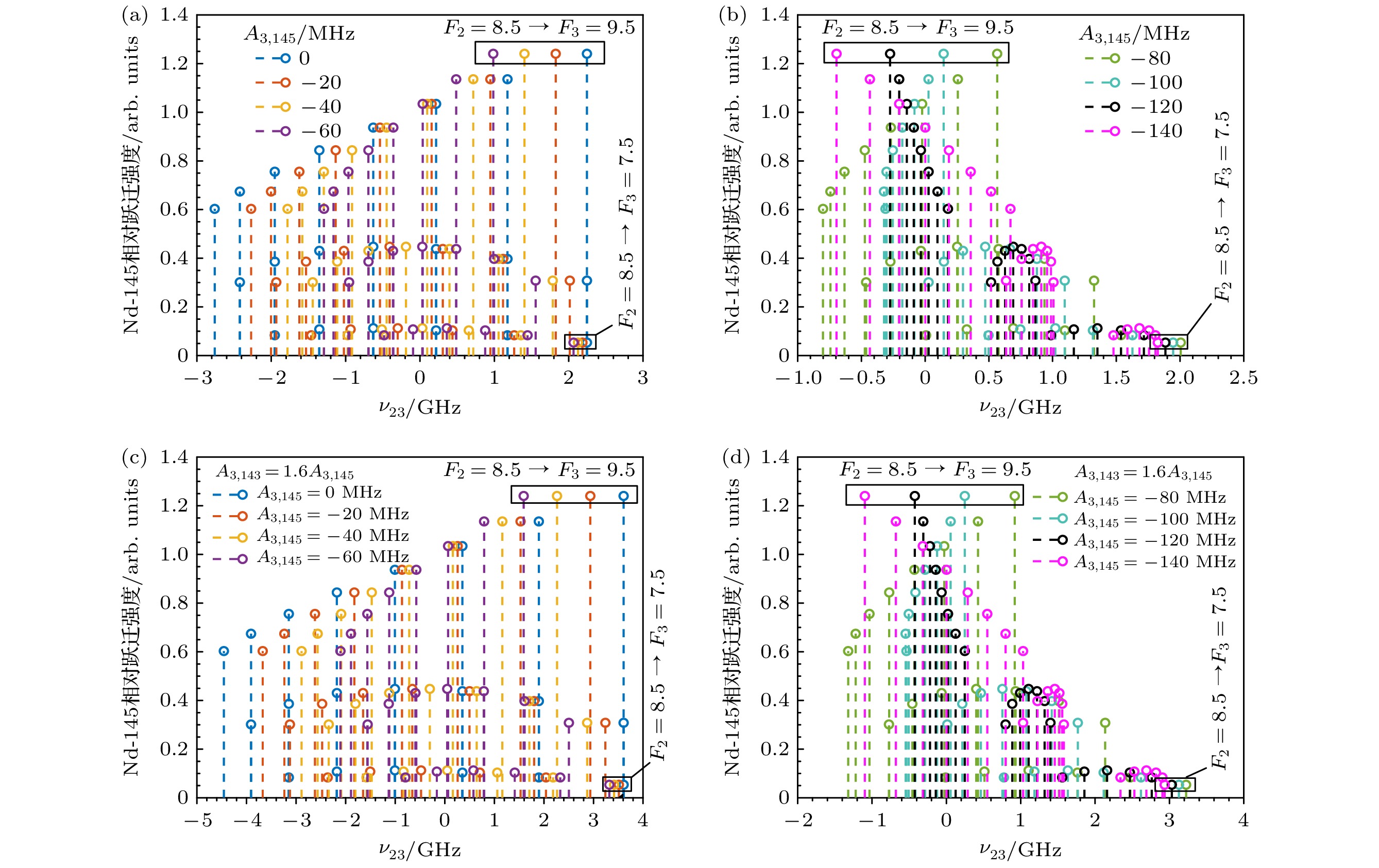
图 9 第二激发态超精细常数A3,145对钕奇同位素第2步跃迁超精细结构的影响, 以B3,145 = 0 MHz, IS23,148 = 0 GHz为示例 (a) Nd-145, A3,145 = 0 MHz, –20 MHz, –40 MHz, –60 MHz; (b) Nd-145, A3,145 = –80 MHz, –100 MHz, –120 MHz, –140 MHz; (c) Nd-143, A3, 143 = 1.6A3,145, A3,145 = 0 MHz, –20 MHz, –40 MHz, –60 MHz; (d) Nd-143, A3,143 = 1.6A3,145, A3,145 = –80 MHz, –100 MHz, –120 MHz, –140 MHz
Fig. 9. The influences of the second excited state’s hyperfine constant A3,145 on the hyperfine structure of the second transition of Nd odd isotopes, taking B3,145 = 0 MHz, IS23,148 = 0 GHz as an example: (a) Nd-145, A3,145 = 0 MHz, –20 MHz, –40 MHz, –60 MHz; (b) Nd-145, A3,145 = –80 MHz, –100 MHz, –120 MHz, –140 MHz; (c) Nd-143, A3,143 = 1.6A3,145, A3,145 = 0 MHz, –20 MHz, –40 MHz, –60 MHz; (d) Nd-143, A3, 143 = 1.6A3,145, A3,145 = –80 MHz, –100 MHz, –120 MHz, –140 MHz.
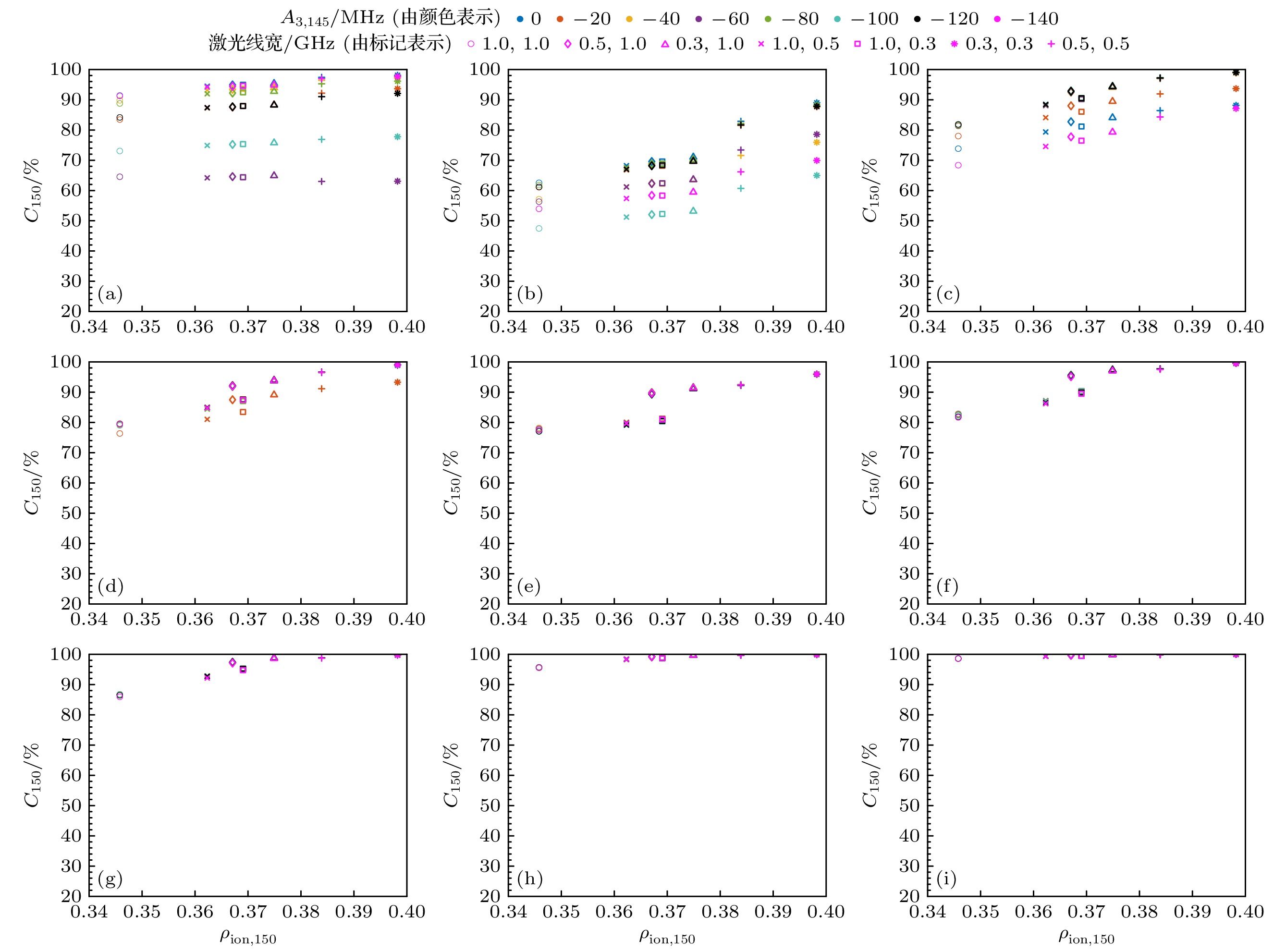
图 10 不同第2步跃迁同位素位移、第二激发态超精细结构下的钕同位素选择性光电离效果 (a) IS23,148 = –1500 MHz; (b) IS23,148 = –1000 MHz; (c) IS23,148 = –500 MHz; (d) IS23,148 = –300 MHz; (e) IS23,148 = 0.0 MHz; (f) IS23,148 = 300 MHz; (g) IS23,148 = 500 MHz; (h) IS23,148 = 1000 MHz; (i) IS23,148 = 1500 MHz
Fig. 10. The selective photoionization effects of Nd isotopes under different combinations of the second transition’s isotope shifts and the second excited state’s hyperfine structures: (a) IS23,148 = –1500 MHz; (b) IS23,148 = –1000 MHz; (c) IS23,148 = –500 MHz; (d) IS23,148 = –300 MHz; (e) IS23,148 = 0.0 MHz; (f) IS23,148 = 300 MHz; (g) IS23,148 = 500 MHz; (h) IS23,148 = 1000 MHz; (i) IS23,148 = 1500 MHz.
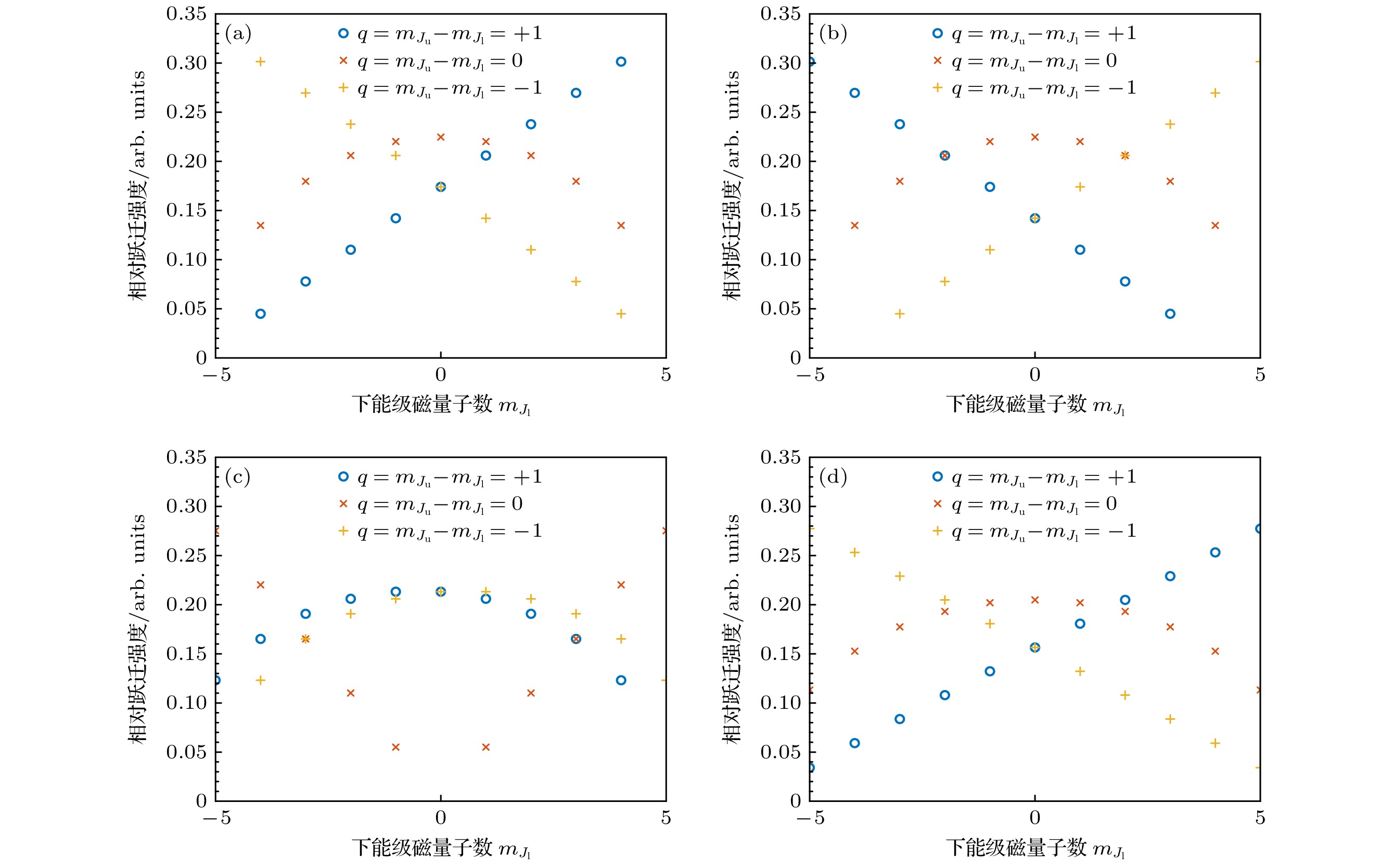
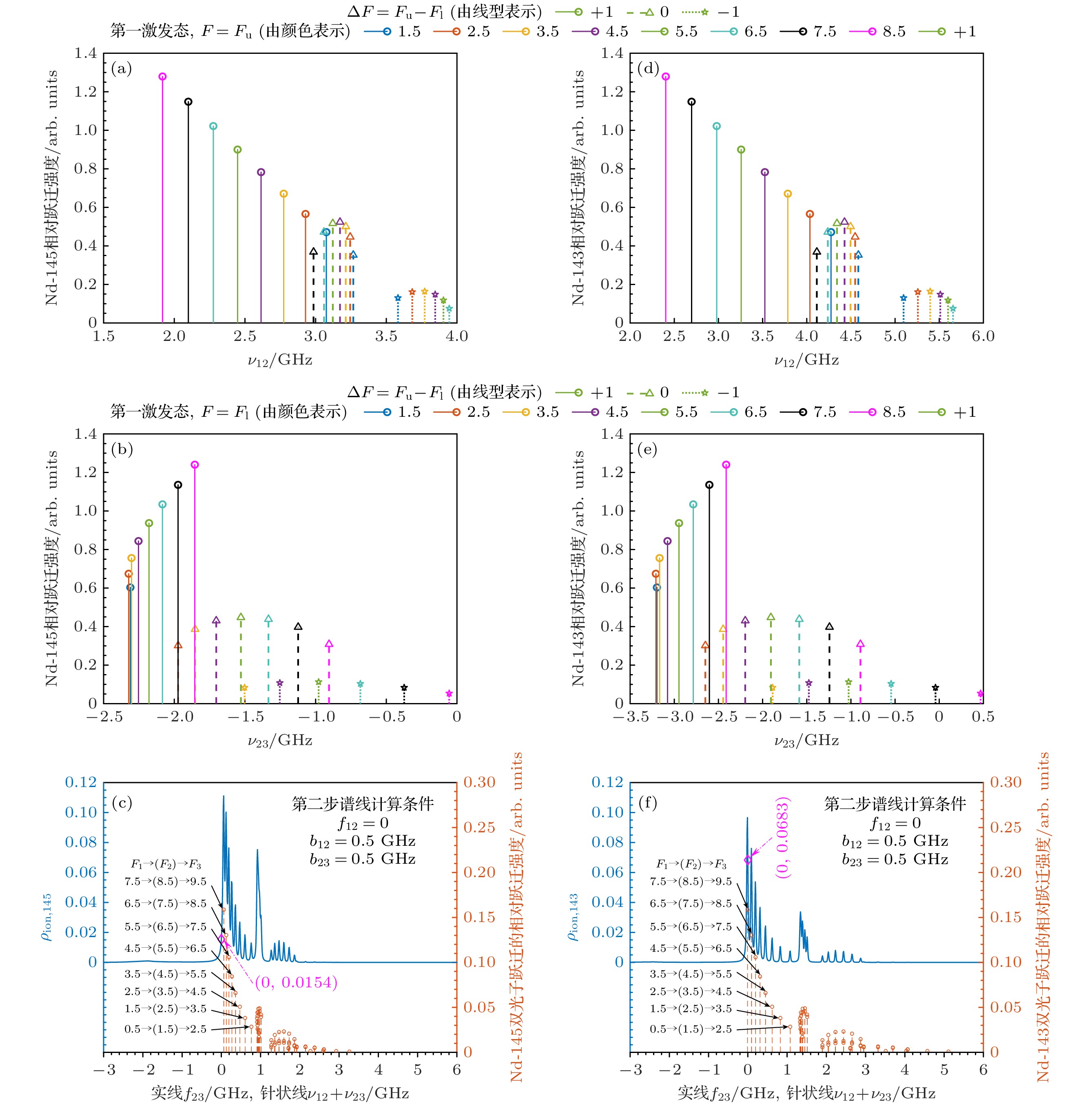
图 11 钕奇同位素超精细跃迁通道 (a) 路径一λ1, Nd-145; (b) 假定λ2, Nd-145; (c) Nd-145第2步谱线和λ1+λ2双光子跃迁; (d) 路径一λ1, Nd-143; (e) 假定λ2, Nd-143; (f) Nd-143第2步谱线和λ1+λ2双光子跃迁
Fig. 11. The hyperfine transition paths of Nd odd isotopes: (a) λ1 of Scheme No. 1, Nd-145; (b) the imagined λ2, Nd-145; (c) the second spectral line and λ1+λ2 two-photon transition of Nd-145; (d) λ1 of Scheme No. 1, Nd-143; (e) the imagined λ2, Nd-143; (f) the second spectral line and λ1+λ2 two-photon transition of Nd-143.
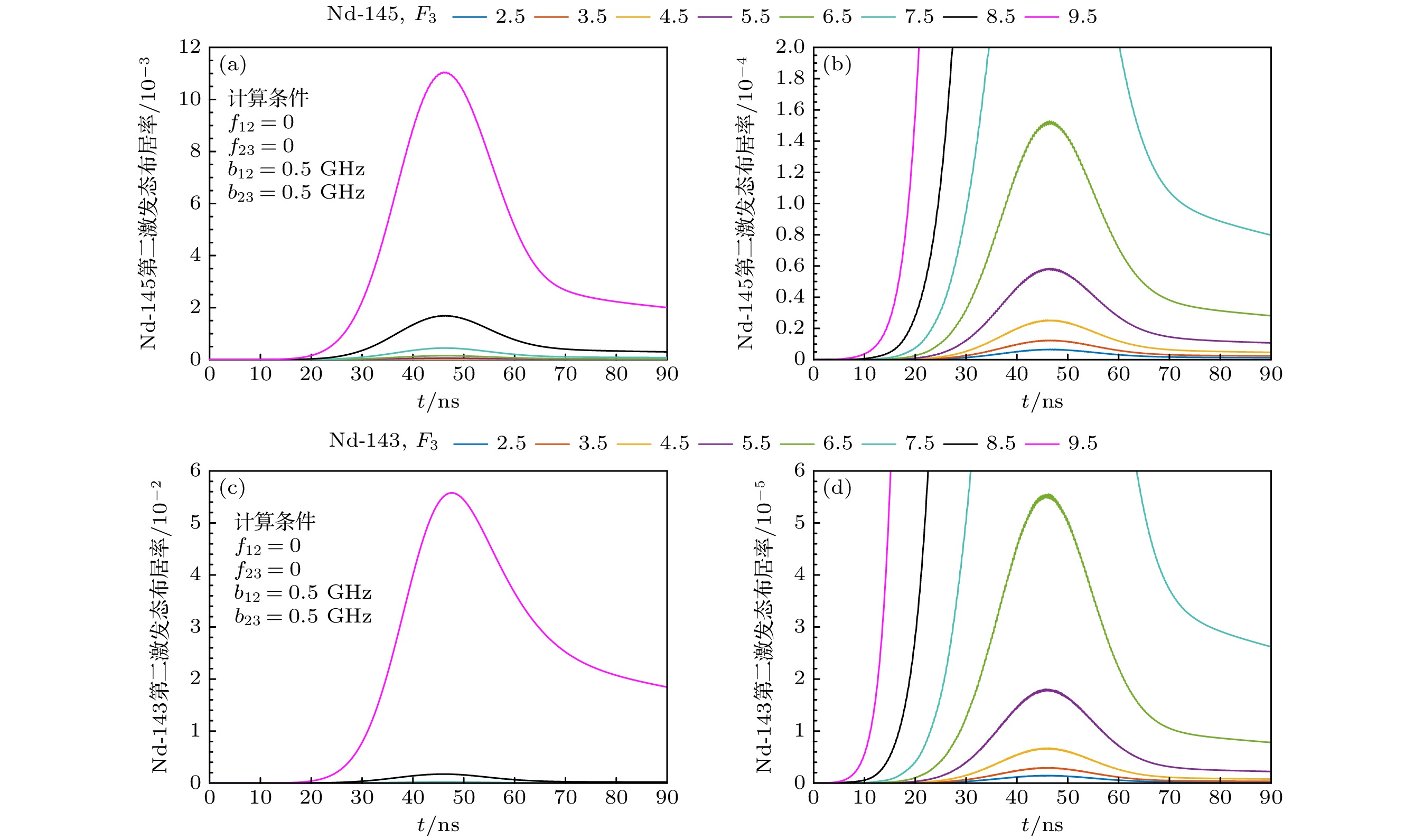
图 12 钕奇同位素第二激发态布居率随作用时间的变化图 (a) Nd-145; (b) Nd-145, 纵轴[0, 2×10–4]的局部放大图; (c) Nd-143; (d) Nd-143, 纵轴[0, 6×10–5]的局部放大图
Fig. 12. The population of the second excited state of Nd odd isotopes versus time: (a) Nd-145; (b) Nd-145, the partial enlarged view of the vertical axis in the range of [0, 2×10–4]; (c) Nd-143; (d) Nd-143, the partial enlarged view of the vertical axis in the range of [0, 6×10–5].
表 1 钕天然同位素
Table 1. Natural Nd isotopes.
钕同位素 Nd-150 Nd-148 Nd-146 Nd-145 Nd-144 Nd-143 Nd-142 天然丰度c0/% 5.62 5.73 17.22 8.30 23.85 12.17 27.11 核自旋In 0 0 0 7/2 0 7/2 0 衰变 2νββ 或 0νββ→Sm-150 — — — α → Ce-140 — — 表 2 钕同位素三步电离路径
Table 2. The three-step photoionization scheme of Nd isotopes.
表 3 数值计算中的激光参数取值
Table 3. The laser parameters adopted in the numerical calculation.
参数 第1束激光 第2束激光 第3束激光 时域线型 高斯线型 脉宽 30 ns (FWHM) 时序关系 峰值时刻同步 频域线型 修正的洛伦兹线型 — 截止系数 κ12 = κ23 = 0.2 — 频率 与Nd-150共振, f12 = f23 = 0 — 偏振 平行线偏振 0:1:0 0:1:0 — 混合偏振 1/3:1/3:1/3 1/3:1/3:1/3 — 正交线偏振 0:1:0 1/2:0:1/2 — 表 4 路径一的能级参数
Table 4. The energy parameters of scheme No. 1.
表 5 路径一的同位素位移
Table 5. The isotope shifts of scheme No. 1.
表 6 路径一选择性光电离效果
Table 6. The selective photoionization effects of scheme No. 1.
线宽/GHz 1.0, 1.0 0.5, 1.0 0.3, 1.0 1.0, 0.5 1.0, 0.3 0.5, 0.5 0.3, 0.3 C150/% 49.86 54.81 55.80 54.64 58.86 68.35 61.00 ρion,150 0.3839 0.4071 0.4158 0.3848 0.3849 0.4144 0.4073 表 7 钕同位素假定电离路径的能级参数
Table 7. The energy parameters of the imagined photoionization scheme of Nd isotope.
能级 E/cm–1 J A145/MHz A143/A145 B145/MHz B143/B145 τ/ns 路径一E1 0 [13] 4[29] –121.628[29] 1.60860[29] 64.634[29] 1.897[29] ∞ 路径一E2 16757.037 [13] 5[15] –129.594[15] 1.6099[15] 90.6[15] 1.91[15] 600* 假定E3 34011.04* 可选 † 可调 ‡ 1.6* 0* 1.9* 100* 注: “*”表示假定值, “†”表示在4, 5, 6范围内可选, “‡”表示在(–∞, 0] MHz范围内可调, 根据低能级超精细常数数值, 本文选取的范围为[–140, 0] MHz. 表 8 钕同位素假定电离路径的跃迁参数
Table 8. The transition parameters of the imagined photoionization scheme of Nd isotope.
跃迁 IS148/MHz IS146/IS148 IS145/IS148 IS144/IS148 IS143/IS148 IS142/IS148 β $ \langle J_m | d_{mn}| J_n \rangle $/(×10–30 C·m) 路径一λ1 1126.9[15] 1.78[15] 2.20[15] 2.51[15] 2.93[15] 3.28[15] 0.15† 4.5535 假定λ2 可调 ‡ 1.66* 2* 2.32* 2.66* 3* 0.05* 6.7004 注: “*”表示假定值, “†”表示由理论模型得到的拟合值, “‡”表示在(–∞, ∞) GHz范围内可调, 根据第1步跃迁同位素位移数值, 本文选取的范围为[–1.5, 1.5] GHz. 表 9 第二激发态超精细常数B3,145对钕奇同位素第2步跃迁谱线分裂程度的影响
Table 9. The influences of the second excited state’s hyperfine constant B3,145 on the hyperfine splitting degree of the second transition of Nd odd isotopes.
同位素 超精细常数 Nd-145超精细常数取值A'/MHz 0 –20 –40 –60 –80 –100 –120 –140 谱线分裂程度max(ν23, A, B) – min(ν23, A, B)/GHz Nd-145 B = –0.3A, A = A' 5.006 4.456 3.906 3.356 2.806 2.268 2.160 2.520 B = –0.5A, A = A' 5.006 4.452 3.898 3.345 2.791 2.254 2.143 2.500 B = –0.7A, A = A' 5.006 4.450 3.893 3.337 2.781 2.245 2.131 2.487 B = –1.0A, A = A' 5.006 4.447 3.888 3.330 2.771 2.236 2.120 2.473 Nd-143 B = –0.3A, A = 1.6A' 8.064 7.184 6.304 5.424 4.544 3.676 3.456 4.032 B = –0.5A, A = 1.6A' 8.064 7.178 6.292 5.406 4.520 3.654 3.429 4.000 B = –0.7A, A=1.6A' 8.064 7.174 6.284 5.394 4.504 3.639 3.410 3.979 B= –1.0A, A=1.6A' 8.064 7.170 6.276 5.382 4.488 3.625 3.392 3.957 表 10 第二激发态超精细常数B3,145对钕奇同位素第2步跃迁超精细跃迁通道共振位置的影响
Table 10. The influences of the second excited state’s hyperfine constant B3,145 on the resonance frequencies of hyperfine transition paths of Nd odd isotopes’ the second transition.
同位素 超精细常数 Nd-145超精细常数取值A'/MHz 0 –20 –40 –60 –80 –100 –120 –140 共振位置最大差异值max(|ν23, A, B – ν23, A, 0|)/MHz Nd-145 B = –0.3A, A = A' 0 2.4 4.8 7.2 9.6 11.9 14.3 16.7 B = –0.5A, A = A' 0 4.0 8.0 11.9 15.9 19.9 23.9 27.8 B = –0.7A, A = A' 0 5.6 11.1 16.7 22.3 27.8 33.4 39.0 B = –1.0A, A = A' 0 8.0 15.9 23.9 31.8 39.2 47.7 55.7 Nd-143 B = –0.3A, A = 1.6A' 0 3.8 7.6 11.5 15.3 19.1 22.9 26.7 B = –0.5A, A =1.6A' 0 6.4 12.7 19.1 25.5 31.8 38.2 44.6 B = –0.7A, A=1.6A' 0 8.9 17.8 26.7 35.6 44.6 53.5 62.4 B = –1.0A, A = 1.6A' 0 12.7 25.5 38.2 50.9 63.6 76.4 89.1 表 11 Nd-150丰度最低时的钕同位素选择性光电离效果
Table 11. The selective photoionization effects of Nd isotopes in the case of the lowest Nd-150 abundance.
线宽/GHz 丰度/% Nd-150 Nd-148 Nd-146 Nd-145 Nd-144 Nd-143 Nd-142 1.0, 1.0 47.45 24.25 2.66 6.69 0.54 18.26 0.14 0.5, 1.0 52.04 20.13 1.76 5.41 0.39 20.17 0.11 0.3, 1.0 53.16 19.23 1.64 5.20 0.37 20.30 0.10 1.0, 0.5 51.22 20.98 1.80 5.42 0.40 20.08 0.11 1.0, 0.3 52.23 20.14 1.69 5.21 0.38 20.24 0.10 0.3, 0.3 64.99 6.85 0.71 3.01 0.22 24.14 0.08 0.5, 0.5 60.70 11.03 0.93 3.60* 0.26 23.39† 0.08 注: 表中工况如图10(b)中的青色标记所示, f12 = f23 = 0, IS23,148 = –1000 MHz, A3,145 = –100 MHz; “*”, “†”对应的奇同位素第二激发态布居率随时间的变化曲线分别与图12(a), (b)相对应. 表 12 钕偶同位素共振位置
Table 12. The resonance frequency of Nd even isotopes.
共振位置 Nd-150 Nd-148 Nd-146 Nd-144 Nd-142 ν12/MHz 0 1126.9 2009.2 2827.7 3700 ν23/MHz 0 –1000 –1660 –2320 –3000 ν12+ν23/MHz 0 126.9 349.2 507.7 700 注: 表中工况如图10(b)中的青色标记所示, IS23,148 = –1000 MHz, A3,145 = –100 MHz. -
[1] Akhmedzhanov R A, Gushchin L A, Nizov N A, Nizov V A, Sobgayda D A, Zelensky I V 2024 JETP Lett. 119 834
 Google Scholar
Google Scholar
[2] Liang P J, Liu X, Li P Y, Zhou Z Q, Li C F, Guo G C 2020 J. Opt. Soc. Am. B 37 1653
 Google Scholar
Google Scholar
[3] Broderick K, Lusk R, Hinderer J, Griswold J, Boll R, Garland M, Heilbronn L, Mirzadeh S 2019 Appl. Radiat. Isot. 144 54
 Google Scholar
Google Scholar
[4] Hu F, Cutler C S, Hoffman T, Sieckman G, Volkert W A, Jurisson S S 2002 Nucl. Med. Biol. 29 423
 Google Scholar
Google Scholar
[5] Committee A 2015 Standard Practice for Analysis of Spent Nuclear Fuel to Determine Selected Isotopes and Estimate Fuel Burnup
[6] Suryanarayana M V 2022 Sci. Rep. 12 11471
 Google Scholar
Google Scholar
[7] Barabash A S, Belli P, Bernabei R, Boiko R S, Cappella F, Caracciolo V, Cerulli R, Danevich F A, Fang D L, Ferella F, Incicchitti A, Kobychev V V, Konovalov S I, Laubenstein M, Leoncini A, Merlo V, Nisi S, Niţescu O, Poda D V, Polischuk O G, Shcherbakov I B K, Šimkovic F, Timonina A, Tinkova V S, Tretyak V I, Umatov V I 2025 Eur. Phys. J. C 85 174
 Google Scholar
Google Scholar
[8] https://www.isotopes.gov/products/neodymium
[9] Letokhov V, Ryabov E (Trigg G L ed) 2004 Encyclopedia of Applied Physics (New York: Wiley) pp1015–1028
[10] Babichev A P, Grigoriev I S, Grigoriev A I, Dorovskii A P, D'Yachkov A B, Kovalevich S K, Kochetov V A, Kuznetsov V A, Labozin V P, Matrakhov A V, Mironov S M, Nikulin S A, Pesnya A V, Timofeev N I, Firsov V A, Tsvetkov G O, Shatalova G G 2005 Quantum Electron. 35 879
 Google Scholar
Google Scholar
[11] Grigoriev I, Diachkov A, Kovalevich S, Labosin V, Mironov S, Nikulin S, Pesnia A, Firsov V, Shatalova G, Tsvetkov G 2003 Proc. SPIE Int. Soc. Opt. Eng. 5121 406
[12] D'Yachkov A B, Kovalevich S K, Labozin V P, Mironov S M, Panchenko V Y, Firsov V A, Tsvetkov G O, Shatalova G G 2012 Quantum Electron. 42 953
 Google Scholar
Google Scholar
[13] Kramida A, Ralchenko Y, Reader J, (NIST ASD Team) 2024 NIST Atomic Spectra Database (Gaithersburg, MD: National Institute of Standards and Technology
[14] Miyabe M, Iwata Y, Tomita H, Morita M, Sakamoto T 2024 Spectrochim. Acta Part B At. Spectrosc. 221 107036
 Google Scholar
Google Scholar
[15] van Leeuwen K A H, Eliel E R, Post B H, Hogervorst W 1981 Z. Phys. A 301 95
 Google Scholar
Google Scholar
[16] Zyuzikov A D, Mishin V I, Fedoseev V N 1988 Opt. Spectrosc. 64 287
[17] D'Yachkov A B, Gorkunov A A, Labozin A V, Mironov S M, Panchenko V Y, Firsov V A, Tsvetkov G O 2018 Quantum Electron. 48 75
 Google Scholar
Google Scholar
[18] 张钧尧, 熊静逸, 魏少强, 李云飞, 卢肖勇 2023 72 193203
 Google Scholar
Google Scholar
Zhang J Y, Xiong J Y, Wei S Q, Li Y F, Lu X Y 2023 Acta Phys. Sin. 72 193203
 Google Scholar
Google Scholar
[19] Campbell P, Moore I D, Pearson M R 2016 Prog. Part. Nucl. Phys. 86 127
 Google Scholar
Google Scholar
[20] Yang X F, Wang S J, Wilkins S G, Ruiz R F G 2023 Prog. Part. Nucl. Phys. 129 104005
 Google Scholar
Google Scholar
[21] Lu X Y, Wang L D 2023 Chin. Phys. B 32 53204
 Google Scholar
Google Scholar
[22] Lu X Y, Wang L D 2024 Appl. Radiat. Isot. 210 111334
 Google Scholar
Google Scholar
[23] Demtröder W 2008 Laser Spectroscopy: Vol. 1 Basic Principles (Berlin: Springer) pp5–60
[24] Greenland P T 1990 Contemp. Phys. 31 405
 Google Scholar
Google Scholar
[25] Axner O, Gustafsson J, Omenetto N, Winefordner J D 2004 Spectrochim. Acta Part B At. Spectrosc. 59 1
 Google Scholar
Google Scholar
[26] Agarwal G S 1970 Phys. Rev. A 1 1445
 Google Scholar
Google Scholar
[27] Lambropoulos P, Lyras A 1989 Phys. Rev. A 40 2199
 Google Scholar
Google Scholar
[28] Blagoev K B, Komarovskii V A 1994 At. Data Nucl. Data Tables 56 1
 Google Scholar
Google Scholar
[29] Childs W J, Goodman L S 1972 Phys. Rev. A 6 1772
 Google Scholar
Google Scholar
[30] Shen X P, Wang W L, Zhai L H, Deng H, Xu J, Yuan X L, Wei G Y, Wang W, Fang S, Su Y Y, Li Z M 2018 Spectrochim. Acta Part B At. Spectrosc. 145 96
 Google Scholar
Google Scholar
[31] Lu X Y, Wang L D 2025 J. Phys. B: At. Mol. Opt. Phys. 58 025001
 Google Scholar
Google Scholar
[32] Wakasugi M, Horiguchi T, Guo Jin W, Sakata H, Yoshizawa Y 1990 J. Phys. Soc. Jpn. 59 2700
 Google Scholar
Google Scholar
计量
- 文章访问数: 622
- PDF下载量: 20
- 被引次数: 0













 下载:
下载: