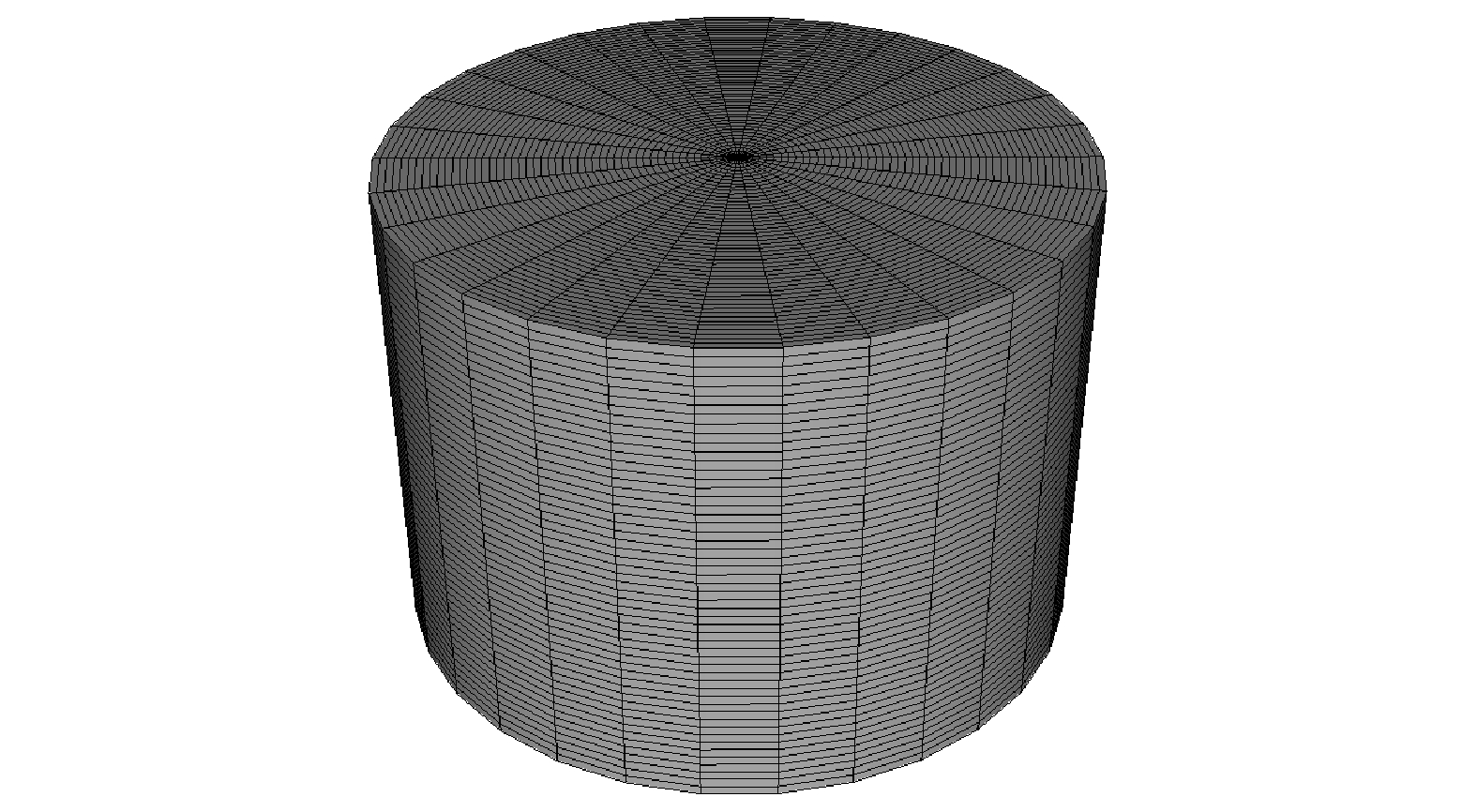
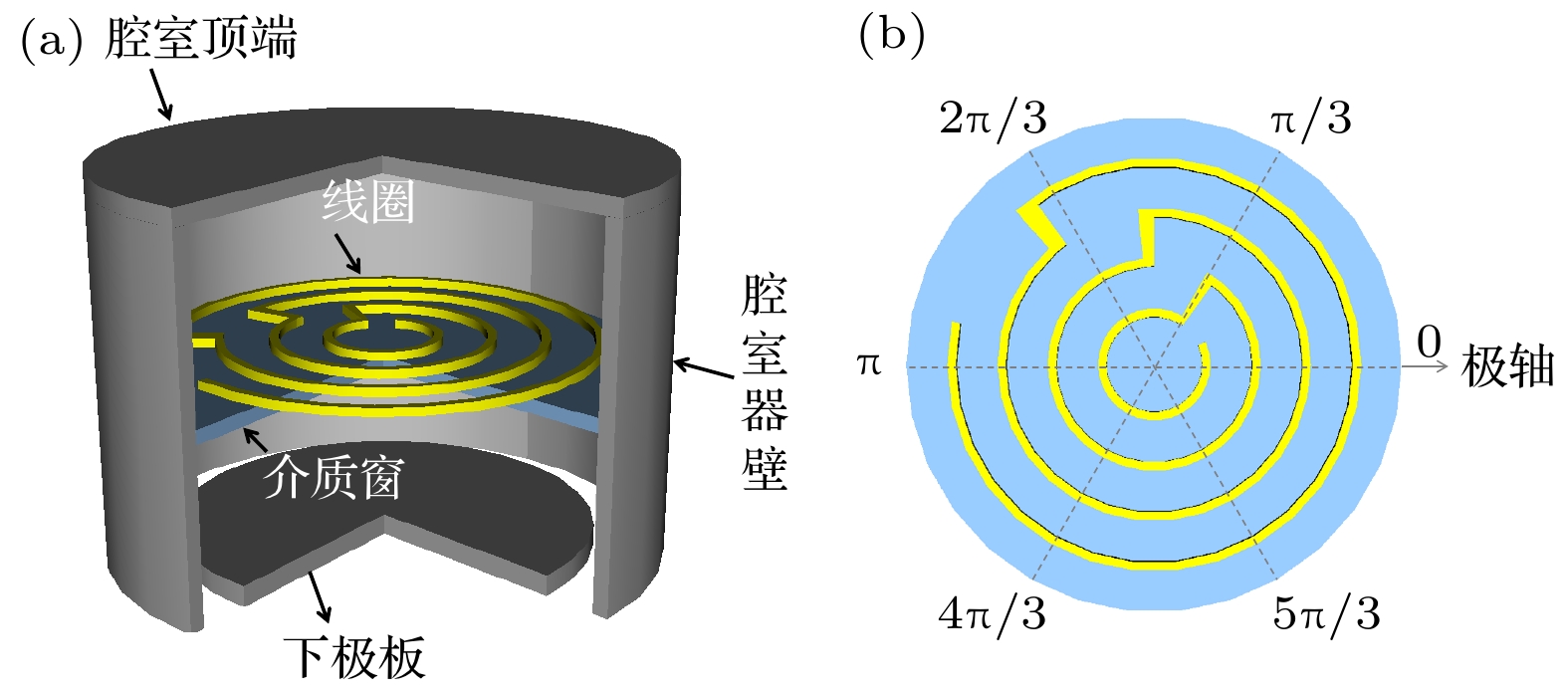
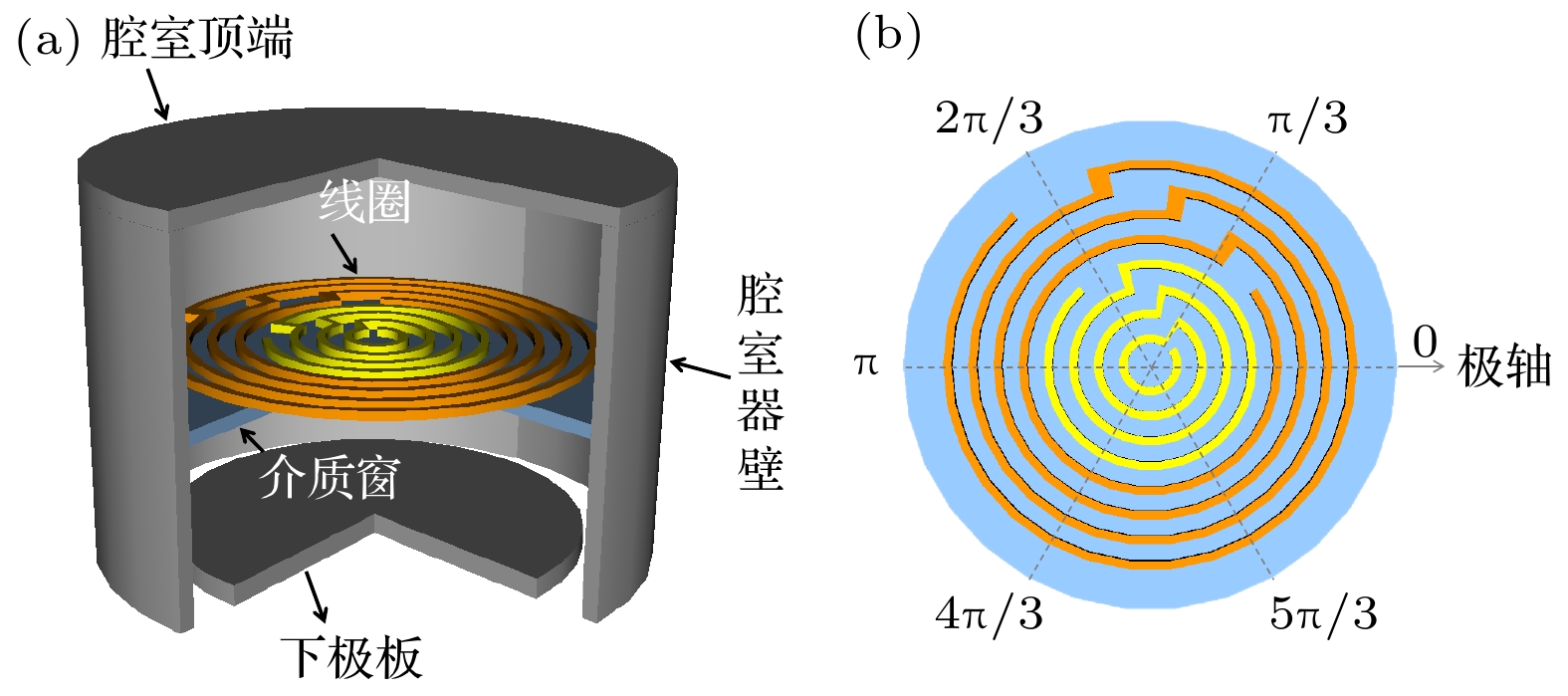
-
In this paper, the effect of the coil structure, as well as the gas pressure, on the spatial distribution of an inductively coupled argon plasma is numerically investigated based on our developed three-dimensional fluid model. The model is based on a modified ambipolar diffusion model, in which the electron density is solved under the quasi-neutral condition, the ion density and neutral particle density are obtained by solving continuity equations, and the ion flux is achieved by solving the full momentum balance equation. In addition, the inductive electric field is governed by the Maxwell equations, which are solved in the frequency domain. The results show that the electron density is nonuniform along the azimuthal direction due to the asymmetry of the coil structure, and the uniformity becomes better as gas pressure decreases. Besides, the plasma azimuthal uniformity can also be improved by reducing the opening of the coil. As the coil radius increases, the plasma density decreases, while the radial uniformity of the plasma improves, and the azimuthal uniformity deteriorates. In addition, the influence of the current amplitude ratio between the inner coil and outer coil on the plasma uniformity in dual-coil discharge is also investigated. It is found that the plasma radial uniformity becomes better by reducing the inter-to-outer coil current amplitude ratio. The results obtained in this work demonstrate that the plasma uniformity can be improved by optimizing the coil structure and adjusting the discharge parameters, which is of significant importance in etching and deposition processes.
-
Keywords:
- inductively coupled plasma /
- three-dimensional fluid simulation /
- plasma uniformity /
- coil structure
[1] Lieberman M A, Lichtenberg A J 2005 Principles of Plasma Discharges and Materials Processing (New York: Wiley) pp350–351
[2] 王友年, 宋远红, 张钰如 2024 射频等离子体物理基础(北京: 科学出版社) 第314页
Wang Y N, Song Y H, Zhang Y R 2024 Fundamentals of Radio-frequency Plasma Physics (Beijing: Science Press) p314
[3] Rauf S, Kenney J, Collins K S 2009 J. Appl. Phys. 105 103301
Google Scholar
[4] Kenney J, Rauf S, Collins K S 2009 J. Appl. Phys. 106 103302
Google Scholar
[5] Agarwal A, Bera K, Kenney J, Likhanskii A, Rauf S 2017 J. Phys. D: Appl. Phys. 50 424001
Google Scholar
[6] Ventzek P L, Sommerer T J, Hoekstra R J, Kushner M J 1993 Appl. Phys. Lett. 63 605
Google Scholar
[7] Thorsteinsson E, Gudmundsson J 2010 J. Phys. D: Appl. Phys. 43 115201
Google Scholar
[8] Thorsteinsson E, Gudmundsson J 2010 J. Phys. D: Appl. Phys. 43 115202
Google Scholar
[9] Hjartarson A, Thorsteinsson E, Gudmundsson J 2010 Plasma Sources Sci. Technol. 19 065008
Google Scholar
[10] Takao Y, Kusaba N, Eriguchi K, Ono K 2010 J. Appl. Phys. 108 093309
Google Scholar
[11] Mattei S, Nishida K, Onai M, Lettry L, Tran M Q, Hatayama A 2017 J. Comput. Phys. 350 891
Google Scholar
[12] Kushner M J 2009 J. Phys. D: Appl. Phys. 42 194013
Google Scholar
[13] Sun X Y, Zhang Y R, Li X C, Wang Y N 2015 Phys. Plasmas 22 053508
Google Scholar
[14] Wang Y H, Wei L, Zhang Y R, Wang Y N 2015 Chin. Phys. B 24 095203
Google Scholar
[15] Wu H M, Yu B W, Li M, Yang Y 2002 IEEE Trans. Plasma Sci. 25 1
Google Scholar
[16] Kushner M J, Collison W Z, Grapperhaus M J, Holland J P, Barnes M S 1996 J. Appl. Phys. 80 1337
Google Scholar
[17] Panagopoulos T, Kim D, Midha V, Economou D J 2002 J. Appl. Phys. 91 2687
Google Scholar
[18] Brcka J 2016 Jpn. J. Appl. Phys. 55 07LD08
Google Scholar
[19] 赵明亮, 张钰如, 高飞, 宋远红, 王友年 2023 力学学报 55 2891
Google Scholar
Zhao M L, Zhang Y R, Gao F, Song Y H, Wang Y N 2023 Chin. J. Theor. Appl. Mech. 55 2891
Google Scholar
[20] De Bleecker K, Bogaerts A, Gijbels R, Goedheer W 2004 Phys. Rev. E 69 056409
Google Scholar
[21] Ariskin D, Schweigert I, Alexandrov A, Bogaerts A, Peeters F M 2009 J. Appl. Phys. 105 063305
Google Scholar
[22] Lee C, Lieberman M 1995 J. Vac. Sci. Technol. A 13 368
Google Scholar
-
图 3 (a)单线圈腔室结构示意图; (b)单组线圈
Fig. 3. Schematic diagram of (a) the single-coil chamber structure and (b) the single coil.
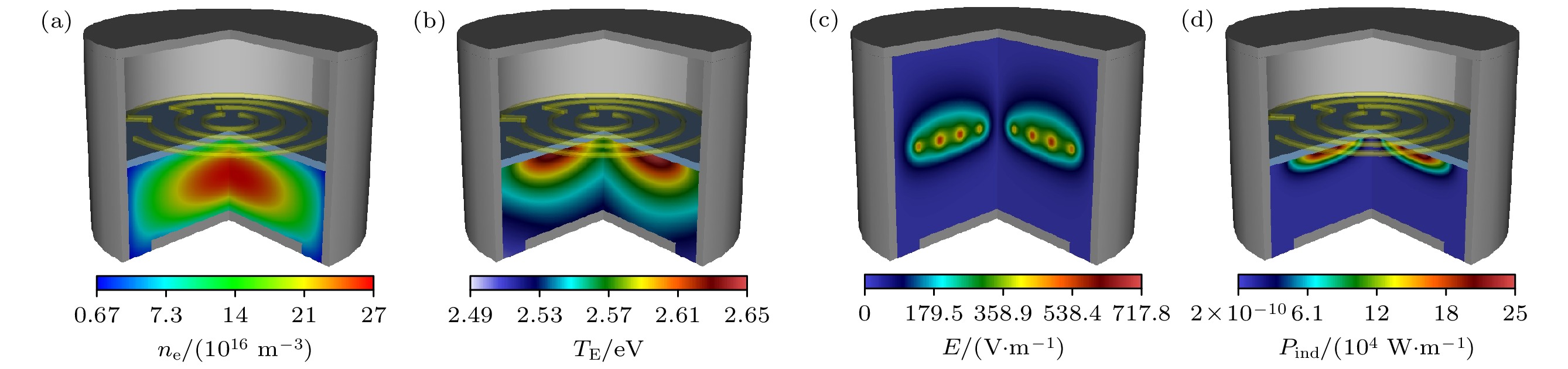
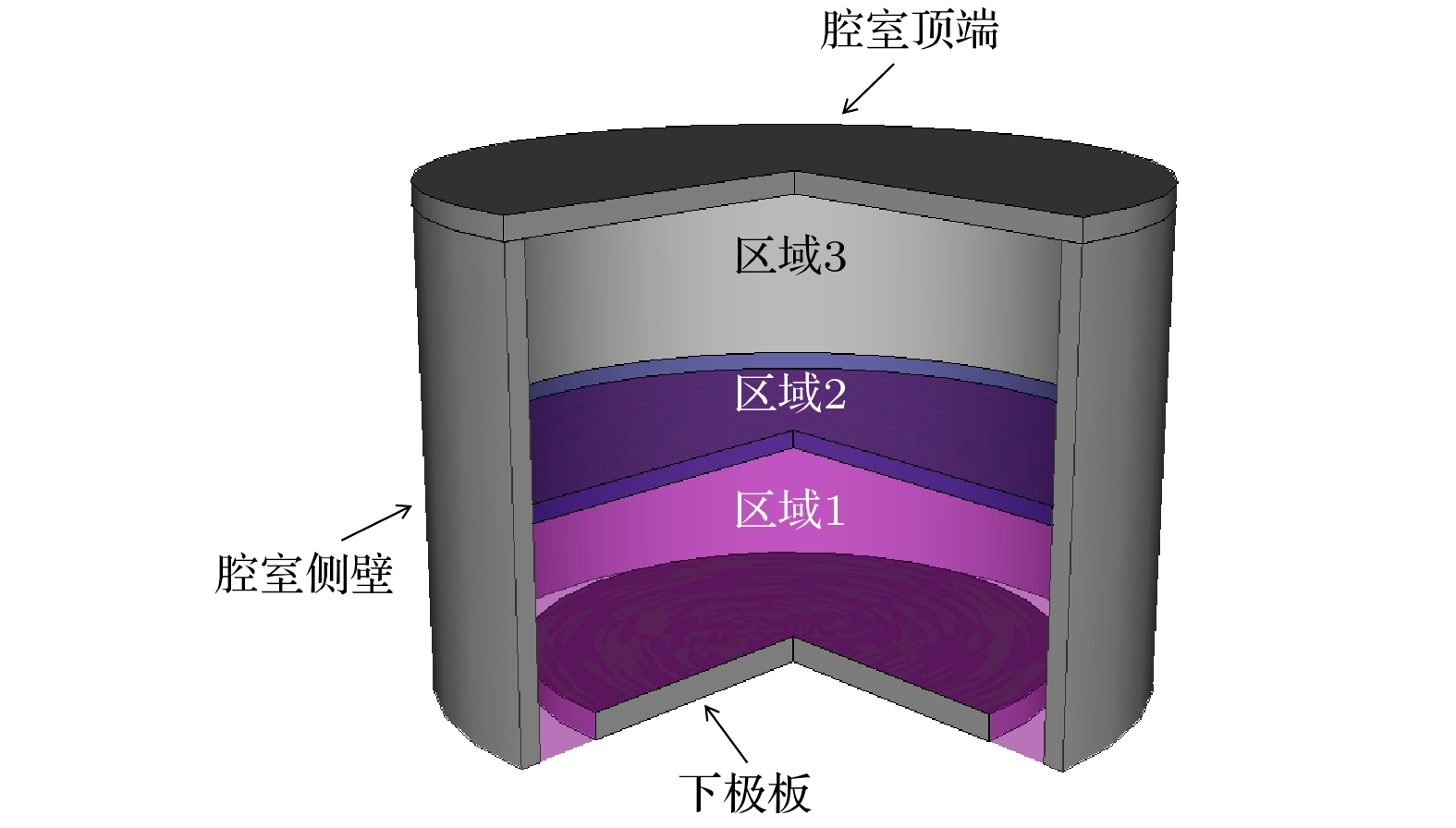
图 4 (a)电子密度、(b)电子温度、(c)感应电场幅值以及(d)感性沉积功率密度的三维空间分布, 其中气压为2 Pa, 放电功率100 W
Fig. 4. Three-dimensional spatial distribution of the (a) electron density, (b) electron temperature, (c) induced electric field amplitude, and (d) induced deposited power density. The gas pressure is 2 Pa, the discharge power is 100 W.
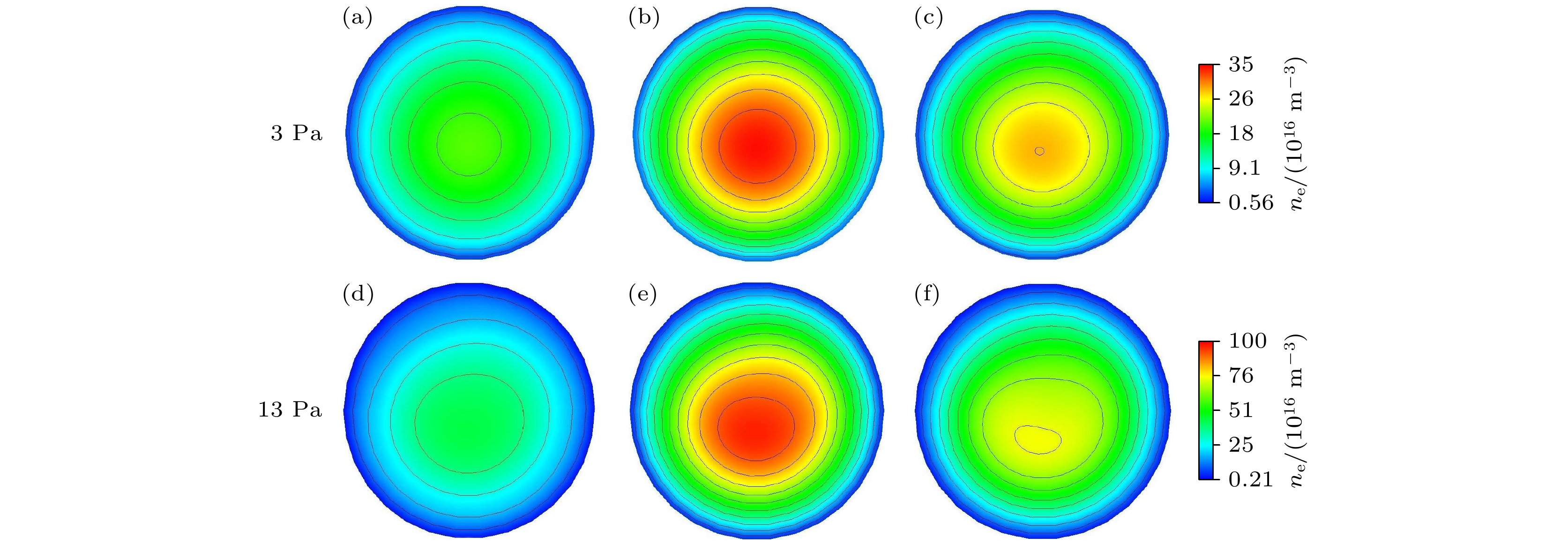
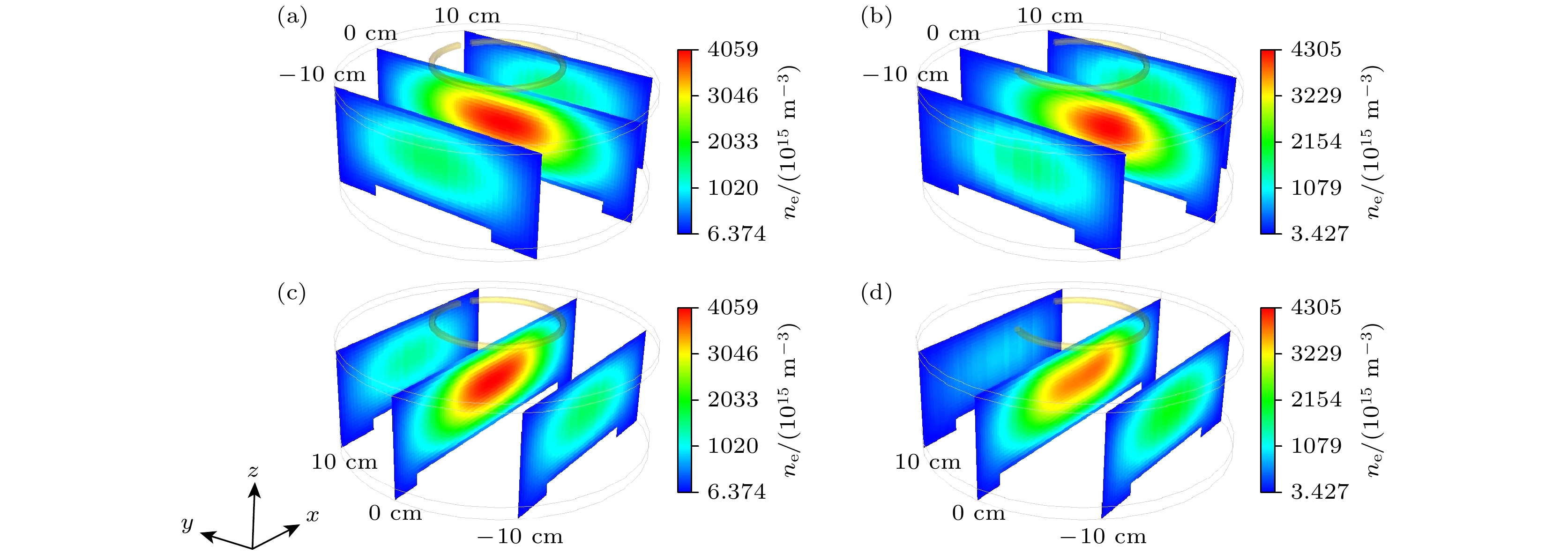
图 5 不同轴向位置的$r{\text{-}}\phi $平面上的电子密度的分布(气压分别为3 Pa和13 Pa, 功率为100 W) (a), (d) 介质窗下方8 cm; (b), (e) 介质窗下方5 cm; (c), (f) 介质窗下方2 cm
Fig. 5. Distribution of electron density in the $r{\text{-}}\phi $ cross section for different axial positions: (a), (d) 8 cm below the quartz window; (b), (e) 5 cm below the quartz window; (c), (f) 2 cm below the quartz window. The gas pressure is 3 Pa and 13 Pa, the power is 100 W
图 6 基片台上方1 cm处的$r{\text{-}}\phi $平面的电子密度分布(气压为2 Pa) (a) 200 W; (b) 300 W; (c) 400 W; (d) 500 W
Fig. 6. Distribution of electron density in the $r{\text{-}}\phi $ plane which is 1 cm above the substrate: (a) 200 W; (b) 300 W; (c) 400 W; (d) 500 W. The gas pressure is 2 Pa.
图 7 不同线圈的开口弧度的单匝线圈 (a) ${\text{π}}/15$; (b) ${\text{π/}}5$; (c) ${\text{π/}}3$; (d) $7{\text{π/}}15$
Fig. 7. Single circle coil with different opening sizes: (a) ${\text{π}}/15$; (b) ${\text{π/}}5$; (c) ${\text{π/}}3$; (d) $7{\text{π/}}15$.
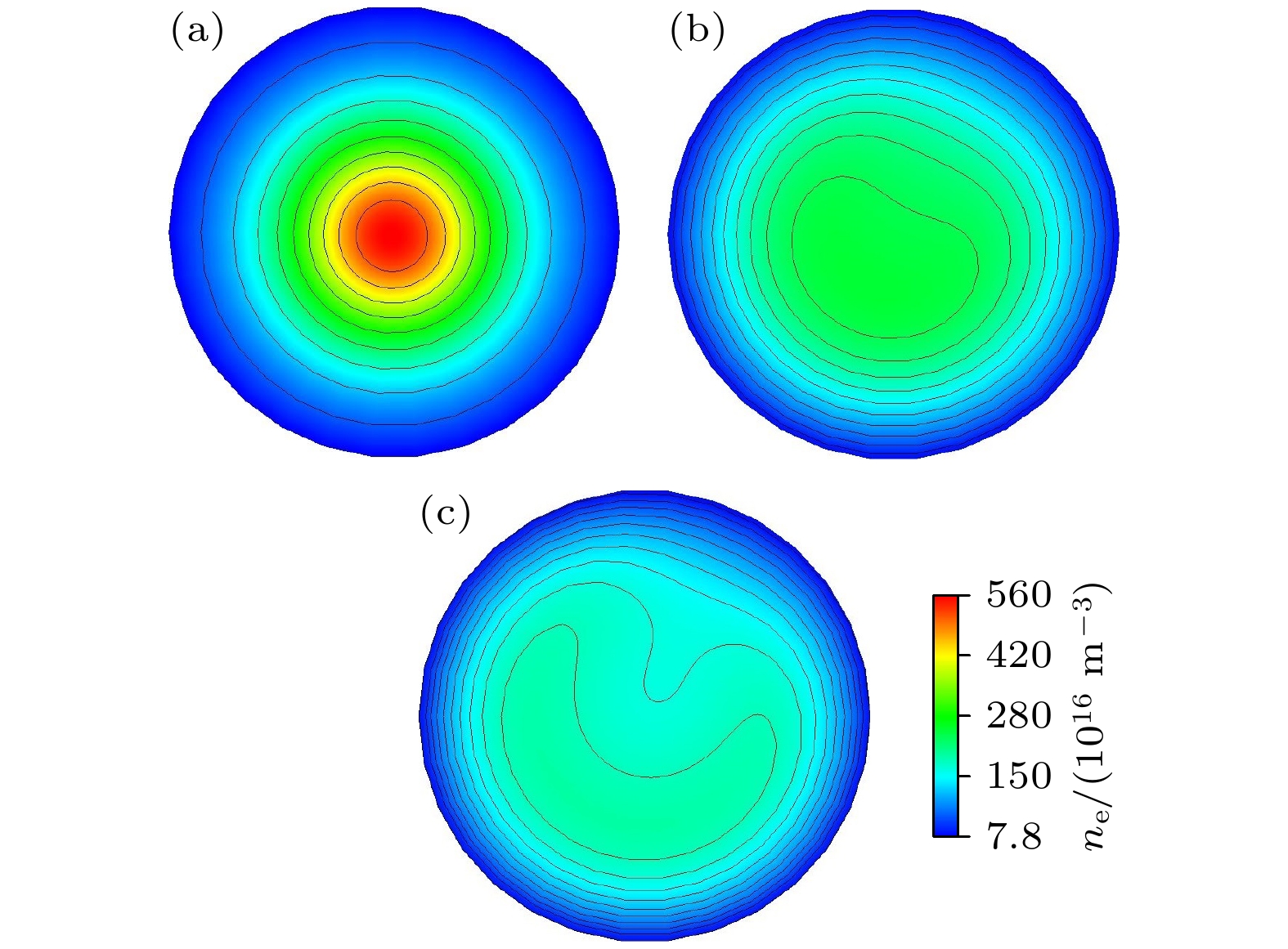
图 8 气压为12 Pa, 功率为300 W时, 线圈开口的大小对于电子密度环向分布的影响 (a) ${\text{π}}/15$; (b) ${\text{π/}}5$; (c) ${\text{π/}}3$; (d) $7{\text{π/}}15$
Fig. 8. Effect of the size of the coil opening on the azimuthal distribution of electron density: (a) ${\text{π}}/15$; (b) ${\text{π/}}5$; (c) ${\text{π/}}3$; (d) $7{\text{π/}}15$
图 9 气压为12 Pa, 功率为300 W时, (a), (b)不同$x$轴方向位置的$y{\text{-}}z$平面上的电子密度的分布, 线圈开口弧度分别为${\text{π}}/15$和$7{\text{π/}}15$; (c), (d)不同$y$轴方向位置的$x{\text{-}}z$平面上的电子密度的分布, 线圈开口弧度分别为${\text{π}}/15$和$7{\text{π/}}15$
Fig. 9. (a), (b) Distributions of electron density in the $y{\text{-}}z$ plane at different x-direction positions with coil openings of ${\text{π}}/15$ and $7{\text{π/}}15$; (c), (d) the distributions of electron density in the $x{\text{-}}z$ plane at different y-direction positions with coil openings of ${\text{π}}/15$ and $7{\text{π/}}15$. The gas pressure is 12 Pa and the power is 300 W.
图 10 线圈半径对电子密度环向分布的影响 (a) 3 cm; (b) 9 cm; (c) 12 cm
Fig. 10. Effect of coil radius on the azimuthal distribution of electron density: (a) 3 cm; (b) 9 cm; (c) 12 cm.
图 11 (a)双线圈腔室结构示意图; (b)内外双线圈
Fig. 11. (a) Schematic diagram of the dual-coil chamber structure; (b) the internal and external dual coil.
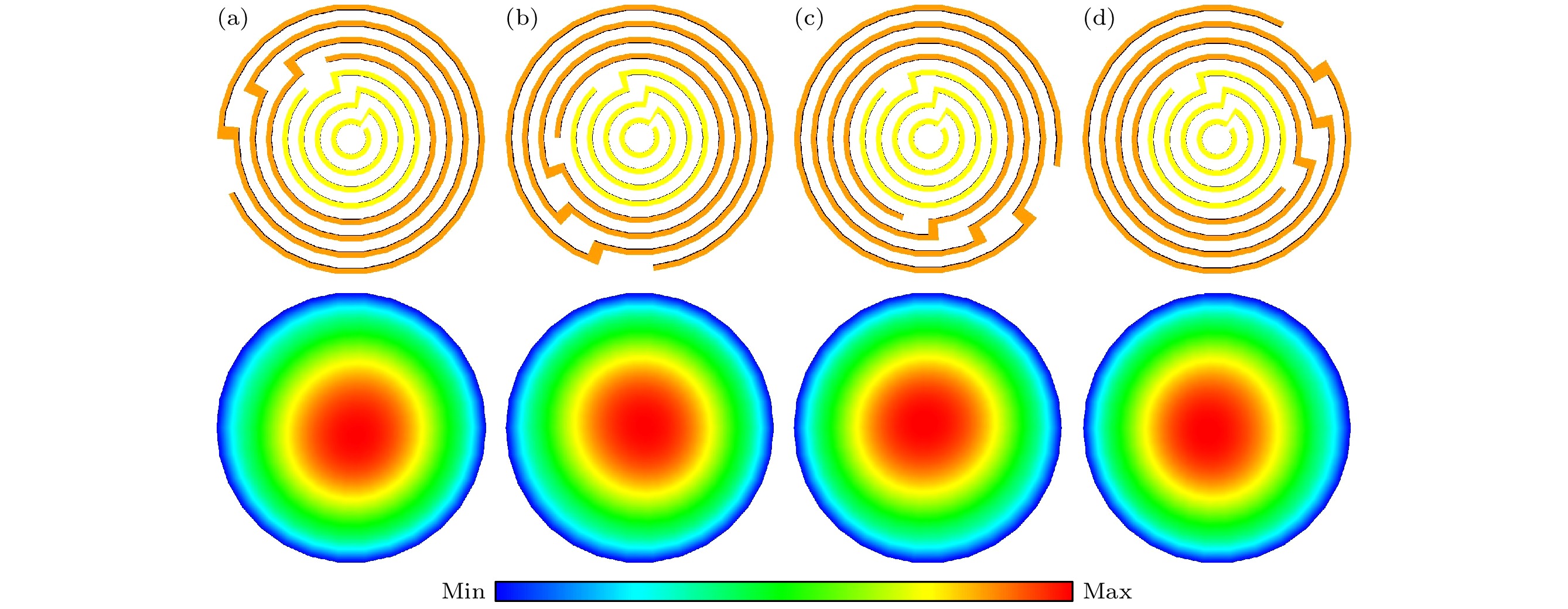
图 12 不同的内外线圈的相对位置下, 电子密度在$r{\text{-}}\phi $平面上的分布(气压为12 Pa, 功率为300 W, 内外线圈电流幅值比为1∶1) (a) case 1; (b) case 2; (c) case 3; (d) case 4
Fig. 12. Distribution of electron density in the $r{\text{-}}\phi $ plane for different relative positions of the inner and outer coils: (a) case 1; (b) case 2; (c) case 3; (d) case 4. The pressure is 12 Pa, the power is 300 W, and the coil current ratio is 1∶1.
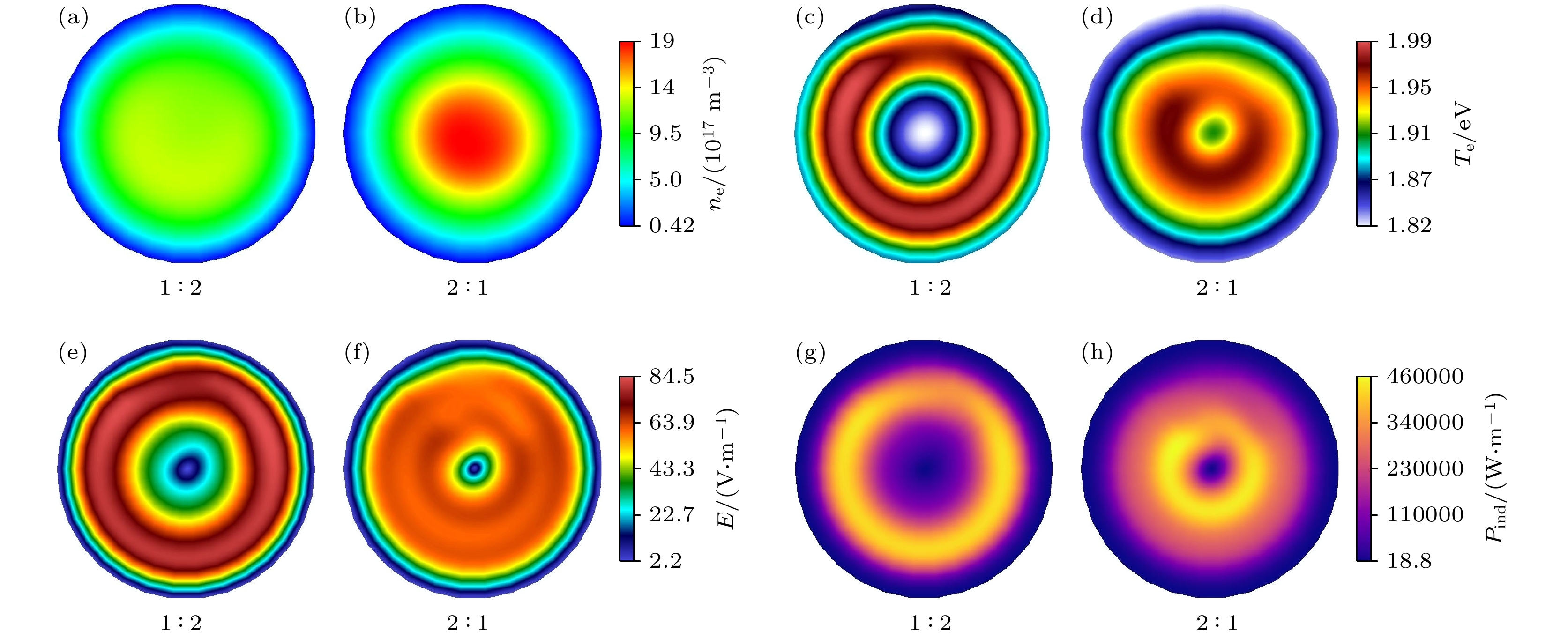
图 13 不同的内外线圈电流幅值比下, (a), (b)电子密度、(c), (d)电子温度、(e), (f)感性沉积功率密度和(g), (h)感应电场的幅值在$r{\text{-}}\phi $平面上的分布, 气压为12 Pa, 功率为300 W
Fig. 13. Distribution of (a), (b) electron density, (c), (d) electron temperature, (e), (f) induced deposition power density and (g), (h) amplitude of induced electric field in the $r{\text{-}}\phi $ plane for different relative positions of the inner and outer coils. The pressure is 12 Pa and the power is 300 W.
表 1 氩等离子体中的碰撞反应及速率系数
Table 1. Collision reactions and rate coefficients in argon plasma.
编号 反应表达式 反应系数/(m3·s–1) 文献 1 ${\text{e + Ar}} \to {\text{e + Ar}}$ $ 2.336 \times {10^{ - 14}}T_{\text{e}}^{1.609}\exp \left[ {0.0618{{\left( {\ln {T_{\text{e}}}} \right)}^2} - 0.1171{{\left( {\ln {T_{\text{e}}}} \right)}^3}} \right] $ [1] 2 ${\text{e + Ar}} \to {\text{e + A}}{{\text{r}}^*}$ $2.48 \times {10^{ - 14}}T_{\text{e}}^{0.33}\exp \left( { - 12.78/{T_{\text{e}}}} \right)$ [1] 3 ${\text{e + Ar}} \to 2{\text{e + A}}{{\text{r}}^ + }$ $2.34 \times {10^{ - 14}}T_{\text{e}}^{0.59}\exp \left( { - 17.44/{T_{\text{e}}}} \right)$ [1] 4 ${\text{e + A}}{{\text{r}}^*} \to 2{\text{e + A}}{{\text{r}}^ + }$ $2.05 \times {10^{ - 13}}\exp \left( { - 4.95/{T_{\text{e}}}} \right)$ [22] 5 ${\text{e + A}}{{\text{r}}^*} \to {\text{e + Ar}}$ $2.0 \times {10^{ - 13}}$ [22] 6 $ {\text{A}}{{\text{r}}^*}{\text{ + A}}{{\text{r}}^*}{\text{ }} \to {\text{Ar + A}}{{\text{r}}^ + }{\text{ + e}} $ $6.2 \times {10^{ - 16}}$ [22] 注: 其中电子温度用电子伏(eV)为单位. 
下载: 导出CSV
-
[1] Lieberman M A, Lichtenberg A J 2005 Principles of Plasma Discharges and Materials Processing (New York: Wiley) pp350–351
[2] 王友年, 宋远红, 张钰如 2024 射频等离子体物理基础(北京: 科学出版社) 第314页
Wang Y N, Song Y H, Zhang Y R 2024 Fundamentals of Radio-frequency Plasma Physics (Beijing: Science Press) p314
[3] Rauf S, Kenney J, Collins K S 2009 J. Appl. Phys. 105 103301
Google Scholar
[4] Kenney J, Rauf S, Collins K S 2009 J. Appl. Phys. 106 103302
Google Scholar
[5] Agarwal A, Bera K, Kenney J, Likhanskii A, Rauf S 2017 J. Phys. D: Appl. Phys. 50 424001
Google Scholar
[6] Ventzek P L, Sommerer T J, Hoekstra R J, Kushner M J 1993 Appl. Phys. Lett. 63 605
Google Scholar
[7] Thorsteinsson E, Gudmundsson J 2010 J. Phys. D: Appl. Phys. 43 115201
Google Scholar
[8] Thorsteinsson E, Gudmundsson J 2010 J. Phys. D: Appl. Phys. 43 115202
Google Scholar
[9] Hjartarson A, Thorsteinsson E, Gudmundsson J 2010 Plasma Sources Sci. Technol. 19 065008
Google Scholar
[10] Takao Y, Kusaba N, Eriguchi K, Ono K 2010 J. Appl. Phys. 108 093309
Google Scholar
[11] Mattei S, Nishida K, Onai M, Lettry L, Tran M Q, Hatayama A 2017 J. Comput. Phys. 350 891
Google Scholar
[12] Kushner M J 2009 J. Phys. D: Appl. Phys. 42 194013
Google Scholar
[13] Sun X Y, Zhang Y R, Li X C, Wang Y N 2015 Phys. Plasmas 22 053508
Google Scholar
[14] Wang Y H, Wei L, Zhang Y R, Wang Y N 2015 Chin. Phys. B 24 095203
Google Scholar
[15] Wu H M, Yu B W, Li M, Yang Y 2002 IEEE Trans. Plasma Sci. 25 1
Google Scholar
[16] Kushner M J, Collison W Z, Grapperhaus M J, Holland J P, Barnes M S 1996 J. Appl. Phys. 80 1337
Google Scholar
[17] Panagopoulos T, Kim D, Midha V, Economou D J 2002 J. Appl. Phys. 91 2687
Google Scholar
[18] Brcka J 2016 Jpn. J. Appl. Phys. 55 07LD08
Google Scholar
[19] 赵明亮, 张钰如, 高飞, 宋远红, 王友年 2023 力学学报 55 2891
Google Scholar
Zhao M L, Zhang Y R, Gao F, Song Y H, Wang Y N 2023 Chin. J. Theor. Appl. Mech. 55 2891
Google Scholar
[20] De Bleecker K, Bogaerts A, Gijbels R, Goedheer W 2004 Phys. Rev. E 69 056409
Google Scholar
[21] Ariskin D, Schweigert I, Alexandrov A, Bogaerts A, Peeters F M 2009 J. Appl. Phys. 105 063305
Google Scholar
[22] Lee C, Lieberman M 1995 J. Vac. Sci. Technol. A 13 368
Google Scholar
下载:
计量
- 文章访问数: 517
- PDF下载量: 37
- 被引次数: 0
