-
Pre-Bötzinger复合体是哺乳类动物呼吸节律起源的关键部位. 外周化学感受器可通过监测血液中氧气和二氧化碳浓度的变化, 显著影响呼吸节律. 本文基于pre-Bötzinger复合体神经元, 同时考虑运动池、肺容积、肺氧、血氧以及化学感受器等因素, 建立了电磁感应驱动的闭环呼吸控制模型. 研究发现, 在不同电磁感应驱动下, 系统的缺氧反应受到磁流反馈系数的控制. 通过分岔分析和数值模拟, 揭示了磁流反馈系数对呼吸节律的恢复能力具有显著影响, 并阐明了产生不同缺氧反应的动力学机制. 此外, 研究发现在电磁感应驱动下, 闭环系统中混合簇放电节律能够自动恢复的条件为缺氧扰动前后的分岔结构完全相同; 而当缺氧扰动前后的分岔结构不同, 系统中混合簇放电节律则不能自动恢复. 对于较轻电磁感应驱动下不能自动恢复的情形, 适当增大磁流反馈系数能使系统自动恢复, 这与Hopf分岔、极限环的鞍结分岔密切相关. 本研究有助于理解呼吸中枢与外周化学感受反馈的相互作用对呼吸节律的影响以及外部感应对缺氧反应的控制作用.The pre-Bötzinger complex is a crucial region for generating respiratory rhythms in mammals. Peripheral chemoreceptors have a significant influence on respiratory rhythm by monitoring changes in blood oxygen concentration and carbon dioxide concentration. This study introduces a closed-loop respiratory control model, which is driven by electromagnetic induction and based on the activation of pre-Bötzinger complex neurons. The model incorporates various factors including the motor pool, lung volume, lung oxygen, blood oxygen, and chemoreceptors. The response of the system subjected to the same hypoxic perturbation under different electromagnetic induction is studied, and the control effect of magnetic flux feedback coefficient on the recovery of mixed rhythms is investigated. Using bifurcation analysis and numerical simulations, it is found that the magnetic flux feedback coefficient has a significant influence on the ability to recover respiratory rhythm. The dynamic mechanism of the magnetic flux feedback coefficient on different hypoxic responses in closed-loop systems are revealed. Dynamic analysis indicates that under certain electromagnetic induction, the mixed bursting rhythm in the closed-loop system can autoresuscitate if the bifurcation structure before and after applying hypoxia perturbation are completely identical. However, when the bifurcation structure before and after applying hypoxia perturbation are different, the mixed bursting rhythm in the system cannot autoresuscitate. In addition, for the cases where automatic recovery is not achieved under mild electromagnetic induction, increasing the magnetic flux feedback coefficient appropriately can lead the system to autoresuscitate, which is closely related to the Hopf bifurcation and fold bifurcation of limit cycle. This study contributes to understanding the influence of the interaction between the central respiratory and peripheral chemoreceptive feedback on respiratory rhythm, as well as the control effect of external induction on the hypoxic response.
-
Keywords:
- respiratory rhythm /
- closed-loop respiratory control model /
- bifurcation analysis /
- electromagnetic induction
[1] Smith J C, Ellenberger H H, Ballanyi K, Richter D W, Feldman J L 1991 Science 254 726
Google Scholar
[2] Diekman C O, Thomas P J, Wilson C G 2024 Biol. Cybern. 118 145
Google Scholar
[3] 李胜岐 2008 呼吸系统与疾病 (上海: 上海科学技术出版社) 第29—36页
Li S Q 2008 Respiratory System and Illness (Shanghai: Shanghai Science and Technology Press) pp29–36
[4] Diekman C O, Thomas P J, Wilson C G 2017 J. Neurophysiol. 118 2194
Google Scholar
[5] Del Negro C A, Funk G D, Feldman J L 2018 Nat. Rev. Neurosci. 19 351
Google Scholar
[6] Diekman C O, Wilson C G, Thomas P J 2012 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) San Diego, California USA, August 28–September 1, 2012 p6669
[7] Ge M Y, Jia Y, Xu Y, Yang L J 2018 Nonlinear Dyn. 91 515
Google Scholar
[8] Zhang Y, Xu Y, Yao Z, Ma J 2020 Nonlinear Dyn. 102 1849
Google Scholar
[9] Duan L X, Cao Q Y, Wang Z J, Su J Z 2018 Nonlinear Dyn. 94 1961
Google Scholar
[10] Mostaghimi S, Nazarimehr F, Jafari S, Ma J 2019 Appl. Math. Comput. 348 42
Google Scholar
[11] Liu Y, Ma J, Xu Y, Jia Y 2019 Int. J. Bifurc. Chaos 29 1950156
Google Scholar
[12] 赵晴晴, 刘深泉, 孟盼 2023 云南大学学报(自然科学版) 45 1238
Google Scholar
Zhao Q, Liu S, Meng P 2023 J. Yunnan Univ. Nat. Sci. Ed. 45 1238
Google Scholar
[13] Zhao J Y, Wang Q Y 2021 Nonlinear Dyn. 106 975
Google Scholar
[14] 赵雅琪, 刘谋天, 赵勇, 段利霞 2021 70 120501
Google Scholar
Zhao Y Q, Liu M T, Zhao Y, Duan L X 2021 Acta Phys. Sin. 70 120501
Google Scholar
[15] 梁艳美, 陆博, 古华光 2022 71 230502
Google Scholar
Liang Y M, Lu B, Gu H G 2022 Acta Phys. Sin. 71 230502
Google Scholar
[16] 黎丽, 赵志国, 古华光 2022 71 050504
Google Scholar
Li L, Zhao Z G, Gu H G 2022 Acta Phys. Sin. 71 050504
Google Scholar
[17] Izhikevich E M 2000 Int. J. Bifurc. Chaos 10 1171
Google Scholar
[18] 冀文超, 段利霞, 齐会如 2021 力学学报 53 1733
Google Scholar
Ji W C, Duan L X, Qi H R 2021 Chin. J. Theor. Appl. Mech. 53 1733
Google Scholar
[19] Liu H, Yang Z Q, Yang B J 2023 Nonlinear Dyn. 111 15417
Google Scholar
[20] Zhao Z G, Jia B, Gu H G 2016 Nonlinear Dyn. 86 1549
Google Scholar
[21] Liu M T, Duan L X 2022 Elec. Res. Arch. 30 961
Google Scholar
[22] Ji W C, Liu M T, Duan L X 2021 Neural Plast. 2021 6655933
Google Scholar
[23] Park C, Rubin J E 2013 J. Comput. Neurosci. 34 345
Google Scholar
[24] Diekman C O, Thomas P J, Wilson C G 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, July 18–21, 2018 p5273
-
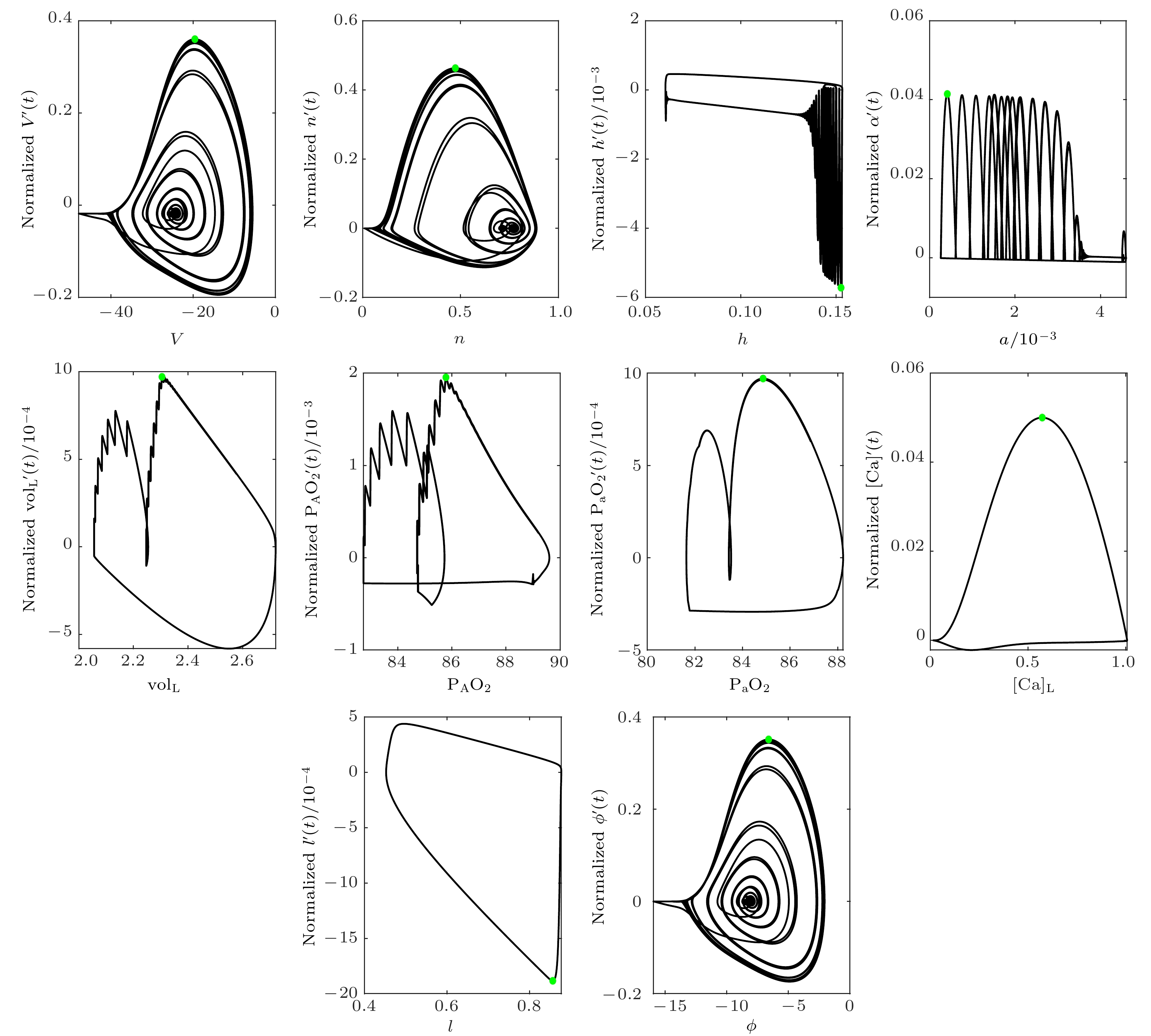
图 1 电磁感应驱动下闭环系统每个变量相对速度的相位图, 绿点表示每个变量的最大相对速度, 参数值见附录A
Fig. 1. Phase diagram of relative speed of each variable in a closed-loop system driven by electromagnetic induction. Green dots indicate the maximum rate $ {v_x} $ of each variable. Defaulted parameter values are shown in Appendix A.
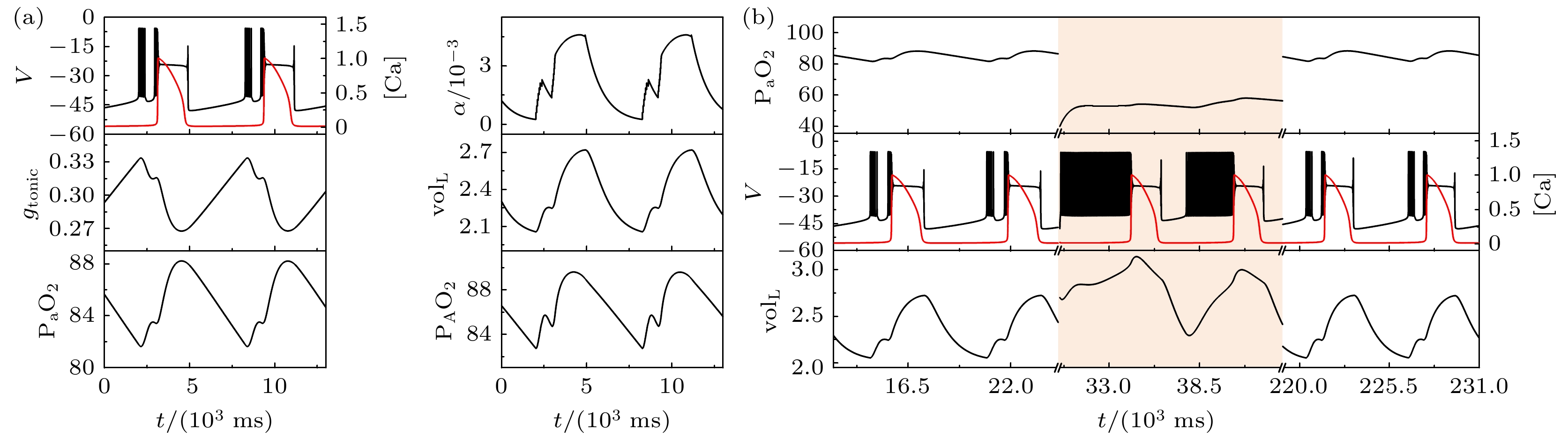
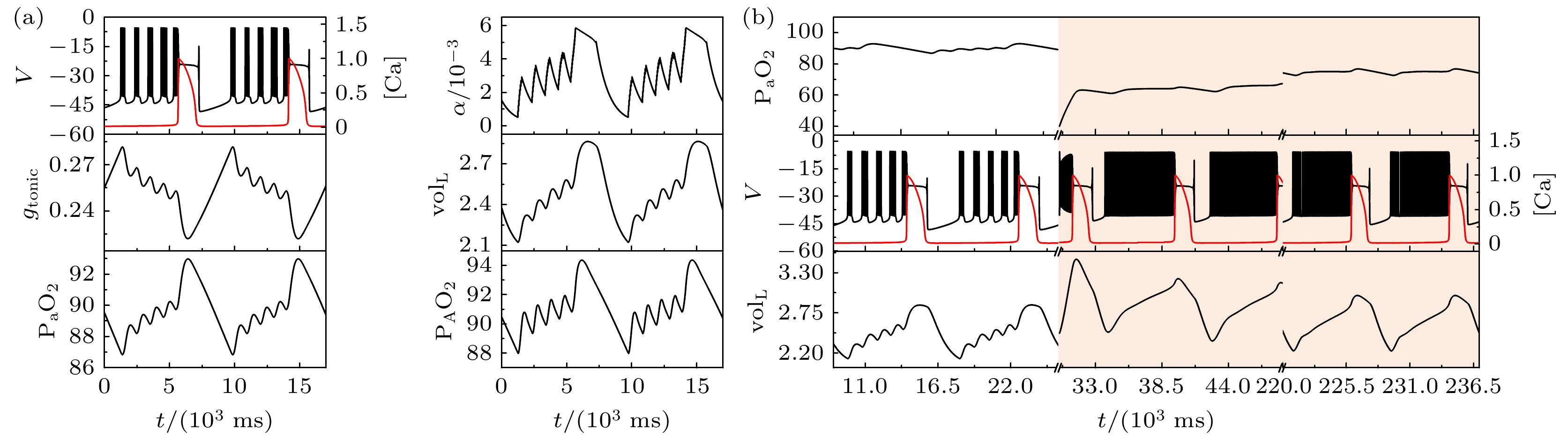
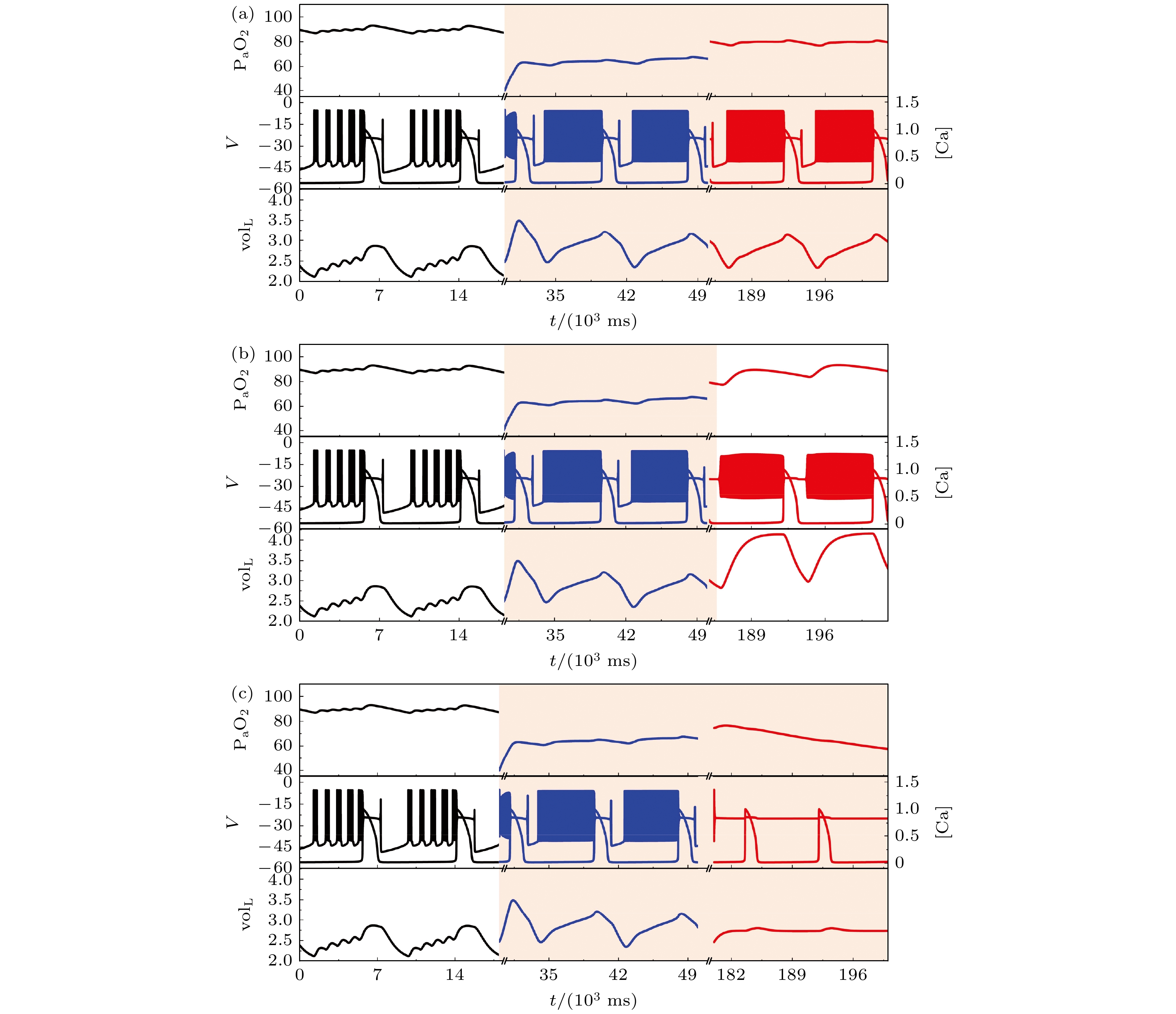
图 2 电磁感应驱动下闭环系统的缺氧反应($ {g_{{\text{NaP}}}} $= 2.3 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L, $ {k_{1}} $= 0.1) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $= 0.1时, 系统可以自动恢复
Fig. 2. Response to transient hypoxia in a closed-loop system driven by electromagnetic induction with $ {g_{{\text{NaP}}}} $ = 2.3 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L and $ {k_{1}} $= 0.1: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When $ {k_{1}} $ = 0.1, the system can automatically recover.
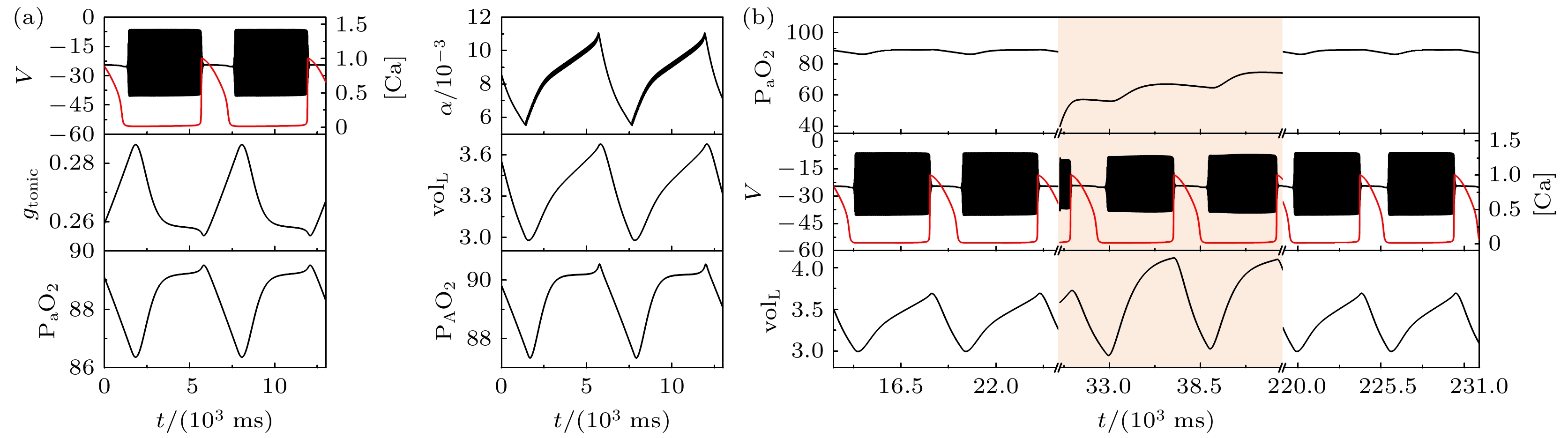
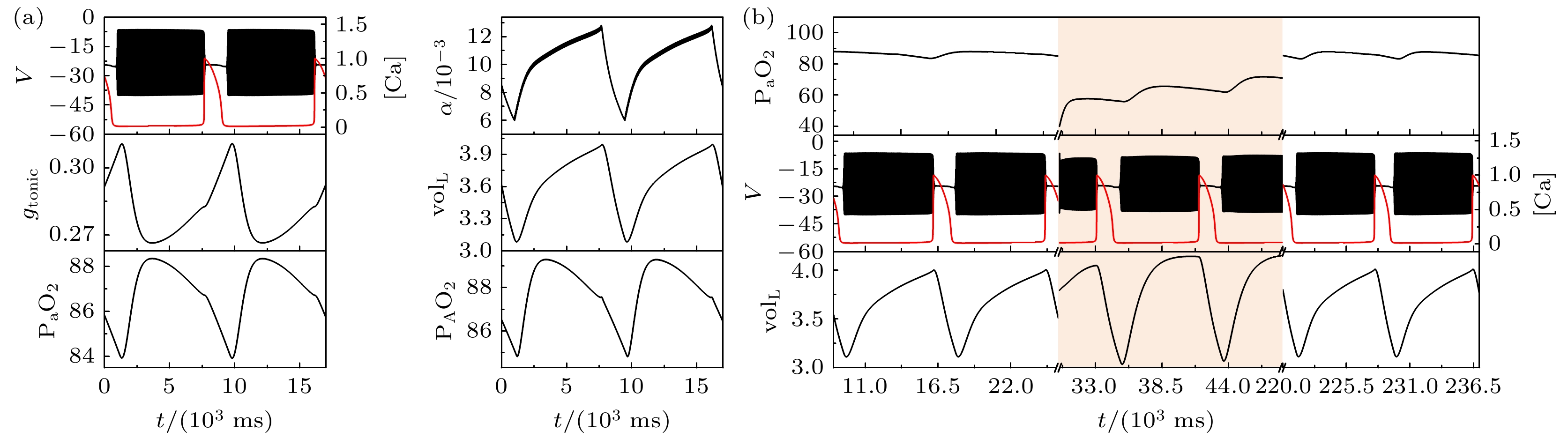
图 3 电磁感应驱动下闭环系统缺的氧反应($ {g_{{\text{NaP}}}} $ = 2.3 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L, $ {k_{1}} $ = 0.5) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $= 0.5时, 系统仍可自动恢复
Fig. 3. Response to transient hypoxia in a closed-loop system driven by electromagnetic induction with $ {g_{{\text{NaP}}}} $ = 2.3 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L and $ {k_{1}} $ = 0.5: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When $ {k_{1}} $ = 0.5, the system can also recover automatically.
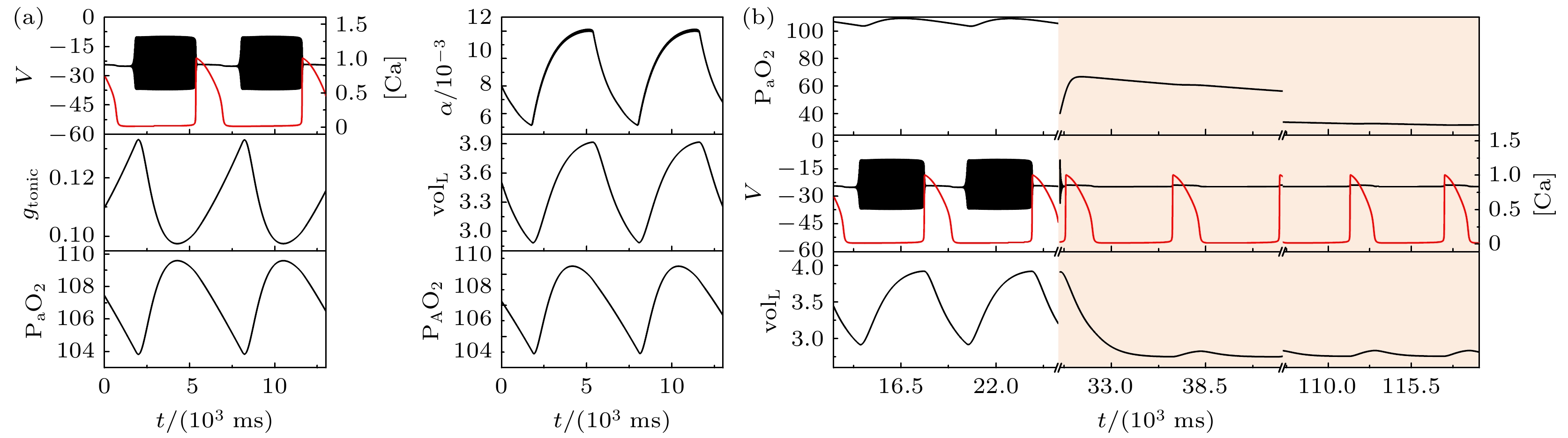
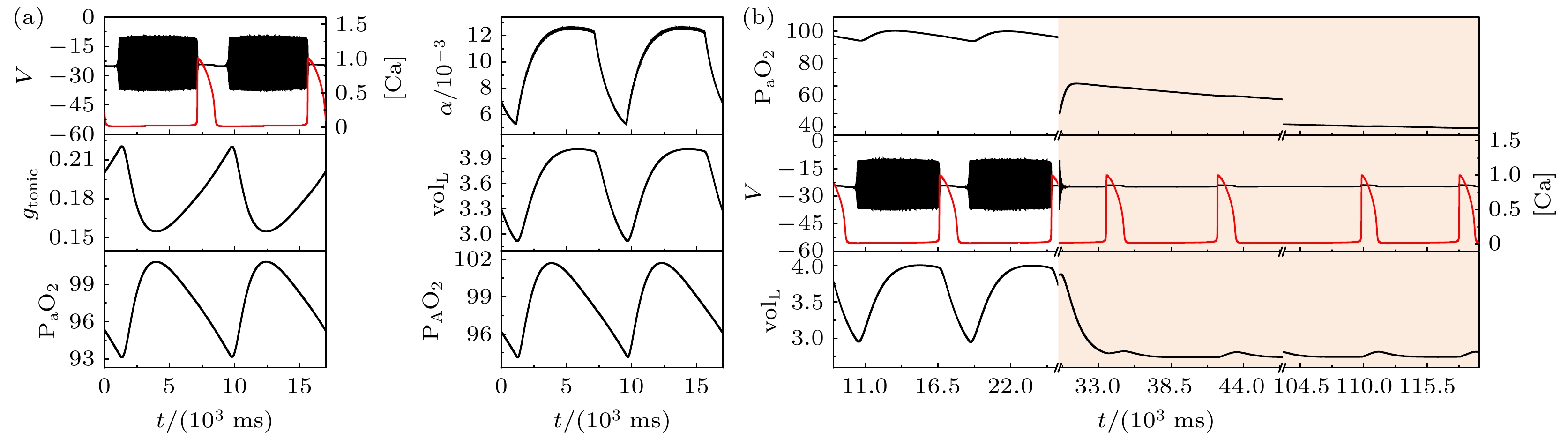
图 4 电磁感应驱动下闭环系统的缺氧反应($ {g_{{\text{NaP}}}} $ = 2.3 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L, $ {k_{1}} $=1) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $ = 1时, 系统却不能自动恢复
Fig. 4. Response to transient hypoxia in a closed-loop system driven by electromagnetic induction with $ {g_{{\text{NaP}}}} $ = 2.3 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.3 μmol/L and $ {k_{1}} $= 1: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When $ {k_{1}} $ = 1, the system cannot automatically recover.
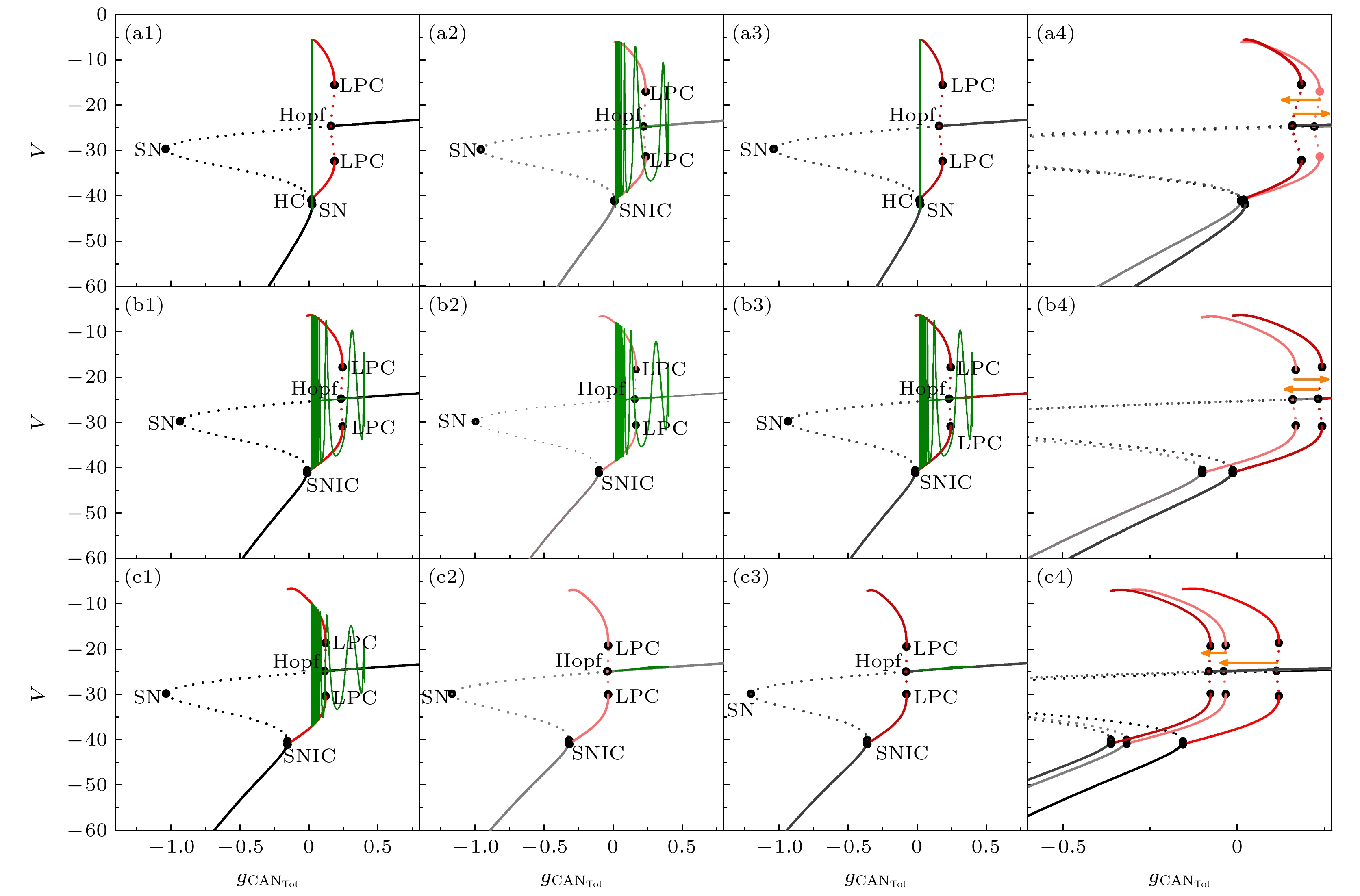
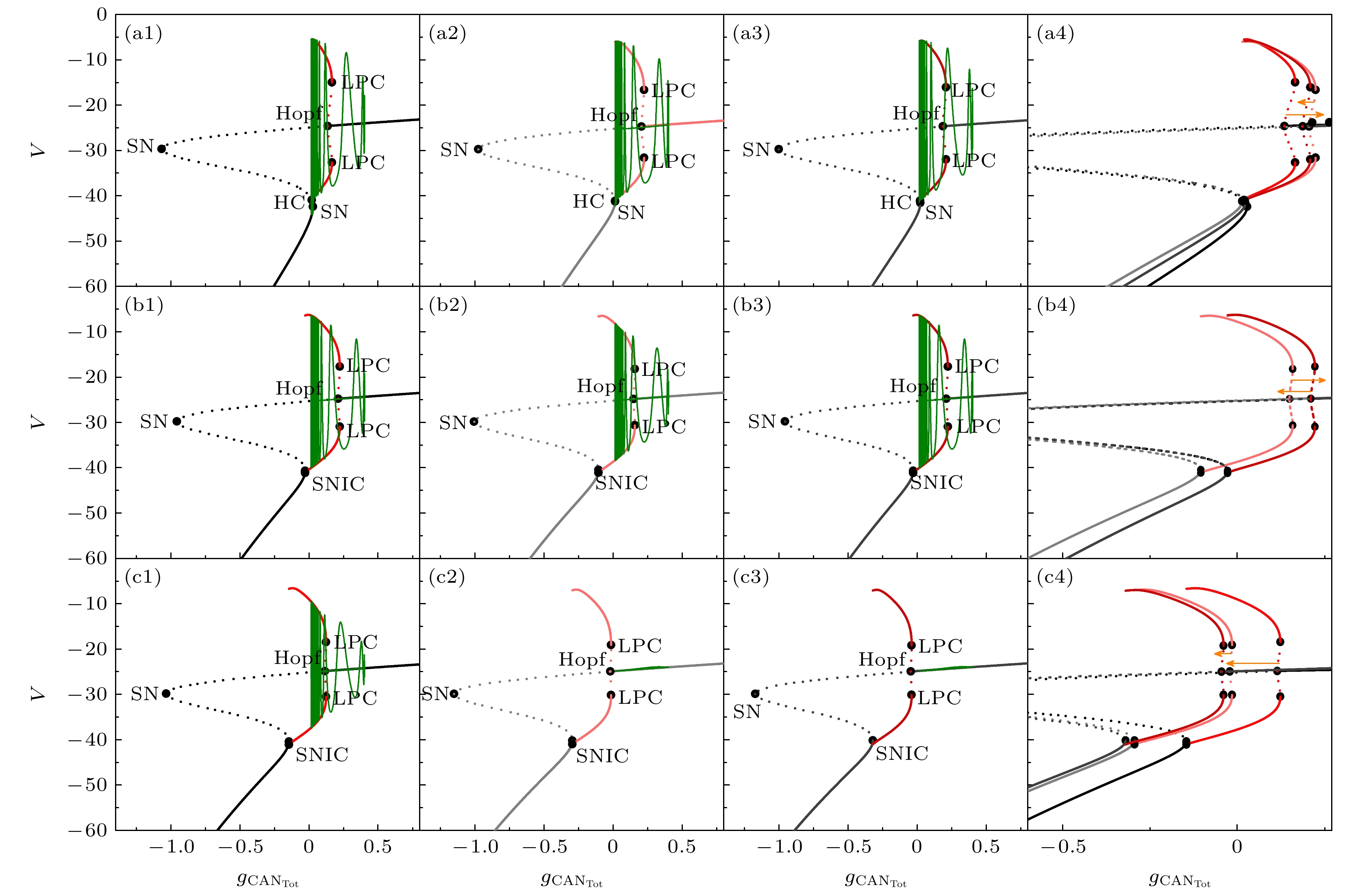
图 5 不同磁流反馈系数$ {k_1} $下, 快子系统的单参数分岔分析, 其中SN, Hopf, LPC, HC和SNIC点分别表示鞍结分岔点、Hopf分岔点、极限环的鞍结分岔点、同宿轨分岔点和不变圆上的鞍结分岔点, 这里(a1)—(a4) $ {k_1} $= 0.1; (b1)—(b4) $ {k_1} $= 0.5; (c1)—(c4) $ {k_1} $= 1
Fig. 5. One-parameter bifurcation analysis of the fast sub-system under different magnetic current feedback coefficients $ {k_1} $. The points SN, Hopf, LPC, HC and SNIC represent the fold bifurcation, Hopf bifurcation, fold bifurcation of limit cycle, homoclinic bifurcation and saddle-node bifurcation on an invariant circle, respectively. (a1)–(a4) $ {k_1} $= 0.1; (b1)–(b4) $ {k_1} $= 0.5; (c1)–(c4) $ {k_1} $= 1.
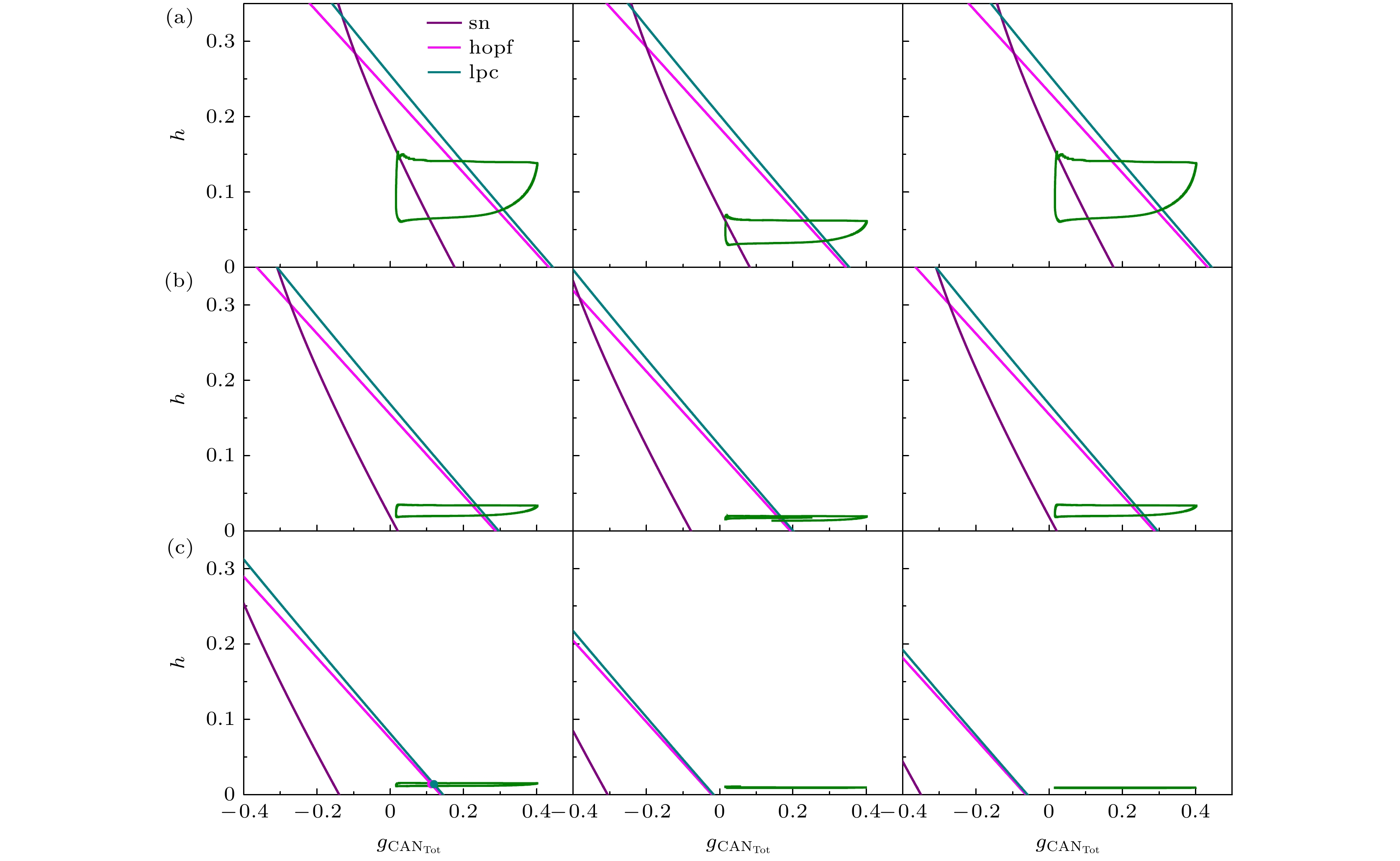
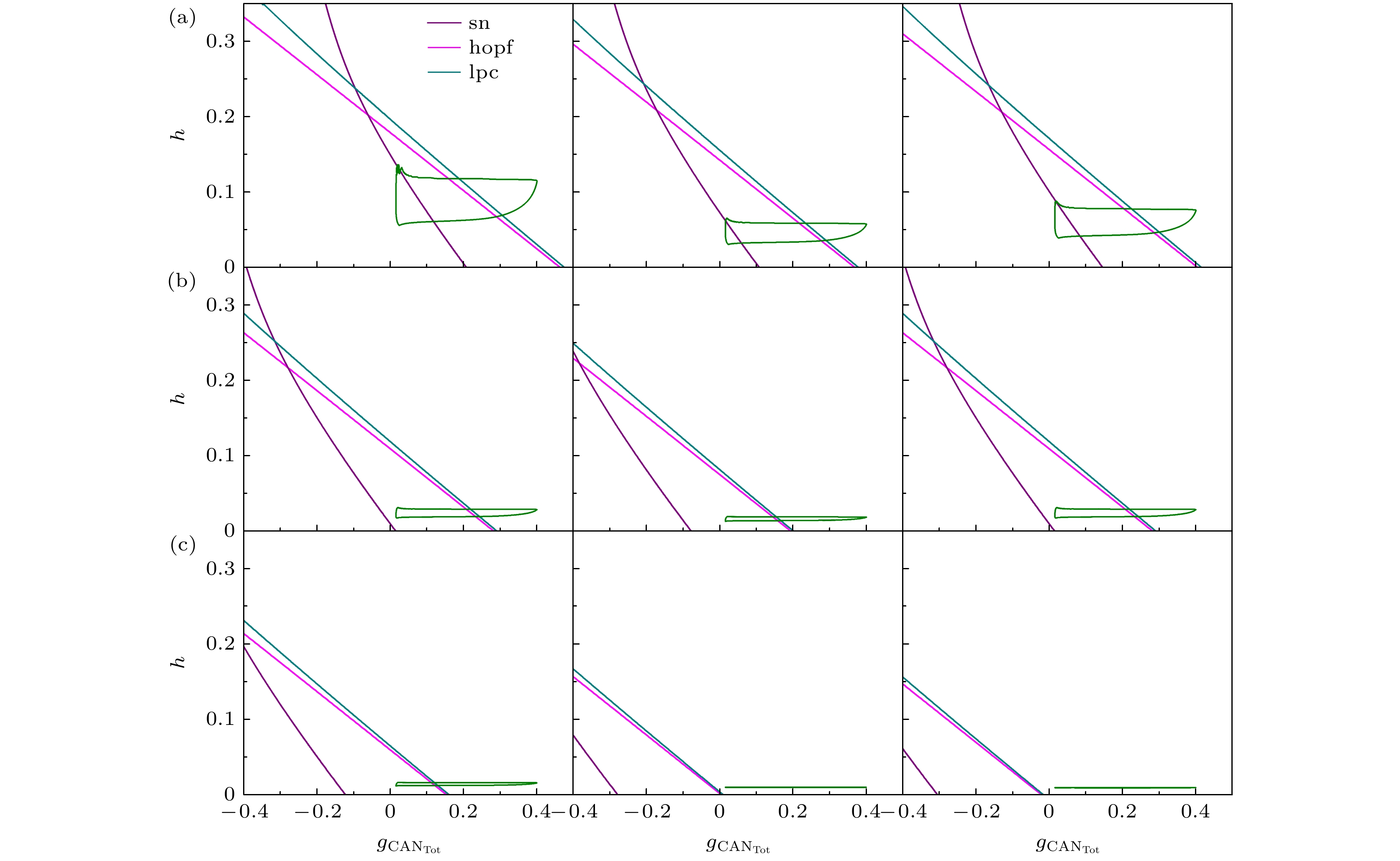
图 6 不同磁流反馈系数$ {k_1} $下, 快子系统的双参数分岔分析, 其中左栏为缺氧干扰前的双参数分岔, 中栏为缺氧干扰后的双参数分岔, 右栏为缺氧干扰后, 系统稳定了的双参数分岔, 这里(a) $ {k_1} $= 0.1; (b) $ {k_1} $= 0.5; (c) $ {k_1} $= 1
Fig. 6. Two-parameter bifurcation analysis of the fast sub-system under different magnetic current feedback coefficients $ {k_1} $. Left is two-parameter bifurcation during eupneic bursting, middle is two-parameter bifurcation after a hypoxic perturbation, right is two-parameter bifurcation of the system stabilized after a hypoxic perturbation. (a) $ {k_1} $ = 0.1; (b) $ {k_1} $ = 0.5; (c) $ {k_1} $= 1.
图 7 电磁感应驱动下的闭环系统($ {g_{{\text{NaP}}}} $= 3.2 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L, $ {k_{1}} $ = 0.1) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $ = 0.1时, 系统不能自动恢复
Fig. 7. Response to transient hypoxia in a closed-loop system driven by electromagnetic induction with $ {g_{{\text{NaP}}}} $ = 3.2 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L and $ {k_{1}} $ = 0.1: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When $ {k_{1}} $= 0.1, the system cannot automatically recover.
图 8 电磁感应驱动下的闭环系统( $ {g_{{\text{NaP}}}} $ = 3.2 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L, $ {k_{1}} $ = 0.5) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $ = 0.5时, 系统却能自动恢复
Fig. 8. Imposed hypoxic event in a closed-loop system driven by electromagnetic induction with $ {g_{{\text{NaP}}}} $ = 3.2 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L and $ {k_{1}} $= 0.5: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When $ {k_{1}} $ = 0.5, the system can automatically recover.
图 9 电磁感应驱动下的闭环系统($ {g_{{\text{NaP}}}} $ = 3.2 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L, $ {k_{1}} $= 0.9) (a)系统的轨迹; (b)系统的缺氧反应; 当$ {k_{1}} $= 0.9时, 系统不能自动恢复
Fig. 9. Imposed hypoxic event in a closed-loop system driven by electromagnetic induction with $ {g_{{\text{NaP}}}} $ = 3.2 ns, $ \left[ {{\text{I}}{{\text{P}}_3}} \right] $ = 1.1 μmol/L and $ {k_{1}} $ = 0.9: (a) Traces from the system during eupneic bursting; (b) traces after a hypoxic perturbation. When $ {k_{1}} $ = 0.9, the system can not automatically recover.
图 10 不同磁流反馈系数$ {k_1} $下, 快子系统的单参数分岔分析 (a1)—(a4) $ {k_1} $ = 0.1; (b1)—(b4) $ {k_1} $ = 0.5; (c1)—(c4) $ {k_1} $ = 0.9
Fig. 10. Single-parameter bifurcation analysis of the fast sub-system under different magnetic current feedback coefficients $ {k_1} $: (a1)–(a4) $ {k_1} $ = 0.1; (b1)–(b4) $ {k_1} $ = 0.5; (c1)–(c4) $ {k_1} $ = 0.9.
图 11 不同磁流反馈系数$ {k_1} $下, 快子系统的双参数分岔分析, 其中左栏为缺氧干扰前的双参数分岔, 中栏为施加缺氧干扰后的双参数分岔, 右栏为施加缺氧干扰后, 系统稳定了的双参数分岔, 这里(a) $ {k_1} $ = 0.1; (b) $ {k_1} $ = 0.5; (c) $ {k_1} $ = 0.9
Fig. 11. Two-parameter bifurcation analysis of the fast sub-system under different magnetic current feedback coefficients $ {k_1} $. Left panel is two-parameter bifurcation during eupneic bursting, middle panel is two-parameter bifurcation after a hypoxic perturbation, right panel is two-parameter bifurcation of the system stabilized after a hypoxic perturbation. (a) $ {k_1} $= 0.1; (b) $ {k_1} $= 0.5; (c) $ {k_1} $= 0.9.
图 12 $ {k_1} $= 0.1时缺氧扰动后系统不能恢复情形下, 增大磁流反馈系数后的反应, 其中黑色和蓝色曲线是$ {k_1} $ = 0.1作用下缺氧扰动前后的时间序列图, 红色曲线是增大磁流反馈系数后的时间序列, 这里(a) $ {k_1} $= 0.2; (b) $ {k_1} $= 0.7; (c) $ {k_1} $= 0.9
Fig. 12. Response to transient hypoxia in a closed-loop system with the increasing magnetic current feedback coefficient , which the system does not recover after a hypoxic perturbation at $ {k_{1}} $= 0.1. The black and blue curves are time series before and after the hypoxic perturbation at $ {k_1} $= 0.1, and the red curve is the time series after increasing the magnetic current feedback coefficient. (a) $ {k_1} $= 0.2; (b) $ {k_1} $= 0.7; (c) $ {k_1} $= 0.9.
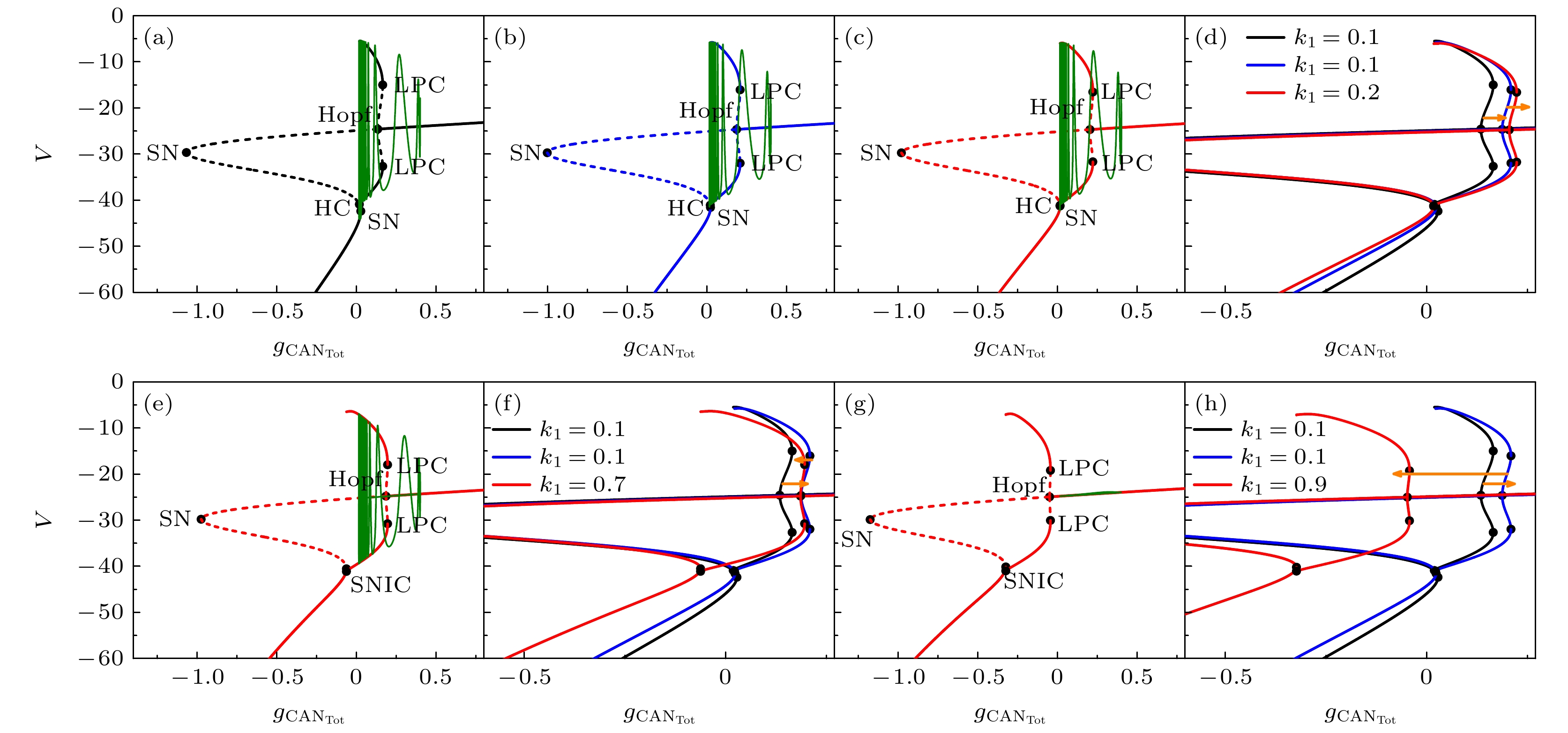
图 13 电磁感应驱动下缺氧扰动前后的单参数分岔分析 (a) $ {k_1} $= 0.1, 缺氧扰动前; (b) $ {k_1} $= 0.1, 缺氧扰动后; (c) $ {k_1} $ = 0.2, h = 0.0667; (d) $ {k_1} $ = 0.1时缺氧扰动前后以及$ {k_1} $= 0.2的叠加图; (e) $ {k_1} $ = 0.7, h = 0.0216; (f) $ {k_1} $= 0.1时缺氧扰动前后以及$ {k_1} $= 0.7的叠加图; (g) $ {k_1} $= 0.9, h = 0.0094; (h) $ {k_1} $= 0.1时缺氧扰动前后以及$ {k_1} $= 0.9的叠加图
Fig. 13. One-parameter bifurcation analysis with before and after hypoxic perturbation driven by electromagnetic induction: (a) Bifurcation structure during eupneic bursting with $ {k_1} $= 0.1; (b) bifurcation structure after a hypoxic perturbation with $ {k_1} $= 0.1; (c) $ {k_1} $= 0.2, h = 0.0667; (d) bifurcation diagrams superposed with before and after hypoxic perturbation when $ {k_1} $= 0.1 and 0.2; (e) $ {k_1} $= 0.7, h = 0.0216; (f) bifurcation diagrams superposed with before and after hypoxic perturbation when $ {k_1} $= 0.1 and 0.7; (g) $ {k_1} $= 0.9, h = 0.0094; (h) bifurcation diagrams superposed with before and after hypoxic perturbation when $ {k_1} $= 0.1 and 0.9.
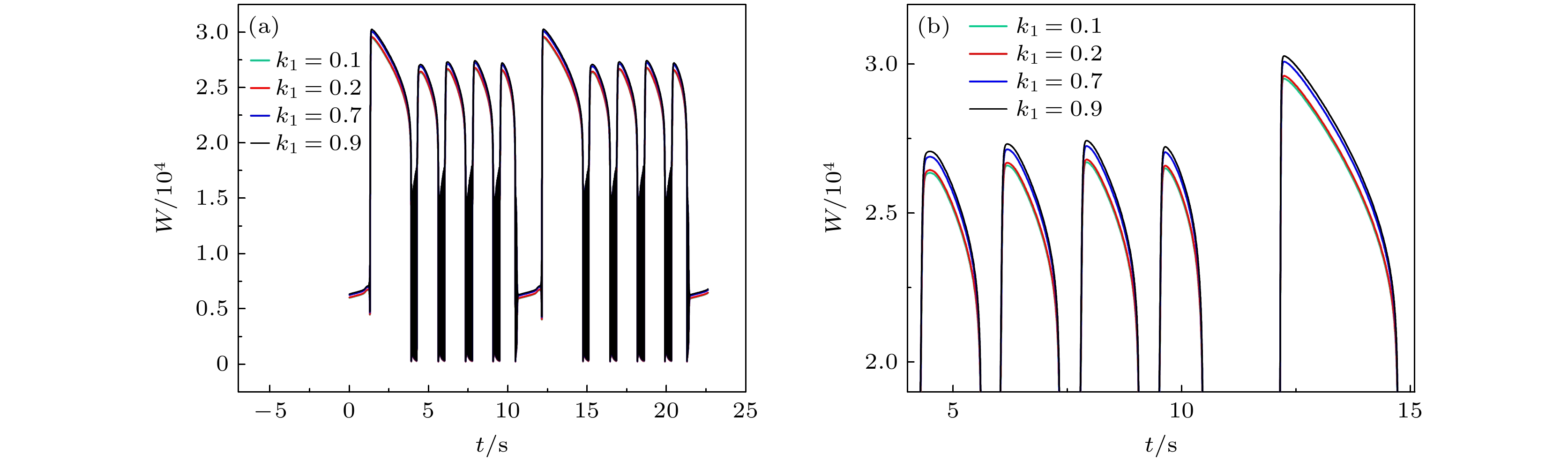
图 14 电磁感应驱动下系统的能量变化 (a) $ {k_1} $ = 0.1, 0.2, 0.7, 0.9时能量随时间的变化; (b) 图(a)的放大图; 参数设置同图12
Fig. 14. Evolution of the energy driven by electromagnetic induction: (a) Evolution of the energy with the parameter $ {k_1} $= 0.1, 0.2, 0.7 and 0.9; (b) the enlargement part of (a). The parameter values are same as that in Fig. 12.
表 1 电磁感应驱动下闭环模型各个变量的最大相对速度
Table 1. The maximum relative speed of each variable in a closed-loop model driven by electromagnetic induction.
变量 $x$ ${\text{vo}}{{\text{l}}_{\text{L}}}$ $ {{\text{P}}_{\text{a}}}{{\text{O}}_{2}} $ l $ {{\text{P}}_{\text{A}}}{{\text{O}}_{2}} $ h ${v_x}$ 0.0009 0.0009 0.0019 0.0020 0.0057 变量 $x$ $\alpha $ [Ca] $ \varphi $ V n ${v_x}$ 0.0415 0.0500 0.3513 0.3601 0.4631 
下载: 导出CSV
参数 取值 参数 取值 参数 取值 C/μF 21 EK/mV –85 $ E_{{\mathrm{L}}} $/mV –58 ${E_{{\text{Na}}}}$ 50 ${E_{{\text{tonic}}}}$/mV 0 ${g_{\text{K}}}$/nS 3.5 ${g_{\text{L}}}$/nS 2.3 ${g_{{\text{NaP}}}}$/nS varied ${g_{{\text{Na}}}}$/nS 8 ${\theta _m}$/mV –34 ${\sigma _m}$/mV –5 ${\theta _n}$/mV –29 ${\sigma _n}$/mV –4 ${\overline \tau _n}$/mV 10 ${\theta _h}$/mV –48 ${\sigma _h}$/mV 5 ${\overline \tau _h}$/mV 10000 ${\theta _p}$/mV –40 $ {\sigma _p} $/mV –6 ${K_{{\text{CAN}}}}$/(μmol·L–1) 0.74 ${n_{{\text{CAN}}}}$ 0.97 ${L_{{\text{I}}{{\text{P}}_{3}}}}$/($ {{\mathrm{p}}{\mathrm{L}}}^{-1}\cdot {{\mathrm{s}}}^{-1} $) 0.27 ${P_{{\text{I}}{{\text{P}}_{3}}}}$/($ {{\mathrm{p}}{\mathrm{L}}}^{-1}\cdot {{\mathrm{s}}}^{-1} $) 31000 $\left[ {{\text{I}}{{\text{P}}_3}} \right]$/(μmol·L–1) varied ${K_{\text{I}}}$/(μmol·L–1) 1.0 ${K_{\text{a}}}$/(μmol·L–1) 0.4 ${{\text{[Ca]}}_{{\text{Tot}}}}$/(μmol·L–1) 1.25 $\sigma $ 0.185 ${V_{{\text{SERCA}}}}$/(amol·s–1) 400 ${K_{{\text{SERCA}}}}$/(μmol·L–1) 0.2 ${f_m}$/$ {{\mathrm{p}}{\mathrm{L}}}^{-1} $ 0.000025 A/(μmol–1·L·s–1) 0.001 ${K_d}$/(μmol·L–1) 0.4 ${r_a}$/(mmol–1·L·ms–1) 0.001 ${r_d}$/(mmol–1·L·ms–1) 0.001 ${T_{\max }}$/(mmol·L–1) 1 ${V_T}$/mV 2 ${K_P}$/mV 5 ${E_1}$/($ {{\mathrm{m}}{\mathrm{s}}}^{-1} $) 0.0025 ${E_2}$/$ {{\mathrm{m}}{\mathrm{s}}}^{-1} $ 0.4 ${\text{vo}}{{\text{l}}_{0}}$/L 2 ${{\text{P}}_{{\text{ext}}}}{{\text{O}}_{2}}$/mmHg 149.7 ${\tau _{{\text{LB}}}}$/ms 500 R/($ {\mathrm{L}}\cdot {\mathrm{ }}{\mathrm{m}}{\mathrm{m}}{\mathrm{H}}{\mathrm{g}}\cdot {{\mathrm{K}}}^{-1}\cdot {{\mathrm{m}}{\mathrm{o}}{\mathrm{l}}}^{-1} $) 62.364 T/K 310 M/$ {{\mathrm{m}}{\mathrm{s}}}^{-1} $ 8×10–6 ${\beta _{{{\text{O}}_{2}}}}$/($ {\mathrm{m}}{\mathrm{l}}{{\mathrm{O}}}_{2}\cdot {\mathrm{l}}{{\mathrm{b}}{\mathrm{l}}{\mathrm{o}}{\mathrm{o}}{\mathrm{d}}}^{-1}\cdot {{\mathrm{m}}{\mathrm{m}}{\mathrm{H}}{\mathrm{g}}}^{-1} $) 0.03 c 2.5 K/mmHg 26 ${\text{vo}}{{\text{l}}_{\text{B}}}$/L 5 [Hb]/(g·L–1) 150 $\phi $/nS 0.3 ${\theta _{\text{g}}}$/mmHg 85 ${\sigma _{\text{g}}}$/mmHg 30
下载: 导出CSV
-
[1] Smith J C, Ellenberger H H, Ballanyi K, Richter D W, Feldman J L 1991 Science 254 726
Google Scholar
[2] Diekman C O, Thomas P J, Wilson C G 2024 Biol. Cybern. 118 145
Google Scholar
[3] 李胜岐 2008 呼吸系统与疾病 (上海: 上海科学技术出版社) 第29—36页
Li S Q 2008 Respiratory System and Illness (Shanghai: Shanghai Science and Technology Press) pp29–36
[4] Diekman C O, Thomas P J, Wilson C G 2017 J. Neurophysiol. 118 2194
Google Scholar
[5] Del Negro C A, Funk G D, Feldman J L 2018 Nat. Rev. Neurosci. 19 351
Google Scholar
[6] Diekman C O, Wilson C G, Thomas P J 2012 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) San Diego, California USA, August 28–September 1, 2012 p6669
[7] Ge M Y, Jia Y, Xu Y, Yang L J 2018 Nonlinear Dyn. 91 515
Google Scholar
[8] Zhang Y, Xu Y, Yao Z, Ma J 2020 Nonlinear Dyn. 102 1849
Google Scholar
[9] Duan L X, Cao Q Y, Wang Z J, Su J Z 2018 Nonlinear Dyn. 94 1961
Google Scholar
[10] Mostaghimi S, Nazarimehr F, Jafari S, Ma J 2019 Appl. Math. Comput. 348 42
Google Scholar
[11] Liu Y, Ma J, Xu Y, Jia Y 2019 Int. J. Bifurc. Chaos 29 1950156
Google Scholar
[12] 赵晴晴, 刘深泉, 孟盼 2023 云南大学学报(自然科学版) 45 1238
Google Scholar
Zhao Q, Liu S, Meng P 2023 J. Yunnan Univ. Nat. Sci. Ed. 45 1238
Google Scholar
[13] Zhao J Y, Wang Q Y 2021 Nonlinear Dyn. 106 975
Google Scholar
[14] 赵雅琪, 刘谋天, 赵勇, 段利霞 2021 70 120501
Google Scholar
Zhao Y Q, Liu M T, Zhao Y, Duan L X 2021 Acta Phys. Sin. 70 120501
Google Scholar
[15] 梁艳美, 陆博, 古华光 2022 71 230502
Google Scholar
Liang Y M, Lu B, Gu H G 2022 Acta Phys. Sin. 71 230502
Google Scholar
[16] 黎丽, 赵志国, 古华光 2022 71 050504
Google Scholar
Li L, Zhao Z G, Gu H G 2022 Acta Phys. Sin. 71 050504
Google Scholar
[17] Izhikevich E M 2000 Int. J. Bifurc. Chaos 10 1171
Google Scholar
[18] 冀文超, 段利霞, 齐会如 2021 力学学报 53 1733
Google Scholar
Ji W C, Duan L X, Qi H R 2021 Chin. J. Theor. Appl. Mech. 53 1733
Google Scholar
[19] Liu H, Yang Z Q, Yang B J 2023 Nonlinear Dyn. 111 15417
Google Scholar
[20] Zhao Z G, Jia B, Gu H G 2016 Nonlinear Dyn. 86 1549
Google Scholar
[21] Liu M T, Duan L X 2022 Elec. Res. Arch. 30 961
Google Scholar
[22] Ji W C, Liu M T, Duan L X 2021 Neural Plast. 2021 6655933
Google Scholar
[23] Park C, Rubin J E 2013 J. Comput. Neurosci. 34 345
Google Scholar
[24] Diekman C O, Thomas P J, Wilson C G 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, July 18–21, 2018 p5273
下载:
计量
- 文章访问数: 611
- PDF下载量: 30
- 被引次数: 0
