-
电磁感应透明效应是基于原子不同跃迁通道之间的量子相干效应, 可以使得原子系综对于光场的吸收率降低, 甚至接近于0, 同时在原子共振频率附近伴随着强烈的色散, 因而被广泛应用于群速度调控、光脉冲存储和光场的相干调控等领域. 本文基于电磁感应透明效应, 通过信号光场、耦合光场和读取光场操控复现光场, 在4
$f$ 系统的像面上实现了光学图像的加减操作. 相较于通常在频谱面上利用余弦光栅进行滤波的方案, 基于电磁感应透明效应的方案无需制备频谱面滤波掩膜版, 并且只产生正一级和负一级衍射图像, 无0级衍射图像干扰, 可广泛应用于光学图像的动态实时处理.The electromagnetically induced transparency (EIT) effect is a quantum coherence effect between different atomic transition channels. The absorption of the atomic ensemble is significantly reduced or even close to zero, and at the same time, this effect is accompanied by strong spectral dispersion near the resonant frequency of atoms, which is widely used in group velocity control, light pulse storage, and coherent manipulation on the light field. In the light pulse storage based on the EIT effect, the retrieval field is determined by the signal, coupling, and readout fields, enabling the retrieval field to be dynamically controlled by manipulating the spatial frequency components of the interacting light fields. In this paper, according to the EIT effect, we achieve experimentally the optical image addition and subtraction in the imaging plane of a 4$f$ system through the coherent manipulation of the retrieval field via the interacting signal, coupling, and readout fields. Specifically, we first store the spatial frequency spectrum of a double-slit mask in the praseodymium-doped yttrium silicate crystal located in the confocal plane of the 4$f$ system based on the EIT effect. Then, we utilize a specially designed mask containing the target objects and perform spatial filtering by using the spatial frequency spectrum of the double-slit mask through the retrieval of stored light pulse. By moving the double-slit mask, the addition and subtraction between the images of target objects can be achieved in the imaging plane of the 4$f$ system. We present a theoretical model to describe the addition and subtraction between the target images through the EIT-based light pulse storage technique. The experimental results accord well with the theoretical prediction. Compared with the traditional scheme with a cosine grating filtering the spatial frequency spectrum, our method does not require the preparation of a spatial frequency filter, and only produces the first-order positive and negative diffraction images without the influence of the zeroth-order diffraction image. The optical image addition and subtraction based on the EIT effect provide a new approach to optical image processing. This approach is not limited to image addition or subtraction, and it can be extended to achieve more complex operations such as differentiation, enhancement, encryption, and decryption with rational design. Therefore, it can be widely used in areas such as coherent manipulation of light fields and dynamic optical image processing.-
Keywords:
- optical image processing /
- electromagnetically induced transparency /
- optical image addition and subtraction
[1] Alfalou A, Brosseau C 2015 Prog. Optics 60 119
[2] Chakraborty S, Saha A, Bhattacharya K 2014 Optik 125 6466
Google Scholar
[3] Gabor D, Stroke G W, Restrick Ⅲ R C, Funkhouser A T, Brumm D 1965 Phys. Lett. 18 116
Google Scholar
[4] Ebersole J F 1975 Opt. Eng. 14 436
[5] 母国光, 蒋建国, 刘国华 1981 30 1609
Google Scholar
Mu G G, Jiang J H, Liu G H 1981 Acta Phys. Sin. 30 1609
Google Scholar
[6] Liu S, Guo C L, Sheridan J T 2014 Opt. Laser Technol. 57 327
Google Scholar
[7] Harris S E, Field J E, Imamoglu A 1990 Phys. Rev. Lett. 64 1107
Google Scholar
[8] Wang J, Zhu Y, Jiang K J, Zhan M S 2003 Phys. Rev. A 68 063810
Google Scholar
[9] Braje D A, Balić V, Goda S, Yin G Y, Harris S E 2004 Phys. Rev. Lett. 93 183601
Google Scholar
[10] Yan H, Liao K Y, Li J F, Du Y X, Zhang Z M, Zhu S L 2013 Phys. Rev. A 87 055401
Google Scholar
[11] Kash M M, Sautenkov V A, Zibrov A S, Hollberg L, Welch G R, Lukin M D, Rostovtsev Y, Fry E S, Scully M O 1999 Phys. Rev. Lett. 82 5229
Google Scholar
[12] Ham B S, Hubrich C, Halfmann T 1997 Opt. Commun. 144 227
Google Scholar
[13] Heinze G, Hubrich C, Halfmann T 2013 Phys. Rev. Lett. 111 033601
Google Scholar
[14] Qiu T H, Xie M 2017 Phys. Rev. A 96 033844
Google Scholar
[15] Dutton Z, Ruostekoski J 2004 Phys. Rev. Lett. 93 193602
Google Scholar
[16] Hamedi H R, Kudriasov V, Ruseckas J, Juzeliunas G 2018 Opt. Express 26 28249
Google Scholar
[17] Zhao L 2015 Opt. Express 23 29808
Google Scholar
[18] Wang Y F, Li J F, Zhang S C, Su K Y, Zhou Y R, Liao K Y, Du S W, Yan H, Zhu S L 2019 Nat. Photonics 13 346
Google Scholar
[19] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[20] Qiu T H, Ma H Y, Xin P P, Zhao X L, Liu Q, Chen L B, Feng Y C, Yu Z X 2022 Eur. Phys. J. Plus 137 126
[21] Tu Y F, Zhang G G, Zhai Z H, Xu J J 2009 Phys. Rev. A 80 033816
Google Scholar
[22] 翟召辉 2013 博士学位论文 (天津: 南开大学)
Zhai Z H 2013 Ph. D. Dissertation (Tianjin: Nankai University) (in Chinese)
[23] Lvovsky A I, Sanders B C, Tittel W 2009 Nat. Photonics 3 706
Google Scholar
[24] Zhai Z H, Li Z X, Xu J J, Zhang G Q 2013 Phys. Rev. A 88 035807
Google Scholar
[25] Zhai Z H, Dou Y L, Xu J J, Zhang G Q 2011 Phys. Rev. A 83 043825
Google Scholar
[26] Li Z X, Liu J J, Fan H M, Liu J C, Zhang G Q 2017 Sci. Rep. 7 2361
Google Scholar
[27] 李志向, 刘建基, 范洪鸣, 张国权 2017 光学学报 37 0207003
Google Scholar
Li Z X, Liu J J, Fan H M, Zhang G Q 2017 Acta Opt. Sin. 37 0207003
Google Scholar
[28] 涂燕飞 2009 博士学位论文 (天津: 南开大学)
Tu Y F 2009 Ph. D. Dissertation (Tianjin: Nankai University) (in Chinese)
-
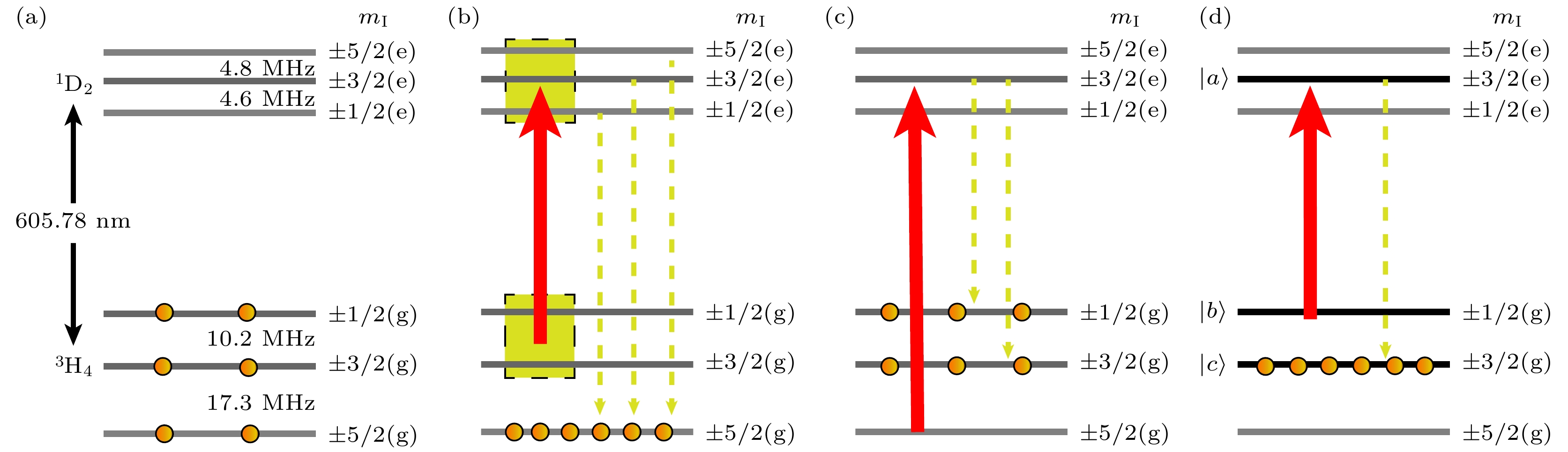
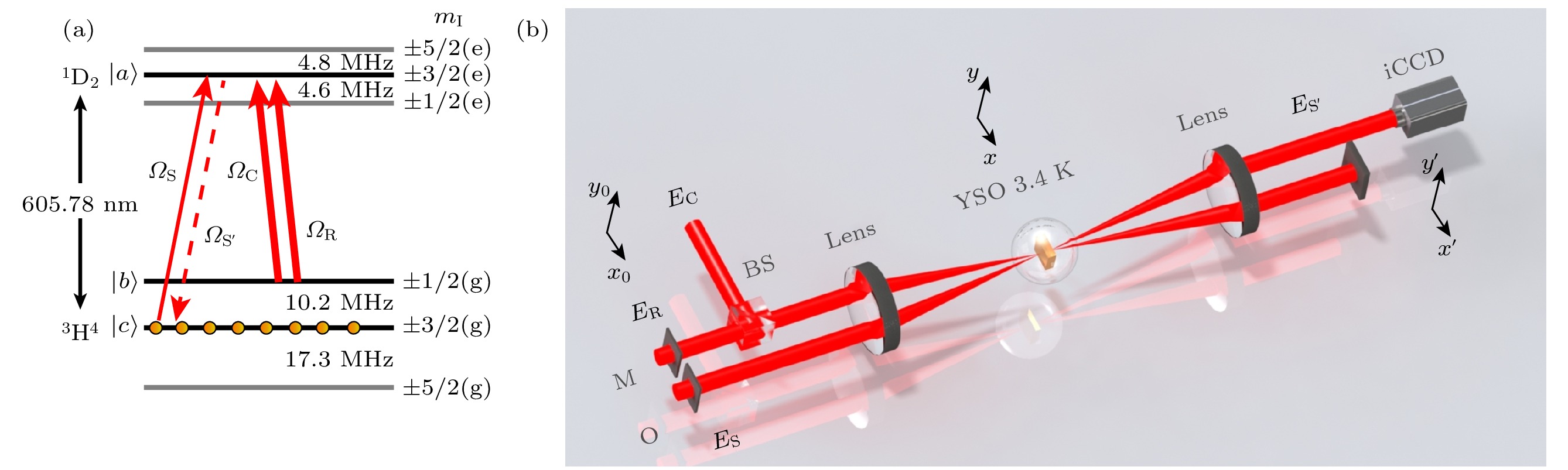
图 1 (a) Pr:YSO晶体中Pr离子参与EIT效应的能级结构图, 其中, ΩS, ΩC, ΩR, ΩS′分别为信号光、耦合光、读取光、复现光对应的拉比频率; (b)基于EIT效应实现图像加减操作的实验装置示意图, 其中, BS为50∶50分束器, Lens为焦距300 mm的凸透镜, iCCD为增强型CCD; 掩膜版M为待处理的图像, 掩膜版O为双缝; Pr:YSO晶体置于3.4 K的低温腔中
Fig. 1. (a) Energy level structure of Pr ions involved in the EIT process in Pr:YSO crystal. Here, ΩS, ΩC, ΩR, ΩS′ are the Rabi frequencies of the signal, coupling, readout, and retrieval fields, respectively. (b) Schematic diagram of the experimental setup for image addition and subtraction based on the EIT effect. Here, BS, 50∶50 beam splitter; Lens, convex lens with a 300-mm focal length; iCCD, intensified CCD. The mask M is the image to be processed, and the mask O is a double-slit mask. The Pr:YSO crystal is placed in a cryogenic vacuum chamber at 3.4 K
图 2 Pr:YSO晶体中电磁感应透明效应Λ型三能级系统初态制备流程图
Fig. 2. Flow diagram to prepare the initial state for the EIT effect with a Λ-type three-level scheme of
$ {\rm Pr}^{3+} $ ions in Pr:YSO crystal
图 3 物面掩膜版 (a)图像相加操作时带有待处理图像的掩膜版; (b)图像相减操作时带有待处理图像的掩膜版; (c)用于制备频谱面滤波光栅的双缝掩膜版
Fig. 3. Masks on the object planes: (a) Mask with the images to be processed for image addition; (b) mask with the images to be processed for image subtraction; (c) double-slit mask used to prepare the diffraction grating filter on the Fourier spectral plane
图 4 光学图像相加理论模拟图(a)和实验结果图(b). 左侧的两个短矩形图案和右侧的单个短矩形图案在像面中心实现了相加
Fig. 4. Theoretical simulation result (a) and the experimental result (b) for optical image addition. The two short rectangles on the left and the single short rectangle on the right are added at the center of the image plane
图 5 光学图像相减理论模拟图(a)和实验结果图(b). 左侧的长矩形图案和右侧的短矩形图案在像面中心实现了相减, 产生了上下两个短矩形图案
Fig. 5. Theoretical simulation result (a) and the experimental result (b) for optical image subtraction. The long rectangle on the left and the short rectangle on the right are subtracted at the center of the image plane, producing two separated short rectangles
-
[1] Alfalou A, Brosseau C 2015 Prog. Optics 60 119
[2] Chakraborty S, Saha A, Bhattacharya K 2014 Optik 125 6466
Google Scholar
[3] Gabor D, Stroke G W, Restrick Ⅲ R C, Funkhouser A T, Brumm D 1965 Phys. Lett. 18 116
Google Scholar
[4] Ebersole J F 1975 Opt. Eng. 14 436
[5] 母国光, 蒋建国, 刘国华 1981 30 1609
Google Scholar
Mu G G, Jiang J H, Liu G H 1981 Acta Phys. Sin. 30 1609
Google Scholar
[6] Liu S, Guo C L, Sheridan J T 2014 Opt. Laser Technol. 57 327
Google Scholar
[7] Harris S E, Field J E, Imamoglu A 1990 Phys. Rev. Lett. 64 1107
Google Scholar
[8] Wang J, Zhu Y, Jiang K J, Zhan M S 2003 Phys. Rev. A 68 063810
Google Scholar
[9] Braje D A, Balić V, Goda S, Yin G Y, Harris S E 2004 Phys. Rev. Lett. 93 183601
Google Scholar
[10] Yan H, Liao K Y, Li J F, Du Y X, Zhang Z M, Zhu S L 2013 Phys. Rev. A 87 055401
Google Scholar
[11] Kash M M, Sautenkov V A, Zibrov A S, Hollberg L, Welch G R, Lukin M D, Rostovtsev Y, Fry E S, Scully M O 1999 Phys. Rev. Lett. 82 5229
Google Scholar
[12] Ham B S, Hubrich C, Halfmann T 1997 Opt. Commun. 144 227
Google Scholar
[13] Heinze G, Hubrich C, Halfmann T 2013 Phys. Rev. Lett. 111 033601
Google Scholar
[14] Qiu T H, Xie M 2017 Phys. Rev. A 96 033844
Google Scholar
[15] Dutton Z, Ruostekoski J 2004 Phys. Rev. Lett. 93 193602
Google Scholar
[16] Hamedi H R, Kudriasov V, Ruseckas J, Juzeliunas G 2018 Opt. Express 26 28249
Google Scholar
[17] Zhao L 2015 Opt. Express 23 29808
Google Scholar
[18] Wang Y F, Li J F, Zhang S C, Su K Y, Zhou Y R, Liao K Y, Du S W, Yan H, Zhu S L 2019 Nat. Photonics 13 346
Google Scholar
[19] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[20] Qiu T H, Ma H Y, Xin P P, Zhao X L, Liu Q, Chen L B, Feng Y C, Yu Z X 2022 Eur. Phys. J. Plus 137 126
[21] Tu Y F, Zhang G G, Zhai Z H, Xu J J 2009 Phys. Rev. A 80 033816
Google Scholar
[22] 翟召辉 2013 博士学位论文 (天津: 南开大学)
Zhai Z H 2013 Ph. D. Dissertation (Tianjin: Nankai University) (in Chinese)
[23] Lvovsky A I, Sanders B C, Tittel W 2009 Nat. Photonics 3 706
Google Scholar
[24] Zhai Z H, Li Z X, Xu J J, Zhang G Q 2013 Phys. Rev. A 88 035807
Google Scholar
[25] Zhai Z H, Dou Y L, Xu J J, Zhang G Q 2011 Phys. Rev. A 83 043825
Google Scholar
[26] Li Z X, Liu J J, Fan H M, Liu J C, Zhang G Q 2017 Sci. Rep. 7 2361
Google Scholar
[27] 李志向, 刘建基, 范洪鸣, 张国权 2017 光学学报 37 0207003
Google Scholar
Li Z X, Liu J J, Fan H M, Zhang G Q 2017 Acta Opt. Sin. 37 0207003
Google Scholar
[28] 涂燕飞 2009 博士学位论文 (天津: 南开大学)
Tu Y F 2009 Ph. D. Dissertation (Tianjin: Nankai University) (in Chinese)
下载:
计量
- 文章访问数: 3718
- PDF下载量: 77
- 被引次数: 0
