部分相干多离轴涡旋矢量光束的传输特性

徐华锋; 张兴宇; 王仁杰

doi:10.7498/aps.73.20231484

摘要

基于相干与偏振的统一理论, 采用傅里叶变换和卷积定理的方法, 研究了携带多个离轴涡旋相位的径向偏振矩形对称余弦-高斯关联结构光束的传输特性. 结果表明, 该光束因其独特的空间相干结构而具有自分裂特性, 可以分裂成4束完全相同的子波瓣. 更重要的是, 多离轴涡旋相位的调制可以作用在每个子波瓣上. 当相干度较大时, 通过调制光束的离轴涡旋数量N₀和光束阶数可以在焦平面处产生具有三角形或正方形等多边形空心光强分布的光斑阵列, 并且每个子波瓣上对应的偏振态呈现倒三角形或斜正方形的椭圆分布. 当相干度较小时, 部分相干光束的空间相干性调控占主导作用, 多离轴涡旋相位的调制效果消失, 每个子波瓣的光强退化成高斯形式分布, 但其偏振态分布仍保持不变, 与光束阶数和相干长度无关. 此外, 当利用障碍物遮挡住其中一个离轴涡旋相位时, 光束仍具有一定的自修复能力. 然而, 若将其中一个离轴涡旋相位完全遮挡住, 此时每个子波瓣的强度分布和偏振态分布都遭到破坏, 会出现不同程度的“缺口”.

关键词:

Abstract

In this paper, we investigate the propagation properties of radially polarized rectangular-symmetric cosine-Gaussian Schell-model (RCGSM) beam with multiple off-axis vortex phases by using Fourier transform and convolution method based on the unified theory of coherence and polarization. The results indicate that the radially polarized RCGSM beam has self-splitting properties and can be split into four identical lobes due to its unique spatial coherence structure. Furthermore, the modulation of multiple off-axis vortex phases can be acted on each lobe. For high coherence, the spot arrays with triangular or square hollow light intensity distribution can be generated in the focal plane by modulating the number of off-axis vortices (N₀) and the beam order, and the corresponding state of polarization on each lobe presents an inverted triangular or oblique square elliptic distribution. However, for small coherence, the modulation effect of multiple off-axis vortex phases disappears and the light intensity of each lobe degenerates into a quasi-Gaussian distribution, whereas its state of polarization keeps invariant, which is independent of the beam order and coherence length. In addition, the beam still has a certain self-healing ability for one of the off-axis vortex phases partially blocked by an obstacle, but it will be destroyed for completely blocking, resulting in a notch on each lobe.

Keywords:

作者及机构信息

安徽理工大学力学与光电物理学院, 淮南　232001

通信作者: 徐华锋, xhfeng716@126.com

基金项目: 安徽省高校自然科学研究项目(批准号: 2023AH051206)和安徽省高等学校省级质量工程项目(批准号: 2022xxkc028)资助的课题.

Authors and contacts

School of Mechanics and Photoelectric Physics, Anhui University of Science and Technology, Huainan 232001, China

Corresponding author: Xu Hua-Feng, xhfeng716@126.com

Funds: Project supported by the Natural Science Foundation of the Higher Education Institutions of Anhui Province, China (Grant No. 2023AH051206) and the Quality Engineering Project of Higher Education of Anhui Province, China (Grant No. 2022xxkc028).

文章全文 : translate this paragraph

参考文献

[1]	Ricklin J C, Davidson F M 2002 J. Opt. Soc. Am. A 19 1794 Google Scholar
[2]	Cai Y J 2011 Proc. SPIE 7924 792402 Google Scholar
[3]	王飞, 余佳益, 刘显龙, 蔡阳健 2018 67 184203 Google Scholar Wang F, Yu J Y, Liu X L, Cai Y J 2018 Acta Phys. Sin. 67 184203 Google Scholar
[4]	Peng D M, Huang Z F, Liu Y L, Chen Y H, Wang F, Ponomarenko S A, Cai Y J 2021 PhotoniX 2 6 Google Scholar
[5]	Chen Y H, Wang F, Cai Y J 2022 Adv. Phys. X 7 2009742 Google Scholar
[6]	许文慧, 宁守琮, 张福才 2021 70 214201 Google Scholar Xu W H, Ning S C, Zhang F C 2021 Acta Phys. Sin. 70 214201 Google Scholar
[7]	Gori F, Santarsiero M 2007 Opt. Lett. 32 3531 Google Scholar
[8]	Gori F, Ramírez-Sánchez V, Santarsiero M, Shirai T 2009 J. Opt. A: Pure Appl. Opt. 11 085706 Google Scholar
[9]	Chen Y H, Gu J X, Wang F, Cai Y J 2015 Phys. Rev. A 91 013823 Google Scholar
[10]	Mei Z R 2014 Opt. Lett. 39 347 Google Scholar
[11]	Chen Y H, Cai Y J 2014 Opt. Lett. 39 2549 Google Scholar
[12]	Mei Z R 2014 Opt. Express 22 13029 Google Scholar
[13]	Liang C H, Wang F, Liu X L, Cai Y J, Korotkova O 2014 Opt. Lett. 39 769 Google Scholar
[14]	Chen Y H, Wang F, Cai Y J 2015 物理学进展 35 51 Google Scholar 陈亚红, 王飞, 蔡阳健 2015 Prog. Phys. 35 51 Google Scholar
[15]	陈亚红, 蔡阳健 2016 光学学报 36 1026002 Google Scholar Chen Y H, Cai Y J 2016 Acta Opt. Sin. 36 1026002 Google Scholar
[16]	曾军, 陈亚红, 刘显龙, 蔡阳健 2019 光学学报 39 1026004 Google Scholar Zeng J, Chen Y H, Liu X L, Cai Y J 2019 Acta Opt. Sin. 39 1026004 Google Scholar
[17]	Willner A E, Huang H, Yan Y, Ren Y, Ahmed N, Xie G 2015 Adv. Opt. Photonics 7 66 Google Scholar
[18]	Ni J C, Wang C W, Zhang C C, Hu Y L, Yang L, Lao Z X, Xu B, Li J W, Wu D, Chu J R 2017 Light Sci. Appl. 6 e17011 Google Scholar
[19]	Ginson G, Courtial J, Padgett M, Vasnetsov M, Pas'ko V, Barnett S, Franke-Arnold S 2004 Opt. Express 12 5448 Google Scholar
[20]	陈康, 马志远, 张明明, 窦建态, 胡友友 2022 71 014203 Google Scholar Cheng K, Ma Z Y, Zhang M M, Dou J T, Hu Y Y 2022 Acta Phys. Sin. 71 014203 Google Scholar
[21]	Zhang H, Zeng J, Lu X Y, Wang Z Y, Zhao C L, Cai Y J 2021 Nanophoto. 11 241 Google Scholar
[22]	Ostrovsky A S, Rickenstorffparrao C, Arrizon V 2013 Opt. Lett. 38 534 Google Scholar
[23]	李阳月, 陈子阳, 刘辉, 蒲继雄 2010 59 1740 Google Scholar Li Y Y, Chen Z Y, Liu H, Pu J X 2010 Acta Phys. Sin. 59 1740 Google Scholar
[24]	Bekshaev A Y, Karamoch A I 2008 Opt. Commun. 281 3597 Google Scholar
[25]	Wang X L, Zhu B W, Dong Y X, Wang S, Zhu Z Q, Bo F, Li X P 2017 Opt. Express 25 26844 Google Scholar
[26]	Xu H F, Zhang R, Sheng Z Q, Qu J 2020 Opt. Express 28 28858 Google Scholar
[27]	Mei Z R, Mao Y H, Wang J X, Shi X H 2023 Opt. Express 31 727 Google Scholar
[28]	Zhan Q W 2009 Adv. Opt. Photon. 1 1 Google Scholar
[29]	刘森森, 宋华冬, 林伟强, 陈旭东, 蒲继雄 2019 68 074201 Google Scholar Liu S S, Song H D, Lin W Q, Chen X D, Pu J X 2019 Acta Phys. Sin. 68 074201 Google Scholar
[30]	Wolf E 2003 Phys. Lett. A 312 263 Google Scholar
[31]	Mei Z R 2017 IEEE Photon. J. 9 6102306 Google Scholar
[32]	Wu G F, Tao C Y 2018 Opt. Commun. 424 86 Google Scholar
[33]	Zhou Y Q, Cui Z W, Han Y P 2022 Opt. Express 30 23448 Google Scholar
[34]	Peng X F, Wang H Y, Liu L, Wang F, Popov S, Cai Y J 2020 Opt. Express 28 31510 Google Scholar
[35]	Liu X L, Peng X F, Liu L, Wu G F, Zhao C L, Wang F, Cai Y J 2017 Appl. Phys. Lett. 110 181104 Google Scholar
[36]	Zeng J, Liang C H, Wang H Y, Wang F, Zhao C L, Gbur G, Cai Y J 2020 Opt. Express 28 11493 Google Scholar
[37]	Korotkova O, Wolf E 2005 Opt. Commun. 246 35 Google Scholar

施引文献

图 1 (a)源平面处第j个离轴涡旋中心与观察点的位置矢量关系; (b)—(d)携带3个离轴涡旋相位(拓扑荷数l = 1)的径向偏振RCGSM光束在源平面处的(b)离轴涡旋相位排列、(c)离轴涡旋相位分布和(d)光强分布

Fig. 1. (a) An illustration of the position vector relationship between the j-th off-axis vortex phase core and the observation point in the initial plane; (b) arrangement of three off-axis vortex phases, (c) phase distribution, and (d) intensity distribution of a radially polarized RCGSM beam carrying three off-axis vortices in the source plane, respectively.

下载: 全尺寸图片幻灯片

图 2 当光束阶数$ m = n = 5 $时, 携带3个离轴涡旋相位的径向偏振RCGSM光束通过薄透镜后的聚焦光强演化

Fig. 2. Evolution of the focused intensity of a radially polarized RCGSM beam carrying three off-axis vortex phases through a thin lens when the beam order $ m = n = 5 $.

下载: 全尺寸图片幻灯片

图 3 当光束阶数$ m = n = 5 $时, 携带4个离轴涡旋相位的径向偏振RCGSM光束的聚焦光强演化

Fig. 3. Evolution of the focused intensity of a radially polarized RCGSM beam carrying four off-axis vortex phases through a thin lens when the beam order $ m = n = 5 $.

下载: 全尺寸图片幻灯片

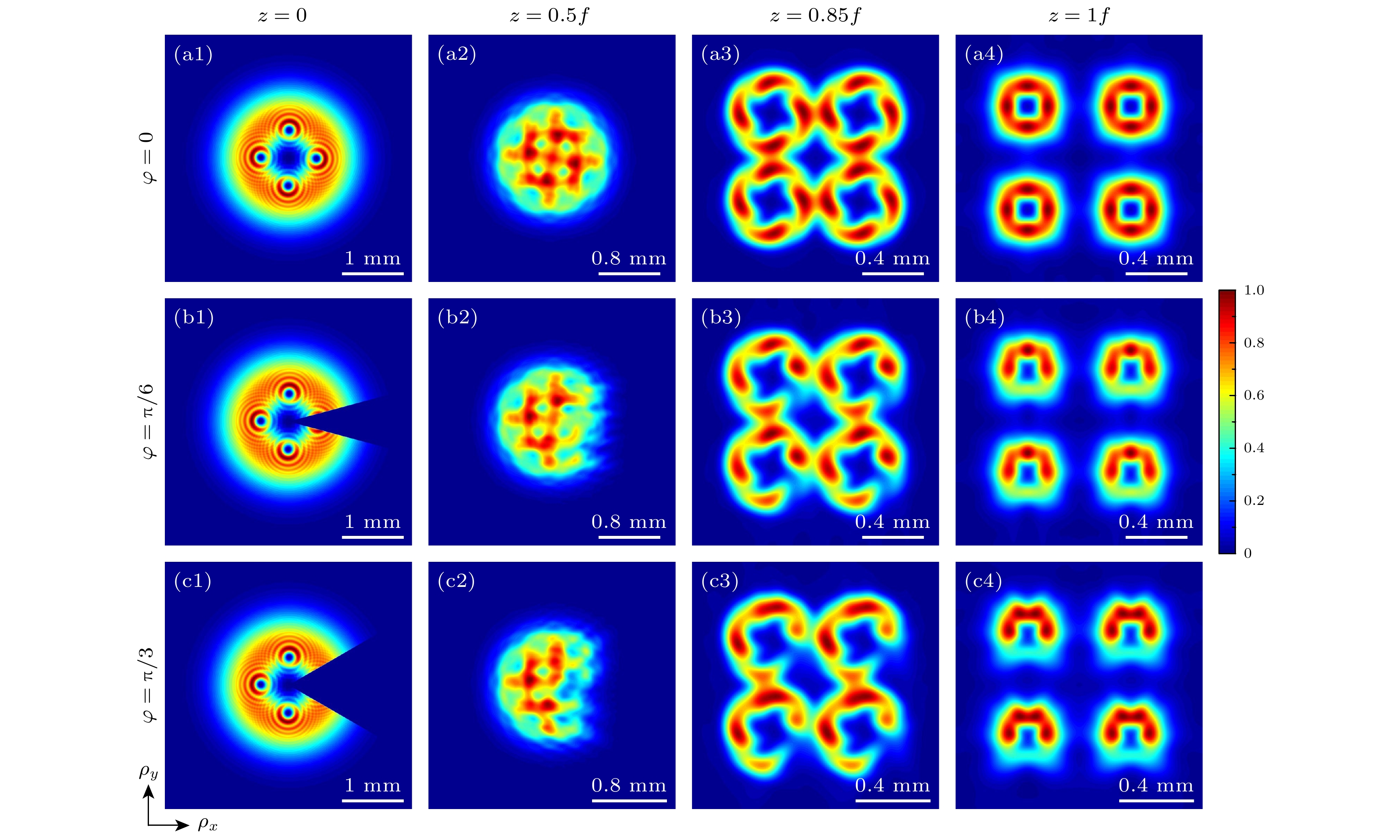
图 4 当光束阶数$ m = n = 5 $和相干长度$ {\delta _0} = 1.5{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{mm}} $时, 携带4个离轴涡旋相位的径向偏振RCGSM光束通过扇形障碍物的聚焦光强演化

Fig. 4. Evolution of the focused intensity of a radially polarized RCGSM beam carrying four off-axis vortex phases after passing through a sector-shaped opaque obstacle when the beam order $ m = n = 5 $ and coherent length $ {\delta _0} = 1.5{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{mm}} $.

下载: 全尺寸图片幻灯片

图 5 携带4个离轴涡旋相位的径向偏振RCGSM光束通过圆形障碍物后的聚焦光强演化($ m = n = 5 $, $ {\delta _0} = 1.5{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{mm}} $)

Fig. 5. Evolution of the focused intensity of a radially polarized RCGSM beam carrying four off-axis vortex phases after passing through a circular obstacle when the beam order $ m = n = 5 $ and coherent length $ {\delta _0} = 1.5{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{mm}} $.

下载: 全尺寸图片幻灯片

图 6 当光束阶数$ {m_0} = {n_0} = 5 $和相干长度$ {\delta _0} = 1.5{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{mm}} $时, 携带多个离轴涡旋相位的径向偏振RCGSM光束通过薄透镜后的偏振态演化情况

Fig. 6. Evolution of the state of polarization of radially polarized RCGSM beams carrying multiple off-axis vortex phases through a thin lens when the beam order $ {m_0} = {n_0} = 5 $ and coherent length $ {\delta _0} = 1.5{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{mm}} $.

下载: 全尺寸图片幻灯片

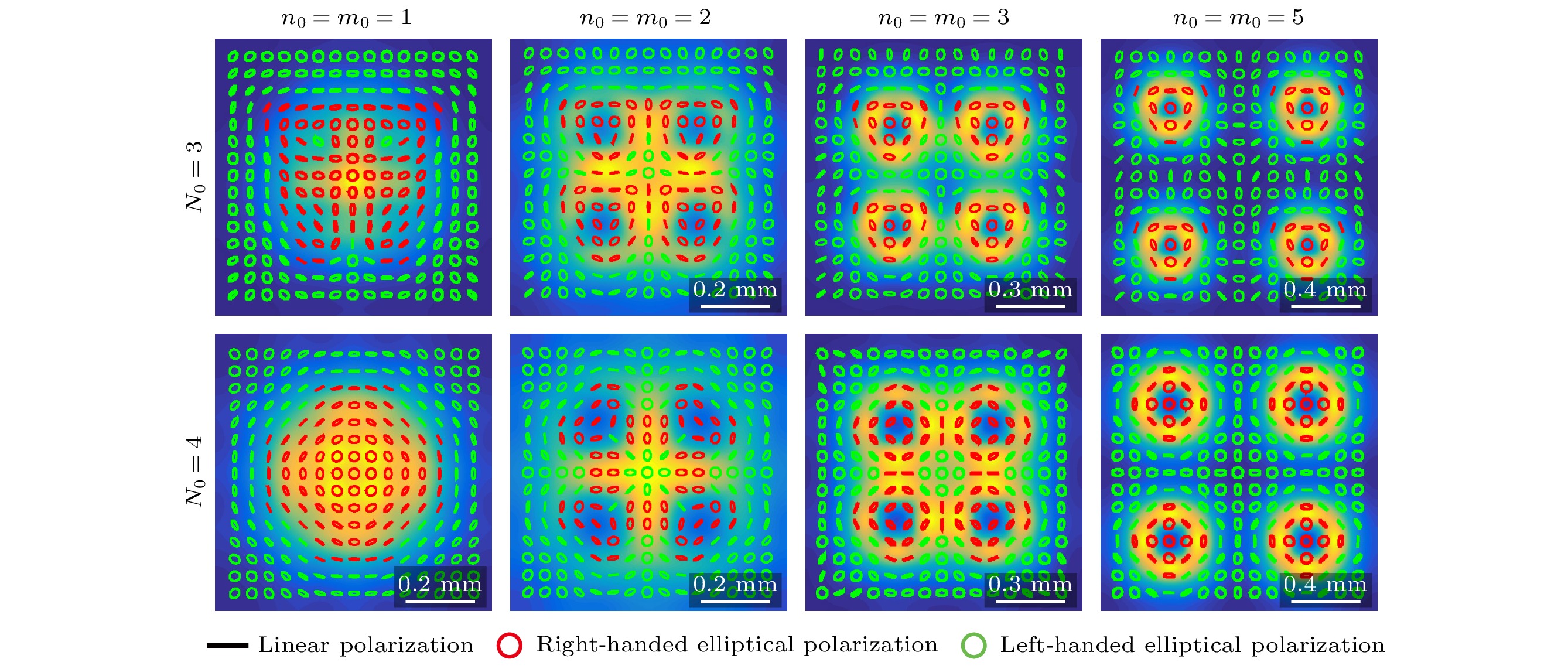
图 7 当相干长度$ {\delta _0} = 1.5{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{mm}} $时, 光束阶数$ {m_0}, {n_0} $对携带多个离轴涡旋相位的径向偏振RCGSM光束在焦平面处偏振态分布的影响

Fig. 7. Influences of beam order $ {m_0}, {n_0} $ on the distribution of the state of polarization of radially polarized RCGSM beams carrying multiple off-axis vortex phases in the focal plane when the coherent length $ {\delta _0} = 1.5{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{mm}} $.

下载: 全尺寸图片幻灯片

图 8 当光束阶数$ {m_0} = {n_0} = 2 $时, 相干长度$ {\delta _0} $对携带多个离轴涡旋相位的径向偏振RCGSM光束在焦平面处偏振态分布的影响

Fig. 8. Influence of coherent length $ {\delta _0} $ on the distribution of the state of polarization of radially polarized RCGSM beams carrying multiple off-axis vortex phases in the focal plane when the beam order $ {m_0} = {n_0} = 2 $.

下载: 全尺寸图片幻灯片

图 9 当光束阶数$ m = n = 2 $和相干长度$ {\delta _0} = 0.5{\text{mm}} $时, 携带多个离轴涡旋相位的径向偏振RCGSM光束通过扇形障碍物后在焦平面处的偏振态分布

Fig. 9. Distribution of the state of polarization in the focal plane for the radially polarized RCGSM beams carrying multiple off-axis vortex phases through a sector-shaped opaque when the beam order $ m = n = 2 $ and the coherent length $ {\delta _0} = 0.5{\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\text{mm}} $.

下载: 全尺寸图片幻灯片

map

[1]	Ricklin J C, Davidson F M 2002 J. Opt. Soc. Am. A 19 1794 Google Scholar
[2]	Cai Y J 2011 Proc. SPIE 7924 792402 Google Scholar
[3]	王飞, 余佳益, 刘显龙, 蔡阳健 2018 67 184203 Google Scholar Wang F, Yu J Y, Liu X L, Cai Y J 2018 Acta Phys. Sin. 67 184203 Google Scholar
[4]	Peng D M, Huang Z F, Liu Y L, Chen Y H, Wang F, Ponomarenko S A, Cai Y J 2021 PhotoniX 2 6 Google Scholar
[5]	Chen Y H, Wang F, Cai Y J 2022 Adv. Phys. X 7 2009742 Google Scholar
[6]	许文慧, 宁守琮, 张福才 2021 70 214201 Google Scholar Xu W H, Ning S C, Zhang F C 2021 Acta Phys. Sin. 70 214201 Google Scholar
[7]	Gori F, Santarsiero M 2007 Opt. Lett. 32 3531 Google Scholar
[8]	Gori F, Ramírez-Sánchez V, Santarsiero M, Shirai T 2009 J. Opt. A: Pure Appl. Opt. 11 085706 Google Scholar
[9]	Chen Y H, Gu J X, Wang F, Cai Y J 2015 Phys. Rev. A 91 013823 Google Scholar
[10]	Mei Z R 2014 Opt. Lett. 39 347 Google Scholar
[11]	Chen Y H, Cai Y J 2014 Opt. Lett. 39 2549 Google Scholar
[12]	Mei Z R 2014 Opt. Express 22 13029 Google Scholar
[13]	Liang C H, Wang F, Liu X L, Cai Y J, Korotkova O 2014 Opt. Lett. 39 769 Google Scholar
[14]	Chen Y H, Wang F, Cai Y J 2015 物理学进展 35 51 Google Scholar 陈亚红, 王飞, 蔡阳健 2015 Prog. Phys. 35 51 Google Scholar
[15]	陈亚红, 蔡阳健 2016 光学学报 36 1026002 Google Scholar Chen Y H, Cai Y J 2016 Acta Opt. Sin. 36 1026002 Google Scholar
[16]	曾军, 陈亚红, 刘显龙, 蔡阳健 2019 光学学报 39 1026004 Google Scholar Zeng J, Chen Y H, Liu X L, Cai Y J 2019 Acta Opt. Sin. 39 1026004 Google Scholar
[17]	Willner A E, Huang H, Yan Y, Ren Y, Ahmed N, Xie G 2015 Adv. Opt. Photonics 7 66 Google Scholar
[18]	Ni J C, Wang C W, Zhang C C, Hu Y L, Yang L, Lao Z X, Xu B, Li J W, Wu D, Chu J R 2017 Light Sci. Appl. 6 e17011 Google Scholar
[19]	Ginson G, Courtial J, Padgett M, Vasnetsov M, Pas'ko V, Barnett S, Franke-Arnold S 2004 Opt. Express 12 5448 Google Scholar
[20]	陈康, 马志远, 张明明, 窦建态, 胡友友 2022 71 014203 Google Scholar Cheng K, Ma Z Y, Zhang M M, Dou J T, Hu Y Y 2022 Acta Phys. Sin. 71 014203 Google Scholar
[21]	Zhang H, Zeng J, Lu X Y, Wang Z Y, Zhao C L, Cai Y J 2021 Nanophoto. 11 241 Google Scholar
[22]	Ostrovsky A S, Rickenstorffparrao C, Arrizon V 2013 Opt. Lett. 38 534 Google Scholar
[23]	李阳月, 陈子阳, 刘辉, 蒲继雄 2010 59 1740 Google Scholar Li Y Y, Chen Z Y, Liu H, Pu J X 2010 Acta Phys. Sin. 59 1740 Google Scholar
[24]	Bekshaev A Y, Karamoch A I 2008 Opt. Commun. 281 3597 Google Scholar
[25]	Wang X L, Zhu B W, Dong Y X, Wang S, Zhu Z Q, Bo F, Li X P 2017 Opt. Express 25 26844 Google Scholar
[26]	Xu H F, Zhang R, Sheng Z Q, Qu J 2020 Opt. Express 28 28858 Google Scholar
[27]	Mei Z R, Mao Y H, Wang J X, Shi X H 2023 Opt. Express 31 727 Google Scholar
[28]	Zhan Q W 2009 Adv. Opt. Photon. 1 1 Google Scholar
[29]	刘森森, 宋华冬, 林伟强, 陈旭东, 蒲继雄 2019 68 074201 Google Scholar Liu S S, Song H D, Lin W Q, Chen X D, Pu J X 2019 Acta Phys. Sin. 68 074201 Google Scholar
[30]	Wolf E 2003 Phys. Lett. A 312 263 Google Scholar
[31]	Mei Z R 2017 IEEE Photon. J. 9 6102306 Google Scholar
[32]	Wu G F, Tao C Y 2018 Opt. Commun. 424 86 Google Scholar
[33]	Zhou Y Q, Cui Z W, Han Y P 2022 Opt. Express 30 23448 Google Scholar
[34]	Peng X F, Wang H Y, Liu L, Wang F, Popov S, Cai Y J 2020 Opt. Express 28 31510 Google Scholar
[35]	Liu X L, Peng X F, Liu L, Wu G F, Zhao C L, Wang F, Cai Y J 2017 Appl. Phys. Lett. 110 181104 Google Scholar
[36]	Zeng J, Liang C H, Wang H Y, Wang F, Zhao C L, Gbur G, Cai Y J 2020 Opt. Express 28 11493 Google Scholar
[37]	Korotkova O, Wolf E 2005 Opt. Commun. 246 35 Google Scholar

[1]	陈康, 马志远, 张明明, 窦健泰, 胡友友. 部分相干幂指数相位涡旋光束的传输特性研究. , 2022, 71(1): 014203. doi: 10.7498/aps.71.20211411
[2]	陈康, 马志远, 张明明, 窦健泰, 胡友友. 部分相干幂指数相位涡旋光束的传输特性研究. , 2021, (): . doi: 10.7498/aps.70.20211411*
[3]	王飞, 余佳益, 刘显龙, 蔡阳健. 部分相干光束经过湍流大气传输研究进展. , 2018, 67(18): 184203. doi: 10.7498/aps.67.20180877
[4]	昌成成, 蒲继雄, 陈子阳, 陈旭东. 非均匀关联随机电磁光束的产生. , 2017, 66(5): 054212. doi: 10.7498/aps.66.054212
[5]	侯鹏程, 钟哲强, 文萍, 张彬. 激光间接驱动球形腔新型光路排布方案. , 2016, 65(2): 024202. doi: 10.7498/aps.65.024202
[6]	朱清智, 沈栋辉, 吴逢铁, 何西. 部分相干光对周期性局域空心光束的影响. , 2016, 65(4): 044103. doi: 10.7498/aps.65.044103
[7]	李杨, 朱竹青, 王晓雷, 贡丽萍, 冯少彤, 聂守平. 离轴椭圆矢量光场传输中的光斑演变. , 2015, 64(2): 024204. doi: 10.7498/aps.64.024204
[8]	张磊, 陈子阳, 崔省伟, 刘绩林, 蒲继雄. 非均匀部分相干光束在自由空间中的传输. , 2015, 64(3): 034205. doi: 10.7498/aps.64.034205
[9]	兰峰, 高喜, 亓丽梅. 基于频率选择表面的双层改进型互补结构太赫兹带通滤波器研究. , 2014, 63(10): 104209. doi: 10.7498/aps.63.104209
[10]	马媛, 季小玲. 倾斜离轴高斯-谢尔模型光束在大气湍流中通过猫眼光学镜头反射光的光强特性. , 2013, 62(9): 094214. doi: 10.7498/aps.62.094214
[11]	郑建洲, 于清旭, 关寿华, 董斌, 曹晓君, 芦永军, 吴云峰. 利用部分相干光和同心角偏差透镜列阵实现二维靶面均匀辐照. , 2012, 61(15): 154205. doi: 10.7498/aps.61.154205
[12]	苏安, 高英俊. 双重势垒一维光子晶体量子阱的光传输特性研究. , 2012, 61(23): 234208. doi: 10.7498/aps.61.234208
[13]	王豆豆, 王丽莉. 新型光学聚合物——Topas环烯烃共聚物微结构光纤的设计及特性分析. , 2010, 59(5): 3255-3259. doi: 10.7498/aps.59.3255
[14]	方春易, 张树仁, 卢俊, 汪剑波, 孙连春. 一种圆孔单元厚屏频率选择表面结构的传输特性研究. , 2010, 59(7): 5023-5027. doi: 10.7498/aps.59.5023
[15]	张永鹏, 刘国治, 邵浩, 杨占峰, 宋志敏, 林郁正. 一维漂移空间内强流电子束的稳态传输特性. , 2009, 58(10): 6973-6978. doi: 10.7498/aps.58.6973
[16]	程科, 吕百达. 四个部分相干点源的完全相消干涉特性. , 2009, 58(1): 250-257. doi: 10.7498/aps.58.250
[17]	李建龙, 吕百达. 基于自适应遗传算法部分相干光整形位相板的优化设计. , 2008, 57(5): 3006-3010. doi: 10.7498/aps.57.3006
[18]	肖瑞, 周朴, 侯静, 姜宗福, 刘明. 激光器的部分相干性对光纤激光器阵列相干合成远场图样的影响. , 2007, 56(2): 819-823. doi: 10.7498/aps.56.819
[19]	王涛, 蒲继雄. 部分相干空心光束在湍流介质中的传输特性. , 2007, 56(11): 6754-6759. doi: 10.7498/aps.56.6754
[20]	季小玲, 汤明玥. 一维线阵离轴高斯光束通过湍流大气的传输特性. , 2006, 55(9): 4968-4973. doi: 10.7498/aps.55.4968

计量

文章访问数: 2447
PDF下载量: 125
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

部分相干多离轴涡旋矢量光束的传输特性