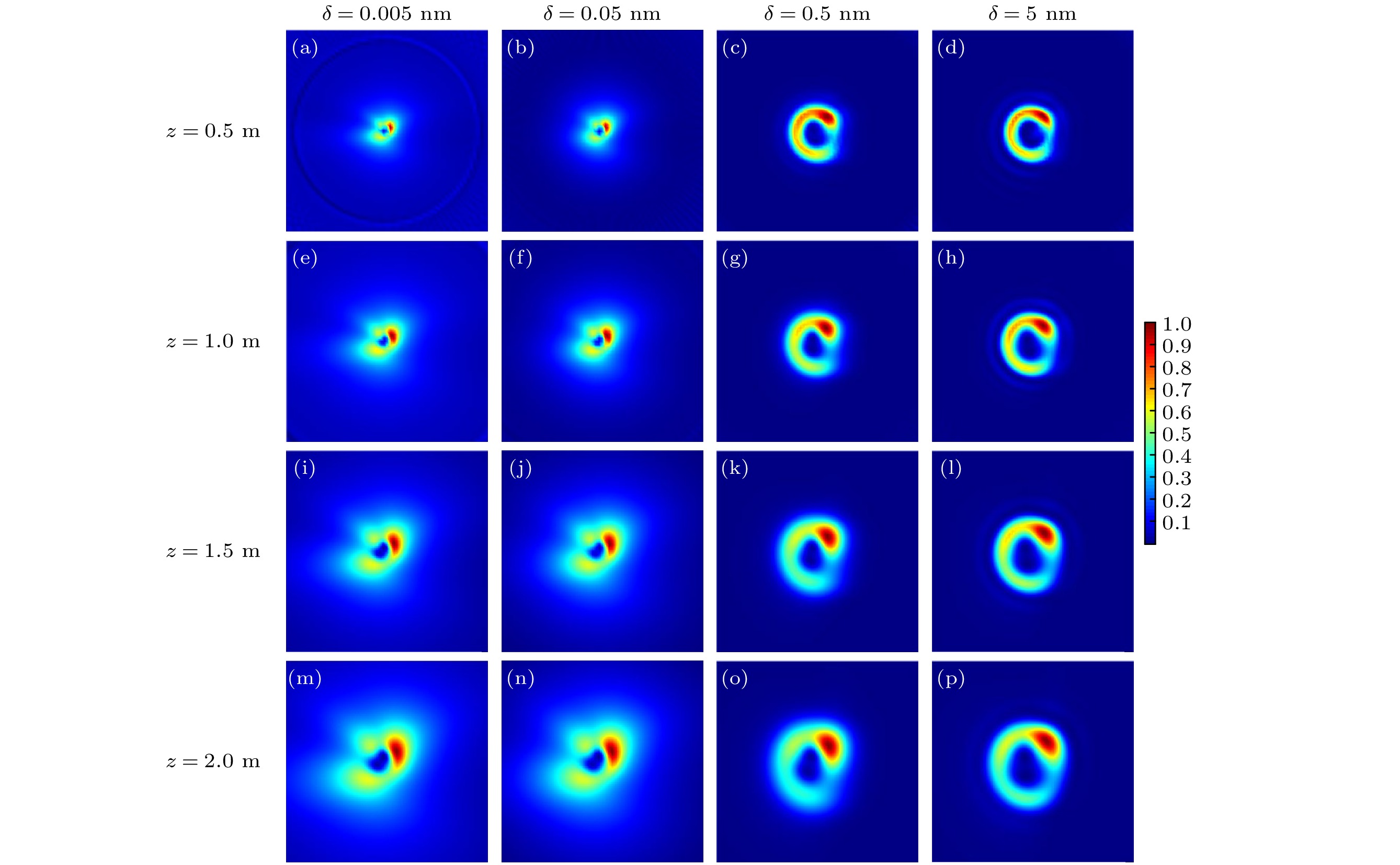
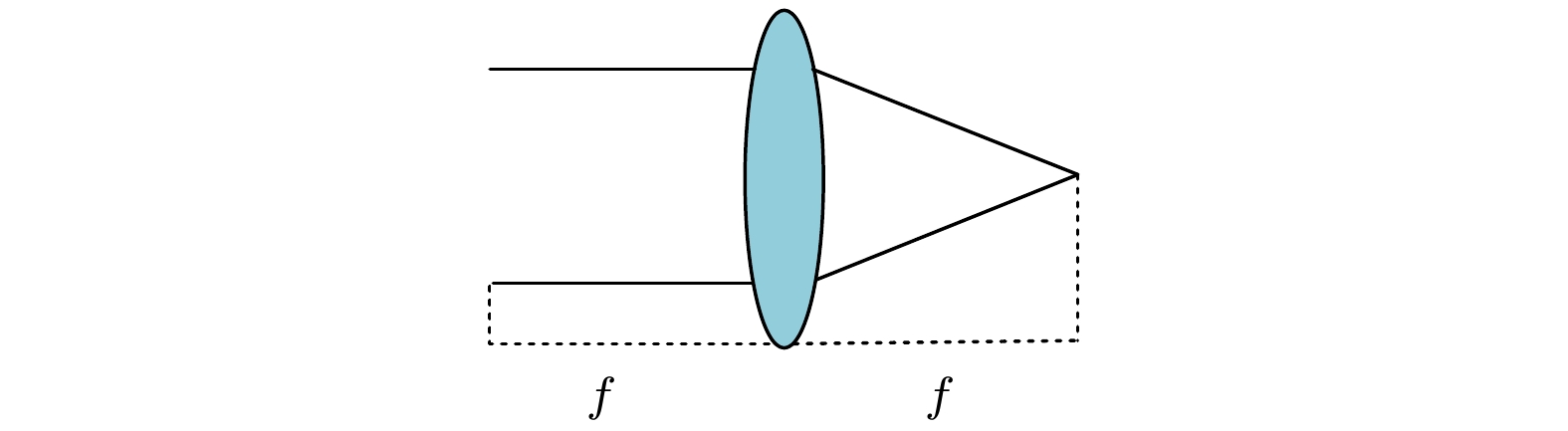
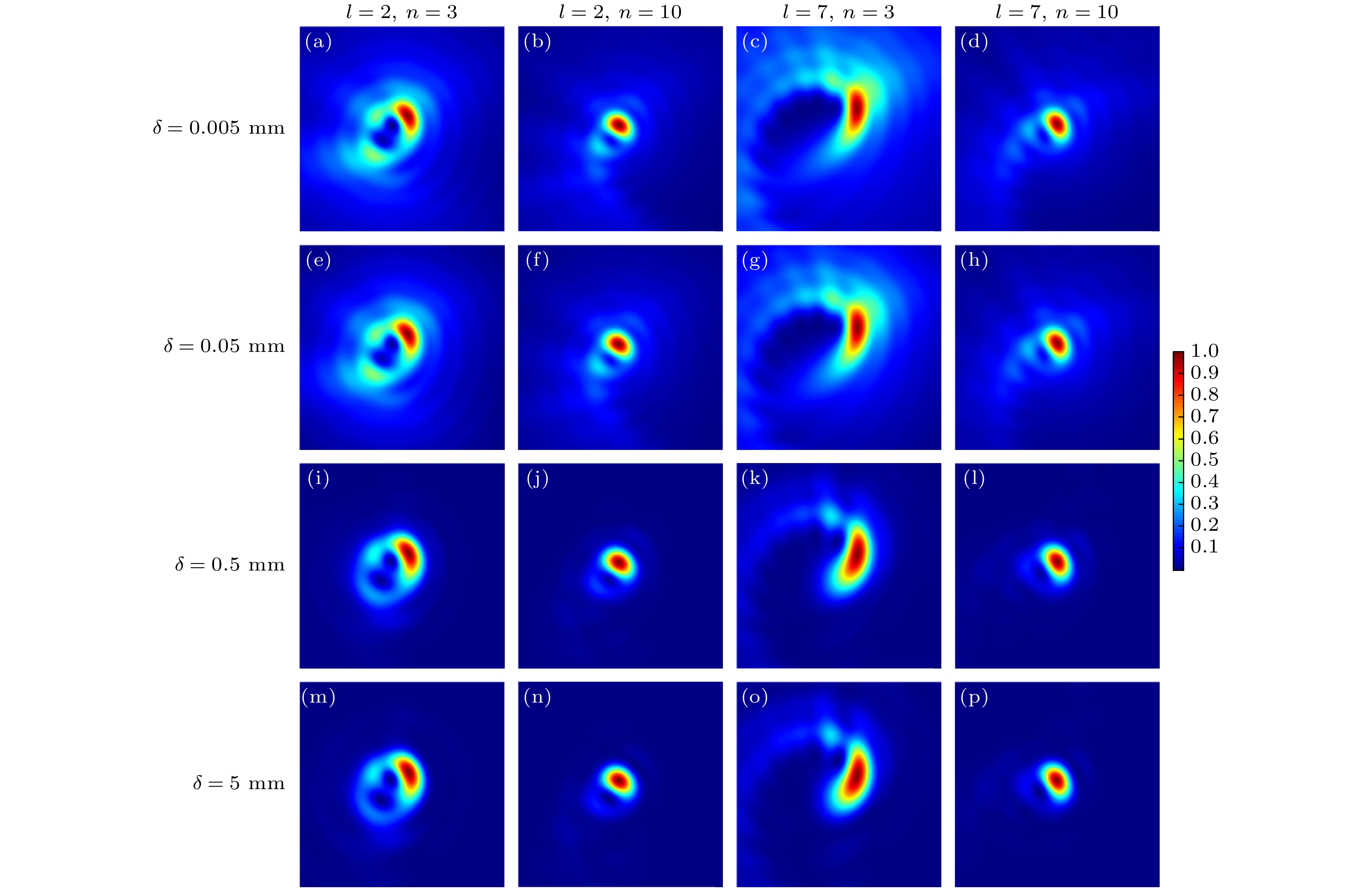
-
本文针对部分相干幂指数相位涡旋光束的传输特性开展研究, 首先建立了部分相干幂指数相位涡旋光束的传输理论模型; 然后, 仿真研究了部分相干幂指数相位涡旋光束在自由空间和ABCD光学系统中的传输特性, 研究结果表明部分相干幂指数相位涡旋光束在自由空间传输时, 拓扑荷数、幂指数和相干长度都对光强的分布有着一定的影响, 而随着传播距离的增大光斑的面积逐渐增大; 当光束在聚焦系统中传输时, 只有拓扑荷数和幂指数的变化会影响光强的分布, 而相干长度对光束整体强度的分布没有太大的影响, 只影响了光斑的质量. 本文研究成果揭示了部分相干幂指数相位涡旋光束的传输特性, 为其在光学捕获等领域的应用打下了理论基础, 对促进新型光场调控理论及应用研究具有重要的意义.In this work, the propagation properties of partially coherent power-exponent-phase vortex beam are studied. Firstly, the propagation model of partially coherent power-exponent-phase vortex beam is established. Then, the propagation properties of partially coherent power-exponent-phase vortex beams in free space and ABCD optical system are simulated. The results show that when power-exponent-phase vortex beams propagate in free space, the topological charge, power order and coherence length have a great influence on the distribution of light intensity, and the area of light spot gradually increases with the increase of propagation distance. When the beam propagates in a focusing system, the changes of topological charge and power order will affect the light intensity distribution, while the coherence length has little effect on the overall intensity distribution of the beam, but only the quality of the spot. The research results of this work reveal the propagation properties of partially coherent power-exponent-phase vortex beam, which will lay a theoretical foundation for its applications in optical capture and other fields, and has important significance in promoting the theory and applications of new light field regulation.
-
Keywords:
- partially coherent beam /
- power-exponent-phase vortex beam /
- propagation properties /
- intensity distribution
[1] Yao A M, Padgett M J 2011 Adv. Opt. Photonics 3 161
Google Scholar
[2] Ng J, Lin Z, Chan C T 2010 Phys. Rev. Lett. 104 103601
Google Scholar
[3] Willner A E, Huang H, Yan Y, Ren Y, Ahmed N, Xie G 2015 Adv. Opt. Photonics 7 66
Google Scholar
[4] Huang K, Liu H, Restuccia S, Mehmood M Q, Mei S T, Giovannini D 2018 Light Sci. Appl. 7 17156
Google Scholar
[5] Ni J, Wang C, Zhang C, Hu Y, Yang L, Lao Z 2017 Light Sci. Appl. 26 e17011
[6] Chow T W, Pechprasarn S, Meng J 2016 Opt. Express 24 10797
Google Scholar
[7] Li P, Liu S, Peng T, Xie G, Gan X, Zhao J 2014 Opt. Express 22 7598
Google Scholar
[8] Lao G, Zhang Z, Zhao D 2016 Opt. Express 24 18082
Google Scholar
[9] Pei Z, Huang S, Chen Y 2021 J. Mod. Opt. 68 224
Google Scholar
[10] Wang F, Liu X, Yuan Y 2013 Opt. Lett. 38 1814
Google Scholar
[11] Yu J, Zhu X, Lin S 2020 Opt. Lett. 45 3824
Google Scholar
[12] Cai Y J, Zhu S Y 2004 Opt. Lett. 29 2716
[13] Clark J N, Huang X, Harder R, Robinson I K 2012 Nat. Commun. 3 1
[14] Zhao C, Cai Y J, Lu X, Eyyuboğlu H T 2009 Opt. Express 17 1753
Google Scholar
[15] Wang F, Cai Y J, Dong Y 2012 Appl. Phys. Lett. 100 051108
Google Scholar
[16] 刘森森, 宋华冬, 林伟强, 陈旭东, 蒲继雄 2019 68 074201
Liu S S, Song H D, Lin W Q, Chen X D, Pu J X 2019 Acta Phys. Sin. 68 074201
[17] Xu H F, Zhou Y, Wu H W 2018 Opt. Express 26 20076
Google Scholar
[18] 张磊, 陈子阳, 崔省伟, 刘绩林, 蒲继雄 2015 64 034205
Zhang L, Chen Z Y, Cui X W, Liu J L, Pu J X 2015 Acta Phys. Sin. 64 034205
[19] 王飞, 余佳益, 刘显龙, 蔡阳健 2018 67 184203
Wang F, Yu J Y, Liu X L, Cai Y J 2018 Acta Phys. Sin. 67 184203
[20] Xu H F, Zhang R, Sheng Z Q 2019 Opt. Express 27 23959
Google Scholar
[21] Dong M, Zhao C L, Cai Y J 2021 Sci. China. Phys. Mech. 64 1
Google Scholar
[22] Liu X, Zeng J, Cai Y J 2019 Adv. Phys. X 4 1626766
[23] Stahl C S D 2018 (The University of North Carolina at Charlotte).
[24] Wolf E 2017 Introduction to the Theory of Coherence and Polarization of Light (Cambridge University Press) p88
[25] Mandel L, Wolf E 1995 Optical Coherence and Quantum Optics (Cambridge University Press) p276
[26] Ma P, Kacerovská B, Khosravi R 2019 Appl. Sci. 9 2084
Google Scholar
[27] Zhao C, Dong Y, Wang Y 2012 Appl. Phys. B 109 345
Google Scholar
[28] Wang T, Pu J, Chen Z 2008 Opt. Eng. 47 036002
Google Scholar
-
图 1 (a), (c) 拓扑荷数l=4的涡旋光束和(b), (d)拓扑荷数l = 4及幂指数n = 2的幂指数相位涡旋光束在源平面上的相位和强度分布
Fig. 1. Phase and intensity distributions of (a), (c) vortex beam (l = 4) and (b), (d) power-exponent-phase vortex beam (l = 4, n = 2) on the source plane.
图 2 部分相干幂指数相位涡旋光束的传输特性与拓扑荷数l和幂指数n的关系
Fig. 2. Relationship between propagation properties of partially coherent power-exponent-phase vortex beams with the topological charge l and power order n
图 3 部分相干幂指数相位涡旋光束传输特性与相干长度δ和传输距离z的关系
Fig. 3. Relationship between propagation properties of partially coherent power-exponent-phase vortex beams with the coherence length δ and propagation distance z.
图 5 相干长度δ = 0.5 mm时, 部分相干幂指数相位涡旋光束聚焦特性与幂指数n、拓扑荷数l的关系
Fig. 5. Relationship between focusing properties of partially coherent power-exponent-phase vortex beams and power order n and topological charge l with coherent length δ = 0.5 mm.
图 6 部分相干幂指数相位涡旋的聚焦特性与相干长度δ的关系
Fig. 6. Relationship between focusing properties of partially coherent power-exponent-phase vortex beams and coherent length δ
-
[1] Yao A M, Padgett M J 2011 Adv. Opt. Photonics 3 161
Google Scholar
[2] Ng J, Lin Z, Chan C T 2010 Phys. Rev. Lett. 104 103601
Google Scholar
[3] Willner A E, Huang H, Yan Y, Ren Y, Ahmed N, Xie G 2015 Adv. Opt. Photonics 7 66
Google Scholar
[4] Huang K, Liu H, Restuccia S, Mehmood M Q, Mei S T, Giovannini D 2018 Light Sci. Appl. 7 17156
Google Scholar
[5] Ni J, Wang C, Zhang C, Hu Y, Yang L, Lao Z 2017 Light Sci. Appl. 26 e17011
[6] Chow T W, Pechprasarn S, Meng J 2016 Opt. Express 24 10797
Google Scholar
[7] Li P, Liu S, Peng T, Xie G, Gan X, Zhao J 2014 Opt. Express 22 7598
Google Scholar
[8] Lao G, Zhang Z, Zhao D 2016 Opt. Express 24 18082
Google Scholar
[9] Pei Z, Huang S, Chen Y 2021 J. Mod. Opt. 68 224
Google Scholar
[10] Wang F, Liu X, Yuan Y 2013 Opt. Lett. 38 1814
Google Scholar
[11] Yu J, Zhu X, Lin S 2020 Opt. Lett. 45 3824
Google Scholar
[12] Cai Y J, Zhu S Y 2004 Opt. Lett. 29 2716
[13] Clark J N, Huang X, Harder R, Robinson I K 2012 Nat. Commun. 3 1
[14] Zhao C, Cai Y J, Lu X, Eyyuboğlu H T 2009 Opt. Express 17 1753
Google Scholar
[15] Wang F, Cai Y J, Dong Y 2012 Appl. Phys. Lett. 100 051108
Google Scholar
[16] 刘森森, 宋华冬, 林伟强, 陈旭东, 蒲继雄 2019 68 074201
Liu S S, Song H D, Lin W Q, Chen X D, Pu J X 2019 Acta Phys. Sin. 68 074201
[17] Xu H F, Zhou Y, Wu H W 2018 Opt. Express 26 20076
Google Scholar
[18] 张磊, 陈子阳, 崔省伟, 刘绩林, 蒲继雄 2015 64 034205
Zhang L, Chen Z Y, Cui X W, Liu J L, Pu J X 2015 Acta Phys. Sin. 64 034205
[19] 王飞, 余佳益, 刘显龙, 蔡阳健 2018 67 184203
Wang F, Yu J Y, Liu X L, Cai Y J 2018 Acta Phys. Sin. 67 184203
[20] Xu H F, Zhang R, Sheng Z Q 2019 Opt. Express 27 23959
Google Scholar
[21] Dong M, Zhao C L, Cai Y J 2021 Sci. China. Phys. Mech. 64 1
Google Scholar
[22] Liu X, Zeng J, Cai Y J 2019 Adv. Phys. X 4 1626766
[23] Stahl C S D 2018 (The University of North Carolina at Charlotte).
[24] Wolf E 2017 Introduction to the Theory of Coherence and Polarization of Light (Cambridge University Press) p88
[25] Mandel L, Wolf E 1995 Optical Coherence and Quantum Optics (Cambridge University Press) p276
[26] Ma P, Kacerovská B, Khosravi R 2019 Appl. Sci. 9 2084
Google Scholar
[27] Zhao C, Dong Y, Wang Y 2012 Appl. Phys. B 109 345
Google Scholar
[28] Wang T, Pu J, Chen Z 2008 Opt. Eng. 47 036002
Google Scholar
下载:
计量
- 文章访问数: 5721
- PDF下载量: 169
- 被引次数: 0
