-
氟化镁微腔光频梳具有体积小、功耗低、光谱覆盖范围广、色散可调控的优势, 在光通信、中红外光谱等领域有着潜在应用前景. 本文研究了氟化镁回音壁模式微瓶腔平台产生的光频梳光谱特性. 为了优化氟化镁微瓶腔光频梳的光谱分布, 利用有限元法迭代求解了瓶腔结构在不同曲率和轴向模式下的二阶色散及高阶色散, 通过分步傅里叶法求解非线性薛定谔方程仿真了不同轴向模式激励下的光频梳光谱演变过程. 结果表明, 在最佳曲率半径下通过低阶轴向模式激励可以实现宽带范围的近零反常色散调谐, 而高阶轴向模式将导致微瓶腔呈现弱正常色散. 在低阶轴向模式下较弱的反常色散使光频梳的带宽得到展宽, 证明了三阶色散和负的四阶色散可以展宽克尔孤子光频梳; 在高阶轴向模式下弱正常色散抑制了克尔光频梳的产生, 拉曼光频梳占主导地位. 在适宜的泵浦条件下通过调控微瓶腔的轴向模式可以实现克尔孤子光频梳和拉曼光频梳的选择性激发. 本文工作的开展将为氟化镁微腔色散设计及宽带克尔孤子光频梳、拉曼光频梳实验调控提供指导意义.
Optical frequency comb has shown great potential applications in many areas including molecular spectroscopy, RF photonics, millimeter wave generation, frequency metrology, atomic clock, and dense/ultra-dense wavelength division multiplexed high speed optical communications. Optical frequency comb in the microresonator supporting whispering-gallery mode has attracted widespread interest because of its advantages such as flexible repetition rate, wide bandwidth, and compact size. The exceptionally long photon lifetime and small modal volume enhance light-matter interaction, which enables us to realize intracavity nonlinear frequency conversions with low pump threshold. With the advantages of small size, low power consumption, wide spectral coverage and adjustable dispersion, the magnesium fluoride microresonator optical frequency comb has potential applications in optical communication and mid-infrared spectroscopy. In this work, the spectral characteristics of the optical frequency comb generated by a magnesium fluoride whispering-gallery mode microbottle resonator platform are investigated. In order to optimize the spectral distribution of the optical frequency comb of the magnesium fluoride microbottle resonator, the second-order dispersion and higher-order dispersion of the bottle resonator structure under different curvatures and axial modes are solved iteratively by the finite element method, and the spectral evolutions of the optical frequency comb under different axial mode excitations are simulated by solving the nonlinear Schrödinger equation through the split-step Fourier method. The results show that near-zero anomalous dispersion tuning can be achieved in a wide bandwidth range by exciting low-order axial mode at an optimal radius of curvature, while the high-order axial mode will lead the microbottle resonator to present the weak normal dispersion. The weaker anomalous dispersion in the lower-order axial mode broadens the bandwidth of the optical comb, demonstrating that the third-order dispersion and the negative fourth-order dispersion can broaden the Kerr soliton optical comb; the weak normal dispersion in the higher-order axial mode suppresses the generation of the Kerr optical comb, and the Raman optical comb dominates. The selective excitation of Kerr soliton combs and Raman combs can be achieved by modulating the axial mode of the microbottle resonator under suitable pumping conditions. The present work provides guidance for designing the dispersion in magnesium fluoride microresonator and the experimental tuning of broadband Kerr soliton optical combs and Raman optical combs. -
Keywords:
- optical microresonator /
- microbottle resonator /
- axial mode /
- dispersion /
- optical frequency comb
[1] 于长秋, 马世昌, 陈志远, 项晨晨, 李海, 周铁军 2021 70 160701
Google Scholar
Yu C Q, Ma S C, Chen Z Y, Xiang C C, Li Hai, Zhou T J 2021 Acta Phys. Sin. 70 160701
Google Scholar
[2] Del’Haye P, Schliesser P, Arcizet O, Wilken T, Holzwarth R, Kippenberg T J 2007 Nature 450 1214
Google Scholar
[3] Kippenberg T J, Holzwarth R, Diddams S A 2011 Science 332 555
Google Scholar
[4] Herr T, Brasch V, Jost J D, Wang C Y, Kondratiev N M, Gorodetsky M L, Kippenberg T J 2014 Nat. Photon. 8 145
Google Scholar
[5] Brasch V, Geiselmann M, Herr T, Lihachev G, Pfeiffer M H, Gorodetsky M L, Kippenberg T J 2016 Science 351 357
Google Scholar
[6] Sayson N L B, Bi T, Ng V, Pham H, Trainor L S, Schwefel H G L, Coen S, Erkintalo M, Murdoch S G 2019 Nat. Photon. 13 701
Google Scholar
[7] Liu J, Weng H, Afridi A A, Li J, Dai J, Ma X, Long H, Zhang Y, Lu Q, Donegan J F, Guo W 2020 Opt. Express 28 19270
Google Scholar
[8] Gu J X, Li X, Qi K, Pu K R, Li Z X, Zhang F, Li T, Xie Z D, Xiao M, Jiang X S 2023 Opt. Lett. 48 1100
Google Scholar
[9] Savchenkov A A, Matsko A B, Liang W, Ilchenko V S, Seidel D, Maleki L 2011 Nat. Photon. 5 293
Google Scholar
[10] Nasir M N M, Murugan G S, Zervas M N 2016 J. Opt. Soc. Am. B 33 1963
Google Scholar
[11] Yin Y H, Niu Y X, Qin H Y, Ding M 2019 J. Lightwave Technol. 37 5571
Google Scholar
[12] Wang M Y, Yang Y, Lu Z Z, Wang W Q, Zhang W F, Xie C F, Zhong H K, Wu L F, Wu T, Tan Q G, Fu Y J, Wang K Y 2021 J. Lightwave Technol. 39 5917
Google Scholar
[13] Jin X Y, Xu X, Gao H R, Wang K Y, Xia H J, Yu L D 2021 Photonics Res. 9 171
Google Scholar
[14] Lecaplain C, Javerzac-Galy C, Gorodetsky M L, Kippenberg T J 2016 Nat. Commun. 7 13383
Google Scholar
[15] Sumetsky M 2004 Opt. Lett. 29 8
Google Scholar
[16] Lin G, Chembo Y K 2015 Opt. Express 23 1594
Google Scholar
[17] Murugan G S, Petrovich M N, Jung Y, Wilkinson J S, Zervas M N 2011 Opt. Express 19 20773
Google Scholar
[18] He Z Q, Sun C Z, Xiong B, Wang J, Hao Z B, Wang L, Han Y J, Li H T, Gan L, Luo Y 2023 Opt. Lett. 48 2182
Google Scholar
[19] Fujii S, Tanabe T 2020 Nanophotonics 9 1087
Google Scholar
[20] Chembo Y K, Grudinin I S, Yu N 2015 Phys. Rev. A 92 043818
Google Scholar
[21] Ghanbari A, Kashaninia A, Sadr A, Saghaei H 2017 Optik 140 545
Google Scholar
[22] 王梦宇, 孟令俊, 杨煜, 钟汇凯, 吴涛, 刘彬, 张磊, 伏燕军, 王克逸 2020 69 234203
Google Scholar
Wang M Y, Meng L J, Yang Y, Zhong H K, Wu T, Liu B, Zhang L, Fu Y J, Wang K Y 2020 Acta Phys. Sin. 69 234203
Google Scholar
[23] Crespo-Ballesteros M, Matsko A B, Sumetsky M 2023 Commun. Phys. 6 52
Google Scholar
[24] Xing T, Xing E, Jia T, Li J, Rong J, Zhou Y, Liu W, Tang J, Liu J 2022 Chin. Phys. B 31 104204
Google Scholar
[25] Fujii S, Kato T, Suzuki R, Hori A, Tanabe T 2018 J. Opt. Soc. Am. B 35 100
Google Scholar
[26] 许凡, 赵妍, 吴宇航, 王文驰, 金雪莹 2022 71 184204
Google Scholar
Xu F, Zhao Y, Wu Y H, Wang W C, Jin X Y 2022 Acta Phys. Sin. 71 184204
Google Scholar
[27] Yang Q F, Yi X, Yang K Y, Vahala K 2017 Nat. Phys. 13 53
Google Scholar
-
图 1 微瓶腔光频梳示意图
Fig. 1. Schematic diagram of the microbottle resonator optical frequency comb.
图 3 (a)不同瓶轴长的色散分布; (b) q = 0的微瓶腔轴向模式场分布
Fig. 3. (a) Dispersion distribution for different bottle axis lengths; (b) axial mode field distribution of the microbottle resonator for q = 0.
图 4 不同最大半径的色散分布 (a)二阶色散; (b)总色散
Fig. 4. Dispersion distribution with different maximum radii: (a) Second order dispersion; (b) total dispersion.
图 5 (a)不同轴向模式的色散分布; (b) $ q=40 $的轴向模式场分布
Fig. 5. (a) Dispersion distribution of different axial modes; (b) axial mode field distribution for q = 40.
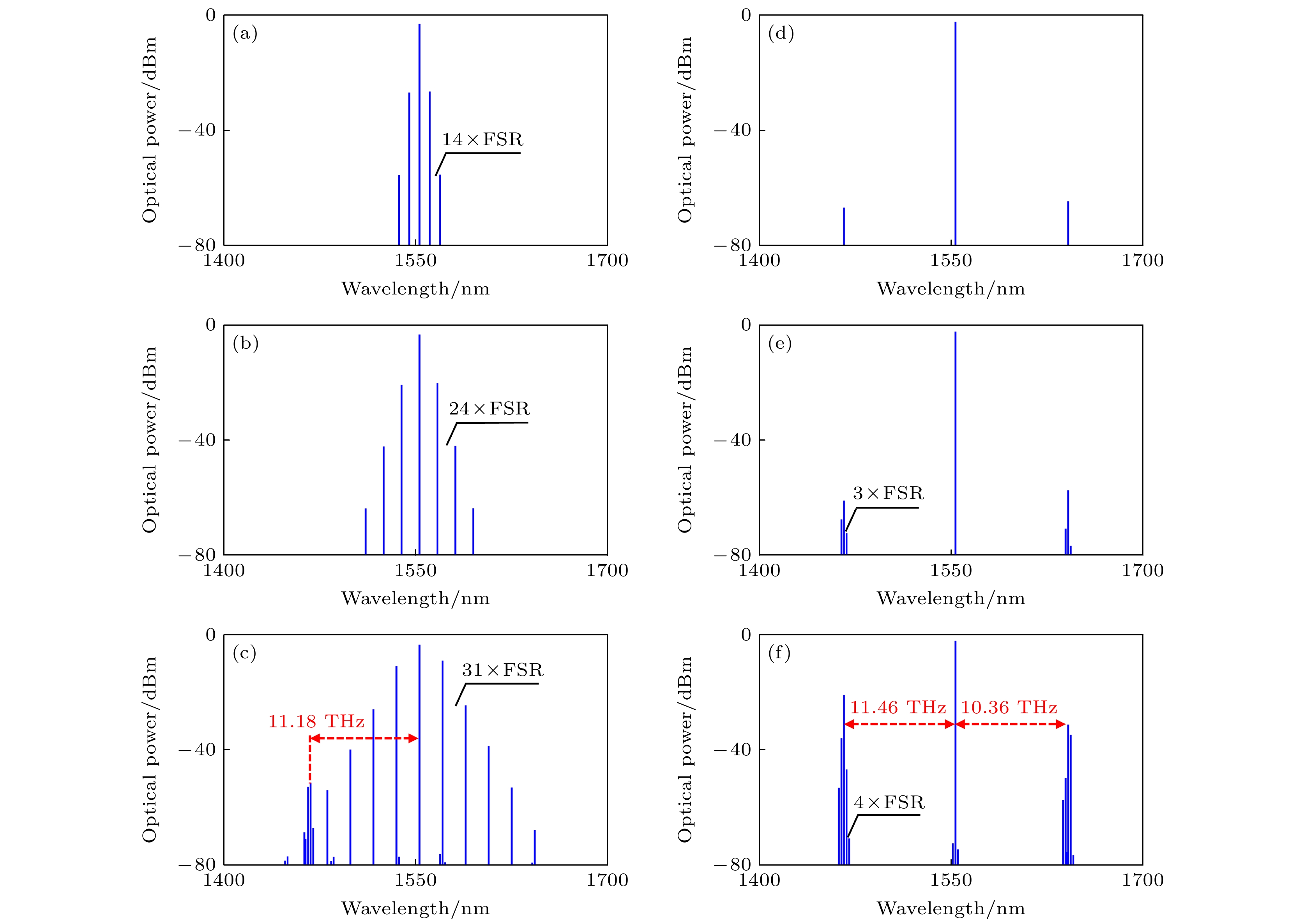
图 6 轴向模式和功率对光频梳光谱演化的影响 (a) q = 0, S = 0.6; (b) q = 40, S = 0.6; (c) q = 40, S = 1.7; (d) q = 80, S = 0.785; (e) q = 80, S = 0.795; (f) q = 80, S = 0.825
Fig. 6. Influences of axial mode and power on the spectral evolution of optical frequency comb: (a) q = 0, S = 0.6; (b) q = 40, S = 0.6; (c) q = 40, S = 1.7; (d) q = 80, S = 0.785; (e) q = 80, S = 0.795; (f) q = 80, S = 0.825.
图 7 不同高阶色散对孤子光频梳的影响 (a)—(c)腔内光谱图; (d)—(f)孤子频域演化图; (g)—(i)孤子时域演化图
Fig. 7. Influence of different higher order dispersions on the soliton optical frequency comb: (a)–(c) Intracavity spectrograms; (d)–(f) soliton frequency domain evolution; (g)–(i) soliton time domain evolution.
-
[1] 于长秋, 马世昌, 陈志远, 项晨晨, 李海, 周铁军 2021 70 160701
Google Scholar
Yu C Q, Ma S C, Chen Z Y, Xiang C C, Li Hai, Zhou T J 2021 Acta Phys. Sin. 70 160701
Google Scholar
[2] Del’Haye P, Schliesser P, Arcizet O, Wilken T, Holzwarth R, Kippenberg T J 2007 Nature 450 1214
Google Scholar
[3] Kippenberg T J, Holzwarth R, Diddams S A 2011 Science 332 555
Google Scholar
[4] Herr T, Brasch V, Jost J D, Wang C Y, Kondratiev N M, Gorodetsky M L, Kippenberg T J 2014 Nat. Photon. 8 145
Google Scholar
[5] Brasch V, Geiselmann M, Herr T, Lihachev G, Pfeiffer M H, Gorodetsky M L, Kippenberg T J 2016 Science 351 357
Google Scholar
[6] Sayson N L B, Bi T, Ng V, Pham H, Trainor L S, Schwefel H G L, Coen S, Erkintalo M, Murdoch S G 2019 Nat. Photon. 13 701
Google Scholar
[7] Liu J, Weng H, Afridi A A, Li J, Dai J, Ma X, Long H, Zhang Y, Lu Q, Donegan J F, Guo W 2020 Opt. Express 28 19270
Google Scholar
[8] Gu J X, Li X, Qi K, Pu K R, Li Z X, Zhang F, Li T, Xie Z D, Xiao M, Jiang X S 2023 Opt. Lett. 48 1100
Google Scholar
[9] Savchenkov A A, Matsko A B, Liang W, Ilchenko V S, Seidel D, Maleki L 2011 Nat. Photon. 5 293
Google Scholar
[10] Nasir M N M, Murugan G S, Zervas M N 2016 J. Opt. Soc. Am. B 33 1963
Google Scholar
[11] Yin Y H, Niu Y X, Qin H Y, Ding M 2019 J. Lightwave Technol. 37 5571
Google Scholar
[12] Wang M Y, Yang Y, Lu Z Z, Wang W Q, Zhang W F, Xie C F, Zhong H K, Wu L F, Wu T, Tan Q G, Fu Y J, Wang K Y 2021 J. Lightwave Technol. 39 5917
Google Scholar
[13] Jin X Y, Xu X, Gao H R, Wang K Y, Xia H J, Yu L D 2021 Photonics Res. 9 171
Google Scholar
[14] Lecaplain C, Javerzac-Galy C, Gorodetsky M L, Kippenberg T J 2016 Nat. Commun. 7 13383
Google Scholar
[15] Sumetsky M 2004 Opt. Lett. 29 8
Google Scholar
[16] Lin G, Chembo Y K 2015 Opt. Express 23 1594
Google Scholar
[17] Murugan G S, Petrovich M N, Jung Y, Wilkinson J S, Zervas M N 2011 Opt. Express 19 20773
Google Scholar
[18] He Z Q, Sun C Z, Xiong B, Wang J, Hao Z B, Wang L, Han Y J, Li H T, Gan L, Luo Y 2023 Opt. Lett. 48 2182
Google Scholar
[19] Fujii S, Tanabe T 2020 Nanophotonics 9 1087
Google Scholar
[20] Chembo Y K, Grudinin I S, Yu N 2015 Phys. Rev. A 92 043818
Google Scholar
[21] Ghanbari A, Kashaninia A, Sadr A, Saghaei H 2017 Optik 140 545
Google Scholar
[22] 王梦宇, 孟令俊, 杨煜, 钟汇凯, 吴涛, 刘彬, 张磊, 伏燕军, 王克逸 2020 69 234203
Google Scholar
Wang M Y, Meng L J, Yang Y, Zhong H K, Wu T, Liu B, Zhang L, Fu Y J, Wang K Y 2020 Acta Phys. Sin. 69 234203
Google Scholar
[23] Crespo-Ballesteros M, Matsko A B, Sumetsky M 2023 Commun. Phys. 6 52
Google Scholar
[24] Xing T, Xing E, Jia T, Li J, Rong J, Zhou Y, Liu W, Tang J, Liu J 2022 Chin. Phys. B 31 104204
Google Scholar
[25] Fujii S, Kato T, Suzuki R, Hori A, Tanabe T 2018 J. Opt. Soc. Am. B 35 100
Google Scholar
[26] 许凡, 赵妍, 吴宇航, 王文驰, 金雪莹 2022 71 184204
Google Scholar
Xu F, Zhao Y, Wu Y H, Wang W C, Jin X Y 2022 Acta Phys. Sin. 71 184204
Google Scholar
[27] Yang Q F, Yi X, Yang K Y, Vahala K 2017 Nat. Phys. 13 53
Google Scholar
下载:
计量
- 文章访问数: 2488
- PDF下载量: 89
- 被引次数: 0
