-
金属玻璃是液态金属在某种程度上的“冻结”, 探明液态金属的结构特征及其在快凝过程中的演化特性, 有助于理解玻璃转变和玻璃形成能力的微结构机制. 为此, 本文采用分子动力学, 模拟研究了液态金属Ta的快凝过程. 并用双体分布函数、最大标准团簇、遗传跟踪等方法, 对快凝Ta的微结构特征及其演化特性进行了表征和分析. 结果表明, 快凝金属Ta的原子组态是各种Kasper团簇及变形结构, 其中占比最高的是Z13 Kasper团簇. 连续遗传起始温度和阶段遗传分数均可用来表征团簇结构遗传能力的大小. 最大标准团簇的对称性可以采用局域对称性参数(LSP)来定量表征, 局域五次对称参数(LSP5)越大其遗传能力越强. 各类团簇在能量区间出现的频率均服从高斯分布, 其平均原子势能期望值(
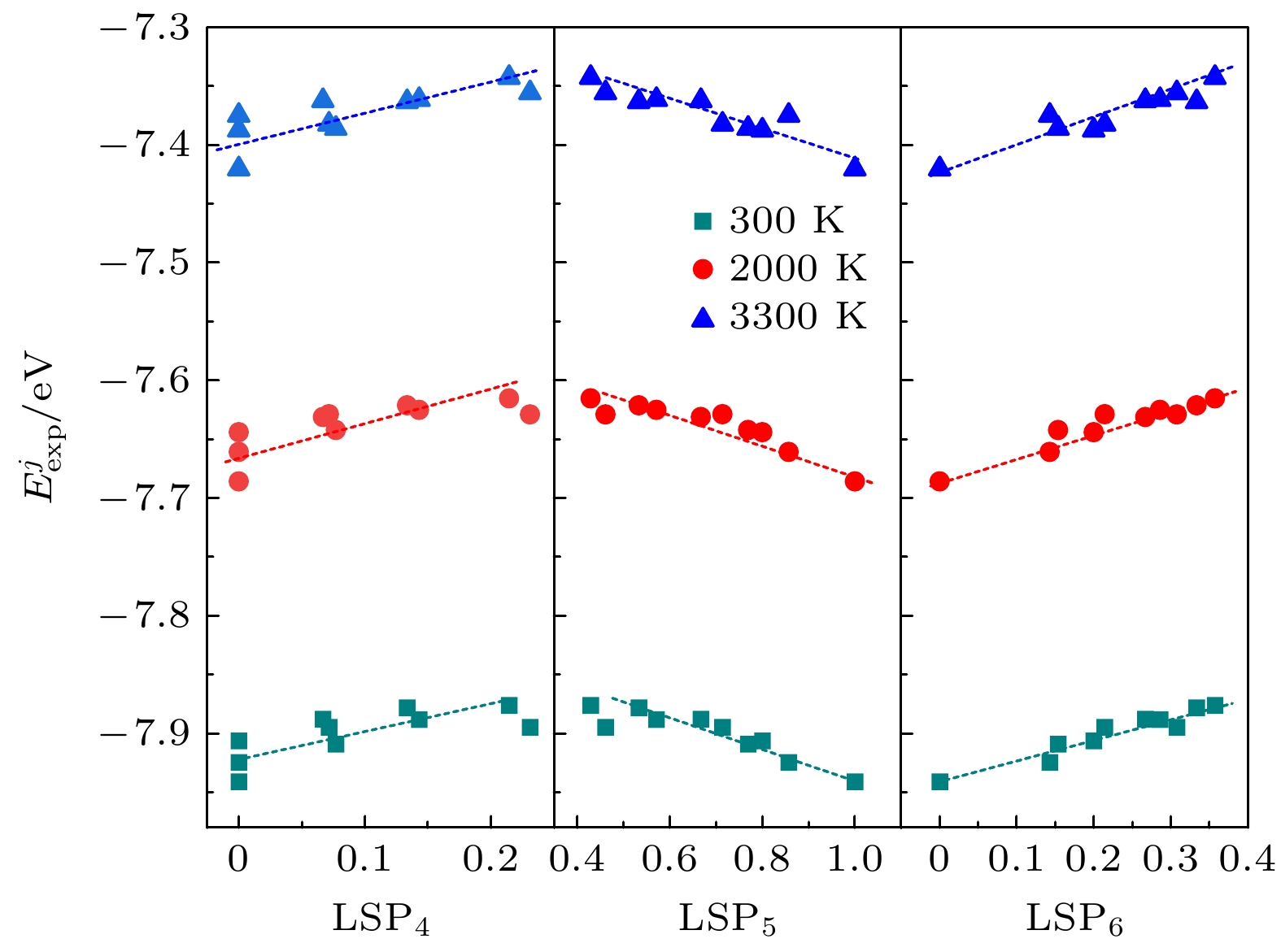
$ {E}_{{\mathrm{e}}{\mathrm{x}}{\mathrm{p}}}^{j} $ )与LSP呈近似线性关系, 且$ {E}_{{\mathrm{e}}{\mathrm{x}}{\mathrm{p}}}^{j} $ 随LSP5的增大而降低. 高的局域五次对称性降低了团簇的平均原子势能, 从而增强了这类团簇的结构遗传能力.Metallic glass (MG) has received intensive attention in the fields of amorphous physics and materials science, owing to its excellent mechanical properties, good corrosion resistance, and large elastic deformation limit. Comparing with traditional oxide glass, the limited glass-forming ability (GFA) seriously restricts the application of MG in engineering. Therefore, the GFA has been a hot scientific issue in the field of amorphous material research. Recently, scientists have fully realized that GFA is closely related to the local atomic structure in liquid as well as its evolution features. Since the MG is called the “freezing” liquid, exploring the correlation of local atomic structures between liquid phase and solid phase under rapid solidification conditions is helpful in understanding the microstructural mechanism of GFA. Therefore, the rapid solidification process of liquid Ta is investigated via molecular dynamics simulation. The pair correlation function (PDF), the largest standard cluster (LSC), and the reverse atomic trajectory tracking methods are used to characterize and analyze the microstructure and its evolution during the rapid solicitation of liquid Ta. The results show that the local atomic configurations of the rapidly solidified Ta are various Kasper clusters as well as their distorted configurations, among of which [1/444, 10/555, 2/666] deformed icosahedron (or Z13 cluster) accounts for the highest proportion. The trend of hereditary ability of clusters revealed by the onset temperature of continuous heredity is consistent well with that by the fraction of staged heredity. The geometric symmetry of clusters can be quantitatively characterized by using the local symmetry parameter (LSP). The hereditary ability of clusters is closely related to their LSP. The local five-fold symmetry is beneficial to enhancing hereditary ability, while local four- and six-fold symmetry are disadvantageous for that. The probability of clusters with the same LSC index emerging in the energy range follows the Gaussian distribution, and the expected average atomic potential energy$ {E}_{\rm exp}^{j} $ is almost linearly related to the LSP, and$ {E}_{\rm exp}^{j} $ decreases with the increase of LSP5. The high local five-fold symmetry reduces the average atomic potential energy of LSC, thereby enhancing its configurational heredity. These findings have guiding significance in improving GFA through regulating the local symmetry of liquid monatomic metals or alloys.-
Keywords:
- molecular dynamics /
- clusters /
- heredity /
- local symmetry
[1] 吴渊, 刘雄军, 吕昭平 2022 物理 51 691
Google Scholar
Wu Y, Liu X J, Lu Z P 2022 Physics 51 691
Google Scholar
[2] 汪卫华 2013 物理学进展 33 177
Wang W H 2013 Prog. Phys. 33 177
[3] 汪卫华 2022 自然杂志 44 173
Google Scholar
Wang W H 2022 Chin. J. Nat. 44 173
Google Scholar
[4] Cheng Y Q, Ma E 2011 Prog. Mater. Sci. 56 379
Google Scholar
[5] Louzguine-Luzgin D V, Miracle D B, Inoue A 2008 Adv. Eng. Mater. 10 1008
Google Scholar
[6] Wei G Y, Cui J Z, Wang W, Guo X X, Ren J L, Wang W H 2022 Phys. Rev. Mater. 6 055601
Google Scholar
[7] 李金富, 李伟 2022 金属学报 58 457
Google Scholar
Li J F, Li W 2022 Acta Metall. Sin. 58 457
Google Scholar
[8] Wang F R, Zhang H P, Li M Z 2018 J. Alloys Compd. 763 392
Google Scholar
[9] Kelton K F, Lee G W, Gangopadhyay A K, Hyers R W, Rathz T J, Rogers J R, Robinson M B, Robinson D S 2003 Phys. Rev. Lett. 90 195504
Google Scholar
[10] Zhang F, Ji M, Fang X W, Sun Y, Wang C Z, Mendelev M I, Kramer M J, Napolitanoa R E, Ho K M 2014 Acta Mater. 81 337
Google Scholar
[11] 高明, 邓永和, 文大东, 田泽安, 赵鹤平, 彭平 2020 69 046401
Google Scholar
Gao M, Deng Y H, Wen D D, Tian Z A, Zhao H P, Peng P 2020 Acta Phys. Sin. 69 046401
Google Scholar
[12] Sandor M T, Ke H B, Wang W H, Wu Y 2013 J. Phys. Condens. Matter. 25 165701
Google Scholar
[13] Peng H L, Li M Z, Wang W H 2011 Phys. Rev. Lett. 106 135503
Google Scholar
[14] Hu Y C, Li F X, Li M Z, Bai H Y, Wang W H 2015 Nat. Commun. 6 8310
Google Scholar
[15] 李茂枝 2017 66 176107
Google Scholar
Li M Z 2017 Acta Phys. Sin. 66 176107
Google Scholar
[16] Xi X K, Li L L, Zhang B, Wang W H, Wu Y 2007 Phys. Rev. Lett. 99 095501
Google Scholar
[17] Wen D D, Deng Y H, Gao M, Tian Z A 2021 Chin. Phys. B 30 076101
Google Scholar
[18] Wen D D, Peng P, Jiang Y Q, Tian Z A, Li W, Liu R S 2015 J. Non-Cryst. Solids 427 199
Google Scholar
[19] Chu W, Shang J X, Yin K B, Ren N N, Hu L N, Zhao Y B, Dong B S 2020 Acta Mater. 196 690
Google Scholar
[20] Zhai X T, Li X, Wang Z, Hu L N, Song K K, Tian Z A, Yue Y Z 2022 Acta Mater. 239 118246
Google Scholar
[21] Zhong L, Wang J W, Sheng H W, Zhang Z, Mao S X 2014 Nature 512 177
Google Scholar
[22] Zhao R, Jiang H Y, Luo P, Sun Y T, Li Z A, Wu W W, Shen L Q, Liu M, Zhao S F, Wen P, Zhang Q H, Gu L, Bai H Y, Wang W H 2020 Appl. Phys. Lett. 117 131903
Google Scholar
[23] Zhang J C, Chen C, Pei Q X, Wan Q, Zhang W X, Sha Z D 2015 Mater. Des. 77 1
Google Scholar
[24] Khmich A, Sbiaai K, Hasnaoui A 2019 J. Non-Cryst. Solids 510 81
Google Scholar
[25] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[26] https://sites.google.com/site/eampotentials/Ta [2020-5-4
[27] Martyna G J, Tobias D J, Klein M L 1994 J. Chem. Phys. 101 4177
Google Scholar
[28] Wu Z W, Li M Z, Wang W H, Song W J, Liu K X 2013 J. Chem. Phys. 138 074502
Google Scholar
[29] Zhang Y, Mattern N, Eckert J 2012 J. Appl. Phys. 111 053520
Google Scholar
[30] 王锦程, 郭灿, 张琪, 唐赛, 李俊杰, 王志军 2018 金属学报 54 204
Google Scholar
Wang J C, Guo C, Zhang Q, Tang S, Li J J, Wang Z J 2018 Acta Metall. Sin. 54 204
Google Scholar
[31] Wen D D, Deng Y H, Dai X Y, Tian Z A, Peng P 2019 Philos. Mag. 99 2904
Google Scholar
[32] Tian Z A, Liu R S, Dong K J, Yu A B 2011 Europhys. Lett. 96 36001
Google Scholar
[33] Honeycutt J D, Andersen H C 1987 J. Phys. Chem. 91 4950
Google Scholar
[34] Wen D D, Deng Y H, Su Y F, Tian Z A 2020 Mod. Phys. Lett. B 34 2050316.
Google Scholar
[35] Deng Y H, Wen D D, Li Y, Peng P 2018 Philos. Mag. 20 1
Google Scholar
[36] Ostwald W 1897 Z. Phys. Chem. 22 289
Google Scholar
-
图 1 液态Ta快凝过程中平均原子势能Esys随温度T的变化
Fig. 1. Temperature (T ) dependence of potential energy (Esys) per atom during the rapid solidification of liquid Ta.
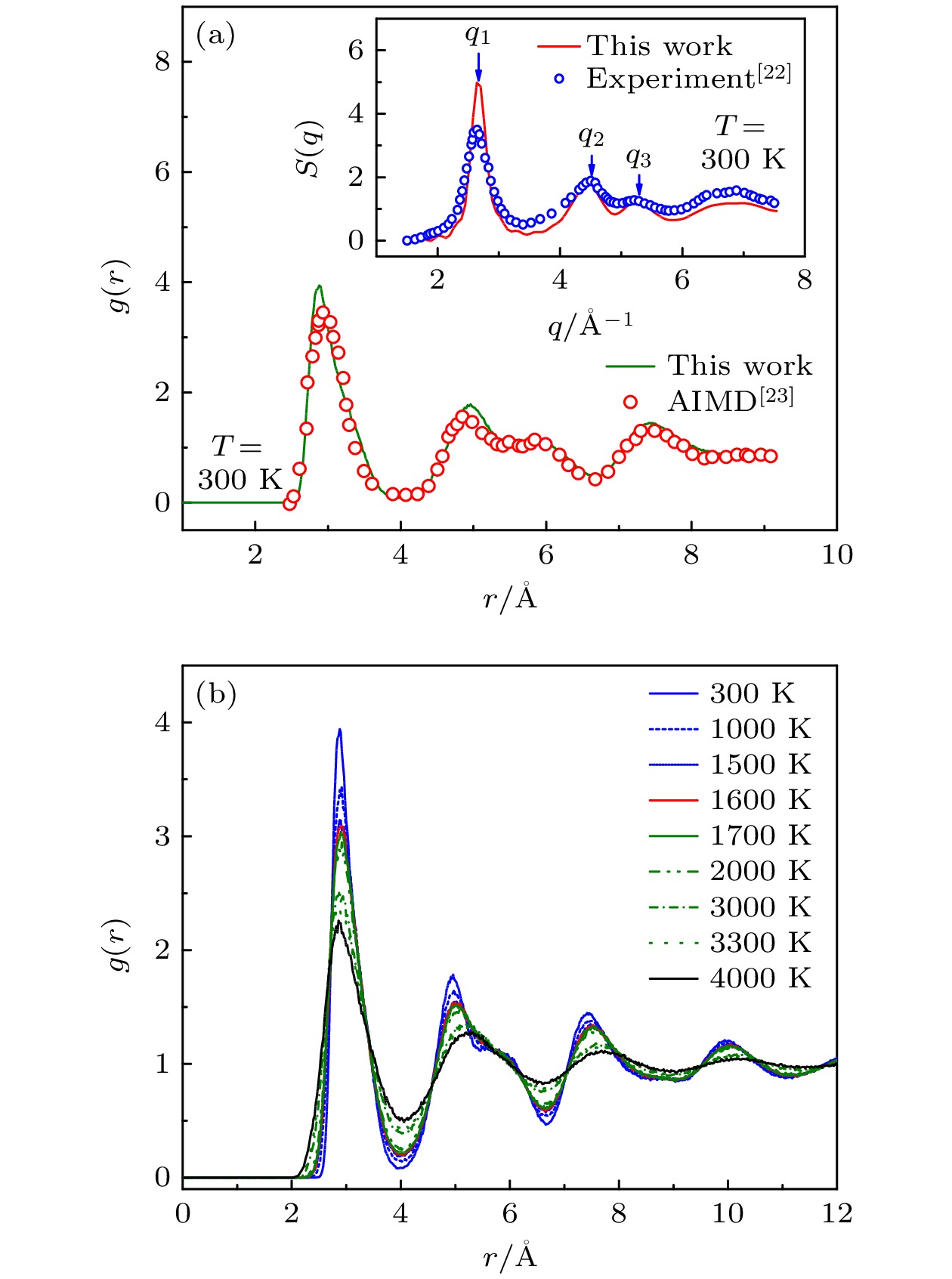
图 2 金属Ta 系统在不同温度下的双体分布函数g(r) (a) MD模拟与AIMD计算结果[23]的比较(T = 300 K), 内插图是MD模拟结构因子S(q)与实验值[22]的比较; (b) g(r)曲线随温度T的演化
Fig. 2. The g(r) curves of metal Ta system at several selected temperatures: (a) Comparison of g(r) for Ta metallic glass at 300 K between present molecular dynamics (MD) simulation and ab-initio MD (AIMD) result[23]; insert is the comparison of S(q) for Ta metallic glass at 300 K between present MD simulation and experimental values[22]; (b) the evolution of g(r) curves with temperature (T ).
图 3 基本原子团簇表征方法和Ta金属玻璃中典型的团簇 (a) 最大标准团簇(LSC) (小球上的编码用于标定原子的局域结构); (b) 共有近邻子团簇(CNS); (c)共有近邻(CNN); (d) Ta金属玻璃中典型LSC结构示意图. 橙色球代表团簇的中心原子; 绿色、灰色、粉色分别代表团簇中具有四次、五次和六次局域对称环境的壳层原子
Fig. 3. Characterization of basic atomic clusters and schematic diagram of typical clusters in Ta metal glass: (a) Topology of largest standard cluster (LSC) (The encoding on the ball is used to identify the local structure of atoms); (b) a common neighbor subcluster (CNS); (c) common near neighbor (CNN); (d) schematic diagram of typical LSC structure in Ta metal glass. The orange sphere represents the central atom of the cluster; green, gray, and pink respectively represent the coordination atoms in the cluster with fourth, fifth, and sixth local symmetric environments.
图 4 Ta金属玻璃中典型LSC的数目分布(a)及其在系统中的占比随温度的演化(b)
Fig. 4. Distribution of typical LSC in Ta metallic glass (a) and their evolution with temperature (b).
图 5 液态Ta快凝过程中典型SRO和MRO的遗传与演化示意图 (a) Z14 SRO的遗传; (b) 由Z12 形成的MRO的遗传与演化. 深蓝色与橙色球分别代表团簇中经遗传得到的壳层与中心原子, 浅蓝色与浅橙色分别代表团簇在演化过程中新增的壳层与中心原子, n与NI分别表示MRO中的原子总数与中心数目
Fig. 5. Schematic diagram of evolution and heredity for a short-range order (SRO) and a typical medium-range order (MRO) in the rapid solidification of liquid Ta: (a) Heredity of Z14 SRO; (b) heredity and evolution of an MRO formed by Z12 basic cluster. The dark blue and orange spheres respectively represent the inherited shell and center atoms in the cluster; while the light blue and light orange represent the newly added shell and center atoms in the evolution of cluster, respectively. n and NI represent the total number of atoms and the number of cores in MRO, respectively.
图 6 Ta快凝过程中典型团簇的遗传起始温度与阶段遗传分数 (a)遗传起始温度Tonset; (b)阶段遗传分数
Fig. 6. Onset temperature as well as the fraction of staged heredity of typical clusters during rapid solidification of liquid Ta: (a) The onset temperature Tonset of typical LSCs; (b) the fraction of staged heredity for different LSCs.
图 7 典型LSC遗传特性与局域对称性参数LSP的关系 (a)遗传起始温度Tonset与LSP的关系; (b)阶段遗传分数fSH与LSP的关系
Fig. 7. Correlation of LSP with the hereditary characteristics of typical LSC: (a) The relationship between Tonset and LSP; (b) correlation of LSP with fSH.
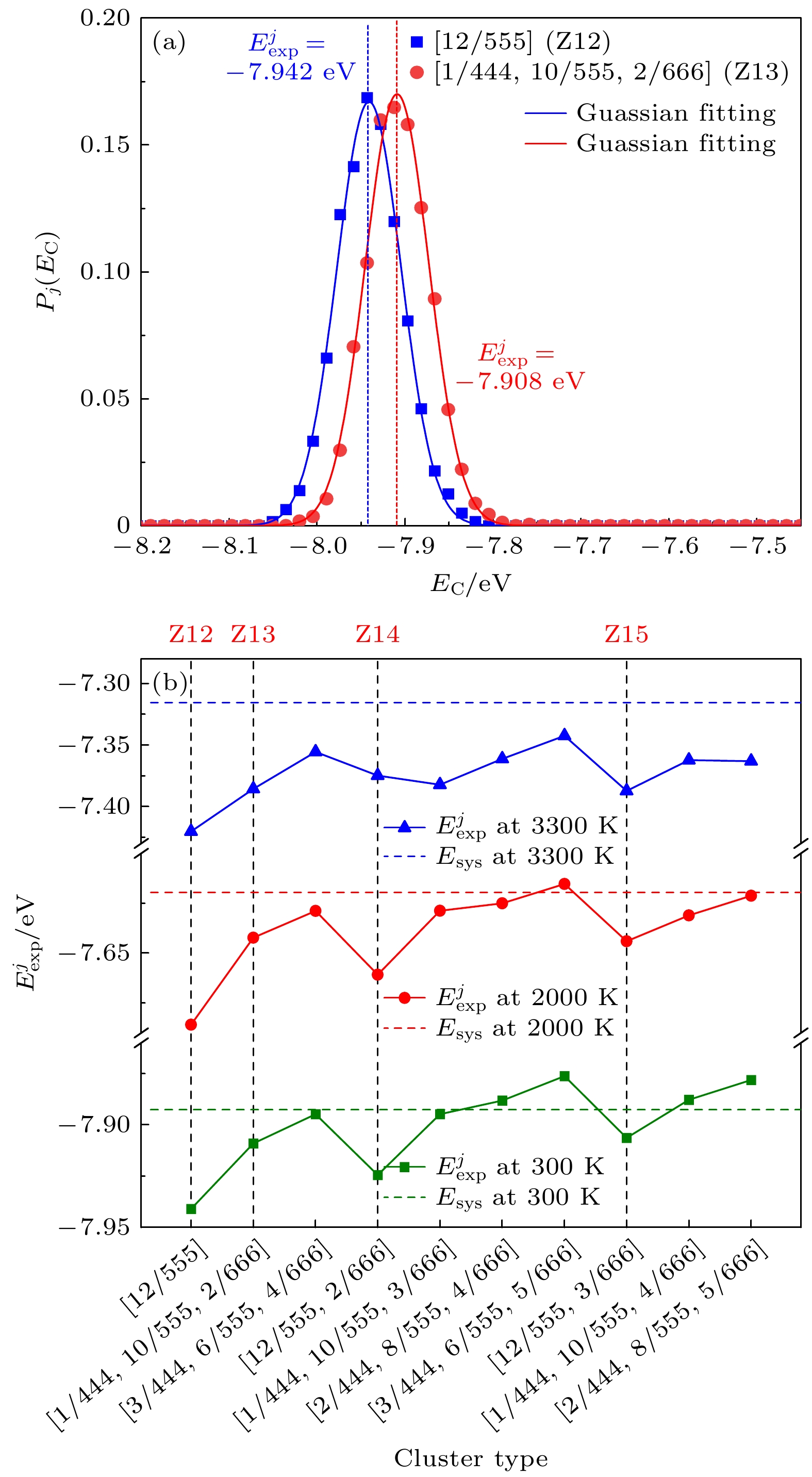
图 8 快凝Ta中典型LSC的平均原子势能 (a) Ta金属玻璃(T = 300 K)中Z12与Z13出现的频率$ P_j({E}_{{\mathrm{C}}} )$随团簇平均原子势能EC的分布; (b)不同温度下典型LSC平均原子势能期望值$ {E}_{{\mathrm{e}}{\mathrm{x}}{\mathrm{p}}}^{j} $
Fig. 8. Potential energy per atom of typical LSC in rapidly solidified metal Ta: (a) The distribution of the fraction of Z12 and Z13 in Ta metallic glass with potential energy per atom $ {E}_{{\mathrm{C}}} $ in LCS (T = 300 K); (b) expected potential energy per atom, $ {E}_{{\mathrm{e}}{\mathrm{x}}{\mathrm{p}}}^{j} $, for typical LSC at different temperatures
图 9 $ {E}_{{\mathrm{e}}{\mathrm{x}}{\mathrm{p}}}^{j} $与局域对称性参数LSP的关系
Fig. 9. Relationship between $ {E}_{{\mathrm{e}}{\mathrm{x}}{\mathrm{p}}}^{j} $ and the local symmetry parameter LSP.
表 1 Ta金属玻璃中典型LSC的局域对称性参数LSP
Table 1. Local symmetry parameters (LSP) of typical LSC in Ta metal glass.
LSC LSP4 LSP5 LSP6 [12/555] (Z12) 0 1.0000 0 [1/444, 10/555, 2/666] (Z13) 0.0769 0.7692 0.1538 [3/444, 6/555, 4/666] 0.2308 0.4615 0.3076 [12/555, 2/666] (Z14) 0 0.8571 0.1429 [1/444, 10/555, 3/666] 0.0714 0.7143 0.2143 [2/444, 8/555, 4/666] 0.1429 0.5714 0.2857 [3/444, 6/555, 5/666] 0.2142 0.4286 0.3571 [12/555, 3/666] (Z15) 0 0.8000 0.2000 [1/444, 10/555, 4/666] 0.0667 0.6667 0.2667 [2/444, 8/555, 5/666] 0.1333 0.5333 0.3333 
下载: 导出CSV
-
[1] 吴渊, 刘雄军, 吕昭平 2022 物理 51 691
Google Scholar
Wu Y, Liu X J, Lu Z P 2022 Physics 51 691
Google Scholar
[2] 汪卫华 2013 物理学进展 33 177
Wang W H 2013 Prog. Phys. 33 177
[3] 汪卫华 2022 自然杂志 44 173
Google Scholar
Wang W H 2022 Chin. J. Nat. 44 173
Google Scholar
[4] Cheng Y Q, Ma E 2011 Prog. Mater. Sci. 56 379
Google Scholar
[5] Louzguine-Luzgin D V, Miracle D B, Inoue A 2008 Adv. Eng. Mater. 10 1008
Google Scholar
[6] Wei G Y, Cui J Z, Wang W, Guo X X, Ren J L, Wang W H 2022 Phys. Rev. Mater. 6 055601
Google Scholar
[7] 李金富, 李伟 2022 金属学报 58 457
Google Scholar
Li J F, Li W 2022 Acta Metall. Sin. 58 457
Google Scholar
[8] Wang F R, Zhang H P, Li M Z 2018 J. Alloys Compd. 763 392
Google Scholar
[9] Kelton K F, Lee G W, Gangopadhyay A K, Hyers R W, Rathz T J, Rogers J R, Robinson M B, Robinson D S 2003 Phys. Rev. Lett. 90 195504
Google Scholar
[10] Zhang F, Ji M, Fang X W, Sun Y, Wang C Z, Mendelev M I, Kramer M J, Napolitanoa R E, Ho K M 2014 Acta Mater. 81 337
Google Scholar
[11] 高明, 邓永和, 文大东, 田泽安, 赵鹤平, 彭平 2020 69 046401
Google Scholar
Gao M, Deng Y H, Wen D D, Tian Z A, Zhao H P, Peng P 2020 Acta Phys. Sin. 69 046401
Google Scholar
[12] Sandor M T, Ke H B, Wang W H, Wu Y 2013 J. Phys. Condens. Matter. 25 165701
Google Scholar
[13] Peng H L, Li M Z, Wang W H 2011 Phys. Rev. Lett. 106 135503
Google Scholar
[14] Hu Y C, Li F X, Li M Z, Bai H Y, Wang W H 2015 Nat. Commun. 6 8310
Google Scholar
[15] 李茂枝 2017 66 176107
Google Scholar
Li M Z 2017 Acta Phys. Sin. 66 176107
Google Scholar
[16] Xi X K, Li L L, Zhang B, Wang W H, Wu Y 2007 Phys. Rev. Lett. 99 095501
Google Scholar
[17] Wen D D, Deng Y H, Gao M, Tian Z A 2021 Chin. Phys. B 30 076101
Google Scholar
[18] Wen D D, Peng P, Jiang Y Q, Tian Z A, Li W, Liu R S 2015 J. Non-Cryst. Solids 427 199
Google Scholar
[19] Chu W, Shang J X, Yin K B, Ren N N, Hu L N, Zhao Y B, Dong B S 2020 Acta Mater. 196 690
Google Scholar
[20] Zhai X T, Li X, Wang Z, Hu L N, Song K K, Tian Z A, Yue Y Z 2022 Acta Mater. 239 118246
Google Scholar
[21] Zhong L, Wang J W, Sheng H W, Zhang Z, Mao S X 2014 Nature 512 177
Google Scholar
[22] Zhao R, Jiang H Y, Luo P, Sun Y T, Li Z A, Wu W W, Shen L Q, Liu M, Zhao S F, Wen P, Zhang Q H, Gu L, Bai H Y, Wang W H 2020 Appl. Phys. Lett. 117 131903
Google Scholar
[23] Zhang J C, Chen C, Pei Q X, Wan Q, Zhang W X, Sha Z D 2015 Mater. Des. 77 1
Google Scholar
[24] Khmich A, Sbiaai K, Hasnaoui A 2019 J. Non-Cryst. Solids 510 81
Google Scholar
[25] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[26] https://sites.google.com/site/eampotentials/Ta [2020-5-4
[27] Martyna G J, Tobias D J, Klein M L 1994 J. Chem. Phys. 101 4177
Google Scholar
[28] Wu Z W, Li M Z, Wang W H, Song W J, Liu K X 2013 J. Chem. Phys. 138 074502
Google Scholar
[29] Zhang Y, Mattern N, Eckert J 2012 J. Appl. Phys. 111 053520
Google Scholar
[30] 王锦程, 郭灿, 张琪, 唐赛, 李俊杰, 王志军 2018 金属学报 54 204
Google Scholar
Wang J C, Guo C, Zhang Q, Tang S, Li J J, Wang Z J 2018 Acta Metall. Sin. 54 204
Google Scholar
[31] Wen D D, Deng Y H, Dai X Y, Tian Z A, Peng P 2019 Philos. Mag. 99 2904
Google Scholar
[32] Tian Z A, Liu R S, Dong K J, Yu A B 2011 Europhys. Lett. 96 36001
Google Scholar
[33] Honeycutt J D, Andersen H C 1987 J. Phys. Chem. 91 4950
Google Scholar
[34] Wen D D, Deng Y H, Su Y F, Tian Z A 2020 Mod. Phys. Lett. B 34 2050316.
Google Scholar
[35] Deng Y H, Wen D D, Li Y, Peng P 2018 Philos. Mag. 20 1
Google Scholar
[36] Ostwald W 1897 Z. Phys. Chem. 22 289
Google Scholar
下载:
计量
- 文章访问数: 2303
- PDF下载量: 70
- 被引次数: 0
