离子阱量子计算规模化的研究进展

吴宇恺; 段路明

doi:10.7498/aps.72.20231128

摘要

离子阱系统是当前实现量子计算最为领先的物理系统之一, 已经在数十量子比特的规模下实现了保真度达到容错量子计算阈值的量子态制备、测量、通用量子逻辑门等基本量子操作. 未来离子阱量子计算的一个重要研究方向, 是在保持量子比特高性能的同时, 进一步扩展量子比特的数量, 最终达到解决实际问题所需的规模. 本文介绍当前离子阱量子计算研究中主流的规模化方案, 如离子输运方案和离子-光子量子网络方案等, 以及各方案中存在的限制因素, 进而探讨如二维离子阵列、双重量子比特等新的规模化方案及其前景.

关键词:

量子计算 /
离子阱 /
量子比特

Abstract

Ion trap is one of the leading physical platforms to implement quantum computation. Currently, high-fidelity elementary quantum operations above the fault-tolerant threshold, including state preparation, measurement and universal gates, have been demonstrated for tens of ionic qubits. One important future research direction is to further enlarge the qubit number to the scale required for solving practical problems while maintaining the high performance of individual qubits. This paper introduces the current mainstream schemes for scalable ion trap quantum computation like quantum charge-coupled device (QCCD) and ion-photon quantum network, and describes the main limiting factors in current research. Then we further explore new schemes to scale up the qubit number like two-dimensional ion crystals and dual-type qubit, and discuss the future research directions.

Keywords:

quantum computation /
ion trap /
qubit

作者及机构信息

吴宇恺^1,2,
段路明^1,2,3

1.
清华大学交叉信息研究院, 北京　100084

2.
合肥国家实验室, 合肥　230088

3.
新基石科学实验室, 北京　100084

通信作者: 段路明, lmduan@tsinghua.edu.cn

基金项目: 科技创新2030—“量子通信与量子计算机”重大项目(批准号: 2021ZD0301601)、新基石科学基金会(新基石研究员项目)、教育部、清华大学自主科研计划、清华大学笃实专项和清华大学科研启动基金资助的课题.

Authors and contacts

1.
Institute for Interdisciplinary Information Sciences, Tsinghua University, Beijing 100084, China

2.
Heifei National Laboratory, Heifei 230088, China

3.
New Cornerstone Science Laboratory, Beijing 100084, China

Corresponding author: Duan Lu-Ming, lmduan@tsinghua.edu.cn

Funds: Project supported by the Innovation Program for Quantum Science and Technology, China (Grant No. 2021ZD0301601), the New Cornerstone Science Foundation through the New Cornerstone Investigator Program, the Ministry of Education of China, the Tsinghua University Initiative Scientific Research Program, China, the Tsinghua University Dushi Program, China, and the Tsinghua University Start-up Fund, China.

文章全文 : translate this paragraph

参考文献

[1]	Cirac J I, Zoller P 1995 Phys. Rev. Lett. 74 4091 Google Scholar
[2]	Moses S A, Baldwin C H, Allman M S, et al. 2023 arXiv 2305.03828
[3]	Ryan-Anderson C, Brown N C, Allman M S, et al. 2022 arXiv 2208.01863
[4]	Bruzewicz C D, Chiaverini J, Mcconnell R, Sage J M 2019 Appl. Phys. Rev. 6 021314 Google Scholar
[5]	Harty T P, Allcock D T C, Ballance C J, Guidoni L, Janacek H A, Linke N M, Stacey D N, Lucas D M 2014 Phys. Rev. Lett. 113 220501 Google Scholar
[6]	Ballance C J, Harty T P, Linke N M, Sepiol M A, Lucas D M 2016 Phys. Rev. Lett. 117 060504 Google Scholar
[7]	Gaebler J P, Tan T R, Lin Y, Wan Y, Bowler R, Keith A C, Glancy S, Coakley K, Knill E, Leibfried D, Wineland D J 2016 Phys. Rev. Lett. 117 060505 Google Scholar
[8]	Egan L, Debroy D M, Noel C, Risinger A, Zhu D, Biswas D, Newman M, Li M, Brown K R, Cetina M, Monroe C 2021 Nature 598 281 Google Scholar
[9]	Zhang J, Pagano G, Hess P W, Kyprianidis A, Becker P, Kaplan H, Gorshkov A V, Gong Z X, Monroe C 2017 Nature 551 601 Google Scholar
[10]	Li B W, Wu Y K, Mei Q X, Yao R, Lian W Q, Cai M L, Wang Y, Qi B X, Yao L, He L, Zhou Z C, Duan L M 2023 PRX Quantum 4 010302 Google Scholar
[11]	Wineland D J, Monroe C, Itano W M, Leibfried D, King B E, Meekhof D M 1998 J. Res. Natl. Inst. Stand. Technol. 103 259 Google Scholar
[12]	Pagano G, Hess P W, Kaplan H B, Tan W L, Richerme P, Becker P, Kyprianidis A, Zhang J, Birckelbaw E, Hernandez M R, Wu Y, Monroe C 2019 Quantum Sci. Technol. 4 014004 Google Scholar
[13]	Yao R, Lian W Q, Wu Y K, Wang G X, Li B W, Mei Q X, Qi B X, Yao L, Zhou Z C, He L, Duan L M 2022 Phys. Rev. A 106 062617 Google Scholar
[14]	Kielpinski D, Monroe C, Wineland D J 2002 Nature 417 709 Google Scholar
[15]	Duan L M, Monroe C 2010 Rev. Mod. Phys. 82 1209 Google Scholar
[16]	Hucul D, Inlek I V, Vittorini G, Crocker C, Debnath S, Clark S M, Monroe C 2015 Nat. Phys. 11 37 Google Scholar
[17]	Stephenson L J, Nadlinger D P, Nichol B C, An S, Drmota P, Ballance T G, Thirumalai K, Goodwin J F, Lucas D M, Ballance C J 2020 Phys. Rev. Lett. 124 110501 Google Scholar
[18]	Ballance C J, Schäfer V M, Home J P, Szwer D J, Webster S C, Allcock D T C, Linke N M, Harty T P, Aude Craik D P L, Stacey D N, Steane A M, Lucas D M 2015 Nature 528 384 Google Scholar
[19]	Sosnova K, Carter A, Monroe C 2021 Phys. Rev. A 103 012610 Google Scholar
[20]	Tan T R, Gaebler J P, Lin Y, Wan Y, Bowler R, Leibfried D, Wineland D J 2015 Nature 528 380 Google Scholar
[21]	Drmota P, Main D, Nadlinger D P, Nichol B C, Weber M A, Ainley E M, Agrawal A, Srinivas R, Araneda G, Ballance C J, Lucas D M 2023 Phys. Rev. Lett. 130 090803 Google Scholar
[22]	Szymanski B, Dubessy R, Dubost B, Guibal S, Likforman J P, Guidoni L 2012 Appl. Phys. Lett. 100 171110 Google Scholar
[23]	Shen C, Duan L M 2014 Phys. Rev. A 90 022332 Google Scholar
[24]	Wang S T, Shen C, Duan L M 2015 Sci. Rep. 5 8555 Google Scholar
[25]	Wu Y K, Liu Z D, Zhao W D, Duan L M 2021 Phys. Rev. A 103 022419 Google Scholar
[26]	Duan L M, Yang H X 2022 China Patent CN112749808B(in Chinese)[段路明, 杨蒿翔 2022 中国专利 CN112749808B
[27]	Yang H X, Ma J Y, Wu Y K, Wang Y, Cao M M, Guo W X, Huang Y Y, Feng L, Zhou Z C, Duan L M 2022 Nat. Phys. 18 1058 Google Scholar
[28]	Allcock D T C, Campbell W C, Chiaverini J, Chuang I L, Hudson E R, Moore I D, Ransford A, Roman C, Sage J M, Wineland D J 2021 Appl. Phys. Lett. 119 214002 Google Scholar
[29]	Feng L, Huang Y Y, Wu Y K, Guo W X, Ma J Y, Yang H X, Zhang L, Wang Y, Huang C X, Zhang C, Yao L, Qi B X, Pu Y F, Zhou Z C, Duan L M 2023 arXiv 2306.14405

施引文献

图 1 清华大学实验团队获得的约500个离子的二维阵列

Fig. 1. A 2D ion crystal with about 500 ions at Tsinghua University.

下载: 全尺寸图片幻灯片

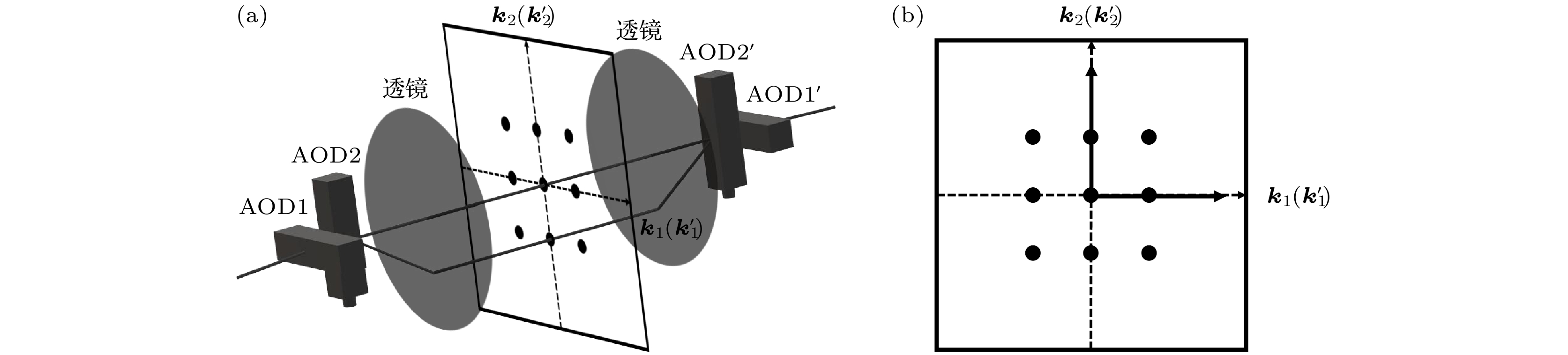
图 2 利用一对正交放置的声光偏转器进行二维单独寻址^[26]. 图中AOD1和AOD2, AOD1' 和AOD2' 各为一对正交放置的声光偏转器, 各自可进行水平和竖直方向的单独寻址

Fig. 2. Individual addressing in 2D through a pair of cross-placed AODs^[26]. Here AOD1 and AOD2, and AOD1' and AOD2', are two pairs of cross-placed AODs, each of which can achieve individual addressing in the horizontal and vertical directions.

下载: 全尺寸图片幻灯片

图 3 镱-171离子的双重类型量子比特方案^[27], 编码在S_1/2和F_7/2超精细能级上的量子比特共振频率不同, 串扰误差小于量子纠错阈值, 且可通过双色窄带激光进行经由D_5/2能级过渡进行相干转换

Fig. 3. Dual-type qubit scheme for ¹⁷¹Yb⁺ ion^[27]. Qubits encoded in S_1/2 and F_7/2 hyperfine levels have distinct resonant frequencies, thus leading to a crosstalk error below the threshold of fault-tolerant quantum computing. The two qubit types can be coherently converted into each other by bichromatic narrow-band laser via intermediate D_5/2 levels.

下载: 全尺寸图片幻灯片

map

[1]	Cirac J I, Zoller P 1995 Phys. Rev. Lett. 74 4091 Google Scholar
[2]	Moses S A, Baldwin C H, Allman M S, et al. 2023 arXiv 2305.03828
[3]	Ryan-Anderson C, Brown N C, Allman M S, et al. 2022 arXiv 2208.01863
[4]	Bruzewicz C D, Chiaverini J, Mcconnell R, Sage J M 2019 Appl. Phys. Rev. 6 021314 Google Scholar
[5]	Harty T P, Allcock D T C, Ballance C J, Guidoni L, Janacek H A, Linke N M, Stacey D N, Lucas D M 2014 Phys. Rev. Lett. 113 220501 Google Scholar
[6]	Ballance C J, Harty T P, Linke N M, Sepiol M A, Lucas D M 2016 Phys. Rev. Lett. 117 060504 Google Scholar
[7]	Gaebler J P, Tan T R, Lin Y, Wan Y, Bowler R, Keith A C, Glancy S, Coakley K, Knill E, Leibfried D, Wineland D J 2016 Phys. Rev. Lett. 117 060505 Google Scholar
[8]	Egan L, Debroy D M, Noel C, Risinger A, Zhu D, Biswas D, Newman M, Li M, Brown K R, Cetina M, Monroe C 2021 Nature 598 281 Google Scholar
[9]	Zhang J, Pagano G, Hess P W, Kyprianidis A, Becker P, Kaplan H, Gorshkov A V, Gong Z X, Monroe C 2017 Nature 551 601 Google Scholar
[10]	Li B W, Wu Y K, Mei Q X, Yao R, Lian W Q, Cai M L, Wang Y, Qi B X, Yao L, He L, Zhou Z C, Duan L M 2023 PRX Quantum 4 010302 Google Scholar
[11]	Wineland D J, Monroe C, Itano W M, Leibfried D, King B E, Meekhof D M 1998 J. Res. Natl. Inst. Stand. Technol. 103 259 Google Scholar
[12]	Pagano G, Hess P W, Kaplan H B, Tan W L, Richerme P, Becker P, Kyprianidis A, Zhang J, Birckelbaw E, Hernandez M R, Wu Y, Monroe C 2019 Quantum Sci. Technol. 4 014004 Google Scholar
[13]	Yao R, Lian W Q, Wu Y K, Wang G X, Li B W, Mei Q X, Qi B X, Yao L, Zhou Z C, He L, Duan L M 2022 Phys. Rev. A 106 062617 Google Scholar
[14]	Kielpinski D, Monroe C, Wineland D J 2002 Nature 417 709 Google Scholar
[15]	Duan L M, Monroe C 2010 Rev. Mod. Phys. 82 1209 Google Scholar
[16]	Hucul D, Inlek I V, Vittorini G, Crocker C, Debnath S, Clark S M, Monroe C 2015 Nat. Phys. 11 37 Google Scholar
[17]	Stephenson L J, Nadlinger D P, Nichol B C, An S, Drmota P, Ballance T G, Thirumalai K, Goodwin J F, Lucas D M, Ballance C J 2020 Phys. Rev. Lett. 124 110501 Google Scholar
[18]	Ballance C J, Schäfer V M, Home J P, Szwer D J, Webster S C, Allcock D T C, Linke N M, Harty T P, Aude Craik D P L, Stacey D N, Steane A M, Lucas D M 2015 Nature 528 384 Google Scholar
[19]	Sosnova K, Carter A, Monroe C 2021 Phys. Rev. A 103 012610 Google Scholar
[20]	Tan T R, Gaebler J P, Lin Y, Wan Y, Bowler R, Leibfried D, Wineland D J 2015 Nature 528 380 Google Scholar
[21]	Drmota P, Main D, Nadlinger D P, Nichol B C, Weber M A, Ainley E M, Agrawal A, Srinivas R, Araneda G, Ballance C J, Lucas D M 2023 Phys. Rev. Lett. 130 090803 Google Scholar
[22]	Szymanski B, Dubessy R, Dubost B, Guibal S, Likforman J P, Guidoni L 2012 Appl. Phys. Lett. 100 171110 Google Scholar
[23]	Shen C, Duan L M 2014 Phys. Rev. A 90 022332 Google Scholar
[24]	Wang S T, Shen C, Duan L M 2015 Sci. Rep. 5 8555 Google Scholar
[25]	Wu Y K, Liu Z D, Zhao W D, Duan L M 2021 Phys. Rev. A 103 022419 Google Scholar
[26]	Duan L M, Yang H X 2022 China Patent CN112749808B(in Chinese)[段路明, 杨蒿翔 2022 中国专利 CN112749808B
[27]	Yang H X, Ma J Y, Wu Y K, Wang Y, Cao M M, Guo W X, Huang Y Y, Feng L, Zhou Z C, Duan L M 2022 Nat. Phys. 18 1058 Google Scholar
[28]	Allcock D T C, Campbell W C, Chiaverini J, Chuang I L, Hudson E R, Moore I D, Ransford A, Roman C, Sage J M, Wineland D J 2021 Appl. Phys. Lett. 119 214002 Google Scholar
[29]	Feng L, Huang Y Y, Wu Y K, Guo W X, Ma J Y, Yang H X, Zhang L, Wang Y, Huang C X, Zhang C, Yao L, Qi B X, Pu Y F, Zhou Z C, Duan L M 2023 arXiv 2306.14405

[1]	熊凡, 陈永聪, 敖平. 热噪声环境下偶极场驱动的量子比特动力学. , 2023, 72(17): 170302. doi: 10.7498/aps.72.20230625
[2]	王宁, 王保传, 郭国平. 硅基半导体量子计算研究进展. , 2022, 71(23): 230301. doi: 10.7498/aps.71.20221900
[3]	施婷婷, 张露丹, 张帅宁, 张威. 两量子比特系统中相互作用对高阶奇异点的影响. , 2022, 0(0): 0-0. doi: 10.7498/aps.71.20220716
[4]	施婷婷, 张露丹, 张帅宁, 张威. 两量子比特系统中相互作用对高阶奇异点的影响. , 2022, 71(13): 130303. doi: 10.7498/aps.70.20220716
[5]	王晨旭, 贺冉, 李睿睿, 陈炎, 房鼎, 崔金明, 黄运锋, 李传锋, 郭光灿. 量子计算与量子模拟中离子阱结构研究进展. , 2022, 71(13): 133701. doi: 10.7498/aps.71.20220224
[6]	张结印, 高飞, 张建军. 硅和锗量子计算材料研究进展. , 2021, 70(21): 217802. doi: 10.7498/aps.70.20211492
[7]	张诗豪, 张向东, 李绿周. 基于测量的量子计算研究进展. , 2021, 70(21): 210301. doi: 10.7498/aps.70.20210923
[8]	廖庆洪, 邓伟灿, 文健, 周南润, 刘念华. 纳米机械谐振器耦合量子比特非厄米哈密顿量诱导的声子阻塞. , 2019, 68(11): 114203. doi: 10.7498/aps.68.20182263
[9]	乌云其木格, 韩超, 额尔敦朝鲁. 色散和杂质对双参量非对称高斯势量子点量子比特的影响. , 2019, 68(24): 247803. doi: 10.7498/aps.68.20190960
[10]	范桁. 量子计算与量子模拟. , 2018, 67(12): 120301. doi: 10.7498/aps.67.20180710
[11]	赵娜, 刘建设, 李铁夫, 陈炜. 超导量子比特的耦合研究进展. , 2013, 62(1): 010301. doi: 10.7498/aps.62.010301
[12]	赵翠兰, 丛银川. 球壳量子点中极化子和量子比特的声子效应. , 2012, 61(18): 186301. doi: 10.7498/aps.61.186301
[13]	姜福仕, 赵翠兰. 量子环中量子比特的声子效应. , 2009, 58(10): 6786-6790. doi: 10.7498/aps.58.6786
[14]	陈英杰, 肖景林. 抛物线性限制势二能级系统量子点量子比特的温度效应. , 2008, 57(11): 6758-6762. doi: 10.7498/aps.57.6758
[15]	尹辑文, 肖景林, 于毅夫, 王子武. 库仑势对抛物量子点量子比特消相干的影响. , 2008, 57(5): 2695-2698. doi: 10.7498/aps.57.2695
[16]	高宽云, 赵翠兰. 量子环中量子比特的性质. , 2008, 57(7): 4446-4449. doi: 10.7498/aps.57.4446
[17]	王子武, 肖景林. 抛物线性限制势量子点量子比特及其光学声子效应. , 2007, 56(2): 678-682. doi: 10.7498/aps.56.678
[18]	董庆瑞. 磁场方向调制的InAs量子点分子量子比特. , 2007, 56(9): 5436-5440. doi: 10.7498/aps.56.5436
[19]	李艳玲, 冯健, 孟祥国, 梁宝龙. 量子比特的普适远程翻转和克隆. , 2007, 56(10): 5591-5596. doi: 10.7498/aps.56.5591
[20]	胡学宁, 李新奇. 量子点接触对单电子量子态的量子测量. , 2006, 55(7): 3259-3264. doi: 10.7498/aps.55.3259

计量

文章访问数: 4630
PDF下载量: 308
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

离子阱量子计算规模化的研究进展