HADAR实验对Fermi-LAT伽马射线源观测的预期研究

孙惠英; 钱祥利; 陈天禄; 单增罗布; 冯有亮; 高启; 苟全补; 郭义庆; 胡红波; 康明铭; 厉海金; 刘成; 刘茂元; 刘伟; 乔冰强; 王旭; 王振; 辛广广; 姚玉华; 袁强; 张毅

doi:10.7498/aps.72.20230977

摘要

高海拔天体辐射探测(high altitude detection of astronomical radiation, HADAR)实验是一个新型的采用纯水作为介质的大气切伦科夫望远镜实验阵列, 其采用大口径半球型透镜来收集大气切伦科夫光, 以实现对10 GeV—10 TeV能量段的伽马射线和宇宙线的探测. HADAR具有低阈能、高灵敏度和传统成像大气切伦科夫望远镜所不具备的大视场优势, 可以对天区进行连续扫描观测, 因此将成为全天伽马源的理想观测仪器和爆发源、时变源的理想搜寻探测器. 本文基于Fermi-LAT的最新伽马射线源表, 详细研究了HADAR实验对这些源的观测能力. 对银河系外的源, 将这些源的能谱加入河外背景光吸收效应外推至甚高能段. 通过对这些源的显著性进行模拟研究, 结果显示HADAR运行一年预期有93个伽马射线源以大于5倍的显著性标准偏差被观测到, 其中包括45个银河系内的源, 39个银河系外的源, 3个未知类型的源和6个未关联类型的源.

关键词:

Abstract

High altitude detection of astronomical radiation (HADAR) is an innovative array of atmospheric Cherenkov telescopes that employs pure water as its medium. By utilizing large-aperture hemispherical lenses, HADAR can capture atmospheric Cherenkov light, enabling the detection of gamma rays and cosmic rays in the energy range of 10 GeV to 10 TeV. Compared to traditional Imaging Atmospheric Cherenkov telescopes, HADAR offers distinct advantages such as a low energy threshold, high sensitivity, and a wide field of view. The telescope mainly consists of a hemispherical lens with a diameter of 5 m acting as a Cherenkov light collector, a cylindrical metal tank with a 4 m radius and 7 m height, and an imaging system at the bottom of the tank. The sky region covered by HADAR is much larger than the current generation of Imaging Atmospheric Cherenkov Telescopes. The field of view of HADAR can reach up to 60 degrees. Its continuous scanning capability allows for comprehensive observations of gamma-ray sources throughout the entire celestial sphere, making it an ideal instrument for studying transient and variable sources. In this study, the observational capabilities of HADAR are thoroughly investigated using the latest 4FGL-DR3 and 4LAC-DR3 gamma-ray source catalogs from Fermi-LAT. For extragalactic sources, the energy spectra in the high energy range have been extrapolated to the very high energy range, taking into account the absorption effect caused by extragalactic background light. By comparing the extrapolated results with existing VHE experimental data, the feasibility of this extrapolation method has been demonstrated. Through simulated analyses of the significance of these sources, it is anticipated that HADAR will detect a total of 93 gamma-ray sources with a significance exceeding 5 standard deviations during one year of operation. These sources comprise 45 galactic sources, 39 extragalactic sources, 3 sources of unknown type, and 6 unassociated sources.

Keywords:

作者及机构信息

1.
山东管理学院智能工程学院, 济南　250357

2.
西藏大学宇宙线教育部重点实验室, 拉萨　850000

3.
中国科学院高能物理研究所粒子天体中心, 北京　100049

4.
中国科学院大学, 北京　100049

5.
四川大学物理学院, 成都　610064

6.
上海交通大学李政道研究所, 上海　200240

7.
苏州空天信息研究院, 苏州　215000

8.
重庆大学物理学院, 重庆　401331

9.
中国科学院紫金山天文台暗物质与空间天文重点实验室, 南京　210023

通信作者: 钱祥利, qianxl@sdmu.edu.cn ; 郭义庆, guoyq@ihep.ac.cn ;

基金项目: 国家自然科学基金(批准号: 12263005, 12005120, 12147218, U1831208, U2031110)和西藏大学宇宙线教育部重点实验室(批准号: KLCR-202201)资助的课题

Authors and contacts

1.
School of Intelligent Engineering, Shandong Management University, Jinan 250357, China

2.
Key Laboratory of Cosmic Rays, Ministry of Education, Tibet University, Lhasa 850000, China

3.
Key Laboratory of Particle Astrophysics, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China

4.
University of Chinese Academy of Sciences, Beijing 100049, China

5.
College of Physics, Sichuan University, Chengdu 610064, China

6.
Tsung-Dao Lee Institute, Shanghai Jiao Tong University, Shanghai 200240, China

7.
Suzhou Aerospace Information Research Institute, Suzhou 215000, China

8.
College of Physics, Chongqing University, Chongqing 401331, China

9.
Key Laboratory of Dark Matter and Space Astronomy, Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210023, China

Corresponding author: Qian Xiang-Li, qianxl@sdmu.edu.cn ; Guo Yi-Qing, guoyq@ihep.ac.cn ;

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12263005, 12005120, 12147218, U1831208, U2031110) and the Key Laboratory of Cosmic Ray of the Ministry of Education of China, Tibet University (Grant No. KLCR-202201)

文章全文 : translate this paragraph

参考文献

[1]	Hinton J A 2004 New Astron. Rev. 48 331 Google Scholar
[2]	Albert J, Aliu E, Anderhub H 2008 Astrophys. J. 674 1037 Google Scholar
[3]	Holder J, Acciari V, Aliu E 2008 4th International Symposium on High Energy Gamma-Ray Astronomy, Heidelberg, Germany, July 7–11, p657
[4]	CTA Consortium 2018 Science with the Cherenkov Telescope Array (Singapore: World Scientific) pp11–26
[5]	Ellison D C, Drury L O’C, Meyer J P 1997 Astrophys. J. 487 197 Google Scholar
[6]	Gaensler B M, Slane P O 2006 Annu. Rev. Astron. Astr. 44 17 Google Scholar
[7]	Abdalla H, Abramowski A, Aharonian F 2018 Astron. Astrophys. 612 A1 Google Scholar
[8]	Abeysekara A U, Archer A, Aune T 2018 Astrophys. J. 861 134 Google Scholar
[9]	Albert A, Alfaro R, Alvarez C 2020 Astrophys. J. 905 76 Google Scholar
[10]	Antonucci R 1993 Annu. Rev. Astron. Astr. 31 473 Google Scholar
[11]	Urry C M, Padovani P 1995 Publ. Astron. Soc. Pac. 107 803 Google Scholar
[12]	Sikora M, Begelman M C, Rees M J 1994 Astrophys. J. 421 153 Google Scholar
[13]	Aharonian F 2000 New. Astron. 5 377 Google Scholar
[14]	Mücke A, Protheroe R J, Engel R, Rachen J P, Stanev T 2003 Astropart. Phys. 18 593 Google Scholar
[15]	Mannheim K, Biermann P L 1989 Astron. Astrophys. 221 211
[16]	Mannheim K 1998 Science 279 684 Google Scholar
[17]	Böttcher M, Reimer A, Sweeney K, Prakash A 2013 Astrophys. J. 768 54 Google Scholar
[18]	Urry C M 1999 Astropart. Phys. 11 159 Google Scholar
[19]	Abdo A A, Ackermann M, Agudo I 2010 Astrophys. J. 716 30 Google Scholar
[20]	Abdo A A, Ackermann M, Ajello M 2010 Astrophys. J. 715 429 Google Scholar
[21]	Xin G G, Yao Y H, Qian X L 2021 Astrophys. J. 923 112 Google Scholar
[22]	Qian X L, Sun H Y, Chen T L 2022 Front. Phys.-Beijing 17 64602 Google Scholar
[23]	Qian X L, Sun H Y, Chen T L 2023 Acta Phys. Sin. 72 049501 [钱祥利, 孙惠英, 陈天禄 2023 72 049501 Google Scholar Qian X L, Sun H Y, Chen T L 2023 Acta Phys. Sin. 72 049501 Google Scholar
[24]	Ajello M, Atwood W B, Baldini L 2017 Astrophys. J. Suppl. S. 232 18 Google Scholar
[25]	Aleksić J, Ansoldi S, Antonelli L A 2016 Astropart. Phys. 72 76 Google Scholar
[26]	Bartoli B, Bernardini P, Bi X J 2013 Astrophys. J. 779 27 Google Scholar
[27]	Abeysekara A U, Alfaro R, Alvarez C 2013 Astropart. Phys. 50 26
[28]	Amenomori M, Bi X J, Chen D 2009 Astrophys. J. 692 61 Google Scholar
[29]	Ma X H, Bi Y J, Cao Z 2022 Chin. Phys. C 46 030001 Google Scholar
[30]	Cai H, Zhang Y, Liu C 2017 J. Instrum. 12 09023
[31]	Chen T L, Liu C, Gao Q 2019 Nucl. Instrum. Meth. A 927 46 Google Scholar
[32]	Atwood W B, Abdo A A, Ackermann M 2009 Astrophys. J. 697 1071 Google Scholar
[33]	Abdollahi S, Acero F, Baldini L 2022 Astrophys. J. Suppl. S. 260 53 Google Scholar
[34]	Ajello M, Baldini L, Ballet J 2022 Astrophys. J. Suppl. S. 263 24 Google Scholar
[35]	Abdollahi S, Acero F, Ackermann M 2020 Astrophys. J. Suppl. S. 247 33 Google Scholar
[36]	Ajello M, Angioni R, Axelsson M 2020 Astrophys. J. 892 105 Google Scholar
[37]	Gilmore R C, Somerville R S, Primack J R, Domínguez A 2012 Mon. Not. R. Astron. Soc. 422 3189 Google Scholar
[38]	Domínguez A, Primack J R, Rosario D J 2011 Mon. Not. R. Astron. Soc. 410 2556 Google Scholar
[39]	Patel S, Maier G, Kaaret P 2021 arXiv: 210806424 [astro-ph.HE
[40]	Ghisellini G, Righi C, Costamante L, Tavecchio F 2017 Mon. Not. R. Astron. Soc. 469 255 Google Scholar
[41]	Abdalla H, Abe H, Acero F 2021 J. Cosmol. Astropart. P. 2021 048 Google Scholar
[42]	Amenomori M, Ayabe S, Chen D 2005 Astrophys. J. 633 1005 Google Scholar
[43]	Aliu E, Archambault S, Arlen T 2012 Astrophys. J. 750 94 Google Scholar
[44]	Abramowski A, Acero F, Aharonian F 2012 Astron. Astrophys. 538 A103 Google Scholar
[45]	Abramowski A, Acero F, Aharonian F 2013 Mon. Not. R. Astron. Soc. 434 1889 Google Scholar
[46]	Aleksić J, Antonelli L A, Antoranz P 2011 Astrophys. J. Lett. 730 L8 Google Scholar
[47]	Aharonian F, Akhperjanian A G, Bazer-Bachi A R 2007 Astron. Astrophys. 470 475 Google Scholar
[48]	Aharonian F, Akhperjanian A G, de Almeida U B 2007 Astron. Astrophys. 475 L9 Google Scholar
[49]	Aleksić J, Ansoldi S, Antonelli L A 2014 Science 346 1080 Google Scholar
[50]	H.E.S.S. Collaboration 2020 Nature 582 356 Google Scholar
[51]	VERITAS Collaboration, VLBA 43 GHz M87 Monitoring Team, H.E.S.S. Collaboration, MAGIC Collaboration 2009 Science 325 444 Google Scholar
[52]	Acero F, Aharonian F, Akhperjanian A G 2009 Science 326 1080 Google Scholar
[53]	Abdalla H, Aharonian F, Benkhali F A 2018 Astron. Astrophys. 617 A73 Google Scholar
[54]	Acciari V A, Aliu E, Arlen T 2009 Nature 462 770 Google Scholar
[55]	Abdo A A, Ackermann M, Ajello M 2010 Astrophys. J. Lett. 709 L152 Google Scholar

施引文献

图 1 HADAR阵列示意图　(a)阵列分布图; (b)单个水透镜详细结构图^[21]

Fig. 1. Schematic of HADAR: (a) Layout of the HADAR experiment; (b) detailed design of a water-lens telescope^[21].

下载: 全尺寸图片幻灯片

图 2 HADAR及其他伽马射线实验的灵敏度曲线对比图^[23]

Fig. 2. Comparisons of the sensitivity of HADAR with other γ-ray instruments^[23]

下载: 全尺寸图片幻灯片

图 3 伽马射线衰减因子与能量的关系图, 分别对应红移为0.03, 0.1, 0.25, 0.5和1.0处的源. 实线代表基于威尔金森微波各向异性探测器卫星(WMAP5)数据的模型, 作为对比, 基于固定参数的WMAP5模型(紫色点划线)和Domínguez模型^[38] (红色点划线)也分别画出. 可以看出伽马射线的衰减主要集中在甚高能段, 随着红移的增加吸收效应逐渐变强, 且衰减逐渐向低能段发展. 低红移时在1—10 TeV能量区间存在一个较平缓的变化^[37]

Fig. 3. Attenuation ${\rm{e}}^{-\tau}$ of gamma-rays versus gamma-ray energy, for sources at z = 0.03, 0.1, 0.25, 0.5 and 1.0. Results are compared for Wilkinson microwave anisotropy probe 5-year (WMAP5, solid) and WMAP5 + fixed (dash-dotted violet) models, as well as the model of Domínguez^[38] (dash-dotted red). Increasing distance causes absorption features to increase in magnitude and appear at lower energies. A plateau can be seen between 1–10 TeV at low redshift^[37]

下载: 全尺寸图片幻灯片

图 4 外推得到的源3C 66A, 1ES 1218+304, PKS 1424+240和PG 1553+113的宽能量段伽马射线谱能量分布图, 可以看出, 采用内禀谱函数加EBL吸收的谱模型能较好地描述能谱的实验观测数据. 其中低能段为Fermi-LAT 4FGL的实验数据(蓝色菱形), VHE能段为VERITAS的实验数据(黄色圆圈代表低态, 黄色圆点代表不同耀发态的数据). 三种不同的红色虚线分别代表不同的谱函数模型, 实线代表Fermi-LAT采用的谱函数. 纵坐标代表观测的流强, 其中包含了EBL的吸收效应

Fig. 4. Gamma-ray spectral energy distribution for the sources 3C 66A, 1ES 1218+304, PKS 1424+240, and PG 1553+113 obtained over a wide energy range by extrapolation. The resulting data show that the spectral models using the intrinsic spectral function and EBL absorption fit the experimental data well. The Fermi-LAT 4FGL data is represented by blue diamonds in the low-energy band, while in the VHE band the VERITAS data is depicted by yellow circles for the low state and yellow dots for the different flaring states. Three different red dashed lines represent different spectral function models, while the solid line represents the Fermi-LAT preferred function. The y-axis represents the flux, which includes the absorption effect of EBL

下载: 全尺寸图片幻灯片

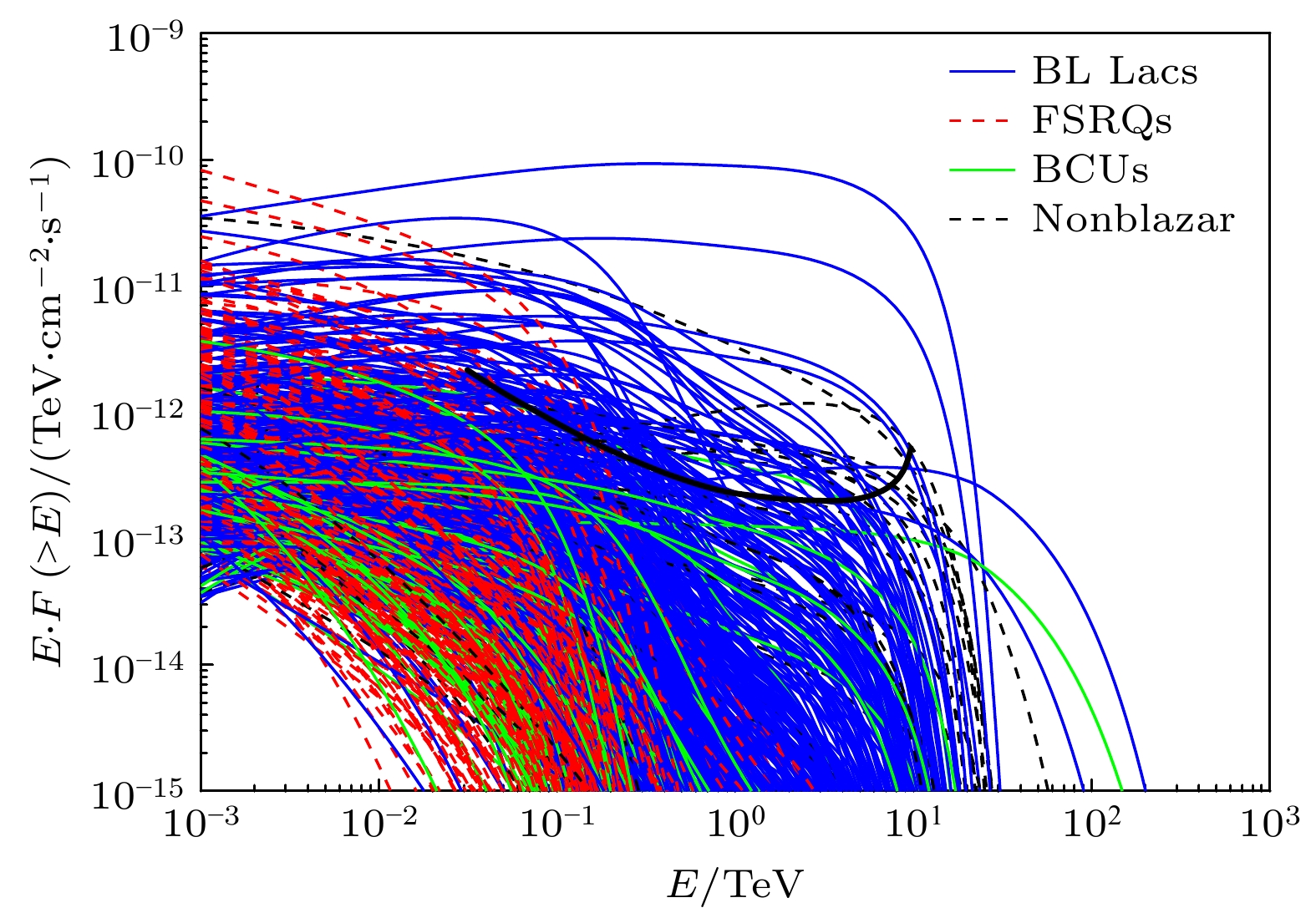
图 5 河外源的预期能谱图, 图中蓝色实线为BL Lacs, 红色虚线为FSRQs, 绿色实线为BCUs, 黑色虚线为Nonblazar AGN, 黑色实线为HADAR运行1 a的灵敏度曲线

Fig. 5. Expected energy spectrum for extragalactic sources. The blue solid line represents BL Lacs, the red dashed line represents FSRQs, the green solid line represents BCUs, the black dashed line represents Nonblazar AGN, and the black solid line indicates the sensitivity of HADAR operating for 1 a

下载: 全尺寸图片幻灯片

图 6 赤道坐标系(J2000 坐标)下HADAR对Fermi-LAT源的观测显著性预期天图, 上面标注为河外源, 下面标注为河内源及未知类型和未关联的源, 显著性显示范围为–3—15

Fig. 6. Expected significance sky map of HADAR observations with respect to Fermi-LAT sources in the equatorial coordinates (J2000 epoch). The map is annotated with extragalactic sources above, and with galactic sources, unknown sources, and unassociated sources below. Significance levels are displayed in the range of –3 to 15

下载: 全尺寸图片幻灯片

表 1 HADAR及其他IACT和EAS实验的性能对比, 表中列出了各实验的名称、覆盖天区、视场、能量阈值、角分辨、观测点源的灵敏度和参考文献

Table 1. Comparison of the performance of HADAR and other IACT/EAS experiments. For each experiment, the name, spatial coverage, field of view, energy threshold, angular resolution, point-source ssensitivity and reference are given.

Experiment	Hemisphere/(N, S)	FOV/sr	Energy threshold	Angular resolution/(°)	Sensitivity/Crab	Ref.
Fermi-LAT 2FHL	space	2.7	10 GeV–2 TeV	0.1°(30 GeV)	3%–4%	[24]
LHAASO-WCDA	N	1.5	100 GeV–30 TeV	0.4°(2 TeV)	< 10%	[29]
HAWC	N	1.5	100 sGeV–10 sTeV	~0.5°	5%–10%	[9]
H.E.S.S.	S	0.006	30 GeV–100 TeV	0.08°	0.4%–2.0%	[7]
MAGIC	N	0.003	50 GeV–10 TeV	~0.1°	~0.7%	[25]
CTA	N, S	0.0048–0.015	20 GeV–300 TeV	0.07°(1 TeV)	0.2%–0.4%	[4]
HADAR	N	0.84	10 GeV–10 TeV	0.4°(100 GeV)	1.3%–2.4%	[22]

下载: 导出CSV

表 2 HADAR视场内4个AGN源的性质参数, 谱的模型参数从4LAC/4FGL导出. 表中从左到右分别为: 4FGL源名称、源对应体、AGN类型、SED分类、红移、模型, 该谱模型下的能量参考值、对应在能量$ E_0 $处的微分流强、谱指数Γ和曲率参数β

Table 2. Property parameters for four AGN sources, where the spectral model parameters are based on 4LAC or 4FGL. Columns from left to right are as follows: 4FGL source name, counterpart, type, class, redshift, model, $ E_0 $, differential flux at $ E_0 $ with the fit model, spectral index Γ, curvature parameter β

4FGL Name	Counterpart	Type	Class	Redshift	Model	E₀/GeV	F₀ /(TeV^–1·cm^–2·s^–1)	Γ	β
J0222.6+4301	3C 66A	BLL	ISP	0.444	LP	1.197	1.03 × 10^–5	1.89	0.04
J1221.3+3010	1ES 1218+304	BLL	EHSP	0.184	PL	4.501	1.83 × 10^–7	1.71	—
J1427.0+2348	PKS 1424+240	BLL	HSP	0.604	LP	1.205	7.03 × 10^–6	1.71	0.06
J1555.7+1111	PG 1553+113	BLL	HSP	0.360	LP	1.802	3.84 × 10^–6	1.54	0.07

下载: 导出CSV

表 3 HADAR预期观测到的Fermi-LAT源的种类和数目

Table 3. Types and numbers of Fermi-LAT sources that HADAR is expected to detect

4FGL-DR3 source classes	Number of sources in 4FGL-DR3	Number of sources in HADAR FOV	Expected to be observed by HADAR in 1 a	Expected to be observed by HADAR in 5 a
Young / Millisecond pulsars	292	106	34	52
PWNe, SNR	63	22	10	13
SNR / PWNe	114	26	0	1
Globular cluster	35	5	0	0
Star-forming region	5	2	1	1
High-mass Binary, Low-mass Binary, Binary, Nova	30	6	0	0
BL Lacs	1458	492	34	66
FSRQs	792	376	2	5
Blazar candidate of uncertain type	1493	88	0	2
Nonblazar AGN (RDG, AGN, SSRQ, CSS, NLSY1, SEY)	71	36	3	8
Starburst galaxy	8	3	0	0
Normal galaxy	6	3	0	0
Unkown	134	48	3	7
Unassociated	2157	592	6	25
Total	6658	1805	93	180

下载: 导出CSV

表 4 HADAR视场内Fermi-LAT河外源的能谱参数及观测信息, 谱的参数从4LAC-DR3导出. 表中从左到右分别为: 4FGL源名称, 源对应体, 赤经, 赤纬, SED分类, 红移, 拟合模型, 该谱模型下的能量参考值, 对应在能量$ E_0 $处的微分流强, 谱指数Γ, 曲率参数β, 有效观测时间, 观测显著性

Table 4. Property parameters for extragalactic sources in HADAR FOV, where the spectral model parameters are derived from 4LAC-DR3. Columns from left to right are as follows: 4FGL source name, counterpart, right ascension, declination, class, redshift, model, $ E_0 $, differential flux at $ E_0 $ with the fit model, spectral index Γ, curvature parameter β, live time and significance

4FGL name	Counterpart	R.A.	Dec.	Type	Redshift	Model	E₀/GeV	F₀/(TeV^–1·cm^–2·s^–1)	Γ	β	Time/h	S/σ
J0112.1+2245	S2 0109+22	18.03	22.75	BLL	0.265	LP	0.769	1.46 × 10^–5	1.99	0.060	277.8	9.05
J0211.2+1051	MG1J021114+1051	32.81	10.86	BLL	0.200	LP	0.922	7.51 × 10^–6	2.02	0.042	196.3	6.47
J0222.6+4302	3C 66A	35.67	43.04	BLL	0.444	LP	1.246	8.40 × 10^–6	1.89	0.046	264.2	17.9
J0319.8+4130	NGC 1275	49.96	41.51	RDG	0.018	LP	0.918	4.36 × 10^–5	2.05	0.069	271.9	54.6
J0521.7+2112	TXS 0518+211	80.44	21.21	bll	0.108	LP	1.541	4.64 × 10^–6	1.86	0.045	271.0	50.2
J0620.7+2643	RX J0620.6+2644	95.18	26.73	bll	0.134	PL	17.415	1.22 × 10^–9	1.55	—	290.3	5.1
J0648.7+1516	RX J0648.7+1516	102.19	15.28	bll	0.179	LP	3.248	1.22 × 10^–7	1.60	0.056	234.3	10.9
J0650.7+2503	1ES 0647+250	102.7	25.05	bll	0.203	LP	2.067	8.44 × 10^–7	1.65	0.041	286.0	32.9
J0738.1+1742	PKS 0735+17	114.54	17.71	bll	0.424	LP	1.623	2.25 × 10^–6	1.97	0.067	251.3	5.2
J0809.8+5218	1ES 0806+524	122.46	52.31	BLL	0.138	LP	1.342	1.91 × 10^–6	1.83	0.023	193.9	15.1
J0915.9+2933	Ton 0396	138.99	29.55	bll	0.190	LP	1.390	9.28 × 10^–7	1.74	0.081	294.7	7.4
J1015.0+4926	1H 1013+498	153.77	49.43	bll	0.212	LP	1.044	6.00 × 10^–6	1.75	0.044	220.0	27.9
J1058.6+5627	TXS 1055+567	164.67	56.46	BLL	0.143	LP	1.102	2.38 × 10^–6	1.86	0.050	149.4	6.1
J1104.4+3812	Mkn 421	166.12	38.21	BLL	0.030	PLEC	1.258	1.79 × 10^–5	1.74	—	284.9	519.6
J1117.0+2013	RBS 0958	169.27	20.23	bll	0.139	PL	1.964	3.12 × 10^–7	1.95	—	266.1	5.0
J1120.8+4212	RBS 0970	170.20	42.20	bll	0.124	LP	2.416	2.11 × 10^–7	1.55	0.046	268.6	23.9
J1150.6+4154	RBS 1040	177.66	41.91	bll	0.320	LP	1.949	4.71 × 10^–7	1.55	0.135	270.0	7.2
J1217.9+3007	B2 1215+30	184.48	30.12	BLL	0.130	LP	1.248	5.77 × 10^–6	1.87	0.043	295.1	37.7
J1221.3+3010	PG 1218+304	185.34	30.17	bll	0.184	LP	2.590	5.27 × 10^–7	1.65	0.029	295.2	37.4
J1221.5+2814	W Comae	185.38	28.24	bll	0.102	LP	0.781	6.00 × 10^–6	2.11	0.024	293.1	5.5
J1230.2+2517	ON 246	187.56	25.30	bll	0.135	LP	0.800	6.66 × 10^–6	2.02	0.056	286.7	5.8
J1230.8+1223	M 87	187.71	12.39	rdg	0.004	LP	1.124	1.30 × 10^–6	2.00	0.036	210.5	5.3
J1417.9+2543	1E 1415.6+2557	214.49	25.72	bll	0.237	LP	8.155	6.13 × 10^–9	1.28	0.138	287.9	5.1
J1427.0+2348	PKS 1424+240	216.76	23.80	BLL	0.604	LP	1.254	5.70 × 10^–6	1.71	0.057	281.8	21.7
J1428.5+4240	H 1426+428	217.13	42.68	bll	0.129	PL	5.135	2.69 × 10^–8	1.65	—	266.1	10.3
J1449.5+2746	B2 1447+27	222.40	27.77	rdg	0.031	PL	14.614	5.37 × 10^–10	1.46	—	292.4	6.8
J1555.7+1111	PG 1553+113	238.93	11.19	BLL	0.360	LP	3.802	1.16 × 10^–6	1.57	0.095	199.5	56.4
J1653.8+3945	Mkn 501	253.47	39.76	BLL	0.033	LP	1.508	3.78 × 10^–6	1.75	0.018	279.5	125.1
J1725.0+1152	1H 1720+117	261.27	11.87	bll	0.180	LP	2.216	7.55 × 10^–7	1.76	0.056	205.9	14.5
J1728.3+5013	I Zw 187	262.08	50.23	bll	0.055	PL	2.983	1.82 × 10^–7	1.79	—	213.2	21.1
J1838.8+4802	GB6J1838+4802	279.71	48.04	bll	0.300	LP	1.631	8.39 × 10^–7	1.78	0.040	231.3	6.7
J1904.1+3627	MG2J190411+3627	286.03	36.45	bll	0.078	PL	5.074	2.01 × 10^–8	1.80	—	289.7	5.8
J2116.2+3339	B2 2114+33	319.06	33.66	bll	0.350	LP	1.653	1.10 × 10^–6	1.75	0.095	294.4	7.1
J2202.7+4216	BL Lac	330.69	42.28	BLL	0.069	LP	0.871	4.07 × 10^–5	2.12	0.059	268.2	27.4
J2232.6+1143	CTA 102	338.15	11.73	FSRQ	1.037	PLEC	1.082	4.34 × 10^–5	2.27	—	204.5	5.9
J2250.0+3825	B3 2247+381	342.51	38.42	bll	0.119	PL	5.338	2.55 × 10^–8	1.74	—	284.2	7.9
J2253.9+1609	3C 454.3	343.50	16.15	FSRQ	0.859	PLEC	0.892	1.32 × 10^–4	2.38	—	240.7	10.9
J2323.8+4210	1ES 2321+419	350.97	42.18	bll	0.059	LP	1.857	5.31 × 10^–7	1.80	0.068	268.7	11.0
J2347.0+5141	1ES 2344+514	356.77	51.70	bll	0.044	LP	1.911	7.15 × 10^–7	1.74	0.039	199.8	29.2

下载: 导出CSV

表 5 HADAR视场内Fermi-LAT河内源的能谱参数及观测信息, 谱的参数从4FGL-DR3导出. 表中从左到右分别为: 4FGL源名称, 源对应体, 赤经, 赤纬, SED分类, 拟合模型, 该谱模型下的能量参考值, 对应在能量$ E_0 $处的微分流强, 谱指数Γ, 曲率参数β, 有效观测时间, 观测显著性

Table 5. Property parameters for galactic sources in HADAR FOV, where the spectral model parameters are derived from 4FGL-DR3. Columns from left to right are as follows: 4FGL source name, counterpart, right ascension, declination, class, model, $ E_0 $, differential flux at $ E_0 $ with the fit model, spectral index Γ, curvature parameter β, live time and significance

4FGL Name	Counterpart	R.A.	Dec.	Type	Model	$ E_0 $/GeV	F₀/(TeV^–1·cm^–2·s^–1)	Γ	β	Time/h	S/σ
J0030.4+0451	PSR J0030+0451	7.61	4.86	MSP	PLEC	1.360	7.36 × 10^–6	2.08	—	130.1	40.6
J0102.8+4839	PSR J0102+4839	15.71	48.66	MSP	PLEC	1.378	1.42 × 10^–6	2.18	—	226.4	6.0
J0106.4+4855	PSR J0106+4855	16.61	48.93	PSR	PLEC	1.578	1.66 × 10^–6	2.11	—	224.2	14.2
J0218.1+4232	PSR J0218+4232	34.53	42.55	MSP	PLEC	0.820	1.20 × 10^–5	2.35	—	266.8	6.2
J0220.1+1155	—	35.04	11.92	—	PL	16.622	3.98 × 10^–10	1.57	—	206.2	5.6
J0340.3+4130	PSR J0340+4130	55.10	41.51	MSP	PLEC	1.659	1.38 × 10^–6	2.03	—	271.9	24.6
J0357.8+3204	PSR J0357+3205	59.46	32.08	PSR	PLEC	1.104	1.26 × 10^–5	2.30	—	295.5	19.3
J0425.6+5522e	SNR G150.3+04.5	66.42	55.37	SNR	LP	7.240	1.19 × 10^–7	1.64	0.047	161.8	123.6
J0534.5+2201i	Crab Nebula	83.63	22.02	PWN	LP	10.000	5.50 × 10^–7	1.75	0.080	274.7	639.6
J0540.3+2756e	Sim 147	85.10	27.94	SNR	LP	1.192	5.50 × 10^–6	2.07	0.081	292.7	11.1
J0554.1+3107	PSR J0554+3107	88.55	31.12	PSR	PLEC	1.066	4.06 × 10^–6	2.34	—	295.5	5.1
J0605.1+3757	PSR J0605+3757	91.28	37.96	MSP	PLEC	1.507	7.88 × 10^–7	2.18	—	285.7	5.3
J0617.2+2234e	IC 443	94.31	22.58	SNR	LP	4.551	2.58 × 10^–6	2.28	0.123	277.1	37.6
J0620.9+2201	—	95.23	22.02	—	PL	20.913	6.45 × 10^–10	1.61	—	274.7	5.7
J0631.5+1036	PSR J0631+1036	97.88	10.60	PSR	PLEC	1.540	2.52 × 10^–6	2.20	—	193.8	11.1
J0631.8+0645	PSR J0631+0646	97.96	6.76	PSR	PLEC	2.258	7.60 × 10^–7	2.22	—	152.9	5.9
J0633.7+0632	PSR J0633+0632	98.44	6.54	PSR	PLEC	1.527	8.13 × 10^–6	2.22	—	150.4	26.3
J0633.9+1746	PSR J0633+1746	98.48	17.77	PSR	PLEC	1.670	3.19 × 10^–4	2.10	—	251.7	575.7
J0650.6+2055	NVSS J065035+205556	102.66	20.93	unk	LP	3.643	4.42 × 10^–8	1.63	0.096	269.6	9.5
J0751.2+1808	PSR J0751+1807	117.80	18.14	MSP	PLEC	1.643	9.45 × 10^–7	2.06	—	254.1	13.1
J1312.7+0050	PSR J1312+0051	198.19	0.84	MSP	PLEC	1.301	2.01 × 10^–6	2.15	—	76.3	5.7
J1554.2+2008	—	238.55	20.15	—	PL	4.619	1.14 × 10^–8	1.82	—	265.6	5.0
J1816.5+4510	PSR J1816+4510	274.15	45.17	MSP	PLEC	1.171	1.48 × 10^–6	2.14	—	251.6	6.1
J1836.2+5925	PSR J1836+5925	279.06	59.43	PSR	PLEC	1.428	6.64 × 10^–5	2.07	—	112.6	388.8
J1846.3+0919	PSR J1846+0919	281.60	9.33	PSR	PLEC	1.458	3.78 × 10^–6	2.19	—	181.0	14.9
J1854.5+2050	—	283.64	20.84	—	PL	103.233	2.68 × 10^–11	1.01	—	269.2	34.8
J1857.7+0246e	HESS J1857+026	284.45	2.77	PWN	PL	6.063	2.25 × 10^–7	2.13	—	103.1	19.5
J1907.9+0602	PSR J1907+0602	286.98	6.04	PSR	PLEC	1.898	1.39 × 10^–5	2.37	—	144.4	31.3
J1910.8+2856	NVSS J191052+285621	287.72	28.94	unk	PL	7.243	6.08 × 10^–9	1.80	—	294.1	7.1
J1911.0+0905	W 49B	287.76	9.09	snr	LP	4.552	7.74 × 10^–7	2.28	0.112	178.6	8.5
J1918.0+0331	NVSS J191803+033032	289.51	3.52	unk	PL	12.647	2.39 × 10^–9	1.72	—	113.0	6.2
J1923.2+1408e	W 51C	290.82	14.14	SNR	LP	2.768	5.08 × 10^–6	2.21	0.109	225.4	25.9
J1924.3+1628	—	291.10	16.48	—	PL	22.893	7.99 × 10^–10	1.76	—	243.1	7.7
J1952.9+3252	PSR J1952+3252	298.25	32.88	PSR	PLEC	1.618	9.92 × 10^–6	2.29	—	295.1	39.3
J1954.3+2836	PSR J1954+2836	298.59	28.60	PSR	PLEC	1.519	8.08 × 10^–6	2.32	—	293.7	23.1
J1958.7+2846	PSR J1958+2846	299.68	28.77	PSR	PLEC	1.356	1.13 × 10^–5	2.35	—	293.9	21.1
J2017.4+0602	PSR J2017+0603	304.35	6.05	MSP	PLEC	1.800	2.20 × 10^–6	1.98	—	144.6	43.2
J2017.9+3625	PSR J2017+3625	304.49	36.43	PSR	PLEC	1.467	6.99 × 10^–6	2.53	—	289.8	5.7
J2021.0+4031e	gamma Cygni	305.27	40.52	SNR	LP	7.758	2.07 × 10^–7	1.88	0.060	276.4	95.9
J2021.1+3651	PSR J2021+3651	305.28	36.86	PSR	PLEC	1.842	2.62 × 10^–5	2.32	—	288.8	114.0
J2028.3+3331	PSR J2028+3332	307.08	33.53	PSR	PLEC	1.467	6.57 × 10^–6	2.32	—	294.6	17.5
J2028.6+4110e	Cygnus X	307.17	41.17	SFR	LP	2.036	2.90 × 10^–5	2.04	0.033	273.5	368.3
J2030.0+3641	PSR J2030+3641	307.51	36.69	PSR	PLEC	1.650	3.92 × 10^–6	2.33	—	289.2	12.6
J2030.9+4416	PSR J2030+4415	307.73	44.27	PSR	PLEC	1.284	6.77 × 10^–6	2.47	—	257.2	5.4
J2032.2+4127	PSR J2032+4127	308.06	41.46	PSR	PLEC	2.918	3.31 × 10^–6	2.26	—	272.2	47.2
J2035.0+3632	PSR J2034+3632	308.76	36.54	MSP	PLEC	2.456	5.99 × 10^–7	2.17	—	289.5	11.3
J2043.3+1711	PSR J2043+1711	310.84	17.19	MSP	PLEC	1.222	3.47 × 10^–6	2.10	—	247.9	20.9
J2055.8+2540	PSR J2055+2539	313.96	25.67	PSR	PLEC	1.279	8.39 × 10^–6	2.18	—	287.7	26.6
J2111.4+4606	PSR J2111+4606	317.86	46.10	PSR	PLEC	1.305	4.84 × 10^–6	2.26	—	245.4	11.9
J2214.6+3000	PSR J2214+3000	333.67	30.01	MSP	PLEC	1.090	5.97 × 10^–6	2.06	—	295.1	28.8
J2301.9+5855e	CTB 109	345.49	58.92	SNR	LP	3.461	1.57 × 10^–7	1.91	0.054	119.2	6.8
J2302.7+4443	PSR J2302+4442	345.69	44.72	MSP	PLEC	2.049	2.04 × 10^–6	2.02	—	254.5	55.8
J2304.0+5406e	—	346.01	54.11	—	LP	14.034	1.58 × 10^–8	1.76	0.127	175.6	18.0
J2323.4+5849	Cas A	350.86	58.82	snr	LP	2.232	1.38 × 10^–6	1.87	0.076	120.5	20.9

下载: 导出CSV

map

[1]	Hinton J A 2004 New Astron. Rev. 48 331 Google Scholar
[2]	Albert J, Aliu E, Anderhub H 2008 Astrophys. J. 674 1037 Google Scholar
[3]	Holder J, Acciari V, Aliu E 2008 4th International Symposium on High Energy Gamma-Ray Astronomy, Heidelberg, Germany, July 7–11, p657
[4]	CTA Consortium 2018 Science with the Cherenkov Telescope Array (Singapore: World Scientific) pp11–26
[5]	Ellison D C, Drury L O’C, Meyer J P 1997 Astrophys. J. 487 197 Google Scholar
[6]	Gaensler B M, Slane P O 2006 Annu. Rev. Astron. Astr. 44 17 Google Scholar
[7]	Abdalla H, Abramowski A, Aharonian F 2018 Astron. Astrophys. 612 A1 Google Scholar
[8]	Abeysekara A U, Archer A, Aune T 2018 Astrophys. J. 861 134 Google Scholar
[9]	Albert A, Alfaro R, Alvarez C 2020 Astrophys. J. 905 76 Google Scholar
[10]	Antonucci R 1993 Annu. Rev. Astron. Astr. 31 473 Google Scholar
[11]	Urry C M, Padovani P 1995 Publ. Astron. Soc. Pac. 107 803 Google Scholar
[12]	Sikora M, Begelman M C, Rees M J 1994 Astrophys. J. 421 153 Google Scholar
[13]	Aharonian F 2000 New. Astron. 5 377 Google Scholar
[14]	Mücke A, Protheroe R J, Engel R, Rachen J P, Stanev T 2003 Astropart. Phys. 18 593 Google Scholar
[15]	Mannheim K, Biermann P L 1989 Astron. Astrophys. 221 211
[16]	Mannheim K 1998 Science 279 684 Google Scholar
[17]	Böttcher M, Reimer A, Sweeney K, Prakash A 2013 Astrophys. J. 768 54 Google Scholar
[18]	Urry C M 1999 Astropart. Phys. 11 159 Google Scholar
[19]	Abdo A A, Ackermann M, Agudo I 2010 Astrophys. J. 716 30 Google Scholar
[20]	Abdo A A, Ackermann M, Ajello M 2010 Astrophys. J. 715 429 Google Scholar
[21]	Xin G G, Yao Y H, Qian X L 2021 Astrophys. J. 923 112 Google Scholar
[22]	Qian X L, Sun H Y, Chen T L 2022 Front. Phys.-Beijing 17 64602 Google Scholar
[23]	Qian X L, Sun H Y, Chen T L 2023 Acta Phys. Sin. 72 049501 [钱祥利, 孙惠英, 陈天禄 2023 72 049501 Google Scholar Qian X L, Sun H Y, Chen T L 2023 Acta Phys. Sin. 72 049501 Google Scholar
[24]	Ajello M, Atwood W B, Baldini L 2017 Astrophys. J. Suppl. S. 232 18 Google Scholar
[25]	Aleksić J, Ansoldi S, Antonelli L A 2016 Astropart. Phys. 72 76 Google Scholar
[26]	Bartoli B, Bernardini P, Bi X J 2013 Astrophys. J. 779 27 Google Scholar
[27]	Abeysekara A U, Alfaro R, Alvarez C 2013 Astropart. Phys. 50 26
[28]	Amenomori M, Bi X J, Chen D 2009 Astrophys. J. 692 61 Google Scholar
[29]	Ma X H, Bi Y J, Cao Z 2022 Chin. Phys. C 46 030001 Google Scholar
[30]	Cai H, Zhang Y, Liu C 2017 J. Instrum. 12 09023
[31]	Chen T L, Liu C, Gao Q 2019 Nucl. Instrum. Meth. A 927 46 Google Scholar
[32]	Atwood W B, Abdo A A, Ackermann M 2009 Astrophys. J. 697 1071 Google Scholar
[33]	Abdollahi S, Acero F, Baldini L 2022 Astrophys. J. Suppl. S. 260 53 Google Scholar
[34]	Ajello M, Baldini L, Ballet J 2022 Astrophys. J. Suppl. S. 263 24 Google Scholar
[35]	Abdollahi S, Acero F, Ackermann M 2020 Astrophys. J. Suppl. S. 247 33 Google Scholar
[36]	Ajello M, Angioni R, Axelsson M 2020 Astrophys. J. 892 105 Google Scholar
[37]	Gilmore R C, Somerville R S, Primack J R, Domínguez A 2012 Mon. Not. R. Astron. Soc. 422 3189 Google Scholar
[38]	Domínguez A, Primack J R, Rosario D J 2011 Mon. Not. R. Astron. Soc. 410 2556 Google Scholar
[39]	Patel S, Maier G, Kaaret P 2021 arXiv: 210806424 [astro-ph.HE
[40]	Ghisellini G, Righi C, Costamante L, Tavecchio F 2017 Mon. Not. R. Astron. Soc. 469 255 Google Scholar
[41]	Abdalla H, Abe H, Acero F 2021 J. Cosmol. Astropart. P. 2021 048 Google Scholar
[42]	Amenomori M, Ayabe S, Chen D 2005 Astrophys. J. 633 1005 Google Scholar
[43]	Aliu E, Archambault S, Arlen T 2012 Astrophys. J. 750 94 Google Scholar
[44]	Abramowski A, Acero F, Aharonian F 2012 Astron. Astrophys. 538 A103 Google Scholar
[45]	Abramowski A, Acero F, Aharonian F 2013 Mon. Not. R. Astron. Soc. 434 1889 Google Scholar
[46]	Aleksić J, Antonelli L A, Antoranz P 2011 Astrophys. J. Lett. 730 L8 Google Scholar
[47]	Aharonian F, Akhperjanian A G, Bazer-Bachi A R 2007 Astron. Astrophys. 470 475 Google Scholar
[48]	Aharonian F, Akhperjanian A G, de Almeida U B 2007 Astron. Astrophys. 475 L9 Google Scholar
[49]	Aleksić J, Ansoldi S, Antonelli L A 2014 Science 346 1080 Google Scholar
[50]	H.E.S.S. Collaboration 2020 Nature 582 356 Google Scholar
[51]	VERITAS Collaboration, VLBA 43 GHz M87 Monitoring Team, H.E.S.S. Collaboration, MAGIC Collaboration 2009 Science 325 444 Google Scholar
[52]	Acero F, Aharonian F, Akhperjanian A G 2009 Science 326 1080 Google Scholar
[53]	Abdalla H, Aharonian F, Benkhali F A 2018 Astron. Astrophys. 617 A73 Google Scholar
[54]	Acciari V A, Aliu E, Arlen T 2009 Nature 462 770 Google Scholar
[55]	Abdo A A, Ackermann M, Ajello M 2010 Astrophys. J. Lett. 709 L152 Google Scholar

[1]	钱祥利, 孙惠英, 陈天禄, 单增罗布, 冯有亮, 高启, 苟全补, 郭义庆, 胡红波, 康明铭, 厉海金, 刘成, 刘茂元, 刘伟, 乔冰强, 王旭, 王振, 辛广广, 姚玉华, 袁强, 张毅. HADAR实验对活动星系核伽马射线辐射观测的预期研究. , 2023, 72(4): 049501. doi: 10.7498/aps.72.20221976
[2]	熊俊, 安红海, 王琛, 张振驰, 矫金龙, 雷安乐, 王瑞荣, 胡广月, 王伟, 孙今人. 长短脉冲联合驱动双层结构靶优化伽马射线的产生. , 2022, 71(21): 215201. doi: 10.7498/aps.71.20212042
[3]	任杰, 阮锡超, 陈永浩, 蒋伟, 鲍杰, 栾广源, 张奇玮, 黄翰雄, 王朝辉, 安琪, 白怀勇, 鲍煜, 曹平, 陈昊磊, 陈琪萍, 陈裕凯, 陈朕, 崔增琪, 樊瑞睿, 封常青, 高可庆, 顾旻皓, 韩长材, 韩子杰, 贺国珠, 何泳成, 洪杨, 黄蔚玲, 黄锡汝, 季筱璐, 吉旭阳, 江浩雨, 姜智杰, 敬罕涛, 康玲, 康明涛, 李波, 李超, 李嘉雯, 李论, 李强, 李晓, 李样, 刘荣, 刘树彬, 刘星言, 穆奇丽, 宁常军, 齐斌斌, 任智洲, 宋英鹏, 宋朝晖, 孙虹, 孙康, 孙晓阳, 孙志嘉, 谭志新, 唐洪庆, 唐靖宇, 唐新懿, 田斌斌, 王丽娇, 王鹏程, 王琦, 王涛峰, 文杰, 温中伟, 吴青彪, 吴晓光, 吴煊, 解立坤, 羊奕伟, 易晗, 于莉, 余滔, 于永积, 张国辉, 张林浩, 张显鹏, 张玉亮, 张志永, 赵豫斌, 周路平, 周祖英, 朱丹阳, 朱科军, 朱鹏. 中国散裂中子源反角白光中子源束内伽马射线研究. , 2020, 69(17): 172901. doi: 10.7498/aps.69.20200718
[4]	强鹏飞, 盛立志, 李林森, 闫永清, 刘哲, 周晓红. X射线聚焦望远镜光学设计. , 2019, 68(16): 160702. doi: 10.7498/aps.68.20190709
[5]	王瑞荣, 安红海, 熊俊, 谢志勇, 王伟. 准单色近平行光束的X射线源. , 2018, 67(24): 240701. doi: 10.7498/aps.67.20180861
[6]	王研, 刘鑫, 黄万霞, 易明皓, 郭金川, 朱佩平. 更正：线焦斑X射线源成像[ 2016，65，219501]. , 2017, 66(8): 089901. doi: 10.7498/aps.66.089901
[7]	朱玥, 张子良, 杨彦佶, 薛荣峰, 崔苇苇, 陆波, 王娟, 陈田祥, 王于仨, 李炜, 韩大炜, 霍嘉, 胡渭, 李茂顺, 张艺, 祝宇轩, 刘苗, 赵晓帆, 陈勇. 硬X射线调制望远镜低能探测器量子效率标定. , 2017, 66(11): 112901. doi: 10.7498/aps.66.112901
[8]	牟欢, 李保权, 曹阳. 基于空间应用的透射式微型微束调制X射线源. , 2016, 65(14): 140703. doi: 10.7498/aps.65.140703
[9]	颜召军, 陈欣扬, 郑立新, 丁媛媛, 朱能鸿. 基于色散干涉图像的拼接望远镜共相零位标定方法研究. , 2016, 65(19): 199501. doi: 10.7498/aps.65.199501
[10]	刘鑫, 易明皓, 郭金川. 线焦斑X射线源成像. , 2016, 65(21): 219501. doi: 10.7498/aps.65.219501
[11]	于树海, 董磊, 刘欣悦, 凌剑勇. 傅里叶望远镜重构图像虚像分析. , 2015, 64(18): 184205. doi: 10.7498/aps.64.184205
[12]	颜召军, 陈欣扬, 杨朋千, 周丹, 郑立新, 朱能鸿. 基于光栅色散干涉条纹的菲佐光干涉望远镜共相检测方法研究. , 2015, 64(14): 149501. doi: 10.7498/aps.64.149501
[13]	廖宏宇, 马晓燠, 郭友明, 饶长辉, 魏凯. 基于AR模型搜索迭代算法的望远镜跟踪误差分析. , 2014, 63(17): 179501. doi: 10.7498/aps.63.179501
[14]	欧建文, 张皓晶, 郑永刚, 张雄. 耀变体S5 0716+714的混沌特性研究. , 2014, 63(4): 049801. doi: 10.7498/aps.63.049801
[15]	黄开, 闫文超, 李明华, 陶孟泽, 陈燕萍, 陈洁, 远晓辉, 赵家瑞, 马勇, 李大章, 高杰, 陈黎明, 张杰. kHz激光与固体靶相互作用产生的X射线源. , 2013, 62(20): 205204. doi: 10.7498/aps.62.205204
[16]	王剑, 赵宗清, 蔡达锋, 黄文忠, 何颖玲, 谷渝秋. Kα射线源半影成像研究. , 2009, 58(10): 7074-7078. doi: 10.7498/aps.58.7074
[17]	徐光, 钱列加, 王韬, 朱鹤元, 范滇元. 用于超短脉冲扩展的时间望远镜. , 2004, 53(1): 93-98. doi: 10.7498/aps.53.93
[18]	孙可煦, 易荣清, 杨家敏, 王红斌, 马洪良, 陈正林, 黄天暄, 崔延莉, 郑志坚, 唐道源, 丁永坤, 温树槐, 江文勉, 赵永宽, 崔明启, 黎刚, 崔聪悟, 唐鄂生. 同步辐射软X射线源用于软X射线探测元件定标. , 1997, 46(4): 650-655. doi: 10.7498/aps.46.650
[19]	吴承伟, 郭杏林. 直流电场中电流变体单链的电学行为及剪切强度. , 1997, 46(8): 1500-1507. doi: 10.7498/aps.46.1500
[20]	张毅波. 切伦科夫自由电子激光中自发辐射与受激辐射的关系. , 1987, 36(10): 1344-1348. doi: 10.7498/aps.36.1344

计量

文章访问数: 3407
PDF下载量: 57
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板