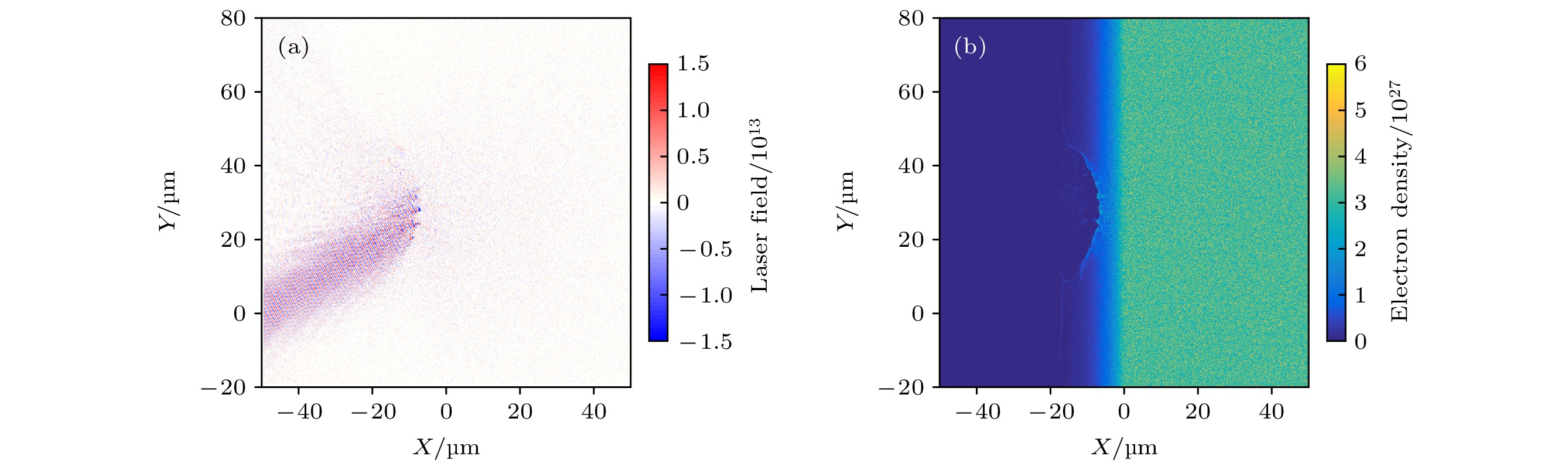
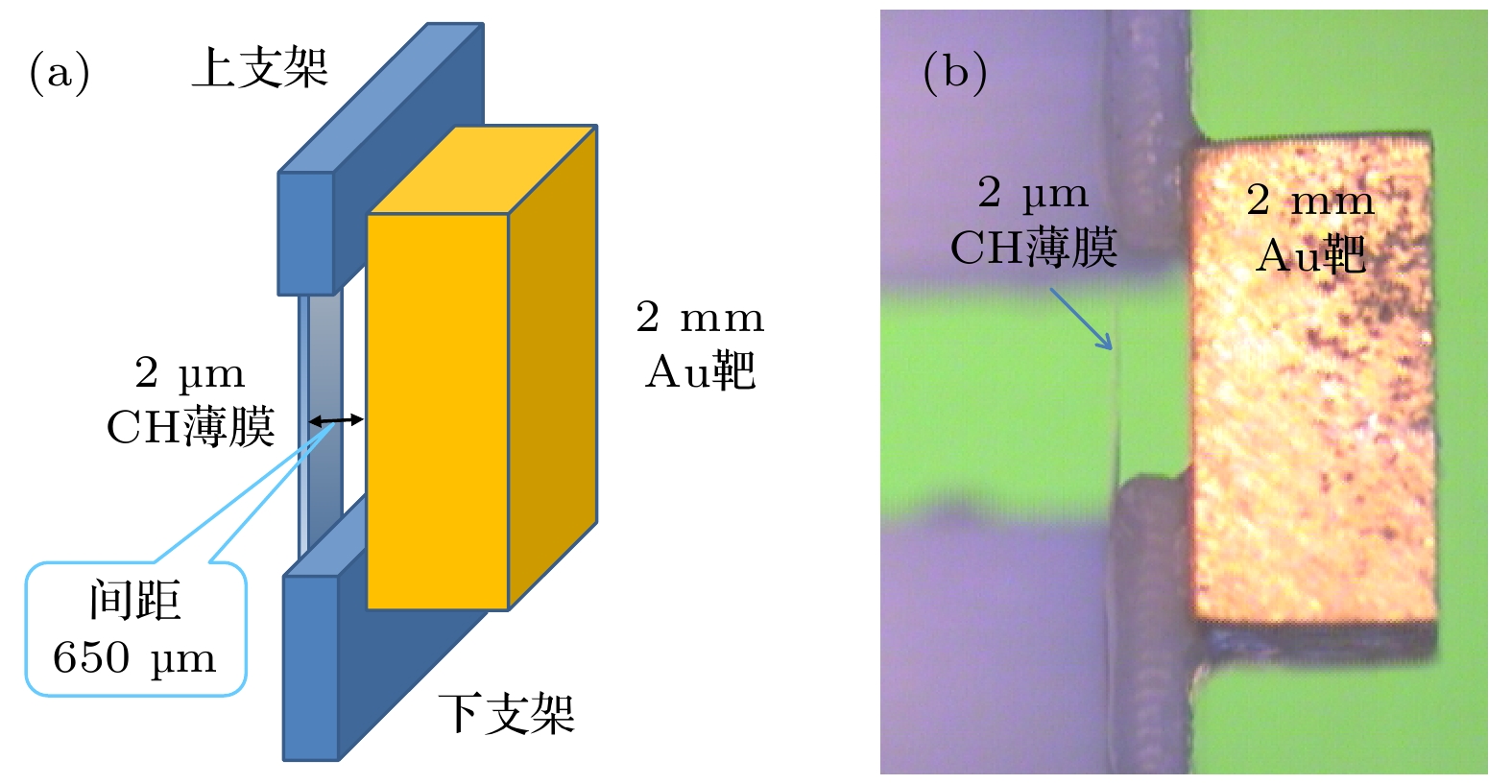
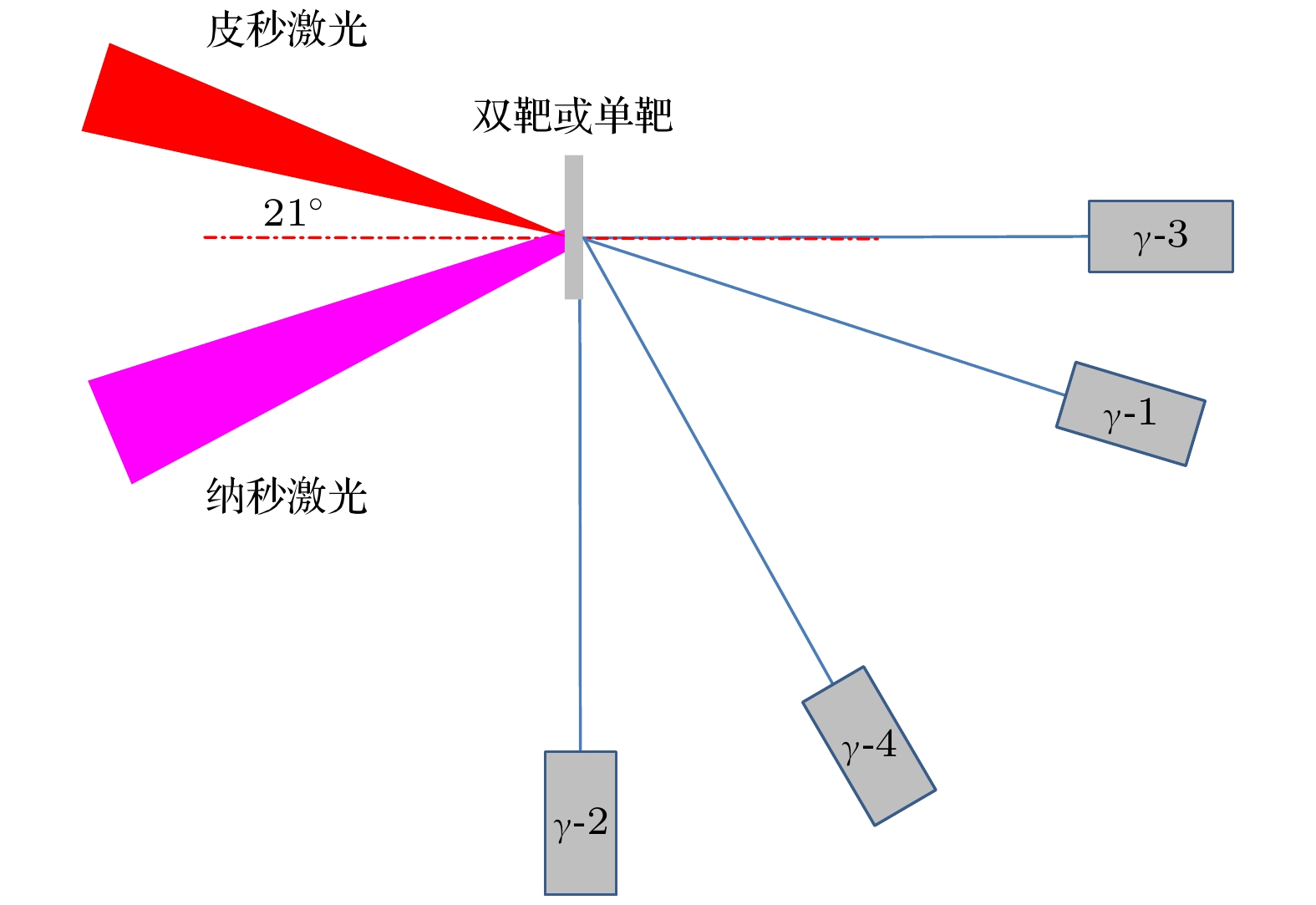
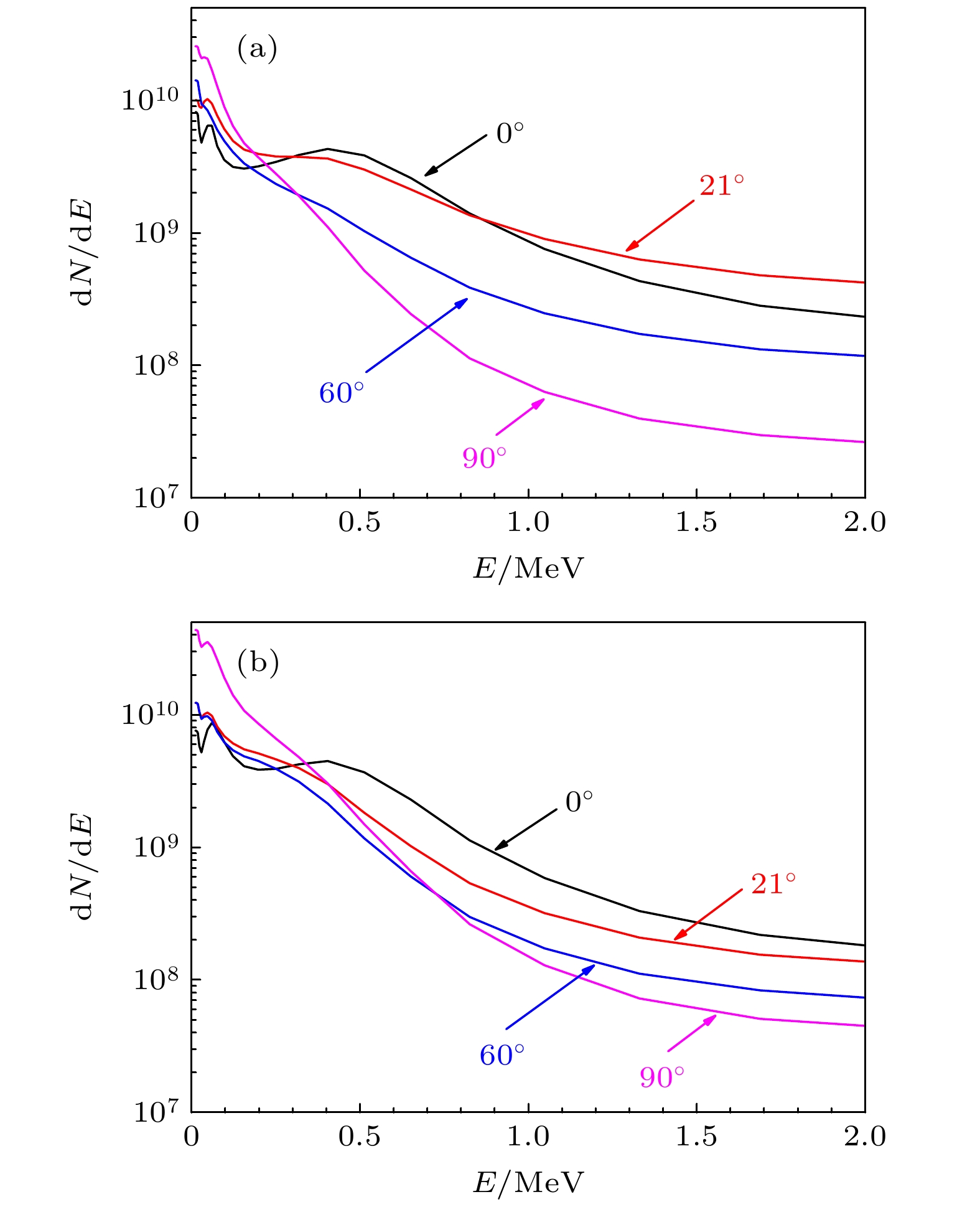
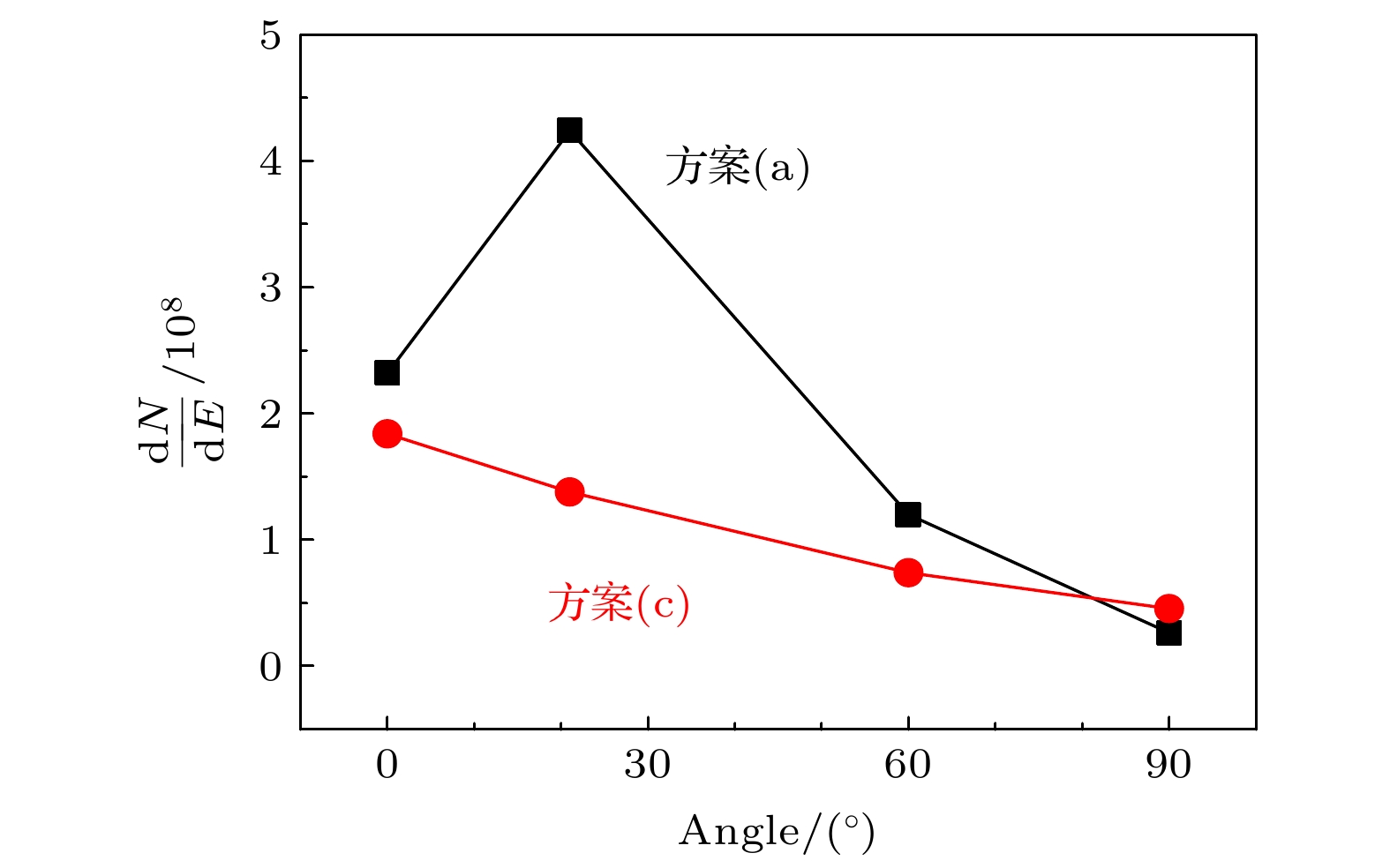
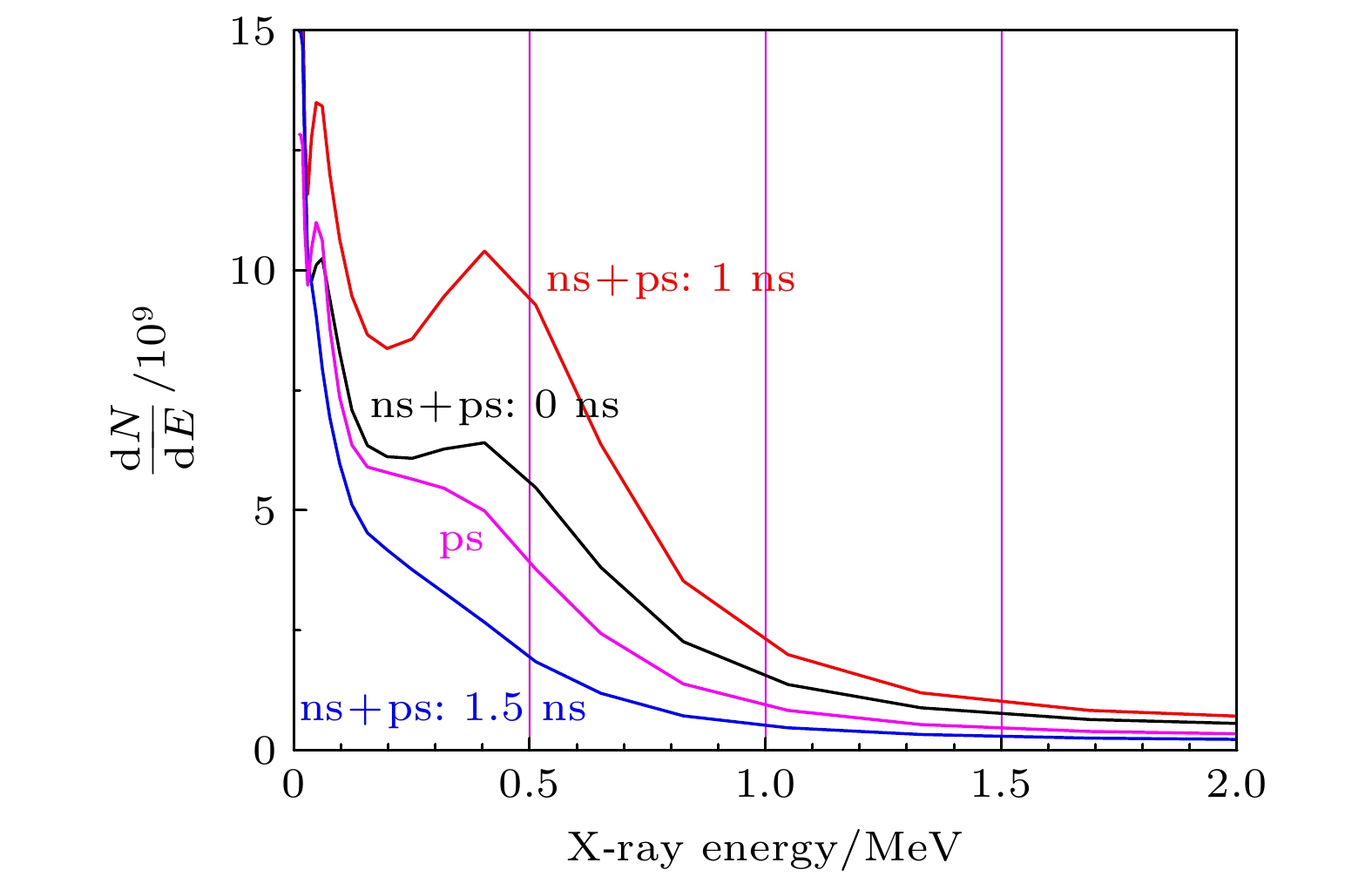
-
在神光-Ⅱ升级及皮秒拍瓦激光装置上, 开展了长短脉冲联合驱动双层结构靶优化伽马射线产生的实验研究. 一束纳秒长脉冲激光预先烧蚀第一层碳氢薄膜靶, 产生等离子体, 经一定时间的自由膨胀后, 形成较大尺度的低密度等离子体. 第二束皮秒短脉冲激光与低密度等离子体相互作用, 通过光场直接加速等非线性加速机制, 将电子加速到相对论量级. 相对论电子束经过传输后在第二层金转换靶上通过轫致辐射的方式产生伽马射线. 该方案能够有效提升超强超短脉冲激光加速产生的相对论电子束流品质, 获得能量更高、发散度更小的相对论电子束, 进而有可能获得品质更高的伽马射线输出.In order to verify that the large-scale low-density plasma has a significant gain effect on the quality of the ultra-hot electron beam in ultra-strong ultra-short pulse laser interactions with matter, on the Shenguang-II upgraded laser facility, we carry out an experimental study on the optimization of relativistic electron beams that combine long and short pulse lasers to generate large-scale low-density pre-plasma. A nanosecond laser is used to ablate the thin hydrocarbon film. After a period of time, a large-scale low-density plasma is formed. The second picosecond short pulse laser then interacts with the formed low-density plasma, and accelerates the electrons to the relativity magnitude. Through the comparative analysis between different experimental conditions in the experiment, it is found that the existence of large-scale low-density plasma significantly increases the intensity of the relativistic electron beam along the laser propagation direction. In the comparative test of three shooting methods (long and short pulse combined driving double-layer target, short pulse driving double-layer target, short pulse driving single-layer target), we find that the energy bands above 1 MeV can be produced by the long pulse and the short pulse jointly driving double-layer target. The gamma-ray intensity is nearly twice that of the other two schemes. In addition, we also find in the experiment that when the time interval between nanosecond-picosecond pulses changes, the pre-plasma electron density and density scale length of the CH film irradiated by the nanosecond laser will be different. When the time interval is 0 ns, the expansion of the plasma is still insufficient, and the density distribution of the pre-plasma is steep. Part of the picosecond laser energy will be reflected at the critical density surface. Insufficient absorption of picosecond laser energy reduces the generation of relativistic electrons.When the time interval is 1 ns, the plasma state is more appropriate. The picosecond laser will form a self-focusing plasma channel in the plasma, thereby efficiently depositing energy, breaking through the energy limit of ponderomotive force acceleration, and obtaining more higher energy relativistic electrons. When the time interval is longer, such as 1.5 ns or more, the plasma can be fully expanded, the electron density becoming too low. Most of the picosecond laser will pass through the pre-plasma, affecting energy deposition and failing to generate more relativistic electrons.
[1] Glinec Y, Faure J, Dain L L, Darbon S, Hosokai T, Santos J J, Lefebvre E, Rousseau J P, Burgy F, Mercier B, Malka V 2005 Phys. Rev. Lett. 94 025003
Google Scholar
[2] Sarri G, Corvan D J, Schumaker W, Cole J M, Piazza A D, Ahmed H, Harvey C, Keitel C H, Krushelnick K, Mangles S P D, Najmudin Z, Symes D, Thomas A G R, Yeung M, Zhao Z, Zepf M 2014 Phys. Rev. Lett. 113 224801
Google Scholar
[3] Ben-Ismail A, Lundh O, Rechatin C, Lim J K, Faure J, Corde S, Malka V 2011 Appl. Phys. Lett. 98 264101
Google Scholar
[4] Sarri G, Schumaker W, Piazza A D, Vargas M, Dromey B, Dieckmann M E, Chvykov V, Maksimchuk A, Yanovsky V, He Z H, Hou B X, Nees J A, Thomas A G R, Keitel C H, Zepf M, Krushelnick K 2013 Phys. Rev. Lett. 110 255002
Google Scholar
[5] Schlenvoigt H P, Haupt K, Debus A, Budde F, Jaroszynski D A 2008 Nat. Phys. 4 130
Google Scholar
[6] Giulietti A, Bourgeois N, Ceccotti T, Davoine X, Dobosz S, D’Oliveira P, Galimberti M, Galy J, Gamucci A, Giulietti D, Gizzi L A, Hamilton D J, Lefebvre E, Labate L, Marquès J R, Monot P, Popescu H, Réau F, Sarri G, Tomassini P, Martin P 2008 Phys. Rev. Lett. 101 105002
Google Scholar
[7] Pomerantz I, McCary E, Meadows A R, Arefiev A, Bernstein A C, Chester C, Cortez J, Donovan M E, Dyer G, Gaul E W, Hamilton D, Kuk D, Lestrade A C, Wang C, Ditmire T, Hegelich B M 2014 Phys. Rev. Lett. 113 184801
Google Scholar
[8] Cowan T E, Hunt A W, Phillips T W, Wilks S C, Perry M D, Brown C, Fountain W, Hatchett S, Johnson J, Key M H, Parnell T, Pennington D M, Snavely R A, Takahashi Y 2000 Phys. Rev. Lett. 84 903
Google Scholar
[9] Sorokovikova A, Arefiev AV, Mcguffey C, Qiao B, Robinson A P L, Wei H S, Mclean H S, Beg F N 2016 Phys. Rev. Lett. 116 155001
Google Scholar
[10] Malka G, Miquel J L 1996 Phys. Rev. Lett. 77 75
Google Scholar
[11] Pukhov A, Meyer-ter-Vehn J 1998 Phys. Plasmas 5 1880
Google Scholar
[12] Culfa O, Tallents G J, Wagenaars E, Ridgers C P, Dance R J, Rossall A K, Gray R J, McKenna P, Brown C D R, James S F, Hoarty D J, Booth N, Robinson A P L, Lancaster K L, Pikuz S A, Faenov A Y, Kampfer T, Schulze K S, Uschmann I, Woolsey N S 2014 Phys. Plasmas 21 043106
Google Scholar
[13] Ting A, Moore C I, Krushelnick K, Manka C, Esarey E, Sprangle P, Hubbard R, Burris H R, Fischer R, Baine M 1997 Phys. Plasmas 4 1889
Google Scholar
[14] Arber T D, Bennett K, Brady C S, Lawrence-Douglas A, Ramsay M G, Sircombe N J, Gillies P, Evans R G, Schmitz H, Bell A R, Ridgers C P 2015 Plasma Phys. Control. Fusion 57 113001
Google Scholar
[15] Gibbon P, Andreev A A, Platonov K Y 2012 Plasma Phys. Control. Fusion 54 045001
Google Scholar
[16] Young P E, Hammer J H, Wilks S C, Kruer W L 1995 Phys. Plasmas 2 2825
Google Scholar
[17] Sarri G, Dieckmann M E, Brown C R D, Cecchetti C A, Hoarty D J, James S F, Jung R, Kourakis I, Schamel H, Willi O, Borghesi M 2010 Phys. Plasmas 17 010701
Google Scholar
[18] Friou A, Lefebvre E, Gremillet L 2012 Phys. Plasmas 19 022704
Google Scholar
[19] Pukhov A, Meyer-Ter-Vehn J N 1996 Phys. Rev. Lett. 76 3975
Google Scholar
[20] Lasinski B F, Langdon A B, Hatchett S P, Key M H, Tabak M 1999 Phys. Plasmas 6 2041
Google Scholar
[21] Li G, Yan R, Ren C, Wang T L, Tonge J, Mori W B 2008 Phys. Rev. Lett. 100 125002
Google Scholar
[22] Arefiev A V, Robinson A, Khudik V N 2015 Phys. Plasmas 81 475810404
Google Scholar
[23] Arefiev A V, Khudik VN, Robinson A, Shvets G, Willingale L, Schollmeier M 2016 Phys. Plasmas 23 056309
Google Scholar
-
图 1 针对出射电子束测量的实验方案示意图 (a)单皮秒激光驱动平面薄膜靶方式; (b)纳秒、皮秒长短脉冲联合驱动平面薄膜靶方式
Fig. 1. Experimental scheme for the measurement of outgoing electron beams: (a) A film target driven by a single ps laser; (b) a film target jointly driven by long ps and short ns pulse lasers.
图 2 由EMS1测量得到的单发次激光入射方向的电子能谱图像 (a)单皮秒激光驱动平面靶; (b) 纳秒、皮秒长短脉冲联合驱动平面靶
Fig. 2. Electron energy spectrum image of the laser incident direction measured by EMS1: (a) A film target driven by a single ps laser; (b) a film target driven by ns and ps lasers.
图 3 由EMS1与EMS2记录图像处理之后的电子能谱分布曲线
Fig. 3. Electronic spectrum distribution curves recorded by EMS1 and EMS2.
图 4 针对带陡峭分布预等离子体层固体靶进行数值模拟的结果 (a)激光场分布; (b)电子密度分布
Fig. 4. Numerical simulation results of a solid target with a steeply distributed pre-plasma: (a) Laser field distribution; (b) electron density distribution.
图 5 针对低密度均匀等离子体进行数值模拟的结果 (a)激光场分布; (b)电子密度分布
Fig. 5. Numerical simulation results for low-density uniform plasma: (a) Laser field distribution; (b) electron density distribution.
图 6 两种情况对应的前向电子能谱模拟结果
Fig. 6. Simulation results of the forward electron spectrum corresponding to the two cases.
图 7 三种产生伽马射线的实验方案示意图 (a)长短脉冲联合驱动双靶; (b)单脉冲驱动双靶; (c)单脉冲驱动单靶
Fig. 7. Experimental schemes for generating gamma rays: (a) Dual targets driven by ns and ps lasers; (b) dual targets driven by a ps laser; (c) a target driven by a ps laser.
图 8 双靶结构示意图(a)及实物照片(b)
Fig. 8. Schematic diagram of dual target structure (a) and actual photo (b).
图 9 三种条件对应的单发次实验伽马射线的能谱分布, 其中a-1, b-1, c-1对应γ-1测量的数据, a-2, b-2, c-2对应γ-2测量的数据
Fig. 9. Spectrum distribution of gamma rays corresponding to the three conditions. a-1, b-1, and c-1 correspond to the data from γ-1, and a-2, b-2, and c-2 correspond to the data from γ-2.
图 10 伽马射线角分布的测量方案示意图
Fig. 10. Experimental schemes for measuring spatial distribution of gamma-ray.
图 11 不同方向测量得到的伽马射线能谱分布 (a)长短脉冲联合驱动双靶; (b)单脉冲驱动单靶
Fig. 11. Spatial distributions of gamma-ray energy spectra: (a) Dual targets driven by ns and ps lasers; (b) a target driven by a ps laser.
图 12 方案(a)与方案(c)的伽马射线能谱空间分布对比
Fig. 12. Comparison of spatial distributions of gamma-ray energy spectra between scheme-(a) and scheme-(c).
图 13 不同时间间隔条件下对应的伽马射线的能谱分布
Fig. 13. Spectrum distribution of gamma rays under different time interval.
表 1 不同能量处3种方案获得的伽马射线强度
Table 1. Gamma ray intensity obtained by the three schemes at different energies.
能量/MeV 伽马射线强度/108 a-1 b-1 c-1 (a – c)/c (b – c)/c 0.5 55.6 38.6 40.1 39% –3.7% 1.0 15.3 9.34 7.79 96% 20% 1.5 7.56 4.58 3.78 100% 21% 2.0 5.60 3.42 2.80 100% 22% 
下载: 导出CSV
-
[1] Glinec Y, Faure J, Dain L L, Darbon S, Hosokai T, Santos J J, Lefebvre E, Rousseau J P, Burgy F, Mercier B, Malka V 2005 Phys. Rev. Lett. 94 025003
Google Scholar
[2] Sarri G, Corvan D J, Schumaker W, Cole J M, Piazza A D, Ahmed H, Harvey C, Keitel C H, Krushelnick K, Mangles S P D, Najmudin Z, Symes D, Thomas A G R, Yeung M, Zhao Z, Zepf M 2014 Phys. Rev. Lett. 113 224801
Google Scholar
[3] Ben-Ismail A, Lundh O, Rechatin C, Lim J K, Faure J, Corde S, Malka V 2011 Appl. Phys. Lett. 98 264101
Google Scholar
[4] Sarri G, Schumaker W, Piazza A D, Vargas M, Dromey B, Dieckmann M E, Chvykov V, Maksimchuk A, Yanovsky V, He Z H, Hou B X, Nees J A, Thomas A G R, Keitel C H, Zepf M, Krushelnick K 2013 Phys. Rev. Lett. 110 255002
Google Scholar
[5] Schlenvoigt H P, Haupt K, Debus A, Budde F, Jaroszynski D A 2008 Nat. Phys. 4 130
Google Scholar
[6] Giulietti A, Bourgeois N, Ceccotti T, Davoine X, Dobosz S, D’Oliveira P, Galimberti M, Galy J, Gamucci A, Giulietti D, Gizzi L A, Hamilton D J, Lefebvre E, Labate L, Marquès J R, Monot P, Popescu H, Réau F, Sarri G, Tomassini P, Martin P 2008 Phys. Rev. Lett. 101 105002
Google Scholar
[7] Pomerantz I, McCary E, Meadows A R, Arefiev A, Bernstein A C, Chester C, Cortez J, Donovan M E, Dyer G, Gaul E W, Hamilton D, Kuk D, Lestrade A C, Wang C, Ditmire T, Hegelich B M 2014 Phys. Rev. Lett. 113 184801
Google Scholar
[8] Cowan T E, Hunt A W, Phillips T W, Wilks S C, Perry M D, Brown C, Fountain W, Hatchett S, Johnson J, Key M H, Parnell T, Pennington D M, Snavely R A, Takahashi Y 2000 Phys. Rev. Lett. 84 903
Google Scholar
[9] Sorokovikova A, Arefiev AV, Mcguffey C, Qiao B, Robinson A P L, Wei H S, Mclean H S, Beg F N 2016 Phys. Rev. Lett. 116 155001
Google Scholar
[10] Malka G, Miquel J L 1996 Phys. Rev. Lett. 77 75
Google Scholar
[11] Pukhov A, Meyer-ter-Vehn J 1998 Phys. Plasmas 5 1880
Google Scholar
[12] Culfa O, Tallents G J, Wagenaars E, Ridgers C P, Dance R J, Rossall A K, Gray R J, McKenna P, Brown C D R, James S F, Hoarty D J, Booth N, Robinson A P L, Lancaster K L, Pikuz S A, Faenov A Y, Kampfer T, Schulze K S, Uschmann I, Woolsey N S 2014 Phys. Plasmas 21 043106
Google Scholar
[13] Ting A, Moore C I, Krushelnick K, Manka C, Esarey E, Sprangle P, Hubbard R, Burris H R, Fischer R, Baine M 1997 Phys. Plasmas 4 1889
Google Scholar
[14] Arber T D, Bennett K, Brady C S, Lawrence-Douglas A, Ramsay M G, Sircombe N J, Gillies P, Evans R G, Schmitz H, Bell A R, Ridgers C P 2015 Plasma Phys. Control. Fusion 57 113001
Google Scholar
[15] Gibbon P, Andreev A A, Platonov K Y 2012 Plasma Phys. Control. Fusion 54 045001
Google Scholar
[16] Young P E, Hammer J H, Wilks S C, Kruer W L 1995 Phys. Plasmas 2 2825
Google Scholar
[17] Sarri G, Dieckmann M E, Brown C R D, Cecchetti C A, Hoarty D J, James S F, Jung R, Kourakis I, Schamel H, Willi O, Borghesi M 2010 Phys. Plasmas 17 010701
Google Scholar
[18] Friou A, Lefebvre E, Gremillet L 2012 Phys. Plasmas 19 022704
Google Scholar
[19] Pukhov A, Meyer-Ter-Vehn J N 1996 Phys. Rev. Lett. 76 3975
Google Scholar
[20] Lasinski B F, Langdon A B, Hatchett S P, Key M H, Tabak M 1999 Phys. Plasmas 6 2041
Google Scholar
[21] Li G, Yan R, Ren C, Wang T L, Tonge J, Mori W B 2008 Phys. Rev. Lett. 100 125002
Google Scholar
[22] Arefiev A V, Robinson A, Khudik V N 2015 Phys. Plasmas 81 475810404
Google Scholar
[23] Arefiev A V, Khudik VN, Robinson A, Shvets G, Willingale L, Schollmeier M 2016 Phys. Plasmas 23 056309
Google Scholar
下载:
计量
- 文章访问数: 3338
- PDF下载量: 51
- 被引次数: 0
