类铝离子钟跃迁能级的超精细结构常数和朗德<i>g</i>因子

王霞; 贾方石; 姚科; 颜君; 李冀光; 吴勇; 王建国

doi:10.7498/aps.72.20230940

摘要

本文利用多组态Dirac-Hartree-Fock方法计算了类铝等电子序列从Si⁺到Kr²³⁺离子基组态3s²3p ²P_{1/2, 3/2}能级的超精细结构常数和朗德g因子. 通过系统评估电子关联效应对Si⁺和Co¹⁴⁺离子中所关心原子参数的影响, 尤其是与内壳层电子相关的关联效应, 构建了可靠精确的计算模型, 除Si⁺离子外, 超精细结构常数和g因子的计算误差分别控制在1%左右和10^–5的量级. 此外, 进一步分析了超精细结构常数中电子部分矩阵元和g因子随原子序数Z的变化规律, 并拟合了这些物理量与Z的定量依赖关系, 利用拟合公式可以快速计算类铝离子在14 ≤ Z ≤ 54区间内任意同位素的超精细结构常数和g因子.

关键词:

Abstract

The highly charged Al-like ions are the potential candidates for the next-generation atomic optical clocks, and their atomic parameters are also useful in plasma and nuclear physics. In the present work, the hyperfine interaction constants and Landé g factors of 3s²3p ²P_{1/2, 3/2} states in the ground configuration for Al-like ions in a range between Si⁺ and Kr²³⁺ ions are calculated by using the multi-configuration Dirac-Hartree-Fock method. Owing to the fact that hyperfine interaction constant is sensitive to electron correlation effects, we systematically investigate its influence on the hyperfine interaction constants, particularly for the high-order correlation related to the 2p electrons. According to this investigation and by taking into account the Breit interaction and QED corrections, we achieve the computational accuracy at a level of 1% and 10^–5 for the hyperfine interaction constants and Landé g factors, respectively, except for the Si⁺ ion. Furthermore, the electronic parts of hyperfine interaction constants and g factors are fitted with functions of atomic number. The deviations between these fitted formulas and the ab initio calculations are less than 2% and 10^–5 for the hyperfine interaction constants and the g factors, respectively. As a result, the hyperfine interaction constants and g factors of all isotopes can be determined for Al-like ions with 14 ≤ Z ≤ 54.

Keywords:

hyperfine structure constant /
Landé g factor /
multi-configuration Dirac-Hartree-Fock method /
electron correlation effect /
Al-like ions

作者及机构信息

1.
北京应用物理与计算数学研究所, 计算物理重点实验室, 北京　100088

2.
复旦大学, 核物理与离子束应用教育部重点实验室, 上海　200433

3.
北京大学工学院, 应用物理与技术研究中心, 北京　100871

通信作者: 李冀光, li_jiguang@iapcm.ac.cn

基金项目: 国家自然科学基金(批准号: 11874090)资助的课题.

Authors and contacts

1.
National Key Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing 100088, China

2.
Key Laboratory of Nuclear Physics and Ion-beam Application, Fudan University, Shanghai 200433, China

3.
Center for Applied Physics and Technology, College of Engineering, Peking University, Beijing 100871, China

Corresponding author: Li Ji-Guang, li_jiguang@iapcm.ac.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11874090).

文章全文 : translate this paragraph

参考文献

[1]	Safronova M S, Budker D, DeMille D, Kimball D F J, Derevianko A, Clark C W 2018 Rev. Mod. Phys. 90 025008 Google Scholar
[2]	Zhang B L, Huang Y, Zhang H Q, Hao Y M, Zeng M Y, Guan H, Gao K L 2020 Chin. Phys. B 29 074209 Google Scholar
[3]	Brewer S M, Chen J S, Hankin A M, Clements E R, Chou C W, Wineland D J, Hume D B, Leibrandt D R 2019 Phys. Rev. Lett. 123 033201 Google Scholar
[4]	Kozlov M G, Safronova M S, López-Urrutia J R C, Schmidt P O 2018 Rev. Mod. Phys. 90 045005 Google Scholar
[5]	Derevianko A, Dzuba V A, Flambaum V V 2012 Phys. Rev. Lett. 109 180801 Google Scholar
[6]	Dzuba V A, Derevianko A, Flambaum V V 2012 Phys. Rev. A 86 054501 Google Scholar
[7]	Dzuba V A, Flambaum V V 2017 Highly Charged Ions for Atomic Clocks and Search for Variation of the Fine Structure Constant (In: Wada M, Schury P, Ichikawa Y (eds) TCP 2014 Springer, Cham.) p79
[8]	Yudin V I, Taichenachev A V, Derevianko A 2014 Phys. Rev. Lett. 113 233003 Google Scholar
[9]	Yu Y, Sahoo B K 2016 Phys. Rev. A 94 062502 Google Scholar
[10]	Li J G, Godefroid M, Wang J G 2016 J. Phys. B: At. Mol. Opt. Phys. 49 115002 Google Scholar
[11]	Lu B, Zhang T X, Chang H, Li J G, Wu Y, Wang J G 2019 Phys. Rev. A 100 012504 Google Scholar
[12]	Goyal A, Khatri I, Singh A K, Mohan M, Sharma R, Singh N 2016 Atoms 4 22 Google Scholar
[13]	Beiersdorfer P, Träbert E, Pinnington E H 2003 Astrophys. J. 587 836 Google Scholar
[14]	Schiffmann S, Brage T, Judge P G, Paraschiv A R, Wang K 2021 Astrophys. J 923 186 Google Scholar
[15]	Booth A J, Blackwell D E 1983 Mon. Not. R. Astro. Soc. 204 777 Google Scholar
[16]	Roederer I U, Lawler J E 2021 Astrophys. J. 912 119 Google Scholar
[17]	Grant I P 2007 Relativistic Quantum Theory of Atoms and Molecules-Theory and Computation (New York: Springer) p393
[18]	Dyall K G, Grant I P, Johnson C T, Parpia F A, Plummer E P 1989 Comput. Phys. Commun. 55 425 Google Scholar
[19]	Jönsson P, Parpia F A, Fischer C F 1996 Comput. Phys. Commun. 96 301 Google Scholar
[20]	Cheng K T, Childs W J 1985 Phys. Rev. A 31 2775 Google Scholar
[21]	Froese C F, Gaigalas G, Jönsson P, Bierón J 2019 Comput. Phys. Commun. 237 184 Google Scholar
[22]	Zhang T X, Xie L Y, Li J G, Lu Z H 2017 Phys. Rev. A 96 012514 Google Scholar
[23]	Li J G, Jönsson P, Godefroid M, Dong C Z, Gaigalas G 2012 Phys. Rev. A 86 052523 Google Scholar
[24]	Kramida A, Ralchenko Yu, Reader J, NIST ASD Team 2022 NIST Atomic Spectra Database
[25]	Stone N J 2005 At. Data Nucl. Data Tables 90 75 Google Scholar
[26]	Pyykkö P 2008 Mol. Phys. 106 1965 Google Scholar

施引文献

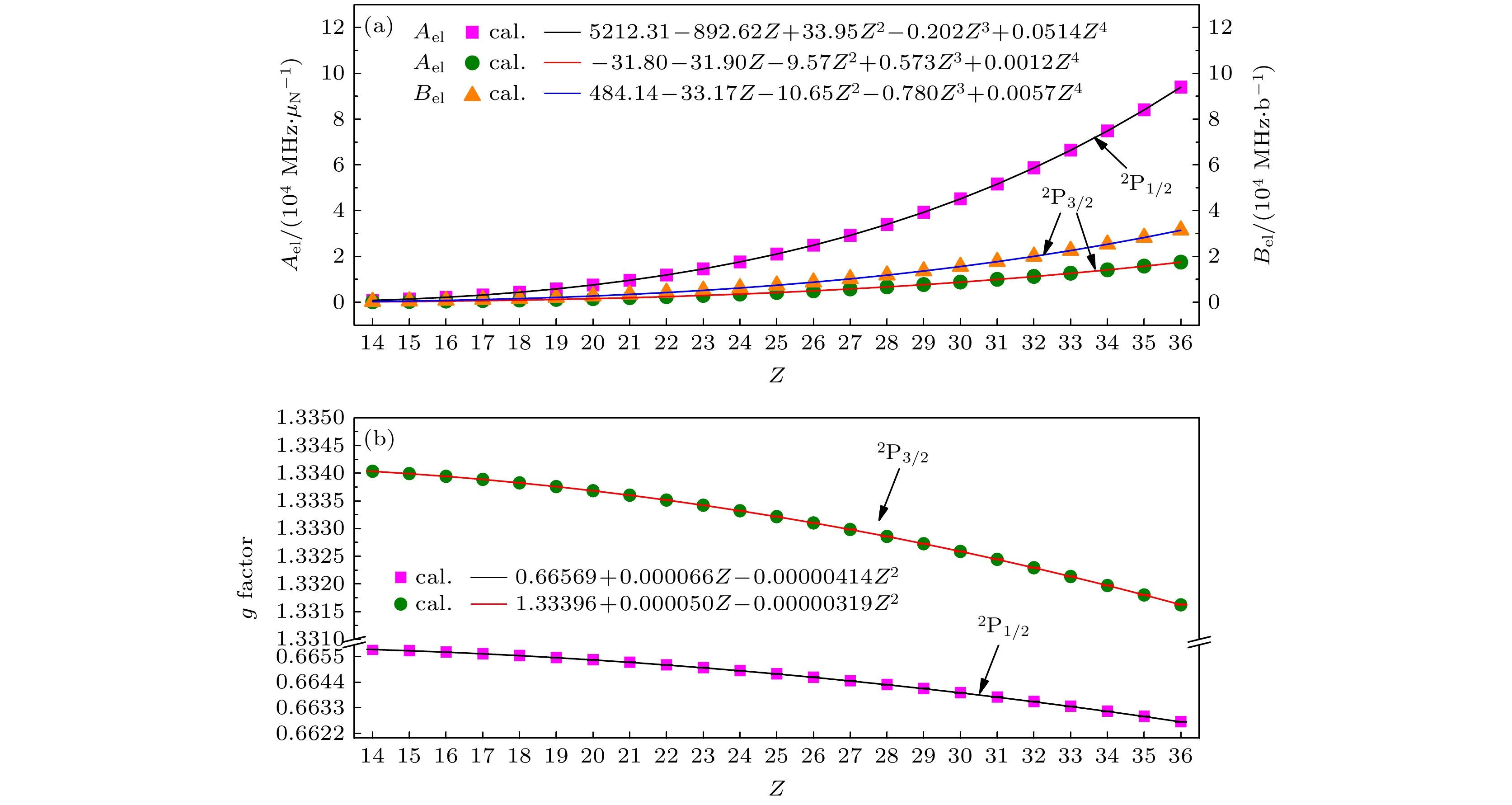
图 1 类铝等电子序列3s²3p ²P_{1/2, 3/2}能级的(a)超精细结构常数电子部分矩阵元A_el和B_el以及(b)朗德g因子随原子序数Z的变化关系. 图中实线表示由拟合公式得出的结果, 散点表示用MCDHF方法从头计算的结果

Fig. 1. (a) Electronic parts of hyperfine structure constants and (b) Landé g factors of 3s²3p ²P_{1/2, 3/2} states of Al-like isoelectronic sequence ions as functions of atomic number. The solid line represents these results obtained by from numerical fitting formula, and the discrete point represents these results obtained by our ab initio calculation using MCDHF method.

下载: 全尺寸图片幻灯片

表 1 Si⁺和Co¹⁴⁺离子3s²3p ²P_{1/2, 3/2}能级的激发能ΔE (cm^–1)随组态空间扩大的收敛趋势. DHF代表单组态计算模型. AO和VO分别代表在每个计算模型下允许被激发的占据轨道和新添加的关联轨道. N_CSF代表相应的组态波函数数目

Table 1. Excitation energies ΔE (in cm^–1) of 3s²3p ²P_{1/2, 3/2} states of Si⁺ and Co¹⁴⁺ ions as functions of various computational models. DHF stands for the single configuration approximation model. AO and VO represent the occupied orbitals allowed to be replaced and the added virtual orbitals in each computational model, respectively. N_CSF represents the corresponding numbers of CSFs.

Model		AO	VO	N_CSF	ΔE
Model		AO	VO	N_CSF	Si⁺	Co¹⁴⁺
DHF		—	—	2	305	23957
VV + CV	1	{3s, 3p}	{4s, 4p, 3d, 4f, 5g}	204	293	23471
	2	{2s, 2p, 3s, 3p}	{5s, 5p, 4d, 5f, 6g}	8577	305	23588
	3	{1s, 2s, 2p, 3s, 3p}	{6s, 6p, 5d, 6f, 6g}	20491	304	23598
	4	{1s, 2s, 2p, 3s, 3p}	{7s, 7p, 6d, 7f, 6g}	33508	304	23605
	5	{1s, 2s, 2p, 3s, 3p}	{8s, 8p, 7d, 7f, 6g}	44508	305	23609
	6	{1s, 2s, 2p, 3s, 3p}	{9s, 9p, 8d, 7f, 6g}	57218	305	23610
	7	{1s, 2s, 2p, 3s, 3p}	{10s, 10p, 9d, 7f, 6g}	71638	305	23611
	8	{1s, 2s, 2p, 3s, 3p}	{11s, 11p, 10d, 7f, 6g}	87768	305	23611
	9	{1s, 2s, 2p, 3s, 3p}	{12s, 12p, 11d, 7f, 6g}	105608	305	23611
	10	{1s, 2s, 2p, 3s, 3p}	{13s, 13p, 12d, 7f, 6g}	125158	305	23611

下载: 导出CSV

表 2 Si⁺和Co¹⁴⁺离子3s²3p ²P_{1/2, 3/2}能级超精细结构常数电子部分矩阵元A_el (MHz/μ_N)和B_el (MHz/b)以及朗德g因子随组态空间扩展的收敛情况. DHF为单组态近似模型

Table 2. Electronic parts of hyperfine structure constants A_el(MHz/μ_N) and B_el(MHz/b) and Landé g factors of 3s²3p ²P_{1/2, 3/2} states in Si⁺ and Co¹⁴⁺ ions as functions of various computational models. DHF stands for the single configuration approximation model.

Model		Si⁺					Co¹⁴⁺
		A_el		B_el	g		A_el		B_el	g
		²P_1/2	²P_3/2	²P_3/2	²P_1/2	²P_3/2	²P_1/2	²P_3/2	²P_3/2	²P_1/2	²P_3/2
DHF		682.2	134.4	248.7	0.6658188	1.3340409	28653	5391	10060	0.6645201	1.3329968
VV + CV	1	647.7	154.5	237.1	0.6658181	1.3340408	27658	5879	9804	0.6645062	1.3330011
	2	741.9	175.0	289.1	0.6658123	1.3340361	28843	6071	10282	0.6644682	1.3329818
	3	783.5	172.2	296.2	0.6658100	1.3340348	29191	5814	10276	0.6644659	1.3329820
	4	799.1	160.4	298.3	0.6658098	1.3340346	29287	5766	10290	0.6644616	1.3329826
	5	799.8	163.2	299.2	0.6658099	1.3340344	29307	5799	10273	0.6644639	1.3329808
	6	800.9	163.4	297.3	0.6658093	1.3340345	29319	5788	10255	0.6644639	1.3329812
	7	801.1	163.9	297.7	0.6658094	1.3340345	29321	5797	10255	0.6644622	1.3329818
	8	802.7	163.7	295.6	0.6658094	1.3340343	29326	5796	10239	0.6644634	1.3329815
	9	802.8	164.0	295.8	0.6658092	1.3340344	29326	5799	10244	0.6644630	1.3329810
	10	802.6	163.9	295.5	0.6658088	1.3340346	29321	5796	10245	0.6644622	1.3329812

下载: 导出CSV

表 3 不同计算模型下Si⁺与Co¹⁴⁺离子3s²3p ²P_{1/2, 3/2}能级的激发能ΔE (cm^–1)、超精细结构常数电子部分矩阵元A_el (MHz/μ_N)和B_el (MHz/b)以及朗德g因子

Table 3. Excitation energies ΔE (cm^–1), electronic parts of hyperfine structure constants A_el (MHz/μ_N) and B_el (MHz/b) and Landé g factors of 3s²3p ²P_{1/2, 3/2} states in Si⁺ and Co¹⁴⁺ ions as functions of various computational models.

Model	Si⁺						Co¹⁴⁺
	ΔE	A_el		B_el	g		ΔE	A_el		B_el	g
	²P_1/2→ ²P_3/2	²P_1/2	²P_3/2	²P_3/2	²P_1/2	²P_3/2	²P_1/2→ ²P_3/2	²P_1/2	²P_3/2	²P_3/2	²P_1/2	²P_3/2
DHF	305	682	134	249	0.665819	1.334041	23957	28653	5391	10060	0.664520	1.332997
VV+CV-10	305	803	164	295	0.665809	1.334035	23611	29321	5796	10245	0.664462	1.332981
+MR₁	305	803	164	296	0.665809	1.334035	23611	29319	5797	10245	0.664462	1.332981
+CC_2p	310	785	150	288	0.665811	1.334036	23656	29287	5757	10232	0.664465	1.332983
+TQ_2p	307	785	160	292	0.665810	1.334036	23618	29245	5784	10229	0.664464	1.332983
+BQ	291	785	160	292	0.665810	1.334036	23044	29230	5788	10211	0.664464	1.332983
CCSD^[9]	—	—	—	—	—	—	22932(13)	—	—	—	—	—
NIST^[24]	287	—	—	—	—	—	22979	—	—	—	—	—

下载: 导出CSV

表 4 类铝等电子序列3s²3p ²P_{1/2, 3/2}能级的超精细结构常数电子部分矩阵元A_el(MHz/μ_N), B_el (MHz/b)和朗德g因子. 括号内的数字表示计算结果相应的不确定度

Table 4. Electronic parts of hyperfine structure constants A_el (MHz/μ_N) and B_el (MHz/b) and Landé g factors of 3s²3p ²P_{1/2, 3/2} states of Al-like isoelectronic sequence ions. Numbers in parentheses represent the computational errors.

Ions	A_el		B_el	g
Ions	²P_1/2	²P_3/2	²P_3/2	²P_1/2	²P_3/2
Si⁺	785(8)	160(8)	292(3)	0.66581	1.33404
P²⁺	1387(14)	290(3)	512(5)	0.66576	1.33399
S³⁺	2172(22)	457(5)	797(8)	0.66570	1.33394
Cl⁴⁺	3160(32)	664(7)	1152(12)	0.66562	1.33389
Ar⁵⁺	4372(44)	914(9)	1585(16)	0.66555	1.33383
K⁶⁺	5828(58)	1212(12)	2104(21)	0.66546	1.33376
Ca⁷⁺	7553(76)	1561(16)	2714(27)	0.66536	1.33368
Sc⁸⁺	9569(96)	1965(20)	3425(34)	0.66526	1.33360
Ti⁹⁺	11902(119)	2430(24)	4243(42)	0.66515	1.33352
V¹⁰⁺	14576(146)	2957(30)	5175(52)	0.66503	1.33342
Cr¹¹⁺	17618(176)	3553(36)	6230(62)	0.66490	1.33332
Mn¹²⁺	21055(211)	4220(42)	7416(74)	0.66476	1.33322
Fe¹³⁺	24916(249)	4964(50)	8740(87)	0.66462	1.33310
Co¹⁴⁺	29230(292)	5788(58)	10211(102)	0.66446	1.33298
Ni¹⁵⁺	34028(340)	6696(67)	11836(118)	0.66430	1.33286
Cu¹⁶⁺	39344(393)	7693(77)	13625(136)	0.66413	1.33273
Zn¹⁷⁺	45209(452)	8783(88)	15587(156)	0.66395	1.33259
Ga¹⁸⁺	51659(517)	9970(100)	17729(177)	0.66377	1.33244
Ge¹⁹⁺	58734(587)	11259(113)	20059(201)	0.66357	1.33229
As²⁰⁺	66469(665)	12654(127)	22588(226)	0.66337	1.33214
Se²¹⁺	74908(749)	14160(142)	25326(253)	0.66316	1.33197
Br²²⁺	84092(841)	15779(158)	28281(283)	0.66294	1.33180
Kr²³⁺	94066(941)	17519(175)	31462(315)	0.66271	1.33162

下载: 导出CSV

表 5 类铝等电子序列3s²3p ²P_{1/2, 3/2}能级的超精细结构常数A, B (MHz)和朗德g因子. 所有核参数μ (μ_N)和Q (mb)均来自于文献[25, 26]. 星号表示用CCSD方法计算的结果^[9]. 括号内的数字表示计算结果相应的不确定度

Table 5. Hyperfine structure constants and g factors of 3s²3p ²P_{1/2, 3/2} states of Al-like isoelectronic sequence ions. Nuclear parameters μ (μ_N) and Q (mb) are taken from Ref. [25, 26]. Asterisk represents these results calculated by CCSD method^[9]. Numbers in parentheses represent the computational uncertainties.

Ion	I	μ	Q	A		B	g
Ion	I	μ	Q	²P_1/2	²P_3/2	²P_3/2	²P_1/2	²P_3/2
⁵¹V¹⁰⁺	7/2	5.1464	–52	21433(214)	4349(43)	–269(3)	0.66503	1.33342
				21456(146)^*	4342(68)^*	–222(6)^*	0.665196^*	1.333460^*
⁵³Cr¹¹⁺	3/2	–0.4743	–150	–5571(56)	–1123(11)	–935(9)	0.66490	1.33332
				–5578(30)^*	–1122(14)^*	–964(10)^*	0.665081^*	1.333363^*
⁵⁵Mn¹²⁺	5/2	3.4669	330	29198(292)	5853(59)	2447(24)	0.66476	1.33322
				29096(3)^*	5821(35)^*	3162(20)^*	0.664957^*	1.333258^*
⁵⁷Fe¹³⁺	1/2	0.09064	160	4517(45)	900(9)	1398(14)	0.66462	1.33310
				4509(39)^*	897(2)^*	961(10)^*	0.664825^*	1.333148^*
⁵⁹Co¹⁴⁺	7/2	4.615	420	38542(39)	7632(76)	4289(43)	0.66446	1.33298
				5245(42)^*	1037(47)^*	3603(40)^*	0.664684^*	1.333032^*
⁶¹Ni¹⁵⁺	3/2	–0.7497	162	–17006(170)	–3348(33)	1917(19)	0.66430	1.33286
				–17016(66)^*	–3345(27)^*	1918(20)^*	0.664536^*	1.332909^*
⁶³Cu¹⁶⁺	3/2	2.2259	–220	58383(584)	11416(114)	–2998(30)	0.66413	1.33273
				58412(254)^*	11416(511)^*	–3012(60)^*	0.664379^*	1.332779^*

下载: 导出CSV

map

[1]	Safronova M S, Budker D, DeMille D, Kimball D F J, Derevianko A, Clark C W 2018 Rev. Mod. Phys. 90 025008 Google Scholar
[2]	Zhang B L, Huang Y, Zhang H Q, Hao Y M, Zeng M Y, Guan H, Gao K L 2020 Chin. Phys. B 29 074209 Google Scholar
[3]	Brewer S M, Chen J S, Hankin A M, Clements E R, Chou C W, Wineland D J, Hume D B, Leibrandt D R 2019 Phys. Rev. Lett. 123 033201 Google Scholar
[4]	Kozlov M G, Safronova M S, López-Urrutia J R C, Schmidt P O 2018 Rev. Mod. Phys. 90 045005 Google Scholar
[5]	Derevianko A, Dzuba V A, Flambaum V V 2012 Phys. Rev. Lett. 109 180801 Google Scholar
[6]	Dzuba V A, Derevianko A, Flambaum V V 2012 Phys. Rev. A 86 054501 Google Scholar
[7]	Dzuba V A, Flambaum V V 2017 Highly Charged Ions for Atomic Clocks and Search for Variation of the Fine Structure Constant (In: Wada M, Schury P, Ichikawa Y (eds) TCP 2014 Springer, Cham.) p79
[8]	Yudin V I, Taichenachev A V, Derevianko A 2014 Phys. Rev. Lett. 113 233003 Google Scholar
[9]	Yu Y, Sahoo B K 2016 Phys. Rev. A 94 062502 Google Scholar
[10]	Li J G, Godefroid M, Wang J G 2016 J. Phys. B: At. Mol. Opt. Phys. 49 115002 Google Scholar
[11]	Lu B, Zhang T X, Chang H, Li J G, Wu Y, Wang J G 2019 Phys. Rev. A 100 012504 Google Scholar
[12]	Goyal A, Khatri I, Singh A K, Mohan M, Sharma R, Singh N 2016 Atoms 4 22 Google Scholar
[13]	Beiersdorfer P, Träbert E, Pinnington E H 2003 Astrophys. J. 587 836 Google Scholar
[14]	Schiffmann S, Brage T, Judge P G, Paraschiv A R, Wang K 2021 Astrophys. J 923 186 Google Scholar
[15]	Booth A J, Blackwell D E 1983 Mon. Not. R. Astro. Soc. 204 777 Google Scholar
[16]	Roederer I U, Lawler J E 2021 Astrophys. J. 912 119 Google Scholar
[17]	Grant I P 2007 Relativistic Quantum Theory of Atoms and Molecules-Theory and Computation (New York: Springer) p393
[18]	Dyall K G, Grant I P, Johnson C T, Parpia F A, Plummer E P 1989 Comput. Phys. Commun. 55 425 Google Scholar
[19]	Jönsson P, Parpia F A, Fischer C F 1996 Comput. Phys. Commun. 96 301 Google Scholar
[20]	Cheng K T, Childs W J 1985 Phys. Rev. A 31 2775 Google Scholar
[21]	Froese C F, Gaigalas G, Jönsson P, Bierón J 2019 Comput. Phys. Commun. 237 184 Google Scholar
[22]	Zhang T X, Xie L Y, Li J G, Lu Z H 2017 Phys. Rev. A 96 012514 Google Scholar
[23]	Li J G, Jönsson P, Godefroid M, Dong C Z, Gaigalas G 2012 Phys. Rev. A 86 052523 Google Scholar
[24]	Kramida A, Ralchenko Yu, Reader J, NIST ASD Team 2022 NIST Atomic Spectra Database
[25]	Stone N J 2005 At. Data Nucl. Data Tables 90 75 Google Scholar
[26]	Pyykkö P 2008 Mol. Phys. 106 1965 Google Scholar

[1]	钟振祥. 氢分子离子超精细结构理论综述. , 2024, 73(20): 203104. doi: 10.7498/aps.73.20241101
[2]	计晨. 原子兰姆位移与超精细结构中的核结构效应. , 2024, 73(20): 202101. doi: 10.7498/aps.73.20241063
[3]	赵国栋, 曹进, 梁婷, 冯敏, 卢本全, 常宏. 镱原子超精细诱导5d6s ³D_1,3→6s² ¹S₀ E2跃迁及超精细常数的精确计算. , 2024, 73(9): 093101. doi: 10.7498/aps.73.20240028
[4]	张天成, 潘高远, 俞友军, 董晨钟, 丁晓彬. 超重元素Og(Z = 118)及其同主族元素的电离能和价电子轨道束缚能. , 2022, 71(21): 213201. doi: 10.7498/aps.71.20220813
[5]	张祥, 卢本全, 李冀光, 邹宏新. Hg⁺离子5d¹⁰6s ²S_1/2→5d⁹6s^{2 2}D_5/2钟跃迁同位素位移和超精细结构的理论研究. , 2019, 68(4): 043101. doi: 10.7498/aps.68.20182136
[6]	陈展斌, 董晨钟. 超精细结构效应对辐射光谱圆极化特性的影响. , 2018, 67(19): 193401. doi: 10.7498/aps.67.20180322
[7]	张斌, 赵健, 赵增秀. 基于多组态含时Hartree-Fock方法研究电子关联对于H2分子强场电离的影响. , 2018, 67(10): 103301. doi: 10.7498/aps.67.20172701
[8]	徐海超, 牛晓海, 叶子荣, 封东来. 铁基超导体系基于电子关联强度的统一相图. , 2018, 67(20): 207405. doi: 10.7498/aps.67.20181541
[9]	张婷贤, 李冀光, 刘建鹏. Al+离子3s2 1S0→3s3p 3,1P1o跃迁同位素偏移的理论研究. , 2018, 67(5): 053101. doi: 10.7498/aps.67.20172261
[10]	余庚华, 刘鸿, 赵朋义, 徐炳明, 高当丽, 朱晓玲, 杨维. 采用相对论多组态Dirac-Hartree-Fock方法对Mg原子同位素位移的理论研究. , 2017, 66(11): 113101. doi: 10.7498/aps.66.113101
[11]	胡峰, 杨家敏, 王传珂, 张继彦, 蒋刚, 朱正和. 电子关联效应对金离子的影响. , 2011, 60(10): 103104. doi: 10.7498/aps.60.103104.1
[12]	刘延君, 董晨钟, 蒋军, 颉录有. 电子与类铍N3+和O4+离子碰撞激发截面的相对论扭曲波计算. , 2009, 58(4): 2320-2327. doi: 10.7498/aps.58.2320
[13]	张书锋, 邓景康, 黄艳茹, 刘昆, 宁传刚. N2价轨道的精细电子动量谱学研究. , 2009, 58(4): 2382-2389. doi: 10.7498/aps.58.2382
[14]	朱婧晶, 苟秉聪. 类氦离子高双激发态电子关联效应的研究. , 2009, 58(8): 5285-5290. doi: 10.7498/aps.58.5285
[15]	姜旻昊, 孟续军. 用Hartree-Fock-Slater-Boltzmann-Saha模型研究等离子体细致组态原子结构及其状态方程. , 2005, 54(2): 587-593. doi: 10.7498/aps.54.587
[16]	苏国林, 任雪光, 张书锋, 宁传刚, 周晖, 李彬, 黄峰, 李桂琴, 邓景康. 环戊烯分子内价轨道1a′的电子动量谱学研究. , 2005, 54(9): 4108-4112. doi: 10.7498/aps.54.4108
[17]	陈志骏, 马洪良, 陈淼华, 李茂生, 施伟, 陆福全, 汤家镛. 单电荷态钡离子超精细结构光谱. , 1999, 48(11): 2038-2041. doi: 10.7498/aps.48.2038
[18]	谭明亮, 朱正和, 赵永宽, 陈晓峰. 类铜Au50+精细结构能级和光谱跃迁的相对论多组态计算. , 1996, 45(10): 1609-1614. doi: 10.7498/aps.45.1609
[19]	王宛珏. 类氮KⅩⅢ,CaⅪⅤ,ScⅩⅤ和TiⅩⅥ精细结构能级和跃迁波长的相对论多组态Dirac-Fock计算. , 1992, 41(5): 726-731. doi: 10.7498/aps.41.726
[20]	潘守甫, 张凤梧. Li原子的超精细结构计算. , 1964, 20(8): 822-824. doi: 10.7498/aps.20.822

计量

文章访问数: 3211
PDF下载量: 136
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

类铝离子钟跃迁能级的超精细结构常数和朗德g因子

Hyperfine interaction constants and Landé g factors of clock states of Al-like ions

摘要

Abstract

作者及机构信息

1.
北京应用物理与计算数学研究所, 计算物理重点实验室, 北京　100088

2.
复旦大学, 核物理与离子束应用教育部重点实验室, 上海　200433

3.
北京大学工学院, 应用物理与技术研究中心, 北京　100871

通信作者: 李冀光, li_jiguang@iapcm.ac.cn

Authors and contacts

Corresponding author: Li Ji-Guang, li_jiguang@iapcm.ac.cn

文章全文 : translate this paragraph

参考文献

施引文献

目录

计量

作者中心

审稿中心

关于期刊

关于我们

搜索

留言板

类铝离子钟跃迁能级的超精细结构常数和朗德g因子

Hyperfine interaction constants and Landé g factors of clock states of Al-like ions

摘要

Abstract

作者及机构信息

1. 北京应用物理与计算数学研究所, 计算物理重点实验室, 北京 100088 2. 复旦大学, 核物理与离子束应用教育部重点实验室, 上海 200433 3. 北京大学工学院, 应用物理与技术研究中心, 北京 100871

通信作者: 李冀光, li_jiguang@iapcm.ac.cn

Authors and contacts

Corresponding author: Li Ji-Guang, li_jiguang@iapcm.ac.cn

文章全文 : translate this paragraph

参考文献

施引文献

目录

计量

出版历程

作者中心

审稿中心

关于期刊

关于我们

1.
北京应用物理与计算数学研究所, 计算物理重点实验室, 北京　100088

2.
复旦大学, 核物理与离子束应用教育部重点实验室, 上海　200433

3.
北京大学工学院, 应用物理与技术研究中心, 北京　100871