-
在镱原子中, 利用
$ {\rm 5d6s \; {^3D_1} \to 6s^2 \; {^1S_0}} $ 跃迁探索宇称破缺效应已经得到了深入的研究. 但是$ {\rm 5d6s\; {^3D_1}} $ 态与基态$ {\rm 6s^2 \; {^1S_0}} $ 之间的M1跃迁和超精细诱导E2跃迁很大程度上影响了宇称破缺信号的探测. 因此, 很有必要精确计算$ {\rm 5d6s\; {^3D_1}} $ 态与基态$ {\rm 6s^2\; {^1S_0}} $ 之间的M1跃迁和超精细诱导E2跃迁的跃迁概率. 本文利用多组态Dirac-Hartree-Fock理论精确计算了$ {\rm 5d6s \; {^3D_1} \to 6s^2 \; {^1S_0}} $ M1跃迁和超精细诱导$ {\rm 5d6s \; ^3D_{1,3} \to 6s^2 \; {^1S_0}} $ E2跃迁的跃迁概率. 计算时详细分析了电子关联效应对跃迁概率的影响. 此外, 还分析了不同微扰态和不同超精细相互作用对跃迁概率的影响. 本文计算的$ {\rm ^3D_{1,2,3}} $ 和$ {\rm ^1D_2} $ 态的超精细常数与实验测量结果符合得很好, 从而证明了本文所用计算模型的合理性. 结合实验测量的超精细常数和本文理论计算所得的核外电子在原子核处的电场梯度, 重新评估了$ ^{173} $ Yb原子核电四极矩$ Q = 2.89(5)\; \rm {b} $ , 评估结果与目前被推荐的结果符合得很好.-
关键词:
- 超精细诱导跃迁 /
- 镱原子 /
- 超精细常数 /
- 多组态Dirac-Hartree-Fock方法
The parity violation effects via the$ {\mathrm{5d6s\; {^3D_1} \to 6s^2 \; {^1S_0}}} $ transition have been extensively investigated in ytterbium atoms. However, the M1 transition between the excitation state$ {\mathrm{5d6s\; {^3D_1}}} $ and the ground state$ {\mathrm{6s^2 \; {^1S_0}}} $ , as well as the hyperfine-induced E2 transition, significantly affects the detection of parity violation signal. Therefore, it is imperative to obtain the accurate transition probabilities for the M1 and hyperfine-induced E2 transitions between the excitation state${\mathrm{ 5d6s\; {^3D_1} }}$ and the ground state$ {\mathrm{6s^2\; {^1S_0}}} $ . In this work, we use the multi-configuration Dirac-Hartree-Fock theory to precisely calculate the transition probabilities for the${\mathrm{ 5d6s \; {^3D_1} \to 6s^2 \; {^1S_0} }}$ M1 and hyperfine-induced${\mathrm{ 5d6s \; ^3D_{1,3} \to 6s^2 \; {^1S_0} }}$ E2 transitions. We extensively analyze the influences of electronic correlation effects on the transition probabilities according to our calculations. Furthermore, we analyze the influences of different perturbing states and various hyperfine interactions on the transition probabilities. The calculated hyperfine constants of the e$ {\mathrm{^3D_{1,2,3}}} $ and${\mathrm{ ^1D_2}} $ states accord well with experimental measurements, validating the rationality of our computational model. By combining experimentally measured hyperfine constants with the theoretically derived electric field gradient of the extra nuclear electrons at the nucleus, we reevaluate the nuclear quadrupole moment of the$ ^{173} $ Yb nucleus as$ Q = 2. 89(5) \;\rm {b} $ , showing that our result is in excellent agreement with the presently recommended value.-
Keywords:
- hyperfine induced transition /
- Yb atom /
- hyperfine constant /
- multi-configuration Dirac-Hartree-Fock method
[1] Bouchiat M, Bouchiat C 1974 J. Phys. 35 899
Google Scholar
[2] Safronova M, Budker D, DeMille D, Kimball D F J, Derevianko A, Clark C W 2018 Rev. Mod. Phys. 90 025008
Google Scholar
[3] Roberts B, Dzuba V, Flambaum V 2015 Annu. Rev. Nucl. Part. Sci. 65 63
Google Scholar
[4] DeMille D 1995 Phys. Rev. Lett. 74 4165
Google Scholar
[5] Tsigutkin K, Dounas Frazer D, Family A, Stalnaker J E, Yashchuk V V, Budker D 2009 Phys. Rev. Lett. 103 071601
Google Scholar
[6] Antypas D, Fabricant A, Stalnaker J E, Tsigutkin K, Flambaum V, Budker D 2019 Nat. Phys. 15 120
Google Scholar
[7] Tsigutkin K, Dounas Frazer D, Family A, Stalnaker J E, Yashchuk V V, Budker D 2010 Phys. Rev. A 81 032114
Google Scholar
[8] Dzuba V, Flambaum V 2011 Phys. Rev. A 83 042514
Google Scholar
[9] Stalnaker J, Budker D, DeMille D, Freedman S, Yashchuk V V 2002 Phys. Rev. A 66 031403
Google Scholar
[10] Sur C, Chaudhuri R K 2007 Phys. Rev. A 76 012509
Google Scholar
[11] Kozlov M, Dzuba V, Flambaum V 2019 Phys. Rev. A 99 012516
Google Scholar
[12] Stone N 2016 At. Data Nucl. Data Tables 111–112 1
Google Scholar
[13] Schwartz C 1955 Phys. Rev. 97 380
Google Scholar
[14] Racah G 1942 Phys. Rev. 62 438
Google Scholar
[15] Andersson M, Jönsson P 2008 Comput. Phys. Commun. 178 156
Google Scholar
[16] Radzig A A, Smirnov B M 2012 Reference Data on Atoms, Molecules, and Ions (Berlin: Springer) p99
[17] Lu B, Lu X, Wang T, Chang H 2022 J. Phys. B: At. Mol. Phys. 55 205002
Google Scholar
[18] Bieroń J, Pyykkö P, Sundholm D, Kellö V, Sadlej A J 2001 Phys. Rev. A 64 052507
Google Scholar
[19] Li J, Godefroid M, Wang J 2016 J. Phys. B: At. Mol. Phys. 49 115002
Google Scholar
[20] Hertel I V, Schulz C P 2014 Atoms, Molecules and Optical Physics (Berlin: Springer) p212
[21] Johnson W R 2007 Atomic Structure Theory (Berlin: Springer) p181
[22] Andersson M, Yao K, Hutton R, Zou Y, Chen C, Brage T 2008 Phys. Rev. A 77 042509
Google Scholar
[23] Li W, Grumer J, Brage T, Jönsson P 2020 Comput. Phys. Commun. 253 107211
Google Scholar
[24] Lu X, Guo F, Wang Y, Feng M, Liang T, Lu B, Chang H 2023 Phys. Rev. A 108 012820
Google Scholar
[25] Johnson W 2010 Can. J. Phys. 89 429
Google Scholar
[26] Grumer J, Brage T, Andersson M, Li J, Jönsson P, Li W, Yang Y, Hutton R, Zou Y 2014 Phys. Scr. 89 114002
Google Scholar
[27] Fischer C F, Brage T, Jönsson P 2022 Computational Atomic Structure: an MCHF Approach (New York: Routledge) p217
[28] Li J, Jönsson P, Godefroid M, Dong C, Gaigalas G 2012 Phys. Rev. A 86 052523
Google Scholar
[29] Jönsson P 1993 Phys. Scr. 48 678
Google Scholar
[30] Jönsson P, Gaigalas G, Fischer C F, Bieroń J, Grant I P, Brage T, Ekman J, Godefroid M, Grumer J, Li J 2023 Atoms 11 68
Google Scholar
[31] Olsen J, Roos B O, Jorgensen P, Jensen H 1988 J. Chem. Phys. 89 2185
Google Scholar
[32] Jönsson P, Godefroid M, Gaigalas G, Ekman J, Grumer J, Li W, Li J, Brage T, Grant I P, Bieroń J, Fischer C F 2023 Atoms 11 7
Google Scholar
[33] Jönsson P, He X, Fischer C F, Grant I 2007 Comput. Phys. Commun. 177 597
Google Scholar
[34] Fischer C F, Gaigalas G, Jönsson P, Bieroń J 2019 Comput. Phys. Commun. 237 184
Google Scholar
[35] Kramida A, Ralchenko Y, Reader J 2023 NIST Atomic Spectra Database (Version 5.11) https://physics.nist.gov/pml/atomic-spectra-database
[36] Bowers C, Budker D, Freedman S, Gwinner G, Stalnaker J, DeMille D 1999 Phys. Rev. A 59 3513
Google Scholar
[37] Beloy K, Sherman J A, Lemke N D, Hinkley N, Oates C W, Ludlow A D 2012 Phys. Rev. A 86 051404
Google Scholar
[38] Ai D, Jin T, Zhang T, Luo L, Liu L, Zhou M, Xu X 2023 Phys. Rev. A 107 063107
Google Scholar
[39] Kronfeldt H D 1998 Phys. Scr. 1998 5
Google Scholar
[40] Porsev S, Rakhlina Y G, Kozlov M 1999 J. Phys. B: At. Mol. Phys. 32 1113
Google Scholar
[41] Holmgren L 1975 Phys. Scr. 12 119
Google Scholar
[42] Zhang T, Xie L, Li J, Lu Z 2017 Phys. Rev. A 96 012514
Google Scholar
[43] Bieroń J, Fischer C F, Jönsson P, Pyykkö P 2008 J. Phys. B: At. Mol. Phys. 41 115002
Google Scholar
[44] Singh A K, Angom D, Natarajan V 2013 Phys. Rev. A 87 012512
Google Scholar
[45] Zehnder A, Boehm F, Dey W, Engfer R, Walter H, Vuilleumier J 1975 Nucl. Phys. A 254 315
Google Scholar
[46] Cheng K, Chen M, Johnson W 2008 Phys. Rev. A 77 052504
Google Scholar
-
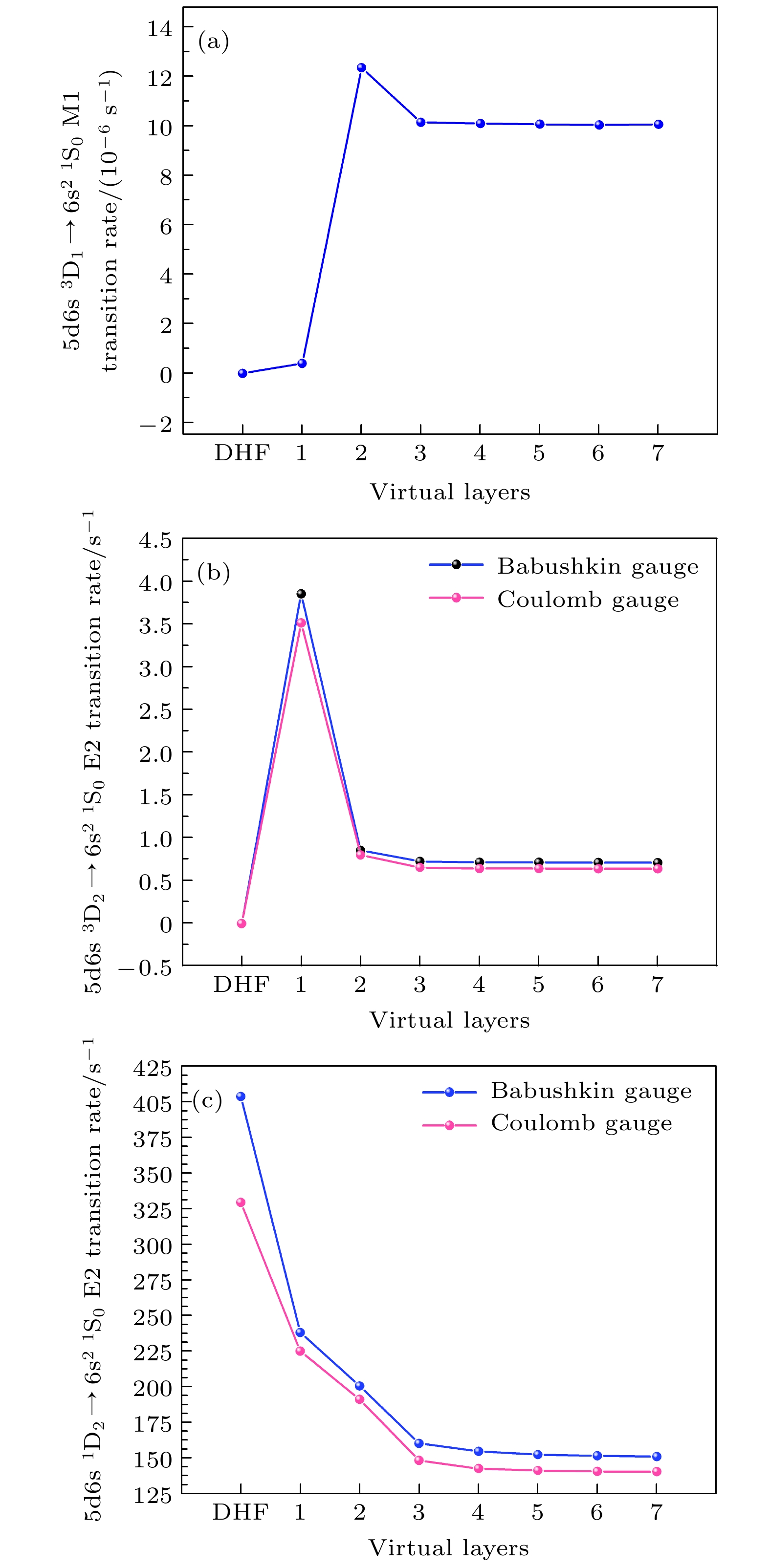
图 1 $ {\rm 5 d6 s \ ^3 D_1 \to 6 s^2 \ ^1 S_0} $ M1跃迁及$ {\rm 5 d6 s \ ^{1, 3}D_2}\to $$ {\rm6 s^2 \ ^1 S_0} $ E2跃迁的跃迁概率随虚轨道扩展的变化
Fig. 1. Transition rates for $ {\rm 5 d6 s \ ^3 D_1 \to 6 s^2 \ ^1 S_0} $ M1 transition and $ {\rm 5 d6 s \ ^{1, 3}D_2 \to 6 s^2 \ ^1 S_0} $ E2 transition as a function of virtual orbital expansion.
表 1 不同计算模型下打开的光谱轨道(active orbitals, AO)、虚轨道(virtual orbitals, VO) 以及模型产生的组态空间内总的组态个数(number of configuration state wavefunctions, NCFs). $ J = 0 $ 表示$ {\rm ^1 S_0} $ 态, $ J = 1, 3 $ 表示$ {\rm ^3 D_{1, 3}} $ 态, 而$ J = 2 $对应$ {\rm ^3 D_{2}} $ 和$ {\rm ^1 D_{2}} $ 态
Table 1. Active orbitals (AO), virtual orbitals (VO) opened under different calculation models, and NCFs is the total number of the configurations in the configuration space. $ J = 0 $ represents $ {\rm ^1 S_0} $ state, $ J = 1, 3 $ represents $ {\rm ^3 D_{1, 3}} $ states, and the $ J = 2 $ corresponds to the $ {\rm ^3 D_{2}} $ and $ {\rm ^1 D_{2}} $ states, respectively.
Models AO VO NCFs $ J = 0 $ $ J = 1 $ $ J = 2 $ $ J = 3 $ DHF 1 1 2 1 VV-1 {$ {\rm 5 d6 s} $;$ {\rm 6 s^2} $} {$ {\rm 7 s, 6 p, 6 d, 5 f, 5 g} $} 15 16 35 24 C5V-2 {$ {\rm 5 s^25 p^65 d6 s} $;$ {\rm 5 s^25 p^66 s^2} $} {$ {\rm 8 s, 7 p, 7 d, 6 f, 6 g, 6 h} $} 336 1954 4361 3213 C4V-3 $ \{{\rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^65 d6 s};{\rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^66 s^2}\} $ {$ {\rm 9 s, 8 p, 8 d, 7 f, 7 g} $} 2896 20054 49368 37668 C4V-4 $ \{\rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^65 d6 s; \rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^66 s^2 \} $ {$ {\rm 10 s, 9 p, 9 d, 8 f, 8 g, 8 h} $} 5058 35649 88596 68104 C4V-5 $ \{{\rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^65 d6 s}; {\rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^66 s^2}\} $ {$ {\rm 11 s, 10 p, 10 d, 9 f, 9 g, 9 h} $} 7822 55699 139251 107472 C4V-6 $ \{{\rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^65 d6 s}; {\rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^66 s^2} \}$ {$ {\rm 12 s, 11 p, 11 d, 10 f, 10 g, 9 h} $} 10681 76208 190245 146319 C4V-7 $ \{{\rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^65 d6 s}; {\rm 4 s^24 p^64 d^{10}4 f^{14}5 s^25 p^66 s^2}\} $ {$ {\rm 13 s, 12 p, 12 d, 11 f, 10 g, 9 h} $} 13213 93967 232975 177889 CC5-7 $ \cup ${$ 5{\mathrm{ s^25 p^65 d6 s}} ; \rm 5 s^25 p^6 s^2 $} {$ {\rm 13 s, 12 p, 12 d, 11 f, 10 g, 9 h} $} 154602 435843 643878 750192 MR-3 $ \cup \{{\rm 5 s^25 p^6 p^2} ; {\rm 5 s^25 p^25 d^2}; {\rm 5 s^2 5 p^46 s^26 d7 d} $ {$ {\rm 9 s, 8 p, 8 d, 7 f, 7 g, 7 h} $} 754484 2123833 3122817 3614260 $ {5 {\mathrm{s}}^25 {\mathrm{p}}^6 {\mathrm{s}}7{\mathrm{ s}}} ; {5 {\mathrm{s}}^25 {\mathrm{p}}^66 {\mathrm{d}}7 {\mathrm{s}}}; {5 {\mathrm{s}}^25 {\mathrm{p}}^45{\mathrm{ d}}6 {\mathrm{s}}^26{\mathrm{ d}}}; $ ${\rm 5 s^25 p^55 d6 s6 p}; {\rm 5 s^25 p^65 f6 p} ; {\rm 5 s^25 p^66 s6 d} $} 
下载: 导出CSV
表 2 不同计算模型下$ {\rm 5 d6 s \ ^3 D_1 \to 6 s^2 \ ^1 S_0} $ M1跃迁的激发能$ \Delta E $($ \rm {cm^{- 1}} $), RME (a.u.)和跃迁概率R($ \rm {s^{- 1}} $). 方括号中的值表示以10为底的指数, 圆括号内的值表示误差
Table 2. Excitation energy $ \Delta E $ (in $ \rm {cm^{- 1}} $), transition probability R (in $ \rm {s^{- 1}} $), and RME (in a.u.) for the $ {\rm 5 d6 s \ ^3 D_1 \to 6 s^2 \ ^1 S_0} $ M1 transition under various computational models. The values in brackets represent exponents with a base of 10, and values in parentheses indicate errors.
下载: 导出CSV
表 3 $ {\rm 5 d6 s \ ^{1, 3}D_2 \to 6 s^2 \ ^1 S_0} $ E2 跃迁的激发能$ \Delta E $($ \rm {cm^{- 1}} $), RME(a.u.) 和跃迁概率R($ \rm {s^{- 1}} $)在不同计算模型下的结果. V表示速度规范, L表示长度规范
Table 3. Excitation energy $ \Delta E $ (in $ \rm {cm^{-1}} $), RME (in a.u.), and transition probability R (in $ \rm {s^{-1}} $) for the $ {\rm 5 d6 s \ ^{1, 3}D_2 \to 6 s^2 \ ^1 S_0} $ E2 transition under various computational models. “V” denotes the velocity gauge, and “L” represents the length gauge.
$ {\rm ^3 D_2 \to {^1 S_0}} $ $ {\rm ^1 D_2 \to {^1 S_0}} $ Models $ \Delta E $ $ \rm{RME_{\rm L}} $ $ \rm{RME_{\rm V}} $ $ R_{\rm L} $ $ R_{\rm V} $ $ \Delta E $ $ \rm{RME_{\rm L}} $ $ \rm{RME_{\rm V}} $ $ R_{\rm L} $ $ R_{\rm V} $ DHF 21114.02 0.05 0.05 0.001 0.001 28822.95 $ - $15.05 $ - $13.59 403.87 329.46 VV-1 25010.57 2.09 2.00 3.85 3.51 26254.24 $ - $15.26 $ - $14.84 238.18 225.08 C4V-7 22406.02 1.18 1.12 0.71 0.64 26208.26 $ - $11.67 $ - $11.26 150.96 140.41 CC5-7 23171.20 0.86 0.85 0.45 0.43 28126.76 $ - $13.55 $ - $12.75 289.61 256.70 MR-3 24685.75 1.21 1.15 1.20 1.10 28313.29 $ - $12.63 $ - $12.84 260.01 232.25 Breit+QED 24553.44 1.18 1.13 1.11 1.02 28206.64 $ - $12.61 $ - $11.94 254.33 228.31 Bowers等[36] 1.12(4) Expt.[36] 1.45(7) NIST[35] 24751.95 27677.67
下载: 导出CSV
表 4 $ {\rm 5 d6 s \ ^{3}D_{1, 2, 3}} $态与$ {\rm ^{1}D_2} $态的磁偶极超精细常数A (MHz)和电四极超精细常数B (MHz)
Table 4. Magnetic dipole hyperfine constant A (in MHz) and electric quadrupole hyperfine constant B (in MHz) for the $ {\rm 5 d6 s \ ^{3}D_{1, 2, 3}} $ and $ {\rm ^{1}D_2} $ states.
$ ^{171} {\mathrm{Yb}}$ $ ^{173} {\mathrm{Yb}}$ Ref. A A B $ {\rm ^3 D_1} $ Expt. $ - $2040(2) 562.8(5) 337(2) [36] $ - $2047(47) [37] $ - $2032.67(17) [38] 563(1) 335(1) [39] Theory $ - $2349 648 249 [11] 596 290 [40] 597 [41] $ - $2119.3 583.79 338.46 This work $ {\rm ^3 D_2} $ Expt. 1315(4) $ - $363.4(10) 487(5) [36] $ - $362(2) 482(22) [39] Theory 1354 $ - $373 387 [11] $ - $351 440 [40] $ - $765 [41] 1314.62 $ - $362.13 491.39 This work $ {\rm ^3 D_3} $ Expt. $ - $430(1) 909(29) [39] Theory $ - $420 728 [40] $ - $477 [41] 1626.97 $ - $448.17 836.5 This work $ {\rm ^1 D_2} $ Expt. 100(18) 1115(89) [39] Theory 131 1086 [40] 465 [41] $ - $313.87 86.46 1053.44 This work
下载: 导出CSV
表 5 不同模型下的EFG(a.u.), 以及重新评估后的$ ^{173} $Yb原子核电四极矩Q(b)
Table 5. The EFG (in a.u.) calculated under different models, along with the reassessment of the nuclear electric quadrupole moment Q (in b) for $ ^{173} $Yb.
Models $ {\rm ^3 D_1} $ $ {\rm ^3 D_2} $ $ {\rm ^3 D_3} $ EFG Q EFG Q EFG Q DHF 0.23 6.09 0.32 6.47 0.55 7.07 C4V-7 0.52 2.75 0.77 2.69 1.29 2.99 CC5-7 0.43 3.26 0.63 3.27 1.10 3.52 MR-3 0.51 2.79 0.74 2.77 1.27 3.04
下载: 导出CSV
表 6 $ ^{171}{\mathrm{Yb}} $和$ ^{173}{\mathrm{Yb}} $原子的超精细诱导$ {\rm 5 d6 s \ {^3 D_{1, 3}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $ E2跃迁的混合系数(a.u.)
Table 6. Mixing coefficients (in a.u.) for the hyperfine-induced $ {\rm 5 d6 s \ {^3 D_{1, 3}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $ E2 transition in $ ^{171} {\mathrm{Yb}}$ and $ ^{173} {\mathrm{Yb}}$.
$ {\rm (^3 D_2, {^3 D_1})} $ $ {\rm (^1 D_2, {^3 D_1})} $ $ F' $ $ \varepsilon_{1}^{{\rm A}} $ $ \varepsilon_{1}^{{\rm B}} $ $ \varepsilon_{1} $ $ \varepsilon_{2}^{{\rm A}} $ $ \varepsilon_{2}^{{\rm B}} $ $ \varepsilon_{2} $ $ ^{171} $Yb 3/2 $ - $1.54[$ - $4] 0 $ - $1.54[$ - $4] 7.1[$ - $6] 0 7.1[$ - $6] 7/2 $ - $7.36[$ - $5] $ - $5.47[$ - $6] $ - $7.91[$ - $5] 3.39[$ - $6] 4.04[$ - $8] 3.43[$ - $6] $ ^{173} $Yb 5/2 $ - $7.17[$ - $5] 3.99[$ - $6] $ - $6.77[$ - $5] 3.30[$ - $6] $ - $2.95[$ - $8] 3.27[$ - $6] 3/2 $ - $5.03[$ - $5] 7.47[$ - $6] $ - $4.28[$ - $5] 2.31[$ - $6] $ - $5.53[$ - $8] 2.26[$ - $6] $ {\rm (^3 D_2, {^3 D_3})} $ $ {\rm (^1 D_2, {^3 D_3})} $ $ F' $ $ \varepsilon_{1}^{{\rm A}} $ $ \varepsilon_{1}^{{\rm B}} $ $ \varepsilon_{1} $ $ \varepsilon_{2}^{{\rm A}} $ $ \varepsilon_{2}^{{\rm B}} $ $ \varepsilon_{2} $ $ ^{171} $Yb 5/2 5.28[$ - $5] 0 5.28[$ - $5] –1.37[$ - $5] 0 $ - $1.37[$ - $5] 9/2 2.35[$ - $5] 2.56[$ - $6] 2.61[$ - $5] $ - $6.13[$ - $6] $ - $3.78[$ - $8] $ - $6.17[$ - $6] 7/2 2.54[$ - $5] $ - $3.46[$ - $7] 2.51[$ - $5] $ - $6.61[$ - $6] 5.1[$ - $9] $ - $6.61[$ - $6] $ ^{173} $Yb 5/2 2.21[$ - $5] $ - $2.41[$ - $6] 1.97[$ - $5] $ - $5.76[$ - $6] 3.55[$ - $8] $ - $5.73[$ - $6] 3/2 1.61[$ - $5] $ - $2.84[$ - $6] 1.32[$ - $5] $ - $4.81[$ - $6] 4.19[$ - $8] $ - $4.14[$ - $6] 1/2 8.40[$ - $6] $ - $1.83[$ - $6] 6.57[$ - $5] $ - $2.19[$ - $6] 2.7[$ - $8] $ - $2.16[$ - $6]
下载: 导出CSV
表 7 $ ^{171} {\mathrm{Yb}}$和$ ^{173} {\mathrm{Yb}}$的超精细诱导$ {\rm 5 d6 s \ {^3 D_{1, 3}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $ E2跃迁的跃迁概率($ \rm s^{- 1} $). $ T_1 $与$ T_2 $分别表示磁偶极超精细相互作用与电四极超精细相互作用下的诱导跃迁概率. $ R_1 $与$ R_3 $表示超精细诱导跃迁$ {\rm 5 d6 s \ {^3 D_{1}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $中$ {\rm ^{3}D_2} $微扰态和$ {\rm ^{1}D_2} $微扰态与$ {\rm {^3 D_{1}}} $态混合后的诱导跃迁概率. $ R_1' $与$ R_3' $表示超精细诱导跃迁$ {\rm 5 d6 s \ {^3 D_{3}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $中$ {\rm ^{3}D_2} $微扰态和$ {\rm ^{1}D_2} $微扰态与$ {\rm {^3 D_{3}}} $态混合后的诱导跃迁概率. 方括号内的数值代表以10 为底的指数, 圆括号内的数值代表误差
Table 7. Transition probabilities (in $ \rm s^{-1} $) for the hyperfine-induced $ {\rm 5 d6 s \ {^3 D_{1, 3}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $ E2 transitions in $ ^{171} {\mathrm{Yb}}$ and $ ^{173} {\mathrm{Yb}}$. T1 and T2 represent the induced transition probabilities under magnetic dipole hyperfine interaction and electric quadrupole hyperfine interaction, respectively. $ R_1 $ and $ R_3 $ represent the transition probabilities in the hyperfine-induced transition $ {\rm 5 d6 s \ {^3 D_{1}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $, where the perturbed states $ {\rm ^{3}D_2} $ and $ {\rm ^{1}D_2} $ are mixed with the $ {\rm {^3 D_{1}}} $ state. Similarly, $ R_1' $ and $ R_3' $ denote the transition probabilities in the hyperfine-induced transition $ {\rm 5 d6 s \ {^3 D_{3}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $, where the perturbed states $ {\rm ^{3}D_2} $ and $ {\rm ^{1}D_2} $ are mixed with the $ {\rm {^3 D_{3}}} $ state. The numerical values in square brackets denote the exponentiation with base 10, while the values in parentheses represent the error.
$ R_1 $ $ R_3 $ Total $ F' $ $ T_1 $ $ T_2 $ $ T_1 $ $ T_2 $ 3/2 1.09[$ - $8] 0 2.64[$ - $9] 0 2.42(23)[$ - $8] 7/2 2.48[$ - $9] 1.37[$ - $11] 6.00[$ - $10] 8.53[$ - $14] 6.13(60)[$ - $9] 5/2 2.35[$ - $9] 7.29[$ - $12] 5.69[$ - $10] 4.55[$ - $14] 4.82(47)[$ - $9] 3/2 1.16[$ - $9] 2.55[$ - $11] 2.80[$ - $10] 1.60[$ - $13] 2.05(20)[$ - $9] $ R_1' $ $ R_3' $ Total $ F' $ $ T_1 $ $ T_2 $ $ T_1 $ $ T_2 $ 5/2 6.41[$ - $10] 0 4.96[$ - $9] 0 9.16(89)[$ - $9] 9/2 1.27[$ - $10] 1.51[$ - $12] 9.85[$ - $10] 3.75[$ - $14] 1.94(18)[$ - $9] 7/2 1.48[$ - $10] 2.74[$ - $14] 1.15[$ - $9] 6.82[$ - $16] 2.10(20)[$ - $9] 5/2 1.12[$ - $10] 1.33[$ - $12] 8.70[$ - $10] 3.30[$ - $14] 1.50(14)[$ - $9] 3/2 5.92[$ - $11] 1.85[$ - $12] 4.58[$ - $10] 4.60[$ - $14] 7.58(74)[$ - $10] 1/2 1.62[$ - $11] 7.68[$ - $13] 1.25[$ - $10] 1.91[$ - $14] 2.02(19)[$ - $10]
下载: 导出CSV
表 8 $ ^{171}{\mathrm{Yb}} $和$ ^{173}{\mathrm{Yb}} $的超精细诱导$ {\rm 5 d6 s \ {^3 D_{1}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $ E2跃迁的跃迁幅度. $ E2_{\rm A} $与$ E2_{\rm B} $分别表示磁偶极超精细相互作用与电四极超精细相互作用下的诱导跃迁幅度. $ E2_{{\rm tot}} $表示磁偶极与电四极超精细相互作用共同作用下的诱导跃迁幅度. 方括号内的数值代表以10为底的指数, 圆括号内的数值代表误差
Table 8. Transition amplitude of the hyperfine-induced $ {\rm 5 d6 s \ {^3 D_{1}}}IF' \to {\rm 6 s^2 \ {^1 S_0}} $ E2 transition in $ ^{171} {\mathrm{Yb}}$ and $ ^{173} {\mathrm{Yb}}$. $ E2_{\rm A} $ and $ E2_{\rm B} $ represent the induced transition amplitudes under the magnetic dipole hyperfine interaction and electric quadrupole hyperfine interaction, respectively. $ E2_{{\rm tot}} $ denotes the induced transition amplitude under the combined influence of magnetic dipole and electric quadrupole hyperfine interactions. The numerical values in square brackets denote the exponentiation with base 10, while the values in parentheses represent the error.
IF Ref. 1/2, 3/2 5/2, 3/2 5/2, 5/5 5/2, 7/2 $ E2_{\rm A} $ 6.43[$ - $4] $ - $3.63[$ - $4] 6.34[$ - $4] $ - $7.52[$ - $4] Kozlov[11] 1.62[$ - $4] $ - $0.53[$ - $4] 9.26[$ - $5] $ - $1.09[$ - $4] This work $ E2_{\rm B} $ 0 $ - $3.90[$ - $5] 2.10[$ - $5] 2.80[$ - $5] Kozlov[11] 0 $ - $7.88[$ - $6] 5.16[$ - $6] 8.16[$ - $6] This work $ E2_{{\rm tot}} $ 6.40(1.0)[$ - $4] $ - $4.00(60)[$ - $4] 6.60(1.0)[$ - $4] $ - $7.20(1.2)[$ - $4] Kozlov[11] 1.62(6)[$ - $4] $ - $4.50(20)[$ - $5] 9.76(41)[$ - $5] $ - $1.01(4)[$ - $4] This work
下载: 导出CSV
-
[1] Bouchiat M, Bouchiat C 1974 J. Phys. 35 899
Google Scholar
[2] Safronova M, Budker D, DeMille D, Kimball D F J, Derevianko A, Clark C W 2018 Rev. Mod. Phys. 90 025008
Google Scholar
[3] Roberts B, Dzuba V, Flambaum V 2015 Annu. Rev. Nucl. Part. Sci. 65 63
Google Scholar
[4] DeMille D 1995 Phys. Rev. Lett. 74 4165
Google Scholar
[5] Tsigutkin K, Dounas Frazer D, Family A, Stalnaker J E, Yashchuk V V, Budker D 2009 Phys. Rev. Lett. 103 071601
Google Scholar
[6] Antypas D, Fabricant A, Stalnaker J E, Tsigutkin K, Flambaum V, Budker D 2019 Nat. Phys. 15 120
Google Scholar
[7] Tsigutkin K, Dounas Frazer D, Family A, Stalnaker J E, Yashchuk V V, Budker D 2010 Phys. Rev. A 81 032114
Google Scholar
[8] Dzuba V, Flambaum V 2011 Phys. Rev. A 83 042514
Google Scholar
[9] Stalnaker J, Budker D, DeMille D, Freedman S, Yashchuk V V 2002 Phys. Rev. A 66 031403
Google Scholar
[10] Sur C, Chaudhuri R K 2007 Phys. Rev. A 76 012509
Google Scholar
[11] Kozlov M, Dzuba V, Flambaum V 2019 Phys. Rev. A 99 012516
Google Scholar
[12] Stone N 2016 At. Data Nucl. Data Tables 111–112 1
Google Scholar
[13] Schwartz C 1955 Phys. Rev. 97 380
Google Scholar
[14] Racah G 1942 Phys. Rev. 62 438
Google Scholar
[15] Andersson M, Jönsson P 2008 Comput. Phys. Commun. 178 156
Google Scholar
[16] Radzig A A, Smirnov B M 2012 Reference Data on Atoms, Molecules, and Ions (Berlin: Springer) p99
[17] Lu B, Lu X, Wang T, Chang H 2022 J. Phys. B: At. Mol. Phys. 55 205002
Google Scholar
[18] Bieroń J, Pyykkö P, Sundholm D, Kellö V, Sadlej A J 2001 Phys. Rev. A 64 052507
Google Scholar
[19] Li J, Godefroid M, Wang J 2016 J. Phys. B: At. Mol. Phys. 49 115002
Google Scholar
[20] Hertel I V, Schulz C P 2014 Atoms, Molecules and Optical Physics (Berlin: Springer) p212
[21] Johnson W R 2007 Atomic Structure Theory (Berlin: Springer) p181
[22] Andersson M, Yao K, Hutton R, Zou Y, Chen C, Brage T 2008 Phys. Rev. A 77 042509
Google Scholar
[23] Li W, Grumer J, Brage T, Jönsson P 2020 Comput. Phys. Commun. 253 107211
Google Scholar
[24] Lu X, Guo F, Wang Y, Feng M, Liang T, Lu B, Chang H 2023 Phys. Rev. A 108 012820
Google Scholar
[25] Johnson W 2010 Can. J. Phys. 89 429
Google Scholar
[26] Grumer J, Brage T, Andersson M, Li J, Jönsson P, Li W, Yang Y, Hutton R, Zou Y 2014 Phys. Scr. 89 114002
Google Scholar
[27] Fischer C F, Brage T, Jönsson P 2022 Computational Atomic Structure: an MCHF Approach (New York: Routledge) p217
[28] Li J, Jönsson P, Godefroid M, Dong C, Gaigalas G 2012 Phys. Rev. A 86 052523
Google Scholar
[29] Jönsson P 1993 Phys. Scr. 48 678
Google Scholar
[30] Jönsson P, Gaigalas G, Fischer C F, Bieroń J, Grant I P, Brage T, Ekman J, Godefroid M, Grumer J, Li J 2023 Atoms 11 68
Google Scholar
[31] Olsen J, Roos B O, Jorgensen P, Jensen H 1988 J. Chem. Phys. 89 2185
Google Scholar
[32] Jönsson P, Godefroid M, Gaigalas G, Ekman J, Grumer J, Li W, Li J, Brage T, Grant I P, Bieroń J, Fischer C F 2023 Atoms 11 7
Google Scholar
[33] Jönsson P, He X, Fischer C F, Grant I 2007 Comput. Phys. Commun. 177 597
Google Scholar
[34] Fischer C F, Gaigalas G, Jönsson P, Bieroń J 2019 Comput. Phys. Commun. 237 184
Google Scholar
[35] Kramida A, Ralchenko Y, Reader J 2023 NIST Atomic Spectra Database (Version 5.11) https://physics.nist.gov/pml/atomic-spectra-database
[36] Bowers C, Budker D, Freedman S, Gwinner G, Stalnaker J, DeMille D 1999 Phys. Rev. A 59 3513
Google Scholar
[37] Beloy K, Sherman J A, Lemke N D, Hinkley N, Oates C W, Ludlow A D 2012 Phys. Rev. A 86 051404
Google Scholar
[38] Ai D, Jin T, Zhang T, Luo L, Liu L, Zhou M, Xu X 2023 Phys. Rev. A 107 063107
Google Scholar
[39] Kronfeldt H D 1998 Phys. Scr. 1998 5
Google Scholar
[40] Porsev S, Rakhlina Y G, Kozlov M 1999 J. Phys. B: At. Mol. Phys. 32 1113
Google Scholar
[41] Holmgren L 1975 Phys. Scr. 12 119
Google Scholar
[42] Zhang T, Xie L, Li J, Lu Z 2017 Phys. Rev. A 96 012514
Google Scholar
[43] Bieroń J, Fischer C F, Jönsson P, Pyykkö P 2008 J. Phys. B: At. Mol. Phys. 41 115002
Google Scholar
[44] Singh A K, Angom D, Natarajan V 2013 Phys. Rev. A 87 012512
Google Scholar
[45] Zehnder A, Boehm F, Dey W, Engfer R, Walter H, Vuilleumier J 1975 Nucl. Phys. A 254 315
Google Scholar
[46] Cheng K, Chen M, Johnson W 2008 Phys. Rev. A 77 052504
Google Scholar
下载:
计量
- 文章访问数: 2688
- PDF下载量: 100
- 被引次数: 0
