-
在以往的腔量子电动力学(QED)系统中原子气通常被处理成单个原子, 从而得到诸如拉比劈裂、单光子阻塞等现象. 受益于超导电路QED的发展, 超导量子比特(SQUID)可以被看成人工原子, 它们之间通过LC谐振子失谐的耦合会构成人工原子间的等效相干耦合. 基于此, 研究了具有相干耦合的多个人工原子对单模腔输入输出的影响, 并从缀饰态的角度对透射谱进行了分析. 结果发现包含多个相干耦合人工原子的单模腔, 其透射谱与只含单个原子的腔显著不同, 更重要的是透射峰的数目并不会随着人工原子数的增加而增加, 最多只有3个透射峰. 为了解释这种透射谱的规律, 应用全量子理论, 计算了整个系统在不含耗散时单能量子情况下的本征值和本征态. 原则上, 有几个粒子, 就会形成几个缀饰态, 理论上就会出现几个透射峰. 然而本文发现存在一些不包含光子成分的缀饰态, 它们并不贡献透射峰. 而原子数增多后会出现透射峰劈裂, 这对应着能级避免交叉现象, 本文从缀饰态角度进行了说明. 从这些缀饰态的具体形式上很多都具有多体纠缠的性质. 因此采用这样一种包含多个相干耦合人工原子的单模腔, 将有利于构建多体纠缠态, 在未来也可以通过透射率的变化, 探知腔内多体纠缠态的形式.In previous cavity quantum electrodynamics (QED) systems, atomic gas is usually treated as single atoms, thereby resulting in phenomena such as Rabi splitting, and single-photon blocking. Benefiting from the development of superconducting circuit QED, the superconducting quantum interference devices (SQUIDs) can be regarded as artificial atoms, and the detuned coupling of them through LC harmonic oscillators will constitute an equivalent coherent coupling between artificial atoms. According to this, we study the effect of multiple artificial atoms with coherent coupling on the input and output of a single-mode cavity, and analyze the transmission spectrum from the perspective of decorated state. We find that single-mode cavities containing multiple artificial atoms with coherent coupling have significantly different transmittances from cavities containing single atoms, the transmission spectra of which are correlated with the coherent coupling coefficients between the artificial atoms, and the coupling coefficients between the cavity modes and the artificial atoms, and we also find that both the cavity mode leakage rate and the artificial atom decay rate are related to each other. And as the number of artificial atoms increases, the number of transmission peaks does not increase, and there are only three transmission peaks at most. In order to explain the law of this transmission spectrum, we quantize both artificial atoms and cavity modes, and calculate the eigenvalues and eigenstates of the whole in a single quantum case. In principle, if there are several particles, they will form several decorative states, and there will theoretically appear several transmission peaks. However, we find that there are some decorated states that do not contain the photonic component and thus do not contribute to the transmission peak. From the specific form of these decorated states, many of them have the property of many-body entanglement. Therefore, using such a single-mode cavity containing multiple coherently coupled artificial atoms, we can construct the required many-body entangled state by simply inputting weak monochromatic light, and at the same time, we can sense the forms of multi-body entanglement states in the cavity through the change of transmittance.
-
Keywords:
- cavity quantum electrodynamics /
- interatomic coherent coupling /
- input-output relationship
[1] Purcell E M 1946 Phys. Rev. 69 681
[2] Jaynes E T, Cummings F W 1963 Proc. IEEE 51 89
Google Scholar
[3] Haroche S, Kleppner D 1989 Phys. Today 42 24
Google Scholar
[4] Gardiner C W, Collett M J 1985 Phys. Rev. A 31 3761
Google Scholar
[5] Auffèves-Garnier A, Simon C, Gérard J M, Poizat J P 2007 Phys. Rev. A 75 053823
Google Scholar
[6] Xia X W, Xu J P, Yang Y P 2014 Phys. Rev. A 90 043857
Google Scholar
[7] Li H Z, Xu J P, Wang D W, Xia X W, Yang Y P, Zhu S Y 2017 Phys. Rev. A 96 013832
Google Scholar
[8] Yang P F, Xia X W, He H, Li S K, Han X, Zhang P, Li G, Zhang P F, Xu J P, Yang Y P, Zhang T C 2019 Phys. Rev. Lett. 123 233604
Google Scholar
[9] Reimann R, Alt W, Kampschulte T, Macha T, Ratschbacher L, Thau N, Yoon S, Meschede D 2015 Phys. Rev. Lett. 114 023601
Google Scholar
[10] Pleinert M O, Zanthier J V, Agarwal G S 2017 Optica 4 000779
Google Scholar
[11] Xu J P, Chang S L, Yang Y P, Zhu S Y, Agarwal G S 2017 Phys. Rev. A 96 013839
Google Scholar
[12] Li N, Jiang H W, Xia X W, Zhu C J, Xie S Y, Xu J P, Yang Y P 2021 Phys. Lett. A 420 127772
Google Scholar
[13] Liu Q, Li M M, Dai K Z, Zhang K, Xue G M, Tan X S, Yu H F, Yu Y 2017 Appl. Phys. Lett. 110 232602
Google Scholar
[14] Rosenberg D, Kim D, Das R, Yost D, Gustavsson S, Hover D, Krantz P, Melville A, Racz L, Samach G O, Weber S J, Yan F, Yoder J L, Kerman A J, Oliver W D 2017 NPJ Quantum Inf. 3 42
Google Scholar
[15] Dunsworth A, Barends R, Chen Y, Chen Z J, Chiaro B, Fowler A, Foxen B, Jeffrey E, Kelly J, Klimov P V, Lucero E, Mutus J Y, Neeley M, Neill C, Quintana C, Roushan P, Sank D, Vainsencher A, Wenner J, White T C, Neven H, Martinis J M, Megrant A 2018 Appl. Phys. Lett. 112 063502
Google Scholar
[16] Nie W, Peng Z H, Nori F, Liu Y X 2020 Phys. Rev. Lett. 124 023603
Google Scholar
[17] Nie W, Liu Y X 2020 Phys. Rev. Res. 2 012076
Google Scholar
[18] Alsing P M, Cardimona D A, Carmichael H J 1992 Phys. Rev. A 45 1793
Google Scholar
[19] Sames C, Chibani H, Hamsen C, Altin P A, Wilk T, Rempe G 2014 Phys. Rev. Lett. 112 043601
Google Scholar
[20] Plankensteiner D, Sommer C, Ritsch H, Genes C 2017 Phys. Rev. Lett. 119 093601
Google Scholar
[21] Lizuain I, Concepción E H, Muga J G 2009 Phys. Rev. A 79 065602
Google Scholar
[22] 鹿利单, 祝连庆, 曾周末, 崔一平, 张东亮, 袁配 2021 70 034204
Google Scholar
Lu L D, Zhu L Q, Zeng Z M, Cui Y P, Zhang D L, Yuan P 2021 Acta Phys. Sin. 70 034204
Google Scholar
-
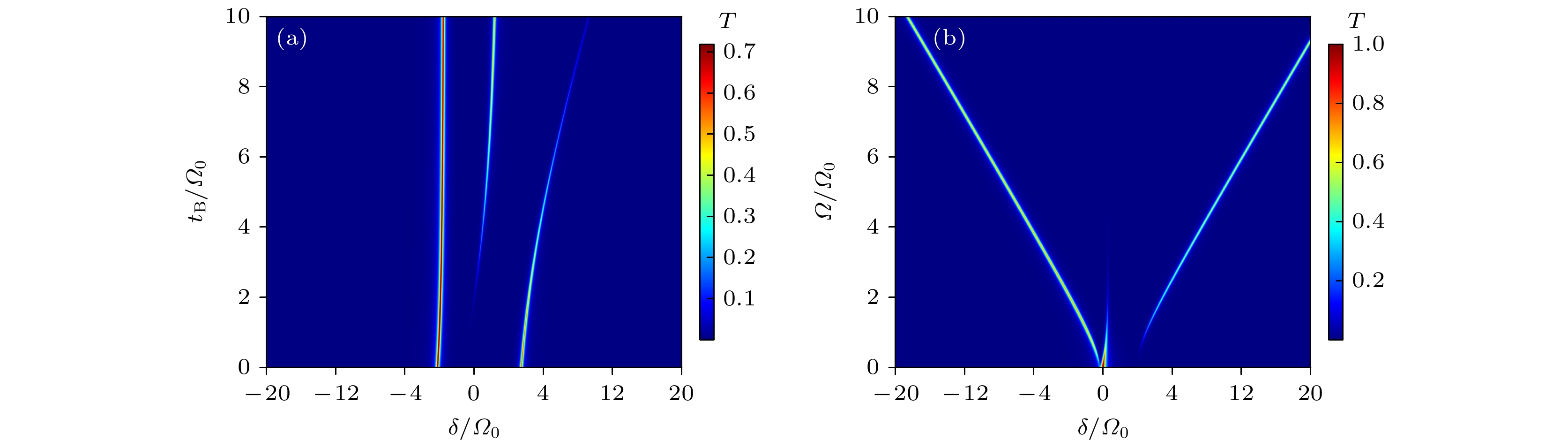
图 2 腔中存在一组共两个人工原子时, 透射率随入射场与腔模失谐
$\delta $ 和原子间耦合$ {t_{\text{A}}} $ 的变化 (a)双原子与腔模的耦合强度一致,${\varOmega _1} = {\varOmega _2} = {\varOmega _0}$ ; (b)双原子与腔模的耦合强度不同,${\varOmega _1} = 2{\varOmega _0}, {\varOmega _2} = 0.1{\varOmega _0}$ , 采用参数$\kappa = \gamma = {\text{0}}{\text{.1}}{\varOmega _0}$ Fig. 2. In the case of a set of altogether two artificial atoms in the cavity, transmittance varies with the detuning
$\delta $ between incident field and cavity mode and interatomic coupling$ {t_{\text{A}}} $ : (a) The coupling strength of diatoms and cavity mode is consistent,${\varOmega _1} = {\varOmega _2} = {\varOmega _0}$ ; (b) the coupling strength between diatoms and cavity modes is different,${\varOmega _1} = 2{\varOmega _0}, {\varOmega _2} = 0.1{\varOmega _0}$ , the parameters are$\kappa = \gamma = {\text{0}}{\text{.1}}{\varOmega _0}$ .
图 3 腔中存在两组共4个人工原子时, (a) 透射谱随原子间耦合强度
${t_{\text{B}}}$ 的变化,$\varOmega = 2{\varOmega _0}$ ; (b) 透射谱随原子与腔模耦合强度$\varOmega $ 的变化,${t_{\text{B}}} = 3{\varOmega _0}$ . 采用参数为${t_{\text{A}}} = {\varOmega _0}, \kappa = 0.2{\varOmega _0}, \gamma = 0.1{\varOmega _0}$ Fig. 3. (a) In the case of two sets of altogether four artificial atoms in the cavity, transmission spectrum varies with the interatomic coupling intensity
${t_{\text{B}}}$ ,$\varOmega = 2{\varOmega _0}$ ; (b) The transmission spectrum varies with the coupling strength$\varOmega $ between the atom and the cavity mode,${t_{\text{B}}} = 3{\varOmega _0}$ . The parameters are${t_{\text{A}}} = {\varOmega _0}, \kappa = 0.2{\varOmega _0}, \gamma = 0.1{\varOmega _0}$ .
图 4 腔中存在3组共6个人工原子时, (a) 透射谱随原子间耦合强度
${t_{\text{B}}}$ 的变化,$\varOmega = 2{\varOmega _0}$ ; (b) 透射谱随原子与腔模耦合强度$\varOmega $ 的变化,${t_{\text{B}}} = 3{\varOmega _0}$ . 采用参数为${t_{\text{A}}} = {\varOmega _0}, \kappa = 0.2{\varOmega _0}, \gamma = 0.1{\varOmega _0}$ , 红圈内为本文定义的劈裂Fig. 4. (a) In the case of three sets of altogether six artificial atoms in the cavity, transmission spectrum varies with the interatomic coupling intensity
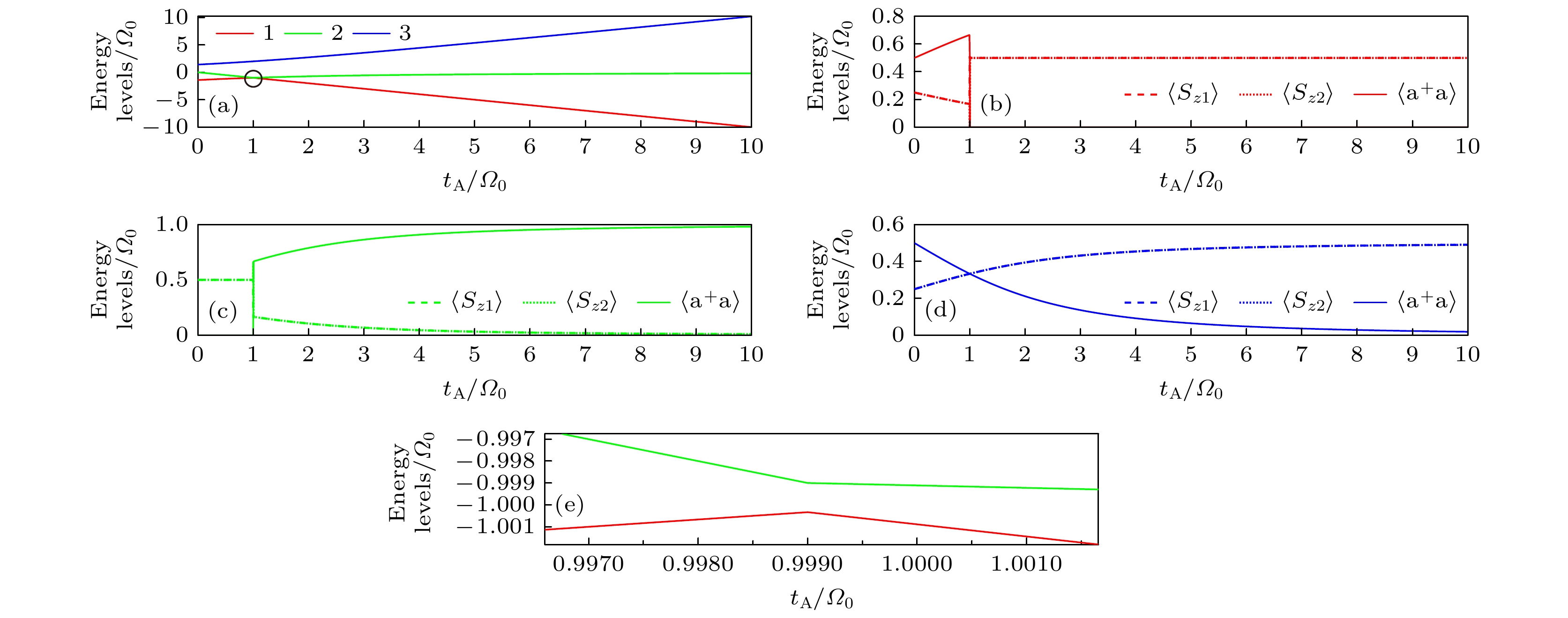
${t_{\text{B}}}$ ,$\varOmega = 2{\varOmega _0}$ ; (b) the transmission spectrum varies with the coupling strength$\varOmega $ between the atom and the cavity mode,${t_{\text{B}}} = 3{\varOmega _0}$ . The parameters are${t_{\text{A}}} = {\varOmega _0}, \kappa = 0.2{\varOmega _0}, \gamma = 0.1{\varOmega _0}$ . The splits defined in this article are circled in red.
图 5 腔内双原子条件下, (a)缀饰态的能级; (b)—(d)各能级对应的原子占据数
$ \left\langle{{S}_{zi}}\right\rangle $ 与腔内平均光子数$ \left\langle{{a}^{+}a}\right\rangle $ 随${t_{\text{A}}}$ 的变化; (e)避免交叉点放大图. 其他参数为${\varOmega _1} = {\varOmega _2} = {\varOmega _0}$ ; 按照本征值从小到大分别用红、绿、蓝三色代表不同的本征态Fig. 5. In the case of two atoms in the cavity, (a) the energy levels of the dressed states; (b)–(d) the corresponding atomic excitation probability of each energy level and the average number of photons in the cavity change with
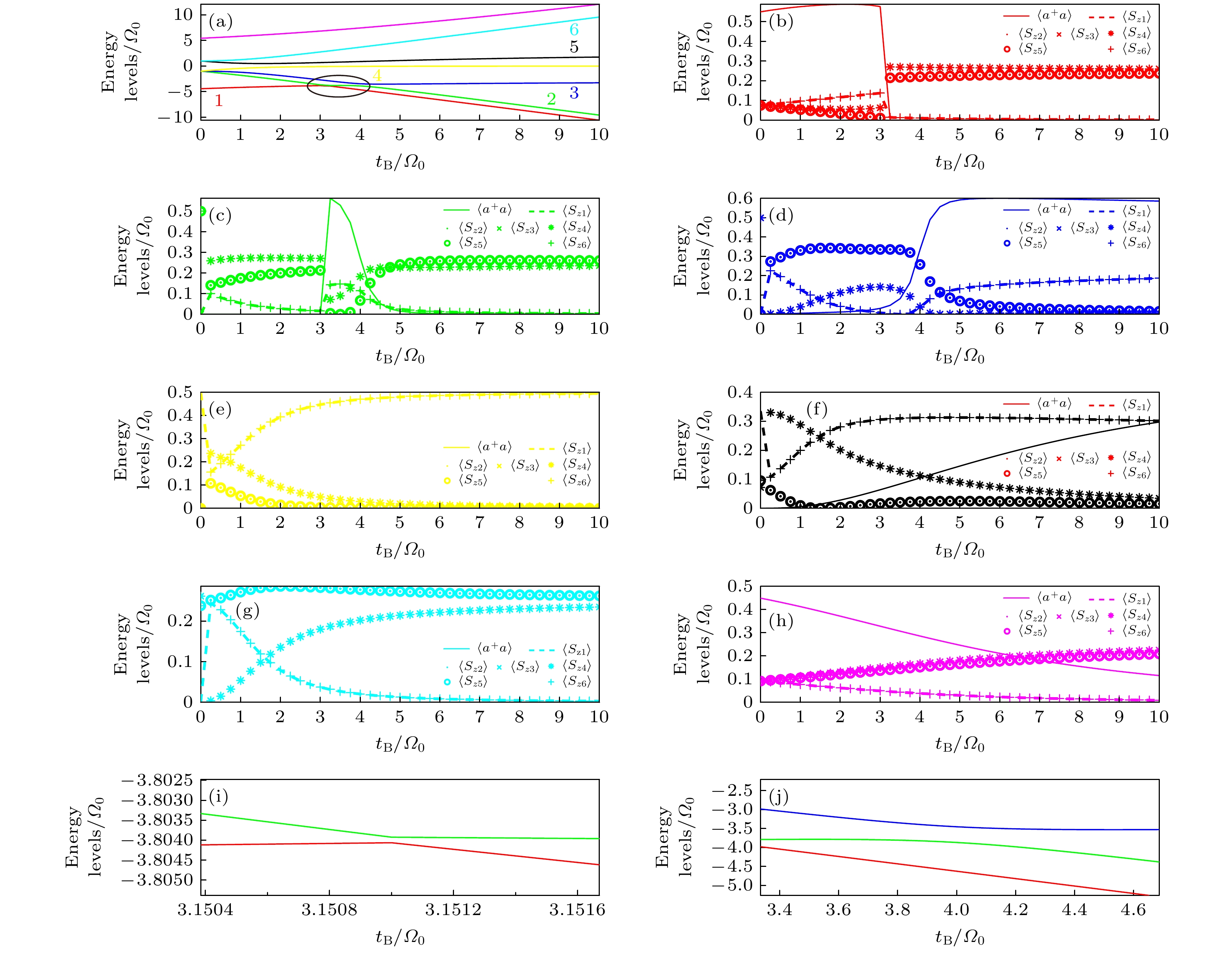
${t_{\text{A}}}$ ; (e) a larger version of avoid crossing points. The parameters are${\varOmega _1} = {\varOmega _2} = {\varOmega _0}$ . The eigen states are represented by red, green, and blue in order of eigen values from smallest to largest.
图 6 腔内六原子条件下, (a)缀饰态的能级; (b)—(h)各能级对应的原子占居数
$ \left\langle{{S}_{zi}}\right\rangle $ 与腔内平均光子数$ \left\langle{{a}^{+}a}\right\rangle $ 随${t_{\text{B}}}$ 的变化; (i), (j)避免交叉点放大图. 采用参数为$\varOmega = 2{\varOmega _0}, {t_{\text{A}}} = {\varOmega _0}$ ; 不同颜色分别代表不同的能级, 并依照本征值的大小编号Fig. 6. In the case of six atoms in the cavity, (a) the energy levels of the dressed states; (b)–(h) the corresponding atomic excitation probability of each energy level and the average number of photons in the cavity change with
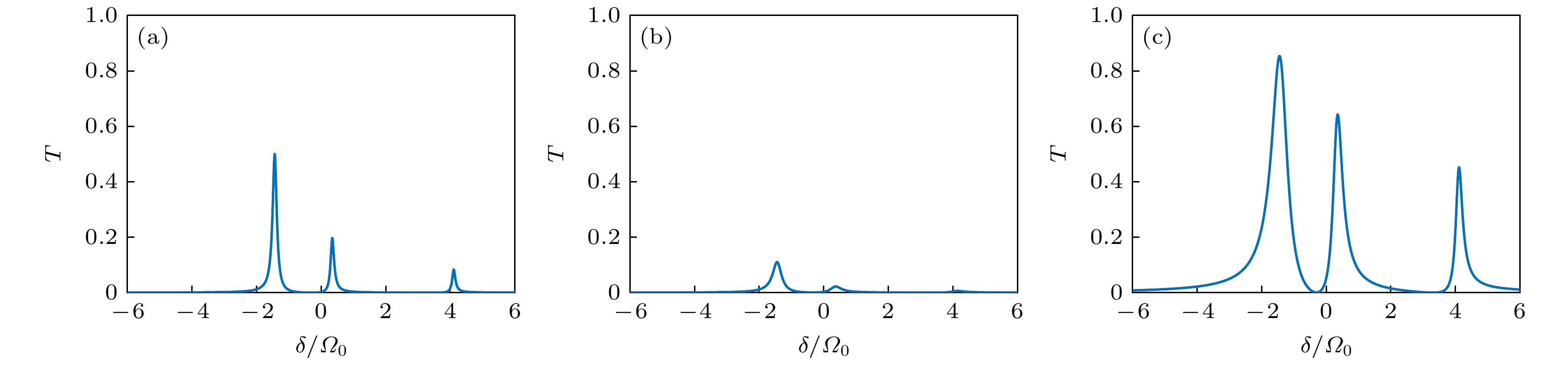
${t_{\text{B}}}$ ; (i), (j) two larger versions of avoid crossing points. The parameters are$\varOmega = 2{\varOmega _0}, {t_{\text{A}}} = {\varOmega _0}$ . Different colors represent different energy levels and are numbered according to the magnitude of the eigenvalue.
图 7 (a)
$\kappa = \gamma = {\text{0}}{\text{.1}}{\varOmega _0}$ 条件下的透射谱; (b)原子自发衰减增大后的透射谱,$ \kappa = {\text{0}}{\text{.1}}{\varOmega _0}, {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} \gamma = {\text{0}}{\text{.5}}{\varOmega _0} $ ; (c)腔的泄漏率增大后的透射谱,$\kappa = {\text{0}}{\text{.5}}{\varOmega _0}, \gamma = {\text{0}}{\text{.1}}{\varOmega _0}$ . 采用参数为$\varOmega = {\varOmega _0}, {t_{\text{A}}} = {\varOmega _0}, {t_{\text{B}}} = 3{\varOmega _0}$ Fig. 7. (a) Transmission spectrum under
$\kappa = \gamma = {\text{0}}{\text{.1}}{\varOmega _0}$ ; (b) the transmission spectrum after the increase of atomic spontaneous attenuation,$ \kappa = {\text{0}}{\text{.1}}{\varOmega _0}, {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} \gamma = {\text{0}}{\text{.5}}{\varOmega _0} $ ; (c) the transmission spectrum after the increase of leakage rate of cavity,$\kappa = {\text{0}}{\text{.5}}{\varOmega _0}, $ $ \gamma = {\text{0}}{\text{.1}}{\varOmega _0}$ . The parameters are$\varOmega = {\varOmega _0}, {t_{\text{A}}} = {\varOmega _0}, {t_{\text{B}}} = 3{\varOmega _0}$ . -
[1] Purcell E M 1946 Phys. Rev. 69 681
[2] Jaynes E T, Cummings F W 1963 Proc. IEEE 51 89
Google Scholar
[3] Haroche S, Kleppner D 1989 Phys. Today 42 24
Google Scholar
[4] Gardiner C W, Collett M J 1985 Phys. Rev. A 31 3761
Google Scholar
[5] Auffèves-Garnier A, Simon C, Gérard J M, Poizat J P 2007 Phys. Rev. A 75 053823
Google Scholar
[6] Xia X W, Xu J P, Yang Y P 2014 Phys. Rev. A 90 043857
Google Scholar
[7] Li H Z, Xu J P, Wang D W, Xia X W, Yang Y P, Zhu S Y 2017 Phys. Rev. A 96 013832
Google Scholar
[8] Yang P F, Xia X W, He H, Li S K, Han X, Zhang P, Li G, Zhang P F, Xu J P, Yang Y P, Zhang T C 2019 Phys. Rev. Lett. 123 233604
Google Scholar
[9] Reimann R, Alt W, Kampschulte T, Macha T, Ratschbacher L, Thau N, Yoon S, Meschede D 2015 Phys. Rev. Lett. 114 023601
Google Scholar
[10] Pleinert M O, Zanthier J V, Agarwal G S 2017 Optica 4 000779
Google Scholar
[11] Xu J P, Chang S L, Yang Y P, Zhu S Y, Agarwal G S 2017 Phys. Rev. A 96 013839
Google Scholar
[12] Li N, Jiang H W, Xia X W, Zhu C J, Xie S Y, Xu J P, Yang Y P 2021 Phys. Lett. A 420 127772
Google Scholar
[13] Liu Q, Li M M, Dai K Z, Zhang K, Xue G M, Tan X S, Yu H F, Yu Y 2017 Appl. Phys. Lett. 110 232602
Google Scholar
[14] Rosenberg D, Kim D, Das R, Yost D, Gustavsson S, Hover D, Krantz P, Melville A, Racz L, Samach G O, Weber S J, Yan F, Yoder J L, Kerman A J, Oliver W D 2017 NPJ Quantum Inf. 3 42
Google Scholar
[15] Dunsworth A, Barends R, Chen Y, Chen Z J, Chiaro B, Fowler A, Foxen B, Jeffrey E, Kelly J, Klimov P V, Lucero E, Mutus J Y, Neeley M, Neill C, Quintana C, Roushan P, Sank D, Vainsencher A, Wenner J, White T C, Neven H, Martinis J M, Megrant A 2018 Appl. Phys. Lett. 112 063502
Google Scholar
[16] Nie W, Peng Z H, Nori F, Liu Y X 2020 Phys. Rev. Lett. 124 023603
Google Scholar
[17] Nie W, Liu Y X 2020 Phys. Rev. Res. 2 012076
Google Scholar
[18] Alsing P M, Cardimona D A, Carmichael H J 1992 Phys. Rev. A 45 1793
Google Scholar
[19] Sames C, Chibani H, Hamsen C, Altin P A, Wilk T, Rempe G 2014 Phys. Rev. Lett. 112 043601
Google Scholar
[20] Plankensteiner D, Sommer C, Ritsch H, Genes C 2017 Phys. Rev. Lett. 119 093601
Google Scholar
[21] Lizuain I, Concepción E H, Muga J G 2009 Phys. Rev. A 79 065602
Google Scholar
[22] 鹿利单, 祝连庆, 曾周末, 崔一平, 张东亮, 袁配 2021 70 034204
Google Scholar
Lu L D, Zhu L Q, Zeng Z M, Cui Y P, Zhang D L, Yuan P 2021 Acta Phys. Sin. 70 034204
Google Scholar
下载:
计量
- 文章访问数: 3529
- PDF下载量: 56
- 被引次数: 0
