-
本文基于最新构建的
${{\rm{SiH}}_2^+}({\tilde{\rm{X}}}{}^{3}{\rm{A}}'')$ 势能面, 运用切比雪夫波包方法, 对初始态为$ \nu = 0, j = 0 $ 的${\text{D}} + {\text{Si}}{{\text{D}}^ + } $ 反应体系在$ 1.0 \times {10^{ - 3}} $ —1.0 eV的碰撞能量范围内进行动力学研究. 通过对角动量量子数$ J \leqslant 110 $ 的所有分波进行计算, 运用耦合态近似和考虑科里奥利耦合效应的精确量子力学两种方法, 得到该反应的反应概率、积分散射截面和速率常数. 文章详细分析了碰撞能量和科里奥利耦合效应对该反应的动力学性质的影响, 并与H+SiH+反应做了对比. 结果表明, 忽略科里奥利耦合效应会使D +SiD+反应积分散射截面和速率常数增大. 与H+SiH+反应动力学相比较, D +SiD+反应的积分反应截面的值较小且随着能量的衰减非常缓慢, 在低能区没有H+SiH+随能量增大而剧烈衰减的情况. 计算发现, 相同温度下, D +SiD+反应速率常数小于H +SiH+反应速率常数, 随着温度的升高, 二者的差距减小. 这表明, 同位素替代对反应的动力学性质有明显的影响.The quantum dynamics calculations are carried out for the title reaction D +SiD+→D2+Si+ to obtain the initial ($ \nu = 0{\text{ }},j = 0 $ )reaction probability, integral cross section (ICS) and rate constant on the potential energy surface (PES) of Gao, Meng and Song. A total of 110 partial waves are calculated by using the Chebyshev wave packet method with full Coriolis coupling (CC) and centrifugal sudden (CS) approximation in a collision energy range from 1.0 × 10–3 to 1.0 eV. The calculated probability decreases with the collision energy increasing except for J≤40. The calculation results indicate that the CS approximation will overestimate or underestimate the reaction probability . The ICS decreases with the collision energy increasing and shows an oscillatory structure due to the$\rm{SiH_2^+} $ well on the reaction path. The results show that the neglect of the Coriolis coupling leads to the overestimation of the cross section and the rate constant. Besides, the discrepancy between the integral cross sections from the CC and CS calculations decreases clearly with collision energy increasing. Comparison with the corresponding results of H+CH+ reaction indicates that isotope substitution reaction makes the cross section and the rate constant underestimated. The resulting integral reaction cross section displays less oscillatory structure, especially in the exact quantum calculation with the full Coriolis coupling effect taken into consideration. The kinetic isotope effect$(\kappa_{\rm H+SiH^+}(T)/\kappa_{\rm D+SiD^+}(T))$ is found to decrease with temperature increasing. It can be seen that the reduced mass of reactant can exert a certain effect on dynamic behavior.-
Keywords:
- Chebyshev wave packet method /
- reaction probability /
- integral cross section /
- rate constant
[1] Bender C F, Schaefer H F 1971 J. Mol. Spectrosc. 37 423
Google Scholar
[2] Stoecklin T, Halvick P 2005 Phys. Chem. Chem. Phys. 7 2446
Google Scholar
[3] Warmbier R, Schneider R 2011 Phys. Chem. Chem. Phys. 13 10285
Google Scholar
[4] Herráez-Aguilar D, Jambrina P G, Menéndez M, Aldegunde J, Warmbier R, Aoiz F J 2014 Phys. Chem. Chem. Phys. 16 24800
Google Scholar
[5] Li Y Q, Zhang P Y, Han K L 2015 J. Chem. Phys. 142 124302
Google Scholar
[6] Guo J, Zhang A J, Zhou Y, Liu J Y, Jia J F, Wu H S 2017 Chem. Phys. Lett. 689 121
Google Scholar
[7] Sundaram P, Manivannan V, Padmanaban R 2017 Phys. Chem. Chem. Phys. 19 20172
Google Scholar
[8] Scheier P, Marsen B, Lonfat M, Schneider W D 2000 Surf. Sci. 458 113
Google Scholar
[9] Maus M, Gantefor G, Eberhardt W 2000 Appl. Phys. A 70 535
Google Scholar
[10] Kasap S, Capper P 2017 Springer Handbook of Electronic and Photonic Materials (Heidelberg: Springer) pp573–576
[11] Zhang Y G, Dou G, Cui J, Yu Y 2018 J. Mol. Struct. 1165 318
Google Scholar
[12] Bauer C, Hirst D M, Hall D I, Sarre P J, Rosmus P J. 1994 Chem. Sot. Faraday Trans. 90 517
Google Scholar
[13] Vach H, Chaâbane N, Peslherbe G H 2002 Chem. Phys. Lett. 352 127
Google Scholar
[14] Chaâbane N, Vach H, Cabarrocas P R I 2004 J. Phys. Chem. A 108 1818
Google Scholar
[15] Gao F, Zhang L L, Zhao W L, Meng Q T, Song Y Z 2019 J. Chem. Phys. 150 224304
Google Scholar
[16] Langhoff S R, Davidson E R 1974 Int. J. Quantum Chem. 8 61
Google Scholar
[17] 高峰 2020 博士学位论文 (济南: 山东师范大学)
Gao F 2020 Ph. D. Dissertation (Jinan: Shandong Normal University) (in Chinese)
[18] Zhao W L, Tan R S, Cao X C, Gao F, Meng Q T 2021 Chin. Phys. B 30 123403
Google Scholar
[19] 王茗馨, 王美山, 杨传路, 刘佳, 马晓光, 王立志 2015 64 043402
Google Scholar
Wang M X, Wang M S, Yang C L, Liu J, Ma X G, Wang L Z 2015 Acta Phys. Sin. 64 043402
Google Scholar
[20] 夏文泽, 于永江, 杨传路 2012 61 223401
Google Scholar
Xia W Z, Yu Y J, Yang C L 2012 Acta Phys. Sin 61 223401
Google Scholar
[21] Guo L, Yang Y F, Fan X X, Ma F C, Li Y Q 2017 Commun. Theor. Phys. 67 549
Google Scholar
[22] Zhang J Z H 1999 Theory and Application of Quantum Molecular Dynamics (Singapore: World Scientific) pp149–150
[23] Lin S Y, Guo H 2003 J. Chem. Phys. 119 11602
Google Scholar
[24] Mandelshtam V A, Taylor H S 1995 J. Chem. Phys. 102 7390
Google Scholar
[25] Mandelshtam V A, Taylor H S 1995 J. Chem. Phys. 103 2903
Google Scholar
[26] Tal-Ezer H, Kosloff R 1984 J. Chem. Phys. 81 3967
Google Scholar
[27] Neuhauser D, Baer M, Judson R S, Kouri D J 1990 J. Chem. Phys. 93 312
Google Scholar
[28] Althorpe S C 2001 J. Chem. Phys. 114 1601
Google Scholar
[29] Zhai H C, Lin S Y 2015 Chem. Phys. 455 57
Google Scholar
[30] Bowman J M 1991 J. Phys. Chem. 95 4960
Google Scholar
[31] Gray S K, Goldfield, E M, Schatz G C, Balint-Kurti G G 1999 Phys. Chem. Chem. Phys. 1 1141
Google Scholar
[32] Clary D C 1984 Mol. Phys. 53 3
Google Scholar
[33] Chu T S, Han K L 2008 Phys. Chem. Chem. Phys. 10 2431
Google Scholar
[34] De Fazio D, Castillo J F 1999 Phys. Chem. Chem. Phys. 1 1165
Google Scholar
[35] Lu R F, Wang Y H, Deng K M, 2013 J. Comput. Chem. 34 1735
Google Scholar
-
图 1
${\rm{Si{H}}}_2^+(\rm{X^2A_1}) $ 势能面(∠[H-Si-H] = 118.38º), 图中等势线间隔为0.2 eV, 红色实线为最小能量路径Fig. 1. The PES of
${\rm{Si{H}}}_2^+ $ (X2A1) for bending angle∠[H-Si-H] = 118.38º starting from–5.82 eV, the contour drawn with an increment of 0.2 eV, the solid red line is minimum energy path.
图 2 最小能量路径(∠[D-Si-D]分别为30°, 60°, 90°, 120°, 180°)
Fig. 2. The MEP of different approaching angles (∠[D-Si-D] = 30°, 60°, 90°, 120°, 180°)for the title reaction.
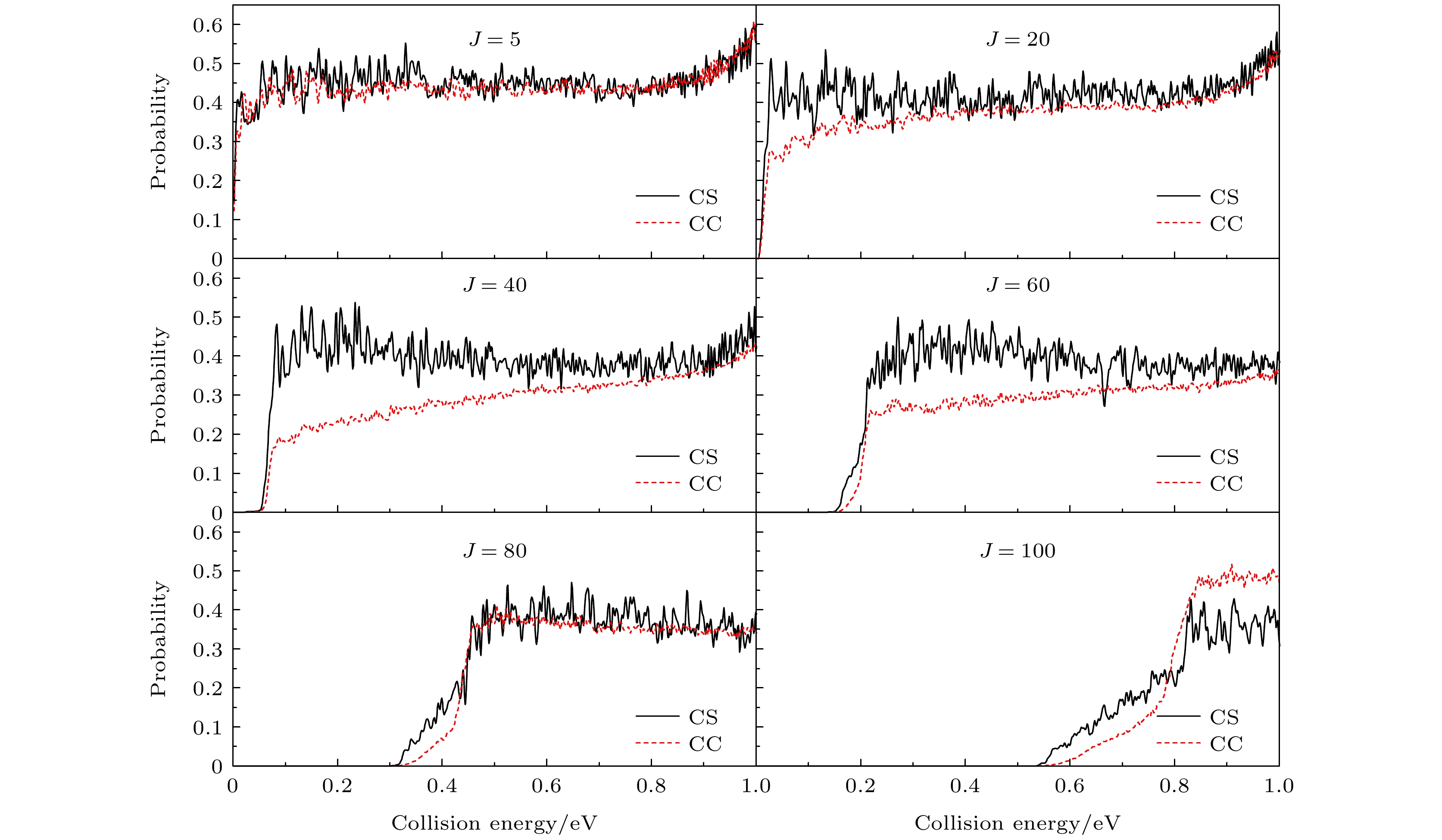
图 3
$ {\text{D}} + {\text{Si}}{{\text{D}}^ + } \to {{\text{D}}_2} + {\text{S}}{{\text{i}}^ + } $ 反应不同分波 (J = 5, 20, 40, 60, 80, 100)的反应概率随碰撞能量的变化, 黑色实线对应CS概率, 红色虚线对应CC概率Fig. 3. The reaction probabilities of CC and CS calculations for
$ {\text{D}} + {\text{Si}}{{\text{D}}^ + } \to {{\text{D}}_2} + {\text{S}}{{\text{i}}^ + } $ reaction at J = 5, 20, 40, 60, 80, and 100, The black soid line is for CS probability and the red dashed line is for CC probability.
图 4 不同的角动量量子数下H+SiH+与D+SiD+的CC反应概率, 黑色实线对应H+SiH+反应, 红色虚线对应D+SiD+反应
Fig. 4. The reaction probabilities of CC calculations for H +SiH+ and D +SiD+ reactions at J = 10, 20, 40, 60, 80, and 90. The black solid line is for H + SiH+ reaction and the red dashed line is for D +SiD+ reaction.
图 5 H + SiH+与D + SiD+反应 ICS 随着碰撞能量的变化(1.0 ×10–3—1.0 eV)
Fig. 5. The ICSs of CS and CC calculations for H+ SiH+ and D +SiD+ reactions over collision energy of 3 1.0 ×10–3—1.0 eV.
图 6 H+ SiH+和
$ {\text{D}} + {\text{Si}}{{\text{D}}^ + } $ 反应速率常数随温度的变化Fig. 6. Variation of reaction rate constant of H+ SiH+ and
$ {\text{D}} + {\text{Si}}{{\text{D}}^ + } $ with temperature.表 1 波包计算中的数值参量(除特殊说明, 均采用原子单位 a.u.)
Table 1. Model parameters of wave packet calculation (The atomic unit is used in the calculation unlessotherwise stated).
坐标取值范围和基组数 吸收势 初始波包 光谱控制 流计算的位置 传播步数 $ R \in (0.2, \, 22) \; ({N_R} = 383) $
$ r \in (0.5, \, 16) \; ({N_r} = 255) $
$ \gamma \in (0, \, {180^ \circ }) \; ({N_\gamma } = 200) $$ {R_d} = 18.0 \;\; {d_R} = 0.0005 $
$ {r_d} = 14.0 \;\; {d_r} = 0.001 $$ {R_0} = 16.0 $
$ {E_0} = 0.15{\text{ eV}} $
$ \delta = 0.3 $1.0 $ {r_f} = 13.8 $ 50000 
下载: 导出CSV
-
[1] Bender C F, Schaefer H F 1971 J. Mol. Spectrosc. 37 423
Google Scholar
[2] Stoecklin T, Halvick P 2005 Phys. Chem. Chem. Phys. 7 2446
Google Scholar
[3] Warmbier R, Schneider R 2011 Phys. Chem. Chem. Phys. 13 10285
Google Scholar
[4] Herráez-Aguilar D, Jambrina P G, Menéndez M, Aldegunde J, Warmbier R, Aoiz F J 2014 Phys. Chem. Chem. Phys. 16 24800
Google Scholar
[5] Li Y Q, Zhang P Y, Han K L 2015 J. Chem. Phys. 142 124302
Google Scholar
[6] Guo J, Zhang A J, Zhou Y, Liu J Y, Jia J F, Wu H S 2017 Chem. Phys. Lett. 689 121
Google Scholar
[7] Sundaram P, Manivannan V, Padmanaban R 2017 Phys. Chem. Chem. Phys. 19 20172
Google Scholar
[8] Scheier P, Marsen B, Lonfat M, Schneider W D 2000 Surf. Sci. 458 113
Google Scholar
[9] Maus M, Gantefor G, Eberhardt W 2000 Appl. Phys. A 70 535
Google Scholar
[10] Kasap S, Capper P 2017 Springer Handbook of Electronic and Photonic Materials (Heidelberg: Springer) pp573–576
[11] Zhang Y G, Dou G, Cui J, Yu Y 2018 J. Mol. Struct. 1165 318
Google Scholar
[12] Bauer C, Hirst D M, Hall D I, Sarre P J, Rosmus P J. 1994 Chem. Sot. Faraday Trans. 90 517
Google Scholar
[13] Vach H, Chaâbane N, Peslherbe G H 2002 Chem. Phys. Lett. 352 127
Google Scholar
[14] Chaâbane N, Vach H, Cabarrocas P R I 2004 J. Phys. Chem. A 108 1818
Google Scholar
[15] Gao F, Zhang L L, Zhao W L, Meng Q T, Song Y Z 2019 J. Chem. Phys. 150 224304
Google Scholar
[16] Langhoff S R, Davidson E R 1974 Int. J. Quantum Chem. 8 61
Google Scholar
[17] 高峰 2020 博士学位论文 (济南: 山东师范大学)
Gao F 2020 Ph. D. Dissertation (Jinan: Shandong Normal University) (in Chinese)
[18] Zhao W L, Tan R S, Cao X C, Gao F, Meng Q T 2021 Chin. Phys. B 30 123403
Google Scholar
[19] 王茗馨, 王美山, 杨传路, 刘佳, 马晓光, 王立志 2015 64 043402
Google Scholar
Wang M X, Wang M S, Yang C L, Liu J, Ma X G, Wang L Z 2015 Acta Phys. Sin. 64 043402
Google Scholar
[20] 夏文泽, 于永江, 杨传路 2012 61 223401
Google Scholar
Xia W Z, Yu Y J, Yang C L 2012 Acta Phys. Sin 61 223401
Google Scholar
[21] Guo L, Yang Y F, Fan X X, Ma F C, Li Y Q 2017 Commun. Theor. Phys. 67 549
Google Scholar
[22] Zhang J Z H 1999 Theory and Application of Quantum Molecular Dynamics (Singapore: World Scientific) pp149–150
[23] Lin S Y, Guo H 2003 J. Chem. Phys. 119 11602
Google Scholar
[24] Mandelshtam V A, Taylor H S 1995 J. Chem. Phys. 102 7390
Google Scholar
[25] Mandelshtam V A, Taylor H S 1995 J. Chem. Phys. 103 2903
Google Scholar
[26] Tal-Ezer H, Kosloff R 1984 J. Chem. Phys. 81 3967
Google Scholar
[27] Neuhauser D, Baer M, Judson R S, Kouri D J 1990 J. Chem. Phys. 93 312
Google Scholar
[28] Althorpe S C 2001 J. Chem. Phys. 114 1601
Google Scholar
[29] Zhai H C, Lin S Y 2015 Chem. Phys. 455 57
Google Scholar
[30] Bowman J M 1991 J. Phys. Chem. 95 4960
Google Scholar
[31] Gray S K, Goldfield, E M, Schatz G C, Balint-Kurti G G 1999 Phys. Chem. Chem. Phys. 1 1141
Google Scholar
[32] Clary D C 1984 Mol. Phys. 53 3
Google Scholar
[33] Chu T S, Han K L 2008 Phys. Chem. Chem. Phys. 10 2431
Google Scholar
[34] De Fazio D, Castillo J F 1999 Phys. Chem. Chem. Phys. 1 1165
Google Scholar
[35] Lu R F, Wang Y H, Deng K M, 2013 J. Comput. Chem. 34 1735
Google Scholar
-
[1] 周勇. F+CHD3→HF+CD3反应C—H伸缩振动激发的量子动力学研究. , 2024, 73(9): 098201. doi: 10.7498/aps.73.20231832 [2] 赵文丽, 宋玉志, 马超, 高峰, 孟庆田. 基于一个新SiH2(11A′)势能面的H+SiH反应动力学研究. , 2024, 73(20): 203401. doi: 10.7498/aps.73.20240859 [3] 赵文丽, 王永刚, 张路路, 岳大光, 孟庆田. 基于新CH2( ${\tilde {\bf{X}}{}^3}{\bf{A''}}$ )势能面的${\bf C}{\bf({}^3}{\bf{P})} + {\bf{H}_2(}{\bf X^1}\Sigma _{\bf g}^ + {\bf )} $ $ \to {\bf H({}^2}{\bf S}) + {\bf CH}{(\bf{}^2}\Pi ) $ 反应量子波包动力学. , 2020, 69(8): 083401. doi: 10.7498/aps.69.20200132[4] 袁方园, 朱子亮. D + DBr反应的态-态动力学研究. , 2020, 69(11): 113401. doi: 10.7498/aps.69.20200321 [5] 袁美玲, 李文涛. O++H2 → OH++H反应的动力学研究. , 2019, 68(8): 083401. doi: 10.7498/aps.68.20182141 [6] 李文涛, 于文涛, 姚明海. 采用量子含时波包方法研究H/D+Li2LiH/LiD+Li反应. , 2018, 67(10): 103401. doi: 10.7498/aps.67.20180324 [7] 吕子瑶, 潘雨佳, 王长顺. 不同类型偶氮材料光致双折射的温度特性研究. , 2017, 66(24): 244203. doi: 10.7498/aps.66.244203 [8] 张静, 魏巍, 高守宝, 孟庆田. H+Li2: 一个典型的释能反应体系及其含时动力学研究. , 2015, 64(6): 063101. doi: 10.7498/aps.64.063101 [9] 何晶, 苗强, 吴德伟. 微波-光波变电长度缩比条件下目标雷达散射截面相似性研究. , 2014, 63(20): 200301. doi: 10.7498/aps.63.200301 [10] 梁达川, 魏明贵, 谷建强, 尹治平, 欧阳春梅, 田震, 何明霞, 韩家广, 张伟力. 缩比模型的宽频时域太赫兹雷达散射截面(RCS)研究. , 2014, 63(21): 214102. doi: 10.7498/aps.63.214102 [11] 徐国亮, 刘培, 刘彦磊, 张琳, 刘玉芳. 准经典轨线法研究交换反应H(D)+SH/SD的动力学性质. , 2013, 62(22): 223402. doi: 10.7498/aps.62.223402 [12] 臧华平, 李文峰, 令狐荣锋, 程新路, 杨向东. 钠分子同位素替代对低温下的He-Na2冷碰撞体系转动激发积分散射截面的影响. , 2011, 60(2): 020304. doi: 10.7498/aps.60.020304 [13] 李文峰, 令狐荣锋, 程新路, 杨向东. 氦同位素原子与钠分子碰撞转动激发积分散射截面的理论计算. , 2010, 59(7): 4591-4597. doi: 10.7498/aps.59.4591 [14] 王斌, 冯灏, 孙卫国, 曾阳阳, 戴伟. 低能电子与氢分子碰撞的振动激发积分散射截面的研究. , 2009, 58(10): 6932-6937. doi: 10.7498/aps.58.6932 [15] 刘会师, 忻向军, 尹霄丽, 余重秀, 张琦. 切比雪夫光混沌发生器的优化. , 2009, 58(4): 2231-2234. doi: 10.7498/aps.58.2231 [16] 戴 伟, 冯 灏, 孙卫国, 唐永建, 申 立, 于江周. 用振动密耦合方法研究低能电子与N2分子碰撞的振动激发微分散射截面. , 2008, 57(1): 143-148. doi: 10.7498/aps.57.143 [17] 李民权, 陶小俊, 赵 瑾, 吴先良. 基于辛Runge-Kutta-Nystrom方法的雷达散射截面计算. , 2007, 56(4): 2115-2118. doi: 10.7498/aps.56.2115 [18] 张程华, 邱 巍, 辛俊丽, 牛英煜, 王晓伟, 王京阳. 电子碰撞下氢原子单离化反应三重微分散射截面的计算. , 2003, 52(10): 2449-2452. doi: 10.7498/aps.52.2449 [19] 白丽华, 张庆刚, 刘新国. D+CD4→CD3+D2反应的四维量子散射计算. , 2003, 52(11): 2774-2780. doi: 10.7498/aps.52.2774 [20] 金石琦, 徐至展. e-Ar(3p54s,J=2)的微分散射截面. , 1998, 47(10): 1621-1624. doi: 10.7498/aps.47.1621
下载:
计量
- 文章访问数: 2518
- PDF下载量: 40
- 被引次数: 0
