-
地球重力场信息是大地测量学、地球物理学、地球动力学等学科所必需的重要基础信息, 重力场测绘是获取地球重力场信息的有效手段. 相比于卫星、海洋、航空重力场测绘, 车载重力场测绘具有灵活性强、空间分辨率高、精度高等优点. 基于相对重力仪和高精度绝对重力基准点可以实现陆域小范围重力场测绘, 但相对重力仪存在零点漂移, 不适用于长基线、大范围的陆域测绘. 本文基于小型化原子重力仪搭建了一套车载绝对重力快速测绘系统, 在郊区安静外场环境, 由12个测点约3 km的测绘结果评估仪器的内符合精度为0.123 mGal (1 Gal = 10–2 m/s2), 外符合精度为0.112 mGal, 并在闹市复杂外场环境下实现了单点调节时间小于2 min, 有效测量时间5 min的快速绝对重力测量, 通过19个测点跨区约24 km的重力场快速测绘, 评估仪器的内符合精度为0.162 mGal, 外符合精度为0.169 mGal. 最后将原子重力仪的外场重力场测绘数据与卫星重力模型计算的数据进行了比较, 发现两者的自由空间重力异常数据的整体变化趋势相吻合. 本文为外场绝对重力场快速测绘提供了一种新的方案.The information about Earth’s gravity field is an important basic information necessarily for geodesy, geophysics, geodynamics and other disciplines. The mapping of gravity field is an effective mean to obtain the gravity field information. Compared with the surveying of gravity field based on satellite, ship, and airplane, vehicle-mounted gravity mapping has advantages of strong flexibility, high spatial resolution and high accuracy. A short baseline or a small-scale gravity field mapping can be realized based on the combination of relative gravimeters and the high-precision absolute gravity reference point. However, this method is not suitable for the situation of a long baseline or a large-scale gravity field surveying due to the drift of relative gravimeter. In this work, a vehicle-mounted system for rapid surveying of the absolute gravity field is built up based on a miniaturized atomic gravimeter. The inner precision of the instrument is evaluated to be 0.123 mGal, and the outer precision is 0.112 mGal in a field test which contains 12 points for 3 km distance. Furthermore, with this system, the absolute gravity data are obatined within 2 min for adjusting and 5 min for measuring in downtown for each measured point. A rapid surveying of absolute gravity field for 19 points is carried out and the route covers 24 km. The inner precision of the instrument is evaluated to be 0.162 mGal, and the outer precision is 0.169 mGal. Finally, the free-air gravity anomalies obtained from the measured data of atomic gravimeter and the fitting results of satellite gravity model are analyzed, and it is found that the trends of changing are basically consistent with each other. This paper provides a new proposal for the rapid surveying of the absolute gravity field.
-
Keywords:
- cold atomic gravimeter /
- absolute gravity survey /
- atomic interference
[1] Van Camp M, De Viron O, Watlet A, Meurers B, Francis O, Caudron C 2017 Rev. Geophys. 55 938
Google Scholar
[2] Peters A, Chung K Y, Chu S 1999 Nature 400 849
Google Scholar
[3] Kasevich M, Chu S 1992 Appl. Phys. B 54 321
Google Scholar
[4] Hu Z K, Sun B L, Duan X C, Zhou M K, Chen L L, Zhan S, Zhang Q Z, Luo J 2013 Phys. Rev. A 88 043610
Google Scholar
[5] Freier C, Hauth M, Schkolnik V, Leykauf B, Schilling M, Wziontek H, Scherneck H G, Muller J, Peters A 2016 J. Phys. Conf. Ser. 723 012050
Google Scholar
[6] Wu B, Wang Z Y, Cheng B, Wang Q Y, Xu A P, Lin Q 2014 Metrologia 51 452
Google Scholar
[7] Le Gouët J, Mehlstäubler T E, Kim J, Merlet S, Clairon A, Landragin A, Pereira Dos Santos F 2008 Appl. Phys. B 92 133
Google Scholar
[8] Peters A, Chung K Y, Chu S 2001 Metrologia 38 25
Google Scholar
[9] Hauth M, Freier C, Schkolnik V, Senger A, Schmidt M, Peters A 2013 Appl. Phys. B 113 49
Google Scholar
[10] Schmidt M, Senger A, Hauth M, Freier C, Schkolnik V, Peters A 2011 Gyroscopy Navig. 2 170
Google Scholar
[11] Bodart Q, Merlet S, Malossi N, Dos Santos F P, Bouyer P, Landragin A 2010 Appl. Phys. Lett. 96 134101
Google Scholar
[12] 吴彬, 程冰, 付志杰, 朱栋, 周寅, 翁堪兴, 王肖隆, 林强 2018 67 190302
Google Scholar
Wu B, Cheng B, Fu Z J, Zhu D, Zhou Y, Weng K X, Wang X L, Lin Q 2018 Acta Phys. Sin. 67 190302
Google Scholar
[13] Wu X J, Zi F, Dudley J, Bilotta R J, Canoza P, Muller H 2017 Optica 4 1545
Google Scholar
[14] Zhang X W, Zhong J Q, Tang B, Chen X, Zhu L, Huang P W, Wang J, Zhan M S 2018 Appl. Opt. 57 6545
Google Scholar
[15] Huang P W, Tang B, Chen X, Zhong J Q, Xiong Z Y, Zhou L, Wang J, Zhan M S 2019 Metrologia 56 045012
Google Scholar
[16] Wang S K, Zhao Y, Zhuang W, Li T C, Wu S Q, Feng J Y, Li C J 2018 Metrologia 55 360
Google Scholar
[17] Heine N, Matthias J, Sahelgozin M, Herr W, Abend S, Timmen L, Müller J, Rasel E M 2020 Eur. Phys. J. D 74 174
Google Scholar
[18] Chen B, Long J, Xie H, Li C, Chen L, Jiang B, Chen S 2020 Chin. Opt. Lett. 18 090201
Google Scholar
[19] Zhu D, Zhou Y, Wu B, Weng K X, Wang K N, Cheng B, Lin Q 2021 Appl. Opt. 60 7910
Google Scholar
[20] Gillot P, Francis O, Landragin A, Dos Santos F P, Merlet S 2014 Metrologia 51 L15
Google Scholar
[21] Fu Z J, Wu B, Cheng B, Zhou Y, Weng K X, Zhu D, Wang Z Y, Lin Q 2019 Metrologia 56 025001
Google Scholar
[22] Bidel Y, Carraz O, Charriere R, Cadoret M, Zahzam N, Bresson A 2013 Appl. Phys. Lett. 102 144107
Google Scholar
[23] 程冰, 周寅, 陈佩军, 张凯军, 朱栋, 王凯楠, 翁堪兴, 王河林, 彭树萍, 王肖隆, 吴彬, 林强 2021 70 040304
Google Scholar
Cheng B, Zhou Y, Chen P J, Zhang K J, Zhu D, Wang K N, Weng K X, Wang H L, Peng S P, Wang X L, Wu B, Lin Q 2021 Acta Phys. Sin. 70 040304
Google Scholar
[24] Wu X J, Pagel Z, Malek B S, Nguyen T H, Zi F, Scheirer D S, Muller H 2019 Sci. Adv. 5 eaax0800
Google Scholar
[25] Bidel Y, Zahzam N, Bresson A, Blanchard C, Cadoret M, Olesen A V, Forsberg R 2020 J. Geod. 94 20
Google Scholar
[26] Bidel Y, Zahzam N, Blanchard C, Bonnin A, Cadoret M, Bresson A, Rouxel D, Lequentrec-Lalancette M F 2018 Nat. Commun. 9 9
Google Scholar
[27] Zhang J Y, Xu W J, Sun S D, Shu Y B, Luo Q, Cheng Y, Hu Z K, Zhou M K 2021 AIP Adv. 11 115223
Google Scholar
[28] Guo J, Ma S, Zhou C, Liu J, Wang B, Pan D, Mao H 2021 Preprints 202111.0255.v1
[29] 吴彬, 周寅, 程冰, 朱栋, 王凯楠, 朱欣欣, 陈佩军, 翁堪兴, 杨秋海, 林佳宏, 张凯军, 王河林, 林强 2020 69 060302
Google Scholar
Wu B, Zhou Y, Cheng B, Zhu D, Wang K N, Zhu X X, Chen P J, Weng K X, Yang Q H, Lin J H, Zhang K J, Wang H L, Lin Q 2020 Acta Phys. Sin. 69 060302
Google Scholar
-
图 1 车载绝对重力场快速测绘系统示意图
Fig. 1. Schematic diagram of the vehicle-mounted system for rapid surveying of the absolute gravity field.
图 2 外场环境下的振动噪声功率谱密度
Fig. 2. Power spectral density of the vibration noise in the field.
图 3 车载静态环境下的长扫重力测量结果(单点5 min平均)
Fig. 3. Long-term measured results of gravity on a static truck (each point takes average of 5 minutes).
图 4 车载静态情况下的重力测量灵敏度评估
Fig. 4. Evaluation of sensitivity with the measured gravity data when the truck is stationary.
图 5 杭州市宝寿山测线以及测点分布图, 蓝色实线为测线, 红点表示各测点分布
Fig. 5. Measurement route and the distribution of measured points on Baoshou Mountain in the city of Hangzhou. The blue curve depicts the measurement route and the red points are the measurement locations.
图 6 杭州宝寿山原子重力仪两次测绘的结果及其残差
Fig. 6. Surveyed results of absolute gravity of two repeated measured line and the corresponding residuals obtained by the atomic gravimeter on Baoshou Mountain in the city of Hangzhou.
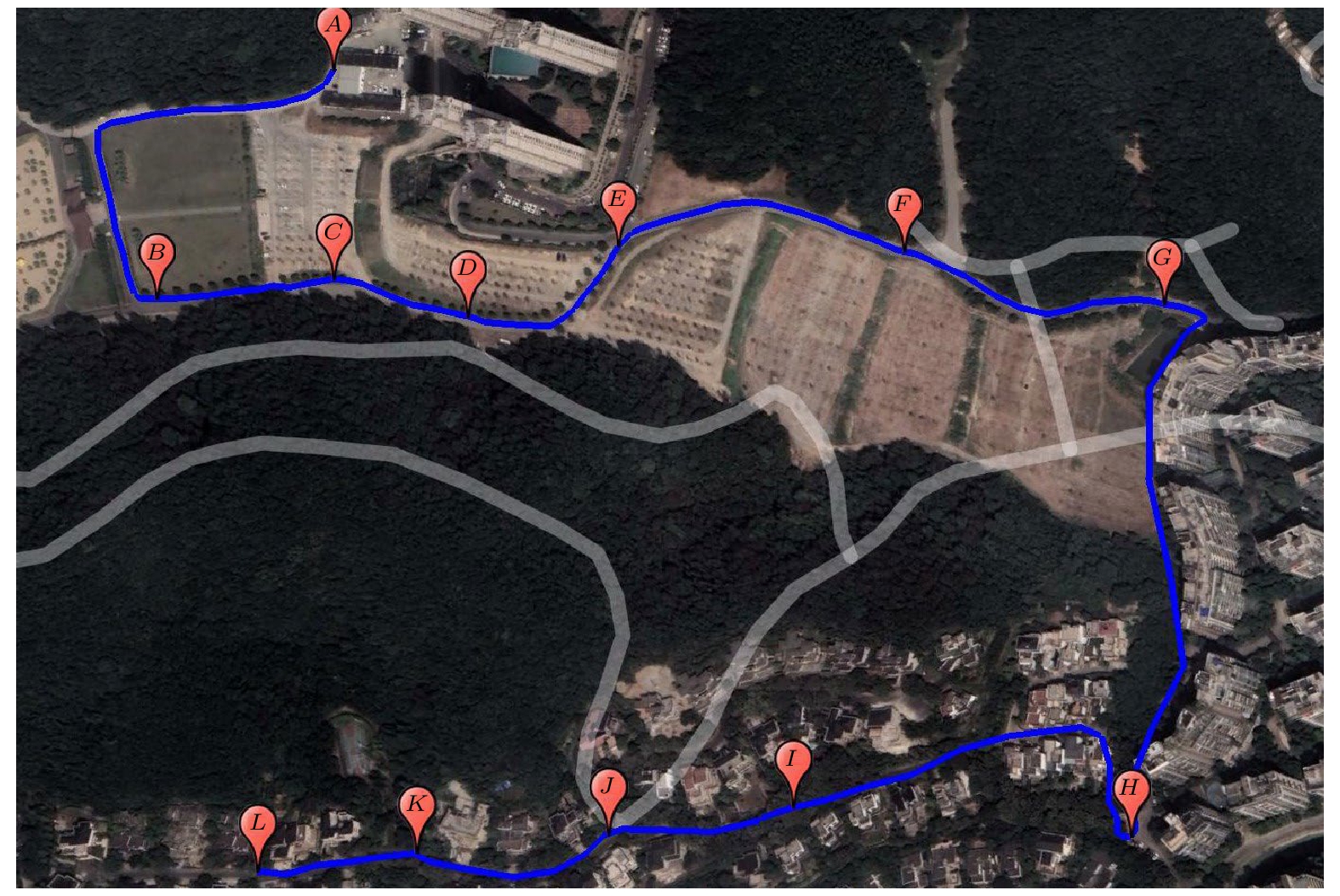
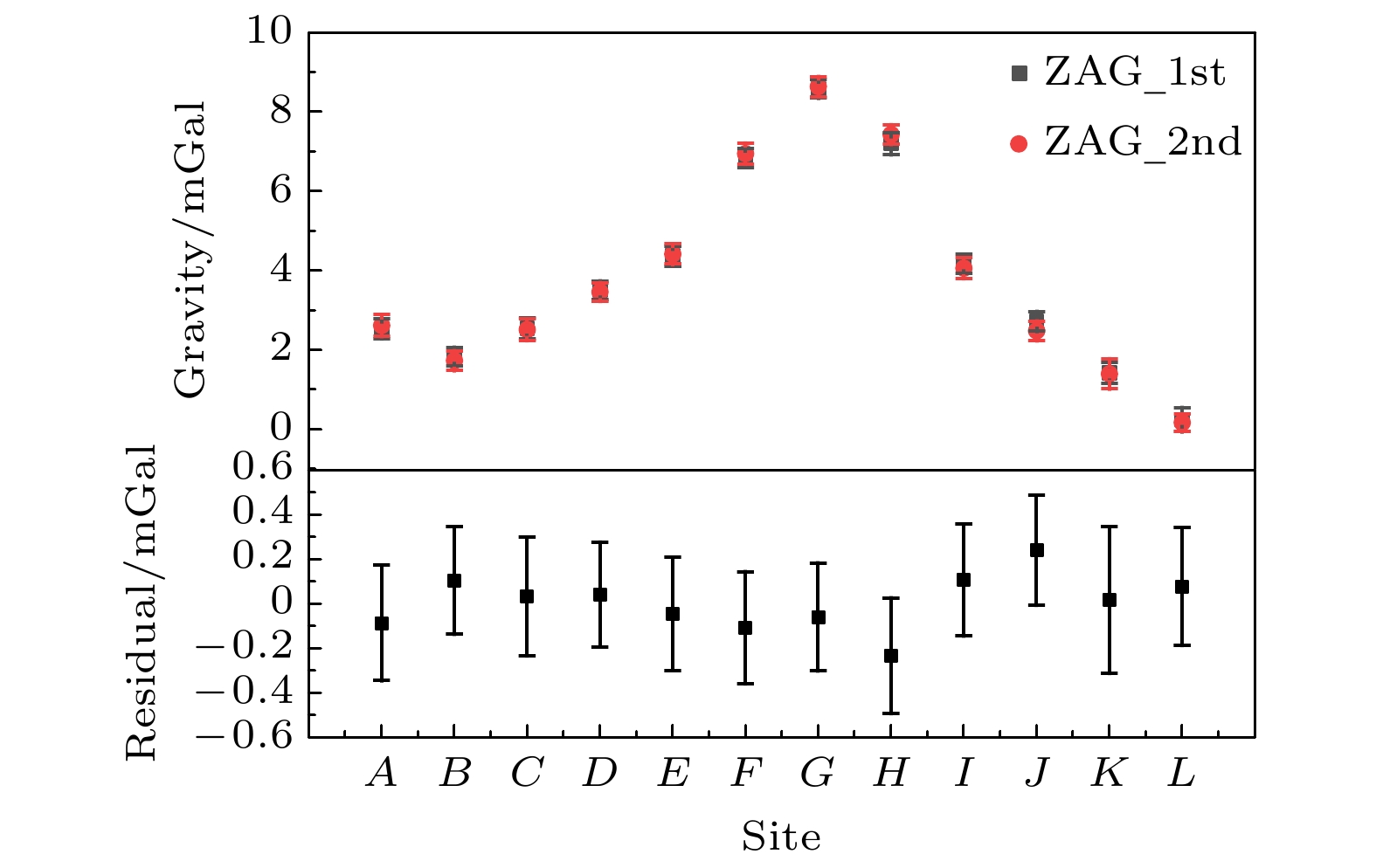
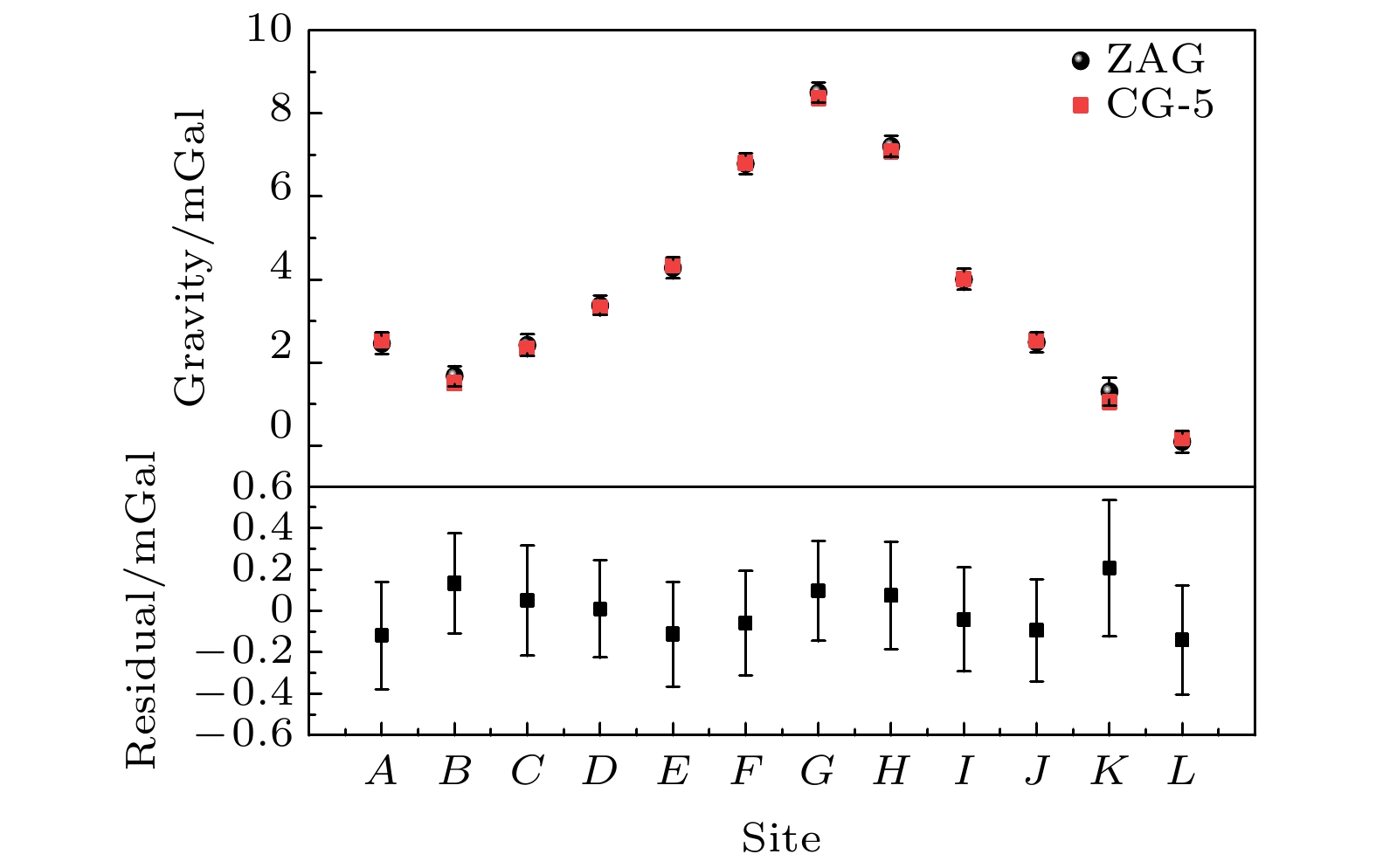
图 7 在杭州宝寿山由原子重力仪与CG-5相对重力仪测绘的数据及两者的残差数据. 图中黑点为原子重力仪两次测绘结果的平均值, 红点为相对重力仪两次测绘结果的平均值
Fig. 7. Gravity data surveyed by atomic gravimeter and relative gravimeter of CG-5 on Baoshou Mountain in Hangzhou city and the residuals data between them. The black dots and red dots are the average values of measured gravity data of two repeated lines with atomic gravimeter and relative gravimeter CG-5, respectively.
图 8 长沙黄兴大道测线及测点分布图, 其中蓝色实线是规划的测线, 红色标记点是各测点位置
Fig. 8. Measurement route and the distribution of measured points on Huangxing Avenue of Changsha city. The blue curve depicts the measurement route and the red marked points are the measurement locations.
图 9 高振动噪声环境下原子重力仪在同一测线两次重力测绘的数据及其残差数据
Fig. 9. Surveyed gravity data of the same line for twice measurements with atomic gravimeter in the environment of high vibration noise and the residuals data.
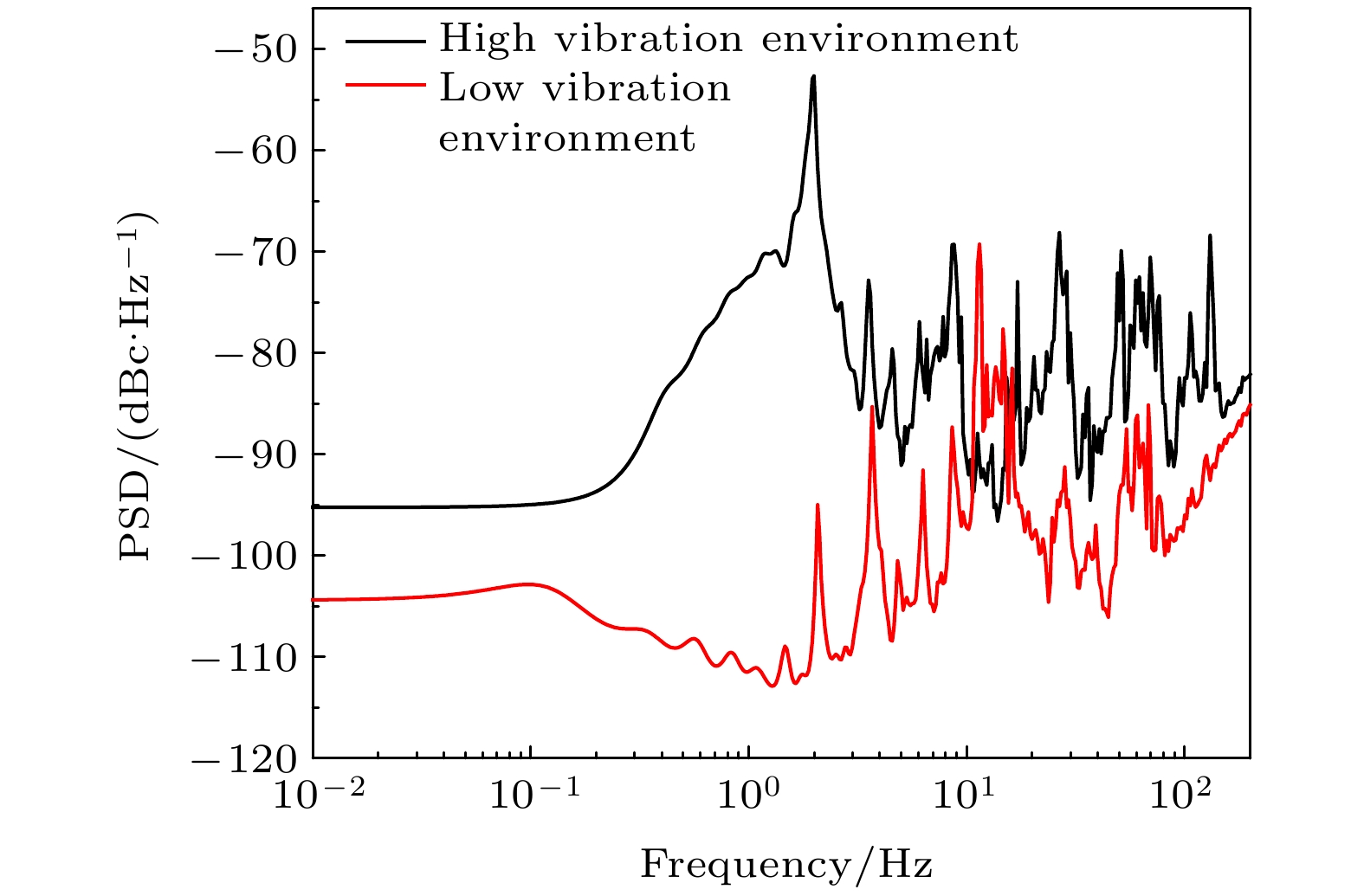
图 10 高振动噪声环境下由原子重力仪与相对重力仪CG-5测绘的数据及两者的残差数据, 图中黑点为原子重力仪两次测绘结果的平均值, 红点为相对重力仪三次测绘结果的平均值
Fig. 10. Gravity data surveyed by atomic gravimeter and relative gravimeter of CG-5 in the environment of high vibration noise and the residuals data between them. The black dots and red dots are the average values of measured gravity data of two repeated lines with atomic gravimeter and three repeated lines with relative gravimeter CG-5, respectively.
图 11 长沙黄兴大道测区高程剖面图(红色倒三角为测点)
Fig. 11. Elevation profile of measurement locations on Huangxing Avenue of Changsha city (the red inverted triangles are the measured points).
图 12 由EGM2008模型拟合获取重力异常分布图
Fig. 12. Distribution map of the gravity anomaly obtained by fitting of the EGM2008 model.
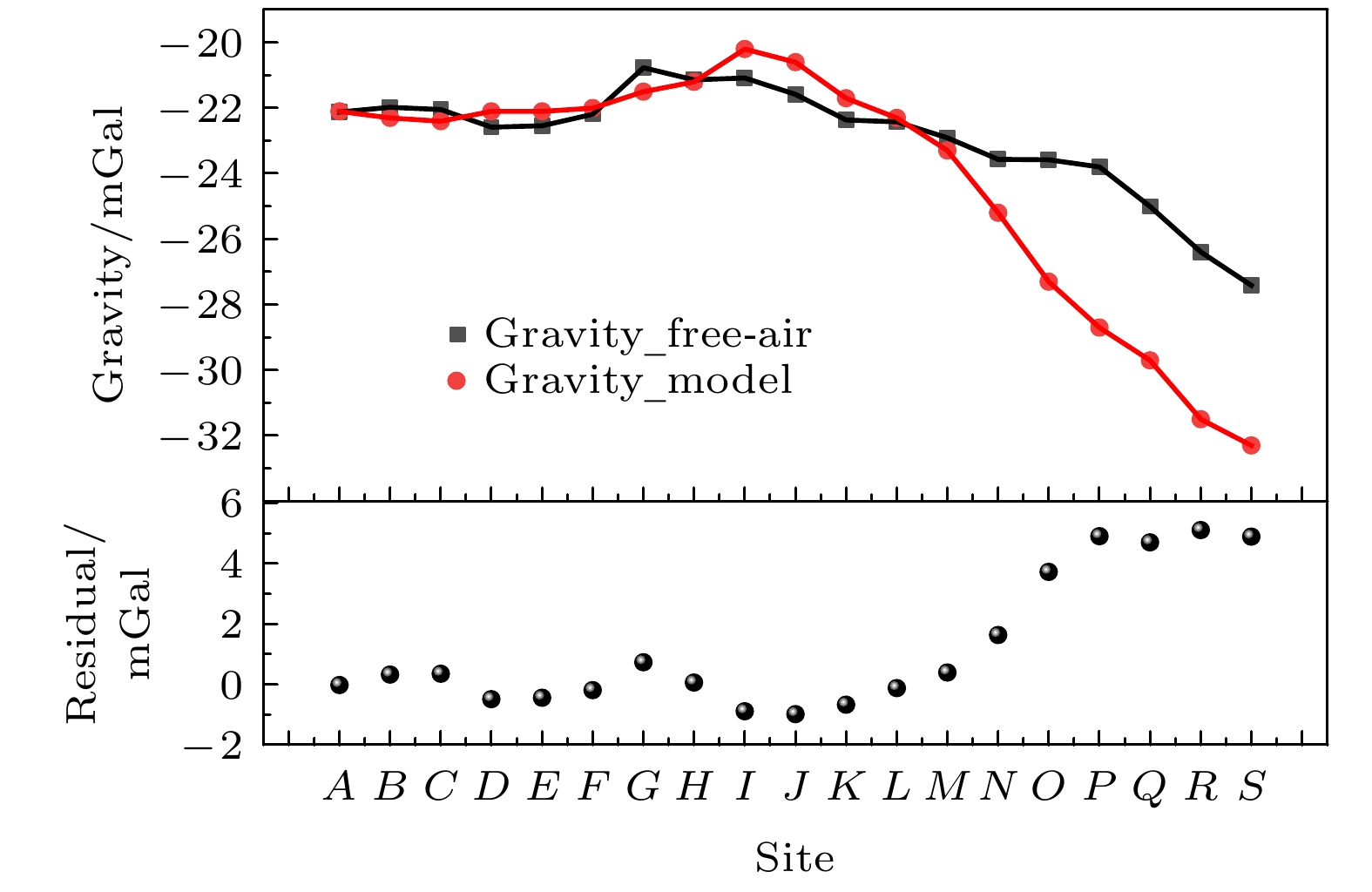
图 13 实测与模型计算的自由空间重力异常数据及其残差, 图中红色点为由卫星重力模型拟合获取的测点自由空间重力异常, 黑色点为原子重力仪测量值改正后的测点自由空间重力异常
Fig. 13. Free-air gravity anomalies obtained by the measured data with atomic gravimeter and the fitting of gravity model and the residual date between them. The black and red dots are the results acquired by atomic gravimeter and the theoretical model, respectively.
表 1 车载快速绝对重力测量系统B类不确定度表
Table 1. Class B uncertainty table for vehicle-mounted rapid absolute gravimetry system
项目 修正量/μGal 不确定度/μGal 科里奥利力效应 39.00 3.06 双光子频移 –13.23 2.52 激光波长 –5.50 1.10 参考频率 0.00 1.00 射频相移 –131.47 10.81 自引力效应 –2.70 0.10 残余边带 –241.56 103.00 其他修正量 0.17 2.00 合成结果 –355.29 103.61 
下载: 导出CSV
-
[1] Van Camp M, De Viron O, Watlet A, Meurers B, Francis O, Caudron C 2017 Rev. Geophys. 55 938
Google Scholar
[2] Peters A, Chung K Y, Chu S 1999 Nature 400 849
Google Scholar
[3] Kasevich M, Chu S 1992 Appl. Phys. B 54 321
Google Scholar
[4] Hu Z K, Sun B L, Duan X C, Zhou M K, Chen L L, Zhan S, Zhang Q Z, Luo J 2013 Phys. Rev. A 88 043610
Google Scholar
[5] Freier C, Hauth M, Schkolnik V, Leykauf B, Schilling M, Wziontek H, Scherneck H G, Muller J, Peters A 2016 J. Phys. Conf. Ser. 723 012050
Google Scholar
[6] Wu B, Wang Z Y, Cheng B, Wang Q Y, Xu A P, Lin Q 2014 Metrologia 51 452
Google Scholar
[7] Le Gouët J, Mehlstäubler T E, Kim J, Merlet S, Clairon A, Landragin A, Pereira Dos Santos F 2008 Appl. Phys. B 92 133
Google Scholar
[8] Peters A, Chung K Y, Chu S 2001 Metrologia 38 25
Google Scholar
[9] Hauth M, Freier C, Schkolnik V, Senger A, Schmidt M, Peters A 2013 Appl. Phys. B 113 49
Google Scholar
[10] Schmidt M, Senger A, Hauth M, Freier C, Schkolnik V, Peters A 2011 Gyroscopy Navig. 2 170
Google Scholar
[11] Bodart Q, Merlet S, Malossi N, Dos Santos F P, Bouyer P, Landragin A 2010 Appl. Phys. Lett. 96 134101
Google Scholar
[12] 吴彬, 程冰, 付志杰, 朱栋, 周寅, 翁堪兴, 王肖隆, 林强 2018 67 190302
Google Scholar
Wu B, Cheng B, Fu Z J, Zhu D, Zhou Y, Weng K X, Wang X L, Lin Q 2018 Acta Phys. Sin. 67 190302
Google Scholar
[13] Wu X J, Zi F, Dudley J, Bilotta R J, Canoza P, Muller H 2017 Optica 4 1545
Google Scholar
[14] Zhang X W, Zhong J Q, Tang B, Chen X, Zhu L, Huang P W, Wang J, Zhan M S 2018 Appl. Opt. 57 6545
Google Scholar
[15] Huang P W, Tang B, Chen X, Zhong J Q, Xiong Z Y, Zhou L, Wang J, Zhan M S 2019 Metrologia 56 045012
Google Scholar
[16] Wang S K, Zhao Y, Zhuang W, Li T C, Wu S Q, Feng J Y, Li C J 2018 Metrologia 55 360
Google Scholar
[17] Heine N, Matthias J, Sahelgozin M, Herr W, Abend S, Timmen L, Müller J, Rasel E M 2020 Eur. Phys. J. D 74 174
Google Scholar
[18] Chen B, Long J, Xie H, Li C, Chen L, Jiang B, Chen S 2020 Chin. Opt. Lett. 18 090201
Google Scholar
[19] Zhu D, Zhou Y, Wu B, Weng K X, Wang K N, Cheng B, Lin Q 2021 Appl. Opt. 60 7910
Google Scholar
[20] Gillot P, Francis O, Landragin A, Dos Santos F P, Merlet S 2014 Metrologia 51 L15
Google Scholar
[21] Fu Z J, Wu B, Cheng B, Zhou Y, Weng K X, Zhu D, Wang Z Y, Lin Q 2019 Metrologia 56 025001
Google Scholar
[22] Bidel Y, Carraz O, Charriere R, Cadoret M, Zahzam N, Bresson A 2013 Appl. Phys. Lett. 102 144107
Google Scholar
[23] 程冰, 周寅, 陈佩军, 张凯军, 朱栋, 王凯楠, 翁堪兴, 王河林, 彭树萍, 王肖隆, 吴彬, 林强 2021 70 040304
Google Scholar
Cheng B, Zhou Y, Chen P J, Zhang K J, Zhu D, Wang K N, Weng K X, Wang H L, Peng S P, Wang X L, Wu B, Lin Q 2021 Acta Phys. Sin. 70 040304
Google Scholar
[24] Wu X J, Pagel Z, Malek B S, Nguyen T H, Zi F, Scheirer D S, Muller H 2019 Sci. Adv. 5 eaax0800
Google Scholar
[25] Bidel Y, Zahzam N, Bresson A, Blanchard C, Cadoret M, Olesen A V, Forsberg R 2020 J. Geod. 94 20
Google Scholar
[26] Bidel Y, Zahzam N, Blanchard C, Bonnin A, Cadoret M, Bresson A, Rouxel D, Lequentrec-Lalancette M F 2018 Nat. Commun. 9 9
Google Scholar
[27] Zhang J Y, Xu W J, Sun S D, Shu Y B, Luo Q, Cheng Y, Hu Z K, Zhou M K 2021 AIP Adv. 11 115223
Google Scholar
[28] Guo J, Ma S, Zhou C, Liu J, Wang B, Pan D, Mao H 2021 Preprints 202111.0255.v1
[29] 吴彬, 周寅, 程冰, 朱栋, 王凯楠, 朱欣欣, 陈佩军, 翁堪兴, 杨秋海, 林佳宏, 张凯军, 王河林, 林强 2020 69 060302
Google Scholar
Wu B, Zhou Y, Cheng B, Zhu D, Wang K N, Zhu X X, Chen P J, Weng K X, Yang Q H, Lin J H, Zhang K J, Wang H L, Lin Q 2020 Acta Phys. Sin. 69 060302
Google Scholar
下载:
计量
- 文章访问数: 4412
- PDF下载量: 128
- 被引次数: 0
