-
探索自驱粒子形状对自组装结构和动力学的影响是软物质研究的前沿课题. 组装基元形成的寡聚体及其动力学是大量粒子形成组装结构的基础. 本文设计了一种“十”字形自驱粒子, 发现其可以形成数种不同构型的寡聚体, 计算了寡聚体(二、三、四聚体)的均方位移、角速度、角速度分布概率、轨迹曲率分布概率等. 寡聚体的运动行为可分为两类: 一类是合力为零但力矩不为零, 寡聚体进行小半径的偏心旋转; 另一类是合力不为零力矩也不为零, 寡聚体呈现大半径的偏心旋转. 寡聚体的平动动力学在短时间尺度(大致约为1—2 s, 与其角速度有关)都呈现超扩散现象, 但转动速度受寡聚体结构影响; 力矩越大, 转动惯量越小, 角速度越大. 对于三聚体, 轨迹曲率与角速度有关, 角速度越大, 曲率也越大.In recent years, active matter has attracted tremendous research interest. Active matter displays many phenomena, such as super-diffusion, huge fluctuation and collective motion. The shape of active agent plays a critical role in the self-assembly of active matter. Understanding the oligomers’ dynamics of active agents is the first step to study the self-assembly of massive agents. Here, we design a self-properlling particle with the “十” shape using the Hexbug robot and investigate the dynamics of oligomers composed of these particles. To track the position of particles, the top of the particles is marked by black cards with white dots in the center. We find that these particles can agglomerate together to form stable oligomers consisting of two, three, or four particles. We study the dynamics by analyzing the trajectory, mean-square displacement, angular velocity, angular velocity distribution and the curvature distribution. We find that the dynamics can be divided into two types. One is the combination of eccentric rotation with small circular radius and irregular translation, which occurs in the system with the zero resultant force and nonzero torque. The other is the eccentric rotation with a large circular radius, which appears in the system in which both the resultant force and torque are not zero. In addition, we find that the translational dynamics of oligomers displays a super diffusion on a short time scale, influenced by the confirguration of oligomers. Further, the larger torque and the smaller moment of inertia result in the bigger angle speed of oligomers. Moreover, we investigate the curvature distribution of the trimer and find that the faster the angle speed of the trimer, the bigger its curvature is.
-
Keywords:
- self-properlled particle /
- “十” shape granule /
- oligomers /
- anomalous dynamics
[1] Jana A D, Manna S C, Rosair G M, Drew M G B, Mostafa G, Ray Chaudhuri N 2007 Cryst. Growth Des. 7 1365
Google Scholar
[2] Janiak C 2000 J. Chem. Soc. , Dalton Trans. 2000 3885
Google Scholar
[3] Schottel B L 2006 J. Am. Chem. Soc. 128 5895
Google Scholar
[4] Nishio M 2004 CrystEngComm 6 130
Google Scholar
[5] Singh N J, Min S K, Kim D Y, Kim K S 2009 J. Chem. Theory Comput. 5 515
Google Scholar
[6] Biswas D, Chakrabarty P P, Saha S, Jana A D, Schollmeyer D, García-Granda S 2013 Inorg. Chim. Acta 408 172
Google Scholar
[7] Packer M J, Dauncey M P, Hunter C A 2000 J. Mol. Biol. 295 71
Google Scholar
[8] de Oliveira B G 2013 Phys. Chem. Chem. Phys. 15 37
Google Scholar
[9] Lee E C, Kim D, Jurečka P, Tarakeshwar P, Hobza P, Kim K S 2007 J. Phys. Chem. A 111 3446
Google Scholar
[10] Yang Z 2021 Cells 10 934
Google Scholar
[11] Ginot F, Theurkauff I, Detcheverry F, Ybert C, Cottin-Bizonne C 2018 Nat. Commun. 9 696
Google Scholar
[12] Mauleon-Amieva A, Allen M P, Royall C P 2021 arXiv: 2107.07934 [cond-mat]
[13] Wensink H H, Löwen H 2008 Phys. Rev. E 78 031409
Google Scholar
[14] Grossmann R, Aranson I S, Peruani F 2020 Nat. Commun. 11 5365
Google Scholar
[15] Fily Y, Marchetti M C 2012 Phys. Rev. Lett. 108 235702
Google Scholar
[16] Deseigne J, Dauchot O, Chaté H 2010 Phys. Rev. Lett. 105 098001
Google Scholar
[17] Wensink H H, Kantsler V, Goldstein R E, Dunkel J 2014 Phys. Rev. E 89 010302
Google Scholar
[18] Prymidis V, Samin S, Filion L 2016 Soft Matter 12 4309
Google Scholar
[19] Redner G S, Hagan M F, Baskaran A 2013 Phys. Rev. Lett. 110 055701
Google Scholar
[20] Andréen D, Jenning P, Napp N, Petersen K 2020 Soft Matter 16 9436
Google Scholar
-
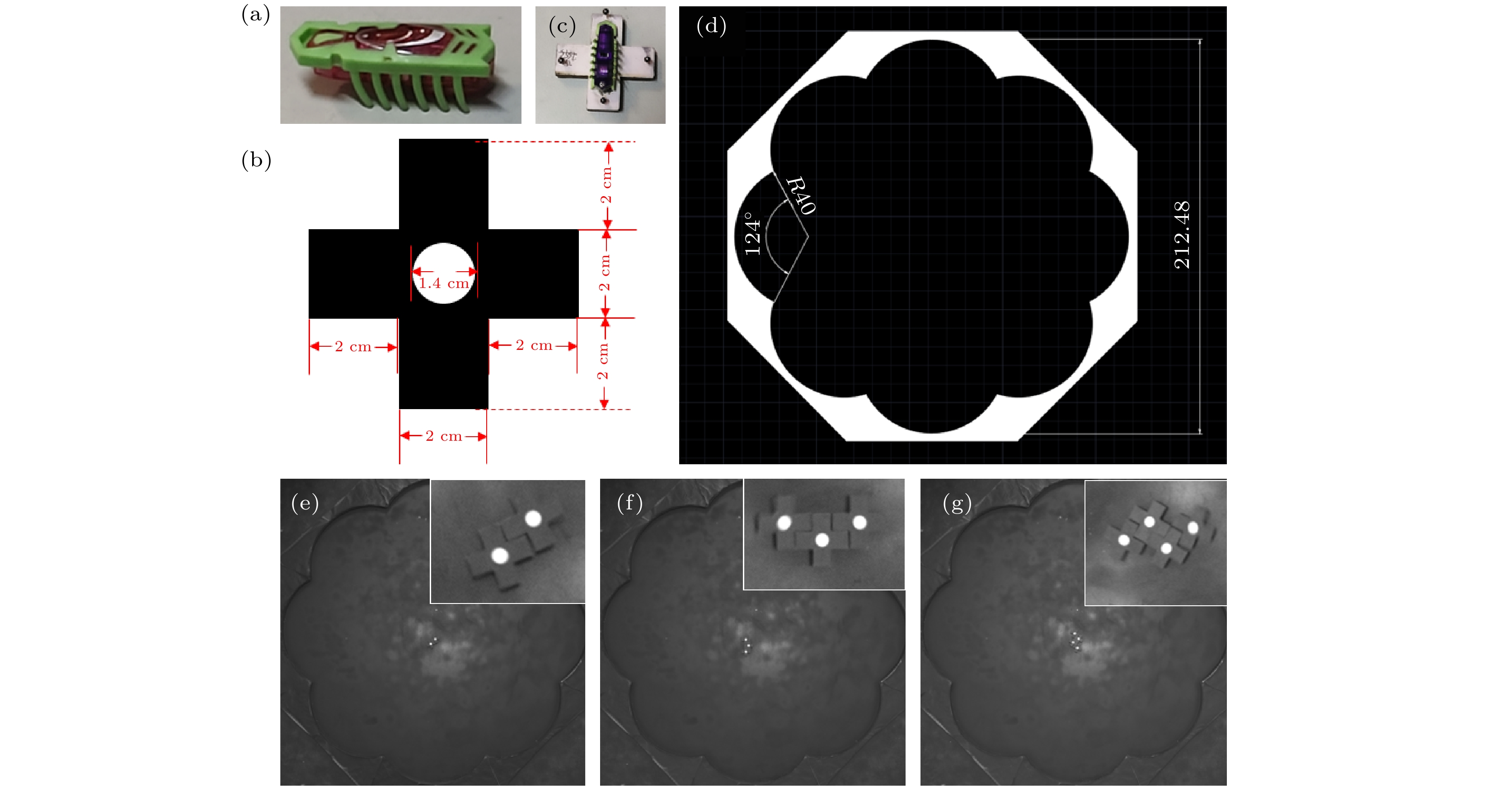
图 1 实验材料与场地 (a) hexbug马达; (b) 识别卡片, 白点用于提取坐标, 数字代表对应部分的尺寸; (c) hexbug马达与“十”字形结构复合体; (d) 实验场地, 数字表示对应尺寸, 白色表示梅花边界; (e)—(g) 二聚体、三聚体、四聚体的初始结构
Fig. 1. Experimental setup: (a) Hexbug motor; (b) identification card, white dots used to extract the coordinate; (c) complex of hexbug motor and “十” structure; (d) experiment field (the white color denotes the plum flower border); (e)–(g) the initial structure of dimer, trimer and tetramer.
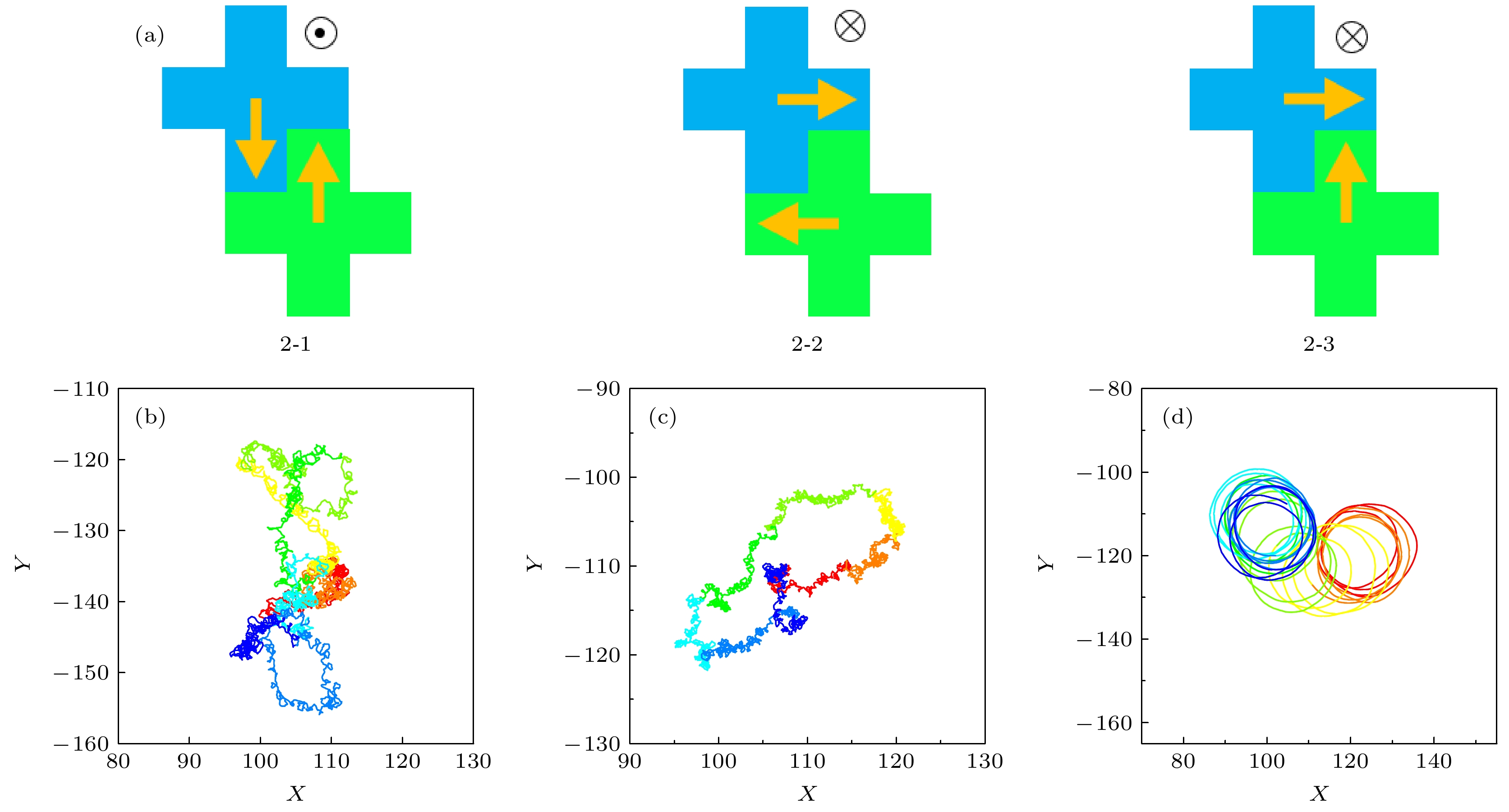
图 2 二聚体构型及运动轨迹 (a) 2-1, 2-2, 2-3为三种构型, 黄色箭头为自驱力方向, 在每个构型右上角标明了旋转方向,
$\otimes $ 表示顺时针旋转,$\odot $ 表示逆时针旋转; (b) 2-1寡聚体的运动轨迹; (c) 寡聚体2-2的运动轨迹; (d) 2-3寡聚体的运动轨迹Fig. 2. Structures and trajectories of three dimers. (a) 2-1, 2-2, 2-3 denote three kinds of arrangements. Yellow arrow is the self-propelled orientation.
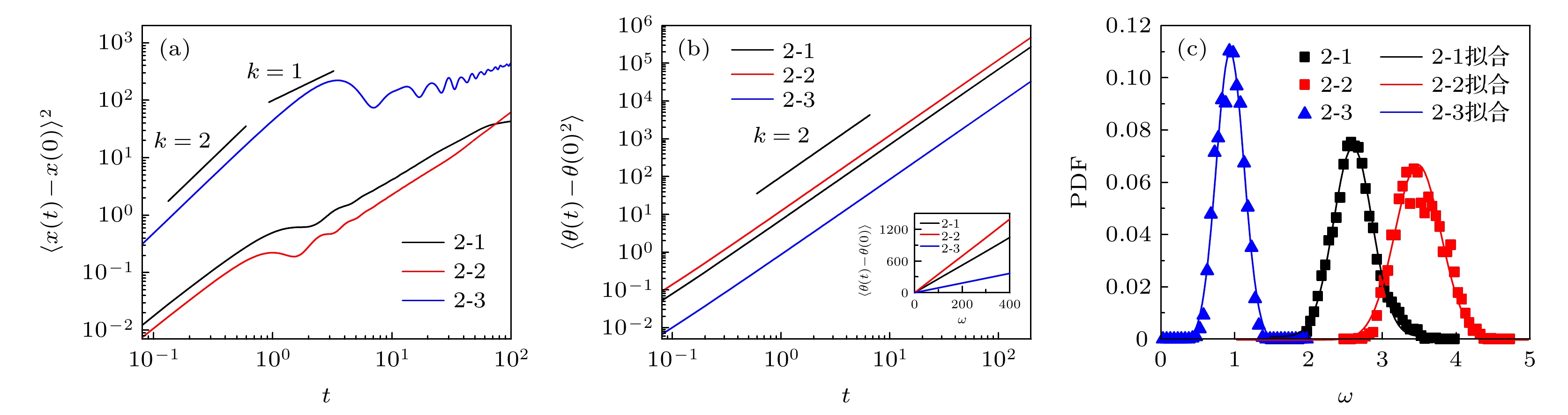
$\otimes $ means clockwise rotation,$\odot $ counterclockwise. (b) 2-1 trajectory; (c) 2-2 trajectory; (d) 2-3 trajectory.
图 3 (a) 三种构型的均方位移; (b) 三种构型的角均方位移, 插图为角平均位移; (c) 三种构型的角速度概率分布, 其中点代表实验数据, 线条为高斯拟合
Fig. 3. (a) MSDs for 2-1, 2-2, 2-3 configurations and their MSADs (b), the inset is mean angle displacement (MAD); (c) angular velocity distribution, where points are the experimental data, lines correspond to Gaussian fitting.
图 4 三粒子寡聚体构型及运动轨迹 (a) 四种构型, 黄色箭头为自推进力方向, 在每个构型旁边标明了旋转方向,
$\otimes$ 表示顺时针旋转,$\odot $ 表示逆时针旋转; (b) 3-1的运动轨迹; (c) 3-2的运动轨迹; (d) 3-3的运动轨迹; (e) 3-4的运动轨迹Fig. 4. Structures and trajectories of three trimers. (a) 3-1, 3-2, 3-3, 3-4 denote four kinds of arrangements. Yellow arrow is the self-propelled orientation.
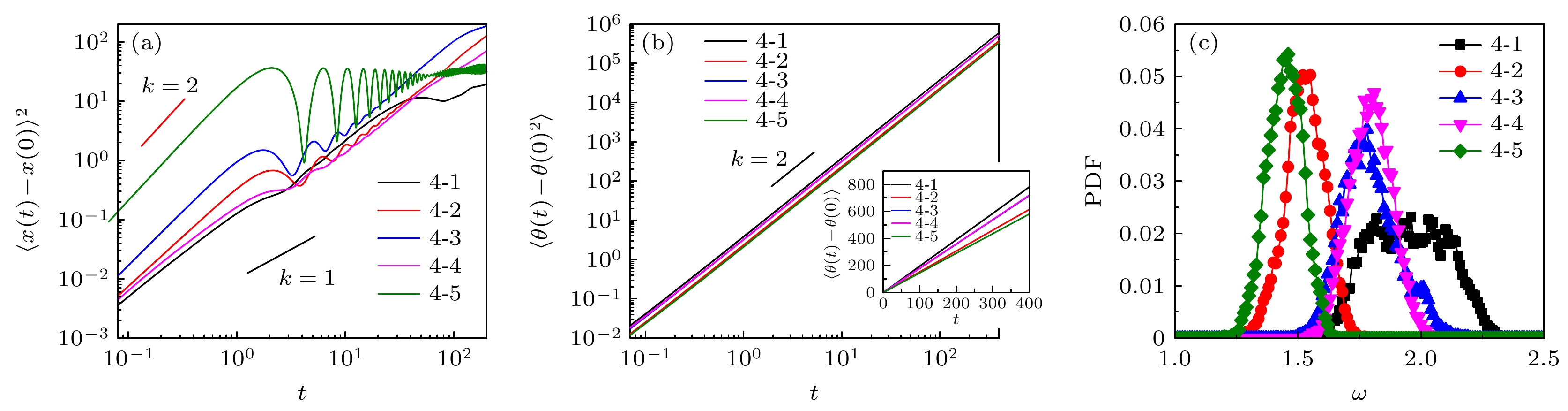
$\otimes $ means clockwise rotation,$\odot $ counterclockwise. (b) 3-1 trajectory; (c) 3-2 trajectory; (d) 3-3 trajectory; (e) 3-4 trajectory.
图 5 (a) 四种构型的均方位移; (b) 四种构型的角均方位移, 插图为角平均位移; (c) 四种构型的角速度概率分布及高斯拟合; (d) 四种构型的曲率概率分布及高斯拟合
Fig. 5. (a) MSDs for 4-1, 4-2, 4-3, 4-4 configurations; (b) MSADs for four configurations, where the inset is mean angle displacement; (c) angular velocity probability distributions and their Gaussian fittings; (d) curvature probability distributions and their Gaussian fittings.
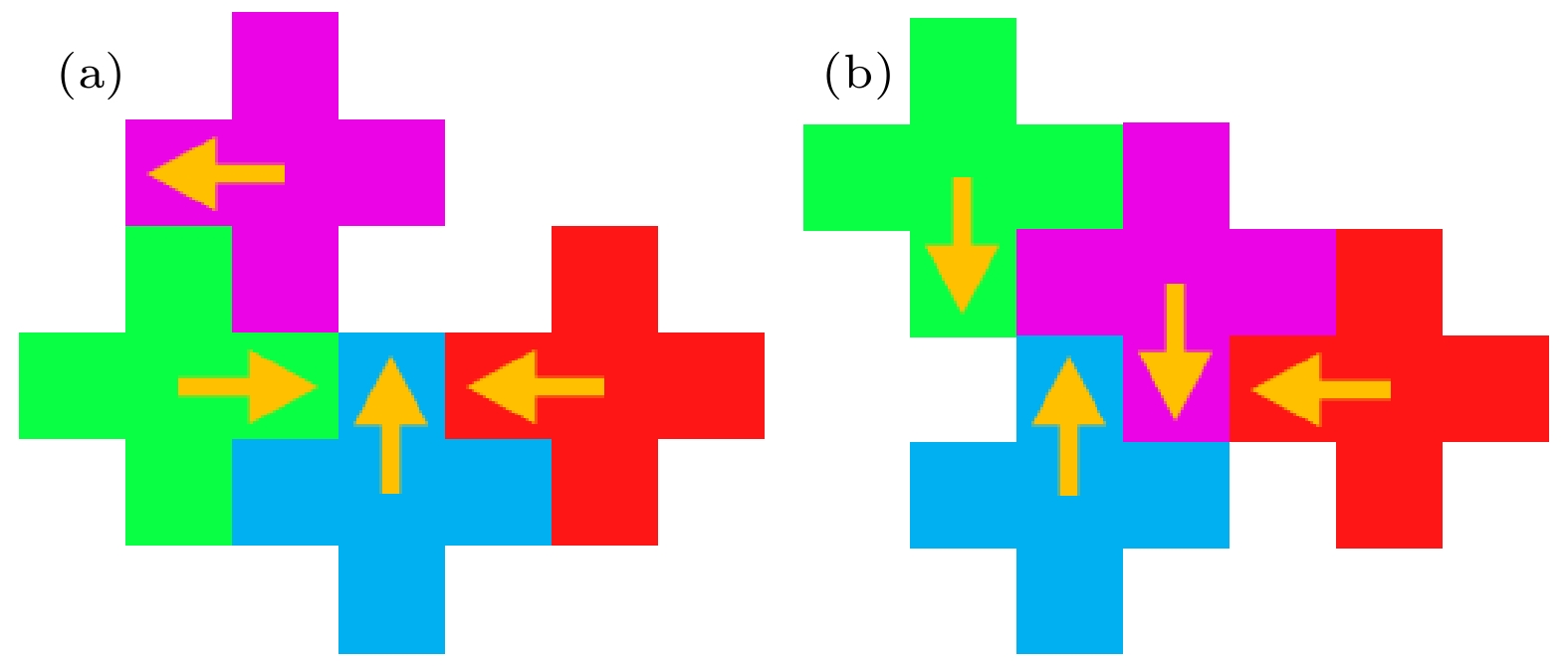
图 6 四粒子寡聚体构型及运动轨迹 (a) 4-1, 4-2, 4-3, 4-4, 4-5为五种构型, 黄色箭头为自推进力方向, 在每个构型旁边标明了旋转方向.
$\otimes $ 表示顺时针旋转,$\odot $ 表示逆时针旋转. (b) 4-1的运动轨迹; (c) 4-2的运动轨迹; (d) 4-3的运动轨迹; (e) 4-4的运动轨迹; (f) 4-5的运动轨迹Fig. 6. Structures and trajectories of five tetramers: (a) 4-1, 4-2, 4-3, 4-4, 4-5 denote five kinds of arrangements. Yellow arrow is the self-propelled orientation.
$\otimes $ means clockwise rotation,$\odot $ counterclockwise. (b) 4-1 trajectory; (c) 4-2 trajectory; (d) 4-3 trajectory; (e) 4-4 trajectory; (f) 4-5 trajectory.
图 7 (a) 五种构型的均方位移; (b) 五种构型的角均方位移, 插图为角平均位移; (c) 五种构型的角速度概率分布
Fig. 7. (a) MSDs for five structures and (b) their MSADs. The inset is mean angle displacement. (c) Angular velocity distributions for five structures.
表 1 角速度的高斯拟合参数值
Table 1. Gaussian fitting parameter value of angular velocity.
参数 2-1构型 2-2构型 2-3构型 均值$ {x}_{\mathrm{c}} $ 2.60 3.48 0.94 σ 0.26 0.31 0.18 
下载: 导出CSV
表 2 角速度的高斯拟合参数值
Table 2. Gaussian fitting parameter value of angular velocity.
参数 3-1构型 3-3构型 3-4构型 中心$ {x}_{\mathrm{c}} $ 1.01 0.68 1.96 方差 0.28 0.16 0.24
下载: 导出CSV
表 3 转动圆周曲率的高斯拟合参数值
Table 3. Gaussian fitting value of curvature.
参数 3-1构型 3-2构型 3-3构型 3-4构型 中心$ {x}_{\mathrm{c}} $ 1.03 1.60 0.69 2.01 方差 0.44 0.50 0.20 0.44
下载: 导出CSV
-
[1] Jana A D, Manna S C, Rosair G M, Drew M G B, Mostafa G, Ray Chaudhuri N 2007 Cryst. Growth Des. 7 1365
Google Scholar
[2] Janiak C 2000 J. Chem. Soc. , Dalton Trans. 2000 3885
Google Scholar
[3] Schottel B L 2006 J. Am. Chem. Soc. 128 5895
Google Scholar
[4] Nishio M 2004 CrystEngComm 6 130
Google Scholar
[5] Singh N J, Min S K, Kim D Y, Kim K S 2009 J. Chem. Theory Comput. 5 515
Google Scholar
[6] Biswas D, Chakrabarty P P, Saha S, Jana A D, Schollmeyer D, García-Granda S 2013 Inorg. Chim. Acta 408 172
Google Scholar
[7] Packer M J, Dauncey M P, Hunter C A 2000 J. Mol. Biol. 295 71
Google Scholar
[8] de Oliveira B G 2013 Phys. Chem. Chem. Phys. 15 37
Google Scholar
[9] Lee E C, Kim D, Jurečka P, Tarakeshwar P, Hobza P, Kim K S 2007 J. Phys. Chem. A 111 3446
Google Scholar
[10] Yang Z 2021 Cells 10 934
Google Scholar
[11] Ginot F, Theurkauff I, Detcheverry F, Ybert C, Cottin-Bizonne C 2018 Nat. Commun. 9 696
Google Scholar
[12] Mauleon-Amieva A, Allen M P, Royall C P 2021 arXiv: 2107.07934 [cond-mat]
[13] Wensink H H, Löwen H 2008 Phys. Rev. E 78 031409
Google Scholar
[14] Grossmann R, Aranson I S, Peruani F 2020 Nat. Commun. 11 5365
Google Scholar
[15] Fily Y, Marchetti M C 2012 Phys. Rev. Lett. 108 235702
Google Scholar
[16] Deseigne J, Dauchot O, Chaté H 2010 Phys. Rev. Lett. 105 098001
Google Scholar
[17] Wensink H H, Kantsler V, Goldstein R E, Dunkel J 2014 Phys. Rev. E 89 010302
Google Scholar
[18] Prymidis V, Samin S, Filion L 2016 Soft Matter 12 4309
Google Scholar
[19] Redner G S, Hagan M F, Baskaran A 2013 Phys. Rev. Lett. 110 055701
Google Scholar
[20] Andréen D, Jenning P, Napp N, Petersen K 2020 Soft Matter 16 9436
Google Scholar
下载:
计量
- 文章访问数: 3385
- PDF下载量: 56
- 被引次数: 0
