-
The teleportation of Werner state in the graphene-based quantum channels under the dephasing environment is studied through the effective low-energy theory in this paper. The results show that the output entanglement normally reaches a higher level as the input entanglement increases, while the performance of the corresponding fidelity is opposite. Given the input state, the greater entanglement in the quantum channel can provide the higher-quality output state. For graphene-based quantum channels, the low temperature and weak Coulomb repulsive potential can decelerate the attenuation of entanglement resources in the dephasing environment. Moreover, when the temperature is lower than 40 K and the coulomb repulsive potential between electrons is less than 6 eV, the average fidelity of the output state reaches more than 80%. These results indicate that graphene has potential applications in quantum information.
-
Keywords:
- graphene nanoribbon /
- Werner state /
- quantum teleportation /
- dephasing
[1] Nielsen M A, Chuang I L 2002 Quantum Computation and Quantum Information (Cambridge: Cambridge University Press)
[2] Davis S I, Peña C, Xie S, Lauk N, Narváez L, Valivarthi R, Allmaras J P, Beyer A D, Gim Y, Hussein M, Iskander G, Kim H L, Korzh B, Mueller A, Rominsky M, Shaw M, Tang D, Wollman E E, Simon C, Spentzouris P, Oblak D, Sinclair N, Spiropulu M 2020 PRX Quantum 1 020317
Google Scholar
[3] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[4] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
Google Scholar
[5] Sangouard N, Simon C, de Riedmatten H, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[6] Gottesman D, Chuang I L 1999 Nature 402 390
Google Scholar
[7] Raussendorf R, Briegel H J 2001 Phys. Rev. Lett. 86 5188
Google Scholar
[8] Chou K S, Blumoff J Z, Wang C S, Reinhold P C, Axline C J, Gao Y Y, Frunzio L, Devoret M H, Jiang L, Schoelkopf R J 2018 Nature 561 368
Google Scholar
[9] Wan Y, Kienzler D, Erickson S D, Mayer K H, Leibfried D 2019 Science 364 875
Google Scholar
[10] 王明宇, 王馨德, 阮东, 龙桂鲁 2021 70 190301
Google Scholar
Wang M Y, Wang X D, Ruan D, Long G L 2021 Acta Phys. Sin. 70 190301
Google Scholar
[11] Bouwmeester D, Pan J W, Mattle K, Eibl M, Zeilinger A 1997 Nature 390 575
Google Scholar
[12] Yin J, Ren J, Lu H, Cao Y, Pan J 2012 Nature 488 185
Google Scholar
[13] Ma X S, Herbst T, Scheidl T, Wang D, Kropatschek S, Naylor W, Wittmann B, Mech A, Kofler J, Anisimova E, Makarov V, Jennewein T, Ursin R, Zeilinger A 2012 Nature 489 269
Google Scholar
[14] Metcalf B J, Spring J B, Humphreys P C, Thomas-Peter N, Barbieri M, Kolthammer W S, Jin X, Langford N K, Kundys D, Gates J C, Smith B J, Smith P G R, Walmsley I A 2014 Nat. Photonics 8 770
Google Scholar
[15] Im D, Lee C, Kim Y, Nha H, Kim M S, Lee S, Kim Y 2021 npj Quantum Inf. 7 86
Google Scholar
[16] Barrett M D, Chiaverini J, Schaetz T, Britton J, Itano W M, Jost J D 2004 Nature 429 737
Google Scholar
[17] Nölleke C, Neuzner A, Reiserer A, Hahn C, Rempe G, Ritter S 2013 Phys. Rev. Lett. 110 140403
Google Scholar
[18] Bao X H, Xu X F, Li C M, Yuan Z S, Lu C Y, Pan J W 2012 Proc. Natl. Acad. Sci. U. S. A. 109 20347
Google Scholar
[19] Krauter H, Salart D, Muschik C A, Petersen J M, Shen H, Fernholz T, Polzik E S 2013 Nat. Phys. 9 400
Google Scholar
[20] Gao W B, Fallahi P, Togan E, Delteil A, Chin Y S, Miguel-Sanchez J, Imamoğlu A 2013 Nat. Commun. 4 2744
Google Scholar
[21] Steffen L, Salathe Y, Oppliger M, Kurpiers P, Baur M, Lang C, Eichler C, Puebla-Hellmann G, Fedorov A, Wallraff A 2013 Nature 500 319
Google Scholar
[22] Pfaff W, Hensen B J, Bernien H, van Dam S B, Blok M S, Taminiau T H, Tiggelman M J, Schouten R N, Markham M, Twitchen D J, Hanson R 2014 Science 345 532
Google Scholar
[23] Huang N, Huang W, Li C 2020 Sci. Rep. 10 3093
Google Scholar
[24] Yu Y, Zhao N, Pei C X, Li W 2021 Commun. Theor. Phys. 73 085103
Google Scholar
[25] Ren J G, Xu P, Yong H L, Zhang L, Liao S K, Yin J, Liu W Y, Cai W Q, Yang M, Li L 2017 Nature 549 70
Google Scholar
[26] Pirandola S, Eisert J, Weedbrook C, Furusawa A, Braunstein S L 2015 Nat. Photonics 9 641
Google Scholar
[27] Bussières F, Clausen C, Tiranov A, Korzh B, Verma V B, Nam S W, Marsili F, Ferrier A, Goldner P, Herrmann H, Silberhorn C, Sohler W, Afzelius M, Gisin N 2014 Nat. Photonics 8 775
Google Scholar
[28] Llewellyn D, Ding Y, Faruque I I, Paesani S, Bacco D, Santagati R, Qian Y, Li Y, Xiao Y, Huber M, Malik M, Sinclair G F, Zhou X, Rottwitt K, O Brien J L, Rarity J G, Gong Q, Oxenlowe L K, Wang J, Thompson M G 2020 Nat. Phys. 16 148
Google Scholar
[29] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[30] Castro Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109
Google Scholar
[31] Wakabayashi K, Sasaki K, Nakanishi T, Enoki T 2010 Sci. Technol. Adv. Mater. 11 054504
Google Scholar
[32] Yazyev O V 2010 Rep. Prog. Phys. 73 056501
Google Scholar
[33] Talirz L, Söde H, Cai J, Ruffieux P, Blankenburg S, Jafaar R, Berger R, Feng X, Müllen K, Passerone D, Fasel R, Pignedoli C A 2013 J. Am. Chem. Soc. 135 2060
Google Scholar
[34] van der Lit J, Boneschanscher M P, Vanmaekelbergh D, Ijäs M, Uppstu A, Ervasti M, Harju A, Liljeroth P, Swart I 2013 Nat. Commun. 4 2023
Google Scholar
[35] Schmidt M J, Golor M, Lang T C, Wessel S 2013 Phys. Rev. B 87 245431
Google Scholar
[36] Golor M, Koop C, Lang T C, Wessel S, Schmidt M J 2013 Phys. Rev. Lett. 111 085504
Google Scholar
[37] Gräfe M, Szameit A 2015 2 D Materials 2 034005
Google Scholar
[38] Burkard G, Bulaev D V, Trauzettel B, Loss D 2007 Nat. Phys. 3 192
Google Scholar
[39] Recher P, Trauzettel B 2010 Nanotechnology 21 302001
Google Scholar
[40] Chen C, Chang Y 2015 Phys. Rev. B 92 245406
Google Scholar
[41] Cimatti I, Bondì L, Serrano G, Malavolti L, Cortigiani B, Velez-Fort E, Betto D, Ouerghi A, Brookes N B, Loth S, Mannini M, Totti F, Sessoli R 2019 Nanoscale Horizons 4 1202
Google Scholar
[42] Guo G, Lin Z, Tu T, Cao G, Li X, Guo G 2009 New J. Phys. 11 123005
Google Scholar
[43] Dragoman D, Dragoman M 2015 Nanotechnology 26 485201
Google Scholar
[44] Dragoman M, Dinescu A, Dragoman D 2018 IEEE Trans. Nanotechnol. 17 362
Google Scholar
[45] Wootters W K 1998 Phys. Rev. Lett. 80 2245
Google Scholar
[46] Werner R F 1989 Phys. Rev. A 40 4277
Google Scholar
[47] Aolita L, de Melo F, Davidovich L 2015 Rep. Prog. Phys. 78 042001
Google Scholar
[48] Bowen G, Bose S 2001 Phys. Rev. Lett. 87 267901
Google Scholar
[49] Jozsa R 1994 J. Mod. Opt. 41 2315
Google Scholar
-
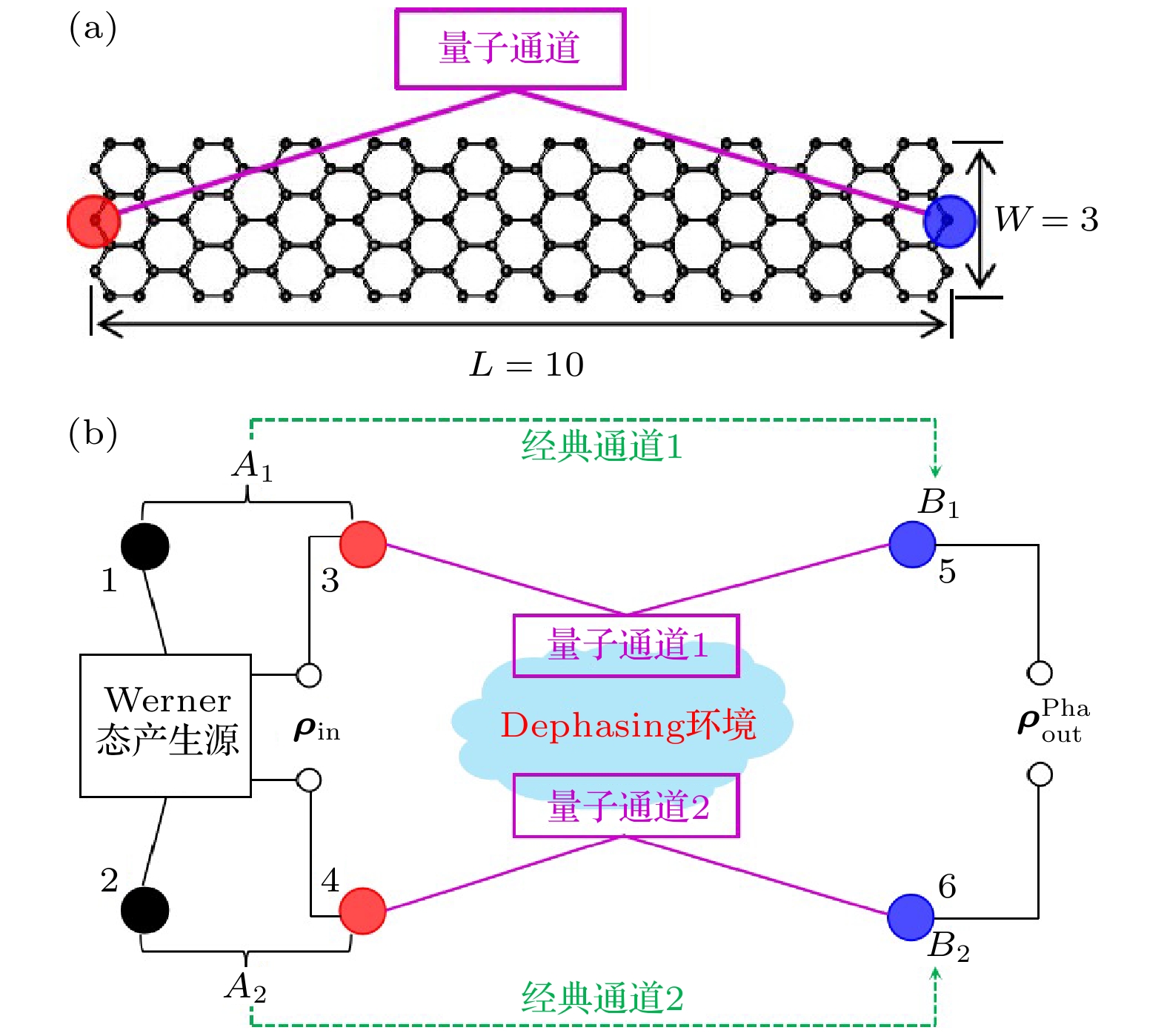
图 1 退相位环境下Werner态在石墨烯基量子通道中的隐形传输原理图 (a) 构建量子通道的特殊石墨烯纳米带(SGNR)几何结构. 带长(L)和带宽(W)分别用沿着扶手椅形和锯齿形边缘的六方格子的数目表征. 红色和蓝色小球表示一对呈反铁磁耦合的电子自旋, 它们就是构建量子通道的物理比特. (b) Werner态的隐形传输原理图. 黑色小球(1, 2)表示产生Werner态的物理比特. 量子通道的物理比特分别由两个尺寸完全相同的SGNR锯齿端上的纠缠粒子对(3, 5)和(4, 6)承担
Fig. 1. Schematic illustration of teleporting the Werner state via the graphene-based quantum channels under the dephasing environment: (a) Lattice geometry of the special graphene nanoribbon (SGNR) used to form quantum channels. The ribbon length (L) and width (W) are characterized by the number of hexagons along the armchair and zigzag direction, respectively. The red and blue particles denote a pair of spins with the antiferromagnetic coupling, which serve as physical qubits to support quantum channels. (b) Schematic illustration of teleporting the Werner state. The black particles (1, 2) are physical qubits used to prepare the Werner state. The physical qubits of quantum channels are supported by two pairs of the entangled spins (3, 5) and (4, 6) in two same SGNRs, respectively.
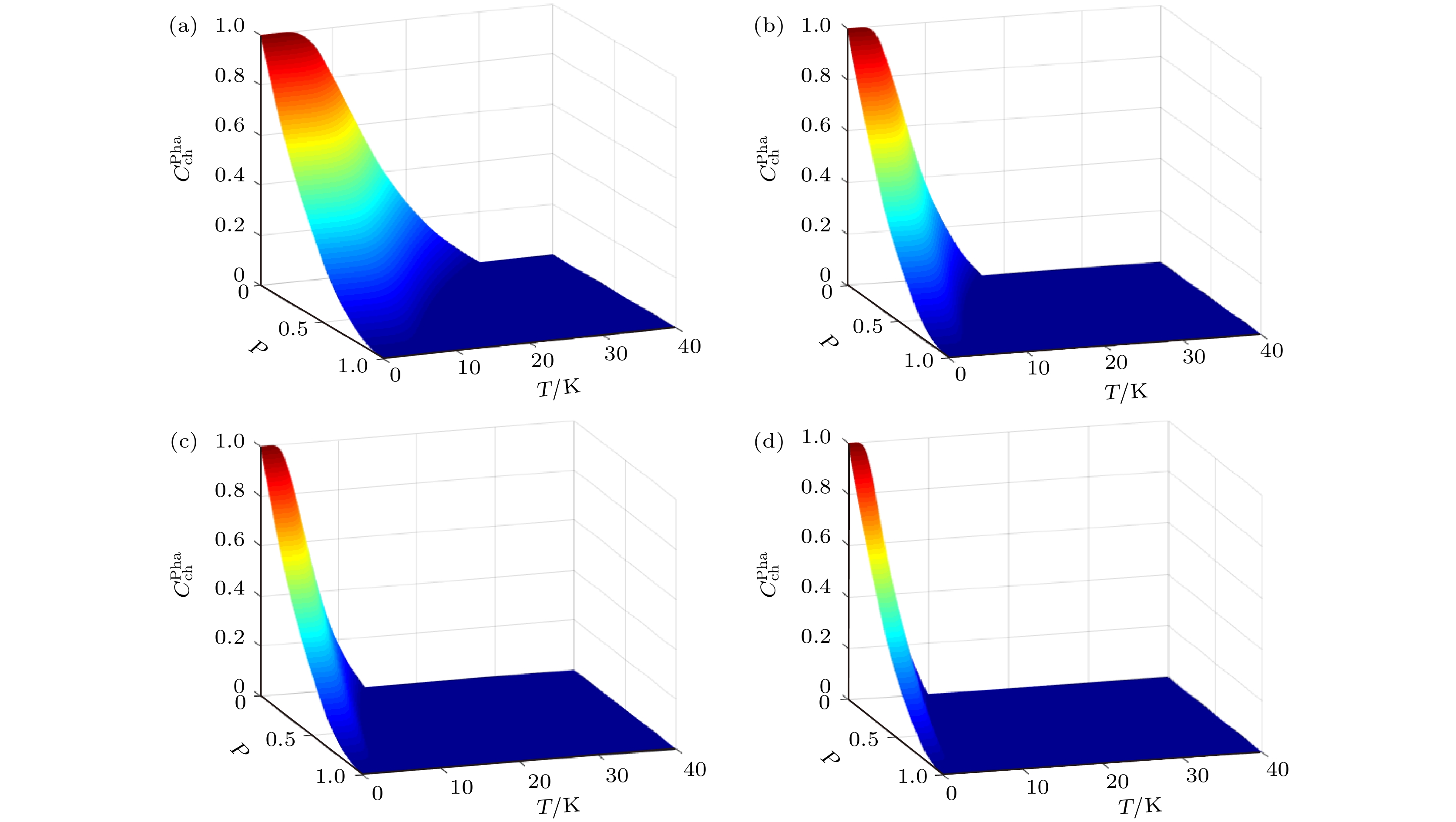
图 2 退相位环境下通道态
$ {\boldsymbol{\rho}} _{{\text{ch}}}^{{\text{Pha}}} $ 的纠缠度$C_{{\text{ch}}}^{{\text{Pha}}}$ 随温度T和出错概率p的变化 (a) U = 2.0 eV; (b) U = 3.5 eV; (c) U = 4.5 eV; (d) U = 6.0 eVFig. 2. Concurrence
$C_{{\text{ch}}}^{{\text{Pha}}}$ for the channel state$ {\boldsymbol{\rho}} _{{\text{ch}}}^{{\text{Pha}}} $ in the dephasing environment as a function of temperature T and probability p: (a) U = 2.0 eV; (b) U = 3.5 eV; (c) U = 4.5 eV; (d) U = 6.0 eV.
图 3 退相位环境下通道态
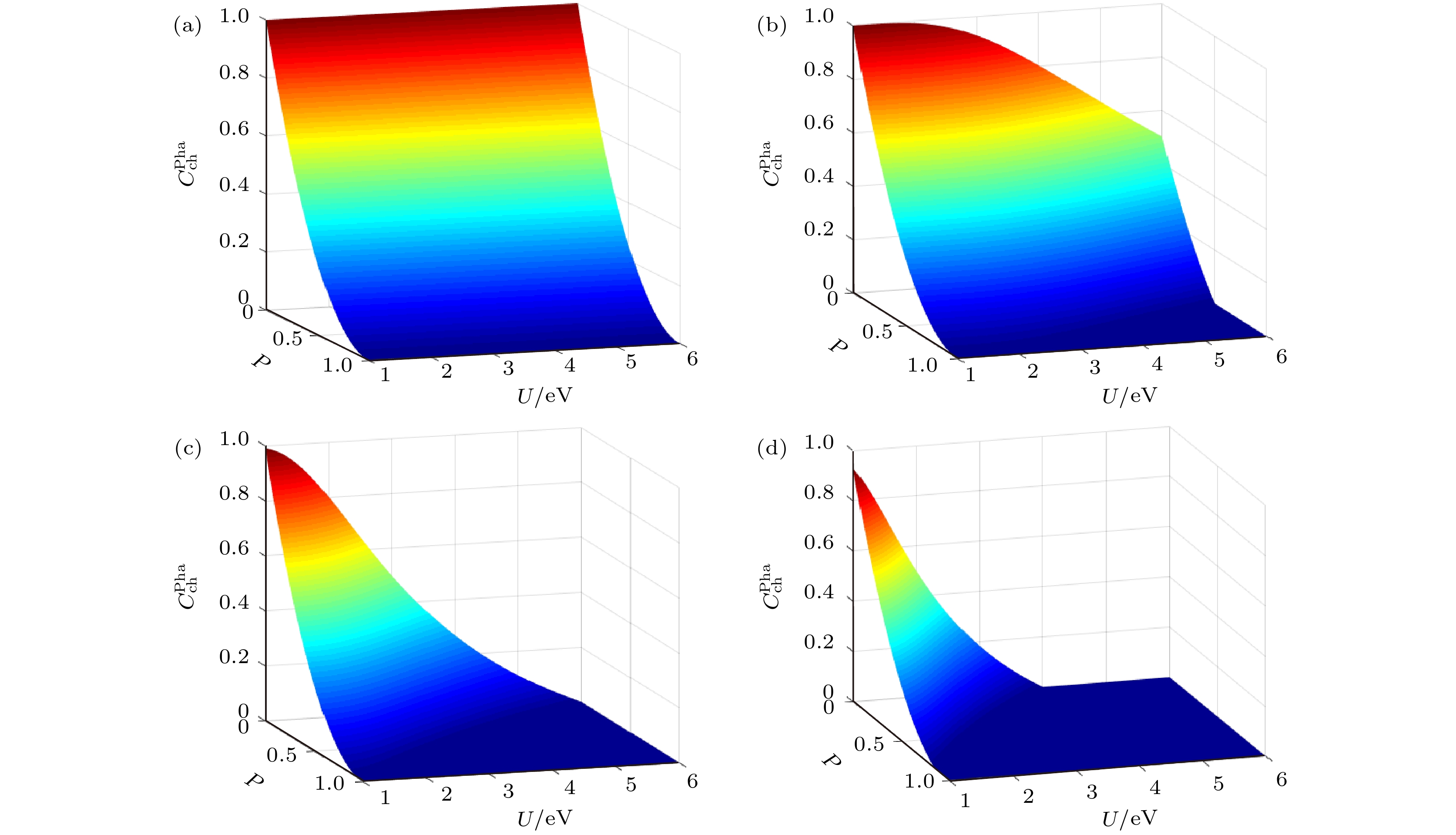
$ {\boldsymbol{\rho}} _{{\text{ch}}}^{{\text{Pha}}} $ 的纠缠度$C_{{\text{ch}}}^{{\text{Pha}}}$ 随库仑排斥势U和出错概率p的变化 (a) T = 0 K, (b) T = 5 K, (c) T = 10 K, (d) T = 15 KFig. 3. Concurrence
$C_{{\text{ch}}}^{{\text{Pha}}}$ for the channel state$ {\boldsymbol{\rho}} _{{\text{ch}}}^{{\text{Pha}}} $ in the dephasing environment as a function of Coulomb repulsion U and probability p: (a) T = 0 K; (b) T = 5 K; (c) T = 10 K; (d) T = 15 K.
图 4 退相位环境下输出态
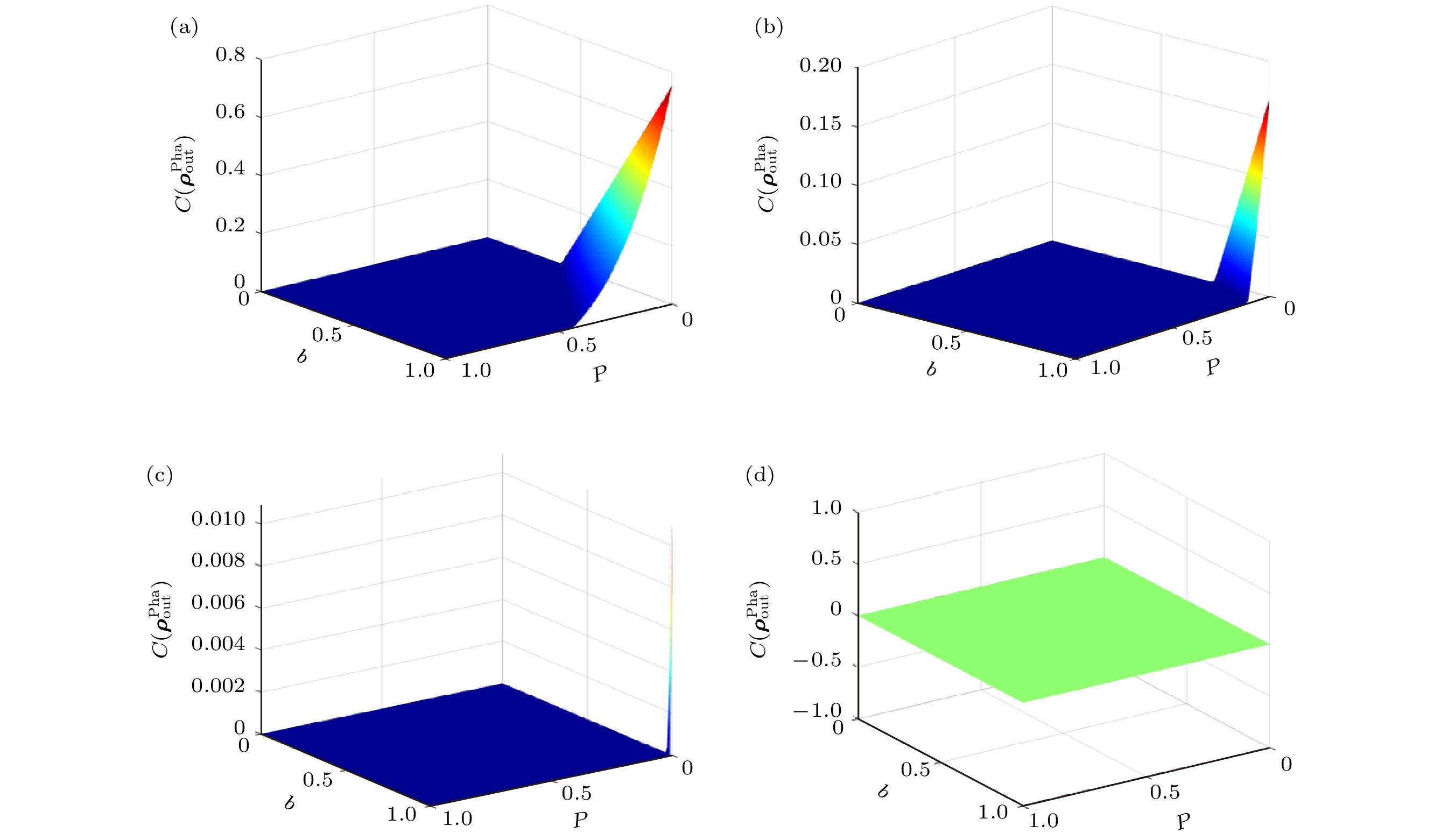
$ {{\rho}} _{out}^{Pha} $ 的纠缠度$C_{out}^{Pha}$ 随参数b和出错概率p的变化 (a) T = 5 K, U = 3.5 eV; (b) T = 5 K, U = 6.0 eV; (c) T = 10 K, U = 3.5 eV; (d) T = 10 K, U = 6.0 eVFig. 4. Concurrence
$C_{{\text{out}}}^{{\text{Pha}}}$ for the output state$ {{\rho}} _{{\text{out}}}^{{\text{Pha}}} $ under the dephasing channel as a function of parameter b and probability p: (a) T = 5 K and U = 3.5 eV; (b) T = 5 K and U = 6.0 eV; (c) T = 10 K and U = 3.5 eV; (d) T = 10 K and U = 6.0 eV.
图 5 退相位环境下输出态
$ {\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}} $ 的保真度$F({{\boldsymbol{\rho}} _{{\text{in}}}}, \;{\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}})$ 随参数b和出错概率p的变化 (a) T = 5 K, U = 3.5 eV; (b) T = 5 K, U = 6.0 eV; (c) T = 10 K, U = 3.5 eV; (d) T = 10 K, U = 6.0 eV.Fig. 5. Fidelity
$F({{\boldsymbol{\rho}} _{{\text{in}}}}, \;{\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}})$ for the output state$ {\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}} $ under the dephasing channel as a function of parameter b and probability p: (a) T = 5 K and U = 3.5 eV; (b) T = 5 K and U = 6.0 eV; (c) T = 10 K and U = 3.5 eV; (d) T = 10 K and U = 6.0 eV.
图 6 退相位环境下输出态
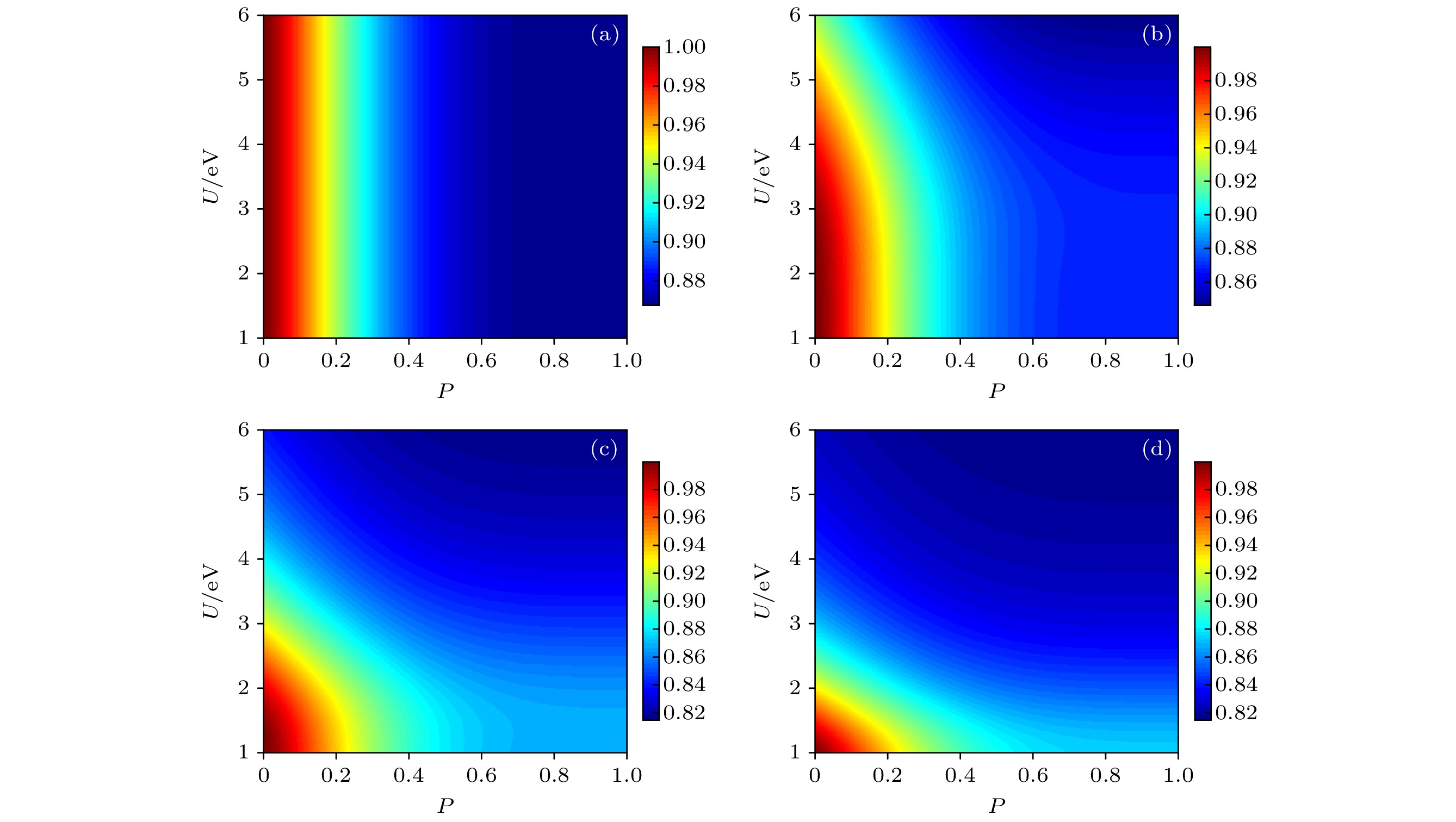
$ {\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}} $ 的平均保真度${F_A}({{\boldsymbol{\rho}} _{{{\rm{in}}} }}, \;{\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}})$ 随出错概率p和温度T的变化 (a) U = 2.0 eV; (b) U = 3.5 eV; (c) U = 4.5 eV; (d) U = 6.0 eV.Fig. 6. Average fidelity
${F_A}({{\boldsymbol{\rho}} _{{\text{in}}}}, \;{\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}})$ of the output state under the dephasing channel as a function of probability p and temperature T: (a) U = 2.0 eV; (b) U = 3.5 eV; (c) U = 4.5 eV; (d) U = 6.0 eV.
图 7 退相位环境下输出态
$ {\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}} $ 的平均保真度${F_A}({{\boldsymbol{\rho}} _{{\text{in}}}}, \;{\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}})$ 随出错概率p和库仑排斥势U的变化 (a) T = 0 K; (b) T = 5 K; (c) T = 10 K; (d) T = 15 KFig. 7. Average fidelity
${F_A}({{\boldsymbol{\rho}} _{{\text{in}}}}, \;{\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}})$ of the output state$ {\boldsymbol{\rho}} _{{\text{out}}}^{{\text{Pha}}} $ under the dephasing channel as a function of probability p and Coulomb repulsion U: (a) T = 0 K; (b) T = 5 K; (c) T = 10 K; (d) T = 15 K, respectively.表 1 Alice执行联合贝尔基测量所得的16种可能结果与对应每种测量结果Bob为复原Werner态所执行的幺正操作
Table 1. Sixteen possible results of joint Bell-state measurements performed by Alice and the unitary operations performed by Bob according to each measurement result for restoring the Werner state.
Alice对A1处的量子比特(1, 3)
和A2处的量子比特(2, 4)执行
联合贝尔基测量后所得结果为了复原Werner态Bob对B1和B2处的量子比特(5,6)
所执行的相应幺正操作$E_0^{{A_1}} \otimes E_0^{{A_2}}$ ${I^{{B_1}}}$, ${I^{{B_2}}}$ $E_0^{{A_1}} \otimes E_1^{{A_2}}$ ${I^{{B_1}}}$, $\sigma _x^{{B_2}}$ $E_0^{{A_1}} \otimes E_2^{{A_2}}$ ${I^{{B_1}}}$, $\sigma _y^{{B_2}}$ $E_0^{{A_1}} \otimes E_3^{{A_2}}$ ${I^{{B_1}}}$, $\sigma _z^{{B_2}}$ $E_1^{{A_1}} \otimes E_0^{{A_2}}$ $\sigma _x^{{B_1}}$, ${I^{{B_2}}}$ $E_1^{{A_1}} \otimes E_1^{{A_2}}$ $\sigma _x^{{B_1}}$, $\sigma _x^{{B_2}}$ $E_1^{{A_1}} \otimes E_2^{{A_2}}$ $\sigma _x^{{B_1}}$, $\sigma _y^{{B_2}}$ $E_1^{{A_1}} \otimes E_3^{{A_2}}$ $\sigma _x^{{B_1}}$, $\sigma _z^{{B_2}}$ $E_2^{{A_1}} \otimes E_0^{{A_2}}$ $\sigma _y^{{B_1}}$, ${I^{{B_2}}}$ $E_2^{{A_1}} \otimes E_1^{{A_2}}$ $\sigma _y^{{B_1}}$, $\sigma _x^{{B_2}}$ $E_2^{{A_1}} \otimes E_2^{{A_2}}$ $\sigma _y^{{B_1}}$, $\sigma _y^{{B_2}}$ $E_2^{{A_1}} \otimes E_3^{{A_2}}$ $\sigma _y^{{B_1}}$, $\sigma _z^{{B_2}}$ $E_3^{{A_1}} \otimes E_0^{{A_2}}$ $\sigma _z^{{B_1}}$, ${I^{{B_2}}}$ $E_3^{{A_1}} \otimes E_1^{{A_2}}$ $\sigma _z^{{B_1}}$, $\sigma _x^{{B_2}}$ $E_3^{{A_1}} \otimes E_2^{{A_2}}$ $\sigma _z^{{B_1}}$, $\sigma _y^{{B_2}}$ $E_3^{{A_1}} \otimes E_3^{{A_2}}$ $\sigma _z^{{B_1}}$, $\sigma _z^{{B_2}}$ 
下载: 导出CSV
-
[1] Nielsen M A, Chuang I L 2002 Quantum Computation and Quantum Information (Cambridge: Cambridge University Press)
[2] Davis S I, Peña C, Xie S, Lauk N, Narváez L, Valivarthi R, Allmaras J P, Beyer A D, Gim Y, Hussein M, Iskander G, Kim H L, Korzh B, Mueller A, Rominsky M, Shaw M, Tang D, Wollman E E, Simon C, Spentzouris P, Oblak D, Sinclair N, Spiropulu M 2020 PRX Quantum 1 020317
Google Scholar
[3] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[4] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
Google Scholar
[5] Sangouard N, Simon C, de Riedmatten H, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[6] Gottesman D, Chuang I L 1999 Nature 402 390
Google Scholar
[7] Raussendorf R, Briegel H J 2001 Phys. Rev. Lett. 86 5188
Google Scholar
[8] Chou K S, Blumoff J Z, Wang C S, Reinhold P C, Axline C J, Gao Y Y, Frunzio L, Devoret M H, Jiang L, Schoelkopf R J 2018 Nature 561 368
Google Scholar
[9] Wan Y, Kienzler D, Erickson S D, Mayer K H, Leibfried D 2019 Science 364 875
Google Scholar
[10] 王明宇, 王馨德, 阮东, 龙桂鲁 2021 70 190301
Google Scholar
Wang M Y, Wang X D, Ruan D, Long G L 2021 Acta Phys. Sin. 70 190301
Google Scholar
[11] Bouwmeester D, Pan J W, Mattle K, Eibl M, Zeilinger A 1997 Nature 390 575
Google Scholar
[12] Yin J, Ren J, Lu H, Cao Y, Pan J 2012 Nature 488 185
Google Scholar
[13] Ma X S, Herbst T, Scheidl T, Wang D, Kropatschek S, Naylor W, Wittmann B, Mech A, Kofler J, Anisimova E, Makarov V, Jennewein T, Ursin R, Zeilinger A 2012 Nature 489 269
Google Scholar
[14] Metcalf B J, Spring J B, Humphreys P C, Thomas-Peter N, Barbieri M, Kolthammer W S, Jin X, Langford N K, Kundys D, Gates J C, Smith B J, Smith P G R, Walmsley I A 2014 Nat. Photonics 8 770
Google Scholar
[15] Im D, Lee C, Kim Y, Nha H, Kim M S, Lee S, Kim Y 2021 npj Quantum Inf. 7 86
Google Scholar
[16] Barrett M D, Chiaverini J, Schaetz T, Britton J, Itano W M, Jost J D 2004 Nature 429 737
Google Scholar
[17] Nölleke C, Neuzner A, Reiserer A, Hahn C, Rempe G, Ritter S 2013 Phys. Rev. Lett. 110 140403
Google Scholar
[18] Bao X H, Xu X F, Li C M, Yuan Z S, Lu C Y, Pan J W 2012 Proc. Natl. Acad. Sci. U. S. A. 109 20347
Google Scholar
[19] Krauter H, Salart D, Muschik C A, Petersen J M, Shen H, Fernholz T, Polzik E S 2013 Nat. Phys. 9 400
Google Scholar
[20] Gao W B, Fallahi P, Togan E, Delteil A, Chin Y S, Miguel-Sanchez J, Imamoğlu A 2013 Nat. Commun. 4 2744
Google Scholar
[21] Steffen L, Salathe Y, Oppliger M, Kurpiers P, Baur M, Lang C, Eichler C, Puebla-Hellmann G, Fedorov A, Wallraff A 2013 Nature 500 319
Google Scholar
[22] Pfaff W, Hensen B J, Bernien H, van Dam S B, Blok M S, Taminiau T H, Tiggelman M J, Schouten R N, Markham M, Twitchen D J, Hanson R 2014 Science 345 532
Google Scholar
[23] Huang N, Huang W, Li C 2020 Sci. Rep. 10 3093
Google Scholar
[24] Yu Y, Zhao N, Pei C X, Li W 2021 Commun. Theor. Phys. 73 085103
Google Scholar
[25] Ren J G, Xu P, Yong H L, Zhang L, Liao S K, Yin J, Liu W Y, Cai W Q, Yang M, Li L 2017 Nature 549 70
Google Scholar
[26] Pirandola S, Eisert J, Weedbrook C, Furusawa A, Braunstein S L 2015 Nat. Photonics 9 641
Google Scholar
[27] Bussières F, Clausen C, Tiranov A, Korzh B, Verma V B, Nam S W, Marsili F, Ferrier A, Goldner P, Herrmann H, Silberhorn C, Sohler W, Afzelius M, Gisin N 2014 Nat. Photonics 8 775
Google Scholar
[28] Llewellyn D, Ding Y, Faruque I I, Paesani S, Bacco D, Santagati R, Qian Y, Li Y, Xiao Y, Huber M, Malik M, Sinclair G F, Zhou X, Rottwitt K, O Brien J L, Rarity J G, Gong Q, Oxenlowe L K, Wang J, Thompson M G 2020 Nat. Phys. 16 148
Google Scholar
[29] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[30] Castro Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109
Google Scholar
[31] Wakabayashi K, Sasaki K, Nakanishi T, Enoki T 2010 Sci. Technol. Adv. Mater. 11 054504
Google Scholar
[32] Yazyev O V 2010 Rep. Prog. Phys. 73 056501
Google Scholar
[33] Talirz L, Söde H, Cai J, Ruffieux P, Blankenburg S, Jafaar R, Berger R, Feng X, Müllen K, Passerone D, Fasel R, Pignedoli C A 2013 J. Am. Chem. Soc. 135 2060
Google Scholar
[34] van der Lit J, Boneschanscher M P, Vanmaekelbergh D, Ijäs M, Uppstu A, Ervasti M, Harju A, Liljeroth P, Swart I 2013 Nat. Commun. 4 2023
Google Scholar
[35] Schmidt M J, Golor M, Lang T C, Wessel S 2013 Phys. Rev. B 87 245431
Google Scholar
[36] Golor M, Koop C, Lang T C, Wessel S, Schmidt M J 2013 Phys. Rev. Lett. 111 085504
Google Scholar
[37] Gräfe M, Szameit A 2015 2 D Materials 2 034005
Google Scholar
[38] Burkard G, Bulaev D V, Trauzettel B, Loss D 2007 Nat. Phys. 3 192
Google Scholar
[39] Recher P, Trauzettel B 2010 Nanotechnology 21 302001
Google Scholar
[40] Chen C, Chang Y 2015 Phys. Rev. B 92 245406
Google Scholar
[41] Cimatti I, Bondì L, Serrano G, Malavolti L, Cortigiani B, Velez-Fort E, Betto D, Ouerghi A, Brookes N B, Loth S, Mannini M, Totti F, Sessoli R 2019 Nanoscale Horizons 4 1202
Google Scholar
[42] Guo G, Lin Z, Tu T, Cao G, Li X, Guo G 2009 New J. Phys. 11 123005
Google Scholar
[43] Dragoman D, Dragoman M 2015 Nanotechnology 26 485201
Google Scholar
[44] Dragoman M, Dinescu A, Dragoman D 2018 IEEE Trans. Nanotechnol. 17 362
Google Scholar
[45] Wootters W K 1998 Phys. Rev. Lett. 80 2245
Google Scholar
[46] Werner R F 1989 Phys. Rev. A 40 4277
Google Scholar
[47] Aolita L, de Melo F, Davidovich L 2015 Rep. Prog. Phys. 78 042001
Google Scholar
[48] Bowen G, Bose S 2001 Phys. Rev. Lett. 87 267901
Google Scholar
[49] Jozsa R 1994 J. Mod. Opt. 41 2315
Google Scholar
下载:
计量
- 文章访问数: 5016
- PDF下载量: 55
- 被引次数: 0
