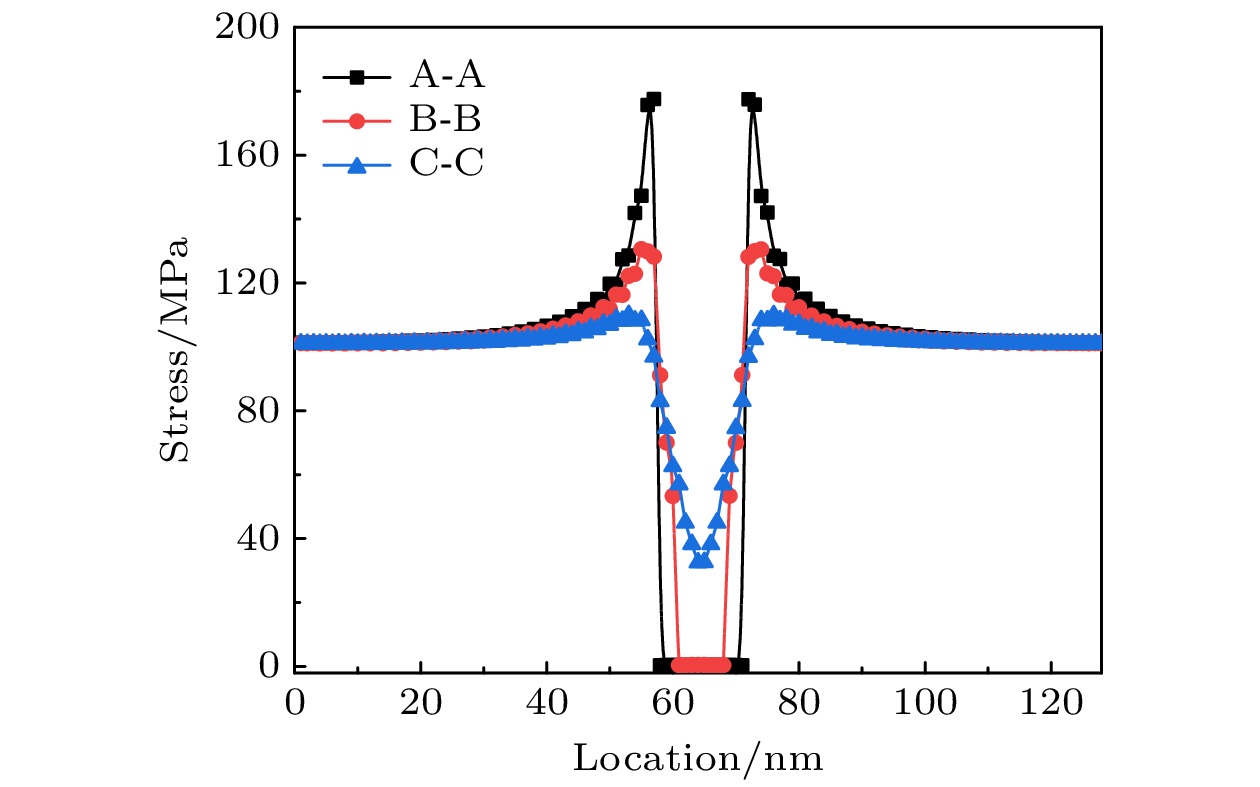
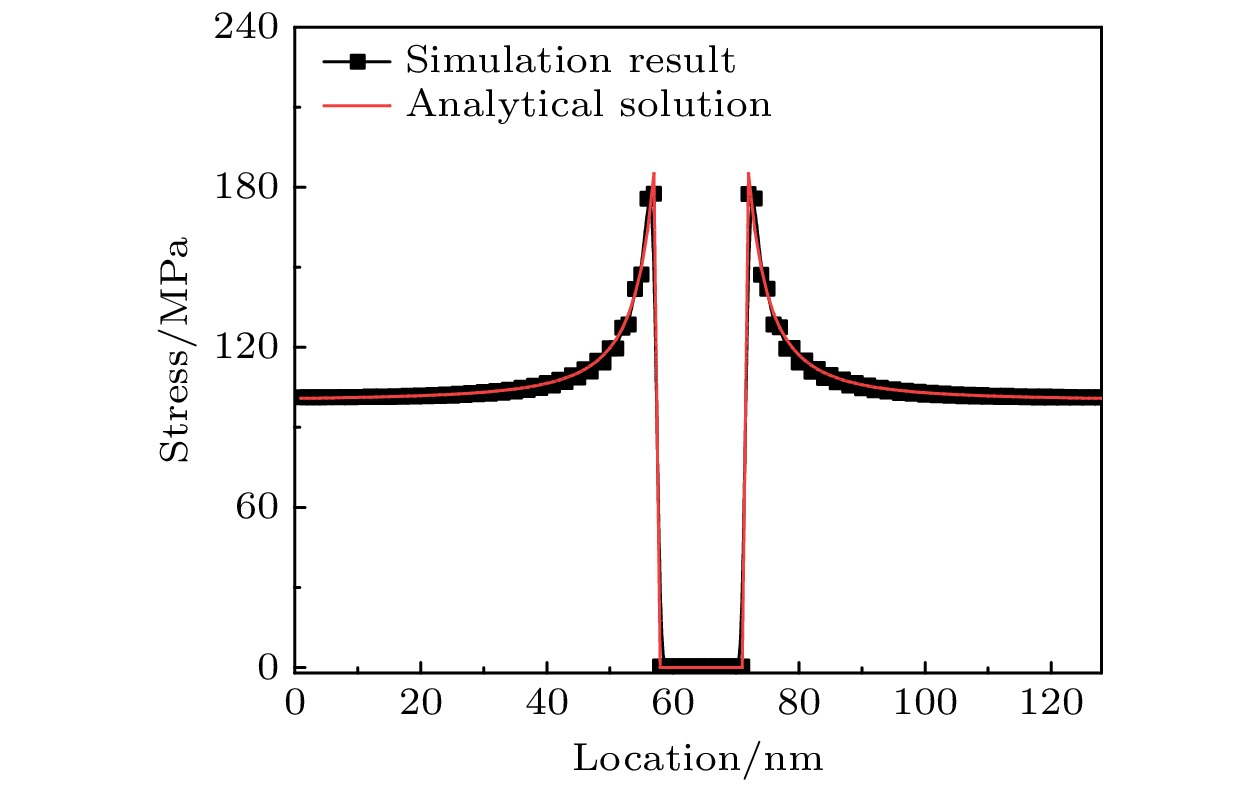
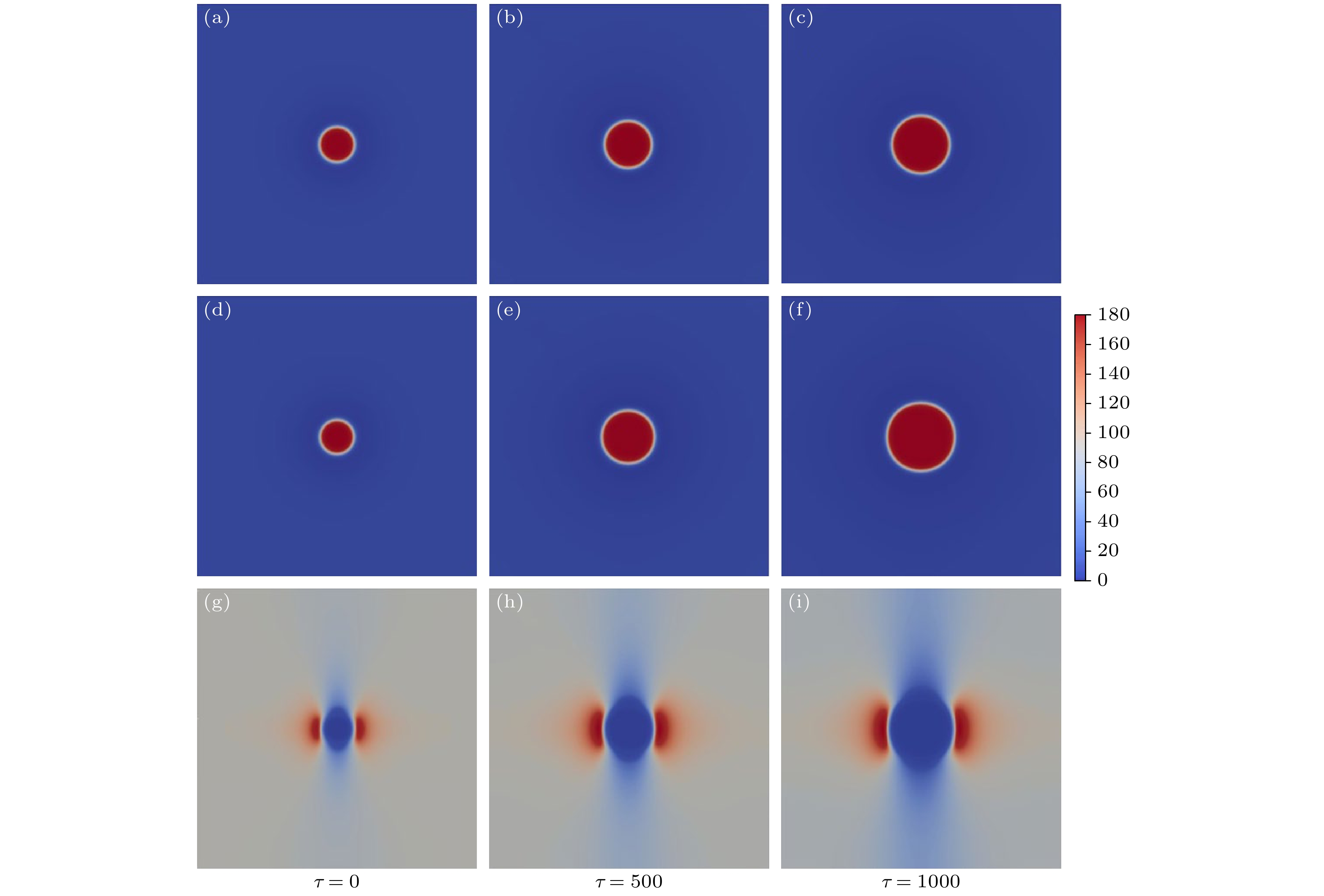
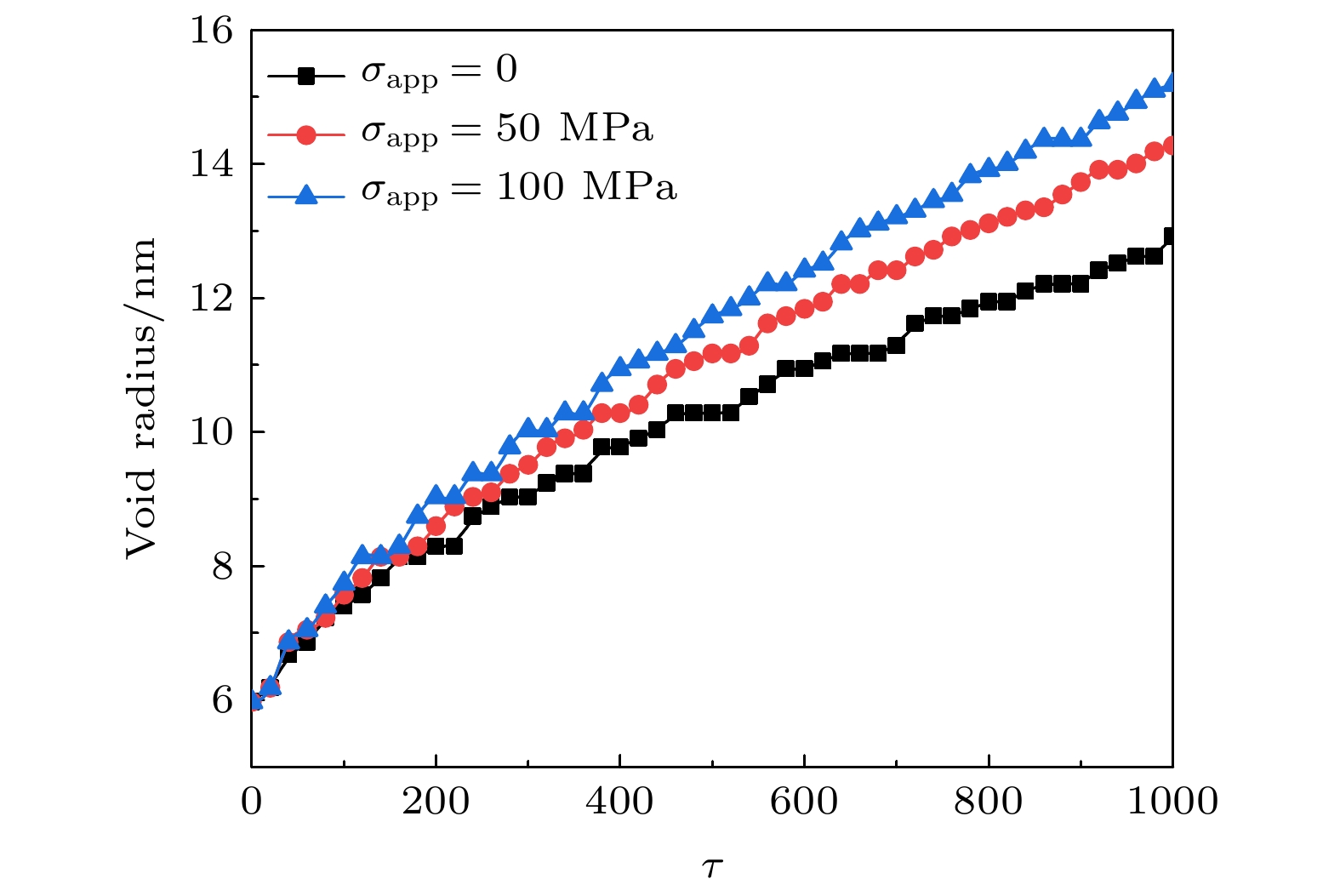
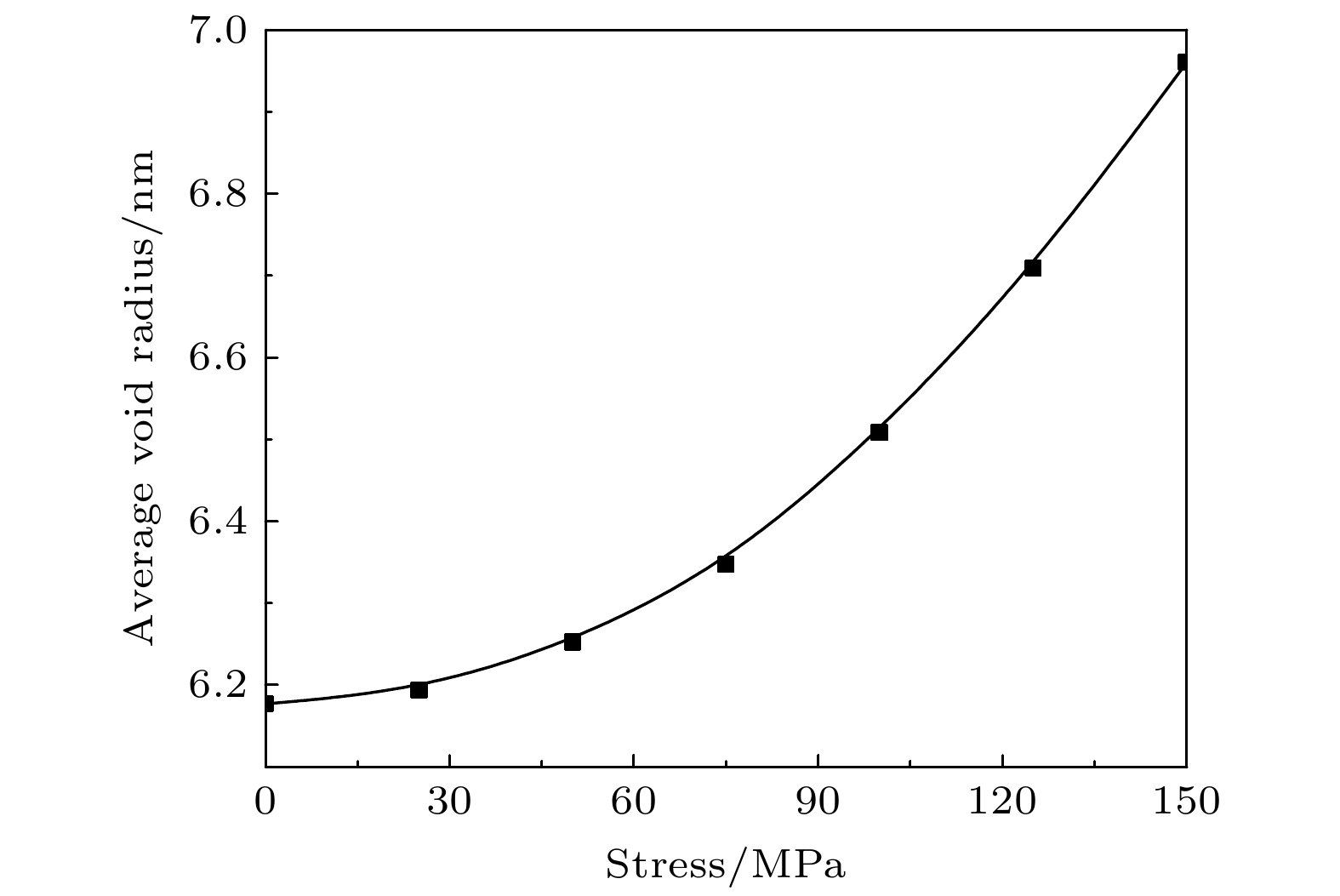
-
本工作建立了外加应力作用下UO2中空洞演化的相场模型. 首先, 使用摄动迭代法求解了弹性平衡方程, 对外加应力下单个空洞周围的应力分布进行了计算, 结果表明空洞边缘有应力集中现象, 模拟得到的应力分布和解析解一致. 然后, 利用相场方法模拟了不同外加应力下单个空洞的演化过程, 结果表明随着外加应力的增大, 空洞的生长速度加快. 最后, 研究了外加应力对多晶体系中晶粒长大和空洞演化的影响, 结果表明, 不同晶粒内的应力大小不同, 应力越小的晶粒越容易长大, 尺寸越大的空洞的边缘应力也越大. 晶间空洞与弯曲晶界存在相互作用, 一方面晶界附近的空洞会生长成透镜状, 另一方面空洞对晶界也有钉扎作用, 能减缓晶界的迁移. 此外, 外加应力会加速多晶系统中空洞的生长, 并且本文计算得到了外加应力与空洞半径的关系, 发现外加应力越大, 空洞的生长越快.Owing to the migration and aggregation of point defects produced by cascade collision, a large number of cavities form easily during irradiation of the uranium dioxide (UO2) that is an important nuclear fuel. In addition, cavities are also inevitably introduced into the ceramic fuel during sintering. Moreover, the creep strain and thermal strain, caused by the extreme environment of high temperature and strong irradiation, significantly increase the applied stress of nuclear fuel. Therefore, it is crucial to investigate the microstructure evolution of the cavities in UO2 fuel under applied stress. In this work, a phase-field model of void evolution in UO2 under applied stress is established. Firstly, the elastic equilibrium equation is solved by the perturbation-iterative method, and the stress distribution around a single void under applied stress is calculated. The results show that the stress concentration is observed at the edge of the void, and the simulated stress distribution is consistent with the theoretically analytical results. Then, the evolution processes of a single void under different applied stresses are simulated by the phase-field model. The results show that the growth rate of void increases with the augment of applied stress. Finally, the effect of applied stress on grain growth and void evolution in polycrystalline are also studied. The results show that the applied stress will accelerate the void growth. With the increase of the applied stress, the effect of the applied stress on accelerating the void evolution increases.
-
Keywords:
- phase field model /
- void evolution /
- grain growth /
- applied stress
[1] Govers K, Lemehov S, Hou M, Verwerft M 2007 J. Nucl. Mater. 366 161
Google Scholar
[2] 杨辉, 冯泽华, 王贺然, 张云鹏, 陈铮, 信天缘, 宋小蓉, 吴璐, 张静 2021 70 054601
Google Scholar
Yang H, Feng Z H, Wang H R, Zhang Y P, Chen Z, Xin T Y, Song X R, Wu L, Zhang J 2021 Acta Phys. Sin. 70 054601
Google Scholar
[3] 孙正阳, 杨超, 柳文波 2020 金属学报 56 1295
Sun Z Y, Yang C, Liu W B 2020 Acta Metall. Sin. 56 1295
[4] Solomon A A 1973 J. Am. Ceram. Soc. 56 164
Google Scholar
[5] Brask D N 1979 J. Nucl. Mater. 83 265
Google Scholar
[6] Porter D L, Takata M L, Wood E L 1983 J. Nucl. Mater. 116 272
Google Scholar
[7] Sahu H K, Jung P 1985 J. Nucl. Mater. 136 154
Google Scholar
[8] Brager H R, Garner F A, Guthrie G L 1977 J. Nucl. Mater. 66 301
Google Scholar
[9] Jiang Y, Liu W, Li W, Sun Z, Xin Y, Chen P, Yun D 2021 Comput. Mater. Sci. 188 110176
Google Scholar
[10] Millett P C, Rokkam S, El-Azab A, Tonks M, Wolf D 2009 Model. Simul. Mater. Sci. Eng. 17 64003
Google Scholar
[11] Brailsford A D, Bullough R, Hayns M R 1976 J. Nucl. Mater. 60 246
Google Scholar
[12] Wiedersich H 1972 Radiat. Eff. Defect. S. 12 111
Google Scholar
[13] Millett P C, El-Azab A, Rokkam S, Tonks M, Wolf D 2011 Comput. Mater. Sci. 50 949
Google Scholar
[14] Millett P C, El-Azab A, Wolf D 2011 Comput. Mater. Sci. 50 960
Google Scholar
[15] Liu W B, Wang N, Ji Y Z, Song P C, Zhang C, Yang Z G, Chen L Q 2016 J. Nucl. Mater. 479 316
Google Scholar
[16] 杨朝曦, 柳文波, 张璁雨, 贺新福, 孙正阳, 贾丽霞, 师田田, 恽迪 2021 70 116101
Google Scholar
Yang Z X, Liu W B, Zhang C Y, He X F, Sun Z Y, Jia L X, Shi T T, Yun D 2021 Acta Phys. Sin. 70 116101
Google Scholar
[17] Hu S Y, Chen L Q 2001 Acta Mater. 49 1879
Google Scholar
[18] Wang J J, Bhattacharyya S, Li Q, Heo T W, Ma X Q, Chen L 2012 Phil. Mag. Lett. 92 327
[19] Kim D, Kim S G, Kim W T, Cho J, Han H N, Cha P 2011 Scr. Mater. 64 1079
Google Scholar
[20] Chang K, Lee G, Kwon J 2016 Radiat. Eff. Defect. S. 171 242
Google Scholar
[21] Salvo M, Sercombe J, Ménard J, Julien J, Helfer T, Désoyer T 2015 J. Nucl. Mater. 456 54
Google Scholar
[22] Cahn J W, Hilliard J E 1958 J. Chem. Phys. 28 258
Google Scholar
[23] Tonks M R, Zhang Y, Butterfield A, Bai X 2015 Model. Simul. Mater. Sci. Eng. 23 45009
Google Scholar
[24] Wang Y U, Jin Y M, Khachaturyan A G 2002 J. Appl. Phys. 92 1351
Google Scholar
[25] Sheng G, Bhattacharyya S, Zhang H, Chang K, Shang S L, Mathaudhu S N, Liu Z K, Chen L Q 2012 Mater. Sci. Eng. A 554 67
Google Scholar
[26] Tonks M, Millett P 2011 Mater. Sci. Eng. A 528 4086
Google Scholar
[27] Yan L L, Liu C Z, Ying Y Z, Zheng C 2014 Chinese Phys. B 23 69102
Google Scholar
[28] Wang Y U, Jin Y M, Khachaturyan A G 2002 J. Appl. Phys. 91 6435
Google Scholar
[29] Moelans N, Blanpain B, Wollants P 2008 Calphad 32 268
Google Scholar
[30] Chen L Q, Shen J 1998 Comput. Phys. Commun. 108 147
Google Scholar
[31] Kang K H, Ryu H J, Song K C, Yang M S 2002 J. Nucl. Mater. 301 242
Google Scholar
[32] Aagesen L K, Schwen D, Tonks M R, Zhang Y 2019 Comput. Mater. Sci. 161 35
Google Scholar
[33] Kinoshita M 1997 J. Nucl. Mater. 248 185
Google Scholar
[34] Freyss M, Petit T, Crocombette J 2005 J. Nucl. Mater. 347 44
Google Scholar
[35] Xiao H, Long C, Chen H, Tian X, Wei T, Zhao Y, Gao W 2015 Appl. Surf. Sci. 351 517
Google Scholar
[36] Chen T, Chen D, Sencer B H, Shao L 2014 J. Nucl. Mater. 452 364
Google Scholar
[37] Fritz I J 1976 J. Appl. Phys. 47 4353
Google Scholar
[38] Jin Y M, Wang Y U, Khachaturyan A G 2003 Philos. Mag. 83 1587
Google Scholar
[39] 徐芝纶 1982 弹性力学(上卷) (北京: 高等教育出版社) 第89页
Xu Z L 1982 Elasticity (Vol. 1) (Beijing: Higher Education Press) p89 (in Chinese)
[40] Wang H, Biswas S, Han Y, Tomar V 2018 Comput. Mater. Sci. 150 169
Google Scholar
[41] Heo T W, Bhattacharyya S, Chen L 2013 Philos. Mag. 93 1468
Google Scholar
[42] Aagesen L K, Gao Y, Schwen D, Ahmed K 2018 Phys. Rev. E 98 23309
Google Scholar
[43] 孙正阳, 王昱天, 柳文波 2020 金属学报 56 1643
Google Scholar
Sun Z Y, Wang L T, Liu W B 2020 Acta Metall. Sin. 56 1643
Google Scholar
[44] Liu W B, Ji Y Z, Tan P K, Zang H, He C H, Yun D, Zhang C, Yang Z G 2016 Materials 9 105
Google Scholar
-
图 1 (a) 初始空洞示意图; (b) 空洞周围应力分布
Fig. 1. (a) Schematic diagram of the initial void; (b) stress distribution with the void.
图 3 模拟结果与解析解的应力分布比较
Fig. 3. Comparison of stress distribution between simulation results and analytical solutions.
图 4 (a)−(c)无应力下空洞演化; (d)−(f) 100 MPa附加应力下空洞演化; (g)−(i)应力分布随时间演化
Fig. 4. (a)−(c) The evolution of void without stress; (d)−(f) the evolution of void with 100 MPa applied stress; (g)−(i) the distribution of stress during the evolution.
图 5 不同应力下空洞半径随时间变化
Fig. 5. The change of void radius with time under different stresses.
图 6 (a)中线应力分布; (b)中线弹性能密度分布
Fig. 6. (a) Stress distribution in the center line; (b) elastic energy density distribution in the center line.
图 7 (a)初始结构示意图; (b)模拟区域的水平中线上的弹性模量分布
Fig. 7. (a) Schematic of initial structure; (b) elastic constants distribution in the center line.
图 8 (a)−(c)晶粒和空洞随时间演化; (d)−(f)演化过程中的应力分布
Fig. 8. (a)−(c) Evolution of grains and void with time; (d)−(f) the distribution of stress during the evolution.
图 9 晶间空洞演化中三个典型截面上应力分布
Fig. 9. Stress distribution along three typical cross sections during intergranular void evolution.
图 11 不同外加应力下的双晶组织((a)—(c))及对应的应力分布((d)—(f)) (a), (d) 50 MPa; (b), (e) 100 MPa; (c), (f) 150 MPa
Fig. 11. The twin-crystal microstructure ((a)–(c)) and the corresponding stress distribution with different applied stresses ((d)–(f)): (a), (d) 50 MPa; (b), (e) 100 MPa; (c), (f) 150 MPa.
图 13 不同外加应力下的多晶组织((a)—(c))和对应的应力分布((d)—(f)) (a), (d) 50 MPa; (b), (e) 100 MPa; (c), (f) 150 MPa
Fig. 13. The polycrystal microstructure ((a)–(c)) and the corresponding stress distribution with different applied stresses ((d)–(f)): (a), (d) 50 MPa; (b), (e) 100 MPa; (c), (f) 150 MPa.
表 1 模拟中使用的UO2参数
Table 1. Parameters of UO2 used in the simulation
参量 符号 取值 参考文献 绝对温度 T 1173 K 玻尔兹曼常数 kB 1.381 × 10–23 J/K 晶格常数 a 0.552 nm [31] 迁移率 L 1.56 × 10–11 m3/(J·s) [32] 梯度自由能参数 κ 3.38 × 10–8 J/m [32] 空位扩散系数 $ {D_{\text{v}}} $ 5.586 × 10–18 m2/s [33] 空位形成能 $ E_{\text{v}}^{\text{f}} $ 5.10 eV [34] 表面能 ${\gamma _{\text{s}}}$ 1.76 eV [35] 晶界能 ${\gamma _{{\text{GB}}}}$ 1.67 eV [36] 弹性模量 C11 389.3 GPa [37] C12 118.7 GPa [37] C44 59.7 GPa [37] 
下载: 导出CSV
-
[1] Govers K, Lemehov S, Hou M, Verwerft M 2007 J. Nucl. Mater. 366 161
Google Scholar
[2] 杨辉, 冯泽华, 王贺然, 张云鹏, 陈铮, 信天缘, 宋小蓉, 吴璐, 张静 2021 70 054601
Google Scholar
Yang H, Feng Z H, Wang H R, Zhang Y P, Chen Z, Xin T Y, Song X R, Wu L, Zhang J 2021 Acta Phys. Sin. 70 054601
Google Scholar
[3] 孙正阳, 杨超, 柳文波 2020 金属学报 56 1295
Sun Z Y, Yang C, Liu W B 2020 Acta Metall. Sin. 56 1295
[4] Solomon A A 1973 J. Am. Ceram. Soc. 56 164
Google Scholar
[5] Brask D N 1979 J. Nucl. Mater. 83 265
Google Scholar
[6] Porter D L, Takata M L, Wood E L 1983 J. Nucl. Mater. 116 272
Google Scholar
[7] Sahu H K, Jung P 1985 J. Nucl. Mater. 136 154
Google Scholar
[8] Brager H R, Garner F A, Guthrie G L 1977 J. Nucl. Mater. 66 301
Google Scholar
[9] Jiang Y, Liu W, Li W, Sun Z, Xin Y, Chen P, Yun D 2021 Comput. Mater. Sci. 188 110176
Google Scholar
[10] Millett P C, Rokkam S, El-Azab A, Tonks M, Wolf D 2009 Model. Simul. Mater. Sci. Eng. 17 64003
Google Scholar
[11] Brailsford A D, Bullough R, Hayns M R 1976 J. Nucl. Mater. 60 246
Google Scholar
[12] Wiedersich H 1972 Radiat. Eff. Defect. S. 12 111
Google Scholar
[13] Millett P C, El-Azab A, Rokkam S, Tonks M, Wolf D 2011 Comput. Mater. Sci. 50 949
Google Scholar
[14] Millett P C, El-Azab A, Wolf D 2011 Comput. Mater. Sci. 50 960
Google Scholar
[15] Liu W B, Wang N, Ji Y Z, Song P C, Zhang C, Yang Z G, Chen L Q 2016 J. Nucl. Mater. 479 316
Google Scholar
[16] 杨朝曦, 柳文波, 张璁雨, 贺新福, 孙正阳, 贾丽霞, 师田田, 恽迪 2021 70 116101
Google Scholar
Yang Z X, Liu W B, Zhang C Y, He X F, Sun Z Y, Jia L X, Shi T T, Yun D 2021 Acta Phys. Sin. 70 116101
Google Scholar
[17] Hu S Y, Chen L Q 2001 Acta Mater. 49 1879
Google Scholar
[18] Wang J J, Bhattacharyya S, Li Q, Heo T W, Ma X Q, Chen L 2012 Phil. Mag. Lett. 92 327
[19] Kim D, Kim S G, Kim W T, Cho J, Han H N, Cha P 2011 Scr. Mater. 64 1079
Google Scholar
[20] Chang K, Lee G, Kwon J 2016 Radiat. Eff. Defect. S. 171 242
Google Scholar
[21] Salvo M, Sercombe J, Ménard J, Julien J, Helfer T, Désoyer T 2015 J. Nucl. Mater. 456 54
Google Scholar
[22] Cahn J W, Hilliard J E 1958 J. Chem. Phys. 28 258
Google Scholar
[23] Tonks M R, Zhang Y, Butterfield A, Bai X 2015 Model. Simul. Mater. Sci. Eng. 23 45009
Google Scholar
[24] Wang Y U, Jin Y M, Khachaturyan A G 2002 J. Appl. Phys. 92 1351
Google Scholar
[25] Sheng G, Bhattacharyya S, Zhang H, Chang K, Shang S L, Mathaudhu S N, Liu Z K, Chen L Q 2012 Mater. Sci. Eng. A 554 67
Google Scholar
[26] Tonks M, Millett P 2011 Mater. Sci. Eng. A 528 4086
Google Scholar
[27] Yan L L, Liu C Z, Ying Y Z, Zheng C 2014 Chinese Phys. B 23 69102
Google Scholar
[28] Wang Y U, Jin Y M, Khachaturyan A G 2002 J. Appl. Phys. 91 6435
Google Scholar
[29] Moelans N, Blanpain B, Wollants P 2008 Calphad 32 268
Google Scholar
[30] Chen L Q, Shen J 1998 Comput. Phys. Commun. 108 147
Google Scholar
[31] Kang K H, Ryu H J, Song K C, Yang M S 2002 J. Nucl. Mater. 301 242
Google Scholar
[32] Aagesen L K, Schwen D, Tonks M R, Zhang Y 2019 Comput. Mater. Sci. 161 35
Google Scholar
[33] Kinoshita M 1997 J. Nucl. Mater. 248 185
Google Scholar
[34] Freyss M, Petit T, Crocombette J 2005 J. Nucl. Mater. 347 44
Google Scholar
[35] Xiao H, Long C, Chen H, Tian X, Wei T, Zhao Y, Gao W 2015 Appl. Surf. Sci. 351 517
Google Scholar
[36] Chen T, Chen D, Sencer B H, Shao L 2014 J. Nucl. Mater. 452 364
Google Scholar
[37] Fritz I J 1976 J. Appl. Phys. 47 4353
Google Scholar
[38] Jin Y M, Wang Y U, Khachaturyan A G 2003 Philos. Mag. 83 1587
Google Scholar
[39] 徐芝纶 1982 弹性力学(上卷) (北京: 高等教育出版社) 第89页
Xu Z L 1982 Elasticity (Vol. 1) (Beijing: Higher Education Press) p89 (in Chinese)
[40] Wang H, Biswas S, Han Y, Tomar V 2018 Comput. Mater. Sci. 150 169
Google Scholar
[41] Heo T W, Bhattacharyya S, Chen L 2013 Philos. Mag. 93 1468
Google Scholar
[42] Aagesen L K, Gao Y, Schwen D, Ahmed K 2018 Phys. Rev. E 98 23309
Google Scholar
[43] 孙正阳, 王昱天, 柳文波 2020 金属学报 56 1643
Google Scholar
Sun Z Y, Wang L T, Liu W B 2020 Acta Metall. Sin. 56 1643
Google Scholar
[44] Liu W B, Ji Y Z, Tan P K, Zang H, He C H, Yun D, Zhang C, Yang Z G 2016 Materials 9 105
Google Scholar
下载:
计量
- 文章访问数: 4567
- PDF下载量: 91
- 被引次数: 0
