-
Owing to the long lifetime of Rydberg atom, easy to operate and easy to control the interaction between Rydberg atoms, Rydberg atom has attracted considerable attention in quantum information and quantum optics fields. Specially, the anti-blockade effect, as a physical resource, can be used to implement various tasks in quantum information processing. Based on the rigid dipole blockade, an ensemble of two-level Rydberg atoms trapped in three magneto-optical traps can be regarded as a superatom. Based on the superatom model, the in-phase and anti-phase dynamics of the three-body Rydberg superatoms are studied by adjusting the numbers of atoms, and the W state and two kinds of maximal entangled states are generated simultaneously. Our work has great potential applications in coherent manipulation and quantum information processing.The numerical simulations are performed based on the superatom model and thereby the formidable obstacle that the Hilbert space dimension grows exponentially with the particle number increasing can be completely removed. As a result, the quantum control and quantum entanglement can be achieved from the single-quanta level to the mesoscopic level.
-
Keywords:
- Rydberg atom /
- superatom /
- dipole blockade /
- quantum entanglement
[1] Jaksch D, Cirac J, Zoller P, Rolston S, Côté R, Lukin M 2000 Phys. Rev. Lett. 85 2208
Google Scholar
[2] Lukin M D, Fleischhauer M, Cote R, Duan L, Jaksch D, Cirac J I, Zoller P 2001 Phys. Rev. Lett. 87 037901
Google Scholar
[3] Li D, Shao X 2018 Phys. Rev. A 98 062338
Google Scholar
[4] Wu J L, Wang Y, Han J X, Su S L, Xia Y, Jiang Y, Song J 2021 Phys. Rev. A 103 012601
Google Scholar
[5] Barredo D, Lienhard V, De Leseleuc S, Lahaye T, Browaeys A 2018 Nature 561 79
Google Scholar
[6] Bannasch G, Killian T, Pohl T 2013 Phys. Rev. Lett. 110 253003
Google Scholar
[7] Beterov I, Tretyakov D, Entin V, Yakshina E, Ryabtsev I, Saffman M, Bergamini S 2020 J. Phys. B:At. Mol. Opt. Phys. 53 182001
Google Scholar
[8] Saffman M 2016 J. Phys. B:At. Mol. Opt. Phys. 49 202001
Google Scholar
[9] Müller M, Diehl S, Pupillo G, Zoller P 2012 Adv. Atom. Mol. Opt. Phys. 61 1
Google Scholar
[10] Schauss P 2018 Quantum Sci. Technol. 3 023001
Google Scholar
[11] Yu S, He X, Xu P, Liu M, Wang J, Zhan M 2012 Chin. Sci. Bull. 57 1931
Google Scholar
[12] Gaëtan A, Miroshnychenko Y, Wilk T, Chotia A, Viteau M, Comparat D, Pillet P, Browaeys A, Grangier P 2009 Nat. Phys. 5 115
Google Scholar
[13] Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nat. Phys. 5 110
Google Scholar
[14] Firstenberg O, Adams C S, Hofferberth S 2016 J. Phys. B: At. Mol. Opt. Phys. 49 152003
Google Scholar
[15] Petrosyan D, Rao D B, Mølmer K 2015 Phys. Rev. A 91 043402
Google Scholar
[16] Saffman M, Walker T 2002 Phys. Rev. A 66 065403
Google Scholar
[17] Maxwell D, Szwer D, Paredes-Barato D, Busche H, Pritchard J D, Gauguet A, Weatherill K J, Jones M, Adams C S 2013 Phys. Rev. Lett. 110 103001
Google Scholar
[18] Gorshkov A V, Nath R, Pohl T 2013 Phys. Rev. Lett. 110 153601
Google Scholar
[19] Gorshkov A V, Otterbach J, Fleischhauer M, Pohl T, Lukin M D 2011 Phys. Rev. Lett. 107 133602
Google Scholar
[20] Tiarks D, Baur S, Schneider K, Dürr S, Rempe G 2014 Phys. Rev. Lett. 113 053602
Google Scholar
[21] Baur S, Tiarks D, Rempe G, Dürr S 2014 Phys. Rev. Lett. 112 073901
Google Scholar
[22] Tresp C, Zimmer C, Mirgorodskiy I, Gorniaczyk H, Paris-Mandoki A, Hofferberth S 2016 Phys. Rev. Lett. 117 223001
Google Scholar
[23] Yu D 2014 Phys. Rev. A 89 063809
Google Scholar
[24] Müller M, Lesanovsky I, Weimer H, Buchler H P, Zoller P 2009 Phys. Rev. Lett. 102 170502
Google Scholar
[25] Olmos B, Li W, Hofferberth S, Lesanovsky I 2011 Phys. Rev. A 84 041607
Google Scholar
[26] Fan C H, Zhang H X, Wu J H 2019 Phys. Rev. A 99 033813 7
[27] Zhang H X, Fan C H, Wu J H 2020 Opt. Express 28 35350
Google Scholar
[28] Weber T, Höning M, Niederprüm T, Manthey T, Thomas O, Guarrera V, Fleischhauer M, Barontini G, Ott H 2015 Nat. Phys. 11 157
Google Scholar
[29] Gaerttner M, Whitlock S, Schoenleber D W, Evers J 2014 Phys. Rev. Lett. 113 233002
Google Scholar
[30] Saffman M, Walker T 2005 Phys. Rev. A 72 022347
Google Scholar
[31] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[32] Carmele A, Vogell B, Stannigel K, Zoller P 2014 New J. Phys. 16 063042
Google Scholar
[33] Yan D, Wang Z H, Ren C N, Gao H, Li Y, Wu J H 2015 Phys. Rev. A 91 023813
Google Scholar
[34] Zhao P Z, Wu X, Xing T H, Xu G F, Tong D M 2018 Phys. Rev. A 98 032313
Google Scholar
[35] Huygens C 1980 Horologium oscillatorium
[36] Pikovsky A, Rosenblum M, Kurths J 2001 Synchronization-A Unified Approach to Nonlinear Science (Cambridge: Cambridge University Press)
[37] Osipov G V, Kurths J, Zhou C 2007 Synchronization in Oscillatory Networks (Springfield: Springer Science & Business Media)
[38] Acebrón J A, Bonilla L L, Vicente C J P, Ritort F, Spigler R 2005 Rev. Mod. Phys. 77 137
Google Scholar
[39] Hillbrand J, Auth D, Piccardo M, Opačak N, Gornik E, Strasser G, Capasso F, Breuer S, Schwarz B 2020 Phys. Rev. Lett. 124 023901
Google Scholar
[40] Karpat G, Yalcinkaya I, Cakmak B 2019 Phys. Rev. A 100 012133
Google Scholar
[41] Karpat G, Yalcinkaya I, Cakmak B 2020 Phys. Rev. A 101 042121
Google Scholar
[42] Gärttner M 2015 Phys. Rev. A 92 013629
Google Scholar
-
图 1 (a) 同一阻塞区域中捕获在三个磁光阱中的原子系综; (b) 二能级单个里德堡原子能级图, 两个里德堡原子相互作用表现为范德瓦尔斯(vdW)势; (c) 超级原子的能级结构: 在严格偶极阻塞条件下, 超级原子(原子系综)可以分为三个较小的超级原子, 每个较小的超级原子由各自光阱中的原子组成
Fig. 1. (a) Schematic diagram of an ensemble of Rydberg atoms trapped in three magneto-optical traps but in the same blockade region; (b) energy structure of the two-level Rydberg atom, two Rydberg atoms interact mediated by vdW potential; (c) energy structure of the superatoms: a superatom representing the ensemble can be divided into three smaller superatoms which are make up of atoms in respective magneto-optical traps.
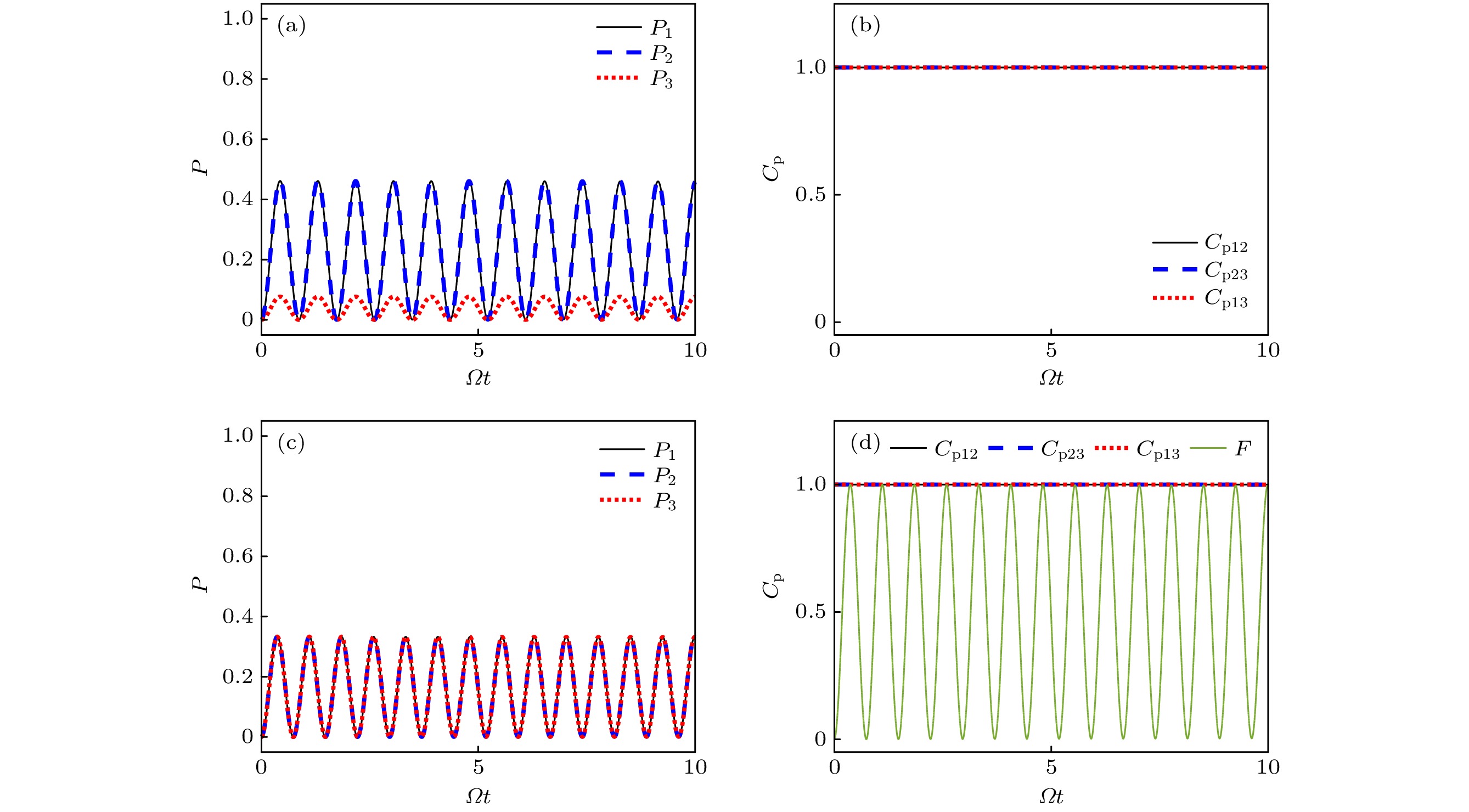
图 2 (a), (c) 超级原子的激发概率P; (b), (d) 皮尔森关联系数
${C_{\rm{p}}}$ (和保真度$F = \left| {\psi \left( t \right)} \right\rangle {\left\langle W \right|^2}$ , 其中$\left| {\psi \left( t \right)} \right\rangle $ 为任意时刻系统的量子态, 而$\left| W \right\rangle = \left( {|{R_1}{G_2}{G_3}\rangle + |{G_1}{R_2}{G_3}\rangle + |{G_1}{G_2}{R_3}\rangle } \right)/\sqrt 3 $ , 见(d)中绿色曲线)的动力学演化. 上图满足$ {n_1} = {n_2} = 6, {n_3} = 1 $ , 而下图满足$ {n_1} = {n_2} = {n_3} = 6 $ . 其他参数有: 拉比频率$\varOmega = 2\;{\rm{MHz}}$ , 自发弛豫速率$\varGamma = 0.002\;{\rm{MHz}}$ , 单光子失谐$\varDelta = 0$ Fig. 2. (a), (c) Dynamical evolution of excitation probability of Rydberg SAsP; (c), (d) Pearson's correlation coefficient
${C_{\rm{p}}}$ (and the fidelity$F = \left| {\psi \left( t \right)} \right\rangle {\left\langle W \right|^2}$ with the quantum state of the system$\left| {\psi \left( t \right)} \right\rangle $ and$\left| W \right\rangle = \left( {|{R_1}{G_2}{G_3}\rangle + |{G_1}{R_2}{G_3}\rangle + |{G_1}{G_2}{R_3}\rangle } \right)/\sqrt 3 $ , see the green curve in Figure (d)). Top:${n_1} = {n_2} = 6$ ,${n_3} = 1$ and bottom:${n_1} = {n_2} = {n_3} = 6$ . Other parameters are Rabi frequency$\varOmega = 2\;{\rm{MHz}}$ , spontaneous emission rate$\Gamma = 0.002\;{\rm{MHz}}$ , and the single-photon detuning$\varDelta = 0$ .
图 3 (a) 皮尔森关联系数
${C_{p12}}$ ; (b) 超级原子的最大里德堡激发概率$P_1^{\max }$ ; (c) 最大并发纠缠度$C_{12}^{\max }$ 作为原子数目$ {n_1}\left( = {{n_2}} \right) $ 和单光子失谐Δ的函数. 演化时间为$\varOmega t = 10$ , 原子数目固定为$ {n_3} = 1 $ , 其他参数同图2Fig. 3. (a) Pearson's correlation coefficient
${C_{{\rm{p}}12}}$ ; (b) maximal excitation probability of Rydberg SA$P_1^{\max }$ ; (c) maximal concurrence$C_{12}^{\max }$ as a function of the number of atoms$ {n_1}\left( = {{n_2}} \right) $ and the single-photon detuning Δ for a fixed number of atoms$ {n_3} = 1 $ . All simulations are done after$\varOmega t = 10$ evolution time. Relevant parameters are the same as in Fig. 2.
图 4 (a) 超级原子的激发概率P和 (b) 皮尔森关联系数
${C_{\rm{p}}}$ 的时间演化曲线; (c) 皮尔森关联系数${C_{\rm{p}}}$ 作为单光子失谐Δ的函数; (d) 最大并发纠缠度$C_{12}^{\max }$ 作为原子数目$ {n_1} $ 的函数. 图(c)和图(d)的演化时间为$\varOmega t = 10$ . 图(a), 图(b)和图(c)图中原子数目为$ {n_1} = {n_2} = 6, {n_3} = 1 $ , 而图(d)中原子数目$ {n_3} = 1 $ . 其他参数同图2Fig. 4. (a) Dynamical evolution of excitation probability of Rydberg SAsP and (b) Pearson's correlation coefficient
${C_{\rm{p}}}$ ; (c) Pearson's correlation coefficient${C_{\rm{p}}}$ as a function of the single-photon detuning Δ; (d) maximal concurrence$C_{12}^{\max }$ as a function of the number of atoms$ {n_1}\left( = {{n_2}} \right) $ . All simulations in Figrue (c)and (d) are done after$\varOmega t = 10$ evolution time. The number of atoms$ {n_1} = {n_2} = 6, {n_3} = 1 $ for Figure (a), Figurue (b) and Figure (c), and$ {n_3} = 1 $ for Figure (d). Relevant parameters are the same as in Fig. 2.
图 5 (a) 超级原子的激发概率P和 (b) 皮尔森关联系数
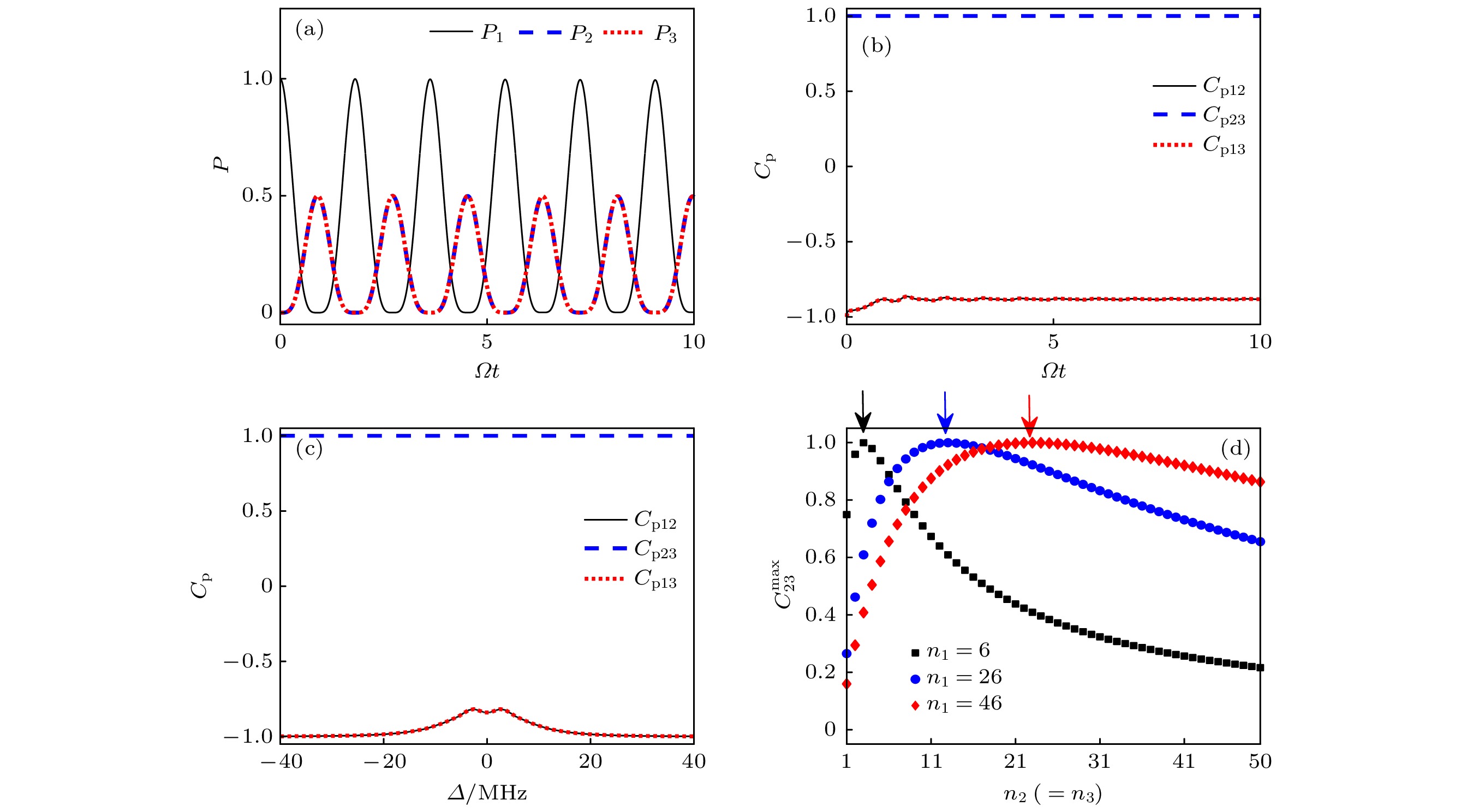
${C_p}$ 的时间演化曲线; (c) 皮尔森关联系数${C_p}$ 作为单光子失谐Δ的函数; (d) 最大纠缠并发纠缠度$C_{23}^{\max }$ 作为原子数目$ {n_2}\left( { = {n_3}} \right) $ 的函数. 图(c)和图(d)的演化时间为$\varOmega t = 10$ . 图(a)、图(b)和图(c)原子数目为$ {n}_{1}=6, {n}_{2}={n}_{3}=3 $ . 其他参数同图2Fig. 5. (a) Dynamical evolution of excitation probability of Rydberg SAsP and (b) Pearson's correlation coefficient
${C_{\rm{p}}}$ ; (c) Pearson's correlation coefficient${C_{\rm{p}}}$ as a function of the single-photon detuning Δ; (d) maximal concurrence$C_{23}^{\max }$ as a function of the number of atoms$ {n_2}\left( { = {n_3}} \right) $ . All simulations in Figure (c)and Figure (d) are done after$\varOmega t = 10$ evolution time. The number of atoms$ {n_1} = 6, \;{n_2} = {n_3} = 3 $ for Fgiure (a), Figure (b) and Figure (c). Relevant parameters are the same as in Fig. 2. -
[1] Jaksch D, Cirac J, Zoller P, Rolston S, Côté R, Lukin M 2000 Phys. Rev. Lett. 85 2208
Google Scholar
[2] Lukin M D, Fleischhauer M, Cote R, Duan L, Jaksch D, Cirac J I, Zoller P 2001 Phys. Rev. Lett. 87 037901
Google Scholar
[3] Li D, Shao X 2018 Phys. Rev. A 98 062338
Google Scholar
[4] Wu J L, Wang Y, Han J X, Su S L, Xia Y, Jiang Y, Song J 2021 Phys. Rev. A 103 012601
Google Scholar
[5] Barredo D, Lienhard V, De Leseleuc S, Lahaye T, Browaeys A 2018 Nature 561 79
Google Scholar
[6] Bannasch G, Killian T, Pohl T 2013 Phys. Rev. Lett. 110 253003
Google Scholar
[7] Beterov I, Tretyakov D, Entin V, Yakshina E, Ryabtsev I, Saffman M, Bergamini S 2020 J. Phys. B:At. Mol. Opt. Phys. 53 182001
Google Scholar
[8] Saffman M 2016 J. Phys. B:At. Mol. Opt. Phys. 49 202001
Google Scholar
[9] Müller M, Diehl S, Pupillo G, Zoller P 2012 Adv. Atom. Mol. Opt. Phys. 61 1
Google Scholar
[10] Schauss P 2018 Quantum Sci. Technol. 3 023001
Google Scholar
[11] Yu S, He X, Xu P, Liu M, Wang J, Zhan M 2012 Chin. Sci. Bull. 57 1931
Google Scholar
[12] Gaëtan A, Miroshnychenko Y, Wilk T, Chotia A, Viteau M, Comparat D, Pillet P, Browaeys A, Grangier P 2009 Nat. Phys. 5 115
Google Scholar
[13] Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nat. Phys. 5 110
Google Scholar
[14] Firstenberg O, Adams C S, Hofferberth S 2016 J. Phys. B: At. Mol. Opt. Phys. 49 152003
Google Scholar
[15] Petrosyan D, Rao D B, Mølmer K 2015 Phys. Rev. A 91 043402
Google Scholar
[16] Saffman M, Walker T 2002 Phys. Rev. A 66 065403
Google Scholar
[17] Maxwell D, Szwer D, Paredes-Barato D, Busche H, Pritchard J D, Gauguet A, Weatherill K J, Jones M, Adams C S 2013 Phys. Rev. Lett. 110 103001
Google Scholar
[18] Gorshkov A V, Nath R, Pohl T 2013 Phys. Rev. Lett. 110 153601
Google Scholar
[19] Gorshkov A V, Otterbach J, Fleischhauer M, Pohl T, Lukin M D 2011 Phys. Rev. Lett. 107 133602
Google Scholar
[20] Tiarks D, Baur S, Schneider K, Dürr S, Rempe G 2014 Phys. Rev. Lett. 113 053602
Google Scholar
[21] Baur S, Tiarks D, Rempe G, Dürr S 2014 Phys. Rev. Lett. 112 073901
Google Scholar
[22] Tresp C, Zimmer C, Mirgorodskiy I, Gorniaczyk H, Paris-Mandoki A, Hofferberth S 2016 Phys. Rev. Lett. 117 223001
Google Scholar
[23] Yu D 2014 Phys. Rev. A 89 063809
Google Scholar
[24] Müller M, Lesanovsky I, Weimer H, Buchler H P, Zoller P 2009 Phys. Rev. Lett. 102 170502
Google Scholar
[25] Olmos B, Li W, Hofferberth S, Lesanovsky I 2011 Phys. Rev. A 84 041607
Google Scholar
[26] Fan C H, Zhang H X, Wu J H 2019 Phys. Rev. A 99 033813 7
[27] Zhang H X, Fan C H, Wu J H 2020 Opt. Express 28 35350
Google Scholar
[28] Weber T, Höning M, Niederprüm T, Manthey T, Thomas O, Guarrera V, Fleischhauer M, Barontini G, Ott H 2015 Nat. Phys. 11 157
Google Scholar
[29] Gaerttner M, Whitlock S, Schoenleber D W, Evers J 2014 Phys. Rev. Lett. 113 233002
Google Scholar
[30] Saffman M, Walker T 2005 Phys. Rev. A 72 022347
Google Scholar
[31] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[32] Carmele A, Vogell B, Stannigel K, Zoller P 2014 New J. Phys. 16 063042
Google Scholar
[33] Yan D, Wang Z H, Ren C N, Gao H, Li Y, Wu J H 2015 Phys. Rev. A 91 023813
Google Scholar
[34] Zhao P Z, Wu X, Xing T H, Xu G F, Tong D M 2018 Phys. Rev. A 98 032313
Google Scholar
[35] Huygens C 1980 Horologium oscillatorium
[36] Pikovsky A, Rosenblum M, Kurths J 2001 Synchronization-A Unified Approach to Nonlinear Science (Cambridge: Cambridge University Press)
[37] Osipov G V, Kurths J, Zhou C 2007 Synchronization in Oscillatory Networks (Springfield: Springer Science & Business Media)
[38] Acebrón J A, Bonilla L L, Vicente C J P, Ritort F, Spigler R 2005 Rev. Mod. Phys. 77 137
Google Scholar
[39] Hillbrand J, Auth D, Piccardo M, Opačak N, Gornik E, Strasser G, Capasso F, Breuer S, Schwarz B 2020 Phys. Rev. Lett. 124 023901
Google Scholar
[40] Karpat G, Yalcinkaya I, Cakmak B 2019 Phys. Rev. A 100 012133
Google Scholar
[41] Karpat G, Yalcinkaya I, Cakmak B 2020 Phys. Rev. A 101 042121
Google Scholar
[42] Gärttner M 2015 Phys. Rev. A 92 013629
Google Scholar
下载:
计量
- 文章访问数: 4518
- PDF下载量: 101
- 被引次数: 0
