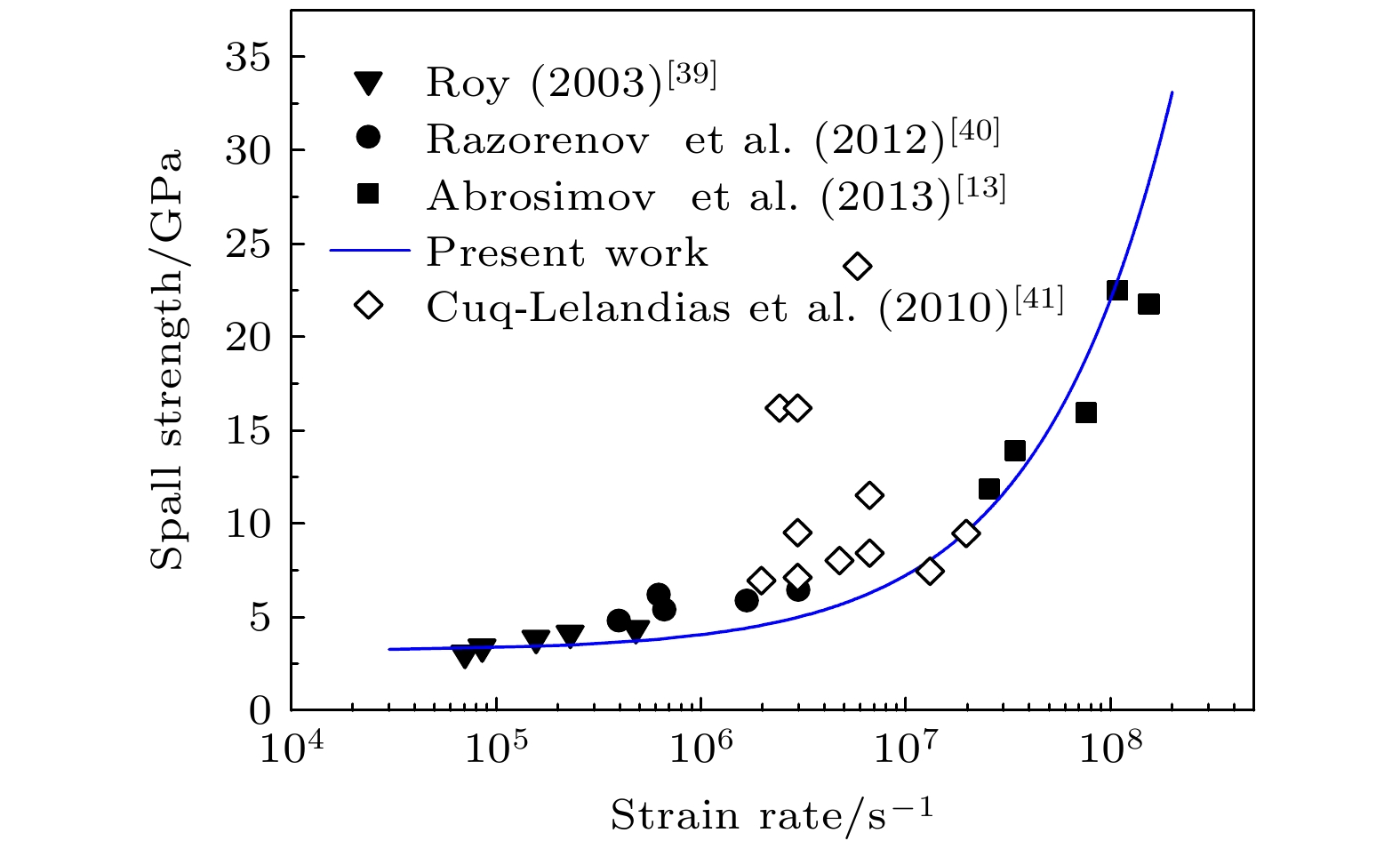
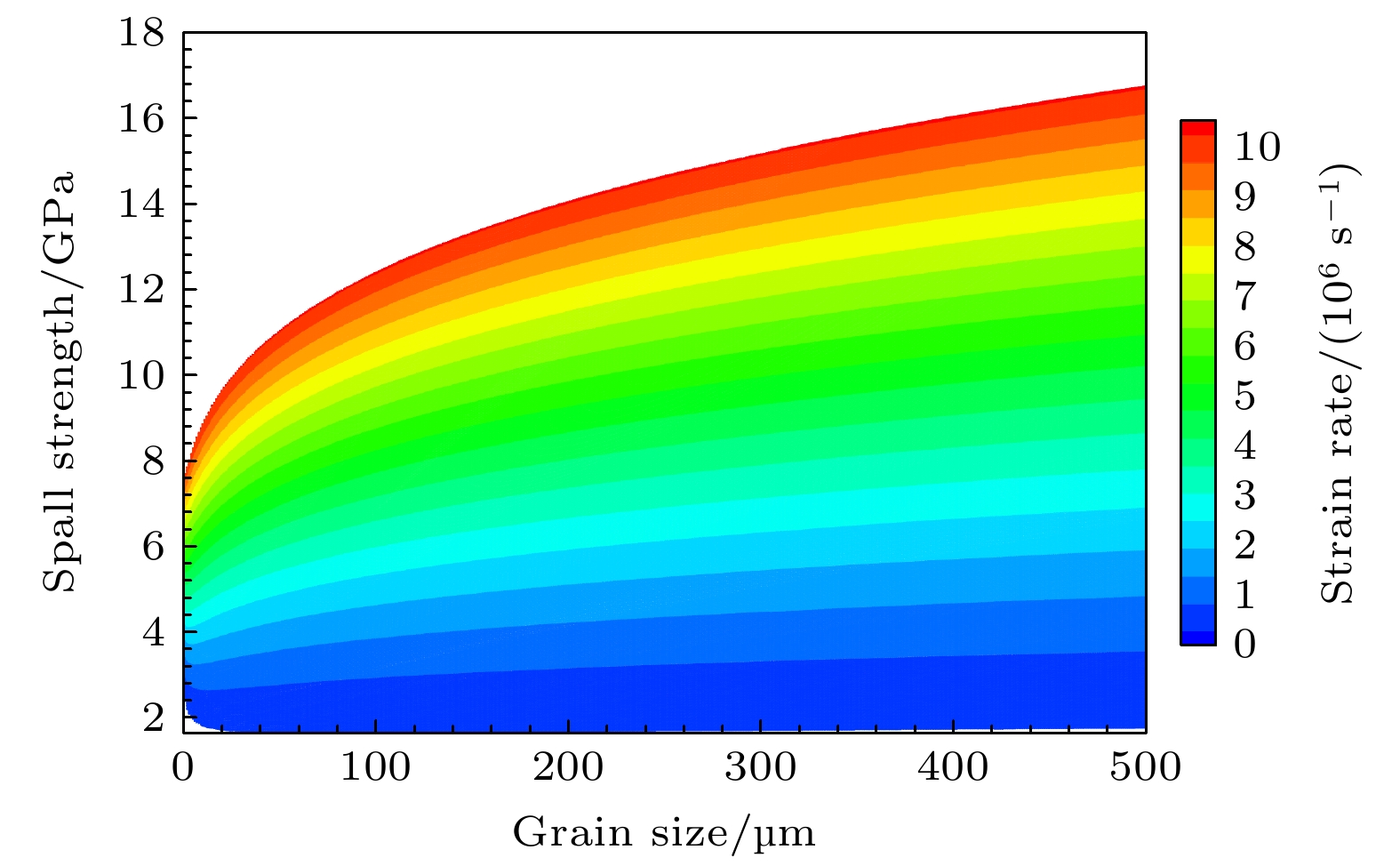
-
层裂强度表征了材料内部最大动态抗拉能力, 并与材料本身的力学性质以及损伤早期演化相关. 建立层裂强度计算的解析表达式, 深入认识层裂强度所包含的微细观物理涵义, 有利于更好地优化延性金属材料的层裂强度. 目前大量的实验表明: 延性金属材料的层裂强度对加载拉伸应变率、温度效应以及材料初始微细观结构具有很强的依赖关系. 本文基于对孔洞成核与增长的损伤早期演化特性的分析, 以及对温度效应和晶粒尺寸与材料本身力学性质之间关系的分析, 给出了简单、实用的层裂强度的解析物理模型, 物理模型的计算结果与典型延性金属高纯铝、铜和钽的层裂强度实验结果基本符合, 从而验证了我们给出的层裂强度模型具有较好的适用性和预测性.When a shockwave, which can be generated by high velocity impact or explosive detonation, reflects from the free surface of a metal, it usually creates tensile stress inside the metal. While the tensile stress is large enough, voids nucleation, growth and coalescence happen inside the metal, causing the metal to spall. As one of the main contents of the spallation damage research, the spallation strength, which is often characterized by features of the free surface velocity history measured in spallation experiments, represents the maximum tensile stress that the material can withstand, and is actually a complex interaction among several competing mechanisms. Optimizing the spallation strengths of metals is important for their applications in the aerospace, automotive, and defense industries, and can be achieved by using the advanced manufacturing strategies, if we can know better the meaning and present analytic model of the spallation strength of metal. A large number of experiments show that the spallation strength of ductile metal is strongly dependent on the tensile strain rate, grain size and temperature of material. Based on the analysis of early spallation evolution and influence of grain size and temperature on the material, a simple analytic model of spallation strength is presented in this paper, which takes into account the effects of strain rate, grain size and temperature in materials. The applicability of this model is verified by comparing the calculated results from the model with the experimental results of spall strength of typical ductile metals such as high purity aluminum, copper, and tantalum.
-
Keywords:
- spall strength /
- void nucleation and early growth /
- grain size /
- temperature /
- tensile strain rate /
- ductile metal
[1] Novikov S A 1967 J. App. Mech. Tech. Phys. 3 109
[2] Stepanov G V 1976 Problemy Prochnosti 8 66
[3] Romanchenko V I, Sepanov G V 1980 J. App. Mech. Tech. Phys. 21 141
[4] Kanel G I 2010 Int. J. Frac. 163 173
Google Scholar
[5] Turley W D, Fensin S J, Hixson R S, Jones D R, La Lone B M, Stevens G D, Thomas S A, Veeser L R 2018 J. App. Phys. 123 55102
Google Scholar
[6] Mallick D D, Zhao M, Parker J, Kannan V, Bosworth B T, Sagapuram D, Foster M A, Ramesh K T 2019 Exp. Mech. 59 1
Google Scholar
[7] Zurek A, Thissell W, Johnson J N, Tonks D, Hixson R. 1996 J. Mater. Process. Technol. 60 261
Google Scholar
[8] 谢普初, 汪小松, 胡昌明, 胡建波, 张凤国, 王永刚 2020 69 034601
Google Scholar
Xie P C, Wang X S, Hu C M, Hu J B, Zhang F G, Wang Y G 2020 Acta Phys. Sin. 69 034601
Google Scholar
[9] Eftis J, Nemes J A, Randles P 1991 Int. J. Plast. 7 15
Google Scholar
[10] Tonks D L, Thissell W R, Schwartz D S 2003 Shock Compression of Condensed Matter (New York: Melville) p507
[11] Kanel G, Razorenov S, Bogatch A, Utkin A, Grady D 1997 Int. J. Impact Eng. 20 467
Google Scholar
[12] Antoun T, Seaman L, Curran D R, Kanel G I, Razorenov S V, Utkin A V 2003 Spall Fracture (New York: Springer-Verlag) p130
[13] Abrosimov S A, Bazhulin A P, Voronov V V, Geras’kin A A, Krasyuk I K, Pashinin P P, Semenov A Yu, Stuchebryukhov I A, Khishchenko K V, Fortov V E 2013 Quantum Electron. 43 246
Google Scholar
[14] Remington T P, Hahn E N, Zhao S, Flanagan R, Mertens J C E, Sabbaghianrad S, Langdon T G, Wehrenberg C E, Maddox B R, Swift D C, Remington B A, Chawla N, Meyers M A 2018 Acta Mater. 158 313
Google Scholar
[15] Zaretsky E B, Kanel G I 2013 J. Appl. Phys. 114 083511
[16] Garkushin G V, Kanel G I, Savinykh A S, Razorenov S V 2016 Int. J. Fract. 197 1
Google Scholar
[17] Zaretsky E B, Kanel G I 2012 J. Appl. Phys. 112 073504
Google Scholar
[18] Bogach A A, Kanel G I, Razorenov S V, Utkin A V, Protasova S G, Sursaeva V G 1998 Phys. Solid State 40 1676
Google Scholar
[19] Trivedi P B, Asay J R, Gupta Y M, Field D P 2007 J. Appl. Phys. 102 083513
Google Scholar
[20] Pedrazas N A, Worthington D L, Dalton D A, Sherek P A, Steucka S P, Quevedo H J, Bernstein A C, Taleff E M, Ditmire T 2012 Mater. Sci. Eng., A 536 117
Google Scholar
[21] Chen X, Asay J R, Dwivedi S K, Field D P 2006 J. Appl. Phys. 99 023528
Google Scholar
[22] Escobedo J P, Dennis-Koller D, Cerreta E K, Patterson B M, Bronkhorst C A, Hansen B L, Tonks D L, Lebensohn R A 2011 J. Appl. Phys. 110 033513
Google Scholar
[23] Chen T, Jiang Z X, Peng H, He H L, Wang L L, Wang Y G 2015 Strain 51 190
Google Scholar
[24] Wilkerson J W, Ramesh K T 2016 Phys. Rev. Lett. 117 215503
Google Scholar
[25] Nguyen T, Luscher D J, Wilkerson J W 2020 J. Mech. Phys. Solids 137 103875
Google Scholar
[26] Seaman L, Curran D R, Shockey D A 1976 J. App. Phys. 47 4814
Google Scholar
[27] Johnson J N 1981 J. App. Phys. 52 2812
Google Scholar
[28] Czarnota C, Jacques N, Mercier S, Molinari A 2008 J. Mech. Phys. Solids 56 1624
Google Scholar
[29] Wilkerson J W 2017 Int. J. Plast. 95 21
Google Scholar
[30] Wright T W, Ramesh K T 2008 J. Mech. Phys. Solids 56 336
Google Scholar
[31] 张凤国, 王裴, 王昆, 周洪强, 赵福祺 2020 防护工程 42 33
Google Scholar
Zhang F G, Wang P, Wang K, Zhou H Q, Zhao F Q 2020 Protective Engineering 42 33
Google Scholar
[32] Wu X Y, Ramesh K T, Wright T W 2003 J. Mech. Phys. Solids 51 1
Google Scholar
[33] Kanel G I, Razorenov S V, Bogatch A, Utkin A V, Fortov V E, Grady D E 1996 J. App. Phys. 79 8310
Google Scholar
[34] Cuq-Lelandais J P, Boustie M, Berthe L, De Rességuier T, Combis P, Colombier J P, Nivard M, Claverie A 2009 J. Phys. D: Appl. Phys. 42 065402
Google Scholar
[35] Moshe E, Eliezer S, Henis Z, Werdiger M, Dekel E, Horovitz Y, Maman S 2000 App. Phys. Lett. 76 1555
Google Scholar
[36] Moshe E, Eliezer S, Deke E, Schwart A J 1998 J. App. Phys. 83 4004
Google Scholar
[37] Kanel G I, Fortov V E, Razorenov S V 2007 Phys. Usp. 50 771
Google Scholar
[38] Bachmann H, Baumung K, Kanel G I, Karov H U, Licht V, Rusch D, Singer J, Stoltz O 1993 Proc. 9th Int. Conf. High Power Particle Beams (Vol. 2) (Springfield, VA: NTIS) p963
[39] Roy G 2003 Ph. D. Dissertation (Poitiers: University of Poitiers)
[40] Razorenov S V, Kanel G I, Garkushin G V, Ignatova O N 2012 Phys. Solid State 54 790
Google Scholar
[41] Cuq-Lelandais J P, Boustie M, Soulard L, Berthe L, De Rességuier T, Combis P, Bontaz-Carion J, Lescoute E 2010 EPJ Web Conferences 10 00014
Google Scholar
[42] 张凤国, 周洪强 2013 62 164601
Google Scholar
Zhang F G, Zhou H Q 2013 Acta Phys. Sin. 62 164601
Google Scholar
[43] Hall E O 1951 Proc. Phys. Soc. London, Ser. B 64 747
Google Scholar
[44] Petch N J 1953 J. Iron Steel Inst. 174 25
[45] Zerilli F J, Armstrong R W 1990 J. App. Phys. 68 1580
Google Scholar
[46] Steinberg D J, Cochran S G, Guinan M W 1980 J. Appl. Phys. 51 1498
Google Scholar
[47] 李茂生, 陈栋泉 2001 高压 15 24
Google Scholar
Li M S, Chen D Q 2001 Chin. J. High Pressure Phys. 15 24
Google Scholar
-
图 1 金属铝材料层裂强度与加载拉伸应变率的关系
Fig. 1. Spall strength in both experimental and calculated results of commercial pure aluminum.
图 2 高纯金属铜层裂强度与加载拉伸应变率的关系
Fig. 2. Spall strength in both experimental and calculated results of pure copper.
图 3 金属钽材料层裂强度与加载拉伸应变率的关系
Fig. 3. Spall strength in both experimental and calculated results of pure tantalum.
图 4 晶粒尺寸对纯钽金属层裂强度的影响
Fig. 4. Experimental data and numerical results show there is a correlation between spall strength and grain size for pure tantalum.
图 5 晶粒尺寸、应变率对纯钽金属层裂强度的影响
Fig. 5. Spall strength vs. grain size and tensile strain rate for pure tantalum.
图 6 初始温度对纯铝材料层裂强度的影响
Fig. 6. Temperature dependence of the spall strength for pure aluminum.
图 7 初始温度、应变率对层裂强度的影响
Fig. 7. Spall strength vs. temperature and tensile strain rate for pure aluminum.
表 1 材料参数以及层裂强度模型参数
Table 1. Material parameters and parameters of spall strength model.
Material 密度$ {\rho }_{0} $/(kg·m–3) 屈服强度$ {Y}_{0} $/GPa 剪切模量$ G $/GPa 体积声速$ {C}_{0}$/(m·s–1) 模型参数$ {N}_{0} $/m–3 Aluminum 2760 0.26 26.5 5240 3.18 × 1017 Copper 8924 0.15 48.4 3910 7.67 × 1015 Tantalum 16690 0.77 69.0 3410 1.01 × 1016 
下载: 导出CSV
-
[1] Novikov S A 1967 J. App. Mech. Tech. Phys. 3 109
[2] Stepanov G V 1976 Problemy Prochnosti 8 66
[3] Romanchenko V I, Sepanov G V 1980 J. App. Mech. Tech. Phys. 21 141
[4] Kanel G I 2010 Int. J. Frac. 163 173
Google Scholar
[5] Turley W D, Fensin S J, Hixson R S, Jones D R, La Lone B M, Stevens G D, Thomas S A, Veeser L R 2018 J. App. Phys. 123 55102
Google Scholar
[6] Mallick D D, Zhao M, Parker J, Kannan V, Bosworth B T, Sagapuram D, Foster M A, Ramesh K T 2019 Exp. Mech. 59 1
Google Scholar
[7] Zurek A, Thissell W, Johnson J N, Tonks D, Hixson R. 1996 J. Mater. Process. Technol. 60 261
Google Scholar
[8] 谢普初, 汪小松, 胡昌明, 胡建波, 张凤国, 王永刚 2020 69 034601
Google Scholar
Xie P C, Wang X S, Hu C M, Hu J B, Zhang F G, Wang Y G 2020 Acta Phys. Sin. 69 034601
Google Scholar
[9] Eftis J, Nemes J A, Randles P 1991 Int. J. Plast. 7 15
Google Scholar
[10] Tonks D L, Thissell W R, Schwartz D S 2003 Shock Compression of Condensed Matter (New York: Melville) p507
[11] Kanel G, Razorenov S, Bogatch A, Utkin A, Grady D 1997 Int. J. Impact Eng. 20 467
Google Scholar
[12] Antoun T, Seaman L, Curran D R, Kanel G I, Razorenov S V, Utkin A V 2003 Spall Fracture (New York: Springer-Verlag) p130
[13] Abrosimov S A, Bazhulin A P, Voronov V V, Geras’kin A A, Krasyuk I K, Pashinin P P, Semenov A Yu, Stuchebryukhov I A, Khishchenko K V, Fortov V E 2013 Quantum Electron. 43 246
Google Scholar
[14] Remington T P, Hahn E N, Zhao S, Flanagan R, Mertens J C E, Sabbaghianrad S, Langdon T G, Wehrenberg C E, Maddox B R, Swift D C, Remington B A, Chawla N, Meyers M A 2018 Acta Mater. 158 313
Google Scholar
[15] Zaretsky E B, Kanel G I 2013 J. Appl. Phys. 114 083511
[16] Garkushin G V, Kanel G I, Savinykh A S, Razorenov S V 2016 Int. J. Fract. 197 1
Google Scholar
[17] Zaretsky E B, Kanel G I 2012 J. Appl. Phys. 112 073504
Google Scholar
[18] Bogach A A, Kanel G I, Razorenov S V, Utkin A V, Protasova S G, Sursaeva V G 1998 Phys. Solid State 40 1676
Google Scholar
[19] Trivedi P B, Asay J R, Gupta Y M, Field D P 2007 J. Appl. Phys. 102 083513
Google Scholar
[20] Pedrazas N A, Worthington D L, Dalton D A, Sherek P A, Steucka S P, Quevedo H J, Bernstein A C, Taleff E M, Ditmire T 2012 Mater. Sci. Eng., A 536 117
Google Scholar
[21] Chen X, Asay J R, Dwivedi S K, Field D P 2006 J. Appl. Phys. 99 023528
Google Scholar
[22] Escobedo J P, Dennis-Koller D, Cerreta E K, Patterson B M, Bronkhorst C A, Hansen B L, Tonks D L, Lebensohn R A 2011 J. Appl. Phys. 110 033513
Google Scholar
[23] Chen T, Jiang Z X, Peng H, He H L, Wang L L, Wang Y G 2015 Strain 51 190
Google Scholar
[24] Wilkerson J W, Ramesh K T 2016 Phys. Rev. Lett. 117 215503
Google Scholar
[25] Nguyen T, Luscher D J, Wilkerson J W 2020 J. Mech. Phys. Solids 137 103875
Google Scholar
[26] Seaman L, Curran D R, Shockey D A 1976 J. App. Phys. 47 4814
Google Scholar
[27] Johnson J N 1981 J. App. Phys. 52 2812
Google Scholar
[28] Czarnota C, Jacques N, Mercier S, Molinari A 2008 J. Mech. Phys. Solids 56 1624
Google Scholar
[29] Wilkerson J W 2017 Int. J. Plast. 95 21
Google Scholar
[30] Wright T W, Ramesh K T 2008 J. Mech. Phys. Solids 56 336
Google Scholar
[31] 张凤国, 王裴, 王昆, 周洪强, 赵福祺 2020 防护工程 42 33
Google Scholar
Zhang F G, Wang P, Wang K, Zhou H Q, Zhao F Q 2020 Protective Engineering 42 33
Google Scholar
[32] Wu X Y, Ramesh K T, Wright T W 2003 J. Mech. Phys. Solids 51 1
Google Scholar
[33] Kanel G I, Razorenov S V, Bogatch A, Utkin A V, Fortov V E, Grady D E 1996 J. App. Phys. 79 8310
Google Scholar
[34] Cuq-Lelandais J P, Boustie M, Berthe L, De Rességuier T, Combis P, Colombier J P, Nivard M, Claverie A 2009 J. Phys. D: Appl. Phys. 42 065402
Google Scholar
[35] Moshe E, Eliezer S, Henis Z, Werdiger M, Dekel E, Horovitz Y, Maman S 2000 App. Phys. Lett. 76 1555
Google Scholar
[36] Moshe E, Eliezer S, Deke E, Schwart A J 1998 J. App. Phys. 83 4004
Google Scholar
[37] Kanel G I, Fortov V E, Razorenov S V 2007 Phys. Usp. 50 771
Google Scholar
[38] Bachmann H, Baumung K, Kanel G I, Karov H U, Licht V, Rusch D, Singer J, Stoltz O 1993 Proc. 9th Int. Conf. High Power Particle Beams (Vol. 2) (Springfield, VA: NTIS) p963
[39] Roy G 2003 Ph. D. Dissertation (Poitiers: University of Poitiers)
[40] Razorenov S V, Kanel G I, Garkushin G V, Ignatova O N 2012 Phys. Solid State 54 790
Google Scholar
[41] Cuq-Lelandais J P, Boustie M, Soulard L, Berthe L, De Rességuier T, Combis P, Bontaz-Carion J, Lescoute E 2010 EPJ Web Conferences 10 00014
Google Scholar
[42] 张凤国, 周洪强 2013 62 164601
Google Scholar
Zhang F G, Zhou H Q 2013 Acta Phys. Sin. 62 164601
Google Scholar
[43] Hall E O 1951 Proc. Phys. Soc. London, Ser. B 64 747
Google Scholar
[44] Petch N J 1953 J. Iron Steel Inst. 174 25
[45] Zerilli F J, Armstrong R W 1990 J. App. Phys. 68 1580
Google Scholar
[46] Steinberg D J, Cochran S G, Guinan M W 1980 J. Appl. Phys. 51 1498
Google Scholar
[47] 李茂生, 陈栋泉 2001 高压 15 24
Google Scholar
Li M S, Chen D Q 2001 Chin. J. High Pressure Phys. 15 24
Google Scholar
下载:
计量
- 文章访问数: 4721
- PDF下载量: 99
- 被引次数: 0
