金属基底上光学偶极纳米天线的自发辐射宽带增强: 表面等离激元直观模型

张炼; 王化雨; 王宁; 陶灿; 翟学琳; 马平准; 钟莹; 刘海涛

doi:10.7498/aps.70.20212290

摘要

本文提出一种具有宽波段自发辐射增强性能的金属基底上光学偶极纳米天线, 实现的总辐射速率与远场辐射速率增强因子分别达到5454和1041, 在近红外波段, 自发辐射增强(Purcell因子超过1000)波长范围达到260 nm, 并且能够实现远场定向辐射. 为了阐明天线性能背后的物理机制, 本文考虑天线臂上表面等离激元激发和多重散射的直观物理过程, 基于Maxwell方程组第一性原理, 建立了一个半解析模型, 能够全面复现天线的辐射特性, 包括总辐射速率、远场辐射速率、远场辐射方向图等. 该模型提供了一个直观的物理图像, 即在模型导出的两个相位匹配条件下, 表面等离激元在天线臂上形成了一对Fabry-Perot共振获得增强, 然后传播到纳米间隙内点辐射源位置和散射到自由空间, 由此分别提高了总辐射速率和远场辐射速率. 并且, 这一对Fabry-Perot共振产生了一对相互靠近的谐振峰, 由此形成了宽波段自发辐射增强. 本文提出的偶极纳米天线可以应用于荧光增强、拉曼散射增强及高速、高亮度纳米光源等领域, 所提出的模型可用于光学天线的物理理解和直观设计.

关键词:

Abstract

Optical nanoantennas can achieve electromagnetic-field enhancement under far-field excitation or spontaneous-emission enhancement under excitation by radiating emitters. Among them, nanoantennas on a metallic substrate (i.e. the so-called nanoparticle-on-mirror antennas) have aroused great research interest due to their ease in forming metallic gaps of sizes down to a few nanometers or even subnanometer. Here we propose an optical dipole nanoantenna on a metallic substrate with a broadband enhancement of spontaneous emission. Its total and radiative emission-rate enhancement factors can reach up to 5454 and 1041, respectively. In the near-infrared band, the wavelength range of spontaneous-emission enhancement (Purcell factor over 1000) can reach 260nm. By changing the width of the slit between the two antenna arms and also the length of the antenna arms, the spontaneous-emission enhancement bandwidth and enhancement factors can be adjusted, respectively, which brings great freedom and simplicity to the design process. The antenna can achieve a strong far-field radiation within a central anglular zone (polar angle θ≤60°) corresponding to a certain numerical aperture of objective lens, and therefore can increase the intensity of the fluorescence collected by the objective lens. Based on the above performances, the antenna can provide a broadband enhancement of spontaneous emission for fluorescent molecules or quantum dots (whose fluorescence spectrum usually covers a certain wavelength range), which is of great significance for the applications such as in high-speed and super-bright nanoscale light sources and high-sensitivity fluorescent-molecule sensing.To clarify the underlying physical mechanisms, we build up a semi-analytical model by considering an intuitive excitation and multiple-scattering process of surface plasmon polaritons (SPPs) that propagate along the antenna arms. All the parameters used in the model (such as the SPP scattering coefficients) are obtained via rigorous calculations based on the first principle of Maxwell's equations without any fitting process, which ensures that the model has a solid electromagnetic foundation and can provide quantitative predictions. The SPP model can comprehensively reproduce all the radiation properties of the antenna, such as the total radiative emission rate and the far-field radiation pattern. Two phase-matching conditions are derived from the model for predicting the antenna resonance, and show that under these conditions, the SPPs on the antenna arms form a pair of Fabry-Perot resonance and therefore are enhanced, and the enhanced SPPs propagate to the emitter in the nanogap (or scattered into the free space), so as to enhance the total spontaneous emission rate (or the far-field radiative emission rate). Besides, this pair of Fabry-Perot resonance results in a pair of resonance peaks close to each other, then enhancing the spontaneous emission with a broadband.

Keywords:

作者及机构信息

1.
南开大学电子信息与光学工程学院, 现代光学研究所, 天津　300350

2.
南开大学, 天津市微尺度光学信息技术科学重点实验室, 天津　300350

3.
郑州师范学院物理与电子工程学院, 郑州　450044

4.
天津大学精密仪器与光电子工程学院, 精密测试技术及仪器国家重点实验室, 天津　300072

通信作者: 刘海涛, liuht@nankai.edu.cn

基金项目: 国家自然科学基金(批准号: 62075104, 61775105)资助的课题.

Authors and contacts

1.
Institute of Modern Optics, College of Electronic Information and Optical Engineering, Nankai University, Tianjin 300350, China

2.
Tianjin Key Laboratory of Micro-scale Optical Information Science and Technology, Nankai University, Tianjin 300350, China

3.
College of Physics and Electronic Engineering, Zhengzhou Normal University, Zhengzhou 450044, China

4.
State Key Laboratory of Precision Measurement Technology and Instruments, School of Precision Instrument and Opto-Electronics Engineering, Tianjin University, Tianjin 300072, China

Corresponding author: Liu Hai-Tao, liuht@nankai.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 62075104, 61775105).

文章全文 : translate this paragraph

参考文献

[1]	Mühlschlegel P, Eisler H J, Martin O J F, Hecht B, Pohl D W 2005 Science 308 1607 Google Scholar
[2]	Novotny L, Van Hulst N 2011 Nat. Photonics 5 83 Google Scholar
[3]	Pelton M 2015 Nat. Photonics 9 427 Google Scholar
[4]	Şendur K, Baran E 2009 Appl. Phys. B 96 325 Google Scholar
[5]	Sederberg S, Elezzabi A Y. 2011 Opt. Express 19 10456 Google Scholar
[6]	El-Toukhy Y M, Hussein M, Hameed M F O, Obayya S S A 2018 Plasmonics 13 503 Google Scholar
[7]	Aizpurua J, Bryant G W, Richter L J, García de Abajo F J, Kelley B K, Mallouk T 2005 Phys. Rev. B 71 235420 Google Scholar
[8]	Yong Z D, Zhang S L, Dong Y J, He S L 2015 Prog. Electromagnet. Res. 153 123 Google Scholar
[9]	Lu G W, Liu J, Zhang T Y, Shen H M, Perriat P, Martini M, Tillement O, Gu Y, He Y B, Wang Y W, Gong Q H 2013 Nanoscale 5 6545 Google Scholar
[10]	Akselrod G M, Argyropoulos C, Hoang T B, Ciracì C, Fang C, Huang J N, Smith D R, Mikkelsen M H 2014 Nat. Photonics 8 835 Google Scholar
[11]	Hoang T B, Akselrod G M, Argyropoulos C, Huang J, Smith D R, Mikkelsen M H 2015 Nat. Commun. 6 7788 Google Scholar
[12]	Kinkhabwala A, Yu Z H, Fan S H, Avlasevich Y, Müllen K, Moerner W E 2009 Nat. Photonics 3 654 Google Scholar
[13]	Muskens O L, Giannini V, Sánchez-Gil J A, Gómez Rivas J 2007 Nano Lett. 7 2871 Google Scholar
[14]	Baibakov M, Patra S, Claude J-B, Moreau A, Lumeau J, Wenger J 2019 ACS Nano 13 8469 Google Scholar
[15]	Barulin A, Claude J-B, Patra S, Bonod N, Wenger J 2019 Nano Lett. 19 7434 Google Scholar
[16]	Rycenga M, Xia X H, Moran C H, Zhou F, Qin D, Li Z Y, Xia Y N 2011 Angew. Chem. Int. Ed. 50 5473 Google Scholar
[17]	Nie S, Emory S R 1997 Science 275 1102 Google Scholar
[18]	Lodahl P, Mahmoodian S, Stobbe S 2015 Rev. Mod. Phys. 87 347 Google Scholar
[19]	Tsakmakidis K L, Boyd R W, Yablonovitch E, Zhang X 2016 Opt. Express 24 17916 Google Scholar
[20]	Suh J Y, Kim C H, Zhou W, Huntington M D, Co D T, Wasielewski M R, Odom T W 2012 Nano Lett. 12 5769 Google Scholar
[21]	Ma R-M, Oulton R F, Sorger V J, Zhang X 2013 Laser Photonics Rev. 7 1 Google Scholar
[22]	Harutyunyan H, Volpe G, Quidant R, Novotny L 2012 Phys. Rev. Lett. 108 217403 Google Scholar
[23]	Butet J, Martin O J F 2015 Plasmonics 10 203 Google Scholar
[24]	Gong T X, Guan F, Wei Z J, Huang W, Zhang X S. 2021 Front. Phys-Lausanne 9 691027 Google Scholar
[25]	Zhang W H, Huang L N, Santschi C, Martin O J F 2010 Nano Lett. 10 1006 Google Scholar
[26]	Fischer H, Martin O J F 2008 Opt. Express 16 9144 Google Scholar
[27]	Yong Z D, Gong C S, Dong Y J, Zhang S L, He S L 2017 RSC Adv. 7 2074 Google Scholar
[28]	Trojak O J, Park S I, Song J D, Sapienza L 2017 Appl. Phys. Lett. 111 021109 Google Scholar
[29]	Zarrabi F B, Naser-Moghadasi M, Heydari S, Maleki M, Arezomand A S 2016 Opt. Commun. 371 34 Google Scholar
[30]	Lumdee C, Yun B F, Kik P G 2014 ACS Photonics 1 1224 Google Scholar
[31]	Baumberg J J, Aizpurua J, Mikkelsen M H, Smith D R 2019 Nat. Mater. 18 668 Google Scholar
[32]	Huang S X, Ming T, Lin Y X, Ling X, Ruan Q F, Palacios T, Wang J F, Kong J, Dresselhaus M, Kong J 2016 Small 12 5190 Google Scholar
[33]	Huang Y, Ma L W, Hou M J, Li J H, Xie Z, Zhang Z J 2016 Sci. Rep. 6 30011 Google Scholar
[34]	Armstrong R E, van Liempt J C, Zijlstra P 2019 J. Phys. Chem. C 123 25801 Google Scholar
[35]	Huang Y, Ma L W, Li J H, Zhang Z J 2017 Nanotechnology 28 105203 Google Scholar
[36]	Purcell E M 1946 Phys. Rev. 69 681
[37]	Lakowicz J R, Fu Y 2009 Laser Photonics Rev. 3 221 Google Scholar
[38]	Agio M 2012 Nanoscale 4 692 Google Scholar
[39]	Li L, Hutter T, Steiner U, Mahajan S 2013 Analyst 138 4574 Google Scholar
[40]	Yoon J K, Kim K, Shin K S 2009 J. Phys. Chem. C 113 1769 Google Scholar
[41]	Alu A, Engheta N 2008 Phys. Rev. Lett. 101 043901 Google Scholar
[42]	Eggleston M S, Messer K, Zhang L M, Yablonovitch E, Wu M C 2015 Proc. Natl. Acad. Sci. U. S. A. 112 1704 Google Scholar
[43]	Fernandez-Garcia R, Rahmani M, Hong M, Maier S A, Sonnefraud Y 2013 Opt. Express 21 12552 Google Scholar
[44]	Calderón J, Álvarez J, Martinez-Pastor J, Hill D 2015 Plasmonics 10 703 Google Scholar
[45]	Cooper C T, Rodriguez M, Blair S, Shumaker-Parry J S 2014 J. Phys. Chem. C 118 1167 Google Scholar
[46]	Jia H, Yang F, Zhong Y, Liu H 2016 Photonics Res. 4 293 Google Scholar
[47]	Lalanne P, Yan W, Vynck K, Sauvan C, Hugonin J P 2018 Laser Photonics Rev. 12 1700113 Google Scholar
[48]	Sauvan C, Hugonin J P, Maksymov I S, Lalanne P 2013 Phys. Rev. Lett. 110 237401 Google Scholar
[49]	Ching E S C, Leung P T, Maassen van den Brink A, Tong S S, Young K 1998 Rev. Mod. Phys. 70 1545 Google Scholar
[50]	Della Valle G, Søndergaard T, Bozhevolnyi S I 2008 Opt. Express 16 6867 Google Scholar
[51]	Taminiau T H, Stefani F D, van Hulst N F 2011 Nano Lett. 11 1020 Google Scholar
[52]	Cubukcu E, Capasso F 2009 Appl. Phys. Lett. 95 201101 Google Scholar
[53]	Hasan S B, Filter R, Ahmed A, Vogelgesang R, Gordon R, Rockstuhl C, Lederer F 2011 Phys. Rev. B 84 195405 Google Scholar
[54]	Kim D, Jeong K Y, Kim J, Ee H S, Kang J H, Park H G Seo M K 2017 Phys. Rev. Appl. 8 054024 Google Scholar
[55]	Chandran A, Barnard E S, White J S, Brongersma M L 2012 Phys. Rev. B 85 085416 Google Scholar
[56]	Filter R, Qi J, Rockstuhl C, Ledere F 2012 Phys. Rev. B 85 125429 Google Scholar
[57]	Wan J, Zhu J, Zhong Y, Liu H 2018 J. Opt. Soc. Am. A: 35 880 Google Scholar
[58]	Jia H, Liu H, Zhong Y 2015 Sci. Rep. 5 8456 Google Scholar
[59]	Zhai X, Wang N, Zhong Y, Liu H 2020 IEEE J. Sel. Top. Quantum Electron. 27 4600815 Google Scholar
[60]	Kotal S, Artioli A, Wang Y, Osterkryger A D, Finazzer M, Fons R, Claudon J, Bleuse J, Gérard J M, 2021 Appl. Phys. Lett. 118 194002 Google Scholar
[61]	Yang J, Kong F M, Li K, Sheng S W 2015 Opt. Commun. 342 230 Google Scholar
[62]	Vesseur E J R, de Abajo F J G, Polman A 2010 Phys. Rev. B 82 165419 Google Scholar
[63]	Edwards A P, Adawi A M 2014 J. Appl. Phys. 115 053101 Google Scholar
[64]	Palik E D 1991 Handbook of Optical Constants of Solids, Part Ⅱ (San Diego: Academic)
[65]	Anger P, Bharadwaj P, Novotny L 2006 Phys. Rev. Lett. 96 113002 Google Scholar
[66]	Liu H T 2010 DIF CODE for Modeling Light Diffraction in Nanostructures (Tianjin: Nankai University)
[67]	Hugonin J P, Lalanne P 2005 J. Opt. Soc. Am. A: 22 1844 Google Scholar
[68]	Vassallo C 1991 Optical Waveguide Concepts (Amsterdam: Elsevier)
[69]	Chang D E, Sørensen A S, Hemmer P R, Lukin M D 2007 Phys. Rev. B 76 035420 Google Scholar
[70]	Li L 1996 J. Opt. Soc. Am. A: 13 1024 Google Scholar
[71]	Li L (edited by Popov E) 2014 Gratings: Theory and Numeric Applications (2nd Ed.) (Marseille: Institut Fresnel, Aix Marseille Université) pp573—574
[72]	Liu H 2013 Opt. Express 21 24093 Google Scholar
[73]	Ortega J M, Rheinboldt W C 1970 Iterative Solution of Nonlinear Equations in Several Variables (New York and London: Academic)
[74]	Li Y, Liu H, Jia H, Bo F, Zhang G, Xu J 2014 J. Opt. Soc. Am. A: 31 2459 Google Scholar
[75]	Yang J, Hugonin J P, Lalanne P 2016 ACS Photonics 3 395 Google Scholar

施引文献

图 1 (a) 金基底上金偶极纳米天线结构示意图; (b1), (b2) 对称点源和反对称点源激励下, SPP模型中的SPP模式系数$a_{\rm sym/asym}^{+/-} $, $b_{\rm sym/asym}^{+/-} $, $c_{\rm sym/asym}^{+/-} $, $d_{\rm sym/asym}^{+/-} $的定义; (c)—(e) SPP模型中用到的SPP散射系数ρ, τ, r, β以及电磁场${\boldsymbol{ \varPsi}} _{{{\rm{SPP, + }}}}^{{{\rm{gap{\text{-}}scattering}}}}$, ${\boldsymbol{ \varPsi}} _{{{\rm{SPP, + }}}}^{{{\rm{end{\text{-}}scattering}}}} $, Ψ_source的定义

Fig. 1. (a) Schematic diagram of the gold dipole nanoantenna on a gold substrate; (b1), (b2) definition of the SPP mode coefficients $a_{\rm sym/asym}^{+/-} $, $b_{\rm sym/asym}^{+/-} $, $c_{\rm sym/asym}^{+/-} $, $d_{\rm sym/asym}^{+/-} $ in the SPP model under excitation by symmetric and anti-symmetric point sources; (c)−(e) definition of the SPP scattering coefficients ρ, τ, r, β and electromagnetic fields ${\boldsymbol{ \varPsi}} _{{{\rm{SPP, + }}}}^{{{\rm{gap{\text{-}}scattering}}}} $, ${\boldsymbol{ \varPsi}} _{{{\rm{SPP, + }}}}^{{{\rm{end{\text{-}}scattering}}}} $, Ψ_source used in the SPP model.

下载: 全尺寸图片幻灯片

图 2 在y-z横截面上SPP基模式电场分量的模值(|E_x|, |E_y|, |E_z|), 在(y, z) = (0, H/2)处满足归一化E_z = 1. 图中叠加的虚线显示了结构的边界

Fig. 2. Moduli of the electric-field components (|E_x|, |E_y|, |E_z|) on the y-z cross section for the fundamental SPP mode satisfying normalization E_z = 1 at (y, z) = (0, H/2). The superimposed dashed lines show the boundaries of the structure.

下载: 全尺寸图片幻灯片

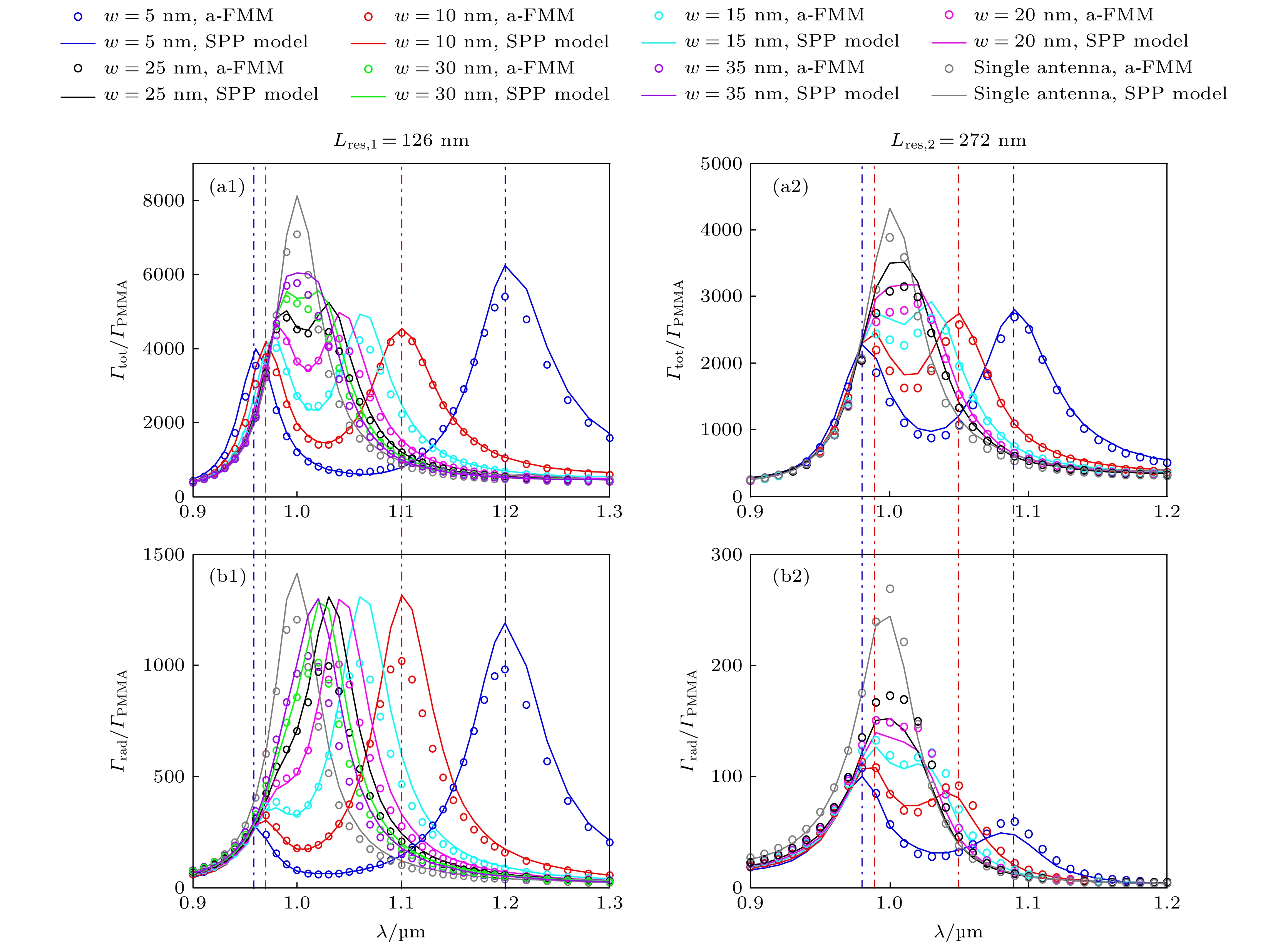
图 3 在单个点源激励下, 偶极纳米天线的归一化总辐射速率Γ_tot/Γ_PMMA((a1), (a2))和归一化远场辐射速率Γ_rad/Γ_PMMA((b1), (b2)), 显示为点源辐射波长λ的函数. 结果分别采用a-FMM严格计算(圆圈)和SPP模型(实线)得到. (a1), (b1)天线臂长L = L_{res, 1} = 126 nm. (a2), (b2) L = L_{res, 2} = 272 nm. 不同天线臂间狭缝宽度w对应不同颜色的曲线. 灰色曲线对应单臂纳米天线的结果. 竖直点划线显示了方程(10)预测的谐振波长

Fig. 3. Normalized total emission rate Γ_tot/Γ_PMMA ((a1), (a2)) and normalized radiative emission rate Γ_rad/Γ_PMMA ((b1), (b2)) of the dipole nanoantenna under a single point-source excitation plotted as functions of the excitation wavelength λ. The results are obtained with the rigorous a-FMM calculation (circles) and the SPP model (solid curves), respectively. (a1), (b1) Antenna arm length L = L_{res, 1} = 126 nm. (a2), (b2) L = L_{res, 2} = 272 nm. Different widths w of the slit between the antenna arms correspond to curves of different colors. The gray curves show the results of a single-arm nanoantenna. The vertical dash-dot lines show the resonant wavelengths predicted by Equation (10).

下载: 全尺寸图片幻灯片

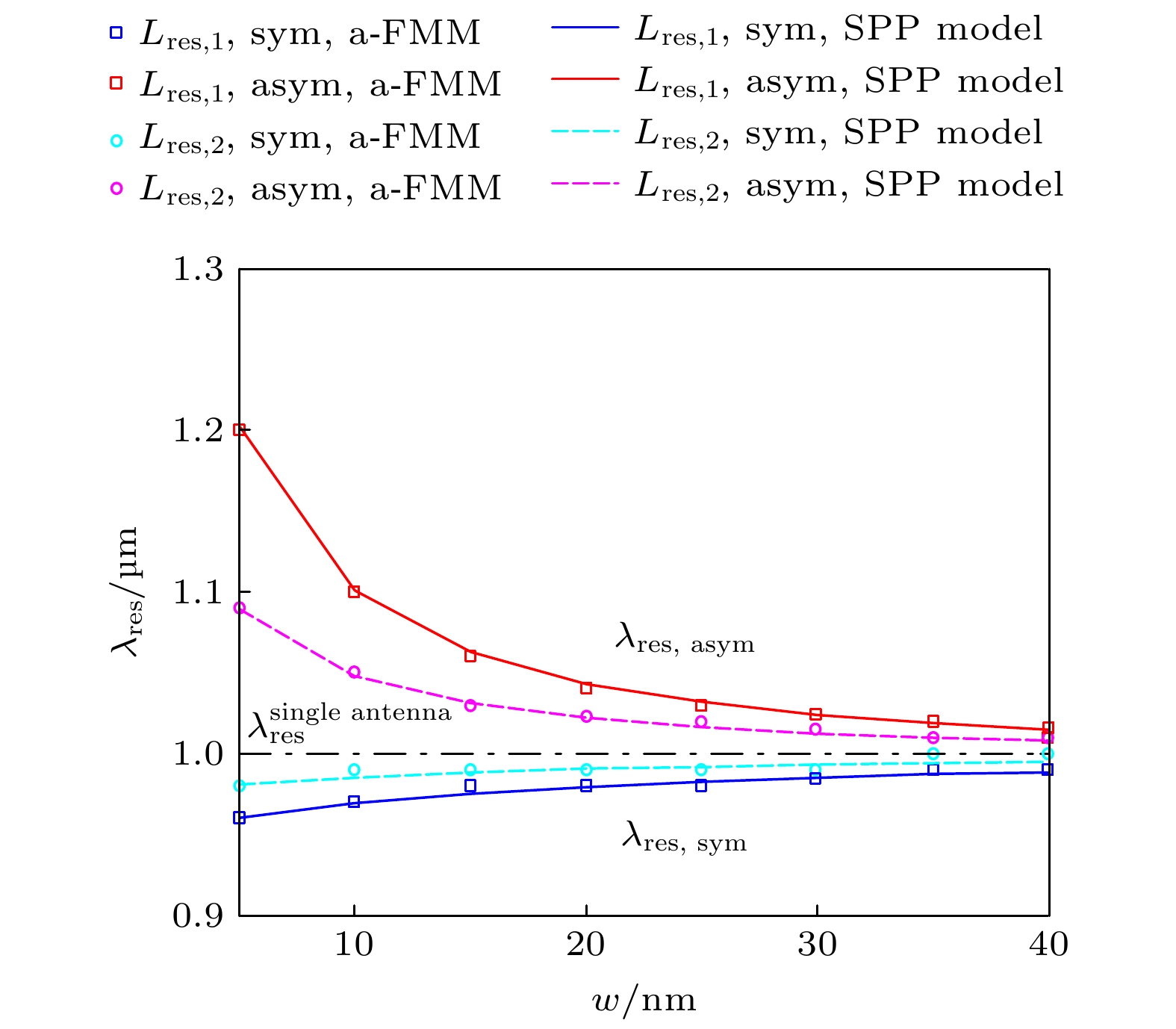
图 4 偶极纳米天线谐振波长λ_res随狭缝宽度w变化的曲线. 图中λ_{res, sym} = λ_{res, 1}, λ_{res, asym} = λ_{res, 2}, λ_{res, 1}, λ_{res, 2}为图3中γ_T或γ_R的谐振波长. 方形、圆圈为a-FMM严格计算结果. 实线、虚线为SPP模型方程(10)预测的结果. 红色、蓝色曲线对应天线臂长L = L_{res, 1} = 126 nm [对应方程(10)中M = N = 1], 洋红、青蓝色曲线对应L = L_{res, 2} = 272 nm(对应M = N = 2). 水平点划线为方程(A5)预测的单臂纳米天线的谐振波长

Fig. 4. Resonant wavelength λ_res of the dipole nanoantenna plotted as a function of the slit width w. There are λ_{res, sym} = λ_{res, 1} and λ_{res, asym} = λ_{res, 2}, with λ_{res, 1} and λ_{res, 2} being the resonant wavelengths of γ_T or γ_R shown in Figure 3. The squares and circles show the results obtained with the rigorous a-FMM calculation. The solid and dashed curves show the predictions of the SPP model Equation (10). The red and blue curves correspond to the antenna arm length L = L_{res, 1} = 126 nm (obtained for M = N = 1 in Equation (10)). The magenta and cyan curves correspond to L = L_{res, 2} = 272 nm (obtained for M = N = 2). The horizontal dash-dot line shows the resonant wavelength of the single-arm nanoantenna predicted by Equation (A5).

下载: 全尺寸图片幻灯片

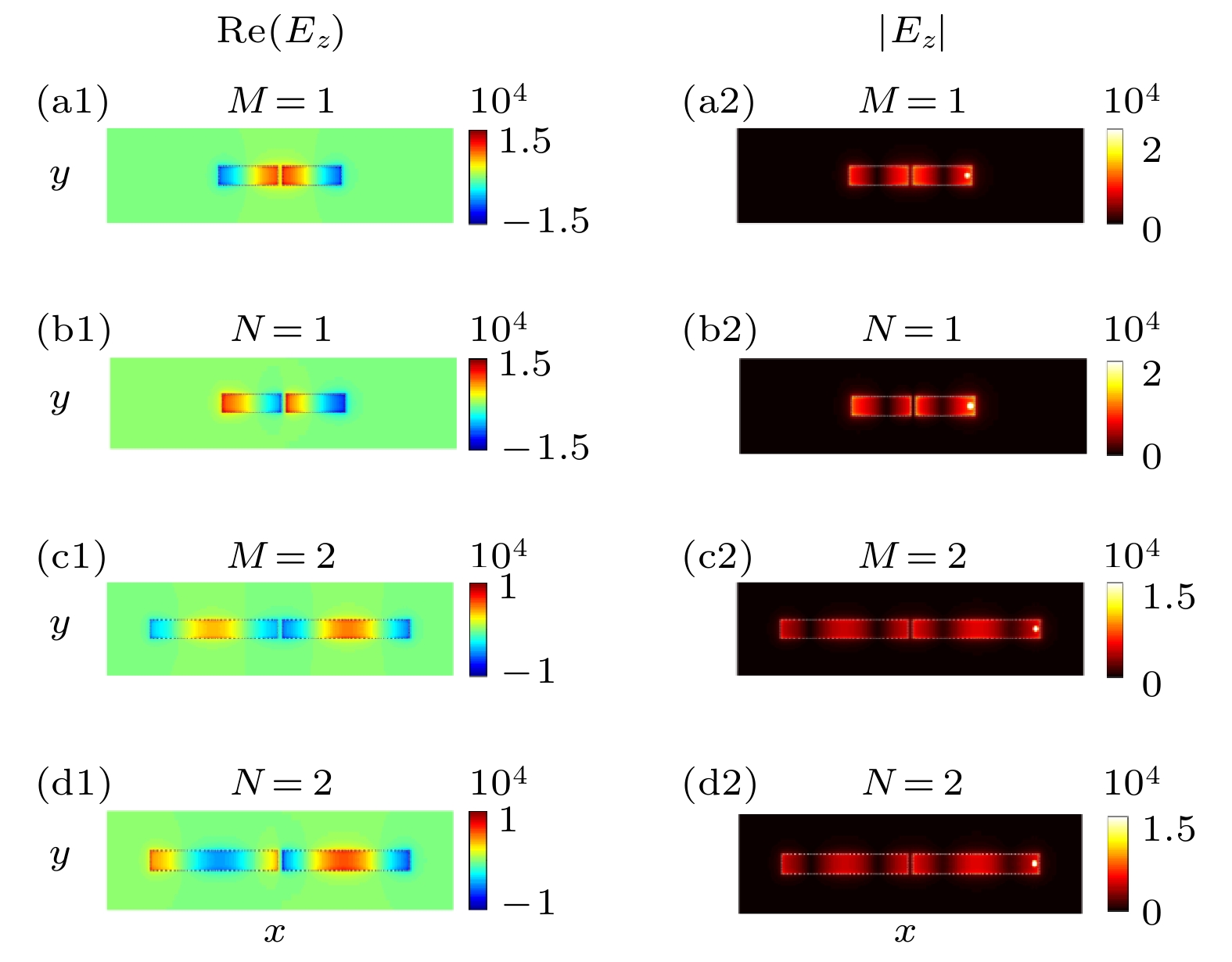
图 5 单个点源激励下, 天线纳米间隙内(z = H下1 nm截面上)主要电场分量E_z的近场分布　(a1), (a2), (b1), (b2) 天线臂长L = L_{res, 1} = 126 nm, λ_{res, sym} = 0.97 μm, λ_{res, asym} = 1.10 μm (分别对应方程(10)中M = 1和N = 1); (c1), (c2), (d1), (d2) L = L_res,2 = 272 nm, λ_res,sym = 0.99 μm, λ_{res, asym} = 1.05 μm (分别对应M = 2和N = 2); (a1)—(d1) 显示了Re(E_z); (a2)—(d2) 显示了|E_z|. E_z做了归一化(除以Γ_PMMA)

Fig. 5. Near-field distribution of the main electric-field component E_z in the antenna nanogap (on the cross-section of 1 nm below z = H) under excitation by a single point source: (a1), (a2), (b1), (b2) For antenna arm length L = L_res,1 = 126 nm and wavelengths λ_res,sym = 0.97 μm, λ_res,asym = 1.10 μm (respectively corresponding to M = 1 and N = 1 in Equation (10)); (c1), (c2), (d1), (d2) for L = L_res,2 = 272 nm and λ_{res, sym} = 0.99 μm, λ_{res, asym} = 1.05 μm (respectively corresponding to M = 2 and N = 2); (a1)−(d1) show Re(E_z); (a2)−(d2) show |E_z|. E_z is normalized (divided by Γ_PMMA).

下载: 全尺寸图片幻灯片

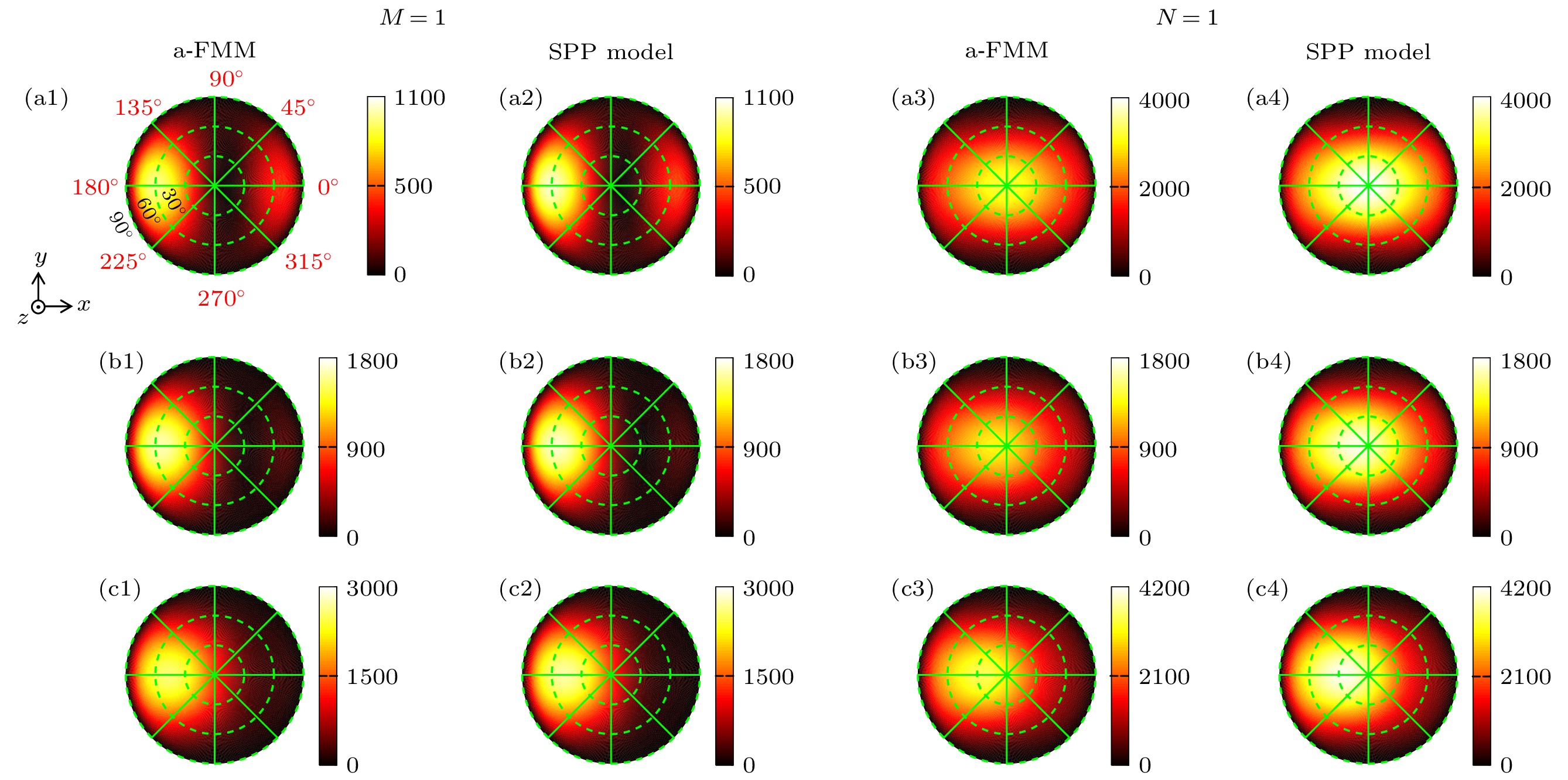
图 6 在单个点源激励下, 偶极纳米天线的远场辐射角分布P(θ, ϕ). 计算选取图4中天线臂长L = L_{res, 1} = 126 nm, 以及不同的天线臂间狭缝宽度w对应的谐振波长λ_{res, sym}(第1, 2列), λ_{res, asym}(第3, 4列) (a1)—(a4) w = 5 nm, λ_{res, sym} = 0.96 μm, λ_{res, asym} = 1.2 μm; (b1) —(b4) w = 15 nm, λ_{res, sym} = 0.98 μm, λ_{res, asym} = 1.06 μm; (c1)—(c4) w = 35 nm, λ_{res, sym} = 0.99 μm, λ_{res, asym} = 1.02 μm. 叠加的圆和径向线分别对应极角θ和方位角ϕ

Fig. 6. Angular distributions P(θ, ϕ) of the far-field emission for the dipole nanoantenna under excitation by a single point source. The calculations are for antenna arm length L = L_{res, 1} = 126 nm and resonance wavelengths λ_{res, sym} (columns 1 and 2) and λ_{res, asym} (columns 3 and 4) corresponding to different widths w of the slit between the antenna arms (as shown in Fig. 4). (a1)−(a4) w = 5 nm, λ_{res, sym} = 0.96 μm, λ_{res, asym} = 1.2 μm; (b1)−(b4) w = 15 nm, λ_{res, sym} = 0.98 μm, λ_{res, asym} = 1.06 μm; (c1)−(c4) w = 35 nm, λ_{res, sym} = 0.99 μm, λ_{res, asym} = 1.02 μm. The superimposed circles and radial lines correspond to the polar angle θ and azimuth angle ϕ, respectively.

下载: 全尺寸图片幻灯片

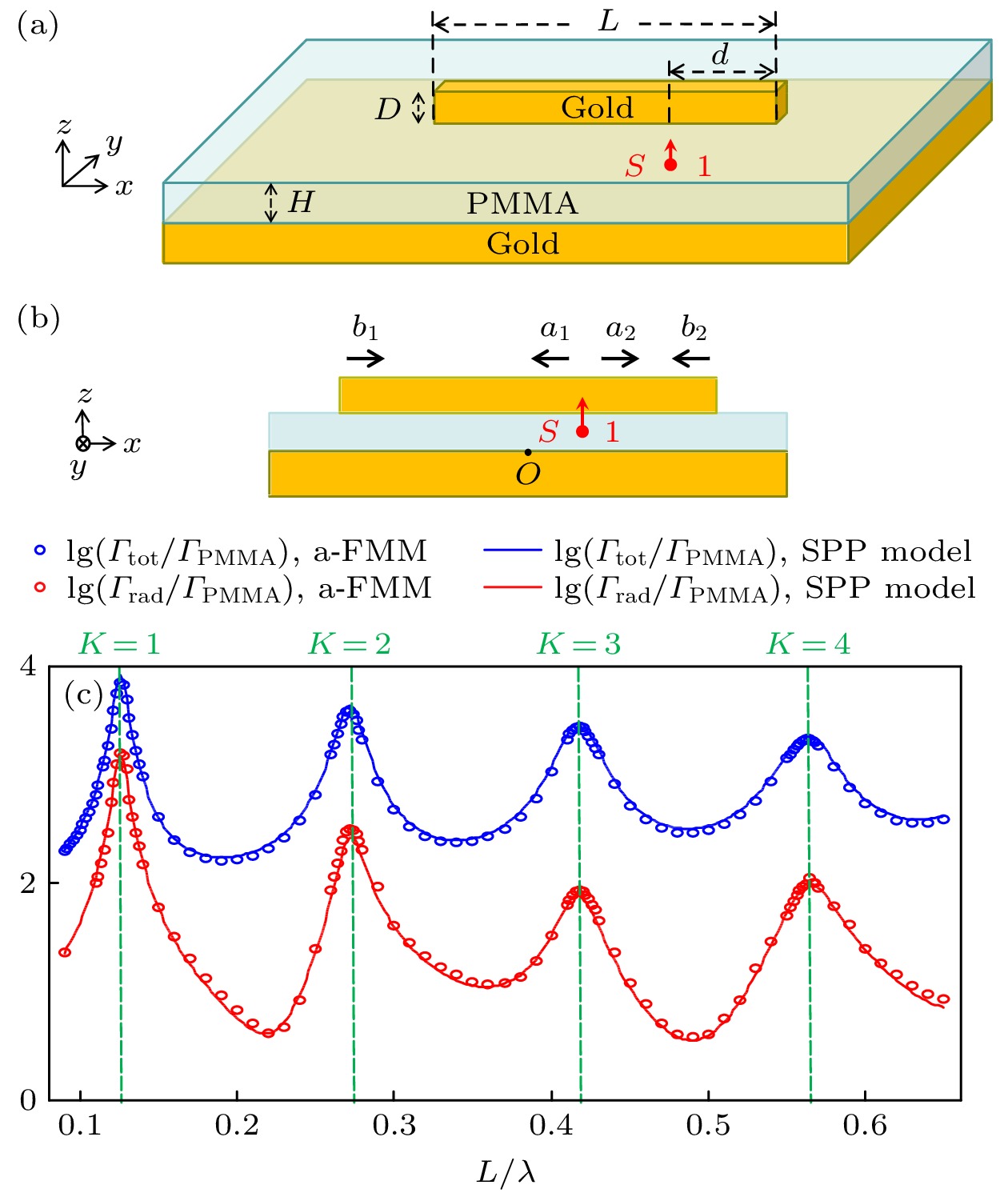
图 A1 (a) 金基底上单臂纳米天线示意图; (b) 在单个点源激励下, SPP模型中SPP模式系数a₁, a₂, b₁, b₂的定义; (c) 归一化总辐射速率Γ_tot/Γ_PMMA(蓝色曲线)和归一化远场辐射速率Γ_rad/Γ_PMMA(红色曲线)随天线臂长L变化的曲线(固定波长λ = 1 μm). 圆圈和实线分别为全波a-FMM, SPP模型的结果. 竖直绿色虚线显示了方程(A5)确定的发生谐振的L

Fig. A1. (a) Schematic diagram of a single-arm nanoantenna on a gold substrate; (b) definition of the SPP mode coefficients a₁, a₂, b₁, b₂ in the SPP model under a single point-source excitation; (c) normalized total emission rate Γ_tot/Γ_PMMA (blue curves) and normalized radiative emssion rate Γ_rad/Γ_PMMA (red curves) of the antenna plotted as functions of the antenna arm length L (for fixed wavelength λ = 1 μm). The circles and solid curves show the results of the full-wave a-FMM and SPP model, respectively. The vertical green dashed lines show the L at resonance determined by Equation (A5).

下载: 全尺寸图片幻灯片

图 B1 偶极天线棱边、棱角圆角化后的俯视图(a)、侧视图(b). 图中红点代表辐射点源

Fig. B1. Top view (a) and side view (b) of the dipole antenna with rounded edges and corners. The red dot represents the emission point source.

下载: 全尺寸图片幻灯片

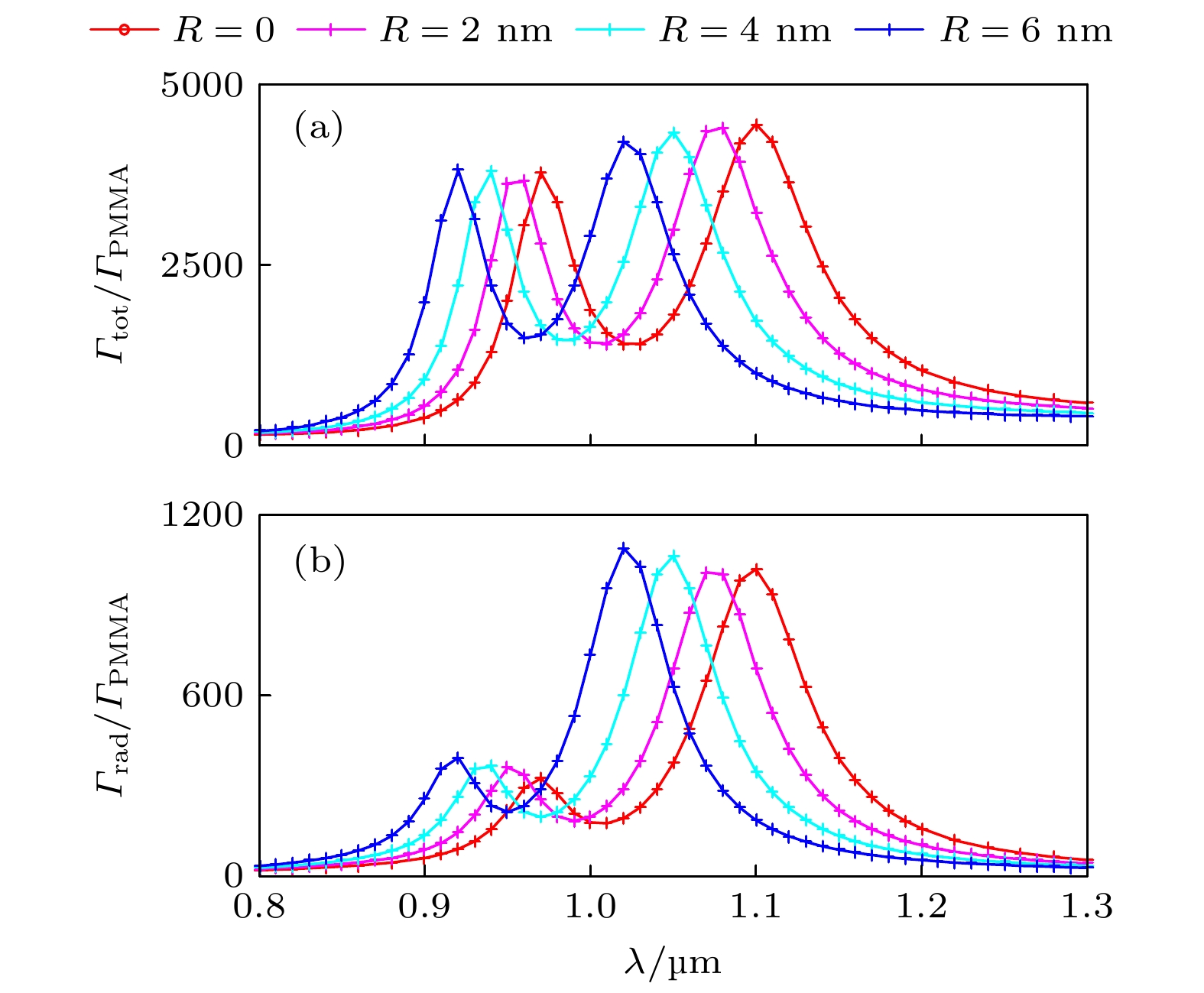
图 B2 对于不同圆角化半径R的偶极天线(对应不同颜色的曲线), 在单个点源激励下, 归一化总辐射速率Γ_tot/Γ_PMMA (a)和归一化远场辐射速率Γ_rad/Γ_PMMA (b)随波长λ变化的曲线. 计算采用a-FMM(红色曲线)和FEM(粉色、青色、蓝色曲线). 选取天线臂长L = L_res,1 = 126 nm, 臂间狭缝宽度w = 10 nm

Fig. B2. For the dipole antenna with different radii R of rounded edges and corners (corresponding to curves of different colors), the normalized total emission rate Γ_tot/Γ_PMMA (a) and normalized radiative emission rate Γ_rad/Γ_PMMA (b) under excitation by a single point source, which are plotted as functions of wavelength λ. The calculation is performed with the a-FMM (red curves) and the FEM (pink, cyan, and blue curves). The antenna arm length is L = L_res,1 = 126 nm, and the width of the slit between the antenna arms is w = 10 nm.

下载: 全尺寸图片幻灯片

map

[1]	Mühlschlegel P, Eisler H J, Martin O J F, Hecht B, Pohl D W 2005 Science 308 1607 Google Scholar
[2]	Novotny L, Van Hulst N 2011 Nat. Photonics 5 83 Google Scholar
[3]	Pelton M 2015 Nat. Photonics 9 427 Google Scholar
[4]	Şendur K, Baran E 2009 Appl. Phys. B 96 325 Google Scholar
[5]	Sederberg S, Elezzabi A Y. 2011 Opt. Express 19 10456 Google Scholar
[6]	El-Toukhy Y M, Hussein M, Hameed M F O, Obayya S S A 2018 Plasmonics 13 503 Google Scholar
[7]	Aizpurua J, Bryant G W, Richter L J, García de Abajo F J, Kelley B K, Mallouk T 2005 Phys. Rev. B 71 235420 Google Scholar
[8]	Yong Z D, Zhang S L, Dong Y J, He S L 2015 Prog. Electromagnet. Res. 153 123 Google Scholar
[9]	Lu G W, Liu J, Zhang T Y, Shen H M, Perriat P, Martini M, Tillement O, Gu Y, He Y B, Wang Y W, Gong Q H 2013 Nanoscale 5 6545 Google Scholar
[10]	Akselrod G M, Argyropoulos C, Hoang T B, Ciracì C, Fang C, Huang J N, Smith D R, Mikkelsen M H 2014 Nat. Photonics 8 835 Google Scholar
[11]	Hoang T B, Akselrod G M, Argyropoulos C, Huang J, Smith D R, Mikkelsen M H 2015 Nat. Commun. 6 7788 Google Scholar
[12]	Kinkhabwala A, Yu Z H, Fan S H, Avlasevich Y, Müllen K, Moerner W E 2009 Nat. Photonics 3 654 Google Scholar
[13]	Muskens O L, Giannini V, Sánchez-Gil J A, Gómez Rivas J 2007 Nano Lett. 7 2871 Google Scholar
[14]	Baibakov M, Patra S, Claude J-B, Moreau A, Lumeau J, Wenger J 2019 ACS Nano 13 8469 Google Scholar
[15]	Barulin A, Claude J-B, Patra S, Bonod N, Wenger J 2019 Nano Lett. 19 7434 Google Scholar
[16]	Rycenga M, Xia X H, Moran C H, Zhou F, Qin D, Li Z Y, Xia Y N 2011 Angew. Chem. Int. Ed. 50 5473 Google Scholar
[17]	Nie S, Emory S R 1997 Science 275 1102 Google Scholar
[18]	Lodahl P, Mahmoodian S, Stobbe S 2015 Rev. Mod. Phys. 87 347 Google Scholar
[19]	Tsakmakidis K L, Boyd R W, Yablonovitch E, Zhang X 2016 Opt. Express 24 17916 Google Scholar
[20]	Suh J Y, Kim C H, Zhou W, Huntington M D, Co D T, Wasielewski M R, Odom T W 2012 Nano Lett. 12 5769 Google Scholar
[21]	Ma R-M, Oulton R F, Sorger V J, Zhang X 2013 Laser Photonics Rev. 7 1 Google Scholar
[22]	Harutyunyan H, Volpe G, Quidant R, Novotny L 2012 Phys. Rev. Lett. 108 217403 Google Scholar
[23]	Butet J, Martin O J F 2015 Plasmonics 10 203 Google Scholar
[24]	Gong T X, Guan F, Wei Z J, Huang W, Zhang X S. 2021 Front. Phys-Lausanne 9 691027 Google Scholar
[25]	Zhang W H, Huang L N, Santschi C, Martin O J F 2010 Nano Lett. 10 1006 Google Scholar
[26]	Fischer H, Martin O J F 2008 Opt. Express 16 9144 Google Scholar
[27]	Yong Z D, Gong C S, Dong Y J, Zhang S L, He S L 2017 RSC Adv. 7 2074 Google Scholar
[28]	Trojak O J, Park S I, Song J D, Sapienza L 2017 Appl. Phys. Lett. 111 021109 Google Scholar
[29]	Zarrabi F B, Naser-Moghadasi M, Heydari S, Maleki M, Arezomand A S 2016 Opt. Commun. 371 34 Google Scholar
[30]	Lumdee C, Yun B F, Kik P G 2014 ACS Photonics 1 1224 Google Scholar
[31]	Baumberg J J, Aizpurua J, Mikkelsen M H, Smith D R 2019 Nat. Mater. 18 668 Google Scholar
[32]	Huang S X, Ming T, Lin Y X, Ling X, Ruan Q F, Palacios T, Wang J F, Kong J, Dresselhaus M, Kong J 2016 Small 12 5190 Google Scholar
[33]	Huang Y, Ma L W, Hou M J, Li J H, Xie Z, Zhang Z J 2016 Sci. Rep. 6 30011 Google Scholar
[34]	Armstrong R E, van Liempt J C, Zijlstra P 2019 J. Phys. Chem. C 123 25801 Google Scholar
[35]	Huang Y, Ma L W, Li J H, Zhang Z J 2017 Nanotechnology 28 105203 Google Scholar
[36]	Purcell E M 1946 Phys. Rev. 69 681
[37]	Lakowicz J R, Fu Y 2009 Laser Photonics Rev. 3 221 Google Scholar
[38]	Agio M 2012 Nanoscale 4 692 Google Scholar
[39]	Li L, Hutter T, Steiner U, Mahajan S 2013 Analyst 138 4574 Google Scholar
[40]	Yoon J K, Kim K, Shin K S 2009 J. Phys. Chem. C 113 1769 Google Scholar
[41]	Alu A, Engheta N 2008 Phys. Rev. Lett. 101 043901 Google Scholar
[42]	Eggleston M S, Messer K, Zhang L M, Yablonovitch E, Wu M C 2015 Proc. Natl. Acad. Sci. U. S. A. 112 1704 Google Scholar
[43]	Fernandez-Garcia R, Rahmani M, Hong M, Maier S A, Sonnefraud Y 2013 Opt. Express 21 12552 Google Scholar
[44]	Calderón J, Álvarez J, Martinez-Pastor J, Hill D 2015 Plasmonics 10 703 Google Scholar
[45]	Cooper C T, Rodriguez M, Blair S, Shumaker-Parry J S 2014 J. Phys. Chem. C 118 1167 Google Scholar
[46]	Jia H, Yang F, Zhong Y, Liu H 2016 Photonics Res. 4 293 Google Scholar
[47]	Lalanne P, Yan W, Vynck K, Sauvan C, Hugonin J P 2018 Laser Photonics Rev. 12 1700113 Google Scholar
[48]	Sauvan C, Hugonin J P, Maksymov I S, Lalanne P 2013 Phys. Rev. Lett. 110 237401 Google Scholar
[49]	Ching E S C, Leung P T, Maassen van den Brink A, Tong S S, Young K 1998 Rev. Mod. Phys. 70 1545 Google Scholar
[50]	Della Valle G, Søndergaard T, Bozhevolnyi S I 2008 Opt. Express 16 6867 Google Scholar
[51]	Taminiau T H, Stefani F D, van Hulst N F 2011 Nano Lett. 11 1020 Google Scholar
[52]	Cubukcu E, Capasso F 2009 Appl. Phys. Lett. 95 201101 Google Scholar
[53]	Hasan S B, Filter R, Ahmed A, Vogelgesang R, Gordon R, Rockstuhl C, Lederer F 2011 Phys. Rev. B 84 195405 Google Scholar
[54]	Kim D, Jeong K Y, Kim J, Ee H S, Kang J H, Park H G Seo M K 2017 Phys. Rev. Appl. 8 054024 Google Scholar
[55]	Chandran A, Barnard E S, White J S, Brongersma M L 2012 Phys. Rev. B 85 085416 Google Scholar
[56]	Filter R, Qi J, Rockstuhl C, Ledere F 2012 Phys. Rev. B 85 125429 Google Scholar
[57]	Wan J, Zhu J, Zhong Y, Liu H 2018 J. Opt. Soc. Am. A: 35 880 Google Scholar
[58]	Jia H, Liu H, Zhong Y 2015 Sci. Rep. 5 8456 Google Scholar
[59]	Zhai X, Wang N, Zhong Y, Liu H 2020 IEEE J. Sel. Top. Quantum Electron. 27 4600815 Google Scholar
[60]	Kotal S, Artioli A, Wang Y, Osterkryger A D, Finazzer M, Fons R, Claudon J, Bleuse J, Gérard J M, 2021 Appl. Phys. Lett. 118 194002 Google Scholar
[61]	Yang J, Kong F M, Li K, Sheng S W 2015 Opt. Commun. 342 230 Google Scholar
[62]	Vesseur E J R, de Abajo F J G, Polman A 2010 Phys. Rev. B 82 165419 Google Scholar
[63]	Edwards A P, Adawi A M 2014 J. Appl. Phys. 115 053101 Google Scholar
[64]	Palik E D 1991 Handbook of Optical Constants of Solids, Part Ⅱ (San Diego: Academic)
[65]	Anger P, Bharadwaj P, Novotny L 2006 Phys. Rev. Lett. 96 113002 Google Scholar
[66]	Liu H T 2010 DIF CODE for Modeling Light Diffraction in Nanostructures (Tianjin: Nankai University)
[67]	Hugonin J P, Lalanne P 2005 J. Opt. Soc. Am. A: 22 1844 Google Scholar
[68]	Vassallo C 1991 Optical Waveguide Concepts (Amsterdam: Elsevier)
[69]	Chang D E, Sørensen A S, Hemmer P R, Lukin M D 2007 Phys. Rev. B 76 035420 Google Scholar
[70]	Li L 1996 J. Opt. Soc. Am. A: 13 1024 Google Scholar
[71]	Li L (edited by Popov E) 2014 Gratings: Theory and Numeric Applications (2nd Ed.) (Marseille: Institut Fresnel, Aix Marseille Université) pp573—574
[72]	Liu H 2013 Opt. Express 21 24093 Google Scholar
[73]	Ortega J M, Rheinboldt W C 1970 Iterative Solution of Nonlinear Equations in Several Variables (New York and London: Academic)
[74]	Li Y, Liu H, Jia H, Bo F, Zhang G, Xu J 2014 J. Opt. Soc. Am. A: 31 2459 Google Scholar
[75]	Yang J, Hugonin J P, Lalanne P 2016 ACS Photonics 3 395 Google Scholar

[1]	苏宇航, 张炼, 陶灿, 王宁, 马平准, 钟莹, 刘海涛. 金属镜面上纳米光学天线阵列自发辐射增强与定向辐射. , 2023, 72(7): 078101. doi: 10.7498/aps.72.20222007
[2]	闫晓宏, 牛亦杰, 徐红星, 魏红. 单个等离激元纳米颗粒和纳米间隙结构与量子发光体的强耦合. , 2022, 71(6): 067301. doi: 10.7498/aps.71.20211900
[3]	张炼, 王化雨, 王宁, 陶灿, 翟学琳, 马平准, 钟莹, 刘海涛. 金属基底上光学偶极纳米天线的自发辐射宽带增强：表面等离激元直观模型. , 2022, 0(0): 0-0. doi: 10.7498/aps.71.20212290
[4]	韩迪仪, 顾阳, 胡涛政, 董雯, 倪亚贤. 双金属/TiO₂纳米管复合结构中增强的光电流. , 2021, 70(3): 038103. doi: 10.7498/aps.70.20201134
[5]	张多多, 刘小峰, 邱建荣. 基于等离激元纳米结构非线性响应的超快光开关及脉冲激光器. , 2020, 69(18): 189101. doi: 10.7498/aps.69.20200456
[6]	周利, 王取泉. 等离激元共振能量转移与增强光催化研究进展. , 2019, 68(14): 147301. doi: 10.7498/aps.68.20190276
[7]	汪涵聪, 李志鹏. 表面增强光学力与光操纵研究进展. , 2019, 68(14): 144101. doi: 10.7498/aps.68.20190606
[8]	李鑫, 吴立祥, 杨元杰. 矩形纳米狭缝超表面结构的近场增强聚焦调控. , 2019, 68(18): 187103. doi: 10.7498/aps.68.20190728
[9]	虞华康, 刘伯东, 吴婉玲, 李志远. 表面等离激元增强的光和物质相互作用. , 2019, 68(14): 149101. doi: 10.7498/aps.68.20190337
[10]	李盼. 表面等离激元纳米聚焦研究进展. , 2019, 68(14): 146201. doi: 10.7498/aps.68.20190564
[11]	刘姿, 张恒, 吴昊, 刘昌. Al纳米颗粒表面等离激元对ZnO光致发光增强的研究. , 2019, 68(10): 107301. doi: 10.7498/aps.68.20190062
[12]	程自强, 石海泉, 余萍, 刘志敏. 银纳米颗粒阵列的表面增强拉曼散射效应研究. , 2018, 67(19): 197302. doi: 10.7498/aps.67.20180650
[13]	王文慧, 张孬. 银纳米线表面等离激元波导的能量损耗. , 2018, 67(24): 247302. doi: 10.7498/aps.67.20182085
[14]	邓红梅, 黄磊, 李静, 陆叶, 李传起. 基于石墨烯加载的不对称纳米天线对的表面等离激元单向耦合器. , 2017, 66(14): 145201. doi: 10.7498/aps.66.145201
[15]	陈聿, 刘垄, 黄忠, 屠林林, 詹鹏. 一维金属光栅嵌入磁性介质纳米结构下的横向磁光克尔效应的增强. , 2016, 65(14): 147302. doi: 10.7498/aps.65.147302
[16]	丁东, 杨仕娥, 陈永生, 郜小勇, 谷锦华, 卢景霄. Al纳米颗粒增强微晶硅薄膜太阳电池光吸收的模拟研究. , 2015, 64(24): 248801. doi: 10.7498/aps.64.248801
[17]	盛世威, 李康, 孔繁敏, 岳庆炀, 庄华伟, 赵佳. 基于石墨烯纳米带的齿形表面等离激元滤波器的研究. , 2015, 64(10): 108402. doi: 10.7498/aps.64.108402
[18]	胡梦珠, 周思阳, 韩琴, 孙华, 周丽萍, 曾春梅, 吴兆丰, 吴雪梅. 紫外表面等离激元在基于氧化锌纳米线的半导体-绝缘介质-金属结构中的输运特性研究. , 2014, 63(2): 029501. doi: 10.7498/aps.63.029501
[19]	朱华, 颜振东, 詹鹏, 王振林. 局域表面等离激元诱导的三次谐波增强效应. , 2013, 62(17): 178104. doi: 10.7498/aps.62.178104
[20]	王垒, 蔡卫, 谭信辉, 向吟啸, 张心正, 许京军. 截面形状对快电子激发纳米双线表面等离激元的影响. , 2011, 60(6): 067305. doi: 10.7498/aps.60.067305

计量

文章访问数: 5688
PDF下载量: 124
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

金属基底上光学偶极纳米天线的自发辐射宽带增强: 表面等离激元直观模型