-
能带理论是凝聚态物理的基石之一, 其应用范围已延伸至许多其他物理领域. 近年来, 众多非厄米物理问题要求将能带理论推广至非厄米体系. 人们在非厄米拓扑体系的研究中发现, 这一推广需要修改能带理论的若干基本概念. 非厄米趋肤效应(non-Hermitian skin effect)这一普遍的非厄米现象导致了布洛赫能带图像的失效以及常规体边对应关系的破坏. 在能谱计算与拓扑不变量定义中, 通常的布里渊区概念需要代之以广义布里渊区(generalized Brillouin zone). 非厄米体系的一系列独特现象可以在广义布里渊区下得到精确刻画. 基于广义布里渊区的非厄米能带理论成功描述并预言了非厄米系统的大量新颖现象. 因其相对布洛赫图像的偏离, 这一理论被称为非布洛赫能带理论(non-Bloch band theory). 本文梳理了广义布里渊区和非布洛赫能带理论的主要概念, 并简要介绍了该理论在非厄米体边对应原理、格林函数、波包动力学、手征衰减和非布洛赫宇称-时间对称性等方面的应用.The energy band theory is one of the cornerstones of condensed matter physics. It also has wide applications in other branches of physics. Recently, a number of questions from non-Hermitian physics call for a generalization of energy band theory to non-Hermitian systems. In the study of non-Hermitian topological states, it has been found that such a generalization necessitates redefinitions of certain fundamental concepts of band theory. In particular, the non-Hermitian skin effect (NHSE) causes the breakdown of Bloch-band picture and conventional bulk-boundary correspondence. To calculate the energy spectra and define topological invariants, the standard Brillouin zone gives way to the generalized Brillouin zone (GBZ). Many intriguing non-Hermitian phenomena, including the non-Hermitian skin effect, can be precisely characterized in terms of the generalized Brillouin zone. The non-Hermitian band theory based on the concept of generalized Brillouin zone, now generally known as the non-Bloch band theory, has successfully described and predicted a number of novel non-Hermitian phenomena. The present article provides a brief introduction to the main concepts of non-Bloch band theory, and its applications in the non-Hermitian bulk-boundary correspondence, Green’s functions, wave dynamics, chiral damping, and non-Bloch parity-time symmetry.
-
Keywords:
- generalized Brillouin zone /
- non-Hermitian skin effect /
- non-Bloch band theory /
- non-Hermitian band theory
[1] Breuer H P, Petruccione F 2006 The Theory of Open Quantum Systems (Oxford: Oxford University Press)
[2] Lindblad G 1976 Commun. Math. Phys. 48 119
Google Scholar
[3] Gorini V, Kossakowski A, Sudarshan E C G 1976 J. Math. Phys. 17 821
Google Scholar
[4] Daley A J 2014 Adv. Phys. 63 77
Google Scholar
[5] Kozii V, Fu L 2017 arXiv: 1708.05841 [cond-mat]
[6] Shen H T, Fu L 2018 Phys. Rev. Lett. 121 026403
Google Scholar
[7] Nagai Y, Qi Y, Isobe H, Kozii V, Fu L 2020 Phys. Rev. Lett. 125 227204
Google Scholar
[8] Papaj M, Isobe H, Fu L 2019 Phys. Rev. B 99 201107
Google Scholar
[9] Bandres M A, Wittek S, Harari G, et al. 2018 Science 359 eaar4005
Google Scholar
[10] Harari G, Bandres M A, Lumer Y, et al. 2018 Science 359 eaar4003
Google Scholar
[11] Zhou H Y, Peng C, Yoon Y, et al. 2018 Science 359 1009
Google Scholar
[12] Ashida Y, Gong Z P, Ueda M 2020 Adv. Phys. 69 249
Google Scholar
[13] Bergholtz E J, Budich J C, Kunst F K 2021 Rev. Mod. Phys. 93 015005
Google Scholar
[14] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[15] Qi X L, Zhang S C 2011 Rev. Mod.Phys. 83 1057
Google Scholar
[16] Chiu C K, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys. 88 035005
Google Scholar
[17] Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004
Google Scholar
[18] Ozawa T, Price H M, Amo A, et al. 2019 Rev. Mod. Phys. 91 015006
Google Scholar
[19] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[20] Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802
Google Scholar
[21] Kunst F K, Edvardsson E, Budich J C, Bergholtz E J 2018 Phys. Rev. Lett. 121 026808
Google Scholar
[22] Lee C H, Thomale R 2019 Phys. Rev. B 99 201103
Google Scholar
[23] Helbig T, Hofmann T, Imhof S, et al. 2020 Nat. Phys. 16 747
Google Scholar
[24] Xiao L, Deng T S, Wang K K, Zhu G Y, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761
Google Scholar
[25] Weidemann S, Kremer M, Helbig T, Hofmann T, Stegmaier A, Greiter M, Thomale R, Szameit A 2020 Science 368 311
Google Scholar
[26] Yokomizo K, Murakami S 2019 Phys. Rev. Lett. 123 066404
Google Scholar
[27] Su W P, Schrieffer J R, Heeger A J 1980 Phys. Rev. B 22 2099
Google Scholar
[28] Wang K K, Li T Y, Xiao L, Han Y W, Yi W, Xue P 2021 arXiv: 2107.14741 [cond-mat]
[29] Ghatak A, Brandenbourger M, van Wezel J, Coulais C 2020 Proc. Natl. Acad. Sci. 117 29561
Google Scholar
[30] Gou W, Chen T, Xie D Z, Xiao T, Deng T S, Gadway B, Yi W, Yan B 2020 Phys. Rev. Lett. 124 070402
Google Scholar
[31] Li L H, Lee C H, Gong J B 2020 Phys. Rev. Lett. 124 250402
Google Scholar
[32] Yoshida T, Mizoguchi T, Hatsugai Y 2020 Phys. Rev. Res. 2 022062
Google Scholar
[33] Scheibner C, Irvine W T M, Vitelli V 2020 Phys. Rev. Lett. 125 118001
Google Scholar
[34] Mandal S, Banerjee R, Ostrovskaya E A, Liew T C H 2020 Phys. Rev. Lett. 125 123902
Google Scholar
[35] Gao P L, Willatzen M, Christensen J 2020 Phys. Rev. Lett. 125 206402
Google Scholar
[36] Zhu X Y, Wang H Q, Gupta S K, Zhang H J, Xie B Y, Lu M H, Chen Y F 2020 Phys. Rev. Res. 2 013280
Google Scholar
[37] Hofmann T, Helbig T, Schindler F, S et al. 2020 Phys. Rev. Res. 2 023265
Google Scholar
[38] Brandenbourger M, Locsin X, Lerner E, Coulais C 2019 Nat. Commun. 10 4608
Google Scholar
[39] Rosa M I N, Ruzzene M 2020 New J. Phys. 22 053004
Google Scholar
[40] Mandal S, Banerjee R, Liew T C H 2021 arXiv: 2103.05480 [cond-mat]
[41] Zhong J, Wang K, Park Y, Asadchy V, Wojcik C C, Dutt A, Fan S H 2021 Phys. Rev. B 104 125416
Google Scholar
[42] Chen Y Y, Li X P, Scheibner C, Vitelli V, Huang G L 2021 Nat. Commun. 12 5935
Google Scholar
[43] Zhang L, Yang Y H, Ge Y, et al. 2021 Nat. Commun. 12 6297
[44] Deng T S, Yi W 2019 Phys. Rev. B 100 035102
Google Scholar
[45] Yang Z S, Zhang K, Fang C, Hu J P 2020 Phys. Rev. Lett. 125 226402
Google Scholar
[46] Li L H, Lee C H, Mu S, Gong J B 2020 Nat. Commun. 11 5491
Google Scholar
[47] Yokomizo K, Murakami S 2021 Phys. Rev. B 104 165117
Google Scholar
[48] Rafi-Ul-Islam S M, Siu Z B, Sahin H, Lee C H, Jalil M B A 2021 arXiv: 2108.02457 [cond-mat]
[49] Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570
Google Scholar
[50] Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651
Google Scholar
[51] Xue W T, Li M R, Hu Y M, Wang Z 2021 Phys. Rev. B 103 L241408
Google Scholar
[52] Zhang K, Yang Z S, Fang C 2020 Phys. Rev. Lett. 125 126402
Google Scholar
[53] Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 246801
Google Scholar
[54] Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801
Google Scholar
[55] Gong Z P, Ashida Y, Kawabata K, Takasan K, Higashikawa S, Ueda M 2018 Phys. Rev. X 8 031079
Google Scholar
[56] Shen H T, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402
Google Scholar
[57] Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015
Google Scholar
[58] Li L H, Mu S, Lee C H, Gong J B 2021 Nat. Commun. 12 5294
Google Scholar
[59] Zhang K, Yang Z S, Fang C 2021 arXiv: 2102.05059 [cond-mat]
[60] Kawabata K, Sato M, Shiozaki K 2020 Phys. Rev. B 102 205118
Google Scholar
[61] Zhang X J, Tian Y, Jiang J H, Lu M H, Chen Y F 2021 Nat. Commun. 12 5377
Google Scholar
[62] Fu Y X, Hu J H, Wan S L 2021 Phys. Rev. B 103 045420
Google Scholar
[63] Edvardsson E, Kunst F K, Bergholtz E J 2019 Phys. Rev. B 99 081302
Google Scholar
[64] Wang H Q, Ruan J W, Zhang H J 2019 Phys. Rev. B 99 075130
Google Scholar
[65] Zhang X Z, Gong J B 2020 Phys. Rev. B 101 045415
Google Scholar
[66] Okugawa R, Takahashi R, Yokomizo K 2020 Phys. Rev. B 102 241202
Google Scholar
[67] Lee C H, Li L H, Gong J B 2019 Phys. Rev. Lett. 123 016805
Google Scholar
[68] Zou D Y, Chen T, He W J, Bao J C, Lee C H, Sun H J, Zhang X D 2021 arXiv: 2104.11260 [cond-mat]
[69] Longhi S 2019 Phys. Rev. Res. 1 023013
Google Scholar
[70] Mao L, Deng T S, Zhang P F 2021 Phys. Rev. B 104 125435
Google Scholar
[71] Longhi S 2020 Phys. Rev. Lett. 124 066602
Google Scholar
[72] Longhi S 2020 Phys. Rev. B 102 201103
Google Scholar
[73] Li T Y, Sun J Z, Zhang Y S, Yi W 2021 Phys. Rev. Res. 3 023022
Google Scholar
[74] Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 170401
Google Scholar
[75] Haga T, Nakagawa M, Hamazaki R, Ueda M 2021 Phys. Rev. Lett. 127 070402
Google Scholar
[76] Liu C H, Zhang K, Yang Z S, Chen S 2020 Phys. Rev. Res. 2 043167
Google Scholar
[77] McDonald A, Clerk A A 2020 Nat. Commun. 11 5382
Google Scholar
[78] McDonald A, Hanai R, Clerk A A 2021 arXiv: 2103.01941 [cond-mat]
[79] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[80] Bender C M 2007 Rep. Prog. Phys. 70 947
Google Scholar
[81] El-Ganainy R, Makris K G, Khajavikhan M, Musslimani Z H, Rotter S, Christodoulides D N 2018 Nat. Phys. 14 11
Google Scholar
[82] Özdemir S K, Rotter S, Nori F, Yang L 2019 Nat. Mater. 18 783
Google Scholar
[83] Miri M A, Alù A 2019 Science 363 eaar7709
Google Scholar
[84] Longhi S 2019 Opt. Lett. 44 5804
Google Scholar
[85] Xiao L, Deng T S, Wang K K, Wang Z, Yi W, Xue P 2021 Phys. Rev. Lett. 126 230402
Google Scholar
[86] Song F, Wang H Y, Wang Z 2021 arXiv: 2102.02230 [cond-mat]
[87] Kawabata K, Okuma N, Sato M 2020 Phys. Rev. B 101 195147
Google Scholar
[88] Li L H, Lee C H, Gong J B 2019 Phys. Rev. B 100 075403
Google Scholar
[89] Liu C H, Jiang H, Chen S 2019 Phys. Rev. B 99 125103
Google Scholar
[90] Yi Y F, Yang Z S 2020 Phys. Rev. Lett. 125 186802
Google Scholar
[91] Yang Z S 2020 arXiv: 2012.03333 [cond-mat]
[92] Yokomizo K, Murakami S 2021 Phys. Rev. B 103 165123
Google Scholar
[93] Jin L, Song Z 2019 Phys. Rev. B 99 081103
Google Scholar
[94] Xu X R, Xu H W, Mandal S, Banerjee R, Ghosh S, Liew T C H 2021 Phys. Rev. B 103 235306
Google Scholar
[95] Okugawa R, Takahashi R, Yokomizo K 2021 Phys. Rev. B 103 205205
Google Scholar
[96] Shiozaki K, Ono S 2021 Phys. Rev. B 104 035424
Google Scholar
[97] Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 054301
Google Scholar
[98] Longhi S 2019 Phys. Rev. B 100 125157
Google Scholar
[99] Zeng Q B, Yang Y B, Xu Y 2020 Phys. Rev. B 101 020201
Google Scholar
[100] Zeng Q B, Xu Y 2020 Phys. Rev. Res. 2 033052
Google Scholar
[101] Kim K M, Park M J 2021 Phys. Rev. B 104 L121101
Google Scholar
[102] Liu Y X, Wang Y C, Liu X J, Zhou Q, Chen S 2021 Phys. Rev. B 103 014203
Google Scholar
[103] Longhi S 2021 Phys. Rev. B 103 144202
Google Scholar
[104] Longhi S 2021 Phys. Rev. B 103 224206
Google Scholar
[105] Liu Q, Li T Y, Xiao L, Wang K K, Yi W, Xue P 2021 arXiv: 2108.01097 [cond-mat]
[106] Claes J, Hughes T L 2021 Phys. Rev. B 103 L140201
Google Scholar
[107] Sun X Q, Zhu P H, Hughes T L 2021 Phys. Rev. Lett. 127 066401
Google Scholar
[108] Panigrahi A, Moessner R, Roy B 2021 arXiv: 2105.05244 [cond-mat]
[109] Schindler F, Prem A 2021 Phys. Rev. B 104 L161106
Google Scholar
[110] Bhargava B A, Fulga I C, van den Brink J, Moghaddam A G 2021 arXiv: 2106.04567 [cond-mat]
[111] Okuma N, Sato M 2021 Phys. Rev. Lett. 126 176601
Google Scholar
[112] Lee C H 2021 Phys. Rev. B 104 195102
[113] Zhang D W, Chen Y L, Zhang G Q, Lang L J, Li Z, Zhu S L 2020 Phys. Rev. B 101 235150
Google Scholar
[114] Mu S, Lee C H, Li L H, Gong J B 2020 Phys. Rev. B 102 081115
Google Scholar
[115] Yoshida T 2021 Phys. Rev. B 103 125145
Google Scholar
[116] Shen R Z, Lee C H 2021 arXiv: 2107.03414 [cond-mat]
[117] Guo C X, Wang X R, Wang C, Kou S P 2020 Phys. Rev. B 101 144439
Google Scholar
[118] Kawabata K, Shiozaki K, Ryu S 2021 Phys. Rev. Lett. 126 216405
Google Scholar
[119] Moustaj A, Eek L, Smith C M 2021 arXiv: 2107.14271 [cond-mat]
-
图 1 (a) 非厄米SSH模型示意图; (b) 开放边界条件下本征态的空间分布, 其中
$|\psi(x)|^2=|\psi_A(x)|^2+|\psi_B(x)|^2$ , 链长$L=40$ ; (c) 非厄米SSH 模型在周期边界条件(黑色虚线)和开放边界条件(蓝色实线)下的能谱; (d) 非厄米SSH 模型的广义布里渊区(蓝色实线), 虚线为布里渊区. 参数值:$t_1=2.5,\; t_2=1,\; \gamma=4/3$ [19]Fig. 1. (a) Sketch of non-Hermitian SSH model; (b) eigenstate profiles under open boundary condition,
$|\psi(x)|^2= $ $ |\psi_A(x)|^2+|\psi_B(x)|^2$ and$L=40$ ; (c) energy spectrum under periodic boundary condition (black dashed lines) and open boundary condition (blue solid lines); (d) generalized Brillouin zone (blue solid line) and Brillouin zone (black dashed line). Parameters:$t_1=2.5,\; t_2= $ $ 1, \gamma=4/3$ [19].
图 2 非厄米体系在开放边界条件下形成以指数衰减的方式局域在边界的“驻波”, 此驻波由
$\beta_1$ 波和$\beta_2$ 波叠加而成Fig. 2. An eigenstate wavefunction under open boundary condition, which is a superposition of the
$\beta_1$ wave and$\beta_2$ wave.
图 3 (a) 具有远程跃迁项
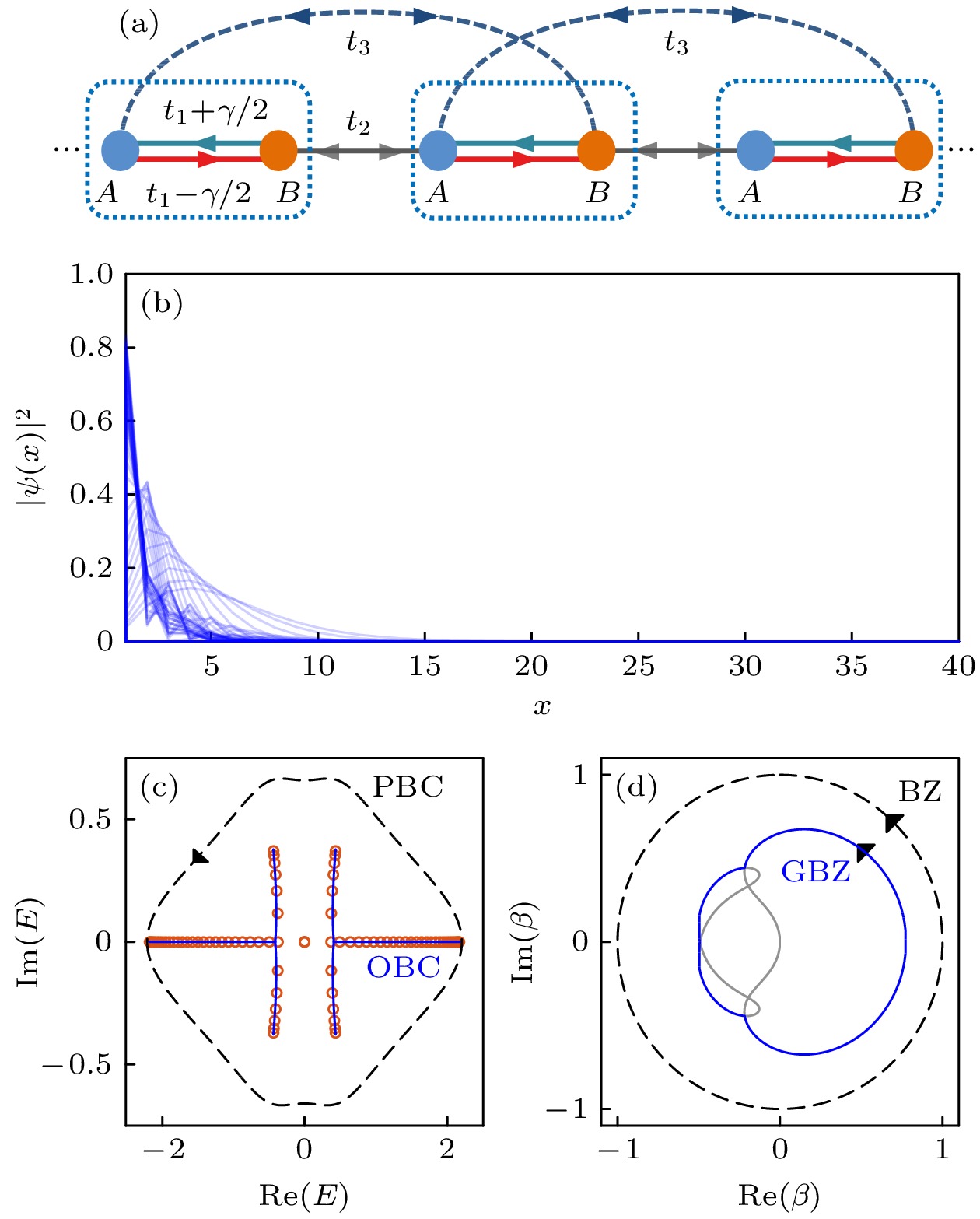
$t_3$ 的非厄米SSH模型示意图; (b) 开放边界条件下本征态的空间分布, 其中$|\psi(x)|^2= $ $ |\psi_A(x)|^2+|\psi_B(x)|^2$ ,$L=40$ ; (c) 周期边界条件(黑色虚线)和开放边界条件(蓝色实线, 通过广义布里渊区计算)下的能谱, 橙色圆点代表直接对角化实空间哈密顿量所得的$L=40$ 系统在开放边界条件下的能谱; (d) 广义布里渊区(蓝色实线)和辅助广义布里渊区(灰色实线), 参数取值:$t_1=1.1,\; t_2=1,\; t_3=0.2,\; \gamma=4/3$ [19]Fig. 3. (a) Sketch of non-Hermitian SSH model with
$t_3$ being the third nearest neighbor hopping term; (b) eigenstate profiles under open boundary condition with$|\psi(x)|^2= $ $ |\psi_A(x)|^2+|\psi_B(x)|^2$ and$L=40$ ; (c) energy spectrum under periodic boundary condition (black dashed lines) and open boundary condition (blue solid lines, calculated from the generalized Brillouin zone). Orange points are eigenenergies from directly diagonalizing the real-space Hamiltonian of an open chain with$L=40$ ; (d) generalized Brillouin zone (blue solid line) and auxiliary generalized Brillouin zone (gray solid line). Parameters:$t_1=1.1 , \;t_2=1, $ $ t_3=0.2, \;\gamma=4/3$ [19].
图 4 (a) 具有非对称次近邻跃迁的非厄米模型示意图; (b) 开放边界条件下系统本征态的空间分布, 其中链长
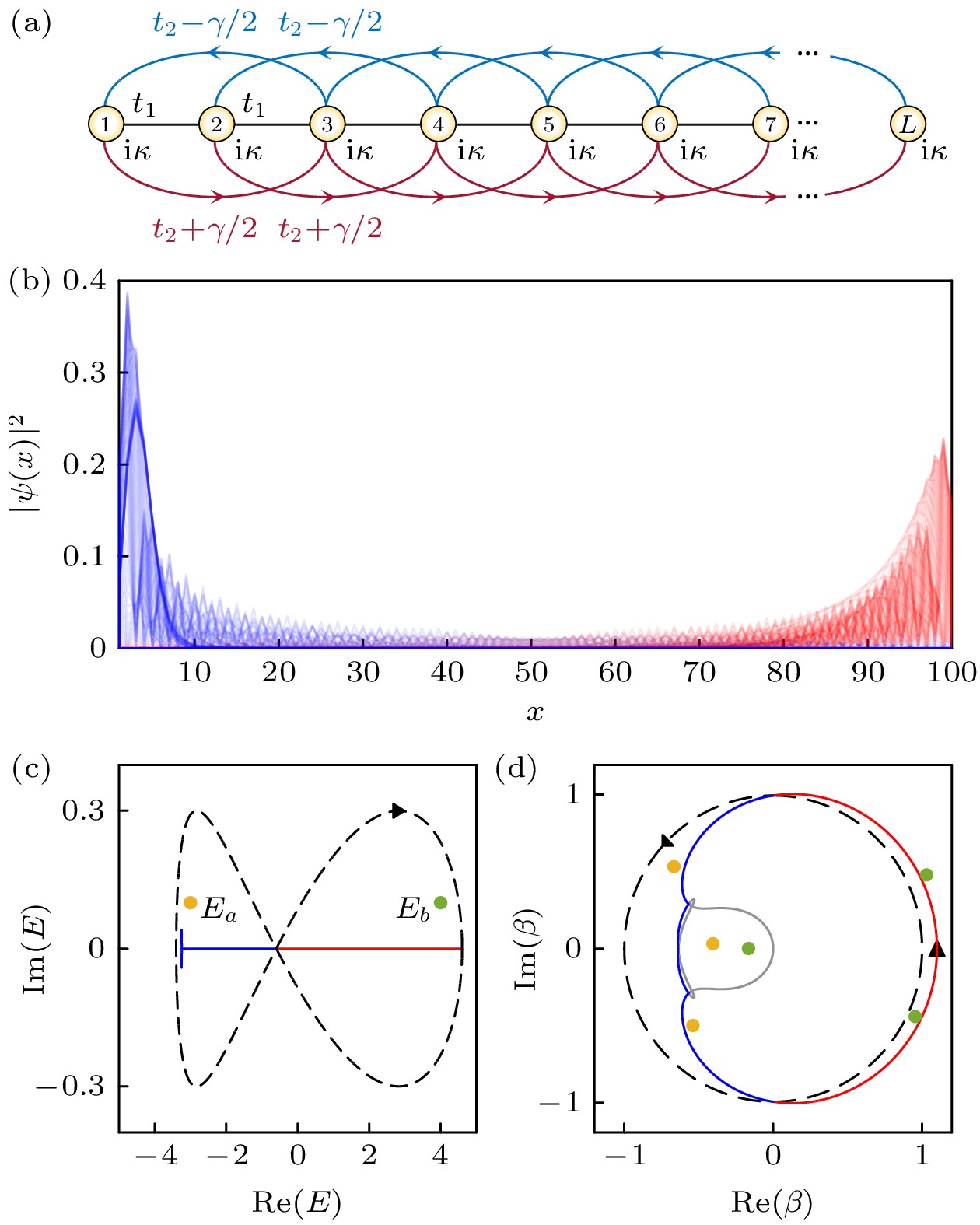
$L= $ $ 100$ , 蓝色表示波函数局域在左边, 红色表示波函数局域在右边; (c) 周期边界条件(虚线)和开放边界条件(实线)下的能谱,$E_a=-3+0.1 {\rm{i}}$ (黄点)和$E_b=4+0.1 {\rm{i}}$ (绿点)为两个能量参照点; (d) 广义布里渊区(红蓝实线), 辅助广义布里渊区$|\beta_1(E)|=|\beta_2(E)|$ (灰色实线), 和布里渊区(黑色虚线),$|\beta_3(E)|=|\beta_4(E)|$ 对应的辅助广义布里渊区在图示区域以外, 黄点和绿点分别为$E_a=h(\beta)$ 和$E_b=h(\beta)$ 的前3个零点$\beta_{1, 2, 3}$ . 参数取值:$t_1 = 2,\; t_2 = 0.3, \;\gamma= 0.3, $ $ \kappa=0$ [51,52]Fig. 4. (a) Sketch of a single-band non-Hermitian model with asymmetric next-nearest-neighbor hoppings; (b) eigenstate profiles under open boundary condition when
$L=100$ . Blue/red eigenstates are localized at the left/right side; (c) energy spectrum under periodic boundary condition (black dashed lines) and open boundary condition (red and blue solid lines),$E_a=-3+0.1 {\rm{i}}$ (yellow point) and$E_b=4+0.1{\rm{ i}}$ (green point) are two reference points; (d) generalized Brillouin zone (red and blue solid line), auxiliary generalized Brillouin zone$|\beta_1(E)|=|\beta_2(E)|$ (gray solid line), and Brillouin zone (black dashed line). Auxiliary generalized Brillouin zone$|\beta_3(E)|=|\beta_4(E)|$ is out of the plot. Yellow and green points are the zeros of$h(\beta)-E_a$ and$h(\beta)-E_b$ , respectively. Parameters:$t_1 = 2, \;t_2 = 0.3, $ $ \gamma= 0.3, \;\kappa=0$ [51,52].
图 5 (a) 非厄米SSH模型在开放边界条件下的能谱模长
$|E|$ 随着参数$t_1$ 的变化, 红色实线表示拓扑零模边界态, 链长$L=40$ ; (b) Non-Bloch拓扑不变量随着$t_1$ 的变化, 参数取值:$t_2=1,\; \gamma=4/3$ [19]Fig. 5. (a) Absolute values of open-boundary eigenenergies
$|E|$ for the non-Hermitian SSH model. Red solid line represents the topological edge zero modes. The chain length$L=40$ . (b) Non-Bloch topological invariant calculated from Eq.(42). Parameters:$t_2=1, \;\gamma=4/3$ [19].
图 6 (a) 方程(34)所描述的非厄米模型在开放边界条件下的非厄米格林函数
$|G_{L1}|$ 和$|G_{1 L}|$ , 实线是利用广义布里渊区计算的理论值; (b)$L=80$ 时的$|G_{40, j}|$ , 蓝线表示根据广义布里渊区公式计算的理论值. 参数取值:$t_1 = t_2 = 1, $ $ \gamma = 4/3, \;\kappa = -0.8, \;\omega = -1.7$ [51]Fig. 6. (a) Non-Hermitian Green’s functions
$|G_{L1}|$ and$|G_{1 L}|$ for the non-Hermitian model in Eq. (34) under open boundary condition. Solid lines are calculated from the generalized Brillouin zone. (b)$|G_{40, j}|$ for$L=80$ . The blue lines are the results from the generalized-Brillouin-zone-based formula. Parameters:$t_1 = t_2 = 1,\; \gamma = 4/3, \;\kappa = $ $ -0.8, \;\omega = -1.7$ [51].
图 7 (a) 布里渊区(蓝色虚线)和广义布里渊区(红色实线).
$\beta_{1, 2, 3}$ 是方程$h(\beta)=\omega$ 在$\kappa=-0.1, \;\omega=4$ 时的根($\beta_4$ 在展示范围之外).$\beta_2$ 位于广义布里渊区和布里渊区之间. (b)$|\beta_2 |$ 随着$\omega, \kappa$ 的变化. (c)$\alpha_\rightarrow$ 随着$\omega, \kappa$ 的变化. (d)$|\beta_2 |$ 和$\alpha_\rightarrow$ 沿着图(c)中虚线$\kappa=-0.1$ 的变化. (e) 和图(a)的区别是$\omega=-3$ , 此时$\beta_3$ 位于广义布里渊区和布里渊区之间. (f)$|\beta_3 |^{-1}$ . (g)$\alpha_\leftarrow$ . (h)$|\beta_3 |^{-1}$ 和$\alpha_\leftarrow$ 沿着图(g)中虚线$\kappa=-0.1$ 的变化. 参数取值:$ t_1 = 2, \;t_2 = 0.3,\; \gamma= 0.3$ [51]Fig. 7. (a) Brillouin zone (blue dashed line) and generalized Brillouin zone (red solid line).
$\beta_{1, 2, 3}$ are the roots of$h(\beta)=\omega$ with$\kappa=-0.1, \;\omega=4$ ($\beta_4$ is out of this plot).$\beta_2$ lies between the Brillouin zone and generalized Brillouin zone. (b)$|\beta_2 |$ as a function of$\omega, \;\kappa$ . (c) Numerical$\alpha_\rightarrow$ as a function of$\omega, \;\kappa$ . (d)$|\beta_2 |$ and$\alpha_\rightarrow$ along the dashed cut$\kappa=-0.1$ in panel (c). (e) The same as panel (a) except that$\omega=-3$ .$\beta_3$ lies between the Brillouin zone and generalized Brillouin zone. (f)$|\beta_3 |^{-1}$ . (g)$\alpha_\leftarrow$ . (h)$|\beta_3 |^{-1}$ and$\alpha_\leftarrow$ along the dashed cut$\kappa=-0.1$ in panel (g). Parameters:$ t_1 = 2,\; t_2 = 0.3,\; \gamma= 0.3$ [51].
图 8 (a) 周期边界条件(黑色虚线)和开放边界条件(红色实线)下的能谱, 蓝点代表鞍点
$\dfrac{\partial E(\beta)}{\partial \beta}=0$ ; (b) 波包初始位置波函数振幅$|\psi(x_0, t)|$ 随时间的演化. 参数取值:$t_1= 1, $ $ t_2=1,\; \gamma=1.5,\; \kappa=-1.2$ Fig. 8. (a) Energy spectrums under periodic boundary condition (black dashed line) and open boundary condition (red solid line). Blue points are the saddle points satisfying
$\dfrac{\partial E(\beta)}{\partial \beta}=0$ . (b) Time evolution of wavefunction amplitude$|\psi(x_0, t)|$ at the initial location$x_0$ . Parameters:$t_1=1, $ $ t_2=1, \;\gamma=1.5, \;\kappa=-1.2$ .
图 9 开放量子系统中的Liouvillian能隙与手征衰减 (a) 具有耗散的开放SSH模型. (b) 衰减矩阵
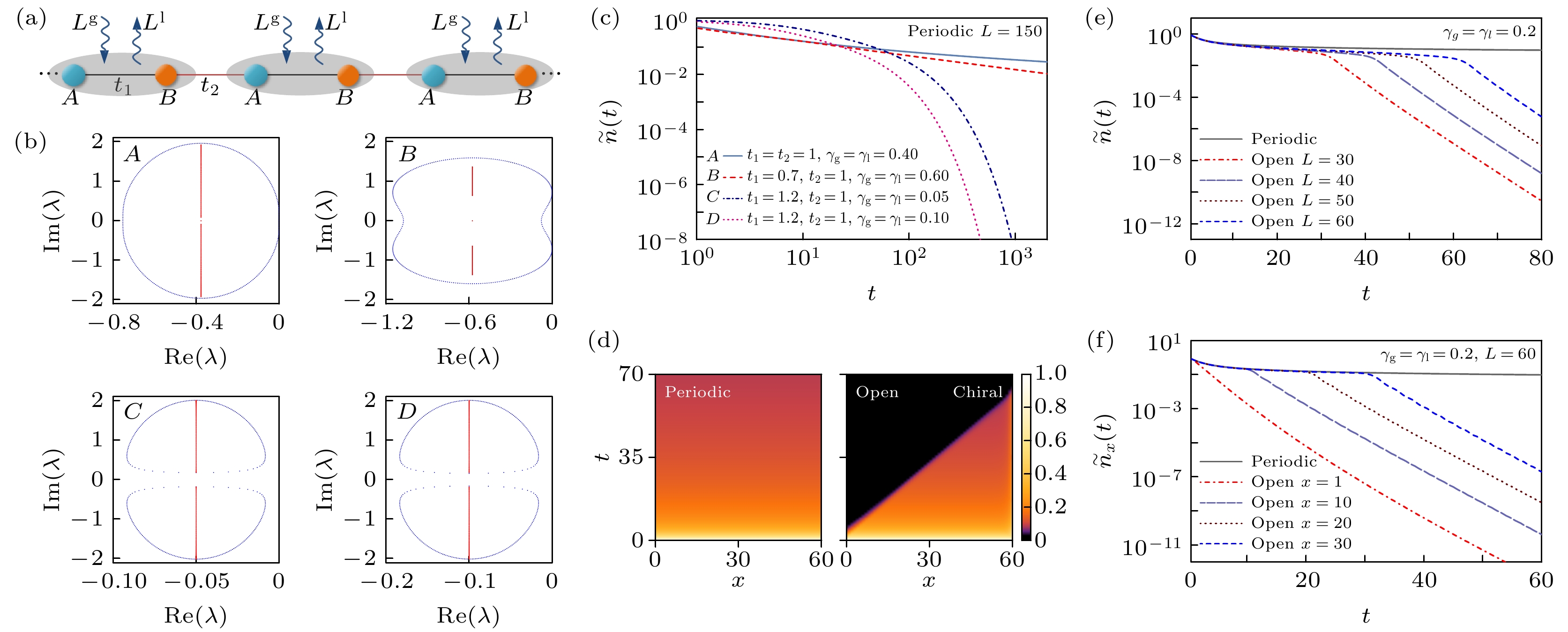
$ {{X}} $ 的本征值. 蓝色代表周期边界条件, 红色代表开放边界条件. A和B ($t_1\leqslant t_2$ )在周期边界条件下的Liouvillian能隙为零而C和D ($t_1> t_2$ )非零. A, B, C, D4种情况在开放边界条件下的Liouvillian能隙均不为零. 4种情况的参数取值见图(c). (c) 平均粒子数偏离值$\tilde n(t)$ 在周期边界条件下的演化. A和B表现为缓慢的代数衰减, 而C和D为指数衰减. (d) 每个格点上的费米子数偏离$\tilde n_x(t)$ 在周期边界条件(左)和开放边界条件(右)下的演化. (e) 不同长度系统中平均费米子数偏离$\tilde n(t)$ 在周期边界条件(实线)和开放边界条件(虚线)下的演化. (f) 费米子数偏离$\tilde n_x(t)$ 在开放边界条件(虚线)下的演化. (d)—(f)的参数为$t_1=t_2=1,\; \gamma_g=\gamma_l=0.2$ . (c)—(f) 中所有演化过程的初态均为全占据态$\prod_{x, s}\hat{c}_{x, s}^\dagger \left| 0 \right\rangle$ [74]Fig. 9. Liouvillian gap and chiral damping in an open quantum system with non-Hermitian skin effect: (a) Sketch of the SSH Hamiltonian
$ {{H}} $ with additional single-particle gain and loss. (b) Eigenenergies of damping matrix$ {{X}} $ . Blue: periodic boundary condition. Red: open boundary condition. The Liouvillian gap under periodic boundary condition is zero for A and B ($t_1\leqslant t_2$ ), while it is nonzero for C and D ($t_1>t_2$ ). Parameter values are shown in panel (c). (c) Time evolution of the fermion number deviation from the steady-state value,$\tilde n(t)$ , of a periodic-boundary chain. The damping is algebraic for A, B and exponential for C, D. (d) Time evolution of site-resolved fermion number deviation from the steady-state values,$\tilde n_x(t)$ , for the periodic boundary condition (left) and open boundary condition (right). (e) Time evolution of$\tilde n(t)$ under periodic boundary conditions (solid curve) and open boundary conditions (dashed curves) for different chain length$L$ . (f) Time evolution of$\tilde n_x(t)$ for an open-boundary chain at different$x$ . Parameters in (d)–(f):$t_1=t_2=1, \;\gamma_g=\gamma_l=0.2$ . The initial state in (c)–(f) is$\prod_{x, s}\hat{c}_{x, s}^\dagger \left| 0 \right\rangle$ [74].
图 10 一维量子行走系统的准能谱虚部
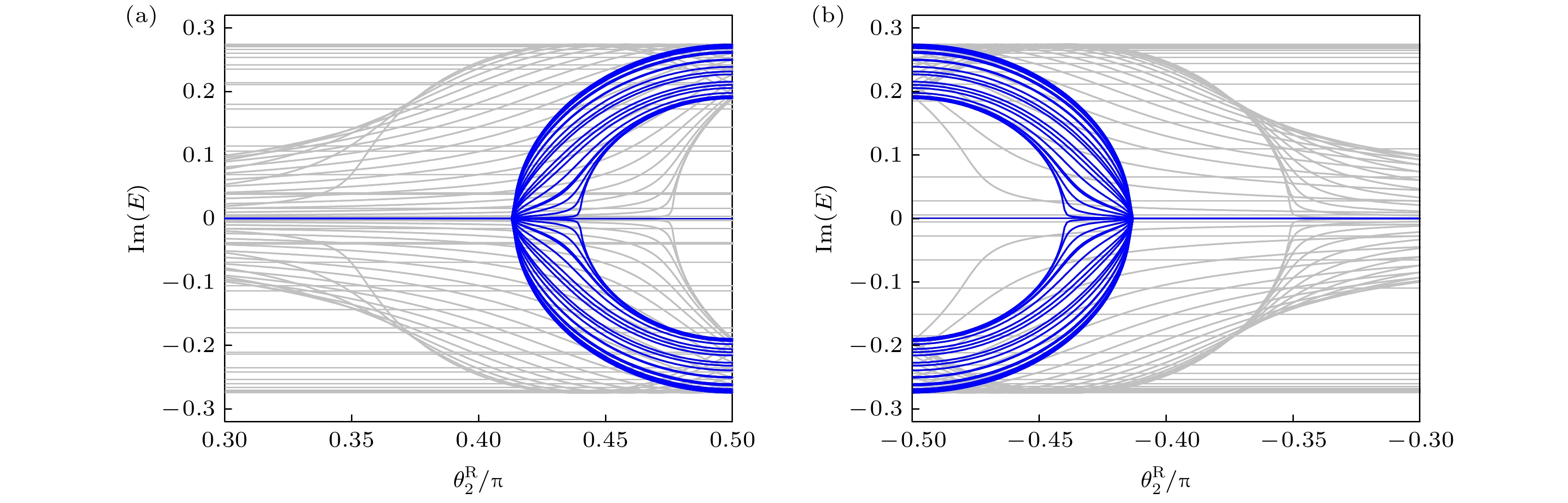
$\operatorname{Im}(E)$ 随着$\theta^{{\rm{R}}}_2$ 的变化. 其他参数为$\theta^{\rm{R}}_1=0.5625\pi,\; \theta^{\rm{L}}_1=-0.0625\pi,\; \gamma=0.2746$ (a)$\theta^{\rm{L}}_2= $ $ 0.75\pi$ ; (b)$\theta^{\rm{L}}_2=-0.9735\pi$ . 蓝色实线和灰色实线分别代表开放边界条件下的非布洛赫能谱和周期边界条件下的布洛赫能谱[85]Fig. 10. Imaginary part of quasienergies
$\operatorname{Im}(E)$ versus$\theta^{{\rm{R}}}_2$ for the experimentally realized one-dimensional quantum walk. Parameter values:$\theta^{\rm{R}}_1=0.5625\pi,\; \theta^{\rm{L}}_1=-0.0625\pi, \;\gamma=0.2746$ : (a)$\theta^{\rm{L}}_2=0.75\pi$ ; (b)$\theta^{\rm{L}}_2=-0.9735\pi$ . Blue and gray lines represent quasi-energies under open boundary condition and periodic boundary condition, respectively[85].
图 11 不同系统在开放边界条件下复数能量数目占比
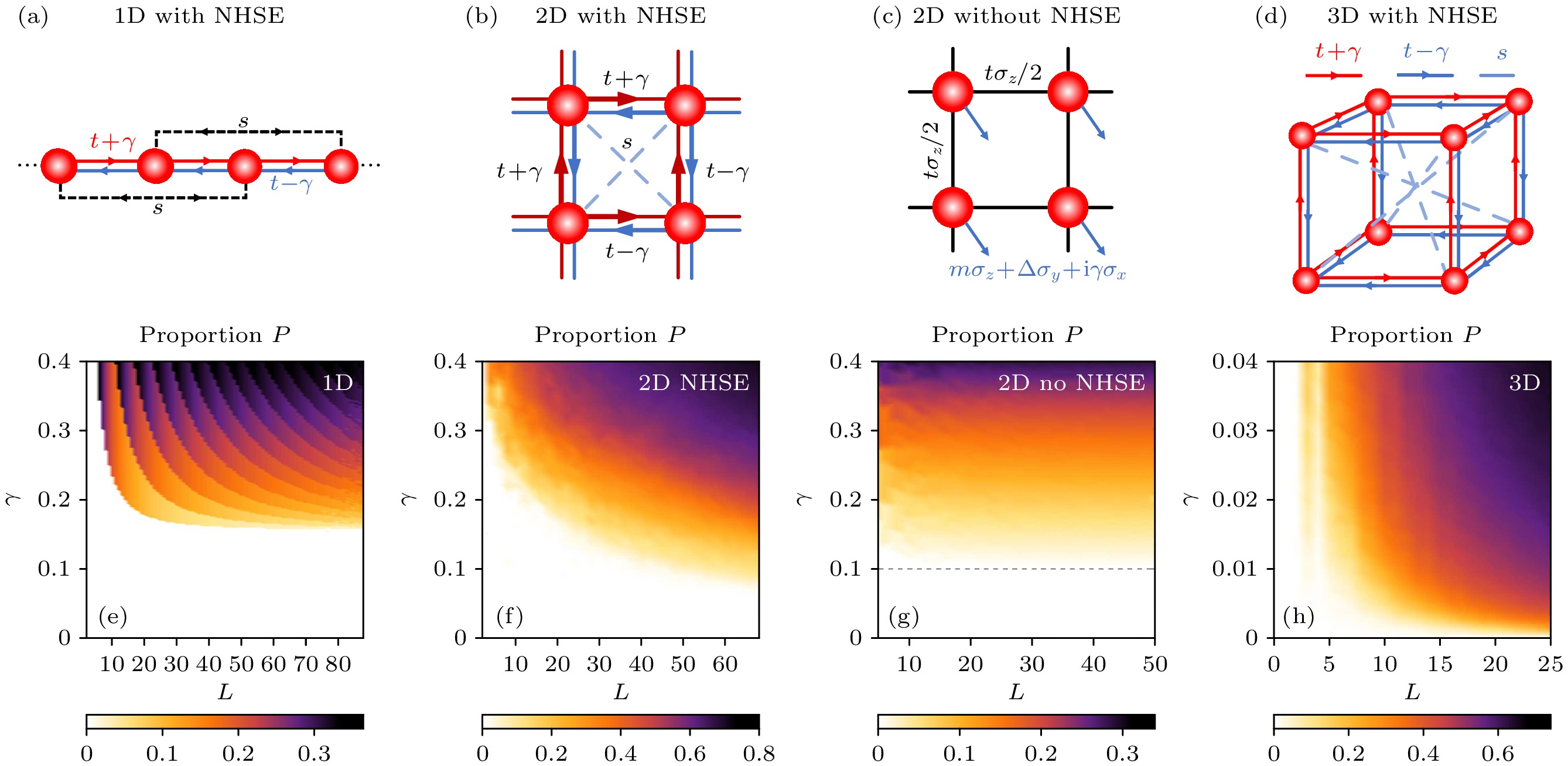
$P$ (a), (e) 长度为$L$ 的链上的$ {{H}}_{1 {\rm{D}}} $ , 其中$t=1,\; s=0.15$ ; (b), (f)$L\times L$ 的正方形上的$ {{H}}_{2 {\rm{D}}}^{\text{skin}} $ , 其中$t=1,\; s=0.3$ ; (c), (g)$L\times L$ 的正方形上的$ {{H}}_{2 {\rm{D}}}^{\text{no skin}} $ , 其中$m=0.5, \;t=0.2, \;\varDelta=0$ ; (d), (h)$L\times L\times L$ 的正方体上的$ {{H}}_{3 {\rm{D}}} $ , 其中$t=1,\; s=0.5$ . (d)中边界格点上有随机势$V=\displaystyle \sum\nolimits_{\boldsymbol{r}\in\text{Boundary}}w(\boldsymbol{r}) \left| {\boldsymbol{r}} \right\rangle \left\langle {\boldsymbol{r}} \right|$ , 其中$w(\boldsymbol{r})$ 在$[-W/2, W/2]$ 中均匀分布且$W=0.7$ . 能量虚部的绝对值$|\operatorname{Im}(E)|>10^{-10}$ 即被视为复数能量[86]Fig. 11. Complex eigenenergies proportion
$P$ for four different systems under open boundary condition: (a), (e)$ {{H}}_{1 {\rm{D}}} $ on a length-$L$ chain with$t=1,\; s=0.15$ ; (b), (f)$ {{H}}_{2 {\rm{D}}}^{\text{skin}} $ on$L\times L$ squares with$t=1,\; s=0.3$ ; (c), (g)$ {{H}}_{2 {\rm{D}}}^{\text{no skin}} $ on$L\times L$ squares with$m=0.5, \;t=0.2,\; \varDelta=0$ ; (d), (h)$ {{H}}_{3 {\rm{D}}} $ on$L\times L\times L$ cubes with$t=1,\; s=0.5$ . For (d), there is an on-site random potential$V=\displaystyle \sum\nolimits_{\mathbf{r}\in\text{Boundary}}w(\boldsymbol{r}) \left| {\boldsymbol{r}} \right\rangle \left\langle {\boldsymbol{r}} \right|$ on boundary sites where$w(\boldsymbol{r})$ is uniformly distributed in$[-W/2, W/2]$ with$W=0.7$ . Numerically, a complex energy holds a nonzero imaginary part if$|\operatorname{Im}(E)|>10^{-10}$ [86]. -
[1] Breuer H P, Petruccione F 2006 The Theory of Open Quantum Systems (Oxford: Oxford University Press)
[2] Lindblad G 1976 Commun. Math. Phys. 48 119
Google Scholar
[3] Gorini V, Kossakowski A, Sudarshan E C G 1976 J. Math. Phys. 17 821
Google Scholar
[4] Daley A J 2014 Adv. Phys. 63 77
Google Scholar
[5] Kozii V, Fu L 2017 arXiv: 1708.05841 [cond-mat]
[6] Shen H T, Fu L 2018 Phys. Rev. Lett. 121 026403
Google Scholar
[7] Nagai Y, Qi Y, Isobe H, Kozii V, Fu L 2020 Phys. Rev. Lett. 125 227204
Google Scholar
[8] Papaj M, Isobe H, Fu L 2019 Phys. Rev. B 99 201107
Google Scholar
[9] Bandres M A, Wittek S, Harari G, et al. 2018 Science 359 eaar4005
Google Scholar
[10] Harari G, Bandres M A, Lumer Y, et al. 2018 Science 359 eaar4003
Google Scholar
[11] Zhou H Y, Peng C, Yoon Y, et al. 2018 Science 359 1009
Google Scholar
[12] Ashida Y, Gong Z P, Ueda M 2020 Adv. Phys. 69 249
Google Scholar
[13] Bergholtz E J, Budich J C, Kunst F K 2021 Rev. Mod. Phys. 93 015005
Google Scholar
[14] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[15] Qi X L, Zhang S C 2011 Rev. Mod.Phys. 83 1057
Google Scholar
[16] Chiu C K, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys. 88 035005
Google Scholar
[17] Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004
Google Scholar
[18] Ozawa T, Price H M, Amo A, et al. 2019 Rev. Mod. Phys. 91 015006
Google Scholar
[19] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[20] Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802
Google Scholar
[21] Kunst F K, Edvardsson E, Budich J C, Bergholtz E J 2018 Phys. Rev. Lett. 121 026808
Google Scholar
[22] Lee C H, Thomale R 2019 Phys. Rev. B 99 201103
Google Scholar
[23] Helbig T, Hofmann T, Imhof S, et al. 2020 Nat. Phys. 16 747
Google Scholar
[24] Xiao L, Deng T S, Wang K K, Zhu G Y, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761
Google Scholar
[25] Weidemann S, Kremer M, Helbig T, Hofmann T, Stegmaier A, Greiter M, Thomale R, Szameit A 2020 Science 368 311
Google Scholar
[26] Yokomizo K, Murakami S 2019 Phys. Rev. Lett. 123 066404
Google Scholar
[27] Su W P, Schrieffer J R, Heeger A J 1980 Phys. Rev. B 22 2099
Google Scholar
[28] Wang K K, Li T Y, Xiao L, Han Y W, Yi W, Xue P 2021 arXiv: 2107.14741 [cond-mat]
[29] Ghatak A, Brandenbourger M, van Wezel J, Coulais C 2020 Proc. Natl. Acad. Sci. 117 29561
Google Scholar
[30] Gou W, Chen T, Xie D Z, Xiao T, Deng T S, Gadway B, Yi W, Yan B 2020 Phys. Rev. Lett. 124 070402
Google Scholar
[31] Li L H, Lee C H, Gong J B 2020 Phys. Rev. Lett. 124 250402
Google Scholar
[32] Yoshida T, Mizoguchi T, Hatsugai Y 2020 Phys. Rev. Res. 2 022062
Google Scholar
[33] Scheibner C, Irvine W T M, Vitelli V 2020 Phys. Rev. Lett. 125 118001
Google Scholar
[34] Mandal S, Banerjee R, Ostrovskaya E A, Liew T C H 2020 Phys. Rev. Lett. 125 123902
Google Scholar
[35] Gao P L, Willatzen M, Christensen J 2020 Phys. Rev. Lett. 125 206402
Google Scholar
[36] Zhu X Y, Wang H Q, Gupta S K, Zhang H J, Xie B Y, Lu M H, Chen Y F 2020 Phys. Rev. Res. 2 013280
Google Scholar
[37] Hofmann T, Helbig T, Schindler F, S et al. 2020 Phys. Rev. Res. 2 023265
Google Scholar
[38] Brandenbourger M, Locsin X, Lerner E, Coulais C 2019 Nat. Commun. 10 4608
Google Scholar
[39] Rosa M I N, Ruzzene M 2020 New J. Phys. 22 053004
Google Scholar
[40] Mandal S, Banerjee R, Liew T C H 2021 arXiv: 2103.05480 [cond-mat]
[41] Zhong J, Wang K, Park Y, Asadchy V, Wojcik C C, Dutt A, Fan S H 2021 Phys. Rev. B 104 125416
Google Scholar
[42] Chen Y Y, Li X P, Scheibner C, Vitelli V, Huang G L 2021 Nat. Commun. 12 5935
Google Scholar
[43] Zhang L, Yang Y H, Ge Y, et al. 2021 Nat. Commun. 12 6297
[44] Deng T S, Yi W 2019 Phys. Rev. B 100 035102
Google Scholar
[45] Yang Z S, Zhang K, Fang C, Hu J P 2020 Phys. Rev. Lett. 125 226402
Google Scholar
[46] Li L H, Lee C H, Mu S, Gong J B 2020 Nat. Commun. 11 5491
Google Scholar
[47] Yokomizo K, Murakami S 2021 Phys. Rev. B 104 165117
Google Scholar
[48] Rafi-Ul-Islam S M, Siu Z B, Sahin H, Lee C H, Jalil M B A 2021 arXiv: 2108.02457 [cond-mat]
[49] Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570
Google Scholar
[50] Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651
Google Scholar
[51] Xue W T, Li M R, Hu Y M, Wang Z 2021 Phys. Rev. B 103 L241408
Google Scholar
[52] Zhang K, Yang Z S, Fang C 2020 Phys. Rev. Lett. 125 126402
Google Scholar
[53] Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 246801
Google Scholar
[54] Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801
Google Scholar
[55] Gong Z P, Ashida Y, Kawabata K, Takasan K, Higashikawa S, Ueda M 2018 Phys. Rev. X 8 031079
Google Scholar
[56] Shen H T, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402
Google Scholar
[57] Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015
Google Scholar
[58] Li L H, Mu S, Lee C H, Gong J B 2021 Nat. Commun. 12 5294
Google Scholar
[59] Zhang K, Yang Z S, Fang C 2021 arXiv: 2102.05059 [cond-mat]
[60] Kawabata K, Sato M, Shiozaki K 2020 Phys. Rev. B 102 205118
Google Scholar
[61] Zhang X J, Tian Y, Jiang J H, Lu M H, Chen Y F 2021 Nat. Commun. 12 5377
Google Scholar
[62] Fu Y X, Hu J H, Wan S L 2021 Phys. Rev. B 103 045420
Google Scholar
[63] Edvardsson E, Kunst F K, Bergholtz E J 2019 Phys. Rev. B 99 081302
Google Scholar
[64] Wang H Q, Ruan J W, Zhang H J 2019 Phys. Rev. B 99 075130
Google Scholar
[65] Zhang X Z, Gong J B 2020 Phys. Rev. B 101 045415
Google Scholar
[66] Okugawa R, Takahashi R, Yokomizo K 2020 Phys. Rev. B 102 241202
Google Scholar
[67] Lee C H, Li L H, Gong J B 2019 Phys. Rev. Lett. 123 016805
Google Scholar
[68] Zou D Y, Chen T, He W J, Bao J C, Lee C H, Sun H J, Zhang X D 2021 arXiv: 2104.11260 [cond-mat]
[69] Longhi S 2019 Phys. Rev. Res. 1 023013
Google Scholar
[70] Mao L, Deng T S, Zhang P F 2021 Phys. Rev. B 104 125435
Google Scholar
[71] Longhi S 2020 Phys. Rev. Lett. 124 066602
Google Scholar
[72] Longhi S 2020 Phys. Rev. B 102 201103
Google Scholar
[73] Li T Y, Sun J Z, Zhang Y S, Yi W 2021 Phys. Rev. Res. 3 023022
Google Scholar
[74] Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 170401
Google Scholar
[75] Haga T, Nakagawa M, Hamazaki R, Ueda M 2021 Phys. Rev. Lett. 127 070402
Google Scholar
[76] Liu C H, Zhang K, Yang Z S, Chen S 2020 Phys. Rev. Res. 2 043167
Google Scholar
[77] McDonald A, Clerk A A 2020 Nat. Commun. 11 5382
Google Scholar
[78] McDonald A, Hanai R, Clerk A A 2021 arXiv: 2103.01941 [cond-mat]
[79] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[80] Bender C M 2007 Rep. Prog. Phys. 70 947
Google Scholar
[81] El-Ganainy R, Makris K G, Khajavikhan M, Musslimani Z H, Rotter S, Christodoulides D N 2018 Nat. Phys. 14 11
Google Scholar
[82] Özdemir S K, Rotter S, Nori F, Yang L 2019 Nat. Mater. 18 783
Google Scholar
[83] Miri M A, Alù A 2019 Science 363 eaar7709
Google Scholar
[84] Longhi S 2019 Opt. Lett. 44 5804
Google Scholar
[85] Xiao L, Deng T S, Wang K K, Wang Z, Yi W, Xue P 2021 Phys. Rev. Lett. 126 230402
Google Scholar
[86] Song F, Wang H Y, Wang Z 2021 arXiv: 2102.02230 [cond-mat]
[87] Kawabata K, Okuma N, Sato M 2020 Phys. Rev. B 101 195147
Google Scholar
[88] Li L H, Lee C H, Gong J B 2019 Phys. Rev. B 100 075403
Google Scholar
[89] Liu C H, Jiang H, Chen S 2019 Phys. Rev. B 99 125103
Google Scholar
[90] Yi Y F, Yang Z S 2020 Phys. Rev. Lett. 125 186802
Google Scholar
[91] Yang Z S 2020 arXiv: 2012.03333 [cond-mat]
[92] Yokomizo K, Murakami S 2021 Phys. Rev. B 103 165123
Google Scholar
[93] Jin L, Song Z 2019 Phys. Rev. B 99 081103
Google Scholar
[94] Xu X R, Xu H W, Mandal S, Banerjee R, Ghosh S, Liew T C H 2021 Phys. Rev. B 103 235306
Google Scholar
[95] Okugawa R, Takahashi R, Yokomizo K 2021 Phys. Rev. B 103 205205
Google Scholar
[96] Shiozaki K, Ono S 2021 Phys. Rev. B 104 035424
Google Scholar
[97] Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 054301
Google Scholar
[98] Longhi S 2019 Phys. Rev. B 100 125157
Google Scholar
[99] Zeng Q B, Yang Y B, Xu Y 2020 Phys. Rev. B 101 020201
Google Scholar
[100] Zeng Q B, Xu Y 2020 Phys. Rev. Res. 2 033052
Google Scholar
[101] Kim K M, Park M J 2021 Phys. Rev. B 104 L121101
Google Scholar
[102] Liu Y X, Wang Y C, Liu X J, Zhou Q, Chen S 2021 Phys. Rev. B 103 014203
Google Scholar
[103] Longhi S 2021 Phys. Rev. B 103 144202
Google Scholar
[104] Longhi S 2021 Phys. Rev. B 103 224206
Google Scholar
[105] Liu Q, Li T Y, Xiao L, Wang K K, Yi W, Xue P 2021 arXiv: 2108.01097 [cond-mat]
[106] Claes J, Hughes T L 2021 Phys. Rev. B 103 L140201
Google Scholar
[107] Sun X Q, Zhu P H, Hughes T L 2021 Phys. Rev. Lett. 127 066401
Google Scholar
[108] Panigrahi A, Moessner R, Roy B 2021 arXiv: 2105.05244 [cond-mat]
[109] Schindler F, Prem A 2021 Phys. Rev. B 104 L161106
Google Scholar
[110] Bhargava B A, Fulga I C, van den Brink J, Moghaddam A G 2021 arXiv: 2106.04567 [cond-mat]
[111] Okuma N, Sato M 2021 Phys. Rev. Lett. 126 176601
Google Scholar
[112] Lee C H 2021 Phys. Rev. B 104 195102
[113] Zhang D W, Chen Y L, Zhang G Q, Lang L J, Li Z, Zhu S L 2020 Phys. Rev. B 101 235150
Google Scholar
[114] Mu S, Lee C H, Li L H, Gong J B 2020 Phys. Rev. B 102 081115
Google Scholar
[115] Yoshida T 2021 Phys. Rev. B 103 125145
Google Scholar
[116] Shen R Z, Lee C H 2021 arXiv: 2107.03414 [cond-mat]
[117] Guo C X, Wang X R, Wang C, Kou S P 2020 Phys. Rev. B 101 144439
Google Scholar
[118] Kawabata K, Shiozaki K, Ryu S 2021 Phys. Rev. Lett. 126 216405
Google Scholar
[119] Moustaj A, Eek L, Smith C M 2021 arXiv: 2107.14271 [cond-mat]
下载:
计量
- 文章访问数: 22272
- PDF下载量: 2141
- 被引次数: 0
