-
开放量子系统在一定程度上可由等效的非厄米哈密顿量来描述, 因此探究非厄米系统的耗散作用有许多重要的现实意义. 本文研究了开边界条件下一维非厄米系统中与耗散强度相关的动力学规律, 发现耗散可诱导边缘爆发重新出现. 粒子在开边界条件下的一维非厄米耗散晶格系统中进行含时演化后, 系统存在边缘爆发即在边缘处有较大的粒子损失概率, 而增大胞内跃迁强度后边缘爆发消失, 研究发现若增大或者减小耗散强度, 边缘爆发会重新出现. 这种重现的与原先的边缘爆发有所不同, 主要表现为粒子的损失概率分布由边缘分布趋向于体分布, 这是由于两种情况下粒子运动方向的概率不同; 更深层的原因与非厄米系统远离宇称-时间对称破缺点有关. 另外还研究了杂质势垒对非厄米动力学中粒子损失概率分布的影响, 结果表明在无耗散的A格点上放置很小的势垒就能明显地阻碍粒子运动, 并且当势垒增大到一定高度后, 其对粒子运动的影响趋于不变.In quantum mechanics, the Hermitian Hamiltonian is generally used to describe the ideal closed quantum system, but in reality, the physical system is closely related to the environment, and the open quantum system coupled to the environment can be described by the equivalent non-Hermitian Hamiltonian to a certain extent. Among them, the dissipation intensity is closely related to the dynamic properties of non-Hermitian quantum systems. Therefore, it is of great practical significance to study how dissipation affects particle loss. In this paper, the dynamic law related to dissipation intensity in a one-dimensional non-Hermitian system under open boundary condition is studied, and it is found that dissipation can induce the recurrence of edge burst. After the time-dependent evolution of the particles in the one-dimensional non-Hermitian dissipative lattice system with open boundary condition, there is an edge burst in the system, that is, there is a large probability of particle loss at the edge, and the edge burst disappears after increasing the intracell hopping. It is found that if the dissipation intensity increases or decreases, the edge burst will reappear. This kind of reappearance is different from the original edge burst, which is mainly manifested in the loss probability distribution of particles from the edge distribution to the bulk distribution, which is due to the difference in probability of particle motion direction between the two cases. Under the re-induced edge burst, the particles move leftward and rightward from their initial positions, and rebound from the left after having reached the boundary, forming a more obvious loss probability at the edge and gradually decreasing to the body area. In the original edge burst, the particles only move to the left with a greater probability, and are ‘trapped’ at the edge to completely dissipated, forming a distribution with an independent loss peak at the edge. The movement to the left is due to the non-Hermitian skin effect. The deeper reason for different movement directions is related to parity-time symmetry. Under the parameter near the parity-time symmetry breaking point, the loss probability of the particle is of unilateral distribution, and the loss probability of the particle moving to both sides is of bilateral distribution when it is far away. This is the description of the dissipation-induced edge burst recurrence phenomenon and its characteristics. In addition, this paper also studies the influence of impurity barrier on the probability distribution of particle loss in non-Hermitian dynamics. The results show that placing a small barrier on the non-dissipative A-site can obviously hinder the particle motion, and when the barrier increases to a certain height, its influence on the particle motion tends to be unchanged. And the barrier at the dissipative B lattice has little effect on the dynamics.
-
Keywords:
- one-dimensional non-Hermitian system /
- dissipations /
- barriers /
- edge burst
[1] Feng L, Ganainy R E, Ge L 2017 Nat. Photonics 11 752
Google Scholar
[2] Feng L, Xu Y L, Fegadolli W S, Lu M H, Oliveira J E B, Almeida V R, Chen Y F, Scherer A 2013 Nat. Mater. 12 108
Google Scholar
[3] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006
Google Scholar
[4] Verstraete F, Wolf M M, Ignacio Cirac J 2009 Nat. Phys. 5 633
Google Scholar
[5] Carmichael H J 1993 Phys. Rev. Lett. 70 2273
Google Scholar
[6] Diehl S, Micheli A, Kantian A, Kraus B, Büchler H P, Zoller P 2008 Nat. Phys. 4 878
Google Scholar
[7] Shen H, Fu L 2018 Phys. Rev. Lett. 121 026403
Google Scholar
[8] Nagai Y, Qi Y, Isobe H, Kozii V, Fu L 2020 Phys. Rev. Lett. 125 227204
Google Scholar
[9] Papaj M, Isobe H, Fu L 2019 Phys. Rev. B 99 201107
Google Scholar
[10] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[11] Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802
Google Scholar
[12] Lee C H, Thomale R 2019 Phys. Rev. B 99 201103
Google Scholar
[13] Longhi S 2022 Phys. Rev. Lett. 128 157601
Google Scholar
[14] Zhang X, Tian Y, Jiang J H, Lu M H, Chen Y F 2021 Nat. Commun. 12 5377
Google Scholar
[15] 胡渝民, 宋飞, 汪忠 2021 70 230307
Google Scholar
Hu Y M, Song F, Wang Z 2021 Acta Phys. Sin. 70 230307
Google Scholar
[16] 侯博, 曾琦波 2022 71 130302
Google Scholar
Hou B, Zeng Q B 2022 Acta Phys. Sin. 71 130302
Google Scholar
[17] 孙思彤, 丁应星, 刘伍明 2022 71 130701
Google Scholar
Sun S T, Ding Y X, Liu W M 2022 Acta Phys. Sin. 71 130701
Google Scholar
[18] 高洁, 杭超 2022 71 133202
Google Scholar
Gao J, Hang C 2022 Acta Phys. Sin. 71 133202
Google Scholar
[19] 潘磊 2022 71 170305
Google Scholar
Pan L 2022 Acta Phys. Sin. 71 170305
Google Scholar
[20] 邓天舒 2022 71 170306
Google Scholar
Deng T S 2022 Acta Phys. Sin. 71 170306
Google Scholar
[21] 陈舒越, 蒋闯, 柯少林, 王兵, 陆培祥 2022 71 174201
Google Scholar
Chen S Y, Jiang C, Ke S L, Wang B, Lu P X 2022 Acta Phys. Sin. 71 174201
Google Scholar
[22] Lee T E 2016 Phys. Rev. Lett. 116 133903
Google Scholar
[23] Mao L, Deng T, Zhang P 2021 Phys. Rev. B 104 125435
Google Scholar
[24] 王利, 贾丽芳, 张云波 2022 71 130501
Google Scholar
Wang L, Jia L F, Zhang Y B 2022 Acta Phys. Sin. 71 130501
Google Scholar
[25] Rudner M S, Levitov L S 2009 Phys. Rev. Lett. 102 065703
Google Scholar
[26] Karski M, Förster L, Choi J M, Steffen A, Alt W, Meschede D, Widera A 2009 Science 325 174
Google Scholar
[27] Broome M A, Fedrizzi A, Lanyon B P, Kassal I, Aspuru-Guzik A, White A G 2010 Phys. Rev. Lett. 104 153602
Google Scholar
[28] Ramasesh V V, Flurin E, Rudner M, Siddiqi I, Yao N Y 2017 Phys. Rev. Lett. 118 130501
Google Scholar
[29] Yan Z, Zhang Y R, Gong M, Wu Y, Zheng Y, Li S, Wang C, Liang F, Lin J, Xu Y, Guo C, Sun L, Peng C Z, Xia K, Deng H, Rong H, You J Q, Nori F, Fan H, Zhu X, Pan J W 2019 Science 364 753
Google Scholar
[30] Xue P, Zhang R, Qin H, Zhan X, Bian Z H, Li J, Sanders B C 2015 Phys. Rev. Lett. 114 140502
Google Scholar
[31] Du J, Li H, Xu X, Shi M, Wu J, Zhou X, Han R 2003 Phys. Rev. A 67 042316
Google Scholar
[32] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2012 Phys. Rev. Lett. 108 010502
Google Scholar
[33] Wang L, Liu Q, Zhang Y B 2021 Chin. Phys. B 30 020506
Google Scholar
[34] Xue W T, Hu Y M, Song F, Wang Z 2022 Phys. Rev. Lett. 128 120401
Google Scholar
[35] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
Google Scholar
[36] Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801
Google Scholar
[37] Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402
Google Scholar
[38] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[39] 唐原江, 梁超, 刘永椿 2022 71 171101
Google Scholar
Tang Y T, Liang C, Liu Y C 2022 Acta Phys. Sin. 71 171101
Google Scholar
[40] 曲登科, 范毅, 薛鹏 2022 71 130301
Google Scholar
Qu D K, Fan Y, Xue P 2022 Acta Phys. Sin. 71 130301
Google Scholar
[41] 施婷婷, 张露丹, 张帅宁, 张威 2022 71 130303
Google Scholar
Shi T T, Zhang L D, Zhang S N, Zhang W 2022 Acta Phys. Sin. 71 130303
Google Scholar
[42] 祝可嘉, 郭志伟, 陈鸿 2022 71 131101
Google Scholar
Zhu K J, Guo Z W, Chen H 2022 Acta Phys. Sin. 71 131101
Google Scholar
[43] 李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江 2022 71 177302
Google Scholar
Li J R, Wang Z A, Xu T T, Zhang L L, Gong W J 2022 Acta Phys. Sin. 71 177302
Google Scholar
[44] 张禧征, 王鹏, 张坤亮, 杨学敏, 宋智 2022 71 174501
Google Scholar
Zhang X Z, Wang P, Zhang K L, Yang X M, Song Z 2022 Acta Phys. Sin. 71 174501
Google Scholar
[45] 范辉颖, 罗杰 2022 71 247802
Google Scholar
Fan H Y, Luo J 2022 Acta Phys. Sin. 71 247802
Google Scholar
[46] Xue W T, Li M R, Hu Y M, Song F, Wang Z 2021 Phys. Rev. B 103 L241408
Google Scholar
-
图 1 一维非厄米耗散晶格模型, 每个原胞由A和B两个子格点组成
Fig. 1. One-dimensional non-Hermitian dissipative lattice model, and each unit cell consists of two sublattices A and B
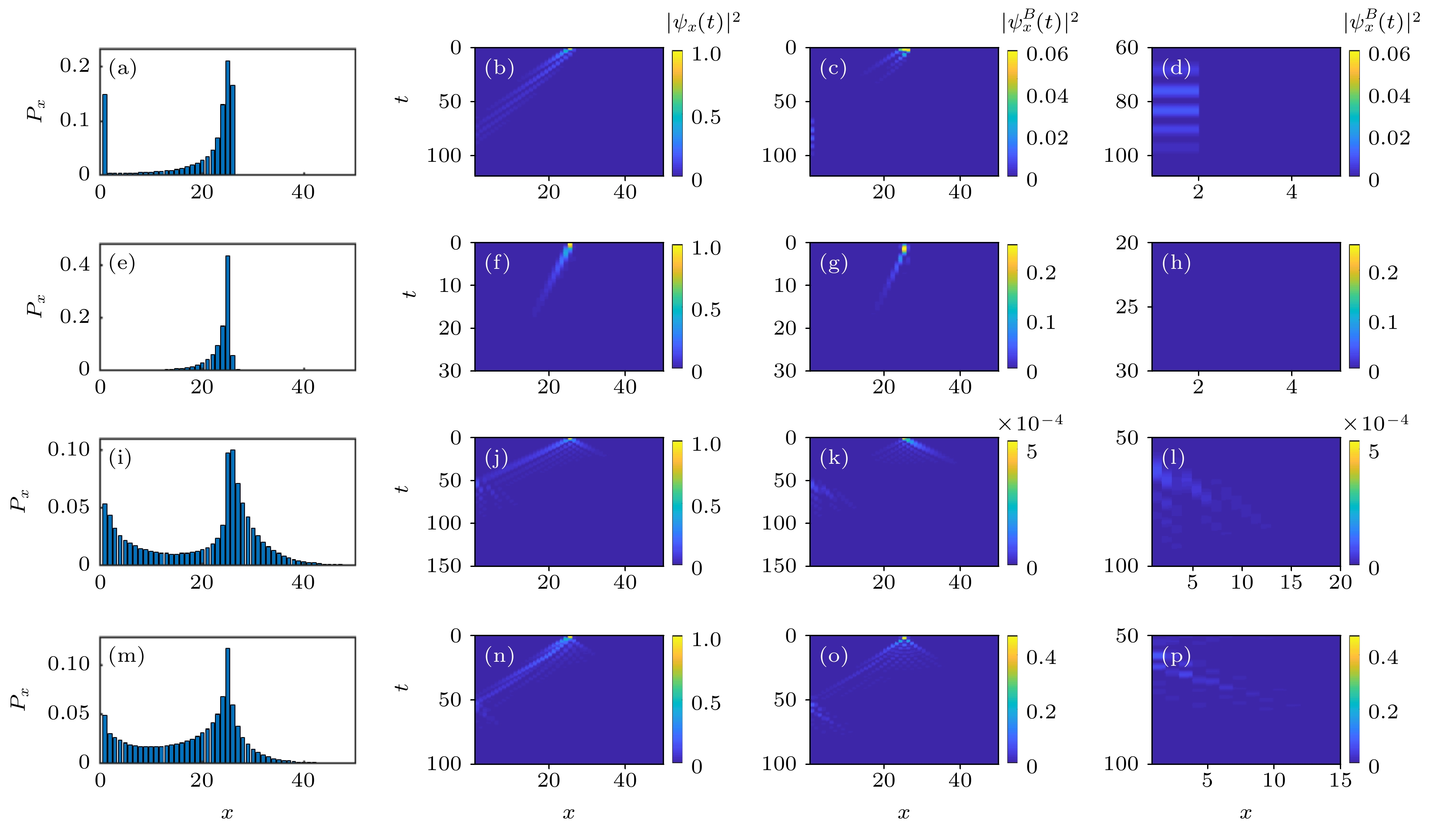
图 2 不同耗散强度下的粒子损失概率分布图和波函数模方的时间演化过程 (a), (e), (i), (m) 粒子损失概率分布图; 其余为波函数模方的时间演化过程. (a)—(d)
$ v{\text{ }} = {\text{ }}0.3 $ ; (e)—(p)$ v{\text{ }} = {\text{ }}0.7 $ ; (a)—(h)$ \gamma = 0.5 $ ; (i)—(l)$ \gamma = 30 $ ; (m)—(p)$ \gamma = 0.05 $ ; 共同参数$ r = 0.5 $ ,$ L = 50 $ ,$ {x_0} = 25 $ Fig. 2. Probability distribution diagram of particle loss and the time evolution process of wave function module square under different dissipation: (a), (e), (i), (m) Distribution of particle loss probability; the rest of the figure is the time evolution process of the norm of the wave function. (a)–(d)
$ v{\text{ }} = {\text{ }}0.3 $ ; (e)–(p)$ v{\text{ }} = {\text{ }}0.7 $ ; (a)–(h)$ \gamma = 0.5 $ ; (i)–(l)$ \gamma = 30 $ ; (m)–(p)$ \gamma = 0.05 $ . Common parameters:$ r = 0.5 $ ,$ L = 50 $ ,$ {x_0} = 25 $ .
图 3 (a)不同初始位置时边缘峰与最小值的相对高度比
$ {P_{{\text{edge}}}}/{P_{\min }} $ ; (b)不同初始位置时边缘峰与整个体系中最大值的相对高度比$ {P_{{\text{edge}}}}/{P_{\max }} $ ; (c)周期性边界条件下能量虚部最大值的模, 插图为$ \gamma {\text{ }} = {30} $ 时开边界条件下本征态的模方$ |\psi _x^{}{|^2} $ 的分布; (d)周期性边界条件下的能量虚部最大值($ \gamma $ 轴取对数), 红线为$ v = r $ 表示胞内胞外跃迁强度相等, 蓝线是PT对称性的分界线$ |\gamma | = 2 v $ . (a)—(c)为双对数坐标,$ v = 0.7 $ ,$ L = 200 $ ; (d)横坐标取$ \ln \gamma $ , 标记4个点,$ \gamma {\text{ }} = {0}{.05} $ 蓝色三角形对应图2(m);$ \gamma = 0.5$ 洋红色十字对应图2(e),$ \gamma {\text{ }} = {30} $ 红色五角星对应图2(i), 以及将图(d)中$ v = 0.3 $ ,$ \gamma {\text{ }} = {0}{.5} $ 标记为黑点对应图2(a). 共同参数$ r = 0.5 $ Fig. 3. (a) Relative height ratio of edge peak to minimum
$ {P_{{\text{edge}}}}/{P_{\min }} $ at different initial positions; (b) relative height ratio of edge peak to maximum in the system$ {P_{{\text{edge}}}}/{P_{\max }} $ ; (c) the modulus of the maximum imaginary part of energy under periodic boundary conditions, the inset shows the distribution of eigenstates$ |\psi _x^{}{|^2} $ under open boundary with$ \gamma {\text{ }} = {30} $ ; (d) maximum energy imaginary part under periodic boundary(axis$ \gamma $ is logarithm), the red line indicates that the intracell and intercell hopping is equal$ v = r $ , and the blue line is the boundary of PT symmetry$ |\gamma | = 2 v $ . (a)–(c) With double logarithmic coordinates,$ v = 0.7 $ ,$ L = 200 $ , (d) abscissa$ \ln \gamma $ . Mark four points:$ \gamma {\text{ }} = {0}{.05} $ blue triangle corresponding to Fig. 2(m);$ \gamma {\text{ }} = {0}{.5} $ magenta cross corresponding to Fig. 2(e);$ \gamma {\text{ }} = {30} $ the red pentagram star corresponding to Fig. 2(i);$ v = 0.3 $ ,$ \gamma = {0}{.5} $ in panel (d) is marked as a black dot corresponding to Fig. 2(a). Common parameters:$ r = 0.5 $ .
图 5 (a)开边界条件下能量本征值虚部随耗散强度的变化,
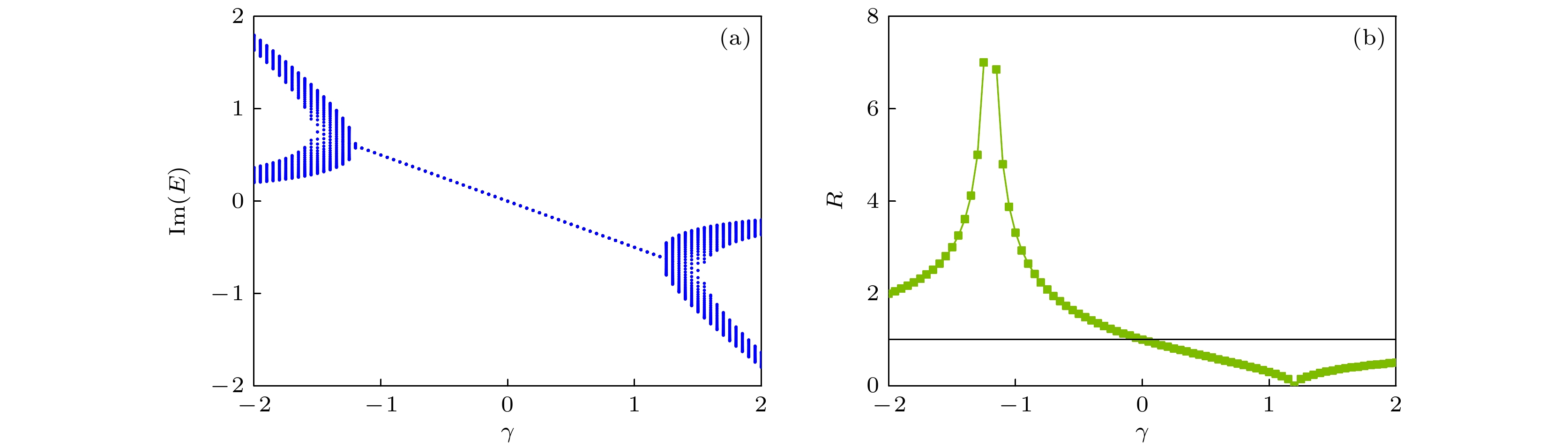
$ L{\text{ }} = {\text{ }}50 $ ; (b)广义布里渊区的半径$ R $ , 黑色直线为$ R = 1 $ 代表布里渊区半径. 共同参数$ r{\text{ }} = {\text{ }}0.5 $ ,$ v{\text{ }} = {\text{ }}0.6 $ Fig. 5. (a) Change of imaginary part of energy eigenvalue with dissipation intensity under open boundary condition with
$ L{\text{ }} = {\text{ }}50 $ ; (b)$ R $ the radius of the generalized Brillouin zone, the black line represents the radius of Brillouin zone with$ R = 1 $ . Common parameters:$ r{\text{ }} = {\text{ }}0.5 $ ,$ v{\text{ }} = {\text{ }}0.6 $ .
图 4 初始位置右侧原胞的损失概率随耗散强度的变化. 右侧原胞位置x 分别取
$ {x_0}{\text{ }} + {\text{ }}3 $ ,$ {x_0}{\text{ }} + {\text{ }}4 $ ,$ {x_0}{\text{ }} + {5} $ ,$ {x_0}{\text{ }} + {6} $ , 其中$ v{\text{ }} = {\text{ }}0.7 $ ,$ L{\text{ }} = {\text{ }}50 $ ,$ {x_0} = 25 $ ,$ r{\text{ }} = {\text{ }}0.5 $ Fig. 4. Loss probability of the right cell at the initial position varies with the dissipation intensity. Right cell position x is taken as
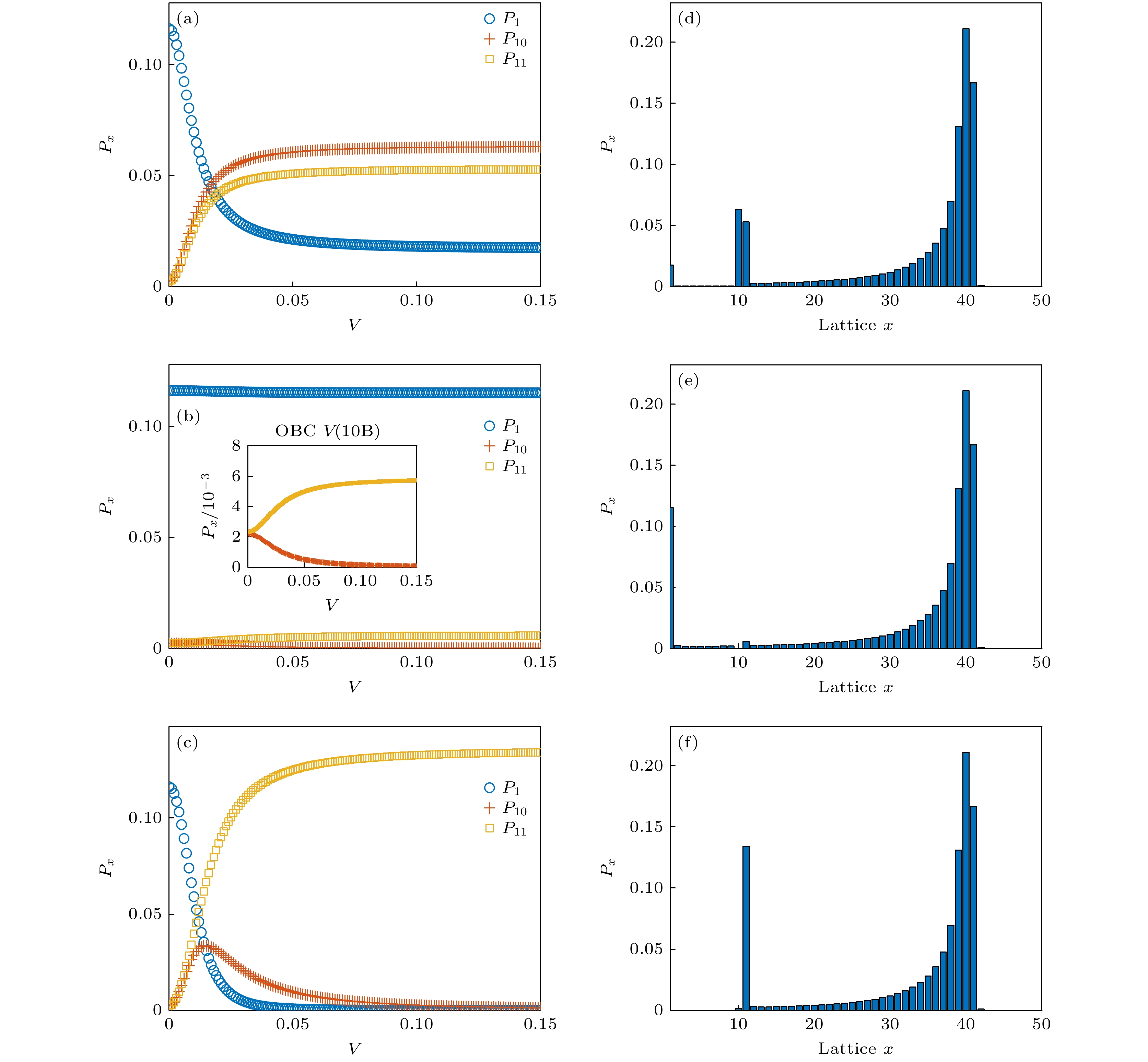
$ {x_0}{\text{ }} + {\text{ }}3 $ ,$ {x_0}{\text{ }} + {\text{ }}4 $ ,$ {x_0}{\text{ }} + {5} $ ,$ {x_0}{\text{ }} + {6} $ respectively with$ v{\text{ }} = {\text{ }}0.7 $ ,$ L{\text{ }} = {\text{ }}50 $ ,$ {x_0} = 25 $ ,$ r{\text{ }} = {\text{ }}0.5 $ .
图 6 在第10个原胞不同格点处放置势垒的粒子损失情况 (a)—(c)在边缘处、杂质原胞处以及杂质原胞相邻原胞上的损失概率
$ {P_1} $ ,$ {P_{10}} $ 和$ {P_{11}} $ , 图(b)中插图为$ {P_{10}} $ 和$ {P_{11}} $ 随势垒变化的细节; (d)—(f)势垒强度$ V = 0.15 $ 时3种势垒设置下的粒子损失概率分布. (a)$ {V_A} = V $ ,$ {V_B} = 0 $ ; (b)$ {V_A} = 0 $ ,$ {V_B} = V $ ; (c)$ {V_A} = {V_B} = V $ ; (d)$ {V_A} = 0.15 $ ,$ {V_B} = 0 $ ; (e)$ {V_A} = 0 $ ,$ {V_B} = 0.15 $ ; (f)$ {V_A} = {V_B} = 0.15 $ . 共同参数$ v = 0.3 $ ,$ r = {\text{ }}0.5 $ ,$ L = 50 $ ,$ {x_0}{\text{ }} = {\text{ }}40 $ ,$ \gamma {\text{ }} = {\text{ }}0.5 $ Fig. 6. Particle loss of the barrier placed at different lattice points of the tenth cell: (a)–(c) Loss probability at the edge, the impurity cell and the adjacent cell of the impurity cell
$ {P_1} $ ,$ {P_{10}} $ and$ {P_{11}} $ , the inset in panel (b) is the detail of$ {P_{10}} $ and$ {P_{11}} $ changing with the barrier; (d)–(f) the probability distribution of particle loss under the three barrier settings with the barrier$ V = 0.15 $ . (a)$ {V_A} = V $ ,$ {V_B} = 0 $ ; (b)$ {V_A} = 0 $ ,$ {V_B} = V $ ; (c)$ {V_A} = {V_B} = V $ ; (d)$ {V_A} = 0.15 $ ,$ {V_B} = 0 $ ; (e)$ {V_A} = 0 $ ,$ {V_B} = 0.15 $ ; (f)$ {V_A} = {V_B} = 0.15 $ . Common parameters$ v = 0.3 $ ,$ r = {\text{ }}0.5 $ ,$ L = 50 $ ,$ {x_0}{\text{ }} = {\text{ }}40 $ ,$ \gamma {\text{ }} = {\text{ }}0.5 $ . -
[1] Feng L, Ganainy R E, Ge L 2017 Nat. Photonics 11 752
Google Scholar
[2] Feng L, Xu Y L, Fegadolli W S, Lu M H, Oliveira J E B, Almeida V R, Chen Y F, Scherer A 2013 Nat. Mater. 12 108
Google Scholar
[3] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006
Google Scholar
[4] Verstraete F, Wolf M M, Ignacio Cirac J 2009 Nat. Phys. 5 633
Google Scholar
[5] Carmichael H J 1993 Phys. Rev. Lett. 70 2273
Google Scholar
[6] Diehl S, Micheli A, Kantian A, Kraus B, Büchler H P, Zoller P 2008 Nat. Phys. 4 878
Google Scholar
[7] Shen H, Fu L 2018 Phys. Rev. Lett. 121 026403
Google Scholar
[8] Nagai Y, Qi Y, Isobe H, Kozii V, Fu L 2020 Phys. Rev. Lett. 125 227204
Google Scholar
[9] Papaj M, Isobe H, Fu L 2019 Phys. Rev. B 99 201107
Google Scholar
[10] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[11] Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802
Google Scholar
[12] Lee C H, Thomale R 2019 Phys. Rev. B 99 201103
Google Scholar
[13] Longhi S 2022 Phys. Rev. Lett. 128 157601
Google Scholar
[14] Zhang X, Tian Y, Jiang J H, Lu M H, Chen Y F 2021 Nat. Commun. 12 5377
Google Scholar
[15] 胡渝民, 宋飞, 汪忠 2021 70 230307
Google Scholar
Hu Y M, Song F, Wang Z 2021 Acta Phys. Sin. 70 230307
Google Scholar
[16] 侯博, 曾琦波 2022 71 130302
Google Scholar
Hou B, Zeng Q B 2022 Acta Phys. Sin. 71 130302
Google Scholar
[17] 孙思彤, 丁应星, 刘伍明 2022 71 130701
Google Scholar
Sun S T, Ding Y X, Liu W M 2022 Acta Phys. Sin. 71 130701
Google Scholar
[18] 高洁, 杭超 2022 71 133202
Google Scholar
Gao J, Hang C 2022 Acta Phys. Sin. 71 133202
Google Scholar
[19] 潘磊 2022 71 170305
Google Scholar
Pan L 2022 Acta Phys. Sin. 71 170305
Google Scholar
[20] 邓天舒 2022 71 170306
Google Scholar
Deng T S 2022 Acta Phys. Sin. 71 170306
Google Scholar
[21] 陈舒越, 蒋闯, 柯少林, 王兵, 陆培祥 2022 71 174201
Google Scholar
Chen S Y, Jiang C, Ke S L, Wang B, Lu P X 2022 Acta Phys. Sin. 71 174201
Google Scholar
[22] Lee T E 2016 Phys. Rev. Lett. 116 133903
Google Scholar
[23] Mao L, Deng T, Zhang P 2021 Phys. Rev. B 104 125435
Google Scholar
[24] 王利, 贾丽芳, 张云波 2022 71 130501
Google Scholar
Wang L, Jia L F, Zhang Y B 2022 Acta Phys. Sin. 71 130501
Google Scholar
[25] Rudner M S, Levitov L S 2009 Phys. Rev. Lett. 102 065703
Google Scholar
[26] Karski M, Förster L, Choi J M, Steffen A, Alt W, Meschede D, Widera A 2009 Science 325 174
Google Scholar
[27] Broome M A, Fedrizzi A, Lanyon B P, Kassal I, Aspuru-Guzik A, White A G 2010 Phys. Rev. Lett. 104 153602
Google Scholar
[28] Ramasesh V V, Flurin E, Rudner M, Siddiqi I, Yao N Y 2017 Phys. Rev. Lett. 118 130501
Google Scholar
[29] Yan Z, Zhang Y R, Gong M, Wu Y, Zheng Y, Li S, Wang C, Liang F, Lin J, Xu Y, Guo C, Sun L, Peng C Z, Xia K, Deng H, Rong H, You J Q, Nori F, Fan H, Zhu X, Pan J W 2019 Science 364 753
Google Scholar
[30] Xue P, Zhang R, Qin H, Zhan X, Bian Z H, Li J, Sanders B C 2015 Phys. Rev. Lett. 114 140502
Google Scholar
[31] Du J, Li H, Xu X, Shi M, Wu J, Zhou X, Han R 2003 Phys. Rev. A 67 042316
Google Scholar
[32] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2012 Phys. Rev. Lett. 108 010502
Google Scholar
[33] Wang L, Liu Q, Zhang Y B 2021 Chin. Phys. B 30 020506
Google Scholar
[34] Xue W T, Hu Y M, Song F, Wang Z 2022 Phys. Rev. Lett. 128 120401
Google Scholar
[35] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
Google Scholar
[36] Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801
Google Scholar
[37] Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402
Google Scholar
[38] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[39] 唐原江, 梁超, 刘永椿 2022 71 171101
Google Scholar
Tang Y T, Liang C, Liu Y C 2022 Acta Phys. Sin. 71 171101
Google Scholar
[40] 曲登科, 范毅, 薛鹏 2022 71 130301
Google Scholar
Qu D K, Fan Y, Xue P 2022 Acta Phys. Sin. 71 130301
Google Scholar
[41] 施婷婷, 张露丹, 张帅宁, 张威 2022 71 130303
Google Scholar
Shi T T, Zhang L D, Zhang S N, Zhang W 2022 Acta Phys. Sin. 71 130303
Google Scholar
[42] 祝可嘉, 郭志伟, 陈鸿 2022 71 131101
Google Scholar
Zhu K J, Guo Z W, Chen H 2022 Acta Phys. Sin. 71 131101
Google Scholar
[43] 李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江 2022 71 177302
Google Scholar
Li J R, Wang Z A, Xu T T, Zhang L L, Gong W J 2022 Acta Phys. Sin. 71 177302
Google Scholar
[44] 张禧征, 王鹏, 张坤亮, 杨学敏, 宋智 2022 71 174501
Google Scholar
Zhang X Z, Wang P, Zhang K L, Yang X M, Song Z 2022 Acta Phys. Sin. 71 174501
Google Scholar
[45] 范辉颖, 罗杰 2022 71 247802
Google Scholar
Fan H Y, Luo J 2022 Acta Phys. Sin. 71 247802
Google Scholar
[46] Xue W T, Li M R, Hu Y M, Song F, Wang Z 2021 Phys. Rev. B 103 L241408
Google Scholar
下载:
计量
- 文章访问数: 3300
- PDF下载量: 132
- 被引次数: 0
