步行通道内行人流拉链现象的生成机理与仿真研究

武鑫森; 岳昊; 刘秋梅; 张旭; 邵春福

doi:10.7498/aps.70.20201626

摘要

以步行通道内的单向行人流为研究对象, 分析研究行人拉链现象的生成机理, 并建立基于Voronoi图的速度修正模型对其仿真研究. 首先, 从行人追求视野最佳和步行舒适的角度分析拉链现象的生成机理, 以行人的视野关注和视野遮挡描述影响行人移动过程中产生拉链偏移的因素; 以行人局部密度描述行人的步行舒适度; 引入拉链敏感系数描述行人客观偏移的意愿程度; 提出单个行人侧向偏移的机制, 获得行人最佳的偏移位置. 然后, 构建基于Voronoi图的行人速度修正仿真模型, 考虑行人是否有偏移倾向的主观意愿, 并嵌入偏移规则, 模拟再现行人的拉链现象. 仿真发现: 行人的拉链层数与通道宽度成正比, 该模型速度密度关系图与实证数据吻合较好; 与不考虑拉链效应相比, 倾向主动进行侧向偏移的行人占比越大, 越有助于提高通道内行人的移动速度、舒适度和空间利用率.

关键词:

Abstract

In this study, the unidirectional pedestrian flow in the corridor is taken as a research object, the generation mechanism of the pedestrian zipper phenomenon is analyzed, and a velocity correction model based on the Voronoi diagram is established for the simulation research. First, the generation mechanism of the pedestrian zipper phenomenon is analyzed from the perspective of optimal visual field and walking comfort of pedestrians. Then the visual attention and visual occlusion of pedestrians are used to describe the factors which affect the zipper deviation during pedestrian movement, the local density of pedestrians is used to describe the walking comfort of pedestrians, the zipper sensitivity coefficient is adopted to describe the willingness of pedestrians to move objectively, and the mechanism of lateral deviation of a single pedestrian is considered to obtain the optimal deviation position of pedestrians. Besides, the Voronoi diagram is introduced to effectively determine the pedestrians surrounding the target pedestrian within the visual field. And the influence of surrounding pedestrians with different distances and directions on the moving velocity of the target pedestrian based on the Voronoi diagram is considered. Then, a velocity correction model of pedestrians based on the Voronoi diagram is constructed, whether the pedestrian has a subjective willingness to deviate is considered, and the deviation rule is embedded to simulate and reproduce the zipper phenomenon of pedestrians. The simulation results truly reproduce the normal pedestrian flow through the corridor and show that our model can overcome the deficiency of the jitter and overlap phenomenon of the traditional social force model. The self-organized pedestrian flow with uniform distribution and the pedestrian zipper effect can also be observed. Furthermore, through the simulation results, we can see that the number of zipper layers for pedestrians is proportional to the width of the corridor. The comparison of simulated pedestrian data with the empirical data indicates that the fundamental diagram of velocity-density relation of our model is in good agreement with the empirical data. A comparison between with and without considering the zipper effect shows that the larger the proportion of pedestrians actively willing to laterally deviate, the more helpful it will be to improve the moving velocity, comfort and space utilization of pedestrians in the corridor.

Keywords:

作者及机构信息

1.
北京交通大学, 综合交通运输大数据应用技术交通运输行业重点实验室, 北京　100044

2.
河南工业大学土木建筑学院, 郑州　450001

通信作者: 岳昊, hyue@bjtu.edu.cn

基金项目: 国家自然科学基金(批准号: 71771013, 71621001)、国家重点研发计划(批准号: 2019YFF0301403)、中央高校基本科研业务费专项资金(批准号: 2019JBM041)和新加坡教育部学术研究基金第二层次(批准号: MOE2016-T2-1-044)资助的课题

Authors and contacts

1.
Key Laboratory of Transport Industry of Big Data Application Technologies for Comprehensive Transport, Ministry of Transport, Beijing Jiaotong University, Beijing 100044, China

2.
College of Civil Engineering and Architecture, Henan University of Technology, Zhengzhou 450001, China

Corresponding author: Yue Hao, hyue@bjtu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 71771013, 71621001), the National Key R&D Program of China (Grant No. 2019YFF0301403), the Special Funds for Fundamental Scientific Research Operation Fees of Central Universities, China (Grant No. 2019JBM041), and the Singapore Ministry of Education (MOE) AcRF Tier 2 (Grant No. MOE2016-T2-1-044)

文章全文 : translate this paragraph

参考文献

[1]	Shiwakoti N, Sarvi M 2013 Transp. Res. C, Emerg. Technol. 37 260 Google Scholar
[2]	Guo R Y, Huang H J, Wong S C 2011 Transp. Res. B, Methodol. 45 490 Google Scholar
[3]	Duives D C, Daamen W, Hoogendoorn S P 2013 Transp. Res. C, Emerg. Technol. 37 193 Google Scholar
[4]	Zheng X, Zhong T, Liu M 2009 Build. Environ. 44 437 Google Scholar
[5]	Blue V J, Adler J L 2000 Transp. Res. Rec. 1710 20 Google Scholar
[6]	Yue H, Wang S, Jia X L, Li J, Shao C F 2016 Simul.: Trans. Soc. Model. Simul. Int. 92 491
[7]	Zhu K, Yang Y, Shi Q 2016 Simul. Model. Pract. Theory. 69 31 Google Scholar
[8]	Burstedde C, Klauck K, Schadschneider A, Zittartz J 2001 Physica A 295 507 Google Scholar
[9]	李明华, 袁振洲, 许痰, 田钧方 2015 64 018903 Google Scholar Li M H, Yuan Z Z, Tian J F 2015 Acta Phys. Sin. 64 018903 Google Scholar
[10]	Yue H, Zhang B Y, Shao C F, Xing Y 2014 Chin. Phys. B 23 050512
[11]	Helbing D, Farkas I, Vicsek T 2000 Nature 407 487 Google Scholar
[12]	Helbing D, Wemer T 2005 Transp. Sci. 39 1 Google Scholar
[13]	Hou L, Liu J G, Pan X, Wang B H 2014 Physica A 400 93 Google Scholar
[14]	Lv W, Song W G, Ma J, Fang Z 2013 IEEE Trans. Intell. Transp. Syst. 14 1753 Google Scholar
[15]	Zhao Y, Li M, Lu X, Tian L, Yu Z, Huang K, Wang Y, Li T 2017 Physica A 465 175 Google Scholar
[16]	Jia X L, Yue H, Tian X, Yin H H 2017 Simul.: Trans. Soc. Model. Simul. Int. 93 1013
[17]	Seer S, Brandle N, Ratti C 2014 Transp. Res. C, Emerg. Technol. 48 212 Google Scholar
[18]	Frank G A, Dorso C O 2011 Physica A 390 2135 Google Scholar
[19]	Seyfried A, Steffen B, Lippert T 2006 Physica A 368 232 Google Scholar
[20]	Parisi D R, Gilman M, Moldovan H 2009 Physica A 388 3600 Google Scholar
[21]	Lakoba T I, Kaup D J, Finkelstein N M 2005 Simul. Model. Pract. Theory. 81 339
[22]	Li S S, Qian D L, Wang J Z 2012 J. Jilin Univ., Eng. Technol. Ed. 42 623
[23]	Johansson A, Helbing D, Shukla P 2007 Adv. Complex Syst. 10 271
[24]	Moussaïd M, Helbing D, Garnier S, Johansson A, Combe M, Theraulaz G 2009 Proc. R. Soc. Biol. Sci. 276 2755 Google Scholar
[25]	Yu WJ, Chen R, Dong L Y, Dai S Q 2005 Phys. Rev. E 72 026112 Google Scholar
[26]	曹自强, 赛斌, 吕欣 2020 69 084203 Google Scholar Cao Z Q, Sai B, Lu X 2020 Acta Phys. Sin. 69 084203 Google Scholar
[27]	Xiao Y, Gao Z Y, Qu Y C, Li X 2016 Transp. Res. C, Emerg. Technol. 68 566 Google Scholar
[28]	Qu Y C, Xiao Y, Wu J J, Tang T, Gao Z Y 2018 Physica A 492 1153 Google Scholar
[29]	Moussaïd M, Helbing D, Theraulaz G 2011 Proc. Natl. Acad. Sci. U. S. A. 108 6884 Google Scholar
[30]	Hoogendoorn S P, Daamen W 2005 Transp. Sci. 39 147 Google Scholar
[31]	Seyfried A, Passon O, Steffen B, Boltes M, Rupprecht T, Klingsch W 2009 Transp. Sci. 43 395 Google Scholar
[32]	Porter E, Hamdar S H, Daamen W 2018 Transportmetrica A 14 468
[33]	Ren X X, Zhang J, Cao S C, Song W G 2019 J. Stat. Mech. 12 123204
[34]	金辉, 郭仁拥 2019 68 020501 Google Scholar Jin H, Guo R Y 2019 Acta Phys. Sin. 68 020501 Google Scholar
[35]	Fruin J J 1971 Pedestrian and Planning Design (New York: Metropolitan Association of Urban Designer and Environmental Planners Inc.)
[36]	张磊, 岳昊, 李梅, 王帅, 米雪玉 2015 64 060505 Google Scholar Zhang L, Yue H, Li M, Wang S, Mi X Y 2015 Acta Phys. Sin. 64 060505 Google Scholar
[37]	Older S J 1968 Traff. Eng. Contr. 10 160
[38]	Mōri M, Tsukaguchi H 1987 Transp. Res. Part A 21 223 Google Scholar
[39]	Zhang J, Klingsch W, Schadschneider A, Seyfried A 2011 J. Statist. Mech. - Theory Exp. 6 P06004
[40]	Weidmann U 1993 Transporttechnik der Fussgänger: Transporttechnische Eigenschaften des Fussgängerverkehrs (Literaturauswertung) (Institut für Verkehrsplanung, Transporttechnik, Strassen- und Eisenbahnbau (IVT), ETH Zürich)
[41]	Hankin B D, Wright R A 1958 J. Oper. Res. Soc. 9 81 Google Scholar

施引文献

图 1 瓶颈中的行人拉链现象^[30]

Fig. 1. Zipper phenomena of pedestrians in a bottleneck^[30].

下载: 全尺寸图片幻灯片

图 2 不同通道宽度下的行人拉链现象^[33]

Fig. 2. Zipper phenomenon of pedestrians under different channel widths^[33].

下载: 全尺寸图片幻灯片

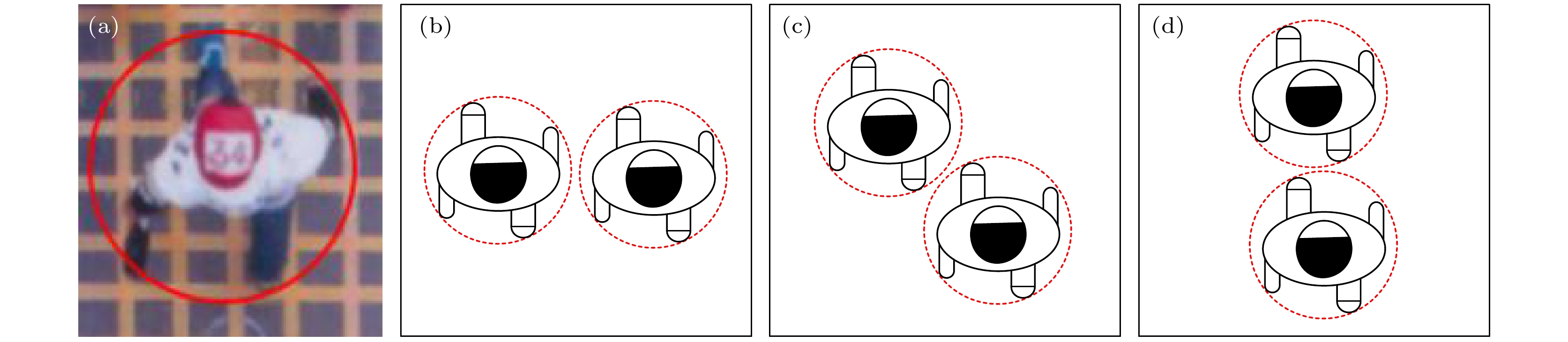
图 3 两相邻行人同方向行走形态　(a)行人行走形态; (b)两行人行走并排形式; (c)两行人行走斜列形式; (d)两行人行走直列形式

Fig. 3. Walking pattern of two adjacent pedestrians in the same direction: (a) The real single pedestrian walking pattern; (b) two adjacent pedestrians walking side by side; (c) two adjacent pedestrians walking in a diagonal pattern; (d) two adjacent pedestrians walking in a straight line.

下载: 全尺寸图片幻灯片

图 4 行人拉链现象表现形式　(a)单列行人截图^[33]与行人直列形式对比; (b)两列行人截图^[33]与行人直列、斜列形式对比; (c)多列行人截图^[33]与行人多种排列形式对比

Fig. 4. Manifestation of pedestrian zipper phenomenon: (a) The comparison of single-column pedestrian screenshot^[33] with pedestrians in-line pattern; (b) the comparison of two-column pedestrian screenshot^[33] with pedestrians in-line and diagonal patterns; (c) the comparison of multi-column pedestrian screenshot^[33] with multiple arrangement patterns of pedestrians.

下载: 全尺寸图片幻灯片

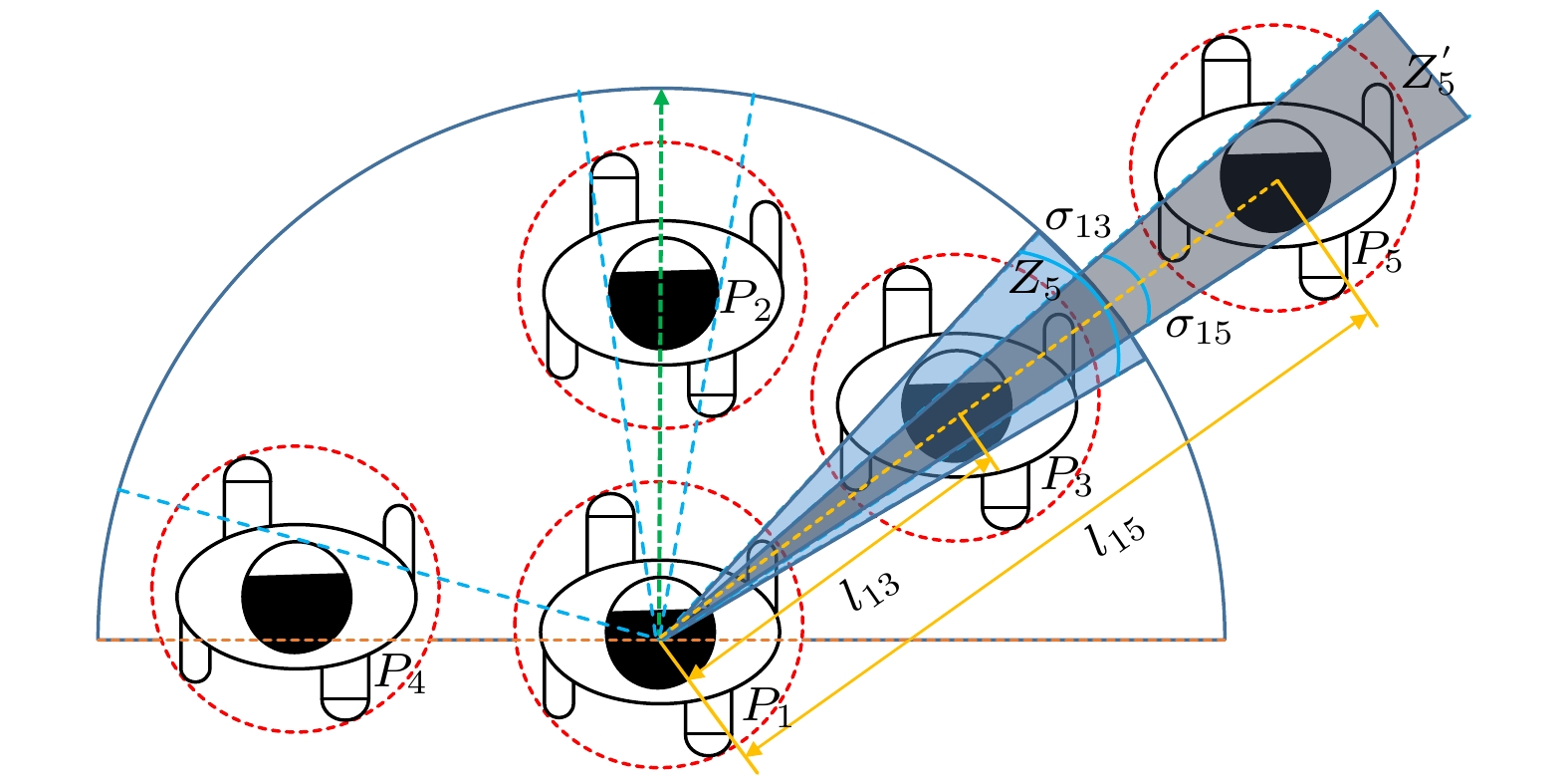
图 5 有效视野区域内的行人视野关注和遮挡(橙色遮挡区域是目标行人最为关注和对目标行人影响最大的区域, 蓝色遮挡区域对目标行人的影响较弱)

Fig. 5. Pedestrian vision attention and occlusion in the effective vision area (the orange shaded area is the area that the target pedestrian pay the most attention to and has the greatest influence on the target pedestrian, while the blue shaded area has a relatively weak influence on the target pedestrian).

下载: 全尺寸图片幻灯片

图 6 不同距离行人对目标行人视野的遮挡程度

Fig. 6. Occlusion degree of the target pedestrian’s vision by surrounding pedestrians at different distances

下载: 全尺寸图片幻灯片

图 7 不同行人局部密度下的拉链现象示意(绿色、黄色、橙色分别表示行人局部密度由低到高)　(a)行人局部密度较低时; (b)行人局部密度较高时

Fig. 7. The zipper phenomenon of pedestrians under different local density (green, yellow and orange respectively represent the local pedestrian density from low to high):(a) When the local pedestrian density is relatively low; (b) when the local pedestrian density is relatively high.

下载: 全尺寸图片幻灯片

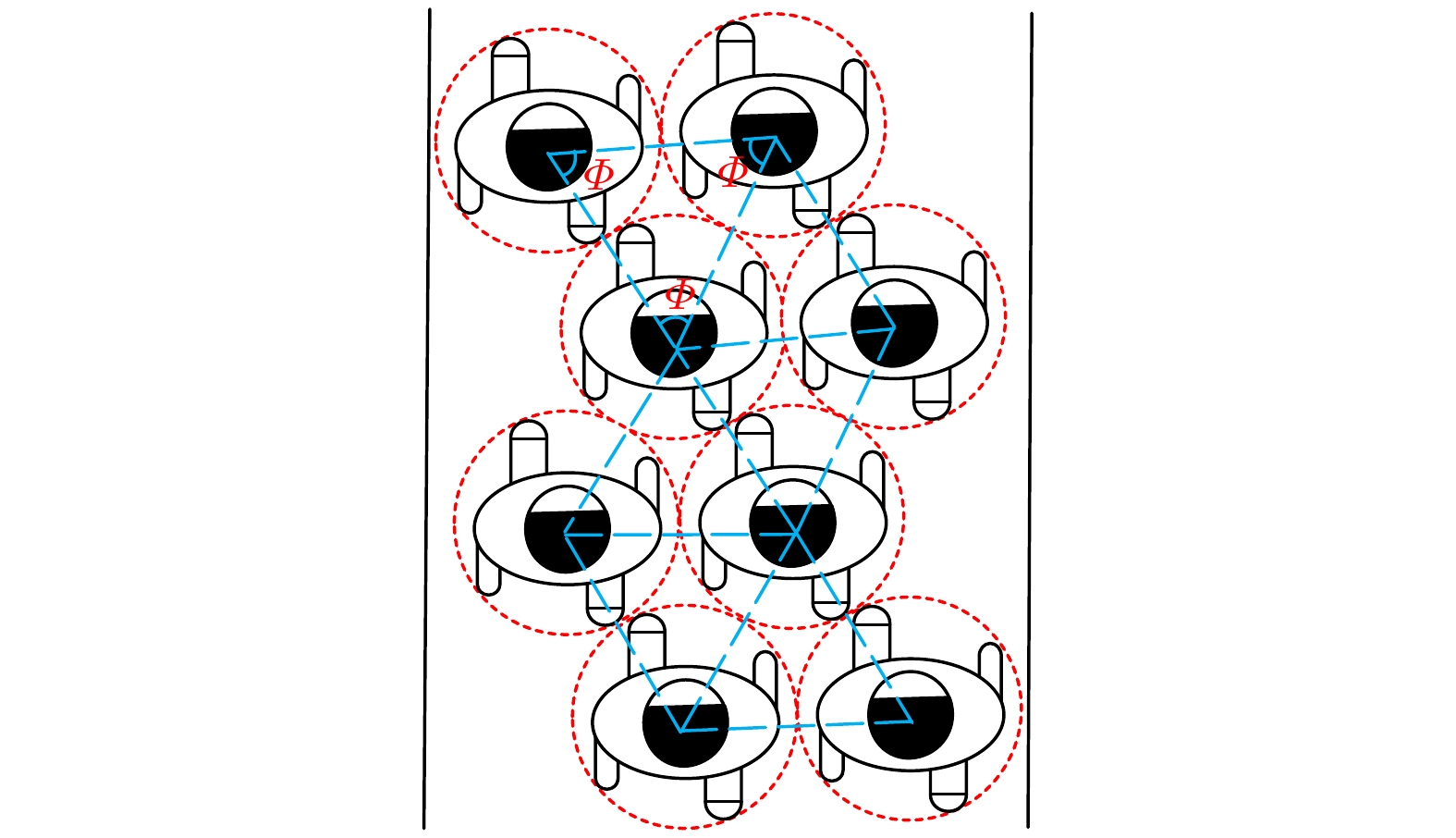
图 8 不同偏离意愿下的拉链现象示意　(a)窄通道行人偏离意愿较低时; (b)窄通道行人偏离意愿较高时; (c) 宽通道行人偏离意愿较高时

Fig. 8. Zipper phenomenon of pedestrians under different deviation intentions: (a) When the deviation intention of pedestrians in narrow corridors is relatively low; (b) when the deviation intention of pedestrians in narrow corridors is relatively high; (c) when the deviation intention of pedestrians in wide corridors is relatively high.

下载: 全尺寸图片幻灯片

图 9 行人拉链效应的稳定形态^[33]

Fig. 9. Stable form of pedestrian zipper effect^[33].

下载: 全尺寸图片幻灯片

图 10 行人拉链效应的最佳形态

Fig. 10. The best form of pedestrian zipper effect.

下载: 全尺寸图片幻灯片

图 11 行人基本单元的拉链稳定状态(阴影区域为目标行人正前方视野遮挡区域, 非阴影区域为目标行人有效可见视野区域)

Fig. 11. Zipper stability state of pedestrian basic unit (the shadow area is the vision occlusion area and the non-shaded area is the effective visible area in front of the target pedestrian).

下载: 全尺寸图片幻灯片

图 12 行人投影区域

Fig. 12. Projection area of pedestrians.

下载: 全尺寸图片幻灯片

图 13 行人拉链效应启动机制示意　(a)行人侧向位移前; (b)行人侧向位移后

Fig. 13. Starting mechanism of pedestrian zipper effect: (a) Before lateral displacement of pedestrians; (b) after lateral displacement of pedestrians.

下载: 全尺寸图片幻灯片

图 14 考虑两侧多个行人的拉链效应偏移情况示意　(a)两侧均满足最佳视野; (b)仅一侧满足最佳视野; (c)两侧妥协后稳定视野

Fig. 14. Deviation of zipper effect when consider multiple pedestrians on both sides: (a) Both sides meet the optimum field of vision; (b) only one side satisfies the optimal field of vision; (c) stabilize visual field after compromise on both sides.

下载: 全尺寸图片幻灯片

图 15 周围行人对目标行人的速度影响

Fig. 15. Velocity effects of surrounding pedestrians on the target pedestrian.

下载: 全尺寸图片幻灯片

图 16 行人拉链效应偏移规则流程图

Fig. 16. Flow diagram of pedestrian zipper effect deviation rules.

下载: 全尺寸图片幻灯片

图 17 有偏移速度的行人侧向偏移示意

Fig. 17. Sideways deviation of pedestrians with deviation velocity.

下载: 全尺寸图片幻灯片

图 18 直通道行人循环流仿真过程截图($w = 3.5\;{\rm{ m}}$, $l = 10\;{\rm{ m}}$, $\kappa = 1$)

Fig. 18. Screenshot of simulation process of pedestrian flow in the straight corridor ($w = 3.5\;{\rm{ m}}$, $l = 10\;{\rm{ m}}$, $\kappa = 1$).

下载: 全尺寸图片幻灯片

图 19 行人#4在不同仿真时间步的拉链效应偏移截图

Fig. 19. Screenshot of zipper effect of pedestrian #4 at different simulation time steps.

下载: 全尺寸图片幻灯片

图 20 行人拉链层数与通道宽度关系

Fig. 20. Relationship between the number of pedestrian zipper layers and the width of the corridor.

下载: 全尺寸图片幻灯片

图 21 直通道单向行人流基本图^[37-41](该模型仿真数据与实证数据(Older^[37], Mori^[38], Zhang^[39], Weidmann^[40], Hankin^[41])进行对比)

Fig. 21. Fundamental diagram of unidirectional pedestrian flow in the corridor^[37-41]. Actual data (Older^[37], Mori^[38], Zhang^[39], Weidmann^[40], Hankin^[41]) are gathered to compare with our model.

下载: 全尺寸图片幻灯片

图 22 不同密度下行人主观偏移意愿占比与行人平均速度关系

Fig. 22. Relationship between the proportion of pedestrian subjective deviation intention and pedestrian average velocity under different overall densities.

下载: 全尺寸图片幻灯片

图 23 不同密度下行人主观偏移意愿占比与行人平均局部密度关系

Fig. 23. Relationship between the proportion of pedestrian subjective deviation intention and pedestrian average local density under different overall densities.

下载: 全尺寸图片幻灯片

表 1 速度修正模型参数取值

Table 1. Parameter values of velocity correction model.

参数	取值	单位	参数	取值
${v_0}$	1	${\rm{m/s}}$	${k_1}$	1
${r_i}$	0.3	${\rm{m}}$	${k_2}$	0.6
${d_1}$	0	${\rm{m}}$	${k_3}$	0.2
${d_2}$	0.5	${\rm{m}}$	${k_4}$	0
${d_3}$	0.25	${\rm{m}}$	${k_5}$	0.8
$\Delta t$	0.5	${\rm{s}}$	${k_6}$	0

下载: 导出CSV

map

[1]	Shiwakoti N, Sarvi M 2013 Transp. Res. C, Emerg. Technol. 37 260 Google Scholar
[2]	Guo R Y, Huang H J, Wong S C 2011 Transp. Res. B, Methodol. 45 490 Google Scholar
[3]	Duives D C, Daamen W, Hoogendoorn S P 2013 Transp. Res. C, Emerg. Technol. 37 193 Google Scholar
[4]	Zheng X, Zhong T, Liu M 2009 Build. Environ. 44 437 Google Scholar
[5]	Blue V J, Adler J L 2000 Transp. Res. Rec. 1710 20 Google Scholar
[6]	Yue H, Wang S, Jia X L, Li J, Shao C F 2016 Simul.: Trans. Soc. Model. Simul. Int. 92 491
[7]	Zhu K, Yang Y, Shi Q 2016 Simul. Model. Pract. Theory. 69 31 Google Scholar
[8]	Burstedde C, Klauck K, Schadschneider A, Zittartz J 2001 Physica A 295 507 Google Scholar
[9]	李明华, 袁振洲, 许痰, 田钧方 2015 64 018903 Google Scholar Li M H, Yuan Z Z, Tian J F 2015 Acta Phys. Sin. 64 018903 Google Scholar
[10]	Yue H, Zhang B Y, Shao C F, Xing Y 2014 Chin. Phys. B 23 050512
[11]	Helbing D, Farkas I, Vicsek T 2000 Nature 407 487 Google Scholar
[12]	Helbing D, Wemer T 2005 Transp. Sci. 39 1 Google Scholar
[13]	Hou L, Liu J G, Pan X, Wang B H 2014 Physica A 400 93 Google Scholar
[14]	Lv W, Song W G, Ma J, Fang Z 2013 IEEE Trans. Intell. Transp. Syst. 14 1753 Google Scholar
[15]	Zhao Y, Li M, Lu X, Tian L, Yu Z, Huang K, Wang Y, Li T 2017 Physica A 465 175 Google Scholar
[16]	Jia X L, Yue H, Tian X, Yin H H 2017 Simul.: Trans. Soc. Model. Simul. Int. 93 1013
[17]	Seer S, Brandle N, Ratti C 2014 Transp. Res. C, Emerg. Technol. 48 212 Google Scholar
[18]	Frank G A, Dorso C O 2011 Physica A 390 2135 Google Scholar
[19]	Seyfried A, Steffen B, Lippert T 2006 Physica A 368 232 Google Scholar
[20]	Parisi D R, Gilman M, Moldovan H 2009 Physica A 388 3600 Google Scholar
[21]	Lakoba T I, Kaup D J, Finkelstein N M 2005 Simul. Model. Pract. Theory. 81 339
[22]	Li S S, Qian D L, Wang J Z 2012 J. Jilin Univ., Eng. Technol. Ed. 42 623
[23]	Johansson A, Helbing D, Shukla P 2007 Adv. Complex Syst. 10 271
[24]	Moussaïd M, Helbing D, Garnier S, Johansson A, Combe M, Theraulaz G 2009 Proc. R. Soc. Biol. Sci. 276 2755 Google Scholar
[25]	Yu WJ, Chen R, Dong L Y, Dai S Q 2005 Phys. Rev. E 72 026112 Google Scholar
[26]	曹自强, 赛斌, 吕欣 2020 69 084203 Google Scholar Cao Z Q, Sai B, Lu X 2020 Acta Phys. Sin. 69 084203 Google Scholar
[27]	Xiao Y, Gao Z Y, Qu Y C, Li X 2016 Transp. Res. C, Emerg. Technol. 68 566 Google Scholar
[28]	Qu Y C, Xiao Y, Wu J J, Tang T, Gao Z Y 2018 Physica A 492 1153 Google Scholar
[29]	Moussaïd M, Helbing D, Theraulaz G 2011 Proc. Natl. Acad. Sci. U. S. A. 108 6884 Google Scholar
[30]	Hoogendoorn S P, Daamen W 2005 Transp. Sci. 39 147 Google Scholar
[31]	Seyfried A, Passon O, Steffen B, Boltes M, Rupprecht T, Klingsch W 2009 Transp. Sci. 43 395 Google Scholar
[32]	Porter E, Hamdar S H, Daamen W 2018 Transportmetrica A 14 468
[33]	Ren X X, Zhang J, Cao S C, Song W G 2019 J. Stat. Mech. 12 123204
[34]	金辉, 郭仁拥 2019 68 020501 Google Scholar Jin H, Guo R Y 2019 Acta Phys. Sin. 68 020501 Google Scholar
[35]	Fruin J J 1971 Pedestrian and Planning Design (New York: Metropolitan Association of Urban Designer and Environmental Planners Inc.)
[36]	张磊, 岳昊, 李梅, 王帅, 米雪玉 2015 64 060505 Google Scholar Zhang L, Yue H, Li M, Wang S, Mi X Y 2015 Acta Phys. Sin. 64 060505 Google Scholar
[37]	Older S J 1968 Traff. Eng. Contr. 10 160
[38]	Mōri M, Tsukaguchi H 1987 Transp. Res. Part A 21 223 Google Scholar
[39]	Zhang J, Klingsch W, Schadschneider A, Seyfried A 2011 J. Statist. Mech. - Theory Exp. 6 P06004
[40]	Weidmann U 1993 Transporttechnik der Fussgänger: Transporttechnische Eigenschaften des Fussgängerverkehrs (Literaturauswertung) (Institut für Verkehrsplanung, Transporttechnik, Strassen- und Eisenbahnbau (IVT), ETH Zürich)
[41]	Hankin B D, Wright R A 1958 J. Oper. Res. Soc. 9 81 Google Scholar

[1]	张琦, 渠静. 基于前摄效应的不耐烦行为建模与双向行人流动态. , 2022, 71(7): 070502. doi: 10.7498/aps.71.20211537
[2]	武鑫森, 岳昊, 刘秋梅, 张旭, 邵春福. L型步行通道内行人转弯行为的实验分析与仿真. , 2021, 70(14): 148901. doi: 10.7498/aps.70.20210055
[3]	曹自强, 赛斌, 吕欣. 行人跟踪算法及应用综述. , 2020, 69(8): 084203. doi: 10.7498/aps.69.20191721
[4]	金辉, 郭仁拥. 基于元胞传输模型的楼梯区域行人运动. , 2019, 68(2): 020501. doi: 10.7498/aps.68.20180912
[5]	董力耘, 陈立, 段晓茵. 基于教室人群疏散实验的行人流建模和模拟. , 2015, 64(22): 220505. doi: 10.7498/aps.64.220505
[6]	张磊, 岳昊, 李梅, 王帅, 米雪玉. 拥堵疏散的行人拥挤力仿真研究. , 2015, 64(6): 060505. doi: 10.7498/aps.64.060505
[7]	方伟, 宋鑫宏. 基于Voronoi图盲区的无线传感器网络覆盖控制部署策略. , 2014, 63(22): 220701. doi: 10.7498/aps.63.220701
[8]	永贵, 黄海军, 许岩. 菱形网格的行人疏散元胞自动机模型. , 2013, 62(1): 010506. doi: 10.7498/aps.62.010506
[9]	陈亮, 郭仁拥, 塔娜. 双出口房间内疏散行人流的仿真和实验研究. , 2013, 62(5): 050506. doi: 10.7498/aps.62.050506
[10]	赵俊英, 金宁德. 两相流相空间多元图重心轨迹动力学特征. , 2012, 61(9): 094701. doi: 10.7498/aps.61.094701
[11]	null. 初始位置布局不平衡的疏散行人流仿真研究. , 2012, 61(13): 130509. doi: 10.7498/aps.61.130509
[12]	谢积鉴, 薛郁. 通过博弈的室内行人疏散动力学研究. , 2012, 61(19): 194502. doi: 10.7498/aps.61.194502
[13]	和兴锁, 李雪华, 邓峰岩. 平面柔性梁的刚-柔耦合动力学特性分析与仿真. , 2011, 60(2): 024502. doi: 10.7498/aps.60.024502
[14]	杨凌霄, 赵小梅, 高自友, 郑建风. 考虑交通出行惯例的双向行人流模型研究. , 2011, 60(10): 100501. doi: 10.7498/aps.60.100501
[15]	温坚, 田欢欢, 薛郁. 考虑次近邻作用的行人交通格子流体力学模型. , 2010, 59(6): 3817-3823. doi: 10.7498/aps.59.3817
[16]	岳昊, 邵春福, 关宏志, 段龙梅. 基于元胞自动机的行人视线受影响的疏散流仿真研究. , 2010, 59(7): 4499-4507. doi: 10.7498/aps.59.4499
[17]	岳昊, 邵春福, 姚智胜. 基于元胞自动机的行人疏散流仿真研究. , 2009, 58(7): 4523-4530. doi: 10.7498/aps.58.4523
[18]	周金旺, 邝华, 刘慕仁, 孔令江. 成对行为对行人疏散动力学的影响研究. , 2009, 58(5): 3001-3007. doi: 10.7498/aps.58.3001
[19]	岳昊, 邵春福, 陈晓明, 郝合瑞. 基于元胞自动机的对向行人交通流仿真研究. , 2008, 57(11): 6901-6908. doi: 10.7498/aps.57.6901
[20]	方励之, 区智. 强耦合的动力学Jahn-Teller效应理论. , 1966, 22(4): 471-486. doi: 10.7498/aps.22.471

计量

文章访问数: 6079
PDF下载量: 94
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板