单轴压缩下Ti<sub>3</sub>B<sub>4</sub>的力学、电学性能及变形机制的第一性原理研究

李君; 刘立胜; 徐爽; 张金咏

doi:10.7498/aps.69.20191194

摘要

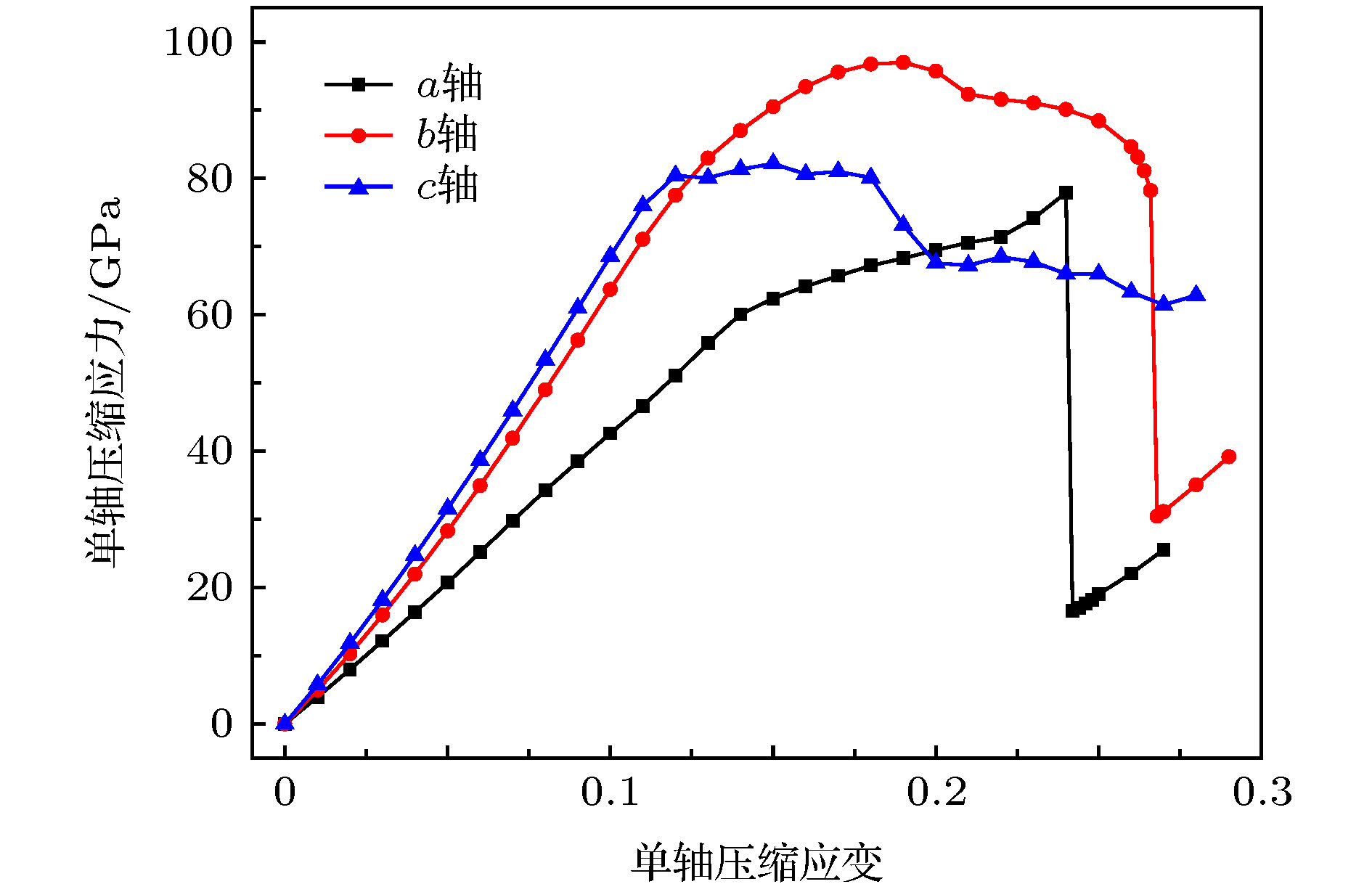
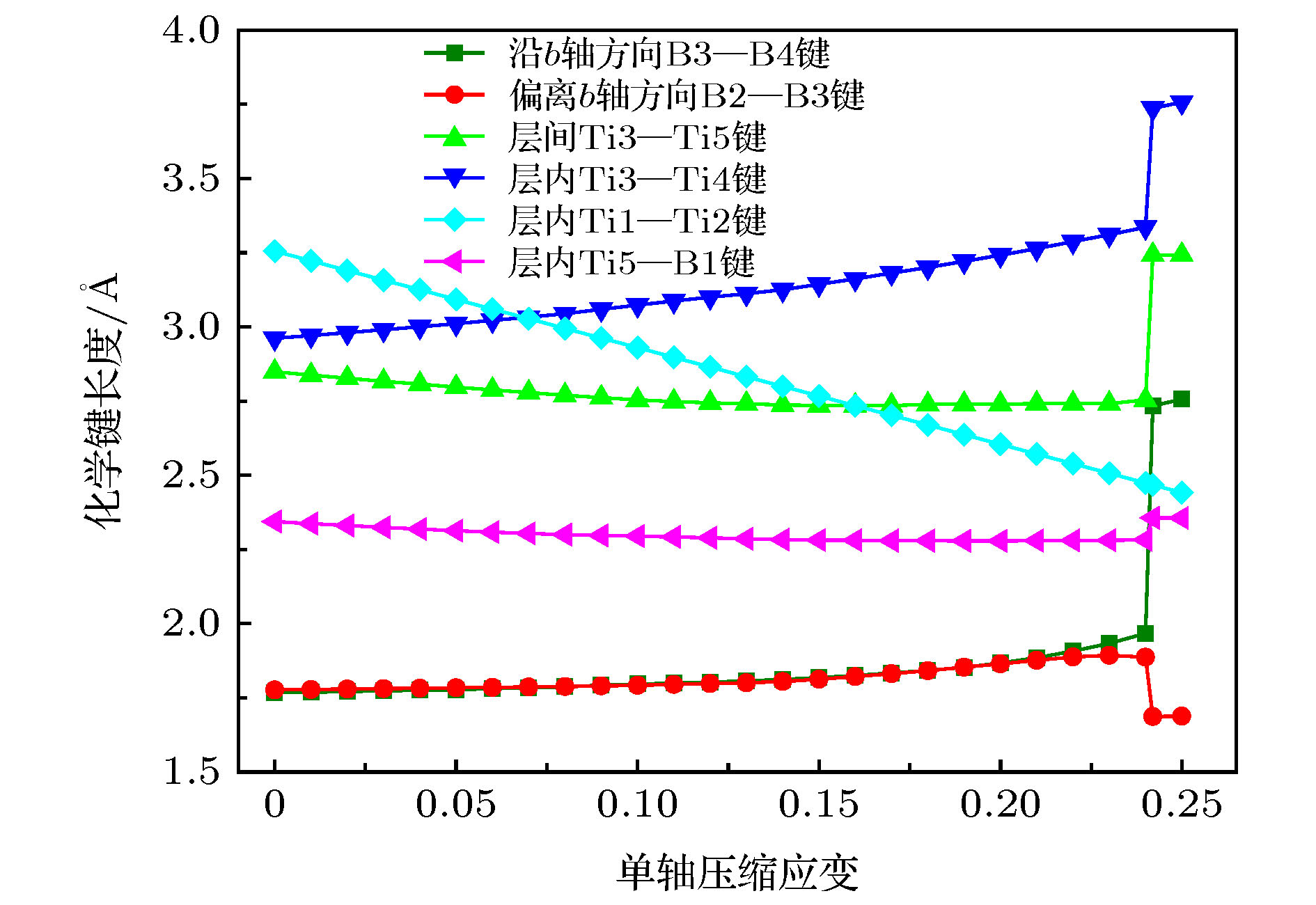
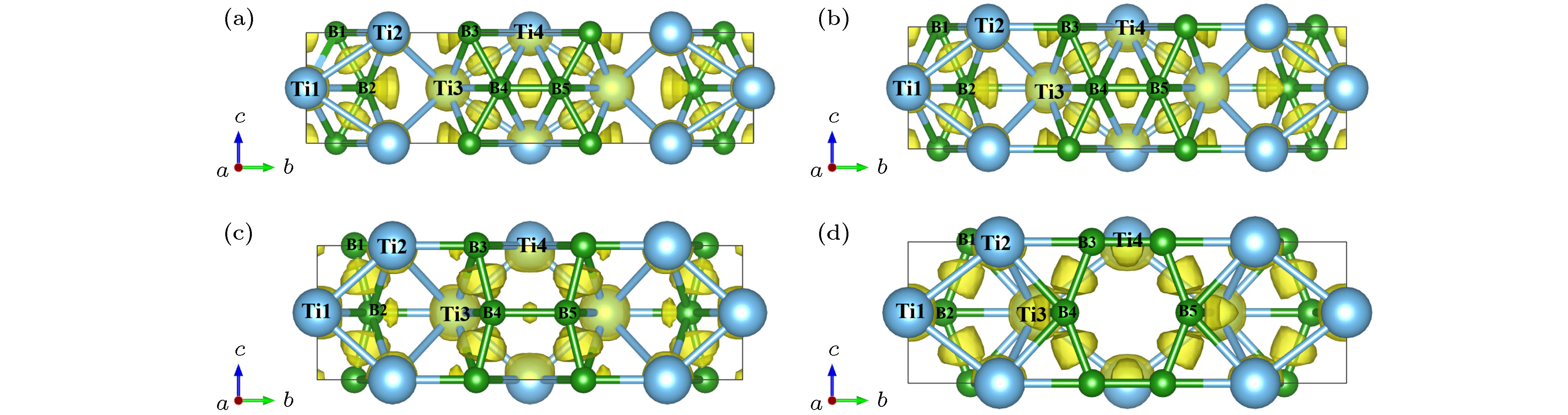
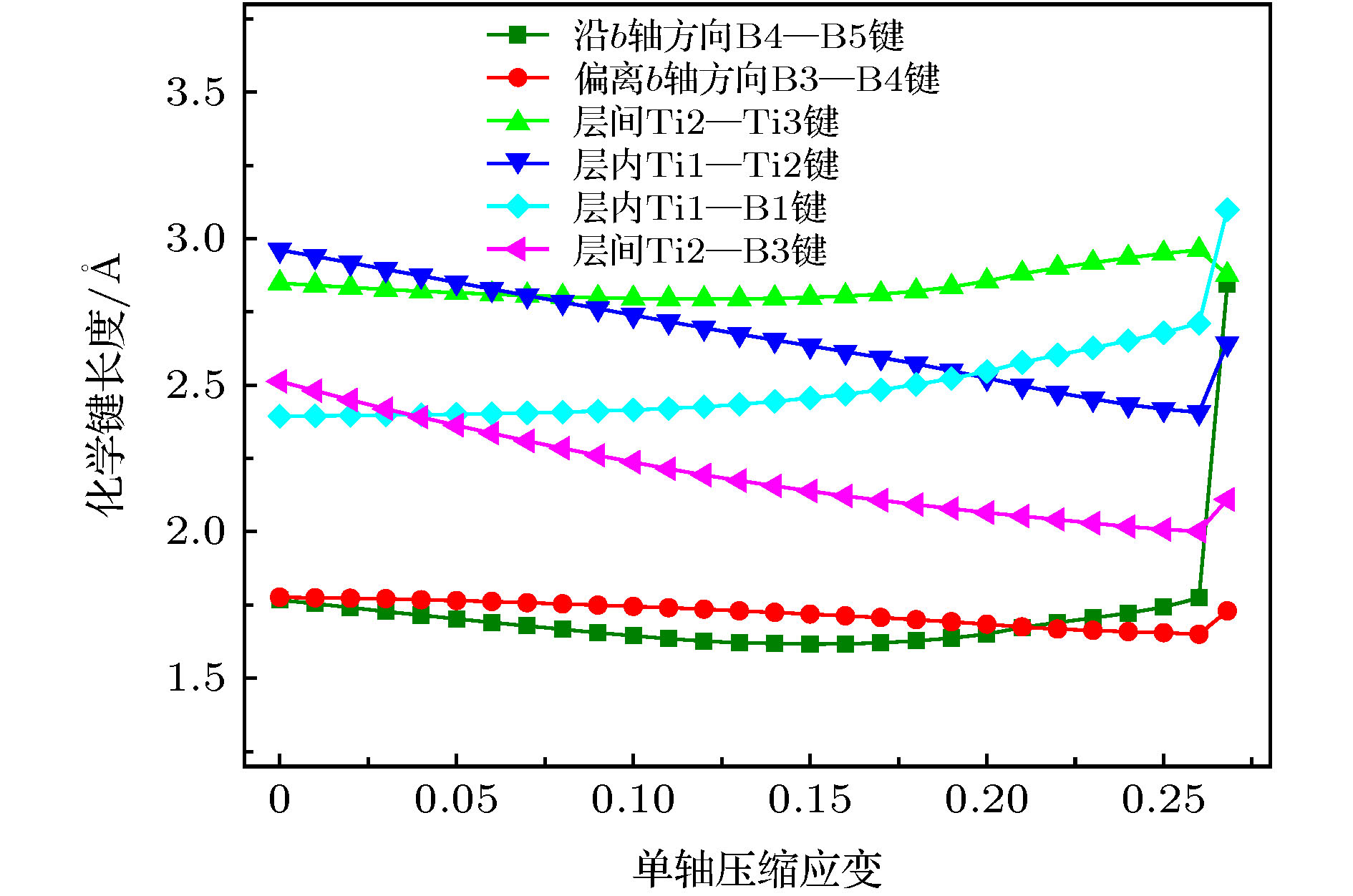
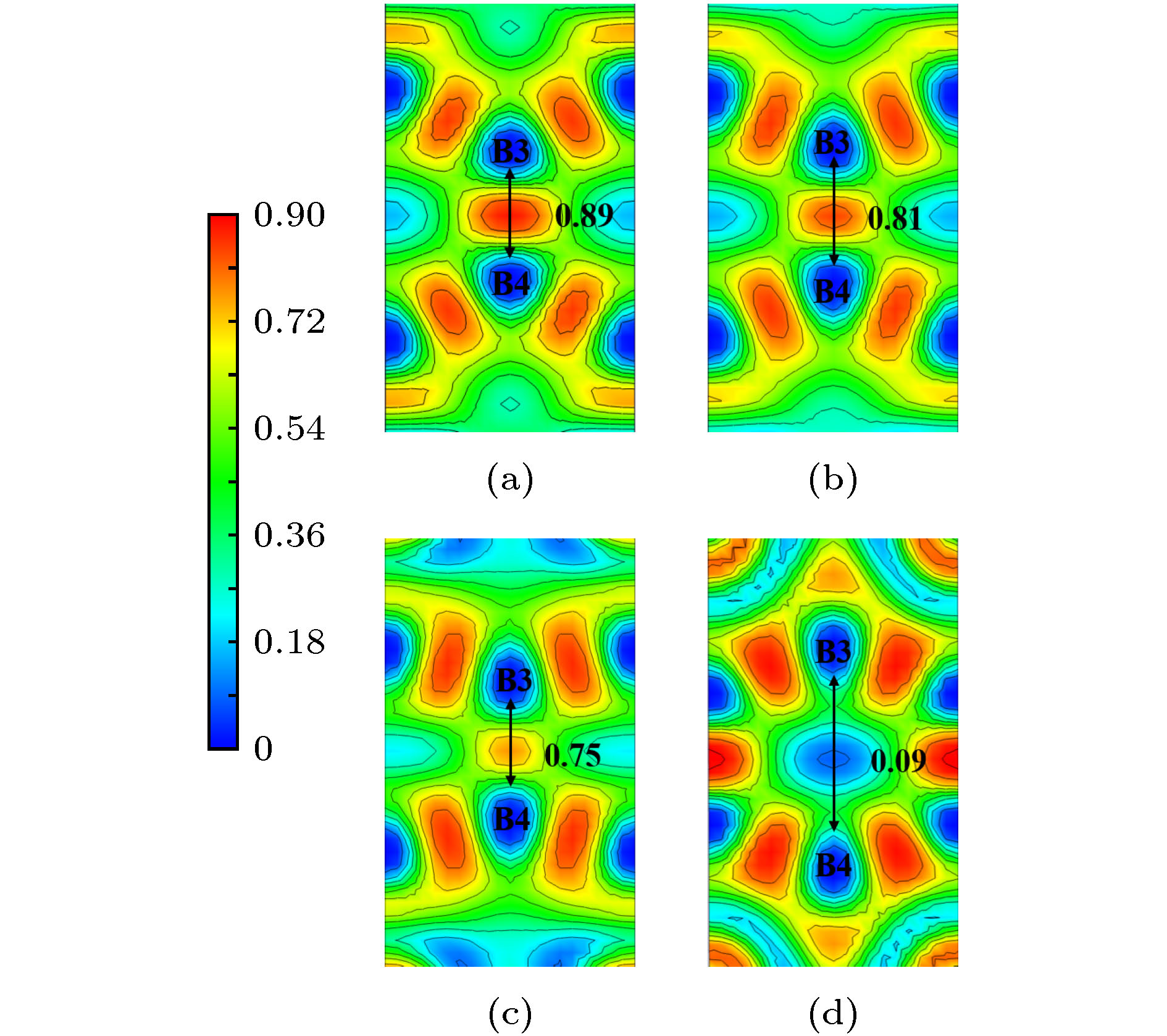
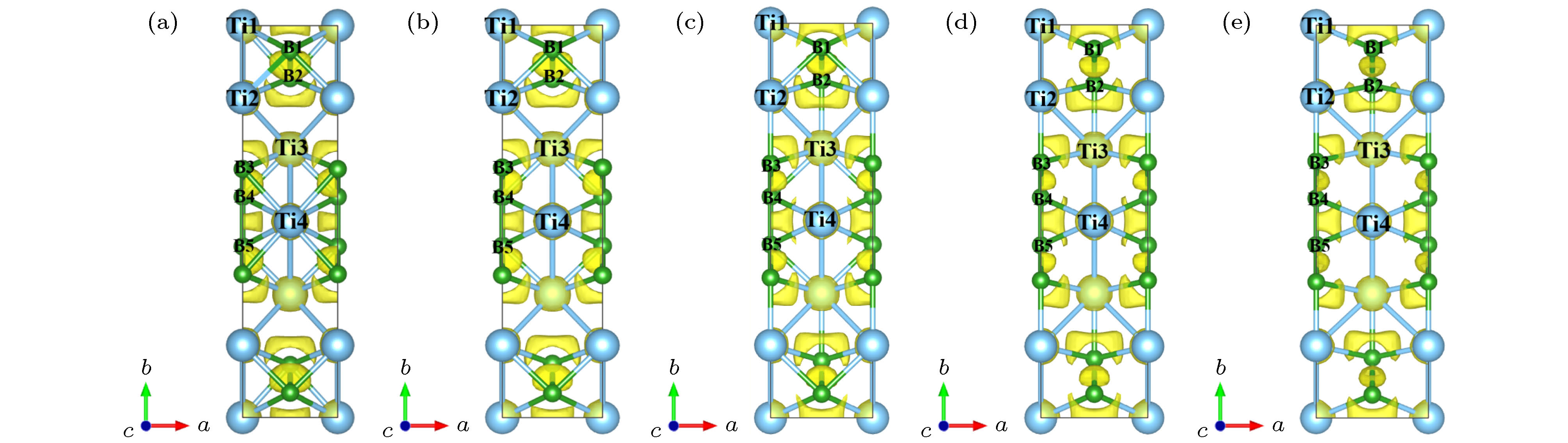
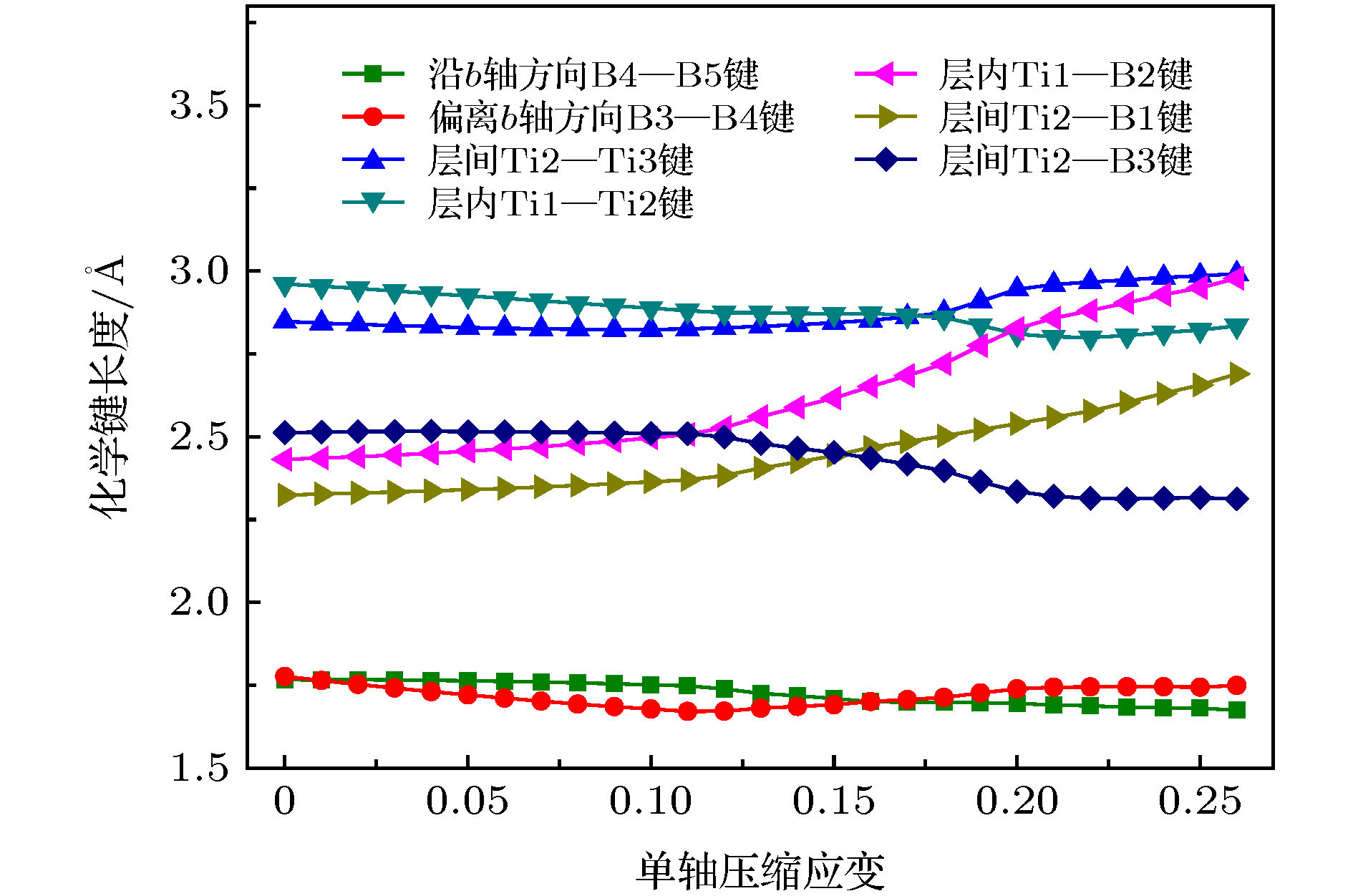
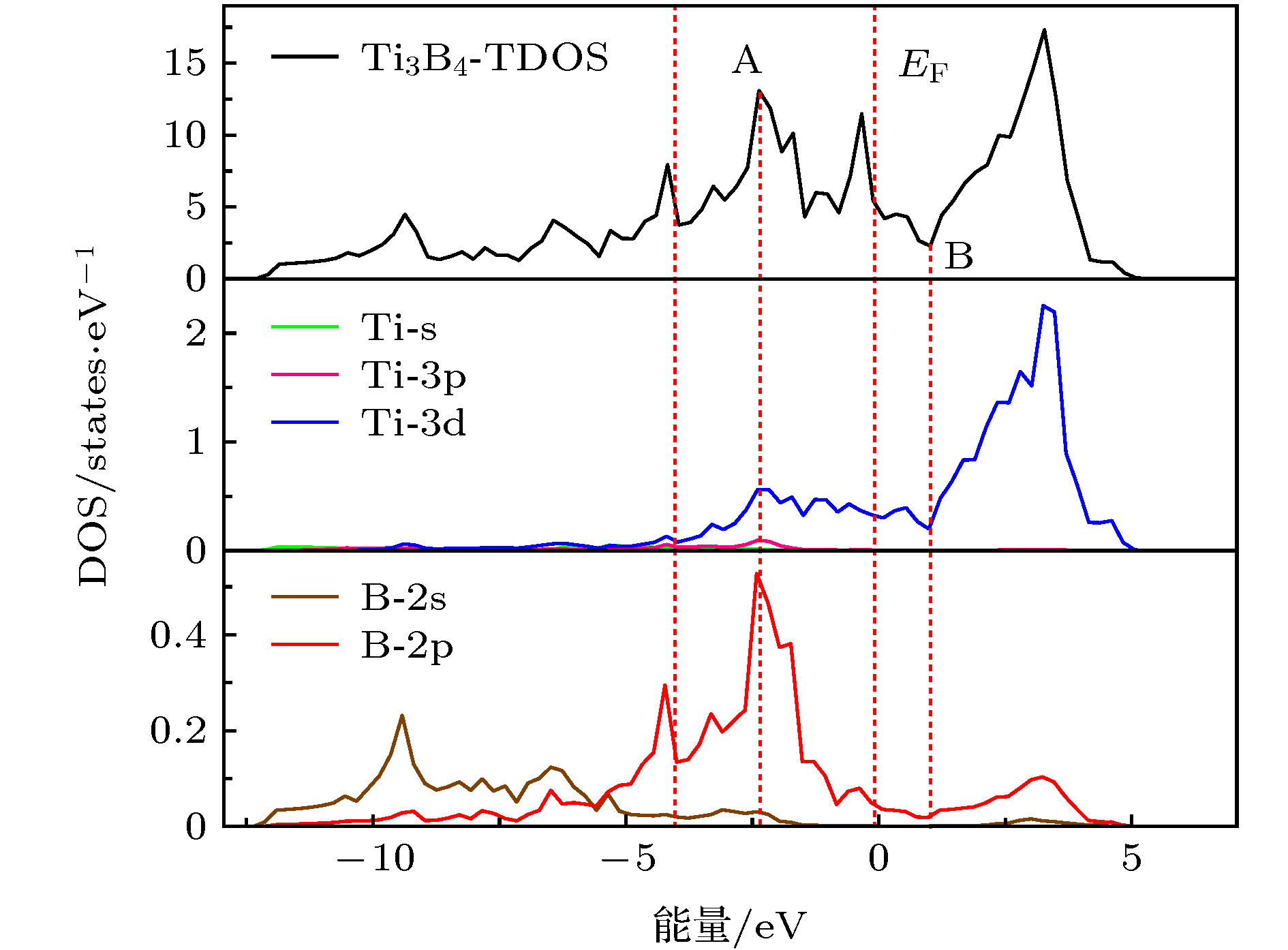
Ti₃B₄作为一种重要的钛硼化合物, 被广泛应用于工业生产和国防军事中. 但是有关Ti₃B₄在外载荷下的变形行为却鲜有报道, 这在很大程度上限制了它的应用. 本文采用基于密度泛函理论的第一性原理方法研究了Ti₃B₄在不同方向单轴压缩下的力学行为、电子结构以及变形机制. 结果表明, 在不同方向单轴压缩下, Ti₃B₄的变形行为表现出很强的各向异性. a轴压缩下, 层内Ti- Ti键减弱使Ti₃B₄承载能力降低, 最终层间Ti-Ti键和沿b轴B-B键断裂造成压缩应力突降; b轴压缩下, 层内Ti-B键减弱和层间Ti-B键增强导致Ti₃B₄承载能力逐渐降低, B-B键断裂导致结构破坏; c轴压缩下, 层内Ti-B键断裂和层间Ti-B键形成使结构稳定性降低. 由态密度分布可知, 在单轴压缩下, 变形后的Ti₃B₄仍然呈现金属性, 但是其共价性能降低. 通过讨论Ti₃B₄在不同方向单轴压缩下的力学行为与微观变形机制可以为改善其宏观性能提供一定的理论指导.

关键词:

Abstract

As an important Ti-B component, Ti₃B₄ has been widely used in industry and military applications. However, its deformation behaviors are not clear, which greatly limits its applications. First-principles methods based on density function theory were employed to investigate the mechanical, electronic properties and deformation mechanisms of Ti₃B₄ under uniaxial compressions along different axis. The results show that the structure underwent a massive change under different axial compressions. Strong anisotropic of deformation behaviors in Ti₃B₄ was observed. The compressive strength along b-axis is the highest in Ti₃B₄ structure. Under a-axis compression, the interaction between intralayer Ti—Ti bonds becomes weaker as the compressive strain increases, causing the partly damage of Ti₃B₄. However, in this process, the structure is not destroyed and can sustain the stress continuously. After that, the interlayer Ti—Ti bonds and the intralyer B—B bonds which are along b-axis, are broken and then it causes the sudden drop in stress, implying that the Ti₃B₄ structure is fully destroyed. Under b-axis compression, the changes of Ti—B bonds in Ti₃B₄ structure lead to the decrease of stress. Similarly, the structure can sustain the stress continuously in the process. Then, the B—B bonds which are along b-axis are broken, resulting in the sudden drop in stress. Under c-axis compression, the formation of interlayer Ti—B bonds and the breakage of intralayer Ti—B bonds result in structural instability of Ti₃B₄. Meanwhile, the deformed Ti₃B₄ still exhibits a metallic feature in the crystalline state after uniaxial compressions. However, there is no noticeable pseudogap in DOS spectra for a-axis and b-axis compressions. While for c-axis compression, there still exists a pseudogap around the Fermi energy, but it moves to the lower energy. And the pseudogap becomes narrower than that of the initial structure, which means that the covalent properties of Ti₃B₄ are reduced after deformations. The present work provides necessary insights in understanding the mechanical behaviors and deformation mechanisms of Ti₃B₄, which is the basis for improving the mechanical performance of Ti₃B₄ at macroscale.

Keywords:

作者及机构信息

1.
武汉理工大学, 新材料力学理论与应用湖北省重点实验室, 武汉　430070

2.
武汉理工大学, 材料复合新技术国家重点实验室, 武汉　430070

3.
武汉理工大学, 先进材料制造装备与技术研究院, 武汉　430070

通信作者: 徐爽, xu_shuang@whut.edu.cn

基金项目: 国家级-国家自然科学基金重点项目(51521001, 51502220, 11402183, U1230107)

Authors and contacts

1.
Hubei Key Laboratory of Theory and Application of Advanced Materials Mechanics, Wuhan University of Technology, Wuhan 430070, China

2.
State Key Laboratory of Advanced Technology for Materials Synthesis and Processing, Wuhan University of Technology, Wuhan 430070, China

3.
Institute of Advanced Material Manufacturing Equipment and Technology, Wuhan University of Technology, Wuhan 430070, China

Corresponding author: Xu Shuang, xu_shuang@whut.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	Li P F, Zhou R L, Zeng X C 2015 ACS Appl. Mater. Interfaces 7 15607 Google Scholar
[2]	Munro R G 2000 J. Res. Nat. Inst. Stand. Technol. 105 709 Google Scholar
[3]	黎军军, 赵学坪, 陶强, 黄晓庆, 朱品文, 崔田, 王欣 2013 62 026202 Google Scholar Li J J, Zhao X P, Tao Q, Huang X Q, Zhu P W, Cui T, Wang X 2013 Acta Phys. Sin. 62 026202 Google Scholar
[4]	Murray J L, Liao P K, Spear K E 1986 Bull. Alloy Phase Diagrams 7 550 Google Scholar
[5]	Spear K E, Mcdowell P, Mcmahon F 1986 J. Am. Ceram. Soc. 69 C-4 Google Scholar
[6]	Huang F, Fu Z Y, Yan A H, Wang W M, Wang H, Zhang J Y, Zhang Q J 2010 Powder Technol. 197 83 Google Scholar
[7]	Panda K B, Ravi Chandran K S 2006 Comput. Mater. Sci. 35 134 Google Scholar
[8]	Ma X Y, Li C R, Du Z M, Zhang W J 2004 J. Alloys Compd. 370 149 Google Scholar
[9]	Yan H Y, Wei Q, Chang S M, Guo P 2011 Trans. Nonferrous Met. Soc. China (English Ed.) 21 1627 Google Scholar
[10]	Tian J Z, Zhao Y H, Wang B, Hou H, Zhang Y M 2018 Mater. Chem. Phys. 209 200 Google Scholar
[11]	Sun L, Gao Y M, Xiao B, Li Y F, Wang G L 2013 J. Alloys Compd. 579 457 Google Scholar
[12]	Zhang X H, Luo X G, Li J P, Hu P, Han J C 2010 Scr. Mater. 62 625 Google Scholar
[13]	Cheng T B, Li W G 2015 J. Am. Ceram. Soc. 98 190 Google Scholar
[14]	Sun M, Wang C Y, Liu J P 2018 Chin. Phys. B 27 077103 Google Scholar
[15]	Arpita Aparajita A N, Sanjay Kumar N R, Chandra Shekar N V, Kalavathi S 2017 Mater. Res. Express 4 096508 Google Scholar
[16]	Tian D C, Wang X B 1992 J. Phys. Condens. Matter 4 8765 Google Scholar
[17]	Mouffok B, Feraoun H, Aourag H 2006 Mater. Lett. 60 1433 Google Scholar
[18]	Vajeeston P, Ravindran P, Ravi C, Asokamani R 2001 Phys. Rev. B 63 045115 Google Scholar
[19]	Wang C L, Yu B H, Huo H L, Chen D, Sun H B 2009 Chin. Phys. B 18 1248 Google Scholar
[20]	Peng F, Fu H Z, Cheng X L 2007 Phys. B Condens. Matter 400 83 Google Scholar
[21]	Xiang H M, Feng Z H, Li Z P, Zhou Y C 2015 J. Appl. Phys. 117 225902 Google Scholar
[22]	Wang M L 2014 Phys. Scr. 89 115702 Google Scholar
[23]	Lu J Q, Qin J N, Chen Y F, Zhang Z W, Lu W J, Zhang D 2010 J. Alloys Compd. 490 118 Google Scholar
[24]	Zhang R, Wang D J, Yuan S J 2017 Mater. Des. 134 250 Google Scholar
[25]	Chen D, Chen Z, Wu Y, Wang M L, Ma N H, Wang H W 2014 Intermetallics 52 64 Google Scholar
[26]	Panda K B, Ravi Chandran K S 2006 Acta Mater. 54 1641 Google Scholar
[27]	Rou S, Ravi Chandran K S 2018 J. Am. Ceram. Soc. 101 4308 Google Scholar
[28]	Wang G L, Li Y F, Gao Y M, Cheng Y H, Ma S Q 2015 Comput. Mater. Sci. 104 29 Google Scholar
[29]	Li J, Liu L S, Xu S, Zhang J Y and She W C 2019 J. Appl. Phys. A 125 222 Google Scholar
[30]	房玉真, 孔祥晋, 王东亭, 崔守鑫, 刘军海 2018 67 117101 Google Scholar Fang Y Z, Kong X J, Wang D T, Cui S X, Liu J H 2018 Acta Phys. Sin. 67 117101 Google Scholar
[31]	丁超, 李卫, 刘菊燕, 王琳琳, 蔡云, 潘沛锋 2018 67 213102 Google Scholar Ding C, Li W, Liu J Y, Wang L L, Cai Y, Pan P F 2018 Acta Phys. Sin. 67 213102 Google Scholar
[32]	刘琪, 管鹏飞 2018 67 178101 Google Scholar Liu Q, Guan P F 2018 Acta Phys. Sin. 67 178101 Google Scholar
[33]	He X, Li J B 2019 Chin. Phys. B 28 037301 Google Scholar
[34]	吕常伟, 王臣菊, 顾建兵 2019 68 077102 Google Scholar Lv C W, Wang C J, Gu J P 2019 Acta Phys. Sin. 68 077102 Google Scholar
[35]	Lu B K, Wang C Y 2018 Chin. Phys. B 27 077104 Google Scholar
[36]	Kresse G 1999 Phys. Rev. B 59 1758 Google Scholar
[37]	Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15 Google Scholar
[38]	Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169 Google Scholar
[39]	Becke A D, Edgecombe K E 1990 J. Chem. Phys. 92 5397 Google Scholar
[40]	Momma K, Izumi F 2011 J. Appl. Crystallogr. (International Union Crystallogr.-IUCr) 44 1272 Google Scholar
[41]	Segall M, Shah R, Pickard C 1996 Phys. Rev. B 54 16317 Google Scholar
[42]	Gull E, Parcollet O, Millis A J 2013 Phys. Rev. Lett. 110 216405 Google Scholar
[43]	王欣, 王发展, 雷哲锋, 王博, 马姗, 王哲, 吴振 2013 62 123101 Google Scholar Wang X, Wang F Z, Lei Z F, Wang B, Ma S, Wang Z, Wu Z 2013 Acta Phys. Sin. 62 123101 Google Scholar

施引文献

图 1 Ti₃B₄的晶体结构　(a) 单晶胞结构; (b) 超晶胞结构. 其中蓝色原子为Ti原子, 绿色原子为B原子

Fig. 1. The crystal structure of Ti₃B₄: (a) The unit cell; (b) the supercell. The blue balls in the figure denote the Ti atoms, and the green balls refer to the B atoms.

下载: 全尺寸图片幻灯片

图 2 Ti₃B₄晶体在单轴压缩载荷下的应力-应变曲线

Fig. 2. The stress-strain relationship of Ti₃B₄ under uniaxial compressions.

下载: 全尺寸图片幻灯片

图 3 a轴压缩时不同应变下Ti₃B₄晶体的结构和ELF分布图　(a) ε = 0.00; (b) ε = 0.10; (c) ε = 0.15; (d) ε = 0.24; (e) ε = 0.242

Fig. 3. The structural and ELF at various strains under a-axis uniaxial compression: (a) ε = 0.00; (b) ε = 0.10; (c) ε = 0.15; (d) ε = 0.24; (e) ε = 0.242.

下载: 全尺寸图片幻灯片

图 4 Ti₃B₄晶体在a轴压缩下化学键长度变化

Fig. 4. Variation of bond lengths as a function of a-axis uniaxial compressive strain.

下载: 全尺寸图片幻灯片

图 5 a轴压缩时临界应变下Ti₃B₄晶体(100)晶面ELF分布图　(a) ε = 0.24; (b) ε = 0.242

Fig. 5. The ELF at critical strains of (100) crystal plane in Ti₃B₄ structure under a-axis uniaxial compression: (a) ε = 0.24; (b) ε = 0.242.

下载: 全尺寸图片幻灯片

图 6 b轴压缩时不同应变下Ti₃B₄晶体的结构和ELF分布图　(a) ε = 0.10; (b) ε = 0.14; (c)ε = 0.26; (d) ε = 0.268

Fig. 6. The structural and ELF at various strains under b-axis uniaxial compression: (a) ε = 0.10; (b) ε = 0.14; (c) ε = 0.26; (d) ε = 0.268.

下载: 全尺寸图片幻灯片

图 7 Ti₃B₄晶体在b轴压缩下化学键长度变化

Fig. 7. Variation of bond lengths as a function of b-axis uniaxial compressive strain.

下载: 全尺寸图片幻灯片

图 8 b轴压缩时临界应变下Ti₃B₄晶体(100)晶面ELF分布图　(a) ε = 0.14; (b) ε = 0.20; (c) ε = 0.26; (d) ε = 0.268

Fig. 8. The ELF at critical strains of (100) crystal plane in Ti₃B₄ structure under b-axis uniaxial compression: (a) ε = 0.14; (b) ε = 0.20; (c) ε = 0.26; (d) ε = 0.268.

下载: 全尺寸图片幻灯片

图 9 c轴压缩时不同应变下Ti₃B₄晶体的结构和ELF分布图　(a) ε = 0.10; (b) ε = 0.13; (c) ε = 0.18; (d) ε = 0.20; (e) ε = 0.26

Fig. 9. The structural and ELF at various strains under c-axis uniaxial compression: (a) ε = 0.10; (b) ε = 0.13; (c) ε = 0.18; (d) ε = 0.20; (e) ε = 0.26.

下载: 全尺寸图片幻灯片

图 10 Ti₃B₄晶体在c轴压缩下化学键长度变化

Fig. 10. Variation of bond lengths in Ti₃B₄ as a function of c-axis uniaxial compressive strain.

下载: 全尺寸图片幻灯片

图 11 Ti₃B₄初始结构的TDOS和PDOS分布

Fig. 11. TDOS and PDOS for undeformed Ti₃B₄.

下载: 全尺寸图片幻灯片

图 12 在单轴压缩下Ti₃B₄结构在临界压缩应变处的TDOS和PDOS分布　(a) ε = 0.242 (a轴); (b) ε = 0.268 (b轴); (c) ε = 0.19 (c轴)

Fig. 12. TDOS and PDOS for Ti₃B₄ at critical strains under uniaxial compressions: (a) ε = 0.242 (a-axis); (b) ε = 0.268 (b-axis); (c) ε = 0.19 (c-axis).

下载: 全尺寸图片幻灯片

表 1 峰值A和谷值B处的Ti原子和B原子的PDOS和Ti₃B₄的TDOS (states/eV)

Table 1. The PDOS of a Ti and a B atom and TDOS of Ti₃B₄ at Peak A and Bottom B (states/eV).

D(Ti-s) D(Ti-3p) D(Ti-3d) D(B-2s) D(B-2p) D(Total)

峰值A 0.0137 0.0959 0.5610 0.0308 0.527 13.0945
谷值B 0.0001 0.0007 0.1996 0.0010 0.019 2.2669

下载: 导出CSV

map

[1]	Li P F, Zhou R L, Zeng X C 2015 ACS Appl. Mater. Interfaces 7 15607 Google Scholar
[2]	Munro R G 2000 J. Res. Nat. Inst. Stand. Technol. 105 709 Google Scholar
[3]	黎军军, 赵学坪, 陶强, 黄晓庆, 朱品文, 崔田, 王欣 2013 62 026202 Google Scholar Li J J, Zhao X P, Tao Q, Huang X Q, Zhu P W, Cui T, Wang X 2013 Acta Phys. Sin. 62 026202 Google Scholar
[4]	Murray J L, Liao P K, Spear K E 1986 Bull. Alloy Phase Diagrams 7 550 Google Scholar
[5]	Spear K E, Mcdowell P, Mcmahon F 1986 J. Am. Ceram. Soc. 69 C-4 Google Scholar
[6]	Huang F, Fu Z Y, Yan A H, Wang W M, Wang H, Zhang J Y, Zhang Q J 2010 Powder Technol. 197 83 Google Scholar
[7]	Panda K B, Ravi Chandran K S 2006 Comput. Mater. Sci. 35 134 Google Scholar
[8]	Ma X Y, Li C R, Du Z M, Zhang W J 2004 J. Alloys Compd. 370 149 Google Scholar
[9]	Yan H Y, Wei Q, Chang S M, Guo P 2011 Trans. Nonferrous Met. Soc. China (English Ed.) 21 1627 Google Scholar
[10]	Tian J Z, Zhao Y H, Wang B, Hou H, Zhang Y M 2018 Mater. Chem. Phys. 209 200 Google Scholar
[11]	Sun L, Gao Y M, Xiao B, Li Y F, Wang G L 2013 J. Alloys Compd. 579 457 Google Scholar
[12]	Zhang X H, Luo X G, Li J P, Hu P, Han J C 2010 Scr. Mater. 62 625 Google Scholar
[13]	Cheng T B, Li W G 2015 J. Am. Ceram. Soc. 98 190 Google Scholar
[14]	Sun M, Wang C Y, Liu J P 2018 Chin. Phys. B 27 077103 Google Scholar
[15]	Arpita Aparajita A N, Sanjay Kumar N R, Chandra Shekar N V, Kalavathi S 2017 Mater. Res. Express 4 096508 Google Scholar
[16]	Tian D C, Wang X B 1992 J. Phys. Condens. Matter 4 8765 Google Scholar
[17]	Mouffok B, Feraoun H, Aourag H 2006 Mater. Lett. 60 1433 Google Scholar
[18]	Vajeeston P, Ravindran P, Ravi C, Asokamani R 2001 Phys. Rev. B 63 045115 Google Scholar
[19]	Wang C L, Yu B H, Huo H L, Chen D, Sun H B 2009 Chin. Phys. B 18 1248 Google Scholar
[20]	Peng F, Fu H Z, Cheng X L 2007 Phys. B Condens. Matter 400 83 Google Scholar
[21]	Xiang H M, Feng Z H, Li Z P, Zhou Y C 2015 J. Appl. Phys. 117 225902 Google Scholar
[22]	Wang M L 2014 Phys. Scr. 89 115702 Google Scholar
[23]	Lu J Q, Qin J N, Chen Y F, Zhang Z W, Lu W J, Zhang D 2010 J. Alloys Compd. 490 118 Google Scholar
[24]	Zhang R, Wang D J, Yuan S J 2017 Mater. Des. 134 250 Google Scholar
[25]	Chen D, Chen Z, Wu Y, Wang M L, Ma N H, Wang H W 2014 Intermetallics 52 64 Google Scholar
[26]	Panda K B, Ravi Chandran K S 2006 Acta Mater. 54 1641 Google Scholar
[27]	Rou S, Ravi Chandran K S 2018 J. Am. Ceram. Soc. 101 4308 Google Scholar
[28]	Wang G L, Li Y F, Gao Y M, Cheng Y H, Ma S Q 2015 Comput. Mater. Sci. 104 29 Google Scholar
[29]	Li J, Liu L S, Xu S, Zhang J Y and She W C 2019 J. Appl. Phys. A 125 222 Google Scholar
[30]	房玉真, 孔祥晋, 王东亭, 崔守鑫, 刘军海 2018 67 117101 Google Scholar Fang Y Z, Kong X J, Wang D T, Cui S X, Liu J H 2018 Acta Phys. Sin. 67 117101 Google Scholar
[31]	丁超, 李卫, 刘菊燕, 王琳琳, 蔡云, 潘沛锋 2018 67 213102 Google Scholar Ding C, Li W, Liu J Y, Wang L L, Cai Y, Pan P F 2018 Acta Phys. Sin. 67 213102 Google Scholar
[32]	刘琪, 管鹏飞 2018 67 178101 Google Scholar Liu Q, Guan P F 2018 Acta Phys. Sin. 67 178101 Google Scholar
[33]	He X, Li J B 2019 Chin. Phys. B 28 037301 Google Scholar
[34]	吕常伟, 王臣菊, 顾建兵 2019 68 077102 Google Scholar Lv C W, Wang C J, Gu J P 2019 Acta Phys. Sin. 68 077102 Google Scholar
[35]	Lu B K, Wang C Y 2018 Chin. Phys. B 27 077104 Google Scholar
[36]	Kresse G 1999 Phys. Rev. B 59 1758 Google Scholar
[37]	Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15 Google Scholar
[38]	Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169 Google Scholar
[39]	Becke A D, Edgecombe K E 1990 J. Chem. Phys. 92 5397 Google Scholar
[40]	Momma K, Izumi F 2011 J. Appl. Crystallogr. (International Union Crystallogr.-IUCr) 44 1272 Google Scholar
[41]	Segall M, Shah R, Pickard C 1996 Phys. Rev. B 54 16317 Google Scholar
[42]	Gull E, Parcollet O, Millis A J 2013 Phys. Rev. Lett. 110 216405 Google Scholar
[43]	王欣, 王发展, 雷哲锋, 王博, 马姗, 王哲, 吴振 2013 62 123101 Google Scholar Wang X, Wang F Z, Lei Z F, Wang B, Ma S, Wang Z, Wu Z 2013 Acta Phys. Sin. 62 123101 Google Scholar

[1]	李巧利, 李慎慎, 肖继军, 陈兆旭. 静水压力作用下(H₂dabco)[K(ClO₄)₃]结构与稳定性的第一性原理研究. , 2024, 73(14): 143101. doi: 10.7498/aps.73.20240477
[2]	张博佳, 安敏荣, 胡腾, 韩腊. 镁中位错和非晶作用机制的分子动力学模拟. , 2022, 71(14): 143101. doi: 10.7498/aps.71.20212318
[3]	安敏荣, 李思澜, 宿梦嘉, 邓琼, 宋海洋. 尺寸依赖的CoCrFeNiMn晶体/非晶双相高熵合金塑性变形机制的分子动力学模拟. , 2022, 71(24): 243101. doi: 10.7498/aps.71.20221368
[4]	张硕鑫, 刘士余, 严达利, 余浅, 任海涛, 于彬, 李德军. Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的结构稳定性和力学性质的第一性原理研究. , 2021, 70(11): 117102. doi: 10.7498/aps.70.20210191
[5]	彭军辉, TikhonovEvgenii. 三元Hf-C-N体系的空位有序结构及其力学性质和电子性质的第一性原理研究. , 2021, 70(21): 216101. doi: 10.7498/aps.70.20210244
[6]	胡雪兰, 卢睿智, 王智隆, 王亚如. Re对Ni₃Al微观结构及力学性质影响的第一原理研究. , 2020, 69(10): 107101. doi: 10.7498/aps.69.20200097
[7]	黄瑞, 李春, 金蔚, GeorgiosLefkidis, WolfgangHübner. 双磁性中心内嵌富勒烯Y₂C₂@C₈₂-C₂(1)中的超快自旋动力学行为. , 2019, 68(2): 023101. doi: 10.7498/aps.68.20181887
[8]	王鹏, 徐建刚, 张云光, 宋海洋. 晶粒尺寸对纳米多晶铁变形机制影响的模拟研究. , 2016, 65(23): 236201. doi: 10.7498/aps.65.236201
[9]	王雪飞, 马静婕, 焦照勇, 张现周. Ti3(SnxAl1-x)C2固溶体电学、力学和热学性能的理论研究. , 2016, 65(20): 206201. doi: 10.7498/aps.65.206201
[10]	王晓媛, 赵丰鹏, 王杰, 闫亚宾. 金属有机框架材料力学、电学及其应变调控特性的第一原理研究. , 2016, 65(17): 178105. doi: 10.7498/aps.65.178105
[11]	曾小波, 朱晓玲, 李德华, 陈中钧, 艾应伟. IrB和IrB2力学性质的第一性原理计算. , 2014, 63(15): 153101. doi: 10.7498/aps.63.153101
[12]	金硕, 孙璐. 带有碳杂质的钨中氢稳定性的第一性原理研究. , 2012, 61(4): 046104. doi: 10.7498/aps.61.046104
[13]	代云雅, 杨莉, 彭述明, 龙兴贵, 周晓松, 祖小涛. 金属氢化物力学性能的第一性原理研究. , 2012, 61(10): 108801. doi: 10.7498/aps.61.108801
[14]	李德华, 苏文晋, 朱晓玲. BC5力学性质的第一性原理计算. , 2012, 61(2): 023103. doi: 10.7498/aps.61.023103
[15]	李青坤, 孙毅, 周玉, 曾凡林. 第一性原理研究bct-C4碳材料的强度性质. , 2012, 61(9): 093104. doi: 10.7498/aps.61.093104
[16]	李青坤, 孙毅, 周玉, 曾凡林. 第一性原理研究hcp-C3碳体环材料的力学性质. , 2012, 61(4): 043103. doi: 10.7498/aps.61.043103
[17]	王晓中, 林理彬, 何捷, 陈军. 第一性原理方法研究He掺杂Al晶界力学性质. , 2011, 60(7): 077104. doi: 10.7498/aps.60.077104
[18]	李德华, 朱晓玲, 苏文晋, 程新路. PtN2的结构和力学性质的第一性原理计算. , 2010, 59(3): 2004-2009. doi: 10.7498/aps.59.2004
[19]	顾娟, 王山鹰, 苟秉聪. Au和3d过渡金属元素混合团簇结构、电子结构和磁性的研究. , 2009, 58(5): 3338-3351. doi: 10.7498/aps.58.3338
[20]	丁迎春, 徐明, 潘洪哲, 沈益斌, 祝文军, 贺红亮. γ-Si3N4在高压下的电子结构和物理性质研究. , 2007, 56(1): 117-122. doi: 10.7498/aps.56.117

计量

文章访问数: 6938
PDF下载量: 109
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

单轴压缩下Ti₃B₄的力学、电学性能及变形机制的第一性原理研究