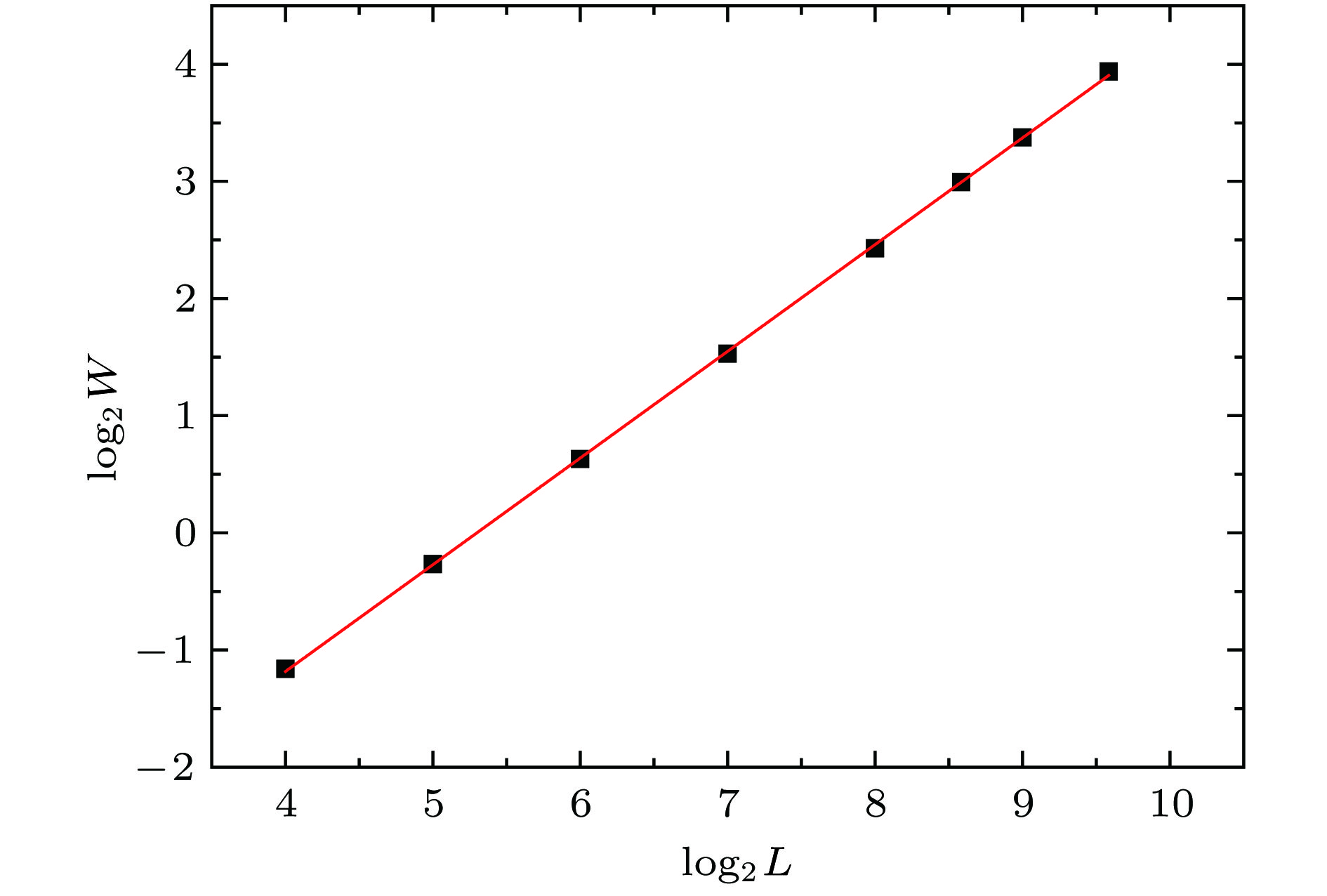
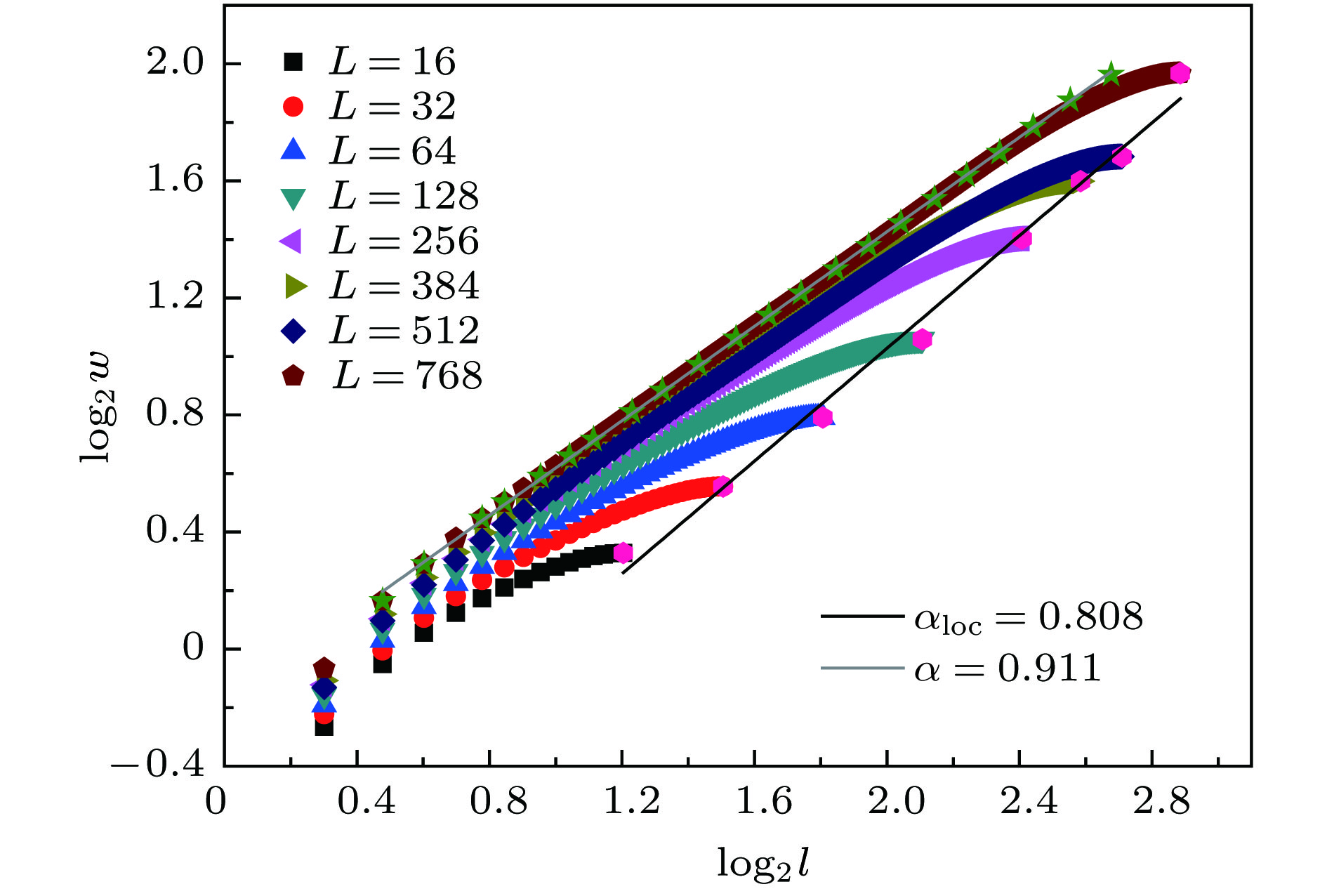
-
石墨烯等材料具有典型的二维蜂巢结构, 而随机电阻丝模型则是研究非均匀材料断裂十分有效的统计物理学模型. 本文尝试对二维蜂巢结构随机电阻丝网络熔断的动力学过程及熔断面性质进行数值模拟分析, 以此来研究二维非均质蜂窝材料熔断的动力学性质和熔断面的动力学标度性质. 模拟研究表明, 二维随机蜂窝网格的熔断动力学过程和熔断面具有明显的标度性质, 得到的熔断面整体和局域粗糙度指数分别为
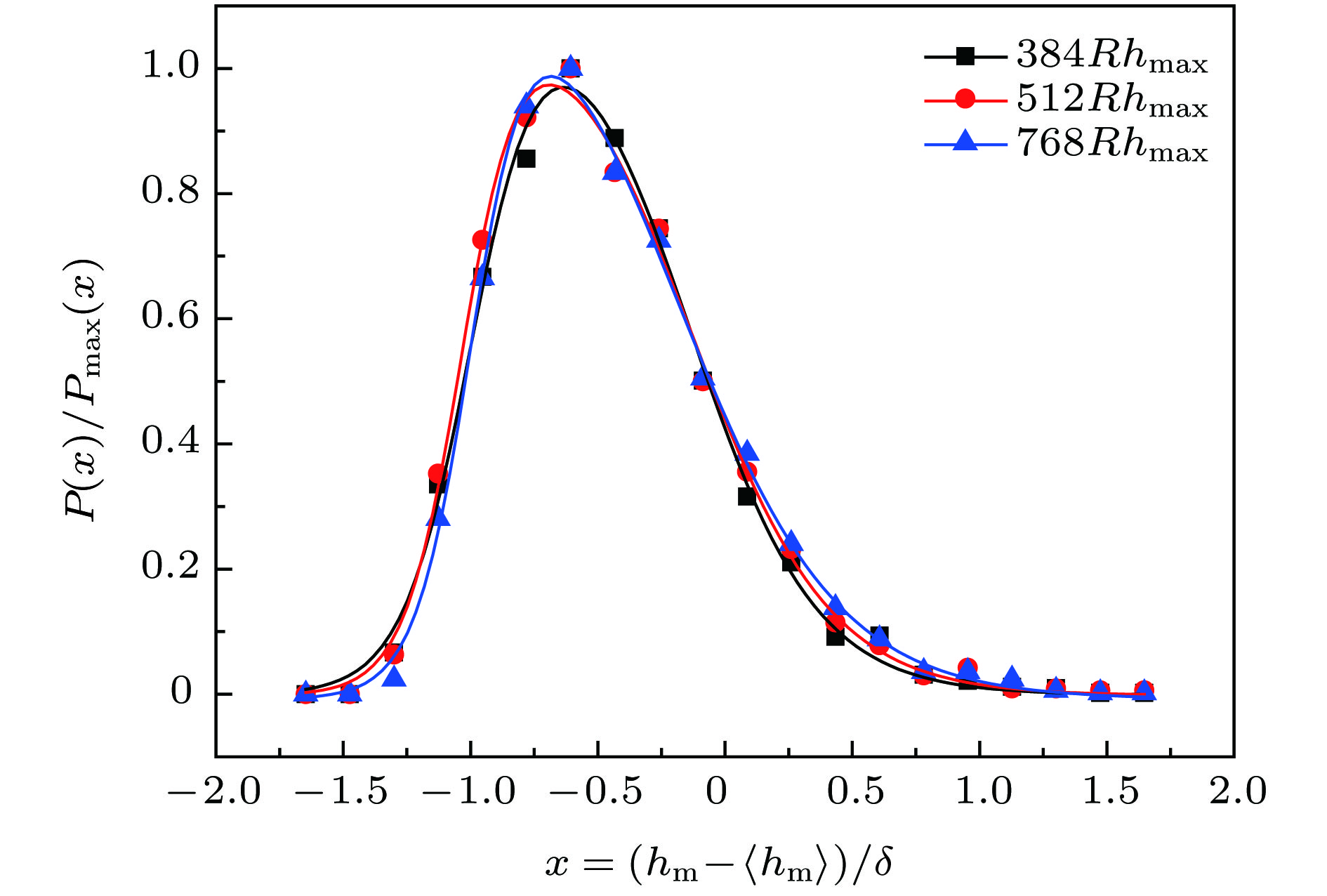
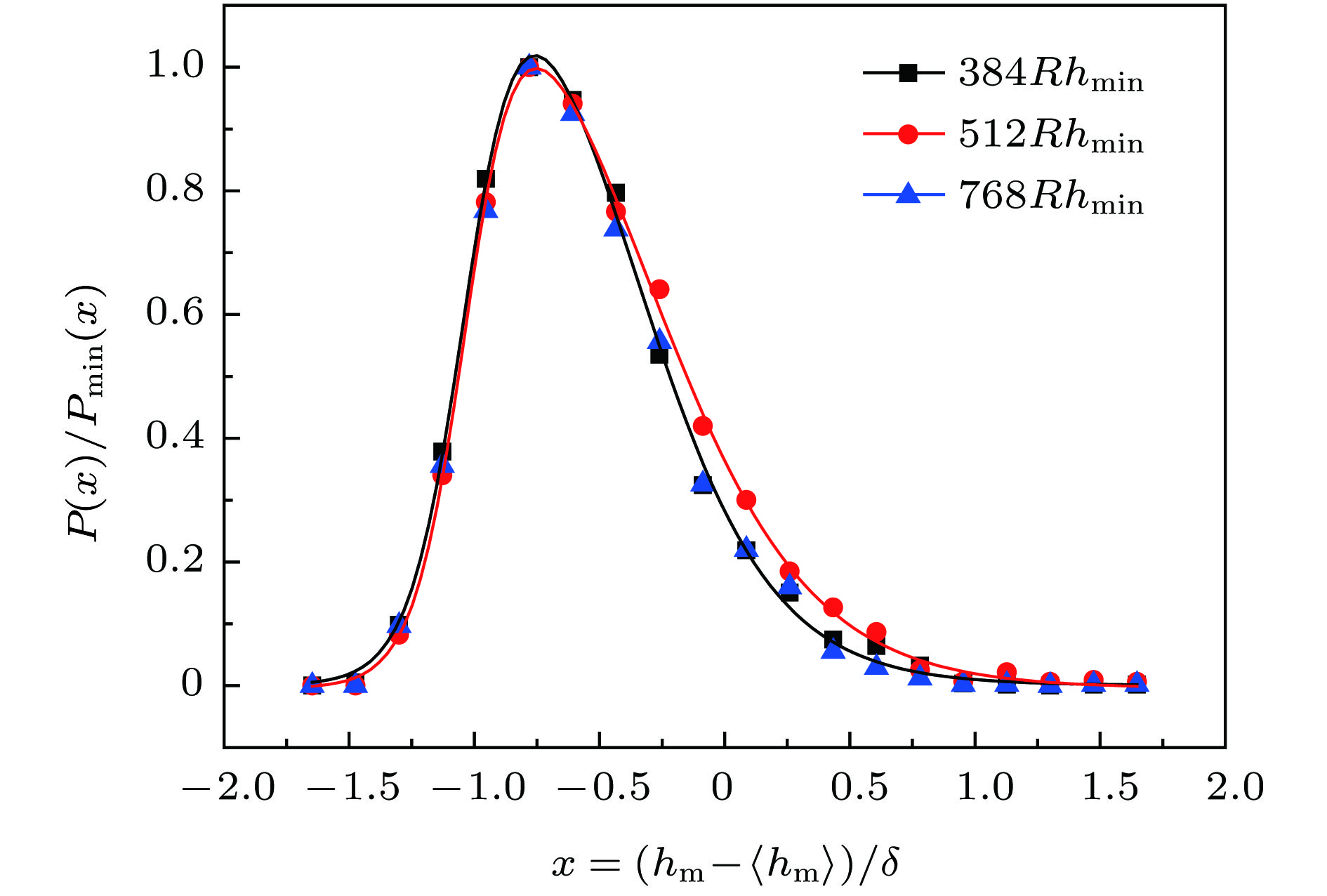
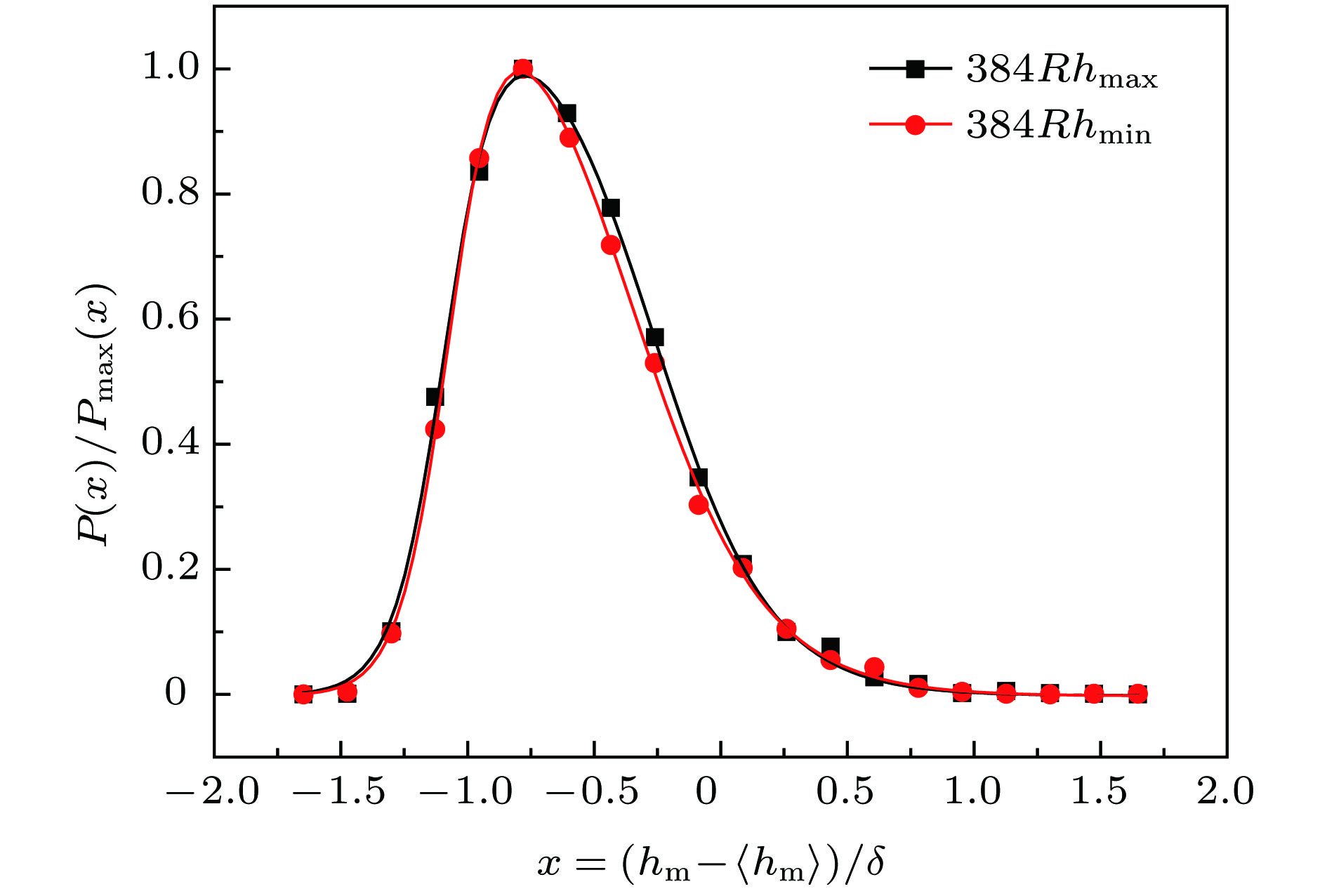
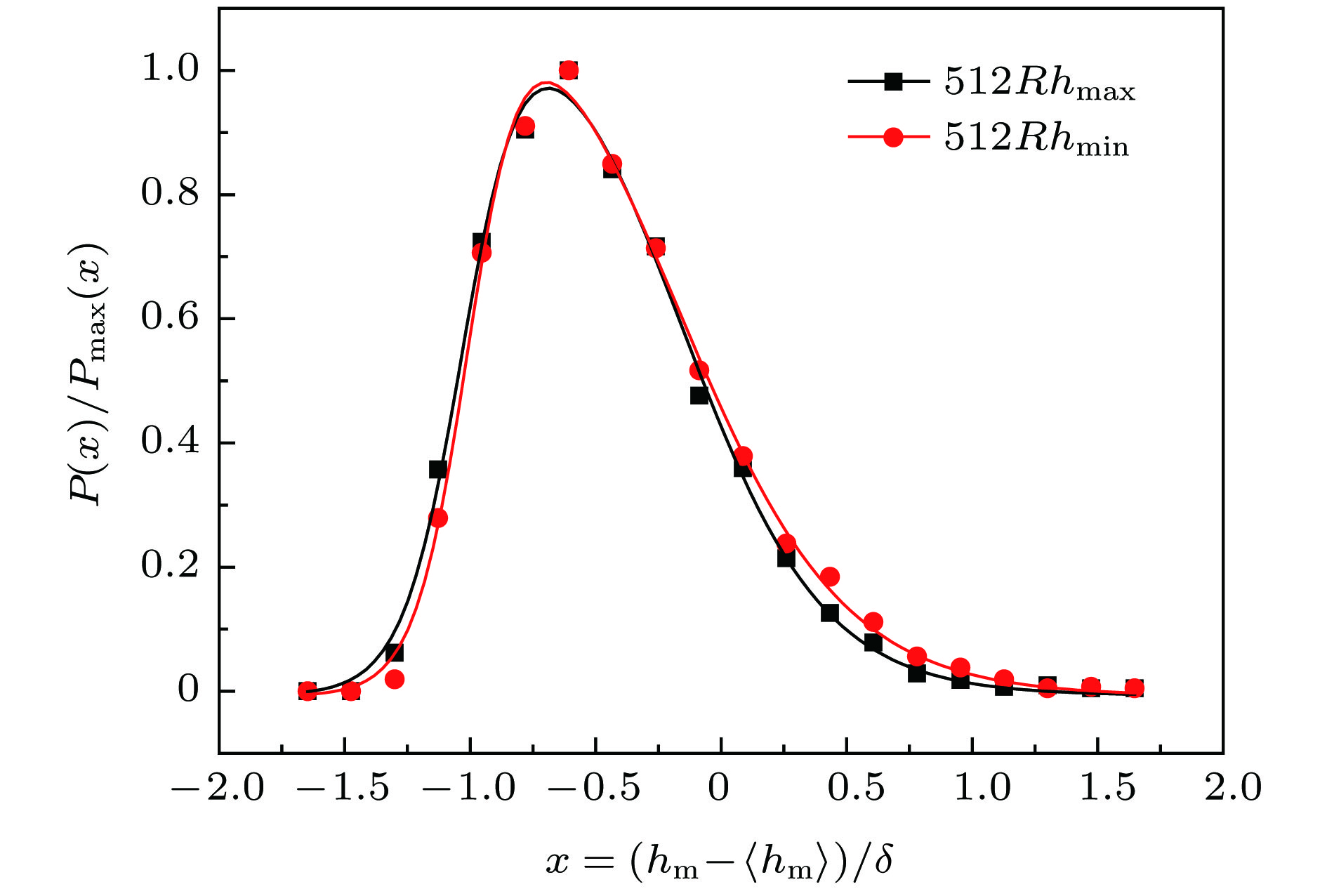
$\alpha = 0.911 \pm 0.005$ 和${\alpha _{{\rm{loc}}}} = 0.808 \pm 0.003$ , 这两者之间的明显差异表明熔断面具有奇异标度性. 通过对熔断面极值高度的分析发现, 熔断面高度的极值统计分布能很好地满足Asym2sig型分布, 而不是最常见的三种极值统计分布. 本文的研究表明, 随机电阻丝模型在模拟非均匀材料的电流熔断过程和熔断表面标度性的分析中同样适用和有效.Graphene and other materials have a typical two-dimensional (2D) honeycomb structure. The random fuse model is a statistical physics model that is very effective in studying the fracture dynamics of heterogeneous materials. In order to study the current fusing process and the properties of the fractured surface of 2D honeycomb structure materials such as graphene, in this paper we attempt to numerically simulate and analyze the fusing process and melting profile properties of the 2D honeycomb structure random fuse network. The results indicate that the surface width exhibits a good scaling behavior and has a linear relationship with the system size, and that the out-of-plane roughness exponent displays a global value of$\alpha = 0.911 \pm 0.005$ and a local value of${\alpha _{{\rm{loc}}}} = 0.808 \pm 0.003$ , approximate to those of the materials studied. The global and local roughness and their difference indicate that the fusing process and the fracture profile exhibit significant scale properties and have a strange scale. On the other hand, by analyzing the extreme values of the fused surface with different system sizes, the extreme heights can be collapsed very well, after a lot of trials and analysis, it is found that the extreme statistical distribution of the height of the fused surface can well satisfy the Asym2sig type distribution. The extreme height distributions of fracture surfaces can be fitted by Asym2Sig distribution, rather than the three kinds of usual extreme statistical distributions, i.e. Weibull, Gumbel, and Frechet distributions. The relative maximal and minimum height distribution of the fused surface at the same substrate size have a good symmetry. In the simulation calculation process of this paper, the coefficient matrix is constructed by using the node analysis method, and the Cholesky decomposition is performed on the coefficient matrix, and then the Sherman-Morrison-Woodbury algorithm is used to quickly invert the coefficient matrix, which greatly optimizes the calculation process and calculation. The efficiency makes the numerical simulation calculation and analysis performed smoothly. The research in this paper indicates that the random fuse model is a very effective theoretical model in the numerical analysis of the scaling properties of rough fracture surfaces, and it is also applicable to the current fusing process of the inhomogeneous material and the scaling surface analysis of the fusing surface. In this paper, it is found that materials with anisotropic structure can also find their fracture mode by energization, and the properties of fracture surface can provide reference for the study of mechanical properties of honeycomb structural materials. It is a very effective statistical physical model, and this will expand the field of applications of random fuse models.-
Keywords:
- graphene honeycomb structure /
- random fuse model /
- roughness /
- extreme statistics
[1] Abergel D S L, Apalkov V, Berashevich J 2010 Adv. Phys. 59 261
Google Scholar
[2] Shin Y J, Gopinadhan K, Narayanapillai K 2013 Appl. Phys. Lett. 102 666
[3] Lu Y H, Shi L, Zhang C, Feng Y P 2009 Phys. Rev. B 80 233410
Google Scholar
[4] Moura M J B, Marder M 2013 Phys. Rev. E 88 032405
Google Scholar
[5] Ghorbanfekr-Kalashami H, Neek-Amal M, Peeters F M 2016 Phys. Rev. B 93 174112
Google Scholar
[6] Alava M J, Nukala P K V V, Zapperi S 2006 Adv. Phys. 55 351
[7] Garcimart'ın A, Guarino A, Bellon L, Ciliberto S 1997 Phys. Rev. Lett. 79 3202
Google Scholar
[8] Maes C, van Moffaert A, Frederix H, Strauven H 1998 Phys. Rev. B 57 4987
[9] Petri A, Paparo G, Vespignani A, Alippi A, Costantini M 1994 Phys. Rev. Lett. 73 3423
Google Scholar
[10] Salminen L I, Tolvanen A I, Alava M J 2002 Phys. Rev. Lett. 89 185503
Google Scholar
[11] Arcangelis L, Redner S, Herrmann H J 1985 J. Phys. Lett. 46 585
Google Scholar
[12] Schramm O 2000 Israel J. Math. 118 221
Google Scholar
[13] Claudio M, Ashivni S, Nukala P K V V, Alava M J, Sethna J P, Zapperi S 2012 Phys. Rev. Lett. 108 065504
Google Scholar
[14] Duxbury P M, Beale P D, Leath P L 1986 Phys. Rev. Lett. 59 155
[15] Nukala P K V V, Srdan S, Zapperi S 2004 J. Stat. Mech. 8 P08001
[16] Toussaint R, Hansen A 2006 Phys. Rev. E 73 046103
Google Scholar
[17] Jan Øystein H B, Hansen A 2008 Phys. Rev. Lett. 100 045501
Google Scholar
[18] Davis T A, Hager W W 1999 Siam J. Matrix Anal. A 22 997
[19] Family F, Vicsek T 1985 J. Phys. A 18 L75
Google Scholar
[20] Xun Z P, Tang G, Han K, Xia H, Hao D P, Li Y 2012 Phys. Rev. E 85 041126
Google Scholar
[21] 寻之朋 2017 离散模型表面界面粗化的动力学标度性质(徐州: 中国矿业大学出版社) 第88页
Xun Z P 2017 The Dynamic Scale Properties of the Surface Roughness of the Discrete Growth Model (Xuzhou: China Mining University Press) p88
[22] Raychaudhuri S, Cranston M, Przybyla C, Shapir Y 2001 Phys. Rev. Lett. 87 136101
Google Scholar
[23] Foltin G, Oerding K, Racz Z, Workman R L, Zia R K P 1994 Phys. Rev. E 50 639
Google Scholar
[24] Majumdar S N, Comtet A 2004 Phys. Rev. Lett. 92 225501
Google Scholar
[25] Derrida B, Lebowitz J L 1998 Phys. Rev. Lett. 80 209
Google Scholar
[26] Majumdar S N, Comtet A 2005 Stat. Phys. 119 777
Google Scholar
[27] Fisher R A, Tippett L H C 1928 Proc. Cambridge Philos. Soc. 24 180
Google Scholar
[28] Bramwell S T, Christensen K, Fortin J, Holdsworth P C W, Jensen H J, Lise S, Lopez J M, Nicodemi M, Pinton J F, Sellitto M 2000 Phys. Rev. Lett. 84 3744
Google Scholar
[29] Antal T, Droz M, Gyorgyi G, Racz Z 2001 Phys. Rev. Lett. 87 240601
Google Scholar
[30] Lee D S 2005 Phys. Rev. Lett. 95 150601
Google Scholar
[31] Lee S B, Jeong H C, Kim J M 2008 J. Stat. Mech. 9 P12013
[32] Wen R J, Tang G, Han K, Xia H, Hao D P, Xun Z P, Chen Y L 2011 Chin. J. Comput. Phys. 28 933
[33] Cui L J, Zhang Y, Zhang M Y, Li W, Zhao X S, Li S G, Wang Y F 2012 J. Environ. Mont. 14 3037
Google Scholar
[34] Brar J 2011 M.S. Thesis (Ottawa: University of Ottawa) pp6－9
[35] 杨毅, 唐刚, 宋丽建, 寻之朋, 夏辉, 郝大鹏 2014 63 150501
Google Scholar
Yang Y, Tang G, Song L J, Xun Z P, Xia H, Hao D P 2014 Acta Phys. Sin. 63 150501
Google Scholar
[36] 杨毅, 唐刚, 张哲, 寻之朋, 宋丽建, 韩奎 2015 64 130501
Google Scholar
Yang Y, Tang G, Zhang Z, Xun Z P, Song L J, Han K 2015 Acta Phys. Sin. 64 130501
Google Scholar
[37] 王晓芳, 杨小玲, 刘洋 2018 化学工程师 274 7
Wang X F, Yang X L, Liu Y 2018 Chemical Engineer. Sum. 274 7
[38] 吴海华, 肖林楠, 王俊, 王亚迪 2018 激光与光电子学进展 55 011417
Wu H H, Xiao L N, Wang J, Wang Y D 2018 Laser Opt. Prog. 55 011417
[39] McGregor D J , Sameh T, William P K 2019 Addit. Manuf. 25 10
Google Scholar
[40] Gibson L J, Ashby M F 1997 Cellular Solids: Structure and Properties (2nd Ed.)(Cambridge: Cambridge University Press) (Cambridge: Cambridge University Press) pp13－19
[41] Soriano J, Ramasco J J, Rodriguez M A, Hernandez-Machado A 2002 Phys. Rev. Lett. 89 026102
Google Scholar
-
图 1 石墨烯蜂巢结构随机电阻丝网络通电熔断示意图
Fig. 1. Schematic diagram of random fuse model electric fuse in graphene honeycomb structure.
图 3 整体表面宽度
$W$ 随系统尺寸$L$ 的对数-对数曲线Fig. 3. The log-logarithmic curve of the global surface width W with the system size L.
图 4 局域表面宽度
$w$ 随局域尺寸$l$ 的对数-对数曲线Fig. 4. The Log-logarithmic curve of local surface width w with local size l.
图 5 不同系统尺寸下石墨烯蜂巢结构随机电阻丝网络熔断面相对极大高度分布
Fig. 5. Relative maximum height distribution of the fracture surface of random fuse model with graphene honeycomb structure under different system sizes.
图 6 不同系统尺寸下石墨烯蜂巢结构随机电阻丝网络熔断面相对极小高度分布
Fig. 6. Relative minimum height distribution of the fracture surface of random fuse model with graphene honeycomb structure under different system sizes.
图 7 不同系统尺寸下石墨烯蜂巢结构随机电阻丝网络熔断面的相对极大高度的半对数分布
Fig. 7. Semi-logarithmic distribution of the relative maximum height of the fracture surface of random fuse model with graphene honeycomb structure under different system sizes.
图 8 不同系统尺寸下石墨烯蜂巢结构随机电阻丝网络熔断面的相对极小高度的半对数分布
Fig. 8. Semi-logarithmic distribution of the relative minimum height of the fracture surface of random fuse model with graphene honeycomb structure under different system sizes.
图 9 系统尺寸L = 384的熔断面的相对极大(小)高度分布
Fig. 9. Relatively maximum (minimum) height distribution of fracture surface with system size L = 384.
图 10 系统尺寸L = 512的熔断面的相对极大(小)高度分布
Fig. 10. Relatively maximum (minimum) height distribution of fracture surface with system size L = 512.
表 1 二维菱形、三角形及石墨烯蜂巢结构电阻丝网络熔断面整体与局域的粗糙度指数
Table 1. Roughness index of the global and local of the burnout surface of two-dimensional diamond, triangle and graphene honeycomb structures.
模型 $\alpha $ ${\alpha _{{\rm{loc}}}}$ 菱形 0.752 ± 0.008 0.758 ± 0.012 三角形 0.772 ± 0.013 0.776 ± 0.003 石墨烯蜂巢结构 0.911 ± 0.005 0.808 ± 0.003 
下载: 导出CSV
表 2 系统尺寸为L = 384, 512, 768时Asym2sig函数拟合的参数
Table 2. Parameters of Asym2sig function fitting when the system size is L = 384, 512, 768.
384 max&min 512 max&min 768 max&min y0 –0.001 ± 0.012 –0.002 ± 0.011 –0.001 ± 0.010 –0.004 ± 0.008 –0.004 ± 0.007 –0.008 ± 0.007 xc –0.57 ± 0.02 –0.58 ± 0.02 –0.59 ± 0.02 –0.70 ± 0.02 –0.68 ± 0.02 –0.72 ± 0.02 A 1.18 ± 0.12 1.15 ± 0.08 1.28 ± 0.11 1.38 ± 0.13 1.38 ± 0.11 1.49 ± 0.15 ${\omega _1}$ 0.85 ± 0.08 0.90 ± 0.06 0.80 ± 0.07 0.65 ± 0.07 0.69 ± 0.06 0.58 ± 0.08 ${\omega _2}$ 0.13 ± 0.02 0.11 ± 0.01 0.11 ± 0.01 0.11 ± 0.01 0.10 ± 0.01 0.12 ± 0.01 ${\omega _3}$ 0.25 ± 0.03 0.27 ± 0.03 0.32 ± 0.03 0.28 ± 0.02 0.33 ± 0.02 0.30 ± 0.02
下载: 导出CSV
-
[1] Abergel D S L, Apalkov V, Berashevich J 2010 Adv. Phys. 59 261
Google Scholar
[2] Shin Y J, Gopinadhan K, Narayanapillai K 2013 Appl. Phys. Lett. 102 666
[3] Lu Y H, Shi L, Zhang C, Feng Y P 2009 Phys. Rev. B 80 233410
Google Scholar
[4] Moura M J B, Marder M 2013 Phys. Rev. E 88 032405
Google Scholar
[5] Ghorbanfekr-Kalashami H, Neek-Amal M, Peeters F M 2016 Phys. Rev. B 93 174112
Google Scholar
[6] Alava M J, Nukala P K V V, Zapperi S 2006 Adv. Phys. 55 351
[7] Garcimart'ın A, Guarino A, Bellon L, Ciliberto S 1997 Phys. Rev. Lett. 79 3202
Google Scholar
[8] Maes C, van Moffaert A, Frederix H, Strauven H 1998 Phys. Rev. B 57 4987
[9] Petri A, Paparo G, Vespignani A, Alippi A, Costantini M 1994 Phys. Rev. Lett. 73 3423
Google Scholar
[10] Salminen L I, Tolvanen A I, Alava M J 2002 Phys. Rev. Lett. 89 185503
Google Scholar
[11] Arcangelis L, Redner S, Herrmann H J 1985 J. Phys. Lett. 46 585
Google Scholar
[12] Schramm O 2000 Israel J. Math. 118 221
Google Scholar
[13] Claudio M, Ashivni S, Nukala P K V V, Alava M J, Sethna J P, Zapperi S 2012 Phys. Rev. Lett. 108 065504
Google Scholar
[14] Duxbury P M, Beale P D, Leath P L 1986 Phys. Rev. Lett. 59 155
[15] Nukala P K V V, Srdan S, Zapperi S 2004 J. Stat. Mech. 8 P08001
[16] Toussaint R, Hansen A 2006 Phys. Rev. E 73 046103
Google Scholar
[17] Jan Øystein H B, Hansen A 2008 Phys. Rev. Lett. 100 045501
Google Scholar
[18] Davis T A, Hager W W 1999 Siam J. Matrix Anal. A 22 997
[19] Family F, Vicsek T 1985 J. Phys. A 18 L75
Google Scholar
[20] Xun Z P, Tang G, Han K, Xia H, Hao D P, Li Y 2012 Phys. Rev. E 85 041126
Google Scholar
[21] 寻之朋 2017 离散模型表面界面粗化的动力学标度性质(徐州: 中国矿业大学出版社) 第88页
Xun Z P 2017 The Dynamic Scale Properties of the Surface Roughness of the Discrete Growth Model (Xuzhou: China Mining University Press) p88
[22] Raychaudhuri S, Cranston M, Przybyla C, Shapir Y 2001 Phys. Rev. Lett. 87 136101
Google Scholar
[23] Foltin G, Oerding K, Racz Z, Workman R L, Zia R K P 1994 Phys. Rev. E 50 639
Google Scholar
[24] Majumdar S N, Comtet A 2004 Phys. Rev. Lett. 92 225501
Google Scholar
[25] Derrida B, Lebowitz J L 1998 Phys. Rev. Lett. 80 209
Google Scholar
[26] Majumdar S N, Comtet A 2005 Stat. Phys. 119 777
Google Scholar
[27] Fisher R A, Tippett L H C 1928 Proc. Cambridge Philos. Soc. 24 180
Google Scholar
[28] Bramwell S T, Christensen K, Fortin J, Holdsworth P C W, Jensen H J, Lise S, Lopez J M, Nicodemi M, Pinton J F, Sellitto M 2000 Phys. Rev. Lett. 84 3744
Google Scholar
[29] Antal T, Droz M, Gyorgyi G, Racz Z 2001 Phys. Rev. Lett. 87 240601
Google Scholar
[30] Lee D S 2005 Phys. Rev. Lett. 95 150601
Google Scholar
[31] Lee S B, Jeong H C, Kim J M 2008 J. Stat. Mech. 9 P12013
[32] Wen R J, Tang G, Han K, Xia H, Hao D P, Xun Z P, Chen Y L 2011 Chin. J. Comput. Phys. 28 933
[33] Cui L J, Zhang Y, Zhang M Y, Li W, Zhao X S, Li S G, Wang Y F 2012 J. Environ. Mont. 14 3037
Google Scholar
[34] Brar J 2011 M.S. Thesis (Ottawa: University of Ottawa) pp6－9
[35] 杨毅, 唐刚, 宋丽建, 寻之朋, 夏辉, 郝大鹏 2014 63 150501
Google Scholar
Yang Y, Tang G, Song L J, Xun Z P, Xia H, Hao D P 2014 Acta Phys. Sin. 63 150501
Google Scholar
[36] 杨毅, 唐刚, 张哲, 寻之朋, 宋丽建, 韩奎 2015 64 130501
Google Scholar
Yang Y, Tang G, Zhang Z, Xun Z P, Song L J, Han K 2015 Acta Phys. Sin. 64 130501
Google Scholar
[37] 王晓芳, 杨小玲, 刘洋 2018 化学工程师 274 7
Wang X F, Yang X L, Liu Y 2018 Chemical Engineer. Sum. 274 7
[38] 吴海华, 肖林楠, 王俊, 王亚迪 2018 激光与光电子学进展 55 011417
Wu H H, Xiao L N, Wang J, Wang Y D 2018 Laser Opt. Prog. 55 011417
[39] McGregor D J , Sameh T, William P K 2019 Addit. Manuf. 25 10
Google Scholar
[40] Gibson L J, Ashby M F 1997 Cellular Solids: Structure and Properties (2nd Ed.)(Cambridge: Cambridge University Press) (Cambridge: Cambridge University Press) pp13－19
[41] Soriano J, Ramasco J J, Rodriguez M A, Hernandez-Machado A 2002 Phys. Rev. Lett. 89 026102
Google Scholar
下载:
计量
- 文章访问数: 7007
- PDF下载量: 37
- 被引次数: 0
