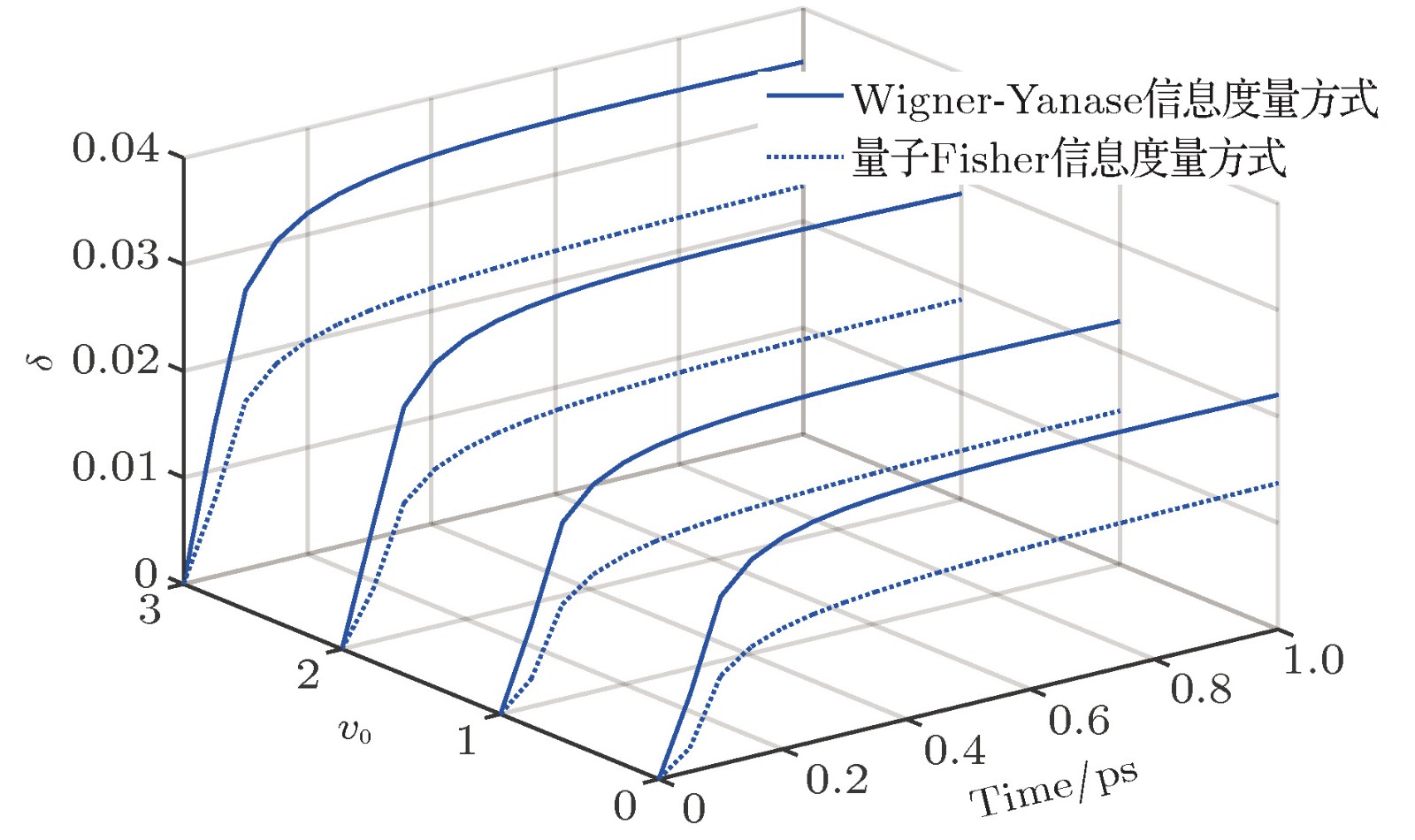
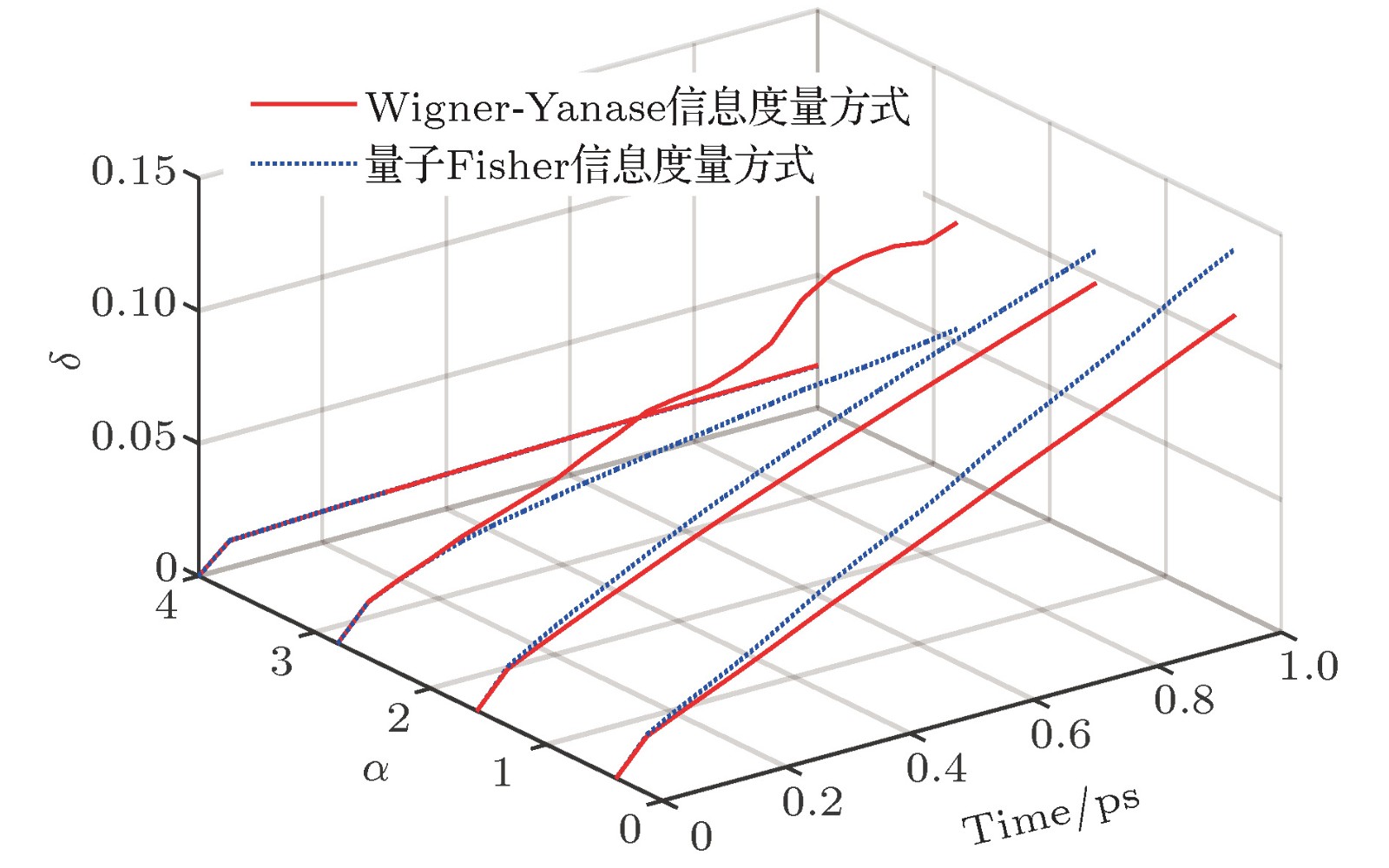
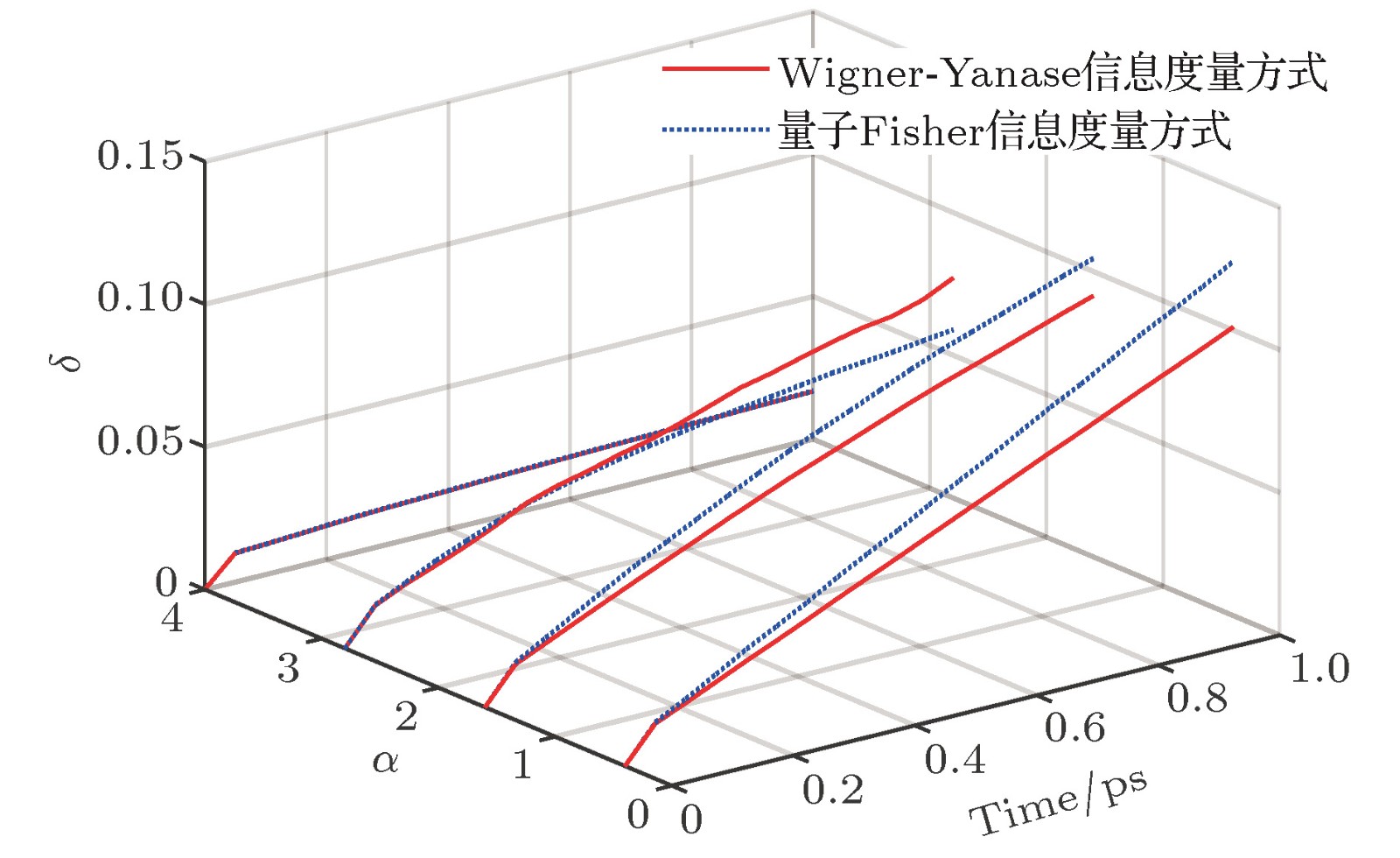
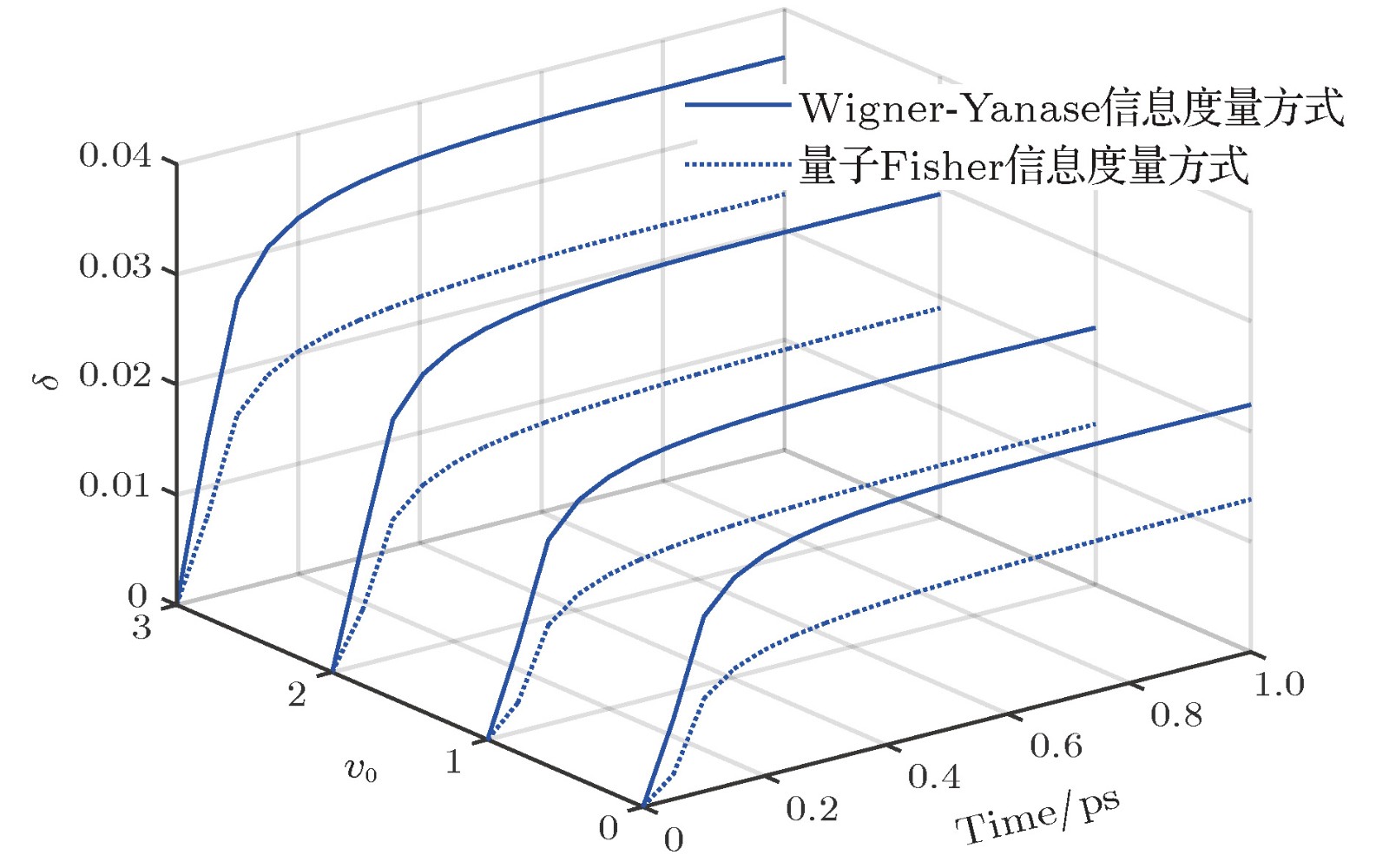
-
Quantum speed limit (QSL) in a quantum system originates from the essential principle of the quantum mechanics. It gives a maximum speed of evolution or a minimum evolution time of the quantum system, which has potential applications in the fields of quantum information, quantum communication and quantum control and so on. In the last decades, the QSL bounds have been explored from the isolated quantum systems to the open quantum systems, several different geometric measures have been adopted to investigate the distinguishability between the initial and the evolved state. The QSL bounds in many systems have been discussed, indicating that the tightness of the QSL metric is related to the researched dynamical system. However, the QSL problem for the molecular system has rarely been reported. The study of the quantum speed limits in the different molecular systems is helpful for realizing the quantum information technology based on the molecules. In this paper, the generalized quantum speed limit metric for linear molecular dynamics is studied by the algebraic approach. The quantum Fisher information metric and the Wigner-Yanase information metric are both used to study the QSLs in the dynamical evolution of the two linear molecules. Here the dynamical evolutions begin with the two kinds of vibrational states, Fock initial state and coherent initial state. The results show that the quantum Fisher information metric is more appropriate than the Wigner-Yanase information metric for HCN and DCN molecules. The relative differences between the generalized geometric QSL and the two geodesic QSL metrics become bigger gradually with the increase of the initial vibrational quantum number. However, the relative difference for the DCN molecule is smaller than for the HCN molecule. The relative difference between the strong coherent states is smaller, which indicates that the generalized geometric quantum speed limit is suitable to describing high-coherent case. In conclusion, the different QSL metrics reveal the discrepancy in the evolution of the molecular system, and the relative difference is related to the initial state of the molecules and molecular parameters. More molecular systems need to be investigated in order to obtain the criteria between the QSL metrics and the molecular parameters.
-
Keywords:
- Lie-algebra /
- quantum speed limit /
- molecules
[1] Anandan J, Aharonov Y 1990 Phys. Rev. Lett. 65 1697
Google Scholar
[2] Margolus N, Levitin L B 1998 Physica D 120 188
Google Scholar
[3] Jones P J, Kok P 2010 Phys. Rev. A 82 022107
Google Scholar
[4] Hegerfeldt G C 2013 Phys. Rev. Lett. 111 260501
Google Scholar
[5] Poggi P M, Lombardo F C, Wisniacki D A 2013 EPL 104 40005
Google Scholar
[6] Deffner S 2014 J. Phys. B 47 145502
Google Scholar
[7] Andersson O, Heydari H 2014 J. Phys. A 47 215301
Google Scholar
[8] Zhang Y J, Han W, Xia Y J, Cao J P, Fan H 2014 Sci. Rep. 4 4890
[9] Wu S X, Zhang Y, Yu C S, Song H S 2015 J. Phys. A 48 045301
Google Scholar
[10] Liu C, Xu Z Y, Zhu S 2015 Phys. Rev. A 91 022102
Google Scholar
[11] Cai X J, Zheng Y J 2017 Phys. Rev. A 95 052104
Google Scholar
[12] Shyshlov D, Babikov D 2012 J. Chem. Phys. 137 194318
Google Scholar
[13] Vatasescu M 2013 Phys. Rev. A 88 063415
Google Scholar
[14] Shyshlov D, Berrios E, Gruebele M, Babikov D 2014 J. Chem. Phys. 141 224306
Google Scholar
[15] 冯海冉, 李鹏, 郑雨军, 丁世良 2010 59 5246
Google Scholar
Feng H R, Li P, Zheng Y J, Ding S L 2010 Acta Phys. Sin. 59 5246
Google Scholar
[16] 郑雨军 2013 分子结构及其代数方法(北京: 科学出版社) 第110—140页, 第179—225页
Zheng Y J 2013 Molecular Structure and Algebraic Methods (Beijing: Science Press) pp110−140, pp179−225 (in Chinese)
[17] Feng H R, Li P, Zheng Y J 2011 Mol. Phys. 109 2633
Google Scholar
[18] Feng H R, Meng X J, Li Peng, Zheng Y J 2014 Chin. Phys. B 23 040305
Google Scholar
[19] Pires D P, Cianciaruso M, Cleri L C, Adesso G, Soares-Pinto D O 2016 Phys. Rev. X 6 021031
[20] Levine R D 1983 Chem. Phys. Lett. 95 87
Google Scholar
[21] Feng H R, Liu Y, Zheng Y J, Ding S L, Ren W Y 2007 Phys. Rev. A 75 063417
Google Scholar
[22] Cooper I L, Gupta R K 1997 Phys. Rev. A 55 4112
Google Scholar
[23] Cooper I L 1998 J. Phys. Chem. A 102 9565
[24] Uhlmann A 1995 Rep. Math. Phys. 36 461
Google Scholar
[25] Gibilisco P, Isola T 2003 J. Math. Phys. (N.Y.)
44 3752 Google Scholar
[26] Theule P, Borget F, Mispelaer F, Danger G, Duvernay F, Guillemin J C, Chiavassa T 2011 Astronomy Astrophysics 534 A64
Google Scholar
[27] Xu D, Xie D, Guo H 2002 J. Chem. Phys. 116 10626
Google Scholar
[28] Feng H R, Ding S L 2007 J. Phys. B 40 69
Google Scholar
-
图 1 Fock态下HCN分子QSL度量相对差
Fig. 1. Relative differences of QSL metrics for the initial Fock states in HCN.
图 2 Fock态下DCN分子QSL度量相对差
Fig. 2. Relative differences of QSL metrics for the initial Fock states in DCN.
图 3 初态为
$ |0,3\rangle $ 时, 两分子采用Wigner-Yanase度量方式时对应的QSL度量相对差Fig. 3. Relative differences of Wigner-Yanase information metric for the initial state
$ |0,3\rangle $ in HCN and DCN molecules.
图 4 相干态下HCN分子QSL度量相对差
Fig. 4. Relative differences of QSL metrics for the coherent states in HCN.
图 5 相干态下DCN分子QSL度量相对差
Fig. 5. Relative differences of QSL metrics for the coherent states in DCN.
-
[1] Anandan J, Aharonov Y 1990 Phys. Rev. Lett. 65 1697
Google Scholar
[2] Margolus N, Levitin L B 1998 Physica D 120 188
Google Scholar
[3] Jones P J, Kok P 2010 Phys. Rev. A 82 022107
Google Scholar
[4] Hegerfeldt G C 2013 Phys. Rev. Lett. 111 260501
Google Scholar
[5] Poggi P M, Lombardo F C, Wisniacki D A 2013 EPL 104 40005
Google Scholar
[6] Deffner S 2014 J. Phys. B 47 145502
Google Scholar
[7] Andersson O, Heydari H 2014 J. Phys. A 47 215301
Google Scholar
[8] Zhang Y J, Han W, Xia Y J, Cao J P, Fan H 2014 Sci. Rep. 4 4890
[9] Wu S X, Zhang Y, Yu C S, Song H S 2015 J. Phys. A 48 045301
Google Scholar
[10] Liu C, Xu Z Y, Zhu S 2015 Phys. Rev. A 91 022102
Google Scholar
[11] Cai X J, Zheng Y J 2017 Phys. Rev. A 95 052104
Google Scholar
[12] Shyshlov D, Babikov D 2012 J. Chem. Phys. 137 194318
Google Scholar
[13] Vatasescu M 2013 Phys. Rev. A 88 063415
Google Scholar
[14] Shyshlov D, Berrios E, Gruebele M, Babikov D 2014 J. Chem. Phys. 141 224306
Google Scholar
[15] 冯海冉, 李鹏, 郑雨军, 丁世良 2010 59 5246
Google Scholar
Feng H R, Li P, Zheng Y J, Ding S L 2010 Acta Phys. Sin. 59 5246
Google Scholar
[16] 郑雨军 2013 分子结构及其代数方法(北京: 科学出版社) 第110—140页, 第179—225页
Zheng Y J 2013 Molecular Structure and Algebraic Methods (Beijing: Science Press) pp110−140, pp179−225 (in Chinese)
[17] Feng H R, Li P, Zheng Y J 2011 Mol. Phys. 109 2633
Google Scholar
[18] Feng H R, Meng X J, Li Peng, Zheng Y J 2014 Chin. Phys. B 23 040305
Google Scholar
[19] Pires D P, Cianciaruso M, Cleri L C, Adesso G, Soares-Pinto D O 2016 Phys. Rev. X 6 021031
[20] Levine R D 1983 Chem. Phys. Lett. 95 87
Google Scholar
[21] Feng H R, Liu Y, Zheng Y J, Ding S L, Ren W Y 2007 Phys. Rev. A 75 063417
Google Scholar
[22] Cooper I L, Gupta R K 1997 Phys. Rev. A 55 4112
Google Scholar
[23] Cooper I L 1998 J. Phys. Chem. A 102 9565
[24] Uhlmann A 1995 Rep. Math. Phys. 36 461
Google Scholar
[25] Gibilisco P, Isola T 2003 J. Math. Phys. (N.Y.)
44 3752 Google Scholar
[26] Theule P, Borget F, Mispelaer F, Danger G, Duvernay F, Guillemin J C, Chiavassa T 2011 Astronomy Astrophysics 534 A64
Google Scholar
[27] Xu D, Xie D, Guo H 2002 J. Chem. Phys. 116 10626
Google Scholar
[28] Feng H R, Ding S L 2007 J. Phys. B 40 69
Google Scholar
下载:
计量
- 文章访问数: 6444
- PDF下载量: 46
- 被引次数: 0
