-
在磁性原子气体中, 偶极弛豫过程将系统的自旋与动能自由度耦合, 从而实现体系动能向塞曼能的转化. 利用光泵浦过程, 可以将偶极弛豫至高自旋态的原子重新泵浦回基态, 实现持续的冷却循环, 有效降低体系温度. 由于单次冷却循环中移除的能量远大于散射光子能量, 这种退磁冷却方案显著提升了冷却效率并减少了原子损失. 本文通过建立结合偶极弛豫与光泵浦过程的态耦合方程, 对镝原子的退磁冷却进行了理论建模与计算, 研究了相关实验参数对冷却效率及冷却极限温度的影响, 确定了实现镝原子玻色-爱因斯坦凝聚的关键实验参数范围和技术指标要求. 结果表明, 在最优实验参数下, 退磁冷却可以在亚秒时间内直接制备大原子数的镝原子玻色-爱因斯坦凝聚, 其冷却效率比传统蒸发冷却高一个数量级.In magnetic atomic gases, the dipolar relaxation process couples the system spin and kinetic degrees of freedom. When the average kinetic energy is significantly lower than the Zeeman splitting, the atoms predominantly occupy the lowest Zeeman state. As the Zeeman splitting approaches the average kinetic energy, some atoms transfer to adjacent Zeeman states through dipolar relaxation, converting kinetic energy into Zeeman energy. By utilizing optical pumping, atoms transferred to higher spin states can be repumped to the ground state, thereby achieving a continuous cooling cycle and effectively lowering the system’s temperature. As the energy removed in a single cooling cycle is much larger than the energy of scattered photons, this demagnetization cooling scheme significantly enhances cooling effciency and reduces atomic loss. In this work, we establish state-coupled equations that incorporate dipolar relaxation and optical pumping to analyze the demagnetization cooling process, modeling the evolution of atom number and temperature during the cooling of $^{164}{\text{Dy}}$ atoms. We develop a strategy to generate an optimal magnetic field waveform by maximizing the demagnetization rate. Based on this strategy, we investigate the influence of crucial experimental parameters on demagnetization cooling and determine their specific ranges for producing large atom number of BEC, including the optical dipole trap frequency, as well as the intensity and polarization purity of the optical pumping light. The results indicate that demagnetization cooling enables the direct preparation of a large number of dysprosium BEC with sub-second timescales, reducing the cooling time by an order of magnitude compared to conventional methods for dysprosium atoms. Furthermore, it could achieve a cooling effciency of $\chi \approx 44.92$, an order of magnitude higher than that of traditional evaporative cooling.
-
Keywords:
- magnetic atoms /
- demagnetization cooling /
- dipolar relaxation /
- optical pumping /
- Bose-Einstein condensate
[1] Lu M, Burdick N Q, Youn S H, Lev B L 2011 Phys. Rev. Lett. 107 190401
Google Scholar
[2] Aikawa K, Frisch A, Mark M, Baier S, Rietzler A, Grimm R, Ferlaino F 2012 Phys. Rev. Lett. 108 210401
Google Scholar
[3] Li X, Luo X, Wang S, Xie K, Liu X P, Hu H, Chen Y A, Yao X C, Pan J W 2022 Science 375 528
Google Scholar
[4] Li X, Wang S, Luo X, et al. 2024 Nature 626 288
Google Scholar
[5] Shao H J, Wang Y X, Zhu D Z, et al. 2024 Nature 632 267
Google Scholar
[6] Chomaz L, Ferrier-Barbut I, Ferlaino F, Laburthe-Tolra B, Lev B L, Pfau T 2022 Rep. Prog. Phys. 86 026401
Google Scholar
[7] Lahaye T, Menotti C, Santos L, Lewenstein M, Pfau T 2009 Rep. Prog. Phys. 72 126401
Google Scholar
[8] Schmitt M, Wenzel M, Böttcher F, Ferrier-Barbut I, Pfau T 2016 Nature 539 259
Google Scholar
[9] Chomaz L, Petter D, Ilzhöfer P, et al. 2019 Phys. Rev. X 9 021012
Google Scholar
[10] Norcia M A, Politi C, Klaus L, Poli E, Sohmen M, Mark M J, Bisset R N, Santos L, Ferlaino F 2021 Nature 596 357
Google Scholar
[11] Tanzi L, Roccuzzo S, Lucioni E, Famà F, Fioretti A, Gabbanini C, Modugno G, Recati A, Stringari S 2019 Nature 574 382
Google Scholar
[12] Baier S, Mark M J, Petter D, Aikawa K, Chomaz L, Cai Z, Baranov M, Zoller P, Ferlaino F 2016 Science 352 201
Google Scholar
[13] Frisch A, Aikawa K, Mark M, Rietzler A, Schindler J, Zupanič E, Grimm R, Ferlaino F 2012 Phys. Rev. A 85 051401
Google Scholar
[14] Maier T, Kadau H, Schmitt M, Griesmaier A, Pfau T 2014 Opt. Lett. 39 3138
Google Scholar
[15] Koch T, Lahaye T, Metz J, Fröhlich B, Griesmaier A, Pfau T 2008 Nat. Phys. 4 218
Google Scholar
[16] Hensler S, Greiner A, Stuhler J, Pfau T 2005 Europhys. Lett. 71 918
Google Scholar
[17] Fattori M, Koch T, Goetz S, Griesmaier A, Hensler S, Stuhler J, Pfau T 2006 Nat. Phys. 2 765
Google Scholar
[18] Volchkov V V, Rührig J, Pfau T, Griesmaier A 2014 Phys. Rev. A 89 043417
Google Scholar
[19] Lounasmaa O V 1975 Phys. Today 2 75
Google Scholar
[20] Schmitt M, Henn E A L, Billy J, Kadau H, Maier T, Griesmaier A, Pfau T 2013 Opt. Lett. 38 637
Google Scholar
[21] Atoneche F, Kastberg A 2017 Eur. J. Phys. 38 045703
Google Scholar
[22] Lecomte M, Journeaux A, Veschambre J, Dalibard J, Lopes R 2024 arXiv: 2407.08702 [cond-mat.quant-gas]
[23] Hensler S, Werner J, Griesmaier A, Schmidt P, Görlitz A, Pfau T, Giovanazzi S, Rzażewski K 2003 Appl. Phys. B 77 765
Google Scholar
[24] Mosk A, Kraft S, Mudrich M, Singer K, Wohlleben W, Grimm R, Weidemüller M 2001 Appl. Phys. B 73 791
Google Scholar
[25] Tang Y, Sykes A, Burdick N Q, Bohn J L, Lev B L 2015 Phys. Rev. A 92 022703
Google Scholar
[26] Olson A J, Niffenegger R J, Chen Y P 2013 Phys. Rev. A 87 053613
Google Scholar
[27] Esry B, Greene C H, Burke Jr J P 1999 Phys. Rev. Lett. 83 1751
Google Scholar
[28] Lecomte M, Journeaux A, Renaud L, Dalibard J, Lopes R 2024 Phys. Rev. A 109 023319
Google Scholar
[29] Rogora C, Cominotti R, Baroni C, Andreoni D, Lamporesi G, Zenesini A, Ferrari G 2024 Phy. Rev. A 110 013319
Google Scholar
[30] Dalfovo F, Giorgini S, Pitaevskii L P, Stringari S 1999 Rev. Mod. Phys. 71 463
Google Scholar
[31] Hamilton M S, Wilson R F, Roberts J L 2014 Eur. Phys. J. D 68 1
Google Scholar
-
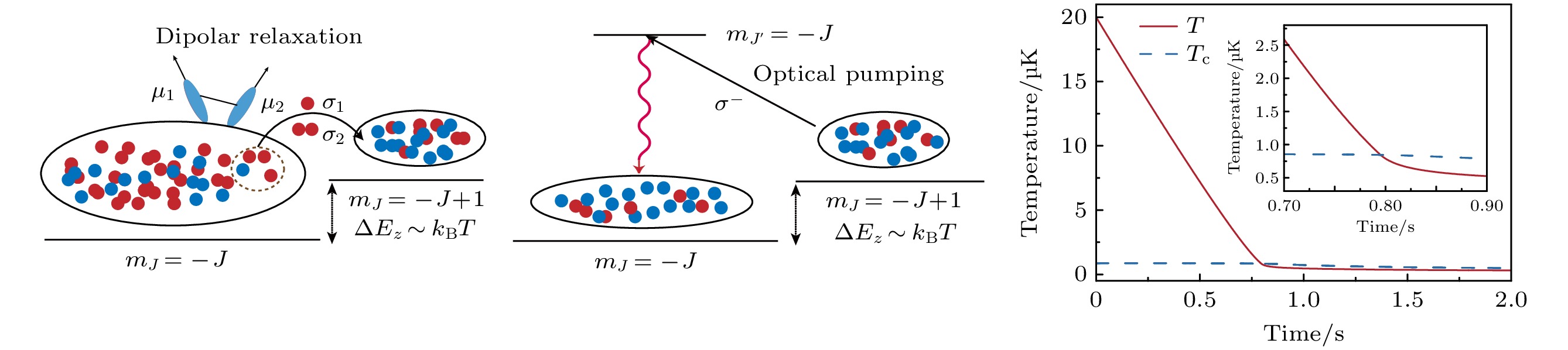
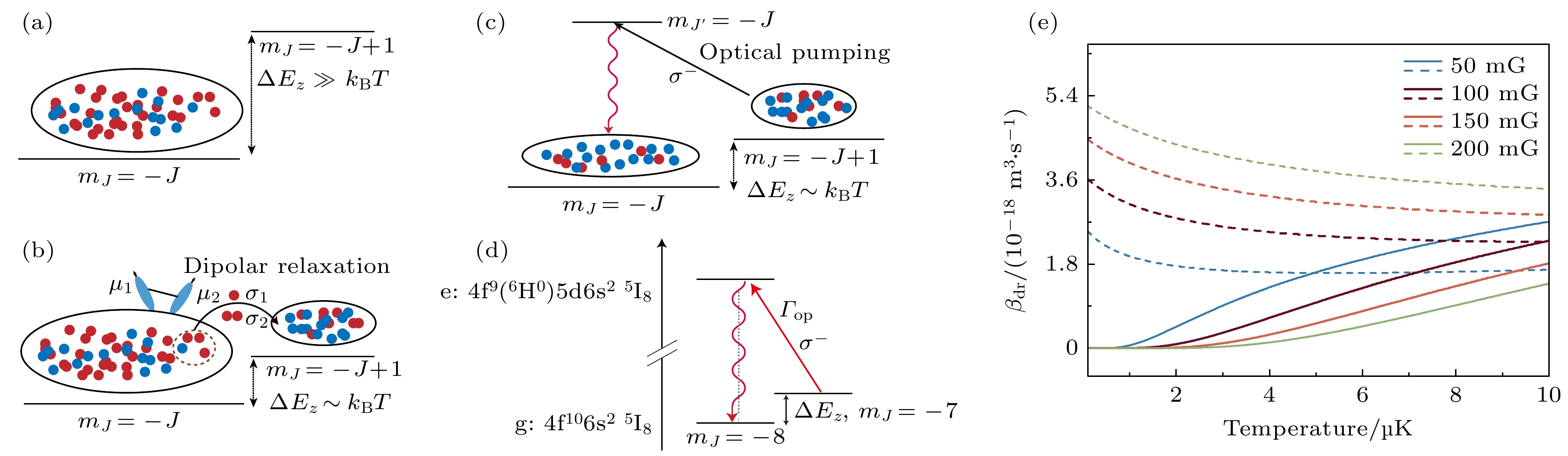
图 1 退磁冷却原理图(图中蓝色与红色实心小球占比表征体系温度. 蓝色小球比例增加, 表示低能原子数量增多, 反映更低的体系温度) (a)当原子的平均动能远小于相邻内态间的塞曼劈裂$ \Delta E_z = g_J\mu_{\text{B}}B $时, 原子极化在最低塞曼态$ m_J = -J $态; (b)随着磁场降低, 当塞曼劈裂与原子平均动能相当时, 部分$ m_J = -J $态的原子通过偶极弛豫转移到$ m_J = -J+1 $的近邻塞曼能级; (c)通过光泵浦过程将原子重新极化回到$ m_J = -J $态; (d)$ ^{164}{\text{Dy}} $原子光泵浦过程示意图, 波长为684 nm的跃迁, 最低塞曼态对$ \sigma^{-} $偏振光表现为暗态; (e) 1—10 µK温度范围内, 不同磁场下$ ^{164}{\text{Dy}} $原子的偶极弛豫系数计算结果(1 G = 10–4 T), 其中实线和虚线分别对应$ \beta_{{\rm{dr}}}^+ $和$ \beta_{{\rm{dr}}}^- $
Fig. 1. Diagram of the principle of demagnetization cooling. The proportion of blue and red solid spheres in the figure represents the system’s temperature. An increase in the proportion of blue spheres indicates a rise in the number of atoms in lower energy states, reflecting a lower temperature of system. (a) When the atom’s average kinetic energy is much lower than the Zeeman splitting $ \Delta E_z = g_J\mu_{\text{B}}B $ between adjacent internal states, the atoms are polarized in the lowest Zeeman state $ m_J = -J $; (b) as the magnetic field is gradually reduced, and the Zeeman splitting becomes comparable to the atom’s average kinetic energy, some atoms in the $ m_J = -J $ state transfer to the adjacent Zeeman state $ m_J = -J+1 $ through dipolar relaxation; (c) the atoms are then pumped back to the $ m_J = -J $ state through an optical pumping process; (d) schematic of the optical pumping process for $ ^{164}{\text{Dy}} $ atoms, in the transition at a wavelength of 684 nm, the lowest Zeeman state behaves as a dark state for $ \sigma^{-} $-polarized light; (e) the calculated results of dipolar relaxation coefficients $ \beta_{{\rm{dr}}}^+ $ and $ \beta_{{\rm{dr}}}^- $ for $ ^{164}{\text{Dy}} $ atoms at different magnetic fields within the temperature range from 1–10 µK; the solid and dashed lines correspond to $ \beta_{{\rm{dr}}}^+ $ and $ \beta_{{\rm{dr}}}^- $, respectively.
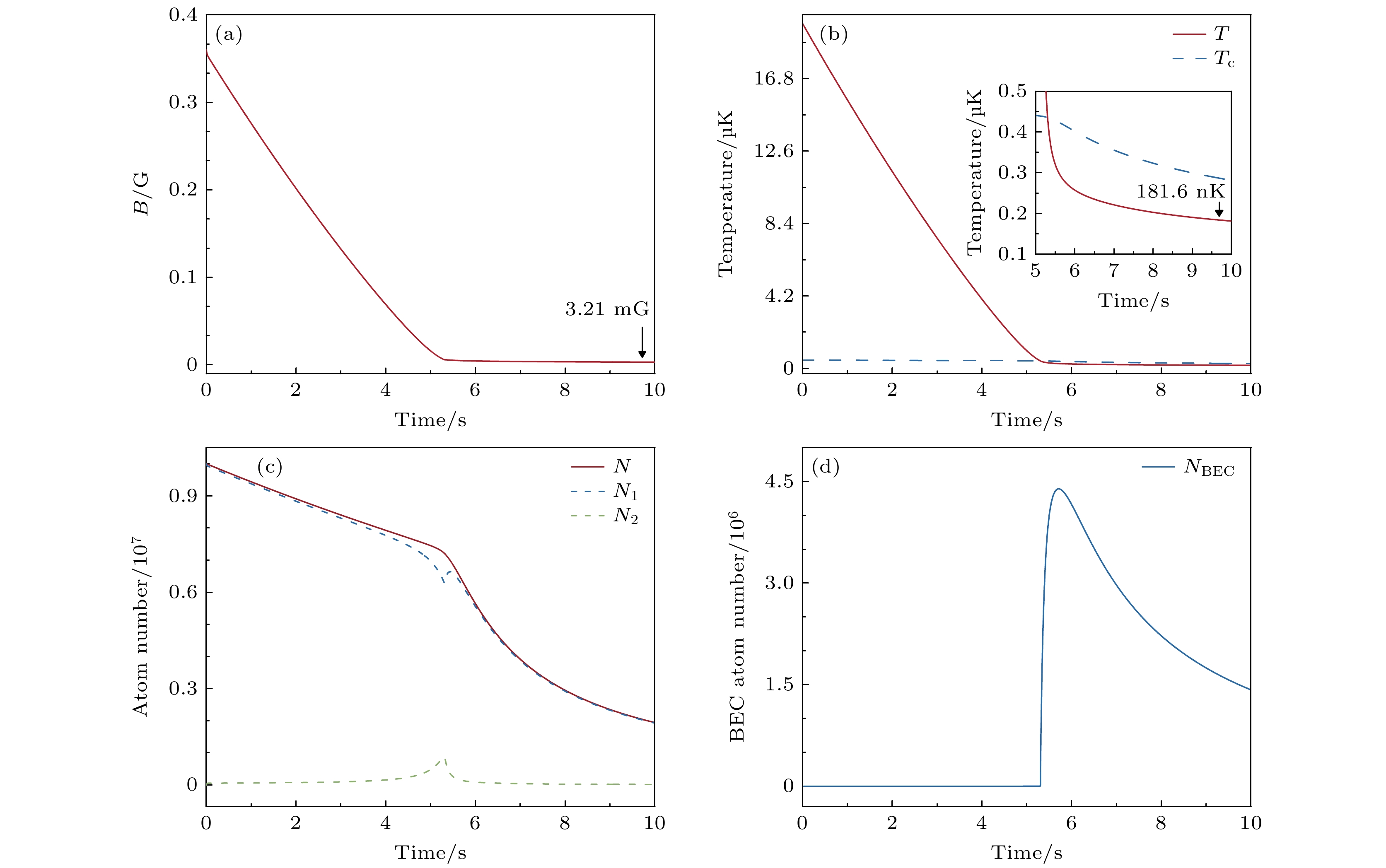
图 2 每个时刻在$ \dot{E}_{{\rm{dip}}} < 0 $条件下, 使$ |\dot{E}_{{\rm{dip}}}| $最大的磁场作为最优磁场, 冷却过程的计算结果(初始时刻, 设定原子数布居为$ N_1 = 1\times10^7 $, $ N_2 = 0 $, 体系温度T = 20 µK, 泵浦光$ \sigma^{-} $偏振成分占比为$ P = 1499/1500 $, 光强和失谐分别为$ I = 500 I_{{\mathrm{s}}} $, $ \varDelta = 200 \varGamma $, 光阱平均阱频率为$ \bar{\omega} = 2\pi\times 50\ {\rm{Hz}}$, 原子寿命$ \tau_{{\rm{bg}}} = 20\ {\rm{s}}$, 三体损失系数$ L_{3} = 5\times \mathrm {10^{-41}~m^{6}/s} $) (a) 最优磁场波形计算结果; (b) 体系温度随时间的演化, 蓝色虚线为BEC临界温度$ T_{\rm{c}} $, 插图为温度低于$ T_{\rm{c}} $后体系温度演化, 在10 s时温度趋于平衡, 此时$ T = 181.6\ {\rm{nK}}$; (c)总原子数(红色实线), $ |J = 8, m_J = -8\rangle $态(蓝色虚线)和$ |J = 8, m_J = -7\rangle $态原子数(绿色虚线)随时间的演化; (d) BEC原子数随时间的演化
Fig. 2. Calculated results of the cooling process under the magnetic field profile that maximizes $ |\dot{E}_{{\rm{dip}}}| $ under the condition $ \dot{E}_{{\rm{dip}}} < 0 $: (a) Calculated optimal magnetic field profile; (b) evolution of the temperature over time, with the blue dashed line representing the BEC critical temperature $ T_{{{\mathrm{c}}}} $ and the inset shows the temperature evolution of the system after it falls below $ T_{\rm{c}} $; at 10 s, the temperature tends towards equilibrium, with $ T = 181.6\ {\rm{nK}} $; (c) time evolution of the total atom number (red solid line), atom numbers of $ |J = 8, m_J = -8\rangle $ (blue dashed line) and $ |J = 8, m_J = -7\rangle $ (green dashed line) states; (d) time evolution of the BEC atom number. Initially, the atomic populations are set to $ N_1 = 1\times10^7 $, $ N_2 = 0 $, with a system temperature of T = 20 µK. The proportion of the $ \sigma^{-} $ polarization in the optical pumping light is $ P = 1499/1500 $, with intensity $ I = 500 I_{{\mathrm{s}}} $ and detuning $ \varDelta = 200 \varGamma $. The mean trapping frequency of the optical dipole trap is $ \bar{\omega} = 2\pi\times 50\ {\rm{Hz}}$, the atomic lifetime is $ \tau_{{\rm{bg}}} = 20\ {\rm{s}}$, and the three-body loss rate is $ L_{3} = 5\times \mathrm{10^{-41} m^{6}/s} $.
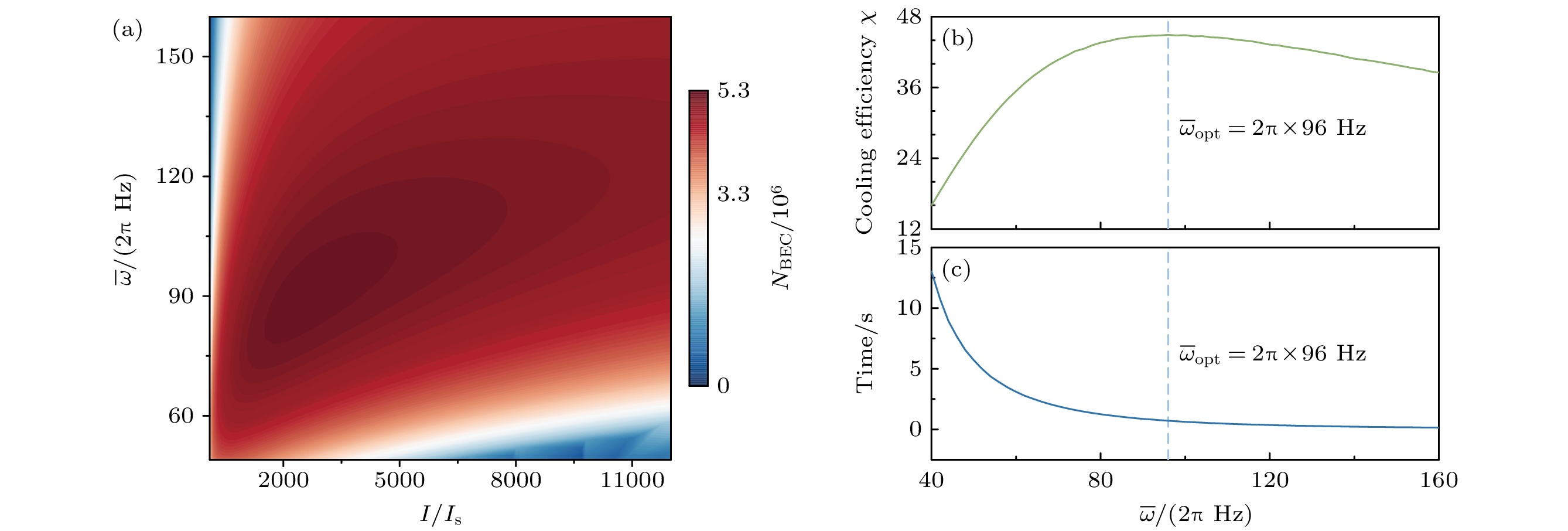
图 3 在与图2相同的其他参数设置和磁场波形优化策略下, 光泵浦光强与平均阱频率$ \bar{\omega} $对冷却过程的影响 (a) 不同泵浦光强与$ \bar{\omega} $下, 可实现的最大BEC原子数; (b)不同$ \bar{\omega} $对应的最优泵浦光强下, 冷却效率$\chi $随$ \bar{\omega} $的变化, 浅蓝色虚线对应$\chi $最大时的$ \bar{\omega} $, 即最优阱频率$ \bar{\omega}_{\text{opt}} = 2{\text{π}} \times 96\ {\rm{Hz}}$; (c)不同$ \bar{\omega} $对应的最优泵浦光强下, 实现最大原子数BEC的冷却时间随$ \bar{\omega} $的变化; 浅蓝色虚线对应$ \bar{\omega}_{\text{opt}} $
Fig. 3. Under the same other parameter settings and magnetic field waveform optimization strategy as in Fig. 2, the influences of optical pumping light intensity and average trap frequency $ \bar{\omega} $ on the cooling process: (a) The maximum achievable atom number of BEC under different $ \bar{\omega} $ and optical pumping light intensities; (b) the cooling efficiency as a function of $ \bar{\omega} $ at the optimal intensity of optical pumping light; the light blue dashed line indicates the value of $ {\omega} $ at which $\chi $ is maximized, representing the optimal trap frequency $ \bar{\omega}_{\text{opt}} = 2{\text{π}} \times 96\ {\rm{Hz}}$; (c) the time required to reach the maximum atom number of BEC as a function of $ \bar{\omega} $ at the optimal intensity of optical pumping light; the light blue dashed line represents $ \bar{\omega}_{\text{opt}} $.
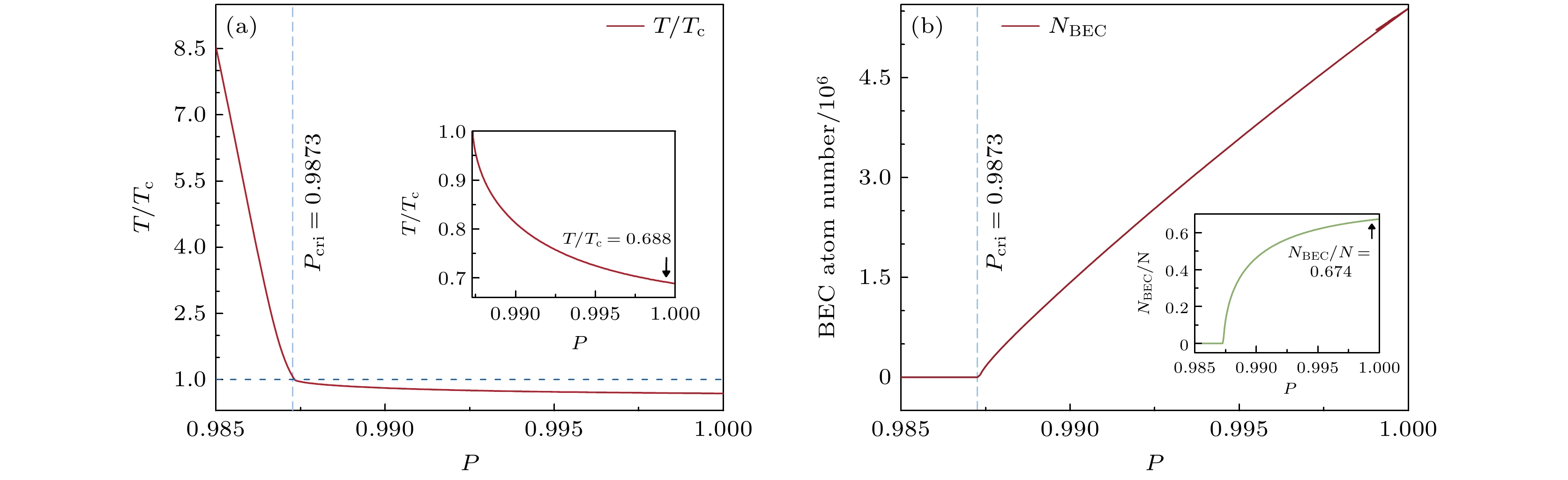
图 4 在与图2相同的其他参数设置和磁场波形优化策略下, 阱频率$ \bar{\omega} = 2\pi\times 90\ {\rm{Hz}} $, 泵浦光强$ I = 2700 I_s $参数下, 泵浦光$ \sigma^- $偏振占比P对冷却过程的影响 (a)相对温度$ T/T_{\rm{c}} $随P的变化; 当$ P < P_{\text{cri}} = 0.9873 $时(浅蓝色虚线), $ T/T_{\rm{c}} > 1 $; 蓝色虚线对应$ T/T_{\rm{c}} = 1 $; 插图为$ P > P_{\text{cri}} $时, $ T/T_{{\rm c}} $随P的变化, 当$ P = 1 $时, $ T/T_{\rm{c}} = 0.688 $; (b) 可实现BEC原子数随P的变化, 当$ P < P_{\text{cri}} = 0.9873 $时(浅蓝色虚线), $ N_{\text{BEC}} = 0 $; 插图为$ N_{\text{BEC}}/N $随P的变化, 当$ P = 1 $时, $ N/N_{\text{BEC}} = 0.674 $
Fig. 4. Under the same parameter settings and magnetic field waveform optimization strategy as in Fig. 2, with a trap frequency of $ \bar{\omega} = 2\pi \times 90\ {\rm{Hz}} $ and an optical pumping light intensity of $ I = 2700 I_s $, the influence of the proportion of the $ \sigma^{-} $ polarization in the optical pumping light on the cooling process. (a) The relative temperature $ T/T_{\rm{c}} $ as a function of P. When $ P < P_{\text{cri}} = 0.9873 $ (light blue dashed line), $ T/T_{\rm{c}} > 1 $. $ T/T_{\rm c} = 0.688 $. The blue dashed line corresponds to $ T/T_{\rm{c}} = 1 $. The inset shows the $T/T_\text{c} $ as a function of P when $ P > P_{\text{cri}} $. When $ P = 1 $, $ T/T_{\rm c} = 0.688 $. (b) The achieved BEC atom number as a function of P. When $ P < P_{\text{cri}} = 0.9873 $ (light blue dashed line), $ N_{\text{BEC}} = 0 $. The inset shows the $ N_{\text{BEC}}/N $ as a function of P. When $ P = 1 $, $ N_{\text{BEC}}/N = 0.674 $.
-
[1] Lu M, Burdick N Q, Youn S H, Lev B L 2011 Phys. Rev. Lett. 107 190401
Google Scholar
[2] Aikawa K, Frisch A, Mark M, Baier S, Rietzler A, Grimm R, Ferlaino F 2012 Phys. Rev. Lett. 108 210401
Google Scholar
[3] Li X, Luo X, Wang S, Xie K, Liu X P, Hu H, Chen Y A, Yao X C, Pan J W 2022 Science 375 528
Google Scholar
[4] Li X, Wang S, Luo X, et al. 2024 Nature 626 288
Google Scholar
[5] Shao H J, Wang Y X, Zhu D Z, et al. 2024 Nature 632 267
Google Scholar
[6] Chomaz L, Ferrier-Barbut I, Ferlaino F, Laburthe-Tolra B, Lev B L, Pfau T 2022 Rep. Prog. Phys. 86 026401
Google Scholar
[7] Lahaye T, Menotti C, Santos L, Lewenstein M, Pfau T 2009 Rep. Prog. Phys. 72 126401
Google Scholar
[8] Schmitt M, Wenzel M, Böttcher F, Ferrier-Barbut I, Pfau T 2016 Nature 539 259
Google Scholar
[9] Chomaz L, Petter D, Ilzhöfer P, et al. 2019 Phys. Rev. X 9 021012
Google Scholar
[10] Norcia M A, Politi C, Klaus L, Poli E, Sohmen M, Mark M J, Bisset R N, Santos L, Ferlaino F 2021 Nature 596 357
Google Scholar
[11] Tanzi L, Roccuzzo S, Lucioni E, Famà F, Fioretti A, Gabbanini C, Modugno G, Recati A, Stringari S 2019 Nature 574 382
Google Scholar
[12] Baier S, Mark M J, Petter D, Aikawa K, Chomaz L, Cai Z, Baranov M, Zoller P, Ferlaino F 2016 Science 352 201
Google Scholar
[13] Frisch A, Aikawa K, Mark M, Rietzler A, Schindler J, Zupanič E, Grimm R, Ferlaino F 2012 Phys. Rev. A 85 051401
Google Scholar
[14] Maier T, Kadau H, Schmitt M, Griesmaier A, Pfau T 2014 Opt. Lett. 39 3138
Google Scholar
[15] Koch T, Lahaye T, Metz J, Fröhlich B, Griesmaier A, Pfau T 2008 Nat. Phys. 4 218
Google Scholar
[16] Hensler S, Greiner A, Stuhler J, Pfau T 2005 Europhys. Lett. 71 918
Google Scholar
[17] Fattori M, Koch T, Goetz S, Griesmaier A, Hensler S, Stuhler J, Pfau T 2006 Nat. Phys. 2 765
Google Scholar
[18] Volchkov V V, Rührig J, Pfau T, Griesmaier A 2014 Phys. Rev. A 89 043417
Google Scholar
[19] Lounasmaa O V 1975 Phys. Today 2 75
Google Scholar
[20] Schmitt M, Henn E A L, Billy J, Kadau H, Maier T, Griesmaier A, Pfau T 2013 Opt. Lett. 38 637
Google Scholar
[21] Atoneche F, Kastberg A 2017 Eur. J. Phys. 38 045703
Google Scholar
[22] Lecomte M, Journeaux A, Veschambre J, Dalibard J, Lopes R 2024 arXiv: 2407.08702 [cond-mat.quant-gas]
[23] Hensler S, Werner J, Griesmaier A, Schmidt P, Görlitz A, Pfau T, Giovanazzi S, Rzażewski K 2003 Appl. Phys. B 77 765
Google Scholar
[24] Mosk A, Kraft S, Mudrich M, Singer K, Wohlleben W, Grimm R, Weidemüller M 2001 Appl. Phys. B 73 791
Google Scholar
[25] Tang Y, Sykes A, Burdick N Q, Bohn J L, Lev B L 2015 Phys. Rev. A 92 022703
Google Scholar
[26] Olson A J, Niffenegger R J, Chen Y P 2013 Phys. Rev. A 87 053613
Google Scholar
[27] Esry B, Greene C H, Burke Jr J P 1999 Phys. Rev. Lett. 83 1751
Google Scholar
[28] Lecomte M, Journeaux A, Renaud L, Dalibard J, Lopes R 2024 Phys. Rev. A 109 023319
Google Scholar
[29] Rogora C, Cominotti R, Baroni C, Andreoni D, Lamporesi G, Zenesini A, Ferrari G 2024 Phy. Rev. A 110 013319
Google Scholar
[30] Dalfovo F, Giorgini S, Pitaevskii L P, Stringari S 1999 Rev. Mod. Phys. 71 463
Google Scholar
[31] Hamilton M S, Wilson R F, Roberts J L 2014 Eur. Phys. J. D 68 1
Google Scholar
下载:
计量
- 文章访问数: 867
- PDF下载量: 121
- 被引次数: 0
