基于微观结构非均匀性理解非晶态聚苯乙烯的应力松弛行为

张婧祺; 郝奇; 吕国建; 熊必金; 乔吉超

doi:10.7498/aps.73.20231240

摘要

研究了非晶态聚苯乙烯材料应力松弛行为与其固有微观结构非均匀性之间的关联, 从基本Maxwell黏弹性模型出发, 到三参量扩展指数方程, 讨论了变形单元特征时间的分布本质及聚合物应力松弛过程中的链段效应. 结果表明, 非晶态聚苯乙烯应力松弛行为呈现典型非指数特征, 单一特征时间的指数衰减形式与有限特征时间的有限谱方法均无法合理描述聚苯乙烯应力松弛行为, 这是由于非晶态聚合物微观结构非均匀性所导致的特征时间谱连续分布. 此外, 本文进一步探究了物理老化导致的应力松弛行为变化, 老化导致体系向更稳定能量状态迁移, 变形单元难以激活, 因而导致应力松弛过程慢化, 特征时间延长.

关键词:

Abstract

The relationship between stress relaxation behavior and inherent microstructural heterogeneity in amorphous polystyrene materials is studied in this work. Starting from the basic Maxwell viscoelastic model and extending to the three-parameter stretched exponential equation, the nature of the distribution of characteristic timescales and the segmental effects during polymer stress relaxation are discussed. The results indicate that the stress relaxation behavior of amorphous polymers exhibits non-exponential characteristics. Neither a single characteristic time with exponential decay nor a finite spectrum method with finite characteristic time can adequately describe the stress relaxation behavior of polystyrene due to the continuous distribution of characteristic timescales resulting from microstructural heterogeneity in amorphous polymers. In addition, the changes in stress relaxation behavior caused by physical aging are explored. Aging leads to a transition of the system towards a more stable energy state, making it difficult to activate the relaxation of the individual units, thus slowing down the stress relaxation process and increasing the characteristic time.

Keywords:

作者及机构信息

1.
西北工业大学伦敦玛丽女王工程学院, 西安　710072

2.
西北工业大学力学与土木建筑学院, 西安　710072

3.
华中科技大学化学与化工学院, 武汉　430074

通信作者: 乔吉超, qjczy@nwpu.edu.cn

基金项目: 国家自然科学基金(批准号: 51971178, 52271153)、陕西省杰出青年基金(批准号: 2021JC-12)和国家级大学生创新创业训练计划(批准号: 202310699002)资助的课题.

Authors and contacts

1.
Queen Mary University of London Engineering School, Northwestern Polytechnical University, Xi’an 710072, China

2.
School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi’an 710072, China

3.
School of Chemistry and Chemical Engineering, Huazhong University of Science and Technology, Wuhan 430074, China

Corresponding author: Qiao Ji-Chao, qjczy@nwpu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 51971178, 52271153), the Outstanding Youth Found of Shaanxi Province, China (Grant No. 2021JC-12), and National College Student Innovation and Entrepreneurship Training Program, China (Grant No. 202310699002).

文章全文 : translate this paragraph

参考文献

[1]	Ozerin A N, Golubev E K, Ivanchev S S, Aulov V A, Kechek’yan A S, Kurkin T S, Ivan’kova E M, Adonin N Y 2022 Polym. Sci. Ser. A 64 73 Google Scholar
[2]	Müller M, Abetz V 2021 Chem. Rev. 121 14189 Google Scholar
[3]	Li Y, Tang S, Abberton B C, Kröger M, Burkhart C, Jiang B, Papakonstantopoulos G J, Poldneff M, Liu W K 2012 Polymer 53 5935 Google Scholar
[4]	Boland C S, Khan U, Ryan G, Barwich S, Charifou R, Harvey A, Backes C, Li Z, Ferreira M S, Möbius M E, Young R J, Coleman J N 2016 Science 354 1257 Google Scholar
[5]	金日光, 华幼卿 2000 高分子物理 (第二版) (北京: 化学工业出版社) Jin R G, Hua Y Q 2000 Polymer Physics (2nd Ed.) (Beijing: Chemical Industry Press
[6]	Hou J X, Svaneborg C, Everaers R, Grest G S 2010 Phys. Rev. Lett. 105 068301 Google Scholar
[7]	Spathis G, Kontou E 2012 Compos. Sci. Technol. 72 959 Google Scholar
[8]	Huang J S, Gibson L J 1991 J. Mater. Sci. 26 637 Google Scholar
[9]	Papanicolaou G C, Zaoutsos S P 2019 Creep and Fatigue in Polymer Matrix Composites (Woodhead Publishing) pp3–59
[10]	Di Marzio E A, Kasianowicz J J 2003 J. Chem. Phys. 119 6378 Google Scholar
[11]	Auhl R, Everaers R, Grest G S, Kremer K, Plimpton S J 2003 J. Chem. Phys. 119 12718 Google Scholar
[12]	Kreer T, Metzger S, Müller M, Binder K, Baschnagel J 2004 J. Chem. Phys. 120 4012 Google Scholar
[13]	Chui C, Boyce M C 1999 Macromolecules 32 3795 Google Scholar
[14]	Perez J 1998 Physics and Mechanics of Amorphous Polymers (CRC Press
[15]	Ediger M D 2000 Annu. Rev. Phys. Chem. 51 99 Google Scholar
[16]	Wang X Y, Xu W S, Zhang H, Douglas J F 2019 J. Chem. Phys. 151 184503 Google Scholar
[17]	Dmowski W, Iwashita T, Chuang C P, Almer J, Egami T 2010 Phys. Rev. Lett. 105 205502 Google Scholar
[18]	Hu Y, Guan P, Li M, Liu C, Yang Y, Bai H, Wang W 2016 Phys. Rev. B 93 214202 Google Scholar
[19]	Smith G D, Borodin O, Paul W 2002 J. Chem. Phys. 117 10350 Google Scholar
[20]	Jin W, Boyd R H 2002 Polymer 43 503 Google Scholar
[21]	Borodin O, Smith G D, Bandyopadhyaya R, Byutner O 2003 Macromolecules 36 7873 Google Scholar
[22]	Smith G D, Paul W, Monkenbusch M, Richter D 2001 J. Chem. Phys. 114 4285 Google Scholar
[23]	Gebremichael Y, Schrøder T B, Starr F W, Glotzer S C 2001 Phys. Rev. E 64 051503 Google Scholar
[24]	Bennemann C, Donati C, Baschnagel J, Glotzer S C 1999 Nature 399 246 Google Scholar
[25]	Etienne S, David L 2007 Philos. Mag. 87 417 Google Scholar
[26]	Lunkenheimer P, Wehn R, Schneider U, Loidl A 2005 Phys. Rev. Lett. 95 055702 Google Scholar
[27]	Bruns M, Hassani M, Varnik F, Hassanpour A, Divinski S, Wilde G 2021 Phys. Rev. Res. 3 013234 Google Scholar
[28]	Pan J, Ivanov Y P, Zhou W H, Li Y, Greer A L 2020 Nature 578 559 Google Scholar
[29]	Pan J, Wang Y X, Guo Q, Zhang D, Greer A L, Li Y 2018 Nat. Commun. 9 560 Google Scholar
[30]	Wunsch J R 2014 Polystyrene-Synthesis, Production and Applications (New York: Nova Science Publishers, Inc.
[31]	张智枢, 顾欣, 杨云云, 蔡绪福 2017 工程科学与技术 49 232 Google Scholar Zhang Z S, Gu X, Yang Y Y, Cai X F 2017 Adv. Eng. Sci. 49 232 Google Scholar
[32]	郝奇, 乔吉超 2022 力学学报 54 3058 Google Scholar Hao Q, Qiao J C 2022 Chin. J. Theo. Appl. Mech. 54 3058 Google Scholar
[33]	Taub A, Spaepen F 1981 J. Mater. Sci. 16 3087 Google Scholar
[34]	Qiao J C, Wang Y J, Zhao L Z, et al. 2016 Phys. Rev. B 94 104203 Google Scholar
[35]	Duan Y J, Zhang L T, Qiao J C, et al. 2022 Phys. Rev. Lett. 129 175501 Google Scholar
[36]	Wagner H, Bedorf D, Küchemann S, Schwabe M, Zhang B, Arnold W, Samwer K 2011 Nat. Mater 10 439 Google Scholar
[37]	黄蓓蓓, 郝奇, 吕国建, 乔吉超 2023 72 136101 Google Scholar Huang B B, Hao Q, Lyu G J, Qiao J C 2023 Acta Phys. Sin. 72 136101 Google Scholar
[38]	Gibbs M R J, Evetts J E, Leake J A 1983 J. Mater. Sci. 18 278 Google Scholar
[39]	Jiao W, Wen P, Peng H L, Bai H Y, Sun B A, Wang W H 2013 Appl. Phys. Lett. 102 101903 Google Scholar
[40]	Lu Z, Shang B, Sun Y, Zhu Z, Guan P, Wang W, Bai H 2016 J. Chem. Phys. 144 144501 Google Scholar
[41]	汪卫华 2013 物理学进展 33 177 Wang W H 2013 Prog. Phys. 33 177
[42]	王峥, 汪卫华 2017 66 176103 Google Scholar Wang Z, Wang W H 2017 Acta Phys. Sin. 66 176103 Google Scholar
[43]	Zhao Y, Shang B, Zhang B, Tong X, Ke H, Bai H, Wang W H 2022 Sci. Adv. 8 eabn3623 Google Scholar
[44]	Casalini R, Roland C M 2009 Phys. Rev. Lett. 102 035701 Google Scholar

施引文献

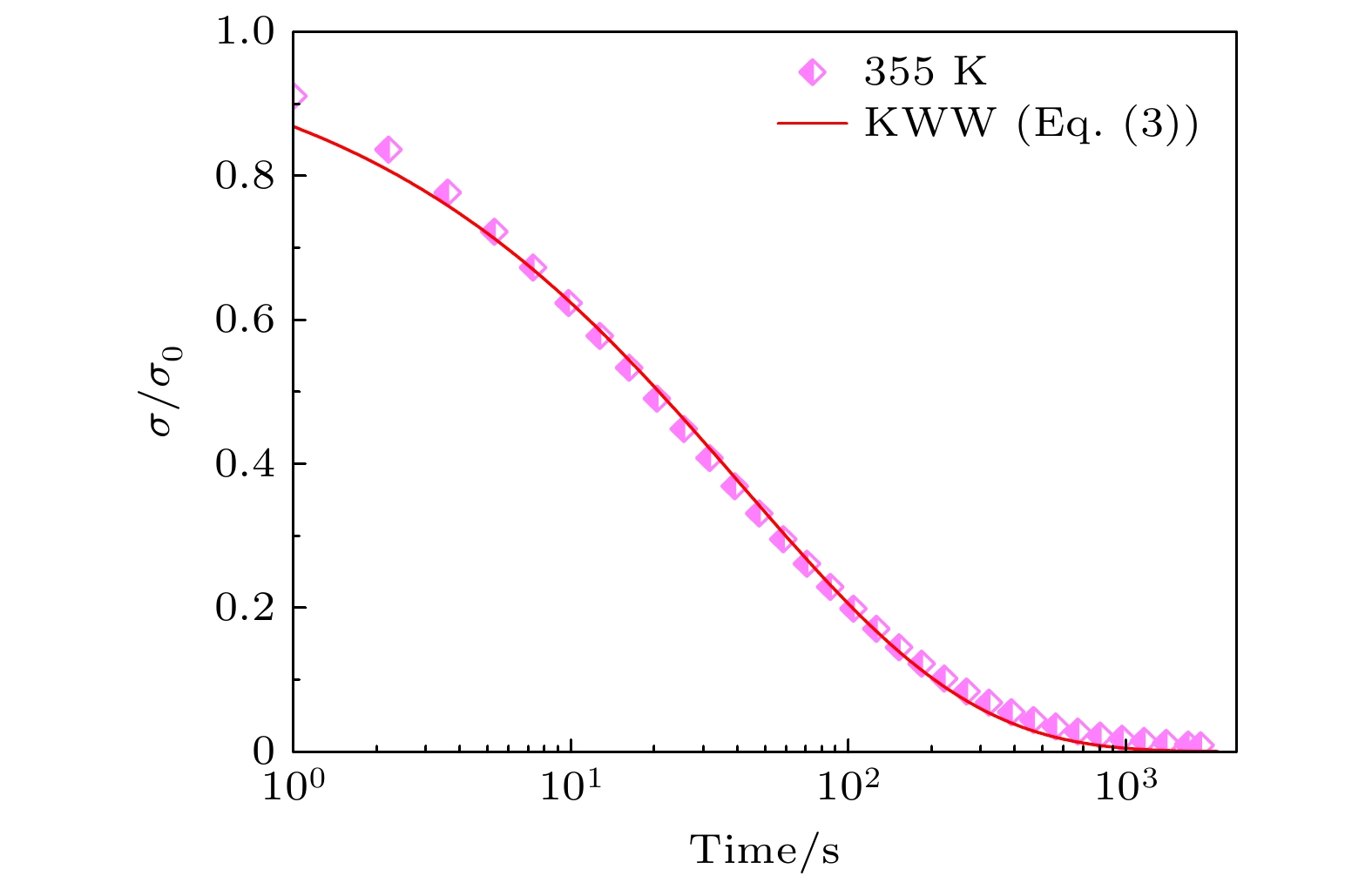
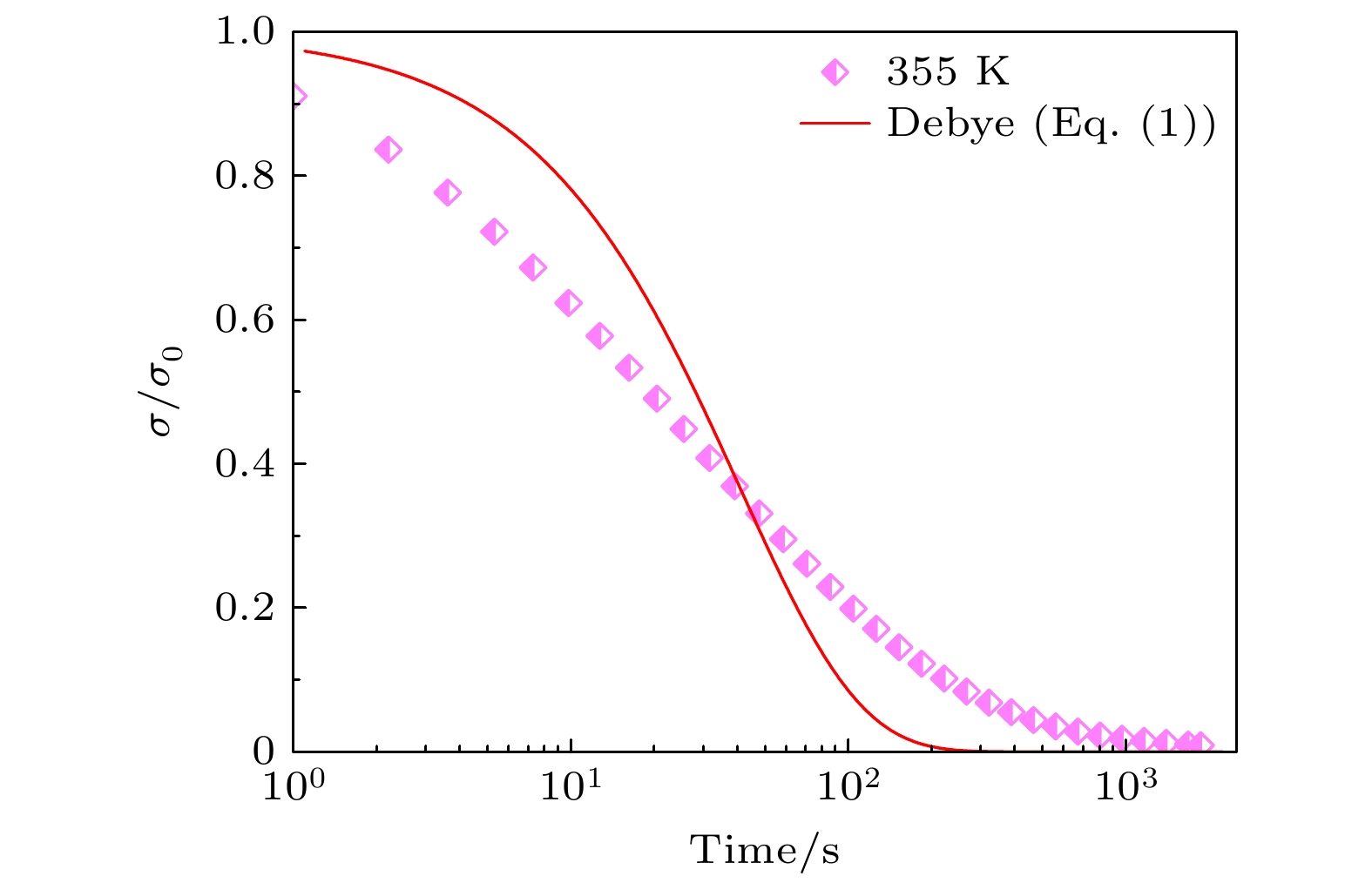
图 1 聚苯乙烯在给定应变0.4%条件下的应力松弛响应. 测试温度为355 K, 加载前保温30 min以使测试环境温度稳定; 红色实线为Maxwell模型 ((1)式)拟合曲线

Fig. 1. Stress response of PS at a given strain of 0.4%. The test temperature is 355 K, and the temperature is kept for 30 min before loading to stabilize the ambient temperature in an equilibrium state. The red solid curve is the least fitting using the Maxwell model (Eq. (1)).

下载: 全尺寸图片幻灯片

图 2 采用(2)式对聚苯乙烯应力松弛响应拟合结果, 其中(a)和(b)中红色实线分别对应于n = 2和n = 4

Fig. 2. Fitting results of stress relaxation response of polystyrene using Eq. (2): (a), (b) The fitting curves of the finite spectrum approach when n = 2 and n = 4, respectively.

下载: 全尺寸图片幻灯片

图 3 应力松弛实验曲线及KWW方程((3)式)最小二乘拟合结果

Fig. 3. Comparison between fitting curve (Eq. (3)) and experiments (symbols) for stress relaxation behavior.

下载: 全尺寸图片幻灯片

图 4 扩展指数方程计算所得应力松弛过程中特征时间分布谱图(绿色区域), 为便于对比, 图3中拟合结果亦被给出

Fig. 4. Characteristic time distribution spectrum of the stress relaxation process calculated by the KWW equation (green area). For comparison, the fitting results in Fig. 3 are also given.

下载: 全尺寸图片幻灯片

图 5 聚苯乙烯在340 K和355 K温度条件下所得(a)应力松弛数据及计算所得(b)激活能谱分布

Fig. 5. (a) Stress relaxation data and (b) calculated activation energy spectrum distribution of polystyrene at temperatures of 340 K and 355 K.

下载: 全尺寸图片幻灯片

图 6 不同温度条件下(340, 345, 350, 355 K)聚苯乙烯应力松弛曲线, 红色实线为扩展指数方程((3)式)拟合结果

Fig. 6. Stress relaxation curves of polystyrene under different temperature conditions (340, 345, 350, 355 K). The red solid curves represent the fitting results of the extended exponential equation (Eq. (3)).

下载: 全尺寸图片幻灯片

图 7 不同温度条件下(340, 345, 350, 355)聚苯乙烯应力松弛曲线, 红色实线为三参数扩展指数方程((6)式)拟合结果

Fig. 7. Stress relaxation curves of polystyrene under different temperature conditions (340, 345, 350, 355 K). The red solid curves represent the fitting results of the three-parameter extended exponential equation (Eq. (6)).

下载: 全尺寸图片幻灯片

图 8 不同老化时间条件下(15, 30, 60, 90, 120 min)聚苯乙烯应力松弛曲线, 测试温度为350 K, 红色实线为三参数扩展指数方程((6)式)拟合结果

Fig. 8. Stress relaxation curves of polystyrene after annealing for different time (15, 30, 60, 90, 120 min). The red solid curves represent the fitting results of the three-parameter extended exponential equation (Eq. (6)).

下载: 全尺寸图片幻灯片

图 9 不同老化时间条件下(15, 30, 60, 90, 120 min)根据(5)式所得聚苯乙烯应力松弛过程中激活能谱分布

Fig. 9. Activation energy spectrum distribution of polystyrene calculated by Eq. (5) after annealing for different time (15, 30, 60, 90, 120 min).

下载: 全尺寸图片幻灯片

map

[1]	Ozerin A N, Golubev E K, Ivanchev S S, Aulov V A, Kechek’yan A S, Kurkin T S, Ivan’kova E M, Adonin N Y 2022 Polym. Sci. Ser. A 64 73 Google Scholar
[2]	Müller M, Abetz V 2021 Chem. Rev. 121 14189 Google Scholar
[3]	Li Y, Tang S, Abberton B C, Kröger M, Burkhart C, Jiang B, Papakonstantopoulos G J, Poldneff M, Liu W K 2012 Polymer 53 5935 Google Scholar
[4]	Boland C S, Khan U, Ryan G, Barwich S, Charifou R, Harvey A, Backes C, Li Z, Ferreira M S, Möbius M E, Young R J, Coleman J N 2016 Science 354 1257 Google Scholar
[5]	金日光, 华幼卿 2000 高分子物理 (第二版) (北京: 化学工业出版社) Jin R G, Hua Y Q 2000 Polymer Physics (2nd Ed.) (Beijing: Chemical Industry Press
[6]	Hou J X, Svaneborg C, Everaers R, Grest G S 2010 Phys. Rev. Lett. 105 068301 Google Scholar
[7]	Spathis G, Kontou E 2012 Compos. Sci. Technol. 72 959 Google Scholar
[8]	Huang J S, Gibson L J 1991 J. Mater. Sci. 26 637 Google Scholar
[9]	Papanicolaou G C, Zaoutsos S P 2019 Creep and Fatigue in Polymer Matrix Composites (Woodhead Publishing) pp3–59
[10]	Di Marzio E A, Kasianowicz J J 2003 J. Chem. Phys. 119 6378 Google Scholar
[11]	Auhl R, Everaers R, Grest G S, Kremer K, Plimpton S J 2003 J. Chem. Phys. 119 12718 Google Scholar
[12]	Kreer T, Metzger S, Müller M, Binder K, Baschnagel J 2004 J. Chem. Phys. 120 4012 Google Scholar
[13]	Chui C, Boyce M C 1999 Macromolecules 32 3795 Google Scholar
[14]	Perez J 1998 Physics and Mechanics of Amorphous Polymers (CRC Press
[15]	Ediger M D 2000 Annu. Rev. Phys. Chem. 51 99 Google Scholar
[16]	Wang X Y, Xu W S, Zhang H, Douglas J F 2019 J. Chem. Phys. 151 184503 Google Scholar
[17]	Dmowski W, Iwashita T, Chuang C P, Almer J, Egami T 2010 Phys. Rev. Lett. 105 205502 Google Scholar
[18]	Hu Y, Guan P, Li M, Liu C, Yang Y, Bai H, Wang W 2016 Phys. Rev. B 93 214202 Google Scholar
[19]	Smith G D, Borodin O, Paul W 2002 J. Chem. Phys. 117 10350 Google Scholar
[20]	Jin W, Boyd R H 2002 Polymer 43 503 Google Scholar
[21]	Borodin O, Smith G D, Bandyopadhyaya R, Byutner O 2003 Macromolecules 36 7873 Google Scholar
[22]	Smith G D, Paul W, Monkenbusch M, Richter D 2001 J. Chem. Phys. 114 4285 Google Scholar
[23]	Gebremichael Y, Schrøder T B, Starr F W, Glotzer S C 2001 Phys. Rev. E 64 051503 Google Scholar
[24]	Bennemann C, Donati C, Baschnagel J, Glotzer S C 1999 Nature 399 246 Google Scholar
[25]	Etienne S, David L 2007 Philos. Mag. 87 417 Google Scholar
[26]	Lunkenheimer P, Wehn R, Schneider U, Loidl A 2005 Phys. Rev. Lett. 95 055702 Google Scholar
[27]	Bruns M, Hassani M, Varnik F, Hassanpour A, Divinski S, Wilde G 2021 Phys. Rev. Res. 3 013234 Google Scholar
[28]	Pan J, Ivanov Y P, Zhou W H, Li Y, Greer A L 2020 Nature 578 559 Google Scholar
[29]	Pan J, Wang Y X, Guo Q, Zhang D, Greer A L, Li Y 2018 Nat. Commun. 9 560 Google Scholar
[30]	Wunsch J R 2014 Polystyrene-Synthesis, Production and Applications (New York: Nova Science Publishers, Inc.
[31]	张智枢, 顾欣, 杨云云, 蔡绪福 2017 工程科学与技术 49 232 Google Scholar Zhang Z S, Gu X, Yang Y Y, Cai X F 2017 Adv. Eng. Sci. 49 232 Google Scholar
[32]	郝奇, 乔吉超 2022 力学学报 54 3058 Google Scholar Hao Q, Qiao J C 2022 Chin. J. Theo. Appl. Mech. 54 3058 Google Scholar
[33]	Taub A, Spaepen F 1981 J. Mater. Sci. 16 3087 Google Scholar
[34]	Qiao J C, Wang Y J, Zhao L Z, et al. 2016 Phys. Rev. B 94 104203 Google Scholar
[35]	Duan Y J, Zhang L T, Qiao J C, et al. 2022 Phys. Rev. Lett. 129 175501 Google Scholar
[36]	Wagner H, Bedorf D, Küchemann S, Schwabe M, Zhang B, Arnold W, Samwer K 2011 Nat. Mater 10 439 Google Scholar
[37]	黄蓓蓓, 郝奇, 吕国建, 乔吉超 2023 72 136101 Google Scholar Huang B B, Hao Q, Lyu G J, Qiao J C 2023 Acta Phys. Sin. 72 136101 Google Scholar
[38]	Gibbs M R J, Evetts J E, Leake J A 1983 J. Mater. Sci. 18 278 Google Scholar
[39]	Jiao W, Wen P, Peng H L, Bai H Y, Sun B A, Wang W H 2013 Appl. Phys. Lett. 102 101903 Google Scholar
[40]	Lu Z, Shang B, Sun Y, Zhu Z, Guan P, Wang W, Bai H 2016 J. Chem. Phys. 144 144501 Google Scholar
[41]	汪卫华 2013 物理学进展 33 177 Wang W H 2013 Prog. Phys. 33 177
[42]	王峥, 汪卫华 2017 66 176103 Google Scholar Wang Z, Wang W H 2017 Acta Phys. Sin. 66 176103 Google Scholar
[43]	Zhao Y, Shang B, Zhang B, Tong X, Ke H, Bai H, Wang W H 2022 Sci. Adv. 8 eabn3623 Google Scholar
[44]	Casalini R, Roland C M 2009 Phys. Rev. Lett. 102 035701 Google Scholar

[1]	张剑, 郝奇, 张浪渟, 乔吉超. 不同力学激励形式探索La基非晶合金微观结构非均匀性. , 2024, 73(4): 046101. doi: 10.7498/aps.73.20231421
[2]	李佳芮, 乐陶然, 尉昊赟, 李岩. 基于脉冲受激布里渊散射光谱的非接触式黏弹性测量. , 2024, 73(12): 127801. doi: 10.7498/aps.73.20231974
[3]	孟绍怡, 郝奇, 王兵, 段亚娟, 乔吉超. 冷却速率对La基非晶合金β弛豫行为和应力弛豫的影响. , 2024, 73(3): 036101. doi: 10.7498/aps.73.20231417
[4]	孟绍怡, 郝奇, 吕国建, 乔吉超. La基非晶合金β弛豫行为: 退火和加载应变的影响. , 2023, 72(7): 076101. doi: 10.7498/aps.72.20222389
[5]	黄蓓蓓, 郝奇, 吕国建, 乔吉超. 锆基非晶合金的动态弛豫和应力松弛. , 2023, 72(13): 136101. doi: 10.7498/aps.72.20230181
[6]	段亚娟, 乔吉超. Pd基非晶合金动态弛豫机制和应力松弛行为. , 2022, 71(8): 086101. doi: 10.7498/aps.71.20212025
[7]	汪杨, 赵伶玲. 单原子Lennard-Jones体黏弹性弛豫时间. , 2020, 69(12): 123101. doi: 10.7498/aps.69.20200138
[8]	姜文龙. 非晶聚苯乙烯和Pd₄₀Ni₁₀Cu₃₀P₂₀玻璃化转变中比热变化的机理和定量研究. , 2020, 69(12): 126401. doi: 10.7498/aps.69.20200331
[9]	许福, 李科锋, 邓旭辉, 张平, 龙志林. 基于分数阶微分流变模型的非晶合金黏弹性行为及流变本构参数研究. , 2016, 65(4): 046101. doi: 10.7498/aps.65.046101
[10]	戴卿, 项楠, 程洁, 倪中华. 圆截面直流道中微粒黏弹性聚焦机理研究. , 2015, 64(15): 154703. doi: 10.7498/aps.64.154703
[11]	廖光开, 龙志林, 许福, 刘为, 张志洋, 杨妙. 基于分数阶流变模型的铁基块体非晶合金黏弹性行为研究. , 2015, 64(13): 136101. doi: 10.7498/aps.64.136101
[12]	杨斌鑫, 欧阳洁. 黏弹性熔体充模流动诱导残余应力模拟. , 2012, 61(23): 234602. doi: 10.7498/aps.61.234602
[13]	熊毅, 张向军, 张晓昊, 温诗铸. 电场作用下5CB液晶分子的近壁面层黏弹性的QCM研究. , 2010, 59(11): 7998-8004. doi: 10.7498/aps.59.7998
[14]	王羽, 欧阳洁, 杨斌鑫. 分数阶Oldroyd-B黏弹性Poiseuille流的Laplace数值反演分析. , 2010, 59(10): 6757-6763. doi: 10.7498/aps.59.6757
[15]	张红平, 欧阳洁, 阮春蕾. 纤维悬浮聚合物熔体描述的均一结构多尺度模型. , 2009, 58(1): 619-630. doi: 10.7498/aps.58.619
[16]	杜启振, 杨慧珠. 裂缝性地层黏弹性地震多波波动方程. , 2004, 53(8): 2801-2806. doi: 10.7498/aps.53.2801
[17]	仪桂云, 董　鹏, 王晓冬, 刘丽霞, 陈胜利. 三维有序大孔聚苯乙烯的制备及表征. , 2004, 53(10): 3311-3315. doi: 10.7498/aps.53.3311
[18]	杜启振, 杨慧珠. 方位各向异性黏弹性介质波场有限元模拟. , 2003, 52(8): 2010-2014. doi: 10.7498/aps.52.2010
[19]	杜启振, 杨慧珠. 线性黏弹性各向异性介质速度频散和衰减特征研究. , 2002, 51(9): 2101-2108. doi: 10.7498/aps.51.2101
[20]	王晓强, 谢二庆, 钱秉中, 贺德衍, 朱智勇, 金运范. 离子辐照对聚苯乙烯低温导电特性的影响. , 2002, 51(5): 1094-1097. doi: 10.7498/aps.51.1094

计量

文章访问数: 2413
PDF下载量: 57
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于微观结构非均匀性理解非晶态聚苯乙烯的应力松弛行为