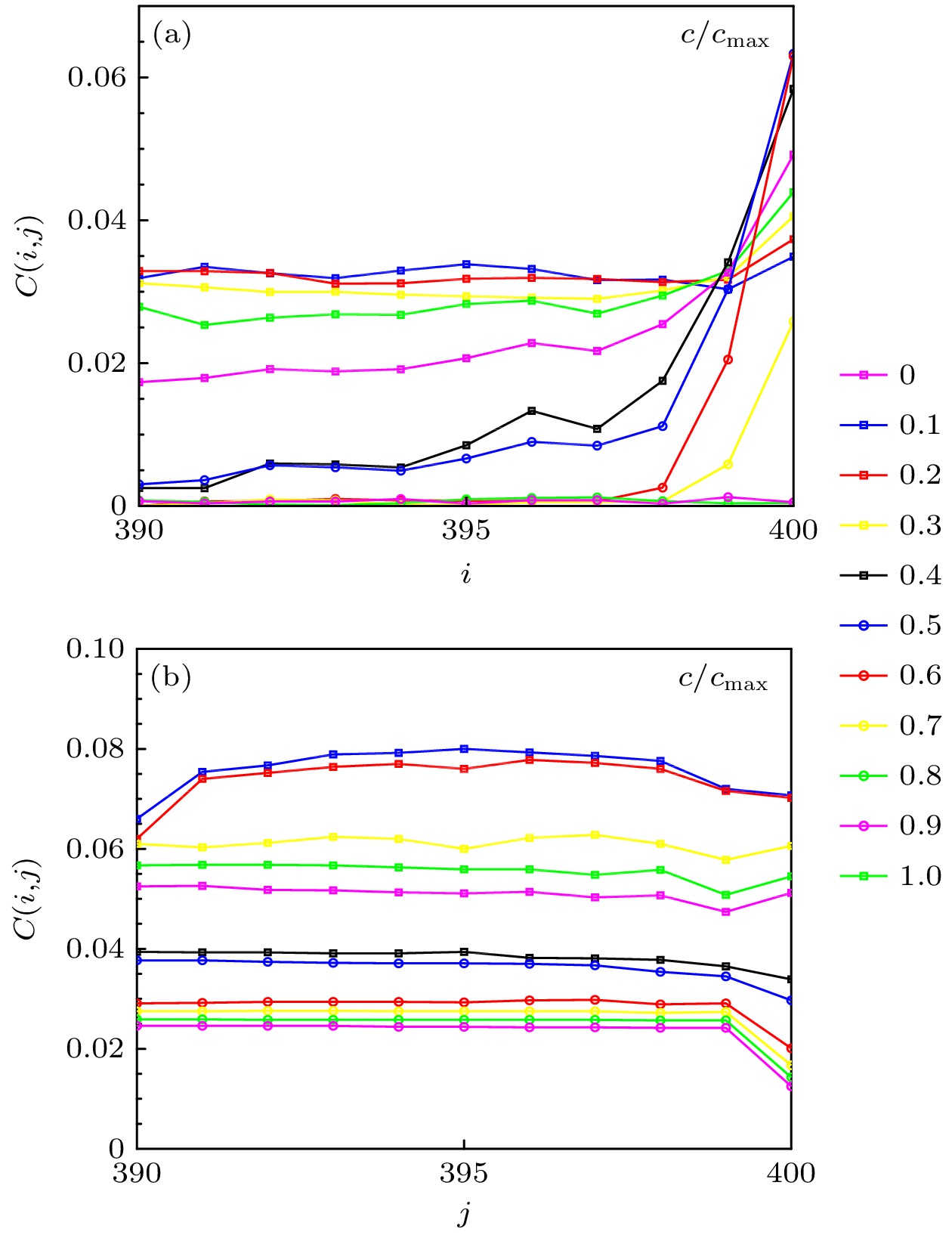
-
利用线性自旋波理论和量子蒙特卡罗方法研究了弯曲应变下六角晶格量子反铁磁体的赝朗道能级. 通过线性自旋波理论, 发现磁赝朗道能级出现在磁子能谱的高能端, 其能级间距与能级指数的平方根成正比. 线性自旋波理论和量子蒙特卡罗方法都显示, 尺寸相同时随着应变强度的逐渐增加, 局域磁化强度逐渐减弱, 应变强度相同的条件下反铁磁序在y方向上连续减弱, 因为上边界处的海森伯链解耦为孤立的垂直链, 导致上边界附近的磁序被破坏. 量子蒙特卡罗方法提供了更精确的反铁磁序演化: 在特定应变强度下上边界处垂直关联不变, 水平关联增加, 从而影响磁化强度, 使局域磁化在上边界处呈上翘趋势. 研究结果有助于理解弯曲应变对自旋激发的影响, 并可能在二维量子磁性材料实验中得以实现.The pseudo-Landau energy levels of a hexagonal lattice quantum antiferromagnet under bending strain are studied by linear spin-wave theory (LSWT) and quantum Monte Carlo method (QMC). Using the linear spin wave theory, the magnetic pseudo-Landau energy level can be found to appear at the high-energy end of the magnon spectrum, and the energy level spacing is proportional to the square root of the energy level index. The linear spin wave theory and the quantum Monte Carlo method both indicate that at the same size, the local magnetization gradually weakens with the gradual increase of the strain strength. Additionally, the antiferromagnetic order continuously weakens in the y-direction under the same strain strength. This occurs because the Heisenberg chain on the upper boundary becomes decoupled into an isolated vertical chain, leading to the destruction of the magnetic order near the upper boundary. The quantum Monte Carlo method provides a more accurate antiferromagnetic sequence evolution, that is, the vertical correlation at the upper boundary is unchanged and the horizontal correlation increases under a specific strain intensity. This affects the magnetization intensity, so that the local magnetization shows an upward trend at the upper boundary. The results contribute to the understanding of the effect of bending strain on spin excitations, and this effect may be observed in two-dimensional quantum magnetic material experiments.
-
Keywords:
- bending strain /
- pseudo-Landau levels /
- linear spin-wave theory /
- quantum Monte Carlo method
[1] Castro-Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109
Google Scholar
[2] Pereira V M, Castro-Neto A H 2009 Phys. Rev. Lett. 103 046801
Google Scholar
[3] Levy N, Burke S A, Meaker K L, Panlasigui M, Zettl A, Guinea F, Castro-Neto A H, Crommie M F 2010 Science 329 544
Google Scholar
[4] Koskinen P 2012 Phys. Rev. B 85 205429
Google Scholar
[5] Nieminen A, Ornigotti M 2022 Phys. Rev. A 106 043517
Google Scholar
[6] Lu W T, Sun Q F, Tian H Y, Zhou B H, Liu H M 2020 Phys. Rev. B 102 125426
Google Scholar
[7] Pereira V M, Castro-Neto A H, Peres N M R 2009 Phys. Rev. B 80 045401
Google Scholar
[8] Sharma A, Kotov V N, Castro-Neto A H 2017 Phys. Rev. B 95 235124
Google Scholar
[9] Vozmediano M A H, Katsnelson M I, Guinea F 2010 Phys. Rep. 496 109
Google Scholar
[10] Torres V, Faria D, Latgé A 2018 Phys. Rev. B 97 165429
Google Scholar
[11] Zhang X, Pan G P, Zhang Y, Kang J, Meng Z Y 2021 Chin. Phys. Lett. 38 077305
Google Scholar
[12] 蔡潇潇, 罗国语, 李志强, 贺言 2021 70 187301
Google Scholar
Cai X X, Luo G Y, Li Z Q, He Y 2021 Acta Phys. Sin. 70 187301
Google Scholar
[13] Li Y F, Chen Z F 2014 Phys. Chem. C 118 1148
Google Scholar
[14] Phan A L, Le D N, Le V H, Roy P 2020 Physica E 121 114084
Google Scholar
[15] Jiang Y C, Gao J 2014 Sci. Rep. 4 6738
Google Scholar
[16] Sun J S, Guo H M, Feng S P 2021 Phys. Rev. Res. 3 043223
Google Scholar
[17] Nayga M M, Rachel S, Vojta M 2019 Phys. Rev. Lett. 123 207204
Google Scholar
[18] Sun J S, Ma N, Ying T, Guo H M, Feng S P 2021 Phys. Rev. B 104 125117
Google Scholar
[19] Zabolotskiy A D, Lozovik Y E 2016 Phys. Rev. B 94 165403
Google Scholar
[20] Toth S, Lake B 2015 J. Phys. Condens. Matter 27 166002
Google Scholar
[21] Liao L, Chen Y 2014 Superlattices Microstruct. 73 82
Google Scholar
[22] Syljuåsen O F, Sandvik A W 2002 Phys. Rev. E 66 046701
Google Scholar
[23] Syljuåsen O F 2003 Phys. Rev. E 67 046701
Google Scholar
[24] Alet F, Wessel S, Troyer M 2005 Phys. Rev. E 71 036706
Google Scholar
[25] Holstein T, Primakoff H 1940 Phys. Rev. 58 1098
Google Scholar
[26] Settnes M, Power S R, Jauho A P 2016 Phys. Rev. B 93 035456
Google Scholar
[27] Yang L, Anantram M P, Han J, Lu J P 1999 Phys. Rev. B 60 13874
Google Scholar
[28] Nikiforov I, Dontsova E, James R D, Dumitrică T 2014 Phys. Rev. B 89 155437
Google Scholar
[29] Wang Z J, Luitz D J, Villadiego I S 2022 Phys. Rev. B 106 125150
Google Scholar
[30] Ma T X, Huang Z B, Hu F M, Lin H Q 2011 Phys. Rev. B 84 121410
Google Scholar
[31] Fang S C, Liu G K, Lin H Q, Huang Z B 2019 Phys. Rev. B 100 115135
Google Scholar
[32] Golor M, Lang T C, Wessel S 2013 Phys. Rev. B 87 155441
Google Scholar
[33] Dai X 2022 Chin. Phys. Lett. 39 050101
Google Scholar
[34] Lu H Y, Li C H, Chen B B, Li W, Qi Y, Meng Z Y 2022 Chin. Phys. Lett. 39 050701
Google Scholar
[35] Wessel S, Jagannathan A, Haas S 2003 Phys. Rev. Lett. 90 177205
Google Scholar
[36] Rostami H, Guinea F, Cappelluti E 2022 Phys. Rev. B 105 195431
Google Scholar
[37] Bussy A, Pizzi G, Gibertini M 2017 Phys. Rev. B 96 165438
Google Scholar
[38] Yadav R, Rachel S, Hozoi L, van den Brink J, Jackeli G 2018 Phys. Rev. B 98 121107
Google Scholar
[39] Liu T Y 2020 Phys. Rev. B 102 045151
Google Scholar
[40] 肖寒, 弭孟娟, 王以林 2021 70 127503
Google Scholar
Xiao H, Mi M J, Wang Y L 2021 Acta Phys. Sin. 70 127503
Google Scholar
[41] Webster L, Yan J A 2018 Phys. Rev. B 98 144411
Google Scholar
[42] Deng Y C, Liu X H, Chen Y Y, Du Z Z, Jiang N, Shen C, Zhang E Z, Zheng H Z, Lu H Z, Wang K Y 2023 Natl. Sci. Rev. 10 nwac154
Google Scholar
-
图 1 (a)弯曲应变下具有锯齿状边缘的内半径为R, 外半径为$R+W$的蜂窝扇形纳米带, 纳米带在x方向具有周期性, y方向的宽度是$L_{y}=6$; (b)弯曲应变下宽度为$L_{y}=200$的纳米带上边界处的晶格放大图. 不同厚度的键表示不同的交换耦合值, 数值标记在旁边
Fig. 1. (a) A honeycomb fan-shaped nanoribbon with jagged edges with an inner radius R and an outer radius $R+W$ under bending strain. The nanoribbon is periodic in the x direction, and the width in the y direction is $L_{y}=6$. (b) Enlarged lattice at the upper boundary of a nanoribbon with a width of $L_{y}=200$ under bending strain. Keys of different thicknesses represent different exchange coupling values, and numerical values are marked next to them.
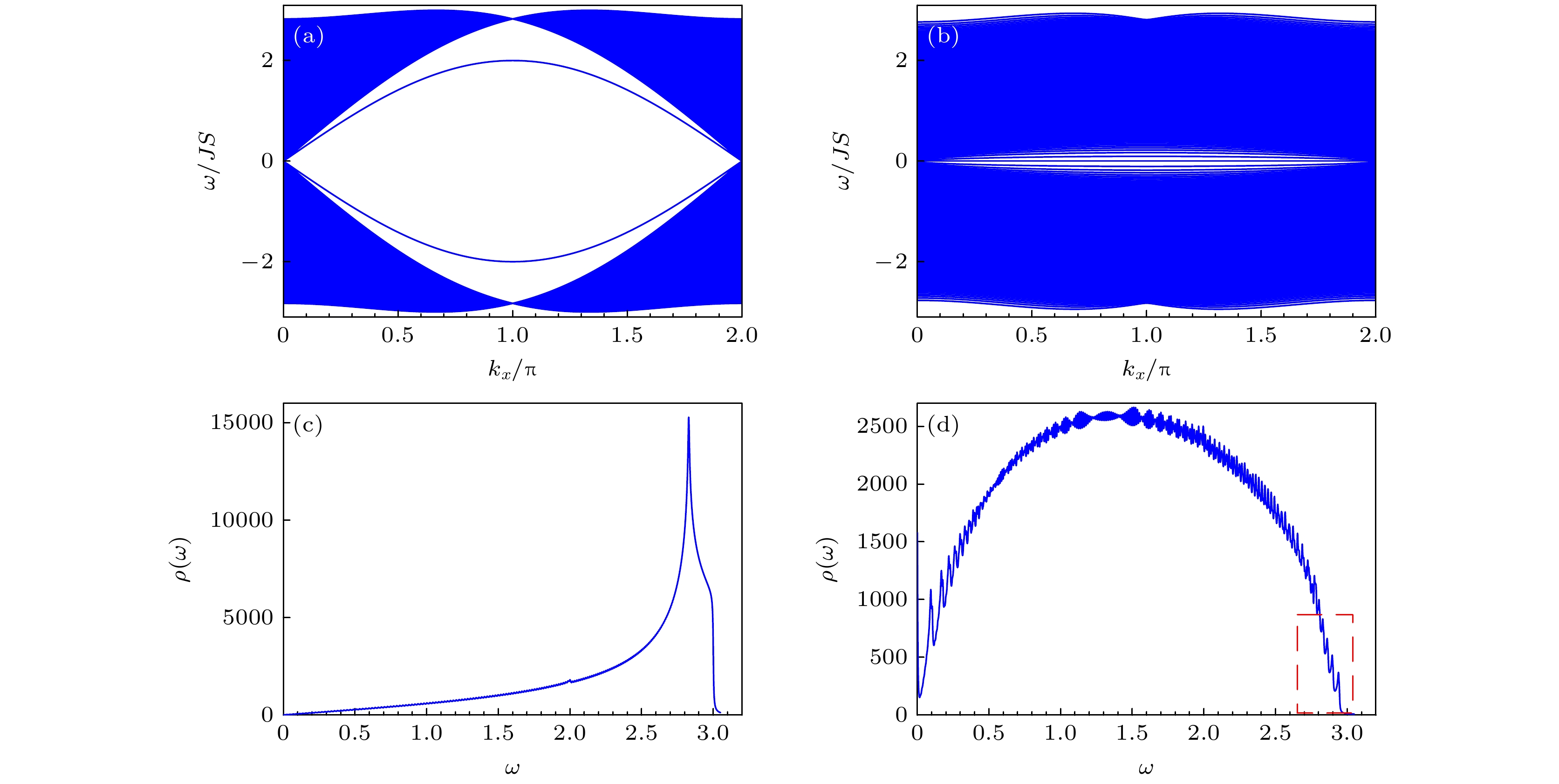
图 2 锯齿状反铁磁蜂窝纳米带的磁子能谱 (a)无应变情况; (b)弯曲应变情况; 图(c)和图(d)是图(a)和图(b)两种情况对应的磁子态密度. 在图(b)和图(d)中, 应变强度为$c/c_{\max}=1$. 图(d)中的红色虚线框内的曲线将放大显示在图3中
Fig. 2. The magnon spectrum of the antiferromagnetic honeycomb nanoribbon: (a) Without strain; (b) under bending strain. Panels (c) and (d) are the magnon density of states corresponding to panels (a) and (b). In panels (b) and (d), the strain strength is $c/c_{\max}=1$. The curve inside the red dashed box in panel (d) will be enlarged as shown in Fig. 3.
图 3 (a)磁子能谱上端态密度; (b)赝朗道能级的能量$\omega_{n}$作为能级指数n的平方根的函数, 实线反映了数据的线性拟合. 图(c)和图(d)是子晶格A和B上的局域磁化率. 在图(a), 图(c)和图(d)中, 应变强度采用$c/c_{\max} = 1$, 线性尺寸Ly = 200, Lx = 20
Fig. 3. (a) The density of states at the upper end of the magnon spectrum; (b) the energy $\omega_{n}$ of the pseudo-Landau level is a function of the square root of the energy level index n, and the solid line reflects the linear fit of the data. Panels (c) and (d) are the local magnetic susceptibility on the sublattices A and B. In panels (a), (c) and (d), the strain strength is $c/c_{\max}=1$, the linear size is $L_{y}=200$, $L_{x}=20$.
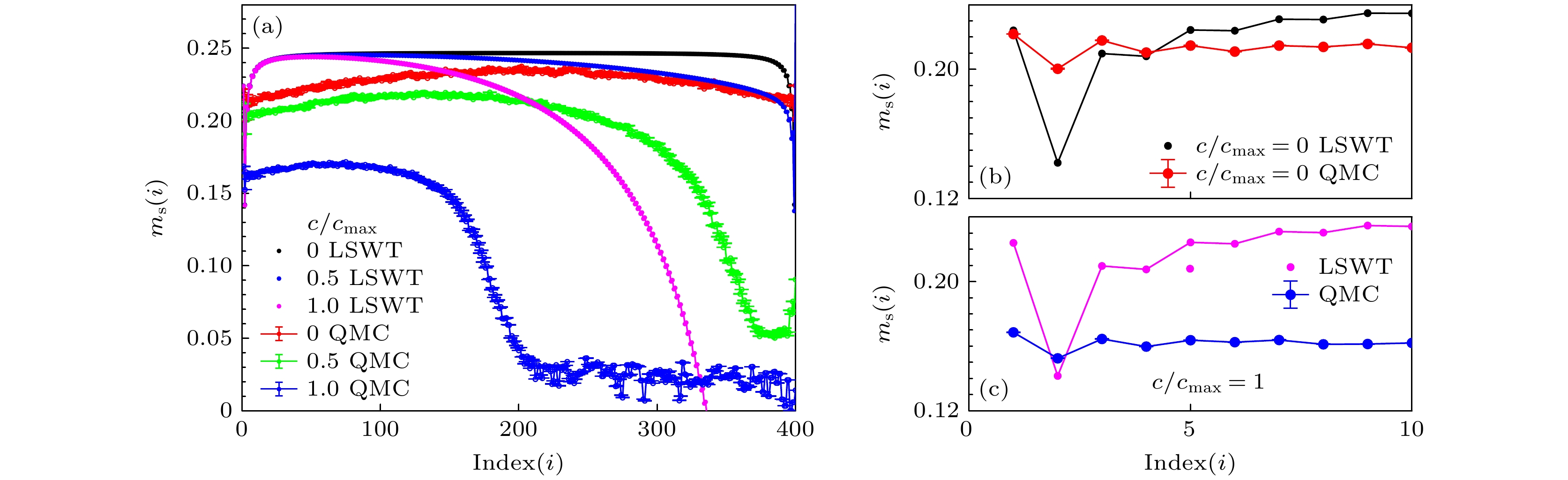
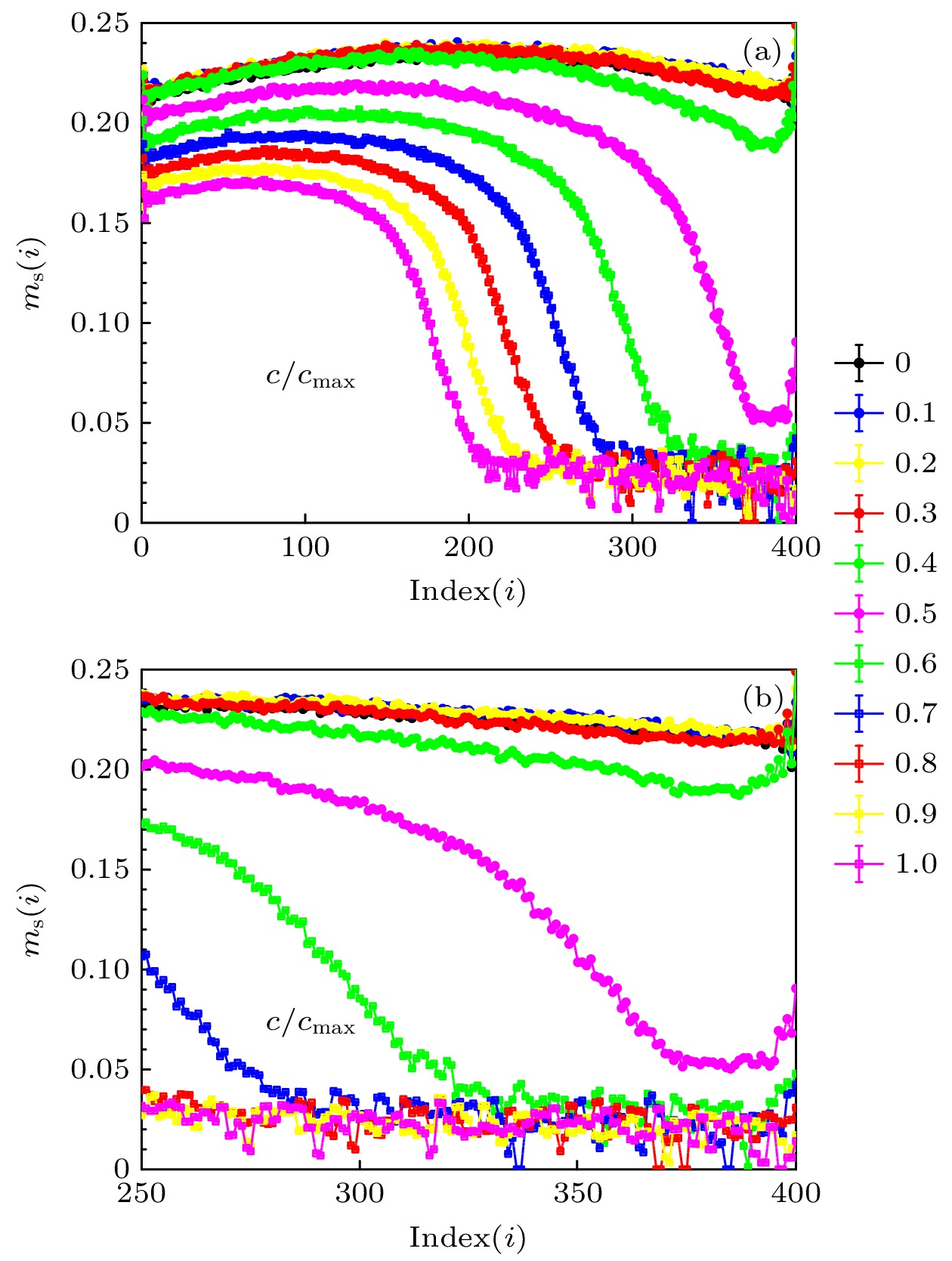
图 4 (a)在应变强度$c/c_{\max}=0, 0.5$和1下, 通过线性自旋波理论和量子蒙特卡罗模拟得到的局域磁化强度. 图(b)和图(c)分别放大了图(a)中无应变和最大应变时靠近下边界的曲线. 计算的格点范围延伸到400 (与此后的图表相同)
Fig. 4. (a) The local magnetization obtained by linear spin wave theory and quantum Monte Carlo simulations under $c/c_{\max}=0$, 0.5 and 1. Panels (b) and (c) magnify the curves near the lower boundary at no strain and maximum strain in panel (a), respectively. The calculated grid point range is extended to 400 (same as charts hereafter).
图 5 在应变强度$c/c_{\max}=0—1$下, 量子蒙特卡罗模拟得到的局域磁化强度 (a) $0—400$号格点上的数值; (b) $250— $$ 400$号格点上的数值
Fig. 5. The local magnetization obtained by quantum Monte Carlo simulations under $c/c_{\max}=0$–1: (a) Values at grid points 0–400; (b) values at grid points 250–400
图 6 在应变强度$c/c_{\max}=0—1$下, 作为zigzag链指数函数的垂直和水平交换耦合
Fig. 6. Under $c/c_{\max}=0$–1, the variation of horizontal bond and vertical bond with the lattice position.
图 7 在$c/c_{\max}=0—1$范围内390—400号格点上的(a)水平关联, (b) 垂直关联
Fig. 7. (a) Horizontal correlations, (b) vertical correlations at grid points 390–400 under $c/c_{\max}=0$–1.
-
[1] Castro-Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109
Google Scholar
[2] Pereira V M, Castro-Neto A H 2009 Phys. Rev. Lett. 103 046801
Google Scholar
[3] Levy N, Burke S A, Meaker K L, Panlasigui M, Zettl A, Guinea F, Castro-Neto A H, Crommie M F 2010 Science 329 544
Google Scholar
[4] Koskinen P 2012 Phys. Rev. B 85 205429
Google Scholar
[5] Nieminen A, Ornigotti M 2022 Phys. Rev. A 106 043517
Google Scholar
[6] Lu W T, Sun Q F, Tian H Y, Zhou B H, Liu H M 2020 Phys. Rev. B 102 125426
Google Scholar
[7] Pereira V M, Castro-Neto A H, Peres N M R 2009 Phys. Rev. B 80 045401
Google Scholar
[8] Sharma A, Kotov V N, Castro-Neto A H 2017 Phys. Rev. B 95 235124
Google Scholar
[9] Vozmediano M A H, Katsnelson M I, Guinea F 2010 Phys. Rep. 496 109
Google Scholar
[10] Torres V, Faria D, Latgé A 2018 Phys. Rev. B 97 165429
Google Scholar
[11] Zhang X, Pan G P, Zhang Y, Kang J, Meng Z Y 2021 Chin. Phys. Lett. 38 077305
Google Scholar
[12] 蔡潇潇, 罗国语, 李志强, 贺言 2021 70 187301
Google Scholar
Cai X X, Luo G Y, Li Z Q, He Y 2021 Acta Phys. Sin. 70 187301
Google Scholar
[13] Li Y F, Chen Z F 2014 Phys. Chem. C 118 1148
Google Scholar
[14] Phan A L, Le D N, Le V H, Roy P 2020 Physica E 121 114084
Google Scholar
[15] Jiang Y C, Gao J 2014 Sci. Rep. 4 6738
Google Scholar
[16] Sun J S, Guo H M, Feng S P 2021 Phys. Rev. Res. 3 043223
Google Scholar
[17] Nayga M M, Rachel S, Vojta M 2019 Phys. Rev. Lett. 123 207204
Google Scholar
[18] Sun J S, Ma N, Ying T, Guo H M, Feng S P 2021 Phys. Rev. B 104 125117
Google Scholar
[19] Zabolotskiy A D, Lozovik Y E 2016 Phys. Rev. B 94 165403
Google Scholar
[20] Toth S, Lake B 2015 J. Phys. Condens. Matter 27 166002
Google Scholar
[21] Liao L, Chen Y 2014 Superlattices Microstruct. 73 82
Google Scholar
[22] Syljuåsen O F, Sandvik A W 2002 Phys. Rev. E 66 046701
Google Scholar
[23] Syljuåsen O F 2003 Phys. Rev. E 67 046701
Google Scholar
[24] Alet F, Wessel S, Troyer M 2005 Phys. Rev. E 71 036706
Google Scholar
[25] Holstein T, Primakoff H 1940 Phys. Rev. 58 1098
Google Scholar
[26] Settnes M, Power S R, Jauho A P 2016 Phys. Rev. B 93 035456
Google Scholar
[27] Yang L, Anantram M P, Han J, Lu J P 1999 Phys. Rev. B 60 13874
Google Scholar
[28] Nikiforov I, Dontsova E, James R D, Dumitrică T 2014 Phys. Rev. B 89 155437
Google Scholar
[29] Wang Z J, Luitz D J, Villadiego I S 2022 Phys. Rev. B 106 125150
Google Scholar
[30] Ma T X, Huang Z B, Hu F M, Lin H Q 2011 Phys. Rev. B 84 121410
Google Scholar
[31] Fang S C, Liu G K, Lin H Q, Huang Z B 2019 Phys. Rev. B 100 115135
Google Scholar
[32] Golor M, Lang T C, Wessel S 2013 Phys. Rev. B 87 155441
Google Scholar
[33] Dai X 2022 Chin. Phys. Lett. 39 050101
Google Scholar
[34] Lu H Y, Li C H, Chen B B, Li W, Qi Y, Meng Z Y 2022 Chin. Phys. Lett. 39 050701
Google Scholar
[35] Wessel S, Jagannathan A, Haas S 2003 Phys. Rev. Lett. 90 177205
Google Scholar
[36] Rostami H, Guinea F, Cappelluti E 2022 Phys. Rev. B 105 195431
Google Scholar
[37] Bussy A, Pizzi G, Gibertini M 2017 Phys. Rev. B 96 165438
Google Scholar
[38] Yadav R, Rachel S, Hozoi L, van den Brink J, Jackeli G 2018 Phys. Rev. B 98 121107
Google Scholar
[39] Liu T Y 2020 Phys. Rev. B 102 045151
Google Scholar
[40] 肖寒, 弭孟娟, 王以林 2021 70 127503
Google Scholar
Xiao H, Mi M J, Wang Y L 2021 Acta Phys. Sin. 70 127503
Google Scholar
[41] Webster L, Yan J A 2018 Phys. Rev. B 98 144411
Google Scholar
[42] Deng Y C, Liu X H, Chen Y Y, Du Z Z, Jiang N, Shen C, Zhang E Z, Zheng H Z, Lu H Z, Wang K Y 2023 Natl. Sci. Rev. 10 nwac154
Google Scholar
下载:
计量
- 文章访问数: 2332
- PDF下载量: 71
- 被引次数: 0
