双层蜂窝状海森伯铁磁体中层间交换耦合相互作用对拓扑相的影响

施洪潮; 唐炳; 刘超飞

doi:10.7498/aps.73.20240437

摘要

层状磁性拓扑材料是最小二维单元下同时具有磁序和拓扑性的材料体系, 研究这一体系可能会观察到新物性和新现象的出现, 因此引起了研究者们的广泛关注. 本文运用线性自旋波理论, 主要研究了层间铁磁耦合的双层蜂窝状海森伯铁磁体中层间交换耦合相互作用对系统拓扑相的影响. 通过计算不同层间交换耦合相互作用强度下的磁子色散关系能得出, 当系统达到两个强度临界值时, 能量较高的两条能带和能量较低的两条能带的带隙在狄拉克点处会依次出现闭合-重新打开现象. 计算能带对应的贝里曲率和陈数后, 发现贝里曲率符号在相应临界值前后会发生反转, 同时陈数也会发生改变, 这证明系统发生了拓扑相变. 此外, 本文研究发现当双层蜂窝状铁磁体发生拓扑相变时, 磁子热霍尔系数变化曲线会相应发生突变. 本研究成果可以为利用双层蜂窝状铁磁材料制作具有更高信息传输能力的自旋电子器件提供理论支撑, 也可以为其他双层铁磁系统的相关研究提供一定的理论参考.

关键词:

Abstract

Layered magnetic topological materials are material systems that exhibit both magnetic ordering and topological properties in their smallest two-dimensional units. Studying these systems may lead to the observation of new physical properties and phenomena, which has attracted considerable attention from researchers. The effect of interlayer exchange coupling interactions on bilayer honeycomb Heisenberg ferromagnets with interlayer coupled topological phase is investigated by using linear spin wave theory. The influence of introducing two additional types of interactions, i.e. interlayer exchange coupling interaction and interlayer easy-axis anisotropy interaction, on the topological phase transition are also explored in this work. By calculating the magnon dispersion relations at various interlayer exchange coupling interaction intensities, it is found that the band gaps of high energy band and low energy band both close and reopen at the Dirac points when the system reaches the critical value of interlayer exchange coupling interaction. In magnon systems, such physical phenomena typically relate to topological phase transitions. When calculating the Berry curvature and Chern numbers for the bands in the aforementioned process, it is found that the sign of the Berry curvature reverses and the Chern numbers change when the critical value of interlayer exchange coupling interaction strength is reached, confirming that a topological phase transition occurs indeed. Introducing two other types of interlayer exchange coupling interactions in this process can lead various novel topological phases to occur in the system. The enhancement of interlayer easy-axis anisotropy interactions is likely to impede the topological phase transitions occurring in the system. We find that a major distinction between bilayer honeycomb ferromagnets and their single-layer counterparts lies in the fact that during a topological phase transition, the sign of the magnon thermal Hall coefficient does not change; on the contrary, abrupt shift in the thermal Hall coefficient curve occurs which can be seen as an indicator of topological phase transition of bilayer honeycomb ferromagnets, and is also reflected in the change in magnon Nernst coefficient. The research results of this work can provide theoretical support for developing novel spintronic devices with enhanced information transmission capabilities by using bilayer honeycomb ferromagnetic materials, and can also provide theoretical reference for studing other bilayer ferromagnetic systems.

Keywords:

作者及机构信息

1.
吉首大学物理与机电工程学院, 吉首　416000

2.
江西理工大学理学院, 赣州　341000

通信作者: 唐炳, bingtangphy@jsu.edu.cn ; 刘超飞, liuchaofei@jxust.edu.cn

基金项目: 国家自然科学基金(批准号: 12064011, 12375014, 11875149)、湖南省教育厅科学研究项目 (批准号: 23A0404)和吉首大学2023年度研究生校级科研项目(批准号: Jdy23052)资助的课题.

Authors and contacts

1.
School of Physics and Mechanical & Electrical Engineering, Jishou University, Jishou 416000, China

2.
School of Science, Jiangxi University of Science and Technology, Ganzhou 341000, China

Corresponding author: Tang Bing, bingtangphy@jsu.edu.cn ; Liu Chao-Fei, liuchaofei@jxust.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12064011, 12375014, 11875149), the Research Foundation of Education Bureau of Hunan Province, China (Grant No. 23A0404) and the School-level Graduate Scientific Research Project Foundation of Jishou University, China (Grant No. Jdy23052).

文章全文 : translate this paragraph

参考文献

[1]	Zhang S Q, Xu R Z, Luo N N, Zou X L 2021 Nanoscale 13 1398 Google Scholar
[2]	Liu Z R, Hua C B, Peng T, Chen R, Zhou B 2023 Phys. Rev. B 107 125302 Google Scholar
[3]	张志东 2015 64 067503 Google Scholar Zhang Z D 2015 Acta Phys. Sin. 64 067503 Google Scholar
[4]	Xu M L, Huang C X, Li Y W, Liu S Y, Zhong X, Jena P, Kan E J, Wang Y C 2020 Phys. Rev. Lett. 124 067602 Google Scholar
[5]	MacDonald A H 2019 Physics 12 12 Google Scholar
[6]	Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Herrero P J 2018 Nature 556 43 Google Scholar
[7]	Tarnopolsky G, Kruchkov A J, Vishwanath A 2019 Phys. Rev. Lett. 122 106405 Google Scholar
[8]	Carr S, Fang S, Jarillo-Herrero P, Kaxiras E 2018 Phys. Rev. B 98 085144 Google Scholar
[9]	Yankowitz M, Chen S, Polshyn H, Zhang Y, Watanabe K, Taniguchi T, Graf D, Young A F, Dean C R 2019 Science 363 1059 Google Scholar
[10]	Ribeiro-Palau R, Zhang C, Watanabe K, Taniguchi T, Hone J, Dean C R 2018 Science 361 690 Google Scholar
[11]	Guerci D, Simon P, Mora C 2021 Phys. Rev. B 103 224436 Google Scholar
[12]	Feng H F, Li Y, Shi Y G, Xie H Y, Li Y Q, Xu Y 2022 Chin. Phys. Lett. 39 077501 Google Scholar
[13]	Cenker J, Huang B, Suri N, Thijssen P, Miller A, Song T, Taniguchi T, Watanabe K 2021 Nat. Phys. 17 20 Google Scholar
[14]	Kang S, Kim K, Kim B H, Kim J, Sim K I, Lee J U, Lee S, Park K, Yun S, Kim T, Nag A, Walters A, Garcia-Fernandez M, Li J, Chapon L, Zhou K J, Son Y W, Kim J H, Cheong H, Park J G 2020 Nature 583 785 Google Scholar
[15]	Zhang H, Feng X, Heitmann T, Kolesnikov A I, Stone M B, Lu Y M 2020 Phys. Rev. B 101 100405 Google Scholar
[16]	Zhang L C, Zhu F, Go D, Lux F R, dos Santos F J, Lounis S, Su Y, Blügel S, Mokrousov Y 2021 Phys. Rev. B 103 134414 Google Scholar
[17]	Ghader D, Khater A 2019 Sci. Rep. 9 15220 Google Scholar
[18]	Van Miert G, Smith C M 2016 Phys. Rev. B 93 035401 Google Scholar
[19]	Wang X S, Wang X R 2021 J. Appl. Phys. 129 151101 Google Scholar
[20]	王振宇, 李志雄, 袁怀洋, 张知之, 曹云姗, 严鹏 2023 72 057503 Google Scholar Wang Z Y, Li Z X, Yuan H Y, Zhang Z Z, Cao Y S, Yan P 2023 Acta Phys. Sin. 72 057503 Google Scholar
[21]	Stauber T, Low T, Gómez-Santos G 2018 Phys. Rev. Lett. 120 046801 Google Scholar
[22]	Ma J J, Wang Z Y, Xu S G, Gao Y X, Zhang Y Y, Dai Q, Lin X, Du S X, Ren J D, Gao H J 2022 Chin. Phys. Lett. 39 047403 Google Scholar
[23]	Hu J W, Zhu S Y, Hu Q Y, Wang Y H, Shen C M, Yang H T, Zhu X S, Huan Q, Xu Y, Gao H J 2024 Chin. Phys. Lett. 41 037401 Google Scholar
[24]	Li X F, Sun R X, Wang S Y, Li X, Liu Z B, Tian J G 2022 Chin. Phys. Lett. 39 037301 Google Scholar
[25]	Liu C F, Wang J 2022 Chin. Phys. Lett. 39 077301 Google Scholar
[26]	Lee J Y 2019 Nat. Commun. 10 5333 Google Scholar
[27]	Zhang Y H, Mao D, Cao Y, Jarillo-Herrero P, Senthil T 2019 Phys. Rev. B 99 075127 Google Scholar
[28]	Po H C, Zou L, Senthil T, Vishwanath A 2019 Phys. Rev. B 99 195455 Google Scholar
[29]	Hao Z, Zimmerman A M, Ledwith P, Khalaf E, Najafabadi D H, Watanabe K, Taniguchi T, Ashvin Vishwanath, Kim P 2021 Science 371 1133 Google Scholar
[30]	Nuckolls K P, Oh M, Wong D, Lian B, Watanabe K, Taniguchi T, Bernevig B A 2020 Nature 588 610 Google Scholar
[31]	Rademaker L, Mellado P 2018 Phys. Rev. B 98 235158 Google Scholar
[32]	Moon P, Koshino M 2014 Phys. Rev. B 90 155406 Google Scholar
[33]	Zhu X C, Guo H M, Feng S P 2021 Chin. Phys. B 30 077505 Google Scholar
[34]	Ghader D 2020 Sci. Rep. 10 16733 Google Scholar
[35]	Zyuzin V A, Kovalev A 2016 Phys. Rev. Lett. 117 217203 Google Scholar
[36]	Huang H, Kariyado T, Hu X 2022 Sci. Rep 12 6257 Google Scholar
[37]	Zhai X, Blanter Y M 2020 Phys. Rev. B 102 075407 Google Scholar
[38]	Ghader D 2022 Physica E 135 114984 Google Scholar
[39]	Kim H, Kim S K 2022 Phys. Rev. B 106 104430 Google Scholar
[40]	Katsura H, Nagaosa N, Lee P A 2010 Phys. Rev. Lett. 104 066403 Google Scholar
[41]	Matsumoto R, Murakami S 2011 Phys. Rev. B 84 184406 Google Scholar
[42]	Owerre S A 2016 J. Appl. Phys. 120 043903 Google Scholar
[43]	Zhang X T, Gao Y H, Chen G 2024 Phys. Rep. 1070 1 Google Scholar
[44]	Lu Y S, Li J L, Wu C T 2021 Phys. Rev. Lett. 127 217202 Google Scholar
[45]	Saito T, Misaki K, Ishizuka H, Nagaosa N 2019 Phys. Rev. Lett. 123 255901 Google Scholar
[46]	Ideue T, Onose Y, Katsura H, Shiomi Y, Ishiwata S, Nagaosa N, Tokura Y 2012 Phys. Rev. B 85 134411 Google Scholar
[47]	Xu H, Cheng S F, Bao S, Wen J S 2022 Progress in Physics 42 159 Google Scholar
[48]	Hirschberger M, Chisnell R, Lee Y S, Ong N P 2015 Phys. Rev. Lett. 115 106603 Google Scholar
[49]	Chisnell R, Helton J S, Freedman D E, Singh D K, Demmel F, Stock C, Nocera D G, Lee Y S 2016 Phys. Rev. B 93 214403 Google Scholar
[50]	McClarty P A, Dong X Y, Gohlke M, Rau J G, Pollmann F, Moessner R, Penc K 2018 Phys. Rev. B 98 060404 Google Scholar
[51]	Rückriegel A, Brataas A, Duine R A 2018 Phys. Rev. B 97 081106 Google Scholar
[52]	Mkhitaryan V V, Ke L 2021 Phys. Rev. B 104 064435 Google Scholar
[53]	Wang S Y, Wang Y, Yan S H, Wang C, Xiang B K, Liang K Y, He Q S, Watanabe K, Taniguchi T, Tian S J, Lei H C, Ji W, Qi Y, Wang Y H 2022 Sci. Bull. 67 2557 Google Scholar
[54]	Diaz S A, Klinovaja J, Loss D 2019 Phys. Rev. Lett. 122 187203 Google Scholar
[55]	McClarty P A 2022 Annu. Rev. Conde. Ma. P 13 171 Google Scholar
[56]	Liu J, Wang L, Shen K 2023 Phys. Rev. B 107 174404 Google Scholar
[57]	Mook A, Plekhanov K, Klinovaja J, Loss D 2021 Phys. Rev. X 11 021061 Google Scholar
[58]	Pirmoradian F, Rameshti B Z, Miri M F, Saeidian S 2018 Phys. Rev. B 98 224409 Google Scholar
[59]	Chen L 2019 Chin. Phys. B 28 078503 Google Scholar
[60]	Zhu H, Shi H C, Tang Z, Tang B 2023 Eur. Phys. J. Plus 138 1 Google Scholar
[61]	Yao S Y, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[62]	Corticelli A, Moessner R, McClarty P A 2022 Phys. Rev. B 105 064430 Google Scholar
[63]	Zhang L, Ren J, Wang J S, Li B 2013 Phys. Rev. B 87 144101 Google Scholar
[64]	Choe D H, Sung H J, Chang K J 2016 Phys. Rev. B 93 125109 Google Scholar
[65]	Rufo S, Lopes N, Continentino M A, Griffith M A R 2019 Phys. Rev. B 100 195432 Google Scholar
[66]	Zhang J S, Chang C Z, Tang P Z, Zhang Z C, Feng X, Li K, Wang L L, Chen X, Liu C X, Duan W H, He K, Xue Q K, Ma X C, Wang Y Y 2013 Science 339 1582 Google Scholar
[67]	孟康康, 赵旭鹏, 苗君, 徐晓光, 赵建华, 姜勇 2018 67 131202 Google Scholar Meng K K, Zhao X P, Miao J, Xu X G, Zhao J H, Jiang Y 2018 Acta Phys. Sin. 67 131202 Google Scholar
[68]	Mook A, Henk J, Mertig I 2014 Phys. Rev. B 90 024412 Google Scholar
[69]	Joshi D G 2018 Phys. Rev. B 98 060405 Google Scholar
[70]	Asano K, Hotta C 2011 Phys. Rev. B 83 245125 Google Scholar
[71]	Fransson J, Black-Schaffer A M, Balatsky A V 2016 Phys. Rev. B 94 075401 Google Scholar
[72]	Pershoguba S S, Banerjee S, Lashley J C, Park J, Agren H, Aeppli G, Balatsky A V 2018 Phys. Rev. X 8 011010 Google Scholar
[73]	Wang D, Bo X Y, Tang F, Wan X G 2019 Phys. Rev. B 99 035160 Google Scholar
[74]	Sun H, Bhowmick D, Yang B, Sengupta P 2023 Phys. Rev. B 107 134426 Google Scholar
[75]	Do S H, Paddison J A M, Sala G, Williams T J, Kaneko K, Kuwahara K, May A F, Yan J, McGuire M A, Stone M B, Lumsden M D, Christianson A D 2022 Phys. Rev. B 106 L060408 Google Scholar
[76]	刘畅, 王亚愚 2023 72 177301 Google Scholar Liu C, Wang Y Y 2023 Acta Phys. Sin. 72 177301 Google Scholar
[77]	孙慧敏, 何庆林 2021 70 127302 Google Scholar Sun H M, He Q L 2021 Acta Phys. Sin. 70 127302 Google Scholar
[78]	Xu C Q, Zhang H D, Carnahan C, Zhang P P, Xiao D, Ke X L 2024 Phys. Rev. B 109 094415 Google Scholar
[79]	Zhang E Z, Chern L E, Kim Y B 2021 Phys. Rev. B 103 174402 Google Scholar
[80]	强晓斌, 卢海舟 2021 70 027201 Google Scholar Qiang X B, Lu H Z 2021 Acta Phys. Sin. 70 027201 Google Scholar
[81]	Kovalev A A, Zyuzin V 2016 Phys. Rev. B 93 161106 Google Scholar
[82]	Bose A, Tulapurkar A A 2019 J. Magn. Magn. Mater. 491 165526 Google Scholar
[83]	Go G, Kim S K 2022 Phys. Rev. B 106 125103 Google Scholar
[84]	Cui Q R, Zeng B W, Cui P, Yu T, Yang H X 2023 Phys. Rev. B 108 L180401 Google Scholar
[85]	Hu C, Zhang D, Yan F G, Li Y C, Lü Q S, Zhu W K, Wei Z K, Chang K M, Wang K Y 2020 Sci. Bull. 65 1072 Google Scholar
[86]	Soriano D, Cardoso C, Fernández-Rossier J 2019 Solid State Commun. 299 113662 Google Scholar
[87]	金哲珺雨, 曾钊卓, 曹云姗, 严鹏 2024 73 017501 Google Scholar Jin Z J Y, Zeng Z Z, Cao Y S, Yan P 2024 Acta Phys. Sin. 73 017501 Google Scholar
[88]	刘恩克 2024 73 017103 Google Scholar Liu E K 2024 Acta Phys. Sin. 73 017103 Google Scholar
[89]	王鹏程, 曹亦, 谢红光, 殷垚, 王伟, 王泽蓥, 马欣辰, 王琳, 黄维 2020 69 117501 Google Scholar Wang P C, Cao Y, Xie H G, Yin Y, Wang W, Wang Z Y, Ma X C, Wang L, Huang W 2020 Acta Phys. Sin. 69 117501 Google Scholar

施引文献

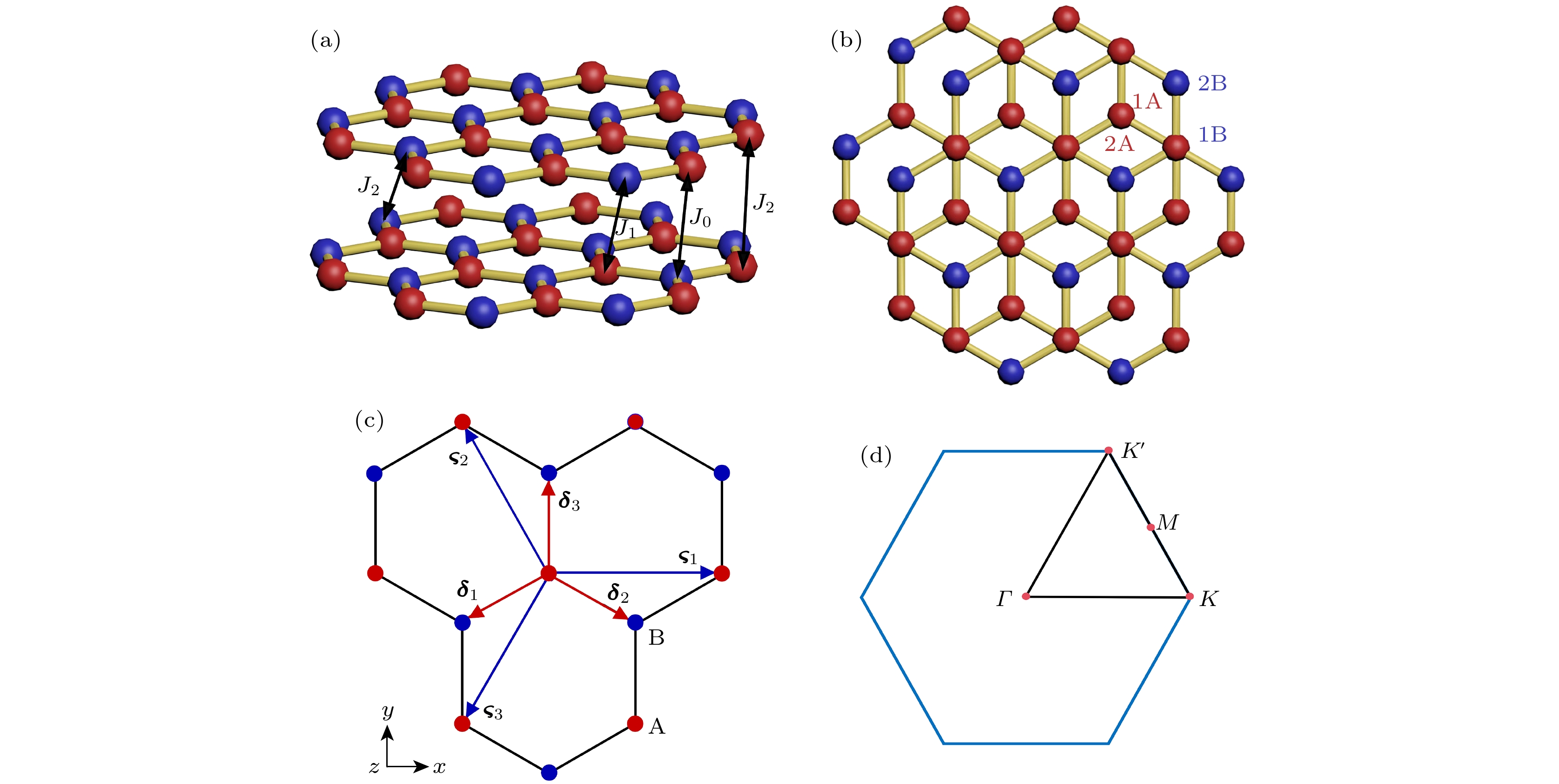
图 1 双层蜂窝状铁磁体晶格结构　(a)侧视图; (b)俯视图; (c)晶格矢量, 最近邻矢量$ {{\boldsymbol{\delta }}_n} $和次近邻矢量$ {{\boldsymbol{\varsigma }}_n} $分别用红色和蓝色箭头表示; (d) 第一布里渊区高对称路径$ { M} {\text{-}} { K}' {\text{-}} \varGamma {\text{-}} { K} {\text{-}} { M} $

Fig. 1. Lattice structure of the bilayer honeycomb ferromagnet: (a) Side view; (b) top view; (c) the lattice vector, the nearest and next-nearest neighbor vectors, $ {{\boldsymbol{\delta }}_n} $ and $ {{\boldsymbol{\varsigma }}_n} $, are represented by red and blue arrows, respectively; (d) the high symmetric path $ { M} {\text{-}} { K}' {\text{-}} \varGamma {\text{-}} { K} {\text{-}} { M} $ in the first Brillouin zone.

下载: 全尺寸图片幻灯片

图 2 双层蜂窝状铁磁体能带结构　(a) $ {J_0} = 0.1 $; (b) $ {J_0} = 0.245 $; (c) $ {J_0} = 0.3 $; (d) $ {J_0} = 0.505 $; (e) $ {J_0} = 0.9 $, 其余参数设置为$ \varGamma '{=}0.1 $, $ {J_1} = {J_2} = 0 $; (f) 带隙图

Fig. 2. Magnon band structures of the bilayer honeycomb ferromagnet: (a) $ {J_0} = 0.1 $; (b) $ {J_0} = 0.245 $; (c) $ {J_0} = 0.3 $; (d) $ {J_0} = $$ 0.505 $; (e) $ {J_0} = 0.9 $, the other parameters are set to $ \varGamma ' = 0.1 $, $ {J_1} = {J_2} = 0 $; (f) gaps as a function of $ {J_0} $.

下载: 全尺寸图片幻灯片

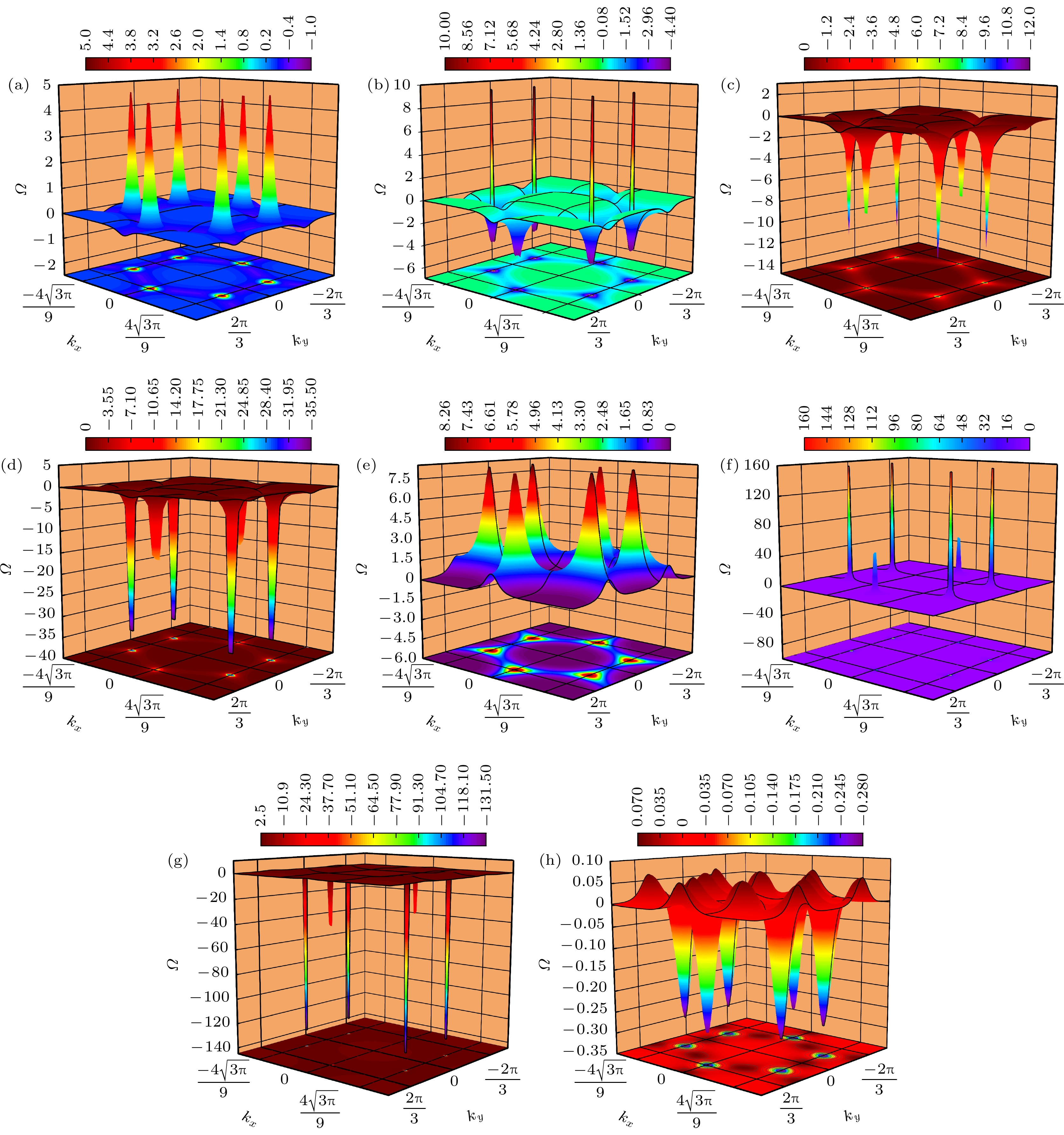
图 3 双层蜂窝状铁磁体最低能带对应的贝里曲率　(a) $ {J_0} = 0.2 $; (b) $ {J_0} = 0.5 $; (c) $ {J_0} = 0.51 $; (d) $ {J_0} = 0.8 $. 双层蜂窝状铁磁体最高能带对应的贝里曲率 (e) $ {J_0} = 0.15 $; (f) $ {J_0} = 0.24 $; (g) $ {J_0} = 0.25 $; (h) $ {J_0} = 0.8 $, 其余参数设置为$ \varGamma '{=}0.1 $, $ {J_1} = {J_2} = 0 $

Fig. 3. Berry curvature of the lowest band in a bilayer honeycomb ferromagnet: (a) $ {J_0} = 0.2 $; (b) $ {J_0} = 0.5 $; (c) $ {J_0} = 0.51 $; (d) $ {J_0} = 0.8 $. Berry curvature of the highest band in a bilayer honeycomb ferromagnet: (e) $ {J_0} = 0.15 $; (f) $ {J_0} = 0.24 $; (g) $ {J_0} = $$ 0.25 $; (h) $ {J_0} = 0.8 $. Other parameters are set to $ \varGamma '{=}0.1 $ and $ {J_1} = {J_2} = 0 $.

下载: 全尺寸图片幻灯片

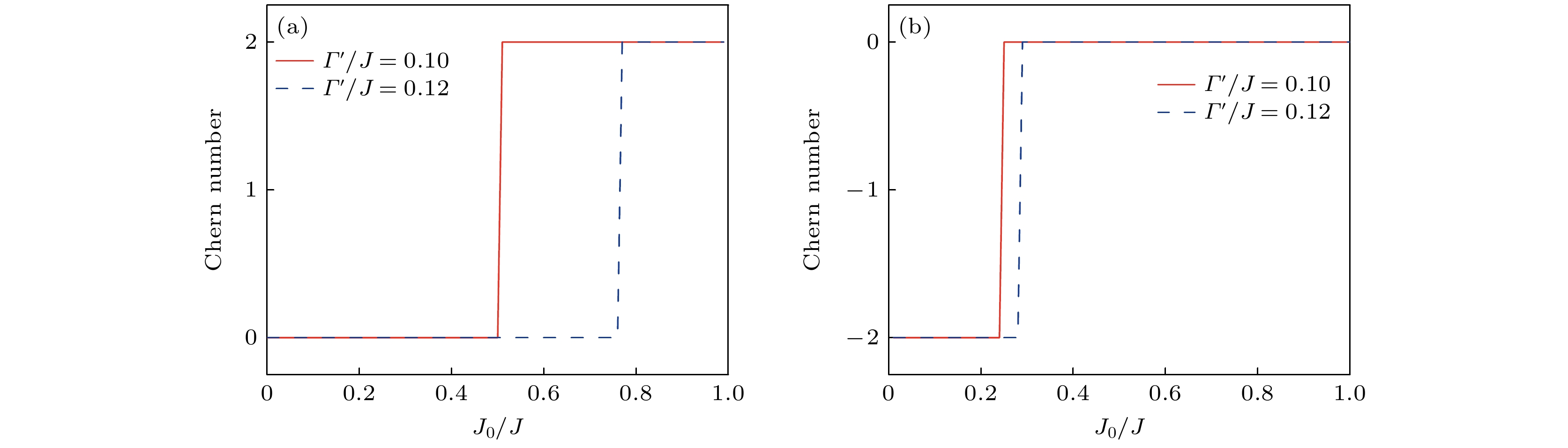
图 4 不同层间易轴各向异性相互作用强度下的陈数随$ {J_0} $强度变化曲线　(a)最低能带; (b)最高能带, 其余参数设置为$ \varGamma ' = 0.1, {J_1} = {J_2} = 0 $

Fig. 4. Chern number as a function of the intensity of interlayer exchange coupling interaction $ {J_0} $ for the different intensity of interlayer easy-axis anisotropy interaction: (a) The lowest band; (b) the highest band, the other parameters are set to $ \varGamma ' = 0.1, $$ {J_1} = {J_2} = 0 $.

下载: 全尺寸图片幻灯片

图 5 陈数随层间交换耦合相互作用J₀和J₁强度变化图　(a)—(d)分别对应能量从高到低的4条能带, 其余参数设置为$ \varGamma ' = 0.1 $

Fig. 5. Chern number as a function of the intensity of the interlayer exchange coupling interaction $ {J_0} $ and $ {J_1} $: (a)–(d) Correspond to four energy bands from high to low energy, the other parameters are set to $ \varGamma ' =0.1 $.

下载: 全尺寸图片幻灯片

图 6 陈数随层间交换耦合相互作用J₀和D强度变化图　(a)—(d)分别对应能量从高到低的4条能带, 其余参数设置为$ \varGamma ' = 0.1 $

Fig. 6. Chern number as a function of the intensity of the interlayer exchange coupling interaction $ {J_0} $ and $ D $: (a)–(d) Correspond to four energy bands from high to low energy, the other parameters are set to $ \varGamma ' = 0.1 $.

下载: 全尺寸图片幻灯片

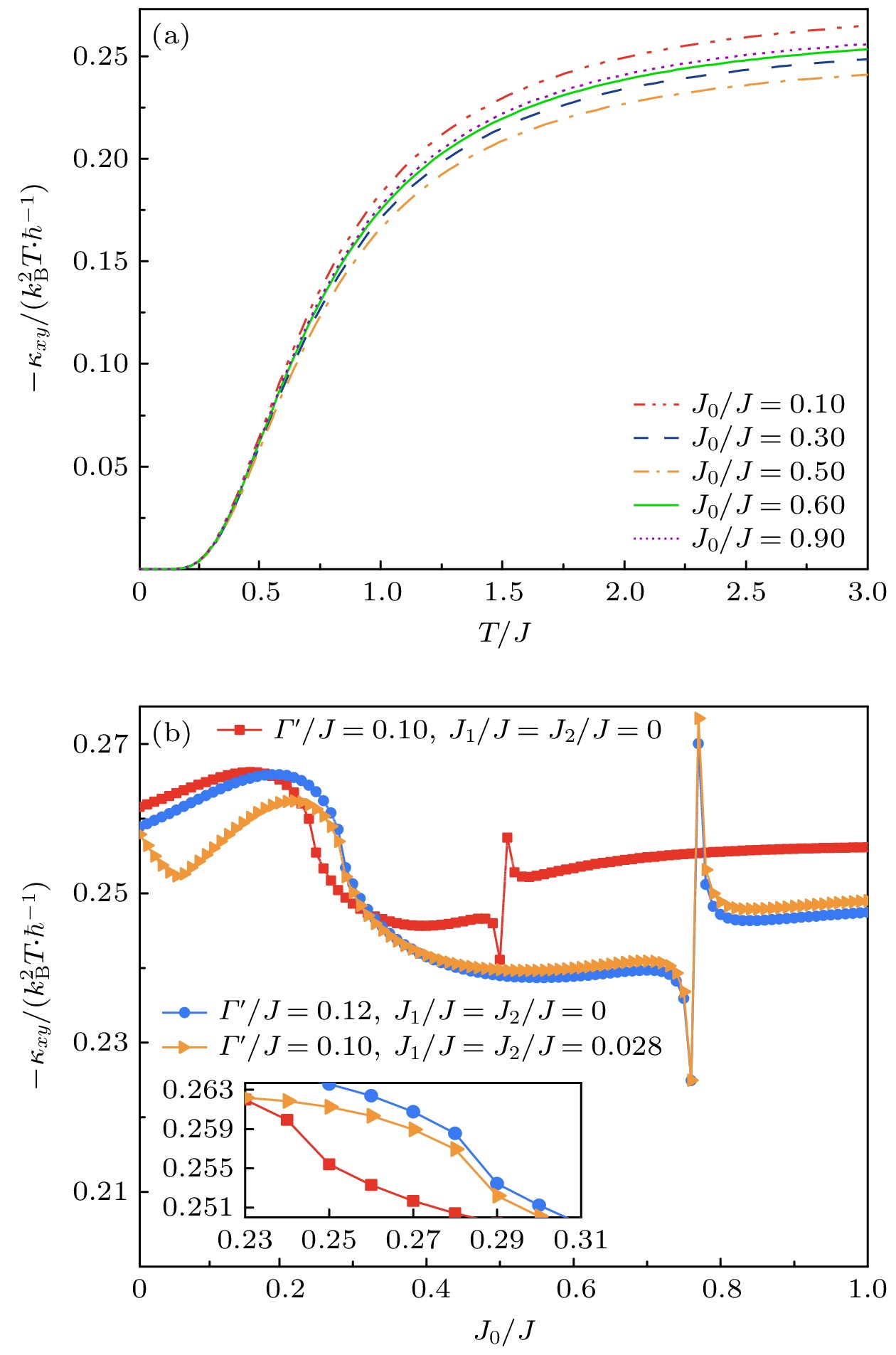
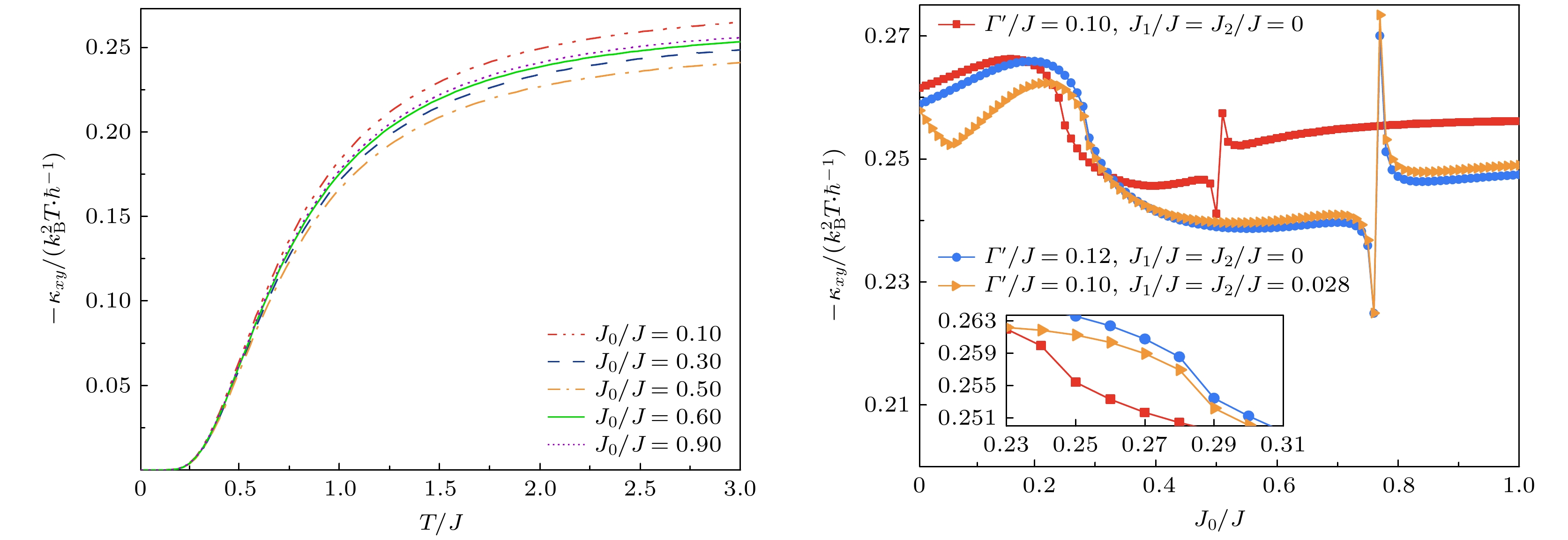
图 7 (a) 不同$ {J_0} $强度下的磁子热霍尔系数随温度变化曲线, 其他参数设置为$ \varGamma '{=}0.1, \;{J_1} = {J_2} = 0 $; (b) 磁子热霍尔系数随$ {J_0} $强度变化曲线

Fig. 7. (a) Thermal Hall conductivity as a function of temperature under different intensity of interlayer exchange coupling interaction $ {J_0} $ with $ \varGamma '{=}0.1, \;{J_1} = {J_2} = 0 $; (b) thermal Hall conductivity as a function of different intensities of interlayer exchange coupling interaction $ {J_0} $.

下载: 全尺寸图片幻灯片

图 8 (a) 不同$ {J_0} $强度下的磁子能斯特系数随温度变化曲线, 其他参数设置为$ \varGamma '{=}0.1, \;{J_1} = {J_2} = 0 $; (b) 磁子能斯特系数随$ {J_0} $强度变化曲线

Fig. 8. (a) Magnon Nernst conductivity as a function of temperature under different intensity of interlayer exchange coupling interaction $ {J_0} $ with $ \varGamma '{=}0.1, \;{J_1} = {J_2} = 0 $; (b) magnon Nernst conductivity as a function of different intensities of interlayer exchange coupling interaction $ {J_0} $.

下载: 全尺寸图片幻灯片

表 1 色散曲线对应的陈数

Table 1. Corresponding Chern numbers of magnon band structures.

参数	陈数
参数	能带1	能带2	能带3	能带4
$ {J_0} = 0.1, \;\varGamma '{=}0.1, \;{J_1} = 0.1, \;{J_2} = {J_3} = 0 $	–2	0	2	0
$ {J_0} = 0.245, \;\varGamma '{=}0.1, \;{J_1} = 0.1, \;{J_2} = {J_3} = 0 $	0	–2	2	0
$ {J_0} = 0.3, \;\varGamma '{=}0.1, \;{J_1} = 0.1, \;{J_2} = {J_3} = 0 $	0	–2	2	0
$ {J_0} = 0.505, \;\varGamma '{=}0.1, \;{J_1} = 0.1, \;{J_2} = {J_3} = 0 $	0	–2	0	2
$ {J_0} = 0.9, \;\varGamma '{=}0.1, \;{J_1} = 0.1, \;{J_2} = {J_3} = 0 $	0	–2	0	2

下载: 导出CSV

表 2 能带对应的陈数

Table 2. Corresponding Chern numbers of magnon band structures.

序号	陈数
序号	能带1	能带2	能带3	能带4
①	0	–2	0	2
②	0	–2	2	0
③	1	–3	2	0
④	–1	–1	2	0
⑤	–3	1	2	0
⑥	–2	0	2	0
⑦	–2	2	0	0
⑧	–1	1	0	0
⑨	–1	0	1	0

下载: 导出CSV

map

[1]	Zhang S Q, Xu R Z, Luo N N, Zou X L 2021 Nanoscale 13 1398 Google Scholar
[2]	Liu Z R, Hua C B, Peng T, Chen R, Zhou B 2023 Phys. Rev. B 107 125302 Google Scholar
[3]	张志东 2015 64 067503 Google Scholar Zhang Z D 2015 Acta Phys. Sin. 64 067503 Google Scholar
[4]	Xu M L, Huang C X, Li Y W, Liu S Y, Zhong X, Jena P, Kan E J, Wang Y C 2020 Phys. Rev. Lett. 124 067602 Google Scholar
[5]	MacDonald A H 2019 Physics 12 12 Google Scholar
[6]	Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Herrero P J 2018 Nature 556 43 Google Scholar
[7]	Tarnopolsky G, Kruchkov A J, Vishwanath A 2019 Phys. Rev. Lett. 122 106405 Google Scholar
[8]	Carr S, Fang S, Jarillo-Herrero P, Kaxiras E 2018 Phys. Rev. B 98 085144 Google Scholar
[9]	Yankowitz M, Chen S, Polshyn H, Zhang Y, Watanabe K, Taniguchi T, Graf D, Young A F, Dean C R 2019 Science 363 1059 Google Scholar
[10]	Ribeiro-Palau R, Zhang C, Watanabe K, Taniguchi T, Hone J, Dean C R 2018 Science 361 690 Google Scholar
[11]	Guerci D, Simon P, Mora C 2021 Phys. Rev. B 103 224436 Google Scholar
[12]	Feng H F, Li Y, Shi Y G, Xie H Y, Li Y Q, Xu Y 2022 Chin. Phys. Lett. 39 077501 Google Scholar
[13]	Cenker J, Huang B, Suri N, Thijssen P, Miller A, Song T, Taniguchi T, Watanabe K 2021 Nat. Phys. 17 20 Google Scholar
[14]	Kang S, Kim K, Kim B H, Kim J, Sim K I, Lee J U, Lee S, Park K, Yun S, Kim T, Nag A, Walters A, Garcia-Fernandez M, Li J, Chapon L, Zhou K J, Son Y W, Kim J H, Cheong H, Park J G 2020 Nature 583 785 Google Scholar
[15]	Zhang H, Feng X, Heitmann T, Kolesnikov A I, Stone M B, Lu Y M 2020 Phys. Rev. B 101 100405 Google Scholar
[16]	Zhang L C, Zhu F, Go D, Lux F R, dos Santos F J, Lounis S, Su Y, Blügel S, Mokrousov Y 2021 Phys. Rev. B 103 134414 Google Scholar
[17]	Ghader D, Khater A 2019 Sci. Rep. 9 15220 Google Scholar
[18]	Van Miert G, Smith C M 2016 Phys. Rev. B 93 035401 Google Scholar
[19]	Wang X S, Wang X R 2021 J. Appl. Phys. 129 151101 Google Scholar
[20]	王振宇, 李志雄, 袁怀洋, 张知之, 曹云姗, 严鹏 2023 72 057503 Google Scholar Wang Z Y, Li Z X, Yuan H Y, Zhang Z Z, Cao Y S, Yan P 2023 Acta Phys. Sin. 72 057503 Google Scholar
[21]	Stauber T, Low T, Gómez-Santos G 2018 Phys. Rev. Lett. 120 046801 Google Scholar
[22]	Ma J J, Wang Z Y, Xu S G, Gao Y X, Zhang Y Y, Dai Q, Lin X, Du S X, Ren J D, Gao H J 2022 Chin. Phys. Lett. 39 047403 Google Scholar
[23]	Hu J W, Zhu S Y, Hu Q Y, Wang Y H, Shen C M, Yang H T, Zhu X S, Huan Q, Xu Y, Gao H J 2024 Chin. Phys. Lett. 41 037401 Google Scholar
[24]	Li X F, Sun R X, Wang S Y, Li X, Liu Z B, Tian J G 2022 Chin. Phys. Lett. 39 037301 Google Scholar
[25]	Liu C F, Wang J 2022 Chin. Phys. Lett. 39 077301 Google Scholar
[26]	Lee J Y 2019 Nat. Commun. 10 5333 Google Scholar
[27]	Zhang Y H, Mao D, Cao Y, Jarillo-Herrero P, Senthil T 2019 Phys. Rev. B 99 075127 Google Scholar
[28]	Po H C, Zou L, Senthil T, Vishwanath A 2019 Phys. Rev. B 99 195455 Google Scholar
[29]	Hao Z, Zimmerman A M, Ledwith P, Khalaf E, Najafabadi D H, Watanabe K, Taniguchi T, Ashvin Vishwanath, Kim P 2021 Science 371 1133 Google Scholar
[30]	Nuckolls K P, Oh M, Wong D, Lian B, Watanabe K, Taniguchi T, Bernevig B A 2020 Nature 588 610 Google Scholar
[31]	Rademaker L, Mellado P 2018 Phys. Rev. B 98 235158 Google Scholar
[32]	Moon P, Koshino M 2014 Phys. Rev. B 90 155406 Google Scholar
[33]	Zhu X C, Guo H M, Feng S P 2021 Chin. Phys. B 30 077505 Google Scholar
[34]	Ghader D 2020 Sci. Rep. 10 16733 Google Scholar
[35]	Zyuzin V A, Kovalev A 2016 Phys. Rev. Lett. 117 217203 Google Scholar
[36]	Huang H, Kariyado T, Hu X 2022 Sci. Rep 12 6257 Google Scholar
[37]	Zhai X, Blanter Y M 2020 Phys. Rev. B 102 075407 Google Scholar
[38]	Ghader D 2022 Physica E 135 114984 Google Scholar
[39]	Kim H, Kim S K 2022 Phys. Rev. B 106 104430 Google Scholar
[40]	Katsura H, Nagaosa N, Lee P A 2010 Phys. Rev. Lett. 104 066403 Google Scholar
[41]	Matsumoto R, Murakami S 2011 Phys. Rev. B 84 184406 Google Scholar
[42]	Owerre S A 2016 J. Appl. Phys. 120 043903 Google Scholar
[43]	Zhang X T, Gao Y H, Chen G 2024 Phys. Rep. 1070 1 Google Scholar
[44]	Lu Y S, Li J L, Wu C T 2021 Phys. Rev. Lett. 127 217202 Google Scholar
[45]	Saito T, Misaki K, Ishizuka H, Nagaosa N 2019 Phys. Rev. Lett. 123 255901 Google Scholar
[46]	Ideue T, Onose Y, Katsura H, Shiomi Y, Ishiwata S, Nagaosa N, Tokura Y 2012 Phys. Rev. B 85 134411 Google Scholar
[47]	Xu H, Cheng S F, Bao S, Wen J S 2022 Progress in Physics 42 159 Google Scholar
[48]	Hirschberger M, Chisnell R, Lee Y S, Ong N P 2015 Phys. Rev. Lett. 115 106603 Google Scholar
[49]	Chisnell R, Helton J S, Freedman D E, Singh D K, Demmel F, Stock C, Nocera D G, Lee Y S 2016 Phys. Rev. B 93 214403 Google Scholar
[50]	McClarty P A, Dong X Y, Gohlke M, Rau J G, Pollmann F, Moessner R, Penc K 2018 Phys. Rev. B 98 060404 Google Scholar
[51]	Rückriegel A, Brataas A, Duine R A 2018 Phys. Rev. B 97 081106 Google Scholar
[52]	Mkhitaryan V V, Ke L 2021 Phys. Rev. B 104 064435 Google Scholar
[53]	Wang S Y, Wang Y, Yan S H, Wang C, Xiang B K, Liang K Y, He Q S, Watanabe K, Taniguchi T, Tian S J, Lei H C, Ji W, Qi Y, Wang Y H 2022 Sci. Bull. 67 2557 Google Scholar
[54]	Diaz S A, Klinovaja J, Loss D 2019 Phys. Rev. Lett. 122 187203 Google Scholar
[55]	McClarty P A 2022 Annu. Rev. Conde. Ma. P 13 171 Google Scholar
[56]	Liu J, Wang L, Shen K 2023 Phys. Rev. B 107 174404 Google Scholar
[57]	Mook A, Plekhanov K, Klinovaja J, Loss D 2021 Phys. Rev. X 11 021061 Google Scholar
[58]	Pirmoradian F, Rameshti B Z, Miri M F, Saeidian S 2018 Phys. Rev. B 98 224409 Google Scholar
[59]	Chen L 2019 Chin. Phys. B 28 078503 Google Scholar
[60]	Zhu H, Shi H C, Tang Z, Tang B 2023 Eur. Phys. J. Plus 138 1 Google Scholar
[61]	Yao S Y, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[62]	Corticelli A, Moessner R, McClarty P A 2022 Phys. Rev. B 105 064430 Google Scholar
[63]	Zhang L, Ren J, Wang J S, Li B 2013 Phys. Rev. B 87 144101 Google Scholar
[64]	Choe D H, Sung H J, Chang K J 2016 Phys. Rev. B 93 125109 Google Scholar
[65]	Rufo S, Lopes N, Continentino M A, Griffith M A R 2019 Phys. Rev. B 100 195432 Google Scholar
[66]	Zhang J S, Chang C Z, Tang P Z, Zhang Z C, Feng X, Li K, Wang L L, Chen X, Liu C X, Duan W H, He K, Xue Q K, Ma X C, Wang Y Y 2013 Science 339 1582 Google Scholar
[67]	孟康康, 赵旭鹏, 苗君, 徐晓光, 赵建华, 姜勇 2018 67 131202 Google Scholar Meng K K, Zhao X P, Miao J, Xu X G, Zhao J H, Jiang Y 2018 Acta Phys. Sin. 67 131202 Google Scholar
[68]	Mook A, Henk J, Mertig I 2014 Phys. Rev. B 90 024412 Google Scholar
[69]	Joshi D G 2018 Phys. Rev. B 98 060405 Google Scholar
[70]	Asano K, Hotta C 2011 Phys. Rev. B 83 245125 Google Scholar
[71]	Fransson J, Black-Schaffer A M, Balatsky A V 2016 Phys. Rev. B 94 075401 Google Scholar
[72]	Pershoguba S S, Banerjee S, Lashley J C, Park J, Agren H, Aeppli G, Balatsky A V 2018 Phys. Rev. X 8 011010 Google Scholar
[73]	Wang D, Bo X Y, Tang F, Wan X G 2019 Phys. Rev. B 99 035160 Google Scholar
[74]	Sun H, Bhowmick D, Yang B, Sengupta P 2023 Phys. Rev. B 107 134426 Google Scholar
[75]	Do S H, Paddison J A M, Sala G, Williams T J, Kaneko K, Kuwahara K, May A F, Yan J, McGuire M A, Stone M B, Lumsden M D, Christianson A D 2022 Phys. Rev. B 106 L060408 Google Scholar
[76]	刘畅, 王亚愚 2023 72 177301 Google Scholar Liu C, Wang Y Y 2023 Acta Phys. Sin. 72 177301 Google Scholar
[77]	孙慧敏, 何庆林 2021 70 127302 Google Scholar Sun H M, He Q L 2021 Acta Phys. Sin. 70 127302 Google Scholar
[78]	Xu C Q, Zhang H D, Carnahan C, Zhang P P, Xiao D, Ke X L 2024 Phys. Rev. B 109 094415 Google Scholar
[79]	Zhang E Z, Chern L E, Kim Y B 2021 Phys. Rev. B 103 174402 Google Scholar
[80]	强晓斌, 卢海舟 2021 70 027201 Google Scholar Qiang X B, Lu H Z 2021 Acta Phys. Sin. 70 027201 Google Scholar
[81]	Kovalev A A, Zyuzin V 2016 Phys. Rev. B 93 161106 Google Scholar
[82]	Bose A, Tulapurkar A A 2019 J. Magn. Magn. Mater. 491 165526 Google Scholar
[83]	Go G, Kim S K 2022 Phys. Rev. B 106 125103 Google Scholar
[84]	Cui Q R, Zeng B W, Cui P, Yu T, Yang H X 2023 Phys. Rev. B 108 L180401 Google Scholar
[85]	Hu C, Zhang D, Yan F G, Li Y C, Lü Q S, Zhu W K, Wei Z K, Chang K M, Wang K Y 2020 Sci. Bull. 65 1072 Google Scholar
[86]	Soriano D, Cardoso C, Fernández-Rossier J 2019 Solid State Commun. 299 113662 Google Scholar
[87]	金哲珺雨, 曾钊卓, 曹云姗, 严鹏 2024 73 017501 Google Scholar Jin Z J Y, Zeng Z Z, Cao Y S, Yan P 2024 Acta Phys. Sin. 73 017501 Google Scholar
[88]	刘恩克 2024 73 017103 Google Scholar Liu E K 2024 Acta Phys. Sin. 73 017103 Google Scholar
[89]	王鹏程, 曹亦, 谢红光, 殷垚, 王伟, 王泽蓥, 马欣辰, 王琳, 黄维 2020 69 117501 Google Scholar Wang P C, Cao Y, Xie H G, Yin Y, Wang W, Wang Z Y, Ma X C, Wang L, Huang W 2020 Acta Phys. Sin. 69 117501 Google Scholar

[1]	. 二维及拓扑自旋物理专题编者按. , 2024, 73(1): 010101. doi: 10.7498/aps.73.010101
[2]	解晓洁, 孙俊松, 秦吉红, 郭怀明. 弯曲应变下六角晶格量子反铁磁体的赝朗道能级. , 2024, 73(2): 020202. doi: 10.7498/aps.73.20231231
[3]	刘恩克. 磁序与拓扑的耦合: 从基础物理到拓扑磁电子学. , 2024, 73(1): 017103. doi: 10.7498/aps.73.20231711
[4]	张世豪, 解博, 彭然, 刘晓迁, 吕昕, 刘健鹏. 莫尔石墨烯体系的新奇电学性质. , 2023, 72(6): 067302. doi: 10.7498/aps.72.20230120
[5]	刘艺舟, 臧佳栋. 磁性斯格明子的研究现状和展望. , 2018, 67(13): 131201. doi: 10.7498/aps.67.20180619
[6]	王一军, 刘洋, 于广华. Pt插层对铁磁/反铁磁界面交换耦合的影响. , 2012, 61(16): 167503. doi: 10.7498/aps.61.167503
[7]	陈东猛, 刘大勇. 双层反铁磁体K3Cu2F7 中轨道序驱动的自旋二聚化. , 2010, 59(10): 7350-7356. doi: 10.7498/aps.59.7350
[8]	曹鸿霞, 张宁. 磁电双层膜层间耦合的弹性力学研究. , 2008, 57(5): 3237-3243. doi: 10.7498/aps.57.3237
[9]	潘靖, 周岚, 陶永春, 胡经国. 外应力场下铁磁/反铁磁双层膜系统中的自旋波. , 2007, 56(6): 3521-3526. doi: 10.7498/aps.56.3521
[10]	许小勇, 潘靖, 胡经国. 交换偏置双层膜中的反铁磁自旋结构及其交换各向异性. , 2007, 56(9): 5476-5482. doi: 10.7498/aps.56.5476
[11]	徐岩, 薛德胜, 左维, 李发伸. 非均匀交换各向异性铁磁介质的非线性表面自旋波. , 2003, 52(11): 2896-2900. doi: 10.7498/aps.52.2896
[12]	李明华, 于广华, 何珂, 朱逢吾, 赖武彦. 具有分隔层Bi的反铁磁/铁磁双层薄膜间的短程交换耦合. , 2002, 51(12): 2854-2857. doi: 10.7498/aps.51.2854
[13]	余登科, 顾强, 汪汉廷, 沈觉涟. 双层Heisenberg反铁磁体中的量子相变. , 1999, 48(13): 169-174. doi: 10.7498/aps.48.169
[14]	田巨平, 王为忠, 姚凯伦. 有机铁磁体中链间次近邻电子跳跃积分诱导的电荷密度波. , 1999, 48(8): 1535-1540. doi: 10.7498/aps.48.1535
[15]	陶瑞宝, 蒲富恪. 具有四次幂交换作用的Heisenberg铁磁体的低温自旋波理论. , 1980, 29(5): 635-643. doi: 10.7498/aps.29.635
[16]	赖武彦, 王鼎盛, 蒲富恪. 圆柱状铁磁体中的偶极-交换自旋波. , 1977, 26(4): 285-292. doi: 10.7498/aps.26.285
[17]	朱砚磬, 王志强. 自旋波-声子耦合对反铁磁体红外吸收谱的影响. , 1966, 22(3): 360-370. doi: 10.7498/aps.22.360
[18]	李荫远, 方励之, 顾世杰. 铁磁体中缺陷对自旋波的影响. , 1963, 19(9): 599-612. doi: 10.7498/aps.19.599
[19]	李荫远, 朱砚磬. 立方铁磁体中的自旋波局域模. , 1963, 19(11): 753-763. doi: 10.7498/aps.19.753
[20]	吴杭生. 铁磁体的超导电理论. , 1963, 19(2): 103-115. doi: 10.7498/aps.19.103

计量

文章访问数: 974
PDF下载量: 42
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板