-
碘化铯(CsI)光阴极响应灵敏度是软X射线条纹相机用于X射线能谱定量诊断的重要参数, 其理论计算具有重要指导意义. 目前的理论解析模型基于薄膜光阴极产生次级电子的一维随机行走模型发展而来, 具体包括X射线正入射、能量大于1 keV条件下的Henke模型, 以及变角度入射、光阴极厚度大于100 nm条件下的Fraser模型, 都存在一定局限性. 本文进一步引入次级电子输运概率的基础表达式, 推导了CsI光阴极在更大参数范围内(X射线能量0.1—10 keV、光阴极厚度10—200 nm)响应灵敏度随X射线能量E、光阴极厚度t、X射线与阴极表面夹角θ变化的一般表达式. 最后, 将本文的理论计算结果与Henke模型、Fraser模型、文献及北京同步辐射的实验数据分别进行了比较和讨论分析, 验证了计算模型的准确性和普适性, 并且为高时间分辨光谱定量测量实验中CsI光阴极的优化设计提供了理论参考.The response sensitivity of CsI photocathode is an important parameter for the quantitative diagnosis of X-ray spectroscopy by soft X-ray streak camera, and its theoretical calculation has important guiding significance. The current theoretical analytical models are based on the one-dimensional random walking model of secondary electrons generated by thin film photocathodes, including the Henke model under the condition of normal incidence of X-rays and energy greater than 1 keV, and the Fraser model under variable angle incidence and photocathode thickness greater than 100 nm, which have certain limitations. In this paper, the basic expression of the probability of secondary electron transmission is introduced, and the general expression of the response sensitivity of CsI photocathode is deduced, which varies with X-ray energy E, photocathode thickness t, and angle θ between X-ray and cathode surface in a larger parameter range (X-ray energy 0.1–10 keV, photocathode thickness 10–200 nm). Finally, the theoretical calculation results of this paper are discussed by comparing it with those from the Henke model, Fraser model, literature data and experimental data on Beijing synchrotron radiation facility, which verifies the accuracy and universality of the computational model, and a theoretical reference is provided for optimally designing the CsI photocathode in high-time-resolution spectrometric quantitative measurement.
-
Keywords:
- secondary electron /
- CsI photocathode /
- X-ray /
- response sensitivity
[1] Regan S P, Delettrez J A, Epstein R, Jaanimagi P A, Yaakobi B 2002 Phys. Plasmas 9 041357
Google Scholar
[2] Baumgaertel J A, Bradley P A, Hsu S C, Cobble J A, Hakel P 2014 Phys. Plasmas 21 052706
Google Scholar
[3] Chen H, Ma T, Nora R, Barrios M A, Scott H A 2017 Phys. Plasmas 24 072715
Google Scholar
[4] 胡昕, 江少恩, 崔延莉, 黄翼翔, 丁永坤, 刘忠礼, 易荣清, 李朝光, 张景和, 张华全 2007 56 1447
Google Scholar
Hu X, Jiang S E, Cui Y L, Huang Y X, Ding Y K, Liu Z L, Yi R Q, Li C G, Zhang J H, Zhang H Q 2007 Acta Phys. Sin. 56 1447
Google Scholar
[5] Dittrich T R, Hammel B A, Keane C J, McEachern R, Turner R E, Haan S W, Suter L J 1994 Phys. Rev. 73 172324
Google Scholar
[6] 乔秀梅, 郑无敌, 高耀明 2015 64 045201
Google Scholar
Qiao X M, Zheng W D, Gao Y M 2015 Acta Phys. Sin. 64 045201
Google Scholar
[7] Henke B L, Knauer J P, Premaratne K 1981 J. Appl. Phys. 52 031509
Google Scholar
[8] 曾鹏, 袁铮, 邓博, 袁永腾, 李志超, 刘慎业, 赵屹东, 洪才浩, 郑雷, 崔明启 2012 61 155209
Google Scholar
Zeng P, Yuan Z, Deng B, Yuan Y T, Li Z C, Liu S Y, Zhao Y D, Hong C H, Zheng L, Cui M Q 2012 Acta Phys. Sin. 61 155209
Google Scholar
[9] 李晋, 胡昕, 樊龙, 陈韬, 杨志文, 邓博, 黎宇坤, 曹柱荣, 刘慎业 2015 强激光与粒子束 27 082003
Google Scholar
Li J, Hu X, Fan L, Chen T, Yang Z W, Deng B, Li Y K, Cao Z R, Liu S Y 2015 High Power Laser and Particle Beams 27 082003
Google Scholar
[10] Fraser G W 1983 Nucl. Instrum. Meth. Phys. Res. 206 251
Google Scholar
[11] Fraser G W 1985 Nucl. Instrum. Meth. Phys. Res. 228 532
Google Scholar
[12] Lowney D P, Heimann P A, Padmore H A 2004 Rev. Sci. Instrum. 75 103131
Google Scholar
[13] 黎宇坤, 陈韬, 李晋, 杨志文, 胡昕, 邓克立, 曹柱荣 2018 67 085203
Google Scholar
Li Y K, Chen T, Li J, Yang Z W, Hu X, Deng K L, Cao Z R 2018 Acta Phys. Sin. 67 085203
Google Scholar
[14] Akkerman A, Gibrekherman A, Breskin A, Chechik R 1992 J. Appl. Phys. 72 5429
Google Scholar
[15] Gibrekhterman A, Akkerman A, Breskin A, Chechik R 1993 J. Appl. Phys. 74 7506
Google Scholar
[16] Kimbrough J R, Bell P M, Christianson G B 2001 Rev. Sci. Instrum. 72 748
Google Scholar
[17] Kane E O 1966 Phys. Rev. 147 335
Google Scholar
[18] Boutboul T, Akkerman A, Gibrekhterman A, Breskin A, Chechikb R 1999 J. Appl. Phys. 86 155841
Google Scholar
[19] 赵凯华, 钟锡华 1982 光学 (北京: 北京大学出版社) 第247页
Zhao K H, Zhong X H 1982 Optics (Beijing: Peking University Press) p247
[20] 黎宇坤, 陈韬, 邓博, 袁铮, 曹柱荣 2014 强激光与粒子束 26 022002
Google Scholar
Li Y K, Chen T, Deng B, Yuan Z, Cao Z R 2014 High Power Laser and Particle Beams 26 022002
Google Scholar
-
图 1 CsI薄膜光阴极次级电子产生、输运和逸出过程示意图
Fig. 1. Schematic diagram for generation, transmission and escape of secondary electrons from CsI photocathode.
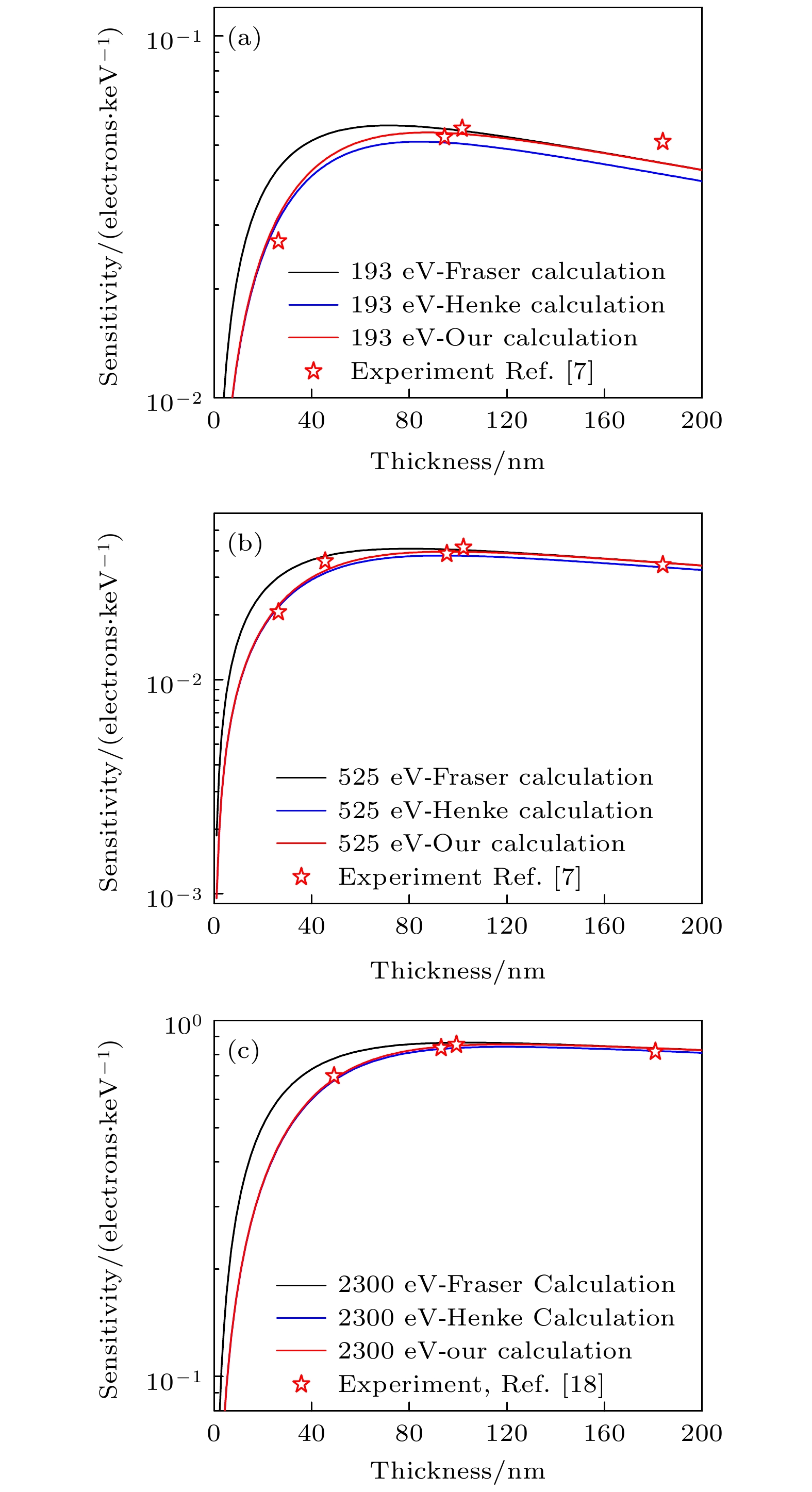
图 2 不同能量 X 射线正入射时, 不同模型计算的 CsI 响应灵敏度随厚度的变化 (a) X 射线能量为 193 eV; (b) X射线能量为 525 eV; (c) X 射线能量为 2300 eV
Fig. 2. Under normal incidence of X-rays with different energy, computed CsI response sensitivity as a function of thickness based on different models: (a) X-ray energy of 193 eV; (b) X-ray energy of 525 eV; (c) X-ray energy of 2300 eV.
图 3 100, 500, 1000 eV的X射线入射时, 不同模型计算的100 nm厚度CsI响应灵敏度随阴极表面夹角的变化
Fig. 3. Comparison of computed 100 nm CsI response sensitivity as a function of angle based on different models at X-ray incidence of 100, 500 and 1000 eV.
图 4 CsI光阴极在北京同步辐射的实验标定结果与本文模型计算结果比较
Fig. 4. Comparison of experimental calibration results of CsI photocathode in Beijing synchrotron radiation with the calculation results of this model.
图 5 三种不同厚度CsI光阴极的响应灵敏度随X射线能量的变化
Fig. 5. Response sensitivity of CsI photocathodes with three different thicknesses as a function of X-ray energy.
-
[1] Regan S P, Delettrez J A, Epstein R, Jaanimagi P A, Yaakobi B 2002 Phys. Plasmas 9 041357
Google Scholar
[2] Baumgaertel J A, Bradley P A, Hsu S C, Cobble J A, Hakel P 2014 Phys. Plasmas 21 052706
Google Scholar
[3] Chen H, Ma T, Nora R, Barrios M A, Scott H A 2017 Phys. Plasmas 24 072715
Google Scholar
[4] 胡昕, 江少恩, 崔延莉, 黄翼翔, 丁永坤, 刘忠礼, 易荣清, 李朝光, 张景和, 张华全 2007 56 1447
Google Scholar
Hu X, Jiang S E, Cui Y L, Huang Y X, Ding Y K, Liu Z L, Yi R Q, Li C G, Zhang J H, Zhang H Q 2007 Acta Phys. Sin. 56 1447
Google Scholar
[5] Dittrich T R, Hammel B A, Keane C J, McEachern R, Turner R E, Haan S W, Suter L J 1994 Phys. Rev. 73 172324
Google Scholar
[6] 乔秀梅, 郑无敌, 高耀明 2015 64 045201
Google Scholar
Qiao X M, Zheng W D, Gao Y M 2015 Acta Phys. Sin. 64 045201
Google Scholar
[7] Henke B L, Knauer J P, Premaratne K 1981 J. Appl. Phys. 52 031509
Google Scholar
[8] 曾鹏, 袁铮, 邓博, 袁永腾, 李志超, 刘慎业, 赵屹东, 洪才浩, 郑雷, 崔明启 2012 61 155209
Google Scholar
Zeng P, Yuan Z, Deng B, Yuan Y T, Li Z C, Liu S Y, Zhao Y D, Hong C H, Zheng L, Cui M Q 2012 Acta Phys. Sin. 61 155209
Google Scholar
[9] 李晋, 胡昕, 樊龙, 陈韬, 杨志文, 邓博, 黎宇坤, 曹柱荣, 刘慎业 2015 强激光与粒子束 27 082003
Google Scholar
Li J, Hu X, Fan L, Chen T, Yang Z W, Deng B, Li Y K, Cao Z R, Liu S Y 2015 High Power Laser and Particle Beams 27 082003
Google Scholar
[10] Fraser G W 1983 Nucl. Instrum. Meth. Phys. Res. 206 251
Google Scholar
[11] Fraser G W 1985 Nucl. Instrum. Meth. Phys. Res. 228 532
Google Scholar
[12] Lowney D P, Heimann P A, Padmore H A 2004 Rev. Sci. Instrum. 75 103131
Google Scholar
[13] 黎宇坤, 陈韬, 李晋, 杨志文, 胡昕, 邓克立, 曹柱荣 2018 67 085203
Google Scholar
Li Y K, Chen T, Li J, Yang Z W, Hu X, Deng K L, Cao Z R 2018 Acta Phys. Sin. 67 085203
Google Scholar
[14] Akkerman A, Gibrekherman A, Breskin A, Chechik R 1992 J. Appl. Phys. 72 5429
Google Scholar
[15] Gibrekhterman A, Akkerman A, Breskin A, Chechik R 1993 J. Appl. Phys. 74 7506
Google Scholar
[16] Kimbrough J R, Bell P M, Christianson G B 2001 Rev. Sci. Instrum. 72 748
Google Scholar
[17] Kane E O 1966 Phys. Rev. 147 335
Google Scholar
[18] Boutboul T, Akkerman A, Gibrekhterman A, Breskin A, Chechikb R 1999 J. Appl. Phys. 86 155841
Google Scholar
[19] 赵凯华, 钟锡华 1982 光学 (北京: 北京大学出版社) 第247页
Zhao K H, Zhong X H 1982 Optics (Beijing: Peking University Press) p247
[20] 黎宇坤, 陈韬, 邓博, 袁铮, 曹柱荣 2014 强激光与粒子束 26 022002
Google Scholar
Li Y K, Chen T, Deng B, Yuan Z, Cao Z R 2014 High Power Laser and Particle Beams 26 022002
Google Scholar
下载:
计量
- 文章访问数: 1869
- PDF下载量: 75
- 被引次数: 0
