-
范德瓦耳斯材料相对扭转到特定角度时, 会出现几乎零色散的莫尔平带, 从而产生一系列关联电子物态, 例如非常规超导、关联绝缘态和轨道磁性等. 在转角双层-双层石墨烯(TDBG)体系中, 能带带宽和拓扑性质可以通过栅极施加的电位移场原位调控, 使该体系成为良好的研究拓扑相变和强关联物理的量子模拟平台. 在一定的电位移场作用下, TDBG中
$ {C}_{2x} $ 对称性破缺, 中性点附近的导带和价带会获得有限的陈数. 能带的拓扑性质与强相互作用驱动的对称性破缺使得可以在低磁场下实现并调控陈绝缘态. 本工作通过制备高质量TDBG器件, 在有限磁场下, 在莫尔原胞填充因子$ \nu $ =1处发现了陈数为4的陈绝缘态. 同时还发现纵向电阻出现电阻峰并随平行磁场或温度升高而增强的现象, 这类似于3He中的Pomeranchuk效应, 推测$ {\rm{\nu }} $ =1处的陈绝缘态或许源于同位旋的极化.-
关键词:
- 转角双层-双层石墨烯 /
- 陈绝缘态 /
- 电子关联
A flat band with nearly zero dispersion can be created by twisting the relative orientation of van der Waals materials, leading to a series of strongly correlated states, such as unconventional superconductivity, correlated insulating state, and orbital magnetism. The bandwidth and topological property of electronic band structure in a twisted double bilayer graphene are tunable by an external displacement field. This system can be an excellent quantum simulator to study the interplay between topological phase transition and strong electron correlation. Theoretical calculation shows that the$ {C}_{2x} $ symmetry in twisted double bilayer graphene (TDBG) can be broken by an electric displacement field, leading the lowest conduction and valence band near charge neutrality to obtain a finite Chern number. The topological properties of the band and the symmetry breaking driven by the strong interaction make it possible to realize and regulate the old insulation state at low magnetic fields. Hence Chern insulator may emerge from this topological non-trivial flat band under strong electron interaction. Here, we observe Chern insulator state with Chern number 4 at filling factor$ \nu =1 $ under a small magnetic field on twisted double bilayer graphene with twist angle 1.48°. Moreover, the longitudinal resistance shows a peak under a parallel magnetic field and increases with temperature or field rising, which is similar to the Pomeranchuk effect in 3He. This phenomenon indicates that Chern insulator at$ \nu =1 $ may originate from isospin polarization.[1] Bistritzer R, MacDonald A H 2011 Proc. Natl. Acad. Sci. U.S.A. 108 12233
Google Scholar
[2] Cao Y, Fatemi V, Demir A, Fang S, Tomarken S L, Luo J Y, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Kaxiras E, Ashoori R C, Jarillo-Herrero P 2018 Nature 556 80
Google Scholar
[3] Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43
Google Scholar
[4] Dean C R, Wang L, Maher P, Forsythe C, Ghahari F, Gao Y, Katoch J, Ishigami M, Moon P, Koshino M, Taniguchi T, Watanabe K, Shepard K L, Hone J, Kim P 2013 Nature 497 598
Google Scholar
[5] Ponomarenko L A, Gorbachev R V, Yu G L, Elias D C, Jalil R, Patel A A, Mishchenko A, Mayorov A S, Woods C R, Wallbank J R, Kruczynski M M, Piot B A, Potemski M, Grigorieva I V, Novoselov K S, Guinea F, Fal’ko V I, Geim A K 2013 Nature 497 594
Google Scholar
[6] Hunt B, Sanchez-Yamagishi J D, Young A F, Yankowitz M, LeRoy B J, Watanabe K, Taniguchi T, Moon P, Koshino M, Jarillo-Herrero P, Ashoori R C 2013 Science 340 1427
Google Scholar
[7] Wang L, Shih E M, Ghiotto A, Xian L, Rhodes D A, Tan C, Claassen M, Kennes D M, Bai Y S, Kim B, Watanabe K, Taniguchi T, Zhu X Y, Hone J, Rubio A, Pasupathy A N, Dean C R 2020 Nat. Mater. 19 861
Google Scholar
[8] Ghiotto A, Shih E M, Pereira G S, Rhodes D A, Kim B, Zang J W, Millis A J, Watanabe K, Taniguchi T, Hone J, Wang L, Dean C R, Pasupathy A N 2021 Nature 597 345
Google Scholar
[9] Serlin M, Tschirhart C L, Polshyn H, Zhang Y, Zhu J, Watanabe K, Taniguchi T, Balents L, Young A F 2020 Science 367 900
Google Scholar
[10] Zhang Y, Tang T T, Girit C, Hao Z, Martin M C, Zettl A, Crommie M F, Shen Y R, Wang F 2009 Nature 459 820
Google Scholar
[11] Koshino M 2019 Phys. Rev. B 99 235406
Google Scholar
[12] Shen C, Chu Y B, Wu Q S, Li N, Wang S P, Zhao Y C, Tang J, Liu J Y, Tian J P, Watanabe K, Taniguchi T, Yang R, Meng Z Y, Shi D X, Yazyev O V, Zhang G Y 2020 Nat. Phys. 16 520
Google Scholar
[13] Liu X M, Hao Z Y, Khalaf E, Lee J Y, Ronen Y, Yoo H, Najafabadi D H, Watanabe K, Taniguchi T, Vishwanath A, Kim P 2020 Nature 583 221
Google Scholar
[14] Cao Y, Rodan-Legrain D, Rubies-Bigorda O, Park J M, Watanabe K, Taniguchi T, Jarillo-Herrero P 2020 Nature 583 215
Google Scholar
[15] He M H, Li Y H, Cai J Q, Liu Y, Watanabe K, Taniguchi T, Xu X D, Yankowitz M 2021 Nat. Phys. 17 26
Google Scholar
[16] Rickhaus P, De-Vries F K, Zhu J H, Portoles E, Zheng G, Masseroni M, Kurzmann A, Taniguchi T, Watanabe K, MacDonald A H, Ihn T, Ensslin K 2021 Science 373 1257
Google Scholar
[17] Liu L, Zhang S H, Chu Y B, Shen C, Huang Y, Yuan Y L, Tian J P, Tang J, Ji Y R, Yang R, Watanabe K, Taniguchi T, Shi D X, Liu J P, Yang W, Zhang G Y 2022 Nat. Commun. 13 3292
Google Scholar
[18] 刘健鹏, 戴希 2020 69 147301
Google Scholar
Liu J P, Dai X 2020 Acta Phys. Sin. 69 147301
Google Scholar
[19] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[20] Kim K, Yankowitz M, Fallahazad B, Kang S, Movva H C, Huang S Q, Larentis S, Corbet C M, Taniguchi T, Watanabe K, Banerjee S K, LeRoy B J, Tutuc E 2016 Nano Lett. 16 1989
Google Scholar
[21] Wang L, Meric I, Huang P Y, Gao Q, Gao Y, Tran H, Taniguchi T, Watanabe K, Campos L M, Muller D A, Guo J, Kim P, Hone J, Shepard K L, Dean C R 2013 Science 342 614
Google Scholar
[22] Haddadi F, Wu Q S, Kruchkov A J, Yazyev O V 2020 Nano Lett. 20 2410
Google Scholar
[23] Rickhaus P, Zheng G, Lado J L, Lee Y J, Kurzmann A, Eich M, Pisoni R, Tong C Y, Garreis R, Gold C, Masseroni M, Taniguchi T, Watanabe K, Ihn T, Ensslin K 2019 Nano Lett. 19 8821
Google Scholar
[24] Wannier G H 1978 Phys. Status Solidi B 88 757
Google Scholar
[25] Thouless D J, Kohmoto M, Nightingale M P, Den-Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[26] Streda P 1982 J. Phys. C: Solid State Phys. 15 L1299
Google Scholar
[27] Wu Q S, Liu J P, Guan Y F, Yazyev O V 2021 Phys. Rev. Lett. 126 056401
Google Scholar
[28] Nuckolls K P, Oh M, Wong D, Lian B, Watanabe K, Taniguchi T, Bernevig B A, Yazdani A 2020 Nature 588 610
Google Scholar
[29] Saito Y, Ge J Y, Rademaker L, Watanabe K, Taniguchi T, Abanin D A, Young A F 2021 Nat. Phys. 17 478
Google Scholar
[30] Das I, Lu X B, Arbeitman J H, Song Z D, Watanabe K, Taniguchi T, Bernevig B A, Efetov D K 2021 Nat. Phys. 17 710
Google Scholar
[31] Bhowmik S, Ghawri B, Leconte N, Appalakondaiah S, Pandey M, Mahapatra P S, Lee D, Watanabe K, Taniguchi T, Jung J, Ghosh A, Chandni U 2022 Nat. Phys. 18 639
Google Scholar
[32] Wang Y X, Li F X, Zhang Z Y 2021 Phys. Rev. B 103 115201
Google Scholar
[33] Saito Y, Yang F Y, Ge J Y, Liu X X, Taniguchi T, Watanabe K, Li J, Berg E, Young A F 2021 Nature 592 220
Google Scholar
[34] Khalaf E, Chatterjee S, Bultinck N, Zaletel M P, Vishwanath A 2021 Sci. Adv. 7 5299
Google Scholar
-
图 1 TDBG器件的电输运测量 (a) 转角为1.48°的TDBG器件光学图; (b) 转角为
$ \theta $ 的TDBG示意图; (c) 转角为$ \theta $ 的迷你布里渊区的示意图; (d)不同电势能作用下(U = 0 meV, U = 20 meV) TDBG的能带图; (e) T = 2 K时, 纵向电阻$ {R}_{xx} $ 随载流子浓度n和电位移场D变化Fig. 1. Transport measurement of TDBG device: (a) Optical image of TDBG device with a twist angle of 1.48°; (b) TDBG with a twist angle
$ \theta $ ; (c) schematic of mini Brillouin zone with a twist angle$ \theta $ ; (d) energy band of TDBG at different electric potential energy U = 0 meV and U = 20 meV; (e) longitudinal resistance$ {R}_{xx} $ versus carrier concentration n and electric displacement field D at T = 2 K.
图 2 低温T = 2 K, D = 0下的磁输运 (a) D = 0时,
$ {R}_{xx} $ 随填充因子$ \nu =4 n/{n}_{{\rm{s}}} $ 和垂直磁场$ {B}_{\perp } $ 的变化; (b) D = 0时, 横向电阻$ {R}_{xy} $ 随填充因子$ \nu =4 n/{n}_{{\rm{s}}} $ 和垂直磁场$ {B}_{\perp } $ 变化; (c) 从(a), (b)中提取得到的朗道能级序列(蓝色)Fig. 2. Magnetotransport of resistance at low temperature of T = 2 K and D = 0: (a) Longitudinal resistance
$ {R}_{xx} $ versus filling factor$ \nu =4 n/{n}_{{\rm{s}}} $ and vertical magnetic field$ {B}_{\perp } $ at D = 0; (b) Hall resistance$ {R}_{xy} $ versus filling factor$ \nu =4 n/{n}_{{\rm{s}}} $ and vertical magnetic field$ {B}_{\perp } $ at D = 0; (c) Landau level (blue) extracted from figure (a) and (b).
图 3 低温(T = 2 K)不同外加电位移场作用下的磁输运性质 (a) D = –0.42 V/nm时, 纵向电阻
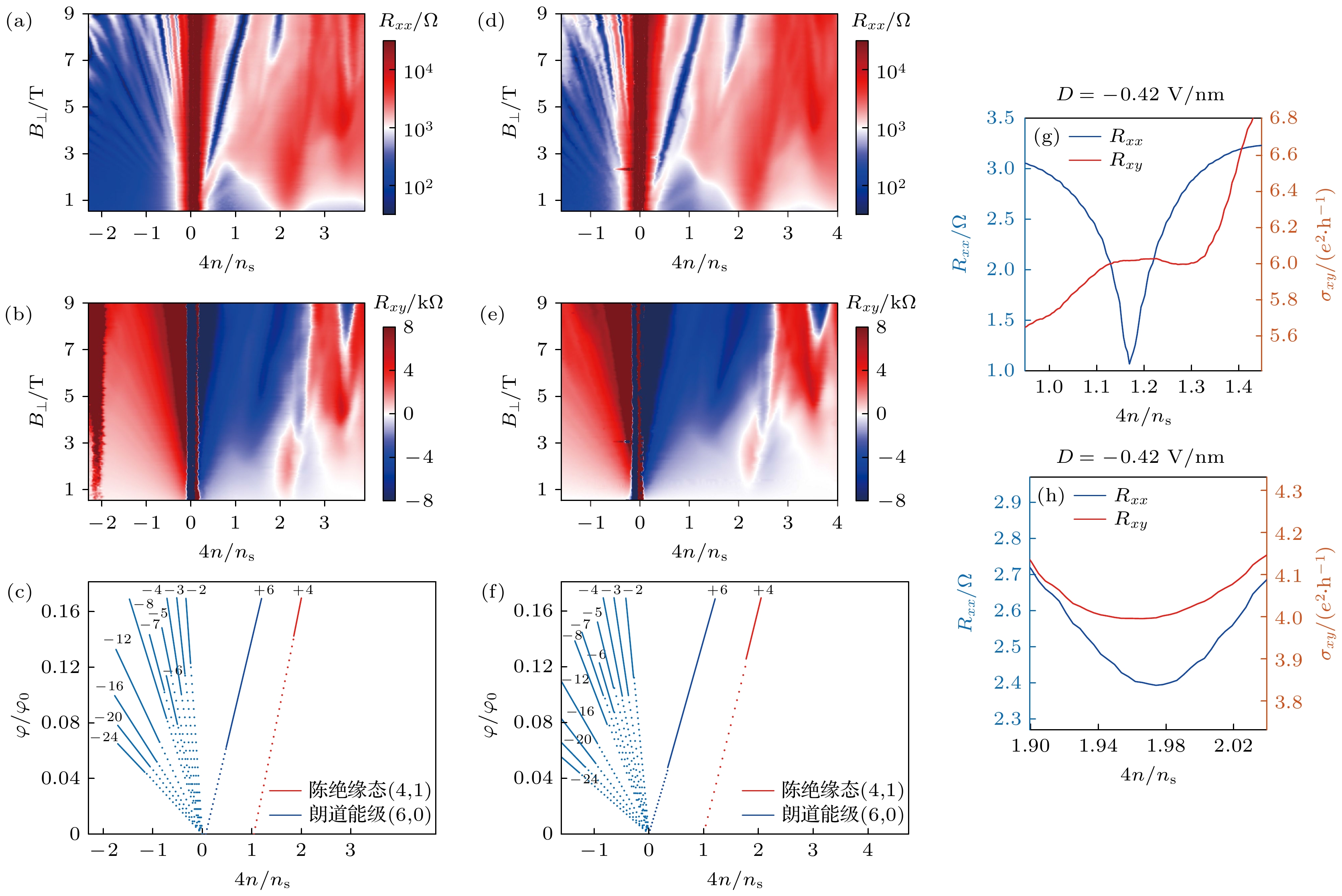
$ {R}_{xx} $ 随填充因子$ \nu $ 和垂直磁场$ {B}_{\perp } $ 的变化; (b) D = –0.42 V/nm时, 横向电阻$ {R}_{xy} $ 随填充因子$ \nu $ 和垂直磁场$ {B}_{\perp } $ 的变化; (c) 从图3(a), (b)中提取得到的朗道能级序列(蓝色)和陈绝缘态(红色); (d) D = 0.5 V/nm时, 纵向电阻$ {R}_{xx} $ 随填充因子$ \nu $ 和垂直磁场$ {B}_{\perp } $ 变化; (e) D = 0.5 V/nm时, 横向电阻$ {R}_{xy} $ 随填充因子$ \nu $ 和垂直磁场$ {B}_{\perp } $ 变化; (f)从图3(d), (e)中提取得到的朗道能级序列(蓝色)和陈绝缘态(红色); (g) 当垂直磁场$ {B}_{\perp } $ = 8.7 T时, (6, 0)所对应朗道能级的纵向电阻$ {R}_{xx} $ 和霍尔电导$ {\sigma }_{xy} $ ; (h) 当垂直磁场$ {B}_{\perp } $ = 8.7 T时, (4, 1)所对应陈绝缘态的纵向电阻$ {R}_{xx} $ 和霍尔电导$ {\sigma }_{xy} $ Fig. 3. Magnetotransport under different electric displacement field at low temperature T = 2 K: (a) Longitudinal resistance
$ {R}_{xx} $ as a function of filling factor$ \nu $ and vertical magnetic field$ {B}_{\perp } $ at D = –0.42 V/nm; (b) Hall resistance$ {R}_{xy} $ as a function of filling factor$ \nu $ and vertical magnetic field$ {B}_{\perp } $ at D = –0.42 V/nm; (c) Landau level (blue) and Chern insulator (red) extracted from Fig. 3(a), (b); (d) longitudinal resistance$ {R}_{xx} $ as a function of filling factor$ \nu $ and vertical magnetic field$ {B}_{\perp } $ at D = 0.5 V/nm; (e) Hall resistance$ {R}_{xy} $ as a function of filling factor$ \nu $ and vertical magnetic field$ {B}_{\perp } $ at D = 0.5 V/nm; (f) Landau level (blue) and Chern insulator (red) extracted from Fig. 3(d) and Fig. 3(e); (g) longitudinal resistance$ {R}_{xx} $ and Hall conductance$ {\sigma }_{xy} $ of (6, 0) state at vertical magnetic field${B}_{\perp } $ = 8.7 T; (h) longitudinal resistance$ {R}_{xx} $ and Hall conductance$ {\sigma }_{xy} $ of (4, 1) state at vertical magnetic field$ {B}_{\perp } $ = 8.7 T.
图 4 温度和平行磁场诱导的极化 (a) B = 0, D = –0.42 V/nm时, 纵向电阻
$ {R}_{xx} $ 随填充因子$ \nu $ 和温度T变化; (b)纵向电阻$ {R}_{xx} $ 随填充因子$ \nu $ 变化, 取自图4(a)的一系列温度下的截线; (c) D = 0时, 一系列不同温度下纵向电阻随$ {R}_{xx} $ 随载流子浓度n变化; (d) T = 0.2 K时, 纵向电阻$ {R}_{xx} $ 作为填充因子$ \nu $ 和平行磁场${B}_{//}$ 函数Fig. 4. Temperature and parallel magnetic field induced polarization: (a) Longitudinal resistance
$ {R}_{xx} $ versus filling factor$ \nu $ and temperature T at B = 0 and D = –0.42 V/nm; (b) longitudinal resistance$ {R}_{xx} $ versus filling factor$ \nu $ extracted from Fig. 4(a) under a series of specific temperature; (c) longitudinal resistance$ {R}_{xx} $ versus carrier concentration n under a series of specific temperature at D = 0; (d) longitudinal resistance$ {R}_{xx} $ as a function of filling factor$ \nu $ and parallel magnetic field${B}_{//}$ at T = 0.2 K. -
[1] Bistritzer R, MacDonald A H 2011 Proc. Natl. Acad. Sci. U.S.A. 108 12233
Google Scholar
[2] Cao Y, Fatemi V, Demir A, Fang S, Tomarken S L, Luo J Y, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Kaxiras E, Ashoori R C, Jarillo-Herrero P 2018 Nature 556 80
Google Scholar
[3] Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43
Google Scholar
[4] Dean C R, Wang L, Maher P, Forsythe C, Ghahari F, Gao Y, Katoch J, Ishigami M, Moon P, Koshino M, Taniguchi T, Watanabe K, Shepard K L, Hone J, Kim P 2013 Nature 497 598
Google Scholar
[5] Ponomarenko L A, Gorbachev R V, Yu G L, Elias D C, Jalil R, Patel A A, Mishchenko A, Mayorov A S, Woods C R, Wallbank J R, Kruczynski M M, Piot B A, Potemski M, Grigorieva I V, Novoselov K S, Guinea F, Fal’ko V I, Geim A K 2013 Nature 497 594
Google Scholar
[6] Hunt B, Sanchez-Yamagishi J D, Young A F, Yankowitz M, LeRoy B J, Watanabe K, Taniguchi T, Moon P, Koshino M, Jarillo-Herrero P, Ashoori R C 2013 Science 340 1427
Google Scholar
[7] Wang L, Shih E M, Ghiotto A, Xian L, Rhodes D A, Tan C, Claassen M, Kennes D M, Bai Y S, Kim B, Watanabe K, Taniguchi T, Zhu X Y, Hone J, Rubio A, Pasupathy A N, Dean C R 2020 Nat. Mater. 19 861
Google Scholar
[8] Ghiotto A, Shih E M, Pereira G S, Rhodes D A, Kim B, Zang J W, Millis A J, Watanabe K, Taniguchi T, Hone J, Wang L, Dean C R, Pasupathy A N 2021 Nature 597 345
Google Scholar
[9] Serlin M, Tschirhart C L, Polshyn H, Zhang Y, Zhu J, Watanabe K, Taniguchi T, Balents L, Young A F 2020 Science 367 900
Google Scholar
[10] Zhang Y, Tang T T, Girit C, Hao Z, Martin M C, Zettl A, Crommie M F, Shen Y R, Wang F 2009 Nature 459 820
Google Scholar
[11] Koshino M 2019 Phys. Rev. B 99 235406
Google Scholar
[12] Shen C, Chu Y B, Wu Q S, Li N, Wang S P, Zhao Y C, Tang J, Liu J Y, Tian J P, Watanabe K, Taniguchi T, Yang R, Meng Z Y, Shi D X, Yazyev O V, Zhang G Y 2020 Nat. Phys. 16 520
Google Scholar
[13] Liu X M, Hao Z Y, Khalaf E, Lee J Y, Ronen Y, Yoo H, Najafabadi D H, Watanabe K, Taniguchi T, Vishwanath A, Kim P 2020 Nature 583 221
Google Scholar
[14] Cao Y, Rodan-Legrain D, Rubies-Bigorda O, Park J M, Watanabe K, Taniguchi T, Jarillo-Herrero P 2020 Nature 583 215
Google Scholar
[15] He M H, Li Y H, Cai J Q, Liu Y, Watanabe K, Taniguchi T, Xu X D, Yankowitz M 2021 Nat. Phys. 17 26
Google Scholar
[16] Rickhaus P, De-Vries F K, Zhu J H, Portoles E, Zheng G, Masseroni M, Kurzmann A, Taniguchi T, Watanabe K, MacDonald A H, Ihn T, Ensslin K 2021 Science 373 1257
Google Scholar
[17] Liu L, Zhang S H, Chu Y B, Shen C, Huang Y, Yuan Y L, Tian J P, Tang J, Ji Y R, Yang R, Watanabe K, Taniguchi T, Shi D X, Liu J P, Yang W, Zhang G Y 2022 Nat. Commun. 13 3292
Google Scholar
[18] 刘健鹏, 戴希 2020 69 147301
Google Scholar
Liu J P, Dai X 2020 Acta Phys. Sin. 69 147301
Google Scholar
[19] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[20] Kim K, Yankowitz M, Fallahazad B, Kang S, Movva H C, Huang S Q, Larentis S, Corbet C M, Taniguchi T, Watanabe K, Banerjee S K, LeRoy B J, Tutuc E 2016 Nano Lett. 16 1989
Google Scholar
[21] Wang L, Meric I, Huang P Y, Gao Q, Gao Y, Tran H, Taniguchi T, Watanabe K, Campos L M, Muller D A, Guo J, Kim P, Hone J, Shepard K L, Dean C R 2013 Science 342 614
Google Scholar
[22] Haddadi F, Wu Q S, Kruchkov A J, Yazyev O V 2020 Nano Lett. 20 2410
Google Scholar
[23] Rickhaus P, Zheng G, Lado J L, Lee Y J, Kurzmann A, Eich M, Pisoni R, Tong C Y, Garreis R, Gold C, Masseroni M, Taniguchi T, Watanabe K, Ihn T, Ensslin K 2019 Nano Lett. 19 8821
Google Scholar
[24] Wannier G H 1978 Phys. Status Solidi B 88 757
Google Scholar
[25] Thouless D J, Kohmoto M, Nightingale M P, Den-Nijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[26] Streda P 1982 J. Phys. C: Solid State Phys. 15 L1299
Google Scholar
[27] Wu Q S, Liu J P, Guan Y F, Yazyev O V 2021 Phys. Rev. Lett. 126 056401
Google Scholar
[28] Nuckolls K P, Oh M, Wong D, Lian B, Watanabe K, Taniguchi T, Bernevig B A, Yazdani A 2020 Nature 588 610
Google Scholar
[29] Saito Y, Ge J Y, Rademaker L, Watanabe K, Taniguchi T, Abanin D A, Young A F 2021 Nat. Phys. 17 478
Google Scholar
[30] Das I, Lu X B, Arbeitman J H, Song Z D, Watanabe K, Taniguchi T, Bernevig B A, Efetov D K 2021 Nat. Phys. 17 710
Google Scholar
[31] Bhowmik S, Ghawri B, Leconte N, Appalakondaiah S, Pandey M, Mahapatra P S, Lee D, Watanabe K, Taniguchi T, Jung J, Ghosh A, Chandni U 2022 Nat. Phys. 18 639
Google Scholar
[32] Wang Y X, Li F X, Zhang Z Y 2021 Phys. Rev. B 103 115201
Google Scholar
[33] Saito Y, Yang F Y, Ge J Y, Liu X X, Taniguchi T, Watanabe K, Li J, Berg E, Young A F 2021 Nature 592 220
Google Scholar
[34] Khalaf E, Chatterjee S, Bultinck N, Zaletel M P, Vishwanath A 2021 Sci. Adv. 7 5299
Google Scholar
下载:
计量
- 文章访问数: 4361
- PDF下载量: 272
- 被引次数: 0
