-
实际量子密钥分发中参数的优化选择能大幅提升系统密钥生成率和最大传输距离, 由于全局搜索算法的成本过大, 本地搜索算法被广泛地应用. 然而该算法存在两个问题, 一是所得解不一定为全局最优解, 二是算法的有效性极大地受制于初始值的选择. 利用蒙特卡罗方法对密钥生成率函数是否为凸函数进行了证明, 并仿真分析了密钥生成率函数在不同参数维度上的特性, 提出了粒子群本地搜索算法并与本地搜索算法进行仿真比较. 结果表明, 密钥生成率函数为非凸函数, 但合理设置初始值, 本地搜索算法仍能求得全局最优解; 在传输距离较远时, 本地搜索算法因难以通过随机取值的方法得到有效的初始值而失效, 粒子群本地搜索算法能克服这一缺点, 以轻微增加算法复杂度为代价, 提升了系统的最大传输距离.The optimal selection of parameters in practical quantum key distribution can greatly improve the key generation rate and maximum transmission distance of the system. Owing to the high cost of global search algorithm, local search algorithm is widely used. However, there are two shortcomings in local search algorithm. One is that the solution obtained is not always the global optimal solution, and the other is that the effectiveness of the algorithm is greatly dependent on the choice of initial value. This paper uses the Monte Carlo method to prove whether the key generation rate function is convex, and also simulates and analyzes the projection of the key generation rate function on each dimension of the parameter, in contrast to the approach in previous article. In order to eliminate the effect of the initial value, this paper proposes the particle swarm local search optimization algorithm which integrates particle swarm optimization algorithm and local search algorithm. The first step is to use the particle swarm optimization to find a valid parameter which leads to nonzero key generation rate, and the second step is to adopt the parameter as the initial value of local search algorithm to derive the global optimal solution. Then, the two algorithms are used to conduct simulation and their results are compared. The results show that the key generation rate function is non-convex because it does not satisfy the definition of a convex function, however, since the key generation rate function has only one non-zero stagnation point, the LSA algorithm can still obtain the global optimal solution with an appropriate initial value. When the transmission distance is relatively long, the local search algorithm is invalid because it is difficult to obtain an effective initial value by random value method. The particle swarm optimization algorithm can overcome this shortcoming and improve the maximum transmission distance of the system at the cost of slightly increasing the complexity of the algorithm.
-
Keywords:
- quantum key distribution /
- particle swarm algorithm /
- measurement device independent protocol /
- optimization of parameters
[1] Shor P W, Preskill J 2000 Phys. Rev. Lett. 85 441
Google Scholar
[2] Pirandola S, Andersen U L, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C, Pereira J L, Razavi M, Shamsul Shaari J, Tomamichel M, Usenko V C, Vallone G, Villoresi P, Wallden P 2020 Adv. Opt. Photonics 12 1012
Google Scholar
[3] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[4] Lo H K, Chau H F 1999 Science 283 2050
Google Scholar
[5] Xu F, Ma X, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002
Google Scholar
[6] Gerhardt I, Liu Q, Lamas-Linares A, Skaar J, Kurtsiefer C, Makarov V 2011 Nat. Commun. 2 349
Google Scholar
[7] Jain N, Stiller B, Khan I, Elser D, Marquardt C, Leuchs G 2016 Contemp. Phys. 57 366
Google Scholar
[8] Lo H K, Ma X, Chen K 2005 Phys. Rev. Lett. 94 230504
Google Scholar
[9] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[10] Gu J, Cao X Y, Fu Y, He Z W, Yin Z J, Yin H L, Chen Z B 2022 Sci. Bull. 67 2167
Google Scholar
[11] Yin H L, Cao W F, Fu Y, Tang Y L, Liu Y, Chen T Y, Chen Z B 2014 Opt. Lett. 39 5451
Google Scholar
[12] Lo H K, Chau H F, Ardehali M 2005 J. Cryptol. 18 133
Google Scholar
[13] Wei Z, Wang W, Zhang Z, Gao M, Ma Z, Ma X 2013 Sci. Rep. 3 2453
Google Scholar
[14] Xu F, Xu H, Lo H K 2014 Phys. Rev. A 89 052333
Google Scholar
[15] Wang W, Lo H K 2019 Phys. Rev. A 100 062334
Google Scholar
[16] Ding H J, Liu J Y, Zhang C M, Wang Q 2020 Quantum Inf. Process. 19 60
Google Scholar
[17] Dong Q, Huang G, Cui W, Jiao R 2022 Quantum Inf. Process. 21 233
Google Scholar
[18] Dong Q, Huang G, Cui W, Jiao R 2021 Quantum Sci. Technol. 7 015014
[19] Lu F Y, Yin Z Q, Wang C, Cui C H, Teng J, Wang S, Chen W, Huang W, Xu B J, Guo G C, Han Z F 2019 J. Opt. Soc. Am. B 36 B92
Google Scholar
[20] Boyd S P, Vandenberghe L 2004 Convex Optimization (New York: Cambridge University Press) p716
[21] 韩宝玲, 赵锐, 罗庆生, 徐峰, 赵嘉珩 2017 北京理工大学学报 37 461
Han B L, Zhao R, Luo Q S, Xu F, Zhao J H 2017 J. Beijing Inst. Technol. 37 461
[22] 蒋丽, 叶润舟, 梁昌勇, 陆文星 2019 计算机工程与应用 55 130
Jiang L, Ye R Z, Liang C Y, Lu W X 2019 Computer Engineering and Applications 55 130
[23] Lucamarini M, Yuan Z L, Dynes J F, Shields A J 2018 Nature 557 400
Google Scholar
[24] Ma X, Zeng P, Zhou H 2018 Phys. Rev. X 8 031043
[25] Zhou L, Lin J, Jing Y, Yuan Z 2023 Nat. Commun. 14 928
Google Scholar
[26] Zeng P, Zhou H, Wu W, Ma X 2022 Nat. Commun. 13 3903
Google Scholar
[27] Xie Y M, Lu Y S, Weng C X, Cao X Y, Jia Z Y, Bao Y, Wang Y, Fu Y, Yin H L, Chen Z B 2022 PRX Quantum. 3 020315
Google Scholar
[28] Ma X, Fung C H F, Razavi M 2012 Phys. Rev. A 86 052305
Google Scholar
[29] Sun S H, Gao M, Li C Y, Liang L M 2013 Phys. Rev. A 87 052329
Google Scholar
[30] Ma X, Qi B, Zhao Y, Lo H K 2005 Phys. Rev. A 72 012326
Google Scholar
[31] Curty M, Xu F, Cui W, Lim C C W, Tamaki K, Lo H K 2014 Nat. Commun. 5 3732
Google Scholar
[32] Xu F, Curty M, Qi B, Lo H K 2013 New J. Phys. 15 113007
Google Scholar
[33] Yang X S 2021 Nature-Inspired Optimization Algorithms (London: Elsevier) pp111–113
[34] Gandomi A H, Yun G J, Yang X S, Talatahari S 2013 Commun. Nonlinear Sci. Numer. Simul. 18 327
Google Scholar
[35] Ursin R, Tiefenbacher F, Schmitt-Manderbach T, et al. 2007 Nat. Phys. 3 481
Google Scholar
-
图 1 凸性判别函数
$ F\left( {\theta , {{\boldsymbol{x}}_1}, {{\boldsymbol{x}}_2}} \right) $ 在10000个随机输入下的取值Fig. 1. Values of convex discriminant function of
$ F\left( {\theta , {{\boldsymbol{x}}_1}, {{\boldsymbol{x}}_2}} \right) $ with 10 thousand random input variables.
图 3 LSA优化时不同初始点对密钥生成率的影响
Fig. 3. Influence of different start point on key rate using LSA optimization.
图 4 利用不同优化算法所得密钥生成率对比
Fig. 4. Comparison among three key rates obtained by different optimization algorithm.
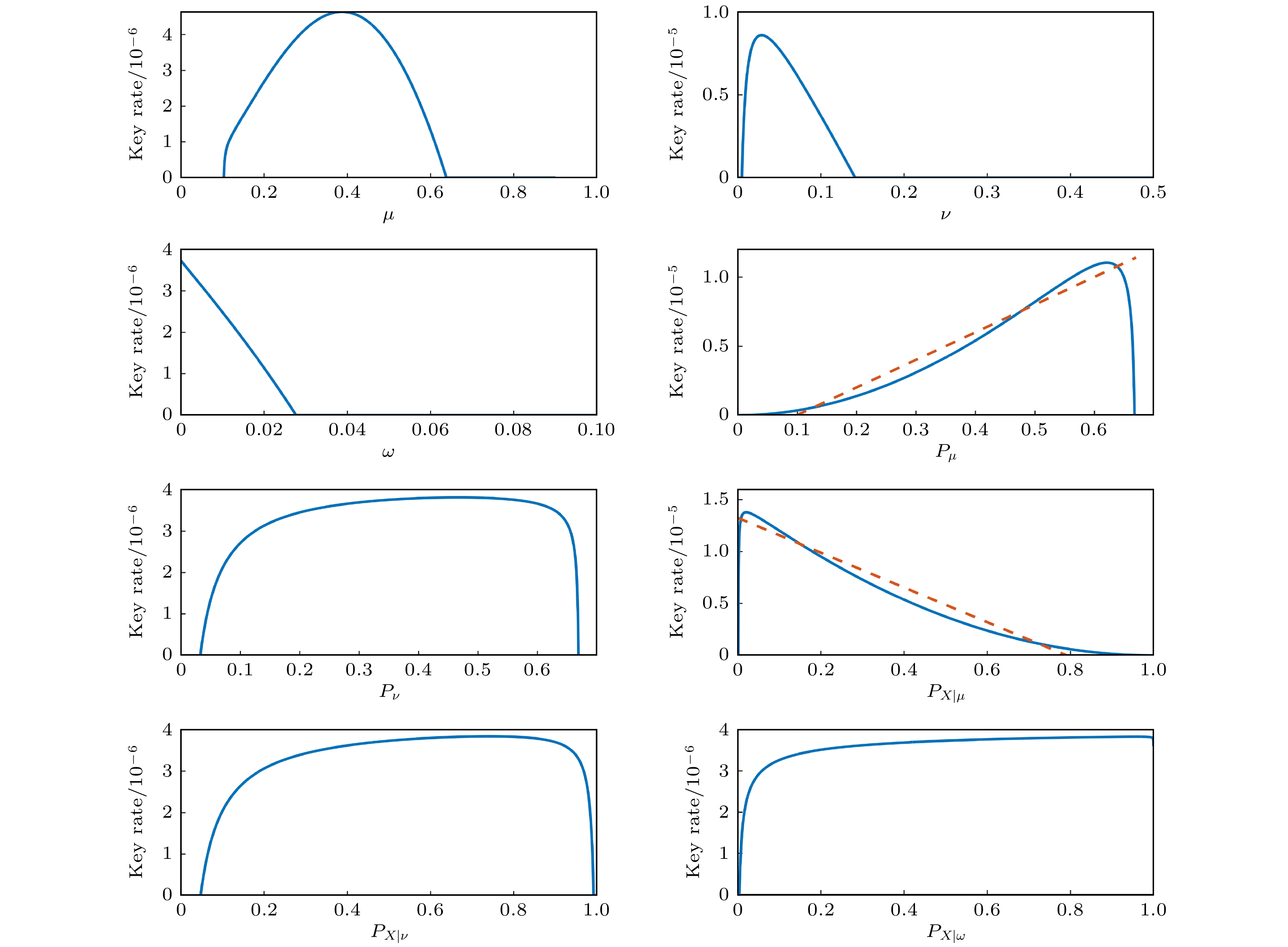
目标函数$ {f_{{\text{LSA}}}}\left( {{x_1}, \cdots , {x_n}} \right) $ 根据经验初始化搜索位置$ {p_0} = \left( {x_1^0, \cdots , x_n^0} \right) $, 初始化迭代次数
t = 0;
while (迭代判决条件) do
for k = 1∶n
对$ {f_{{\text{LSA}}}}\left( {x_1^{t + 1}, \cdots , x_{k - 1}^{t + 1}, x_k^t, x_{k + 1}^t, \cdots , x_n^t} \right) $在$ x_k^t $维度上
进行线性回溯搜索
if ${f_{ {\text{LSA} } } }\left( {x_1^{t + 1}, \cdots , x_{k - 1}^{t + 1}, x_k^{t + 1}, x_{k + 1}^t, \cdots , x_n^t} \right) > $
$ {f_{ {\text{LSA} } } }\left( {x_1^{t + 1}, \cdots , x_{k - 1}^{t + 1}, x_k^t, x_{k + 1}^t, \cdots , x_n^t} \right)$
更新$ x_k^t $为$ x_k^{t + 1} $
$ {p_{t + 1}} = \left( {x_1^{t + 1}, \cdots , x_{k - 1}^{t + 1}, x_k^{t + 1}, x_{k + 1}^t, \cdots , x_n^t} \right) $
else
$ {p_{t + 1}} = \left( {x_1^{t + 1}, \cdots , x_{k - 1}^{t + 1}, x_k^t, x_{k + 1}^t, \cdots , x_n^t} \right) $
end
end
更新迭代次数 t = t + 1
更新搜索位置为$ {p_{t + 1}} $
end
输出最终结果$ \left( {x_1^{t + 1}, \cdots , x_n^{t + 1}} \right) $和$ {f_{{\text{LSA}}}}\left( {x_1^{t + 1}, \cdots , x_n^{t + 1}} \right) $
下载: 导出CSV
目标函数$ f\left( {\boldsymbol{x}} \right) $ 根据经验初始化粒子1的位置$ {{\boldsymbol{x}}_1} $
初始化剩余$ n - 1 $个粒子的位置$ {{\boldsymbol{x}}_i} $和所有粒子的速度$ {{\boldsymbol{\nu }}_i} $
寻找全局最优解$ {{\boldsymbol{g}}_{\text{a}}} $, $ {{\boldsymbol{g}}_{\text{a}}} = \min \left\{ {f\left( {{{\boldsymbol{x}}_1}} \right), \cdots , f\left( {{{\boldsymbol{x}}_n}} \right)} \right\} $
while(迭代判决条件) do
for 所有的粒子 do
更新速度$ {\boldsymbol{\nu }}_i^{t + 1} $
更新位置$ {\boldsymbol{x}}_i^{t + 1} $
计算目标函数在新位置的值
更新当前粒子的历史最优位置$ {\boldsymbol{x}}_i^* $
end
更新全局最优解$ {{\boldsymbol{g}}_{\text{a}}} $
end
输出最终结果$ {\boldsymbol{x}}_i^* $和$ {{\boldsymbol{g}}_{\text{a}}} $
以$ {{\boldsymbol{g}}_{\text{a}}} $为初始点, 采用LSA算法求局部最优解
下载: 导出CSV
表 1 用于仿真分析的相关参数
Table 1. Practical parameters for numerical simulations.
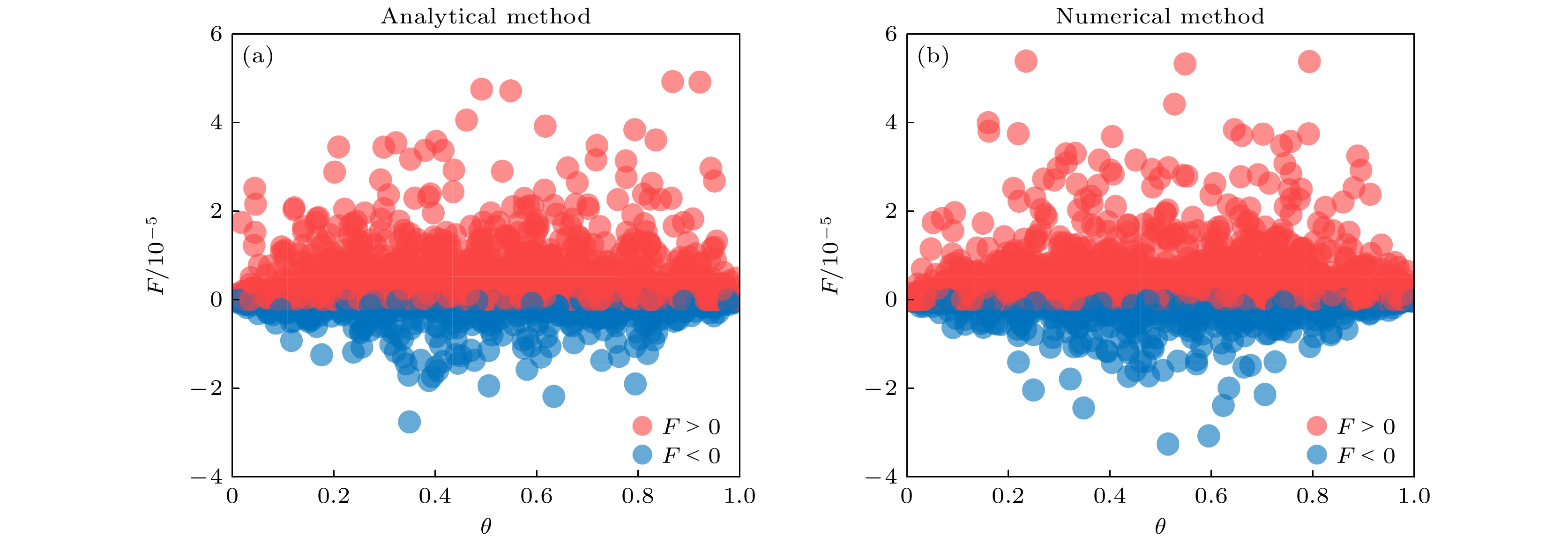
${\eta _{\text{d}}}$/% ${e_{\text{d}}}$/% ${Y_0}$ ${f_{\text{e}}}$ $\chi $ $N$ $\alpha $ 14.5 1.5 $6.02 \times {10^{ - 6}}$ 1.16 ${10^{ - 7}}$ ${10^{12}}$ 0.21
下载: 导出CSV
表 2 可判别密钥生成率非凸的四个点
Table 2. Four points which can be used to discriminate the key rate is non convex function.
参数 $ {{\boldsymbol{x}}_1} $ $ {{\boldsymbol{x}}_2} $ $ {{\boldsymbol{x}}_3} $ $ {{\boldsymbol{x}}_4} $ $ \mu $ 0.40 0.60 0.50 0.075 $ \nu $ 0.037 0.045 0.029 $5.9 \times {10^{ - 3} }$ $ \omega $ $7.9 \times {10^{ - 4} }$ $2.6 \times {10^{ - 3} }$ $2.0 \times {10^{ - 3} }$ $2.57 \times {10^{ - 4} }$ $ {P_\mu } $ 0.15 0.48 0.54 0.020 $ {P_\nu } $ 0.18 0.13 0.26 0.48 $ {P_{{\text{X}}|\mu }} $ 0.8 0.14 0.76 0.14 $ {P_{{\text{X}}|\nu }} $ 0.92 0.56 0.89 0.64 $ {P_{{\text{X}}|\omega }} $ 0.25 0.99 0.54 0.55 $ \theta $ 0.47 0.64 $ F\left( {\theta , {\boldsymbol{x}}, {\boldsymbol{y}}} \right) $ $ - 5.50 \times {10^{ - 6}} $ $ 3.84 \times {10^{ - 6}} $
下载: 导出CSV
表 3 三种优化算法计算资源消耗比较
Table 3. Comparison of computational resource consumption among the three optimization algorithms.
算法 迭代次数 时间/s 密钥生成率 LSA 858 0.12 $ 4.13 \times {10^{ - 6}} $ PSO 40000 4.2 $ 2.97 \times {10^{ - 6}} $ PSLSA 40559 4.29 $ 4.13 \times {10^{ - 6}} $
下载: 导出CSV
-
[1] Shor P W, Preskill J 2000 Phys. Rev. Lett. 85 441
Google Scholar
[2] Pirandola S, Andersen U L, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C, Pereira J L, Razavi M, Shamsul Shaari J, Tomamichel M, Usenko V C, Vallone G, Villoresi P, Wallden P 2020 Adv. Opt. Photonics 12 1012
Google Scholar
[3] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[4] Lo H K, Chau H F 1999 Science 283 2050
Google Scholar
[5] Xu F, Ma X, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002
Google Scholar
[6] Gerhardt I, Liu Q, Lamas-Linares A, Skaar J, Kurtsiefer C, Makarov V 2011 Nat. Commun. 2 349
Google Scholar
[7] Jain N, Stiller B, Khan I, Elser D, Marquardt C, Leuchs G 2016 Contemp. Phys. 57 366
Google Scholar
[8] Lo H K, Ma X, Chen K 2005 Phys. Rev. Lett. 94 230504
Google Scholar
[9] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[10] Gu J, Cao X Y, Fu Y, He Z W, Yin Z J, Yin H L, Chen Z B 2022 Sci. Bull. 67 2167
Google Scholar
[11] Yin H L, Cao W F, Fu Y, Tang Y L, Liu Y, Chen T Y, Chen Z B 2014 Opt. Lett. 39 5451
Google Scholar
[12] Lo H K, Chau H F, Ardehali M 2005 J. Cryptol. 18 133
Google Scholar
[13] Wei Z, Wang W, Zhang Z, Gao M, Ma Z, Ma X 2013 Sci. Rep. 3 2453
Google Scholar
[14] Xu F, Xu H, Lo H K 2014 Phys. Rev. A 89 052333
Google Scholar
[15] Wang W, Lo H K 2019 Phys. Rev. A 100 062334
Google Scholar
[16] Ding H J, Liu J Y, Zhang C M, Wang Q 2020 Quantum Inf. Process. 19 60
Google Scholar
[17] Dong Q, Huang G, Cui W, Jiao R 2022 Quantum Inf. Process. 21 233
Google Scholar
[18] Dong Q, Huang G, Cui W, Jiao R 2021 Quantum Sci. Technol. 7 015014
[19] Lu F Y, Yin Z Q, Wang C, Cui C H, Teng J, Wang S, Chen W, Huang W, Xu B J, Guo G C, Han Z F 2019 J. Opt. Soc. Am. B 36 B92
Google Scholar
[20] Boyd S P, Vandenberghe L 2004 Convex Optimization (New York: Cambridge University Press) p716
[21] 韩宝玲, 赵锐, 罗庆生, 徐峰, 赵嘉珩 2017 北京理工大学学报 37 461
Han B L, Zhao R, Luo Q S, Xu F, Zhao J H 2017 J. Beijing Inst. Technol. 37 461
[22] 蒋丽, 叶润舟, 梁昌勇, 陆文星 2019 计算机工程与应用 55 130
Jiang L, Ye R Z, Liang C Y, Lu W X 2019 Computer Engineering and Applications 55 130
[23] Lucamarini M, Yuan Z L, Dynes J F, Shields A J 2018 Nature 557 400
Google Scholar
[24] Ma X, Zeng P, Zhou H 2018 Phys. Rev. X 8 031043
[25] Zhou L, Lin J, Jing Y, Yuan Z 2023 Nat. Commun. 14 928
Google Scholar
[26] Zeng P, Zhou H, Wu W, Ma X 2022 Nat. Commun. 13 3903
Google Scholar
[27] Xie Y M, Lu Y S, Weng C X, Cao X Y, Jia Z Y, Bao Y, Wang Y, Fu Y, Yin H L, Chen Z B 2022 PRX Quantum. 3 020315
Google Scholar
[28] Ma X, Fung C H F, Razavi M 2012 Phys. Rev. A 86 052305
Google Scholar
[29] Sun S H, Gao M, Li C Y, Liang L M 2013 Phys. Rev. A 87 052329
Google Scholar
[30] Ma X, Qi B, Zhao Y, Lo H K 2005 Phys. Rev. A 72 012326
Google Scholar
[31] Curty M, Xu F, Cui W, Lim C C W, Tamaki K, Lo H K 2014 Nat. Commun. 5 3732
Google Scholar
[32] Xu F, Curty M, Qi B, Lo H K 2013 New J. Phys. 15 113007
Google Scholar
[33] Yang X S 2021 Nature-Inspired Optimization Algorithms (London: Elsevier) pp111–113
[34] Gandomi A H, Yun G J, Yang X S, Talatahari S 2013 Commun. Nonlinear Sci. Numer. Simul. 18 327
Google Scholar
[35] Ursin R, Tiefenbacher F, Schmitt-Manderbach T, et al. 2007 Nat. Phys. 3 481
Google Scholar
下载:
计量
- 文章访问数: 3016
- PDF下载量: 52
- 被引次数: 0
