基于量子长短期记忆网络的量子图像混沌加密方案

王伟杰; 姜美美; 王淑梅; 曲英杰; 马鸿洋; 邱田会

doi:10.7498/aps.72.20230242

摘要

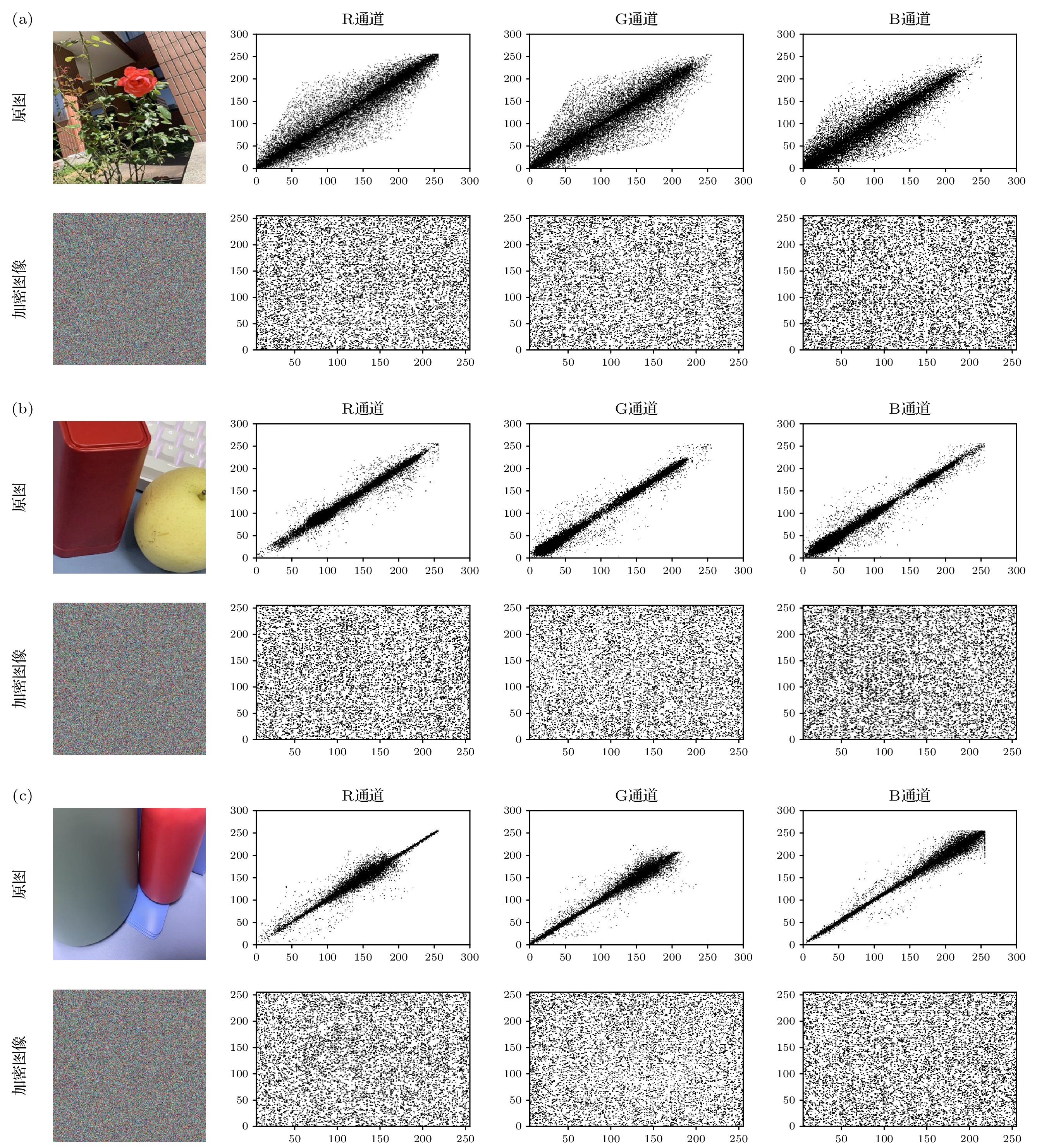
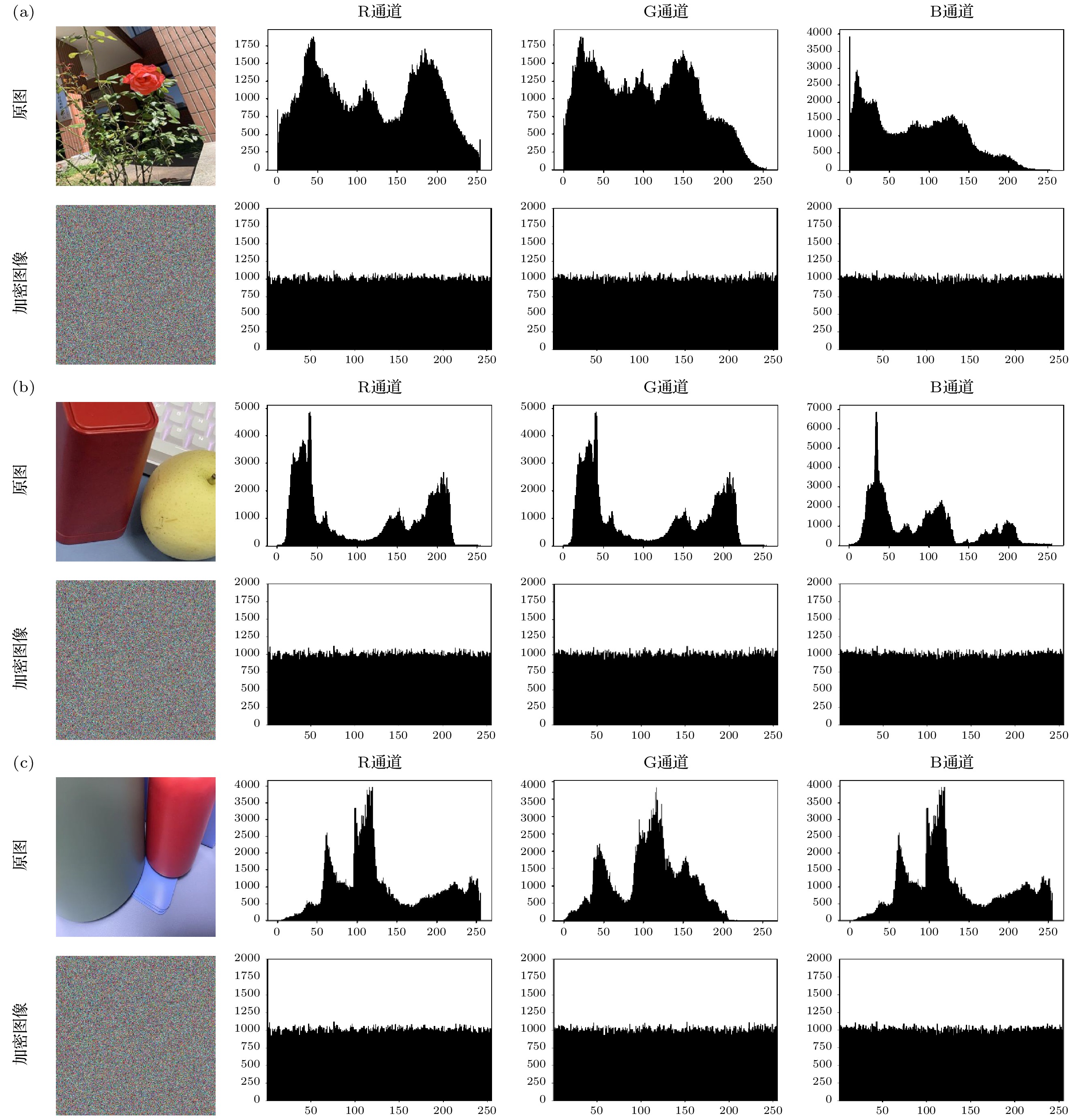
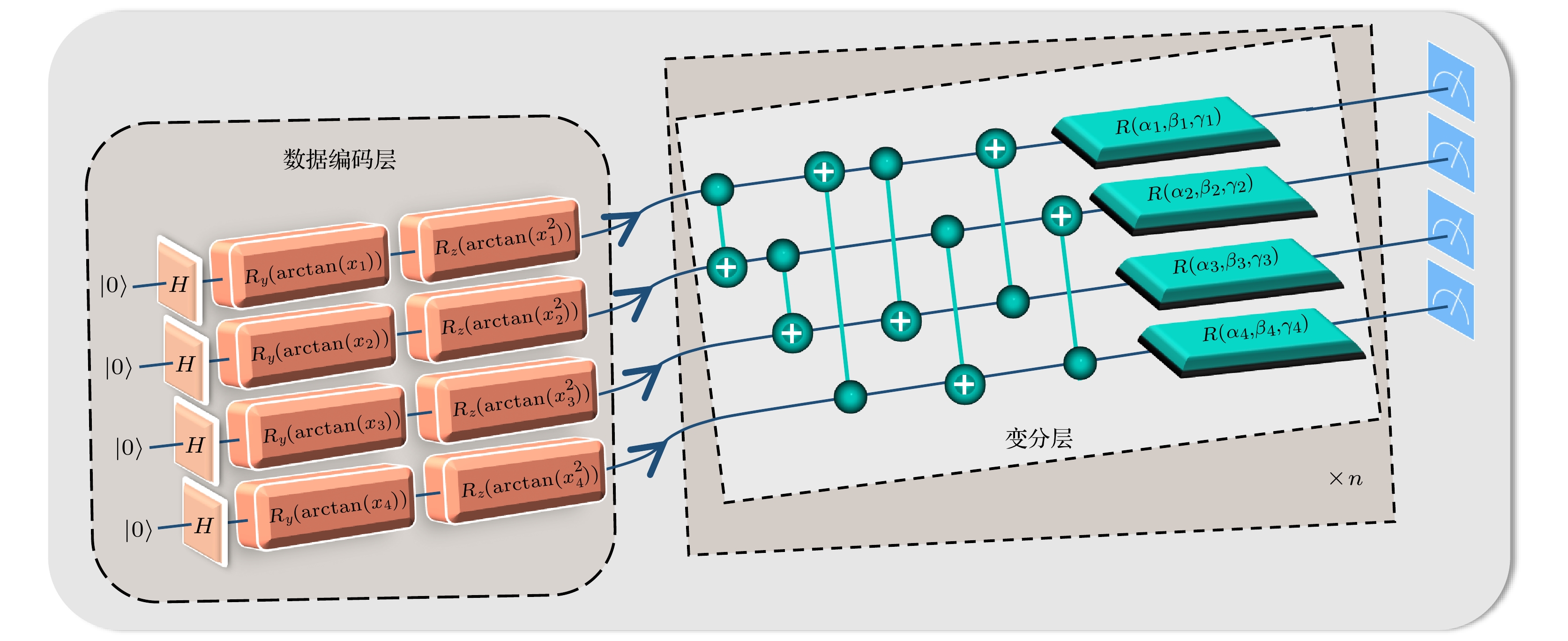
近年来, 图像信息的传输安全性已经成为互联网领域的重要研究方向. 本文提出了一种基于量子长短期记忆(quantum long-short term memory, QLSTM)网络的量子图像混沌加密方案. 结果发现, 因为QLSTM网络具有复杂的结构和较多的参数, 应用QLSTM网络对Lorenz混沌序列进行改进, 其最大Lyapunov指数比原序列提高2.5465%, 比经典长短期记忆(long-short term memory, LSTM)网络改进的序列提高0.2844%, 同时在0—1测试中结果更接近1且更稳定, 因此QLSTM网络改进的序列具备更优异的混沌性能, 更难以被预测, 提高了单一混沌系统加密的安全性. 运用NCQI (novel quantum representation of color digital images) 量子图像表示模型, 将原始图像存储为量子态形式, 利用QLSTM网络改进的序列分别控制三级径向扩散、量子广义Arnold变换和量子W变换, 改变量子图像的灰度值与像素位置, 生成最终的加密图像. 本文提出的加密方案在统计学特性测试中, 实现了RGB三通道平均信息熵均大于7.999, 像素数改变率的平均值达99.6047%, 统一平均变化强度的平均值为33.4613%, 平均相关性为0.0038等, 比其他一些传统方法具有更高的安全性, 能够抵抗常见的攻击方式.

关键词:

Abstract

In recent years, the transmission security of image information has become an important research direction in the internet field. In this work, we propose a quantum image chaos encryption scheme based on quantum long-short term memory (QLSTM) network. We find that because the QLSTM network has a complex structure and more parameters, when the QLSTM network is used to improve the Lorenz chaotic sequence, its largest Lyapunov exponent is 2.5465% higher than that of the original sequence and 0.2844% higher than that the sequence improved by the classical long-short term memory (LSTM) network, while its result is closer to 1 and more stable in the 0–1 test. The improved sequence of QLSTM network has better chaotic performance and is predicted more difficultly, which improves the security of single chaotic system encryption. The original image is stored in the form of quantum states by using the NCQI quantum image representation model, and the improved sequence of QLSTM network is used to control the three-level radial diffusion, quantum generalized Arnold transform and quantum W-transform respectively, so that the gray value and pixel position of the quantum image are changed and the final encrypted image is obtained. The encryption scheme proposed in this work obtains the average information entropy of all three channels of RGB of greater than 7.999, the average value of pixel number change rate of 99.6047%, the average value of uniform average change intensity of 33.4613%, the average correlation of 0.0038, etc. In the test of statistical properties, the encryption scheme has higher security than some other traditional methods and can resist the common attacks.

Keywords:

quantum image encryption /
quantum long-short term memory network /
chaotic systems

作者及机构信息

青岛理工大学理学院, 青岛　266520

通信作者: 邱田会, qiutianhui@qut.edu.cn

基金项目: 山东省自然科学基金(批准号: ZR2021MF049)、山东省自然科学基金联合项目(批准号: ZR2022LLZ012, ZR2021LLZ001)、山东省大学生创新创业训练计划(批准号: S202210429001)和青岛理工大学大学生科技创新项目(批准号: KJCXXM141)资助的课题

Authors and contacts

School of Science, Qingdao University of Technology, Qingdao 266520, China

Corresponding author: Qiu Tian-Hui, qiutianhui@qut.edu.cn

Funds: Project supported by the Natural Science Foundation of Shandong Province, China (Grant No. ZR2021MF049), the Joint Fund of Natural Science Foundation of Shandong Province, China (Grant Nos. ZR2022LLZ012, ZR2021LLZ001), the Innovation and Entrepreneurship Training Program for College Students of Shandong Province, China (Grant No. S202210429001), and the Scientific and Technological Innovation Project for College Students of Qingdao University of Technology, China (Grant No. KJCXXM141)

文章全文 : translate this paragraph

参考文献

[1]	Shakir H R, Mehdi S A A, Hattab A A 2022 Bull. Electr. Eng. Inform. 11 2645 Google Scholar
[2]	王一诺, 宋昭阳, 马玉林, 华南, 马鸿洋 2021 70 230302 Google Scholar Wang Y N, Song Z Y, Ma Y L, Hua N, Ma H Y 2021 Acta Phys. Sin. 70 230302 Google Scholar
[3]	Liu G Z, Li W, Fan X K, Li Z, Wang Y X, Ma H Y 2022 Entropy 24 608 Google Scholar
[4]	Zhao J B, Zhang T, Jiang J W, Fang T, Ma H Y 2022 Sci. Rep. 12 14253 Google Scholar
[5]	Li C Q, Lin D D, Lu J H 2017 IEEE MultiMedia 24 64 Google Scholar
[6]	Li C M, Yang X Z 2022 Optik 260 169042 Google Scholar
[7]	Xian Y J, Wang X Y 2021 Inf. Sci. 547 1154 Google Scholar
[8]	Zhou N R, Hu Y Q, Gong L H, Li G Y 2017 Quantum Inf. Process. 16 164 Google Scholar
[9]	Liu H, Zhao B, Huang L Q 2019 Entropy 21 343 Google Scholar
[10]	Song X H, Wang S, Abd El-Latif A A, Niu X M 2014 Quantum Inf. Process. 13 1765 Google Scholar
[11]	Akhshani A, Akhavan A, Lim S C, Hassan Z 2012 Commun. Nonlinear Sci. Numer. Simul. 17 4653 Google Scholar
[12]	Zhou N R, Huang L X, Gong L H, Zeng Q W 2020 Quantum Inf. Process. 19 284 Google Scholar
[13]	Wang X Y, Su Y I, Luo C, Nian F Z, Teng L 2022 Multimedea Tools Appl. 81 13845 Google Scholar
[14]	Gao Y J, Xie H W, Zhang J, Zhang H 2022 Physia A 598 127334 Google Scholar
[15]	Liu X B, Xiao D, Liu C 2021 Quantum Inf. Process. 20 23 Google Scholar
[16]	Jiang J W, Zhang T, Li W, Wang S M 2023 Quantum Eng. 2023 3746357 Google Scholar
[17]	Zhao J F, Wang S Y, Chang Y X, Li X F 2015 Nonlinear Dyn. 80 1721 Google Scholar
[18]	Chai X L, Fu J Y, Zhang J T, Han D J, Gan Z H 2021 Neural. Comput. Appl. 33 10371 Google Scholar
[19]	Chai X L, Gan Z H, Yuan K, Lu Y, Chen Y R 2017 Chin. Phys. B 26 020504 Google Scholar
[20]	Jiang N, Dong X, Hu H, Ji Z X, Zhang W Y 2019 Int. J. Theor. Phys. 58 979 Google Scholar
[21]	Ge B, Luo H B 2020 Int. J. Autom. Comput. 17 123 Google Scholar
[22]	Hu W B, Dong Y M 2022 J. Appl. Phys. 131 114402 Google Scholar
[23]	刘瀚扬, 华南, 王一诺, 梁俊卿, 马鸿洋 2022 71 170303 Google Scholar Liu H Y, Hua N, Wang Y N, Liang J Q, Ma H Y 2022 Acta Phys. Sin. 71 170303 Google Scholar
[24]	Faqih A, Kamanditya B, Kusumoputro B 2018 International Conference on Computer, Information and Telecommunication Systems (Alsace: IEEE) p1
[25]	Qu J Y, Zhao T, Ye M, Li J Y, Liu C 2020 Neural Process. Lett. 52 1461 Google Scholar
[26]	Yang G C, Zhu T, Wang H, Yang F B 2021 IEEE Trans. Circuits Syst. Express Briefs 69 1487 Google Scholar
[27]	Li Y T, Li Y 2022 Neurocomputing 491 321 Google Scholar
[28]	Li W, Chu P C, Liu G Z, Tian Y B, Qiu T H, Wang S M 2022 Quantum Eng. 2022 5701479 Google Scholar
[29]	Chen G M, Long S, Yuan Z D, Li W Y, Peng J F 2023 Quantum Eng. 2023 2842217 Google Scholar
[30]	Zhang Y, Ni Q 2021 Quantum Eng. 3 e75 Google Scholar
[31]	Wei S J, Chen Y H, Zhou Z R, Long G L 2022 AAPPS Bulletin 32 2 Google Scholar
[32]	Hochreiter S, Schmidhuber J 1997 Neural Comput. 9 1735 Google Scholar
[33]	Kandala A, Mezzacapo A, Temme K, Takita M, Brink M, Chow J M, Gambetta J M 2017 Nature 549 242 Google Scholar
[34]	McClean J R, Romero J, Babbush R, Aspuru-Guzik A 2016 New J. Phys. 18 023023 Google Scholar
[35]	Chen S Y C, Yang C H H, Qi J, Chen P Y, Ma X L, Goan H S 2020 IEEE Access 8 141007 Google Scholar
[36]	Schuld M, Bocharov A, Svore K M, Wiebe N 2020 Phys. Rev. A 101 032308 Google Scholar
[37]	Benedetti M, Lloyd E, Sack S, Fiorentini M 2019 Quantum Sci. Technol. 4 043001 Google Scholar
[38]	Havlicek V, Corcoles A D, Temme K, Harrow A W, Kandala A, Chow J M, Gambetta J M 2019 Nature 567 209 Google Scholar
[39]	Di Sipio R, Huang J H, Chen S Y C, Mangini S, Worring M 2022 ICASSP 2022–2022 IEEE International Conference on Acoustics, Speech and Signal Processing (Singapore: IEEE) p8612
[40]	Sang J Z, Wang S, Li Q 2017 Quantum Inf. Process. 16 42 Google Scholar
[41]	Wu Y L 2008 Electron. Sci. 21 69
[42]	Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Phys. D: Nonlinear Phenomena 16 285 Google Scholar
[43]	赵智鹏, 周双, 王兴元 2021 70 230502 Google Scholar Zhao Z P, Zhou S, Wang X Y 2021 Acta Phys. Sin. 70 230502 Google Scholar
[44]	Gottwald G A, Melbourne I 2004 Proc. R. Soc. London, Ser. A 460 603 Google Scholar
[45]	Sun K H, Liu X, Zhu C X 2010 Chin. Phys. B 19 110510 Google Scholar
[46]	Boriga R, Dascalescu A C, Priescu I 2014 Signal Process. Image Commun. 29 887 Google Scholar
[47]	Raja S S, Mohan V 2014 Int. J. Adv. Eng. Res. 8 1
[48]	Yang Y G, Tian J, Lei H, Zhou Y H, Shi W M 2016 Inf. Sci. 345 257 Google Scholar

施引文献

图 1 VQC的通用架构

Fig. 1. General architecture of VQC

下载: 全尺寸图片幻灯片

图 2 QLSTM网络的循环单元结构

Fig. 2. Cyclic cell structure of QLSTM network

下载: 全尺寸图片幻灯片

图 3 径向扩散　(a)原序列; (b)二位径向扩散; (c)四位径向扩散; (d) 八位径向扩散

Fig. 3. Radial diffusion: (a) Original sequence; (b) two-position radial diffusion; (c) four-position radial diffusion; (d) eight-position radial diffusion

下载: 全尺寸图片幻灯片

图 4 LSTM网络和QLSTM网络改进的序列的LLE曲线

Fig. 4. Largest Lyapunov exponent curves for sequences improved by LSTM network or QLSTM network

下载: 全尺寸图片幻灯片

图 5 Lorenz混沌序列、LSTM网络和QLSTM网络改进的序列的0—1测试图

Fig. 5. 0–1 test images for Lorenz chaotic sequences and sequences improved by LSTM network or QLSTM network

下载: 全尺寸图片幻灯片

图 6 加密和解密的效果图

Fig. 6. Effect of encryption and decryption

下载: 全尺寸图片幻灯片

图 7 加密前后相关性分析对比图

Fig. 7. Comparison of pixel correlation analysis before and after encryption

下载: 全尺寸图片幻灯片

图 8 加密前后直方图分析对比图

Fig. 8. Comparison of histogram analysis before and after encryption

下载: 全尺寸图片幻灯片

表 1 LLE数据对比

Table 1. Comparison of LLE data

序列来源	LLE
Henon映射	0.4192
超混沌Lorenz系统	0.3381
LSTM网络改进的序列^[43]	2.6002
QLSTM网络改进的序列	2.8846

下载: 导出CSV

表 2 0—1测试的数据对比

Table 2. Comparison of from 0–1 test data

序列来源	0—1测试
Henon映射^[45]	0.6173
超混沌Lorenz系统	0.7937
LSTM网络改进的序列^[43]	0.9218
QLSTM网络改进的序列	0.9572

下载: 导出CSV

表 3 加密图像的相关性分析

Table 3. Pixel correlation analysis of encrypted images

图像	通道	水平	垂直	对角
	R	0.0074	0.0031	0.0064
1	G	0.0039	0.0021	0.0019
	B	0.0044	0.0013	0.0058
	R	0.0006	0.0067	0.0026
2	G	0.0017	0.0049	0.0047
	B	0.0057	0.0006	0.0069
	R	0.0003	0.0052	0.0013
3	G	0.0035	0.0005	0.0042
	B	0.0090	0.0029	0.0045

下载: 导出CSV

表 4 加密图像的信息熵

Table 4. Information entropy of encrypted images

图像	R	G	B
1	7.99928	7.99973	7.99951
2	7.99935	7.99908	7.99975
3	7.99912	7.99949	7.99921

下载: 导出CSV

表 5 加密图像的NPCR与UACI

Table 5. NPCR and UACI of encrypted images.

图像	NPCR	UACI
1	99.6048%	33.4604%
2	99.6063%	33.4609%
3	99.6029%	33.4627%

下载: 导出CSV

表 6 NPCR与UACI的对比分析

Table 6. Comparison of NPCR and UACI

算法	平均NPCR	平均UACI
本文	99.6047%	33.4613%
文献[43]	99.604%	33.46%

下载: 导出CSV

map

[1]	Shakir H R, Mehdi S A A, Hattab A A 2022 Bull. Electr. Eng. Inform. 11 2645 Google Scholar
[2]	王一诺, 宋昭阳, 马玉林, 华南, 马鸿洋 2021 70 230302 Google Scholar Wang Y N, Song Z Y, Ma Y L, Hua N, Ma H Y 2021 Acta Phys. Sin. 70 230302 Google Scholar
[3]	Liu G Z, Li W, Fan X K, Li Z, Wang Y X, Ma H Y 2022 Entropy 24 608 Google Scholar
[4]	Zhao J B, Zhang T, Jiang J W, Fang T, Ma H Y 2022 Sci. Rep. 12 14253 Google Scholar
[5]	Li C Q, Lin D D, Lu J H 2017 IEEE MultiMedia 24 64 Google Scholar
[6]	Li C M, Yang X Z 2022 Optik 260 169042 Google Scholar
[7]	Xian Y J, Wang X Y 2021 Inf. Sci. 547 1154 Google Scholar
[8]	Zhou N R, Hu Y Q, Gong L H, Li G Y 2017 Quantum Inf. Process. 16 164 Google Scholar
[9]	Liu H, Zhao B, Huang L Q 2019 Entropy 21 343 Google Scholar
[10]	Song X H, Wang S, Abd El-Latif A A, Niu X M 2014 Quantum Inf. Process. 13 1765 Google Scholar
[11]	Akhshani A, Akhavan A, Lim S C, Hassan Z 2012 Commun. Nonlinear Sci. Numer. Simul. 17 4653 Google Scholar
[12]	Zhou N R, Huang L X, Gong L H, Zeng Q W 2020 Quantum Inf. Process. 19 284 Google Scholar
[13]	Wang X Y, Su Y I, Luo C, Nian F Z, Teng L 2022 Multimedea Tools Appl. 81 13845 Google Scholar
[14]	Gao Y J, Xie H W, Zhang J, Zhang H 2022 Physia A 598 127334 Google Scholar
[15]	Liu X B, Xiao D, Liu C 2021 Quantum Inf. Process. 20 23 Google Scholar
[16]	Jiang J W, Zhang T, Li W, Wang S M 2023 Quantum Eng. 2023 3746357 Google Scholar
[17]	Zhao J F, Wang S Y, Chang Y X, Li X F 2015 Nonlinear Dyn. 80 1721 Google Scholar
[18]	Chai X L, Fu J Y, Zhang J T, Han D J, Gan Z H 2021 Neural. Comput. Appl. 33 10371 Google Scholar
[19]	Chai X L, Gan Z H, Yuan K, Lu Y, Chen Y R 2017 Chin. Phys. B 26 020504 Google Scholar
[20]	Jiang N, Dong X, Hu H, Ji Z X, Zhang W Y 2019 Int. J. Theor. Phys. 58 979 Google Scholar
[21]	Ge B, Luo H B 2020 Int. J. Autom. Comput. 17 123 Google Scholar
[22]	Hu W B, Dong Y M 2022 J. Appl. Phys. 131 114402 Google Scholar
[23]	刘瀚扬, 华南, 王一诺, 梁俊卿, 马鸿洋 2022 71 170303 Google Scholar Liu H Y, Hua N, Wang Y N, Liang J Q, Ma H Y 2022 Acta Phys. Sin. 71 170303 Google Scholar
[24]	Faqih A, Kamanditya B, Kusumoputro B 2018 International Conference on Computer, Information and Telecommunication Systems (Alsace: IEEE) p1
[25]	Qu J Y, Zhao T, Ye M, Li J Y, Liu C 2020 Neural Process. Lett. 52 1461 Google Scholar
[26]	Yang G C, Zhu T, Wang H, Yang F B 2021 IEEE Trans. Circuits Syst. Express Briefs 69 1487 Google Scholar
[27]	Li Y T, Li Y 2022 Neurocomputing 491 321 Google Scholar
[28]	Li W, Chu P C, Liu G Z, Tian Y B, Qiu T H, Wang S M 2022 Quantum Eng. 2022 5701479 Google Scholar
[29]	Chen G M, Long S, Yuan Z D, Li W Y, Peng J F 2023 Quantum Eng. 2023 2842217 Google Scholar
[30]	Zhang Y, Ni Q 2021 Quantum Eng. 3 e75 Google Scholar
[31]	Wei S J, Chen Y H, Zhou Z R, Long G L 2022 AAPPS Bulletin 32 2 Google Scholar
[32]	Hochreiter S, Schmidhuber J 1997 Neural Comput. 9 1735 Google Scholar
[33]	Kandala A, Mezzacapo A, Temme K, Takita M, Brink M, Chow J M, Gambetta J M 2017 Nature 549 242 Google Scholar
[34]	McClean J R, Romero J, Babbush R, Aspuru-Guzik A 2016 New J. Phys. 18 023023 Google Scholar
[35]	Chen S Y C, Yang C H H, Qi J, Chen P Y, Ma X L, Goan H S 2020 IEEE Access 8 141007 Google Scholar
[36]	Schuld M, Bocharov A, Svore K M, Wiebe N 2020 Phys. Rev. A 101 032308 Google Scholar
[37]	Benedetti M, Lloyd E, Sack S, Fiorentini M 2019 Quantum Sci. Technol. 4 043001 Google Scholar
[38]	Havlicek V, Corcoles A D, Temme K, Harrow A W, Kandala A, Chow J M, Gambetta J M 2019 Nature 567 209 Google Scholar
[39]	Di Sipio R, Huang J H, Chen S Y C, Mangini S, Worring M 2022 ICASSP 2022–2022 IEEE International Conference on Acoustics, Speech and Signal Processing (Singapore: IEEE) p8612
[40]	Sang J Z, Wang S, Li Q 2017 Quantum Inf. Process. 16 42 Google Scholar
[41]	Wu Y L 2008 Electron. Sci. 21 69
[42]	Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Phys. D: Nonlinear Phenomena 16 285 Google Scholar
[43]	赵智鹏, 周双, 王兴元 2021 70 230502 Google Scholar Zhao Z P, Zhou S, Wang X Y 2021 Acta Phys. Sin. 70 230502 Google Scholar
[44]	Gottwald G A, Melbourne I 2004 Proc. R. Soc. London, Ser. A 460 603 Google Scholar
[45]	Sun K H, Liu X, Zhu C X 2010 Chin. Phys. B 19 110510 Google Scholar
[46]	Boriga R, Dascalescu A C, Priescu I 2014 Signal Process. Image Commun. 29 887 Google Scholar
[47]	Raja S S, Mohan V 2014 Int. J. Adv. Eng. Res. 8 1
[48]	Yang Y G, Tian J, Lei H, Zhou Y H, Shi W M 2016 Inf. Sci. 345 257 Google Scholar

[1]	杨光, 钞苏亚, 聂敏, 刘原华, 张美玲. 面向图像分类的混合量子长短期记忆神经网络构建方法. , 2023, 72(5): 058901. doi: 10.7498/aps.72.20221924
[2]	赵智鹏, 周双, 王兴元. 基于深度学习的新混沌信号及其在图像加密中的应用. , 2021, 70(23): 230502. doi: 10.7498/aps.70.20210561
[3]	方洁, 姜明浩, 安小宇, 孙军伟. 基于混沌加密和DNA编码的“一图一密”图像加密算法. , 2021, 70(7): 070501. doi: 10.7498/aps.70.20201642
[4]	温贺平, 禹思敏, 吕金虎. 基于Hadoop大数据平台和无简并高维离散超混沌系统的加密算法. , 2017, 66(23): 230503. doi: 10.7498/aps.66.230503
[5]	魏德志, 陈福集, 郑小雪. 基于混沌理论和改进径向基函数神经网络的网络舆情预测方法. , 2015, 64(11): 110503. doi: 10.7498/aps.64.110503
[6]	张玲梅, 张建文, 吴润衡. 具有对应分段系统和指数系统的新混沌系统的Hopf分岔控制研究. , 2014, 63(16): 160505. doi: 10.7498/aps.63.160505
[7]	张宏立, 宋莉莉. 基于量子粒子群算法的混沌系统参数辨识. , 2013, 62(19): 190508. doi: 10.7498/aps.62.190508
[8]	冯朝文, 蔡理, 康强, 张立森. 一种新的三维自治混沌系统. , 2011, 60(3): 030503. doi: 10.7498/aps.60.030503
[9]	刘朝华, 章兢, 张英杰, 李小花, 吴建辉. 一类不确定离散混沌系统的自抗扰控制器与小脑神经网络并行优化控制. , 2011, 60(3): 030701. doi: 10.7498/aps.60.030701
[10]	唐良瑞, 李静, 樊冰, 翟明岳. 新三维混沌系统及其电路仿真. , 2009, 58(2): 785-793. doi: 10.7498/aps.58.785
[11]	张建雄, 唐万生, 徐勇. 一个新的三维混沌系统. , 2008, 57(11): 6799-6807. doi: 10.7498/aps.57.6799
[12]	李文林, 宋运忠. 不确定非线性系统混沌反控制. , 2008, 57(1): 51-55. doi: 10.7498/aps.57.51
[13]	张敏, 胡寿松. 不确定时滞混沌系统的自适应动态神经网络控制. , 2008, 57(3): 1431-1438. doi: 10.7498/aps.57.1431
[14]	杨东升, 张化光, 李爱平, 孟子怡. 基于模糊模型的不同结构的混沌系统同步. , 2007, 56(6): 3121-3126. doi: 10.7498/aps.56.3121
[15]	罗润梓. 一个新混沌系统的脉冲控制与同步. , 2007, 56(10): 5655-5660. doi: 10.7498/aps.56.5655
[16]	牛培峰, 张君, 关新平. 基于遗传算法的统一混沌系统比例-积分-微分神经网络解耦控制研究. , 2007, 56(5): 2493-2497. doi: 10.7498/aps.56.2493
[17]	王杰智, 陈增强, 袁著祉. 一个新的混沌系统及其性质研究. , 2006, 55(8): 3956-3963. doi: 10.7498/aps.55.3956
[18]	卢志刚, 于灵慧, 柳晓菁, 高美静, 吴士昌. 克服扰动的混沌逆控制同步系统. , 2002, 51(10): 2211-2215. doi: 10.7498/aps.51.2211
[19]	关新平, 范正平, 彭海朋, 王益群. 扰动情况下基于RBF网络的混沌系统同步. , 2001, 50(9): 1670-1674. doi: 10.7498/aps.50.1670
[20]	关新平, 唐英干, 范正平, 王益群. 基于神经网络的混沌系统鲁棒自适应同步. , 2001, 50(11): 2112-2115. doi: 10.7498/aps.50.2112

计量

文章访问数: 3880
PDF下载量: 130
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板