-
数值研究了偶极玻色-爱因斯坦凝聚体(Bose-Einstein condensate, BEC) 在环形运动高斯势搅拌时的动力学行为. 当高斯势运动速度和尺寸逐渐变化时, 偶极BEC中将出现稳定层流、涡旋偶极子、Bénard–von Kármán(BvK)涡街以及混乱激发4种模式. 结果表明高斯势在偶极BEC中圆周运动时产生涡街的条件非常苛刻, 只有适当尺寸的高斯势以合适的速度运动时, 尾流中周期性脱落的具有相同旋量的涡旋对稳定的分布在内外两个圆环上, 形成BvK涡街. 在实验参数下进行系统数值计算得到了不同偶极相互作用时的相图, 讨论了偶极相互作用以及高斯势速度和尺寸对不同激发模式的影响. 通过高斯势所受拖拽力的计算, 分析了不同激发的物理学机制.
-
关键词:
- 偶极Bose-Einstein 凝聚 /
- 偶极子 /
- Bénard–von Kármán涡街
The dynamical behaviors of a dipole Bose-Einstein condensate (BEC), which is stirred by a circular moving Gaussian potential, are numerically investigated by using the mean-field theory. In this work, the atom is assumed to polarize along the z-axis. Firstly, the stationary state of the system is obtained by solving the quasi-two-dimensional Gross-Pitaevskki equation numerically under periodic boundary conditions. And then, taking the obtained ground state as the initial condition, the dynamic evolution of the dipole BEC system is studied by the time-splitting Fourier spectrum method. Four types of emissions, namely, the stable laminar flow, vortex dipole, Bénard–von Kármán (BvK) vortex street and irregular turbulence, are observed in the wake when the velocity and size of the Gaussian potential change gradually. When the velocity of the Gaussian potential reaches the critical velocity of vortex excitation, vortex pairs with opposite circulations alternately fall off from the surface of the Gaussian potential. Owing to the interaction between the vortex dipoles, the dipoles rotate around their own centers. Finally, a ring structure will be formed and exist in the wake stably for a long time. With the increase of the velocity of Gaussian potential, the period of dipoles shedding is also shortened. For the appropriate velocity and size of the Gaussian potential, the vortex pairs with the same circulations will periodically fall off from the Gaussian potential and stably distributed on the inner and outer rings, forming BvK vortex street. Our caculation reveals that the conditions for forming BvK vortex street when the dipole BEC is stirred with a circular moving potential are very restricted. When the velocity or size of the Gaussian potential continues to increase, the phenomenon of the periodic vortex pairs shedding in the wake of the Gaussian potential will disappear, and the shedding pattern of the dipole BEC becomes irregular. Using experimental parameters, the parameter ranges of different dipole interactions are obtained through numerical calculation. The influences of dipole interactions, velocity and size of the Gaussian potential on different emission are discussed. In the end, the physical mechanisms of different emissions are analyzed by calculating the drag force acting on Gaussian potential.[1] Kim I, Wu X L 2015 Phys. Rev. E 92 043011
Google Scholar
[2] Crowdy D G, Krishnamurthy V S 2017 Phys. Rev. Fluids 2 114701
Google Scholar
[3] Iima M 2019 Phys. Rev. E 99 062203
Google Scholar
[4] Ponta F L Aref H 2004 Phys. Rev. Lett. 93 084501
Google Scholar
[5] Wille R 1960 Adv. Appl. Mech. 6 273
[6] Williamson C H K 1996 Annu. Rev. Fluid. Mech. 28 477
Google Scholar
[7] Thoraval M J, Takehara K, Etoh T G, Popinet S, Ray P, Josserand C, Zaleski S, Thoroddsen S T 2012 Phys. Rev. Lett. 108 264506
Google Scholar
[8] Reeves M T, Billam T P, Anderson B P, Bradley A S 2015 Phys. Rev. Lett. 114 155302
Google Scholar
[9] Fujimoto K, Tsubota M 2010 Phys. Rev. A 82 043611
Google Scholar
[10] Fujimoto K, Tsubota M 2011 Phys. Rev. A 83 053609
Google Scholar
[11] Sasaki K, Suzuki N, Saito H 2010 Phys. Rev. Lett. 104 150404
Google Scholar
[12] Sasaki K, Suzuki N, Saito H 2011 Phys. Rev. A 83 033602
Google Scholar
[13] Stagg G W, Parker N G, Barenghi C F 2014 J. Phys. B At. Mol. Opt. Phys. 47 095304
Google Scholar
[14] Stagg G W, Allen A J, Barenghi C F, Parker N G 2015 J. Phys. Conf. Ser. 594 012044
Google Scholar
[15] Kwon W J, Moon G, Choi J, Seo S W, Shin Y 2014 Phys. Rev. A 90 063627
Google Scholar
[16] Kwon W J, Moon G, Seo S W, Shin Y 2015 Phys. Rev. A 91 053615
Google Scholar
[17] Kwon W J, Seo S W, Shin Y 2015 Phys. Rev. A 92 033613
Google Scholar
[18] Kwon W J, Kim J H, Seo S W, Shin Y 2016 Phys. Rev. Lett. 117 245301
Google Scholar
[19] Wang D S, Song S W, Xiong B, Liu W M 2011 Phys. Rev. A 84 053607
Google Scholar
[20] Wang L X, Dong B, Chen G P, Han W, Zhang S G, Shi Y R, Zhang X F 2016 Phys. Lett. A 380 435
Google Scholar
[21] Cai Y Y, Matthias R, Lei Z, Bao W Z 2010 Phys. Rev. A 82 043623
Google Scholar
[22] Yi S and You L 2000 Phys. Rev. A 61 041604
Google Scholar
[23] Xi Z H, Zhao Y Z, Shi Y R 2021 Phys. A 572 125866
Google Scholar
[24] Marinescu M andYou L 1998 Phys. Rev. Lett. 81 4596
Google Scholar
[25] Deb B and You L 2001 Phys. Rev. A 64 022717
Google Scholar
[26] Nath R, Pedri P, Santos L 2009 Phys. Rev. Lett. 102 050401
Google Scholar
[27] Giovanazzi S, Gorlitz A, Pfau T, 2002 Phys. Rev. Lett. 89 130401
Google Scholar
[28] Pedri P, Santos L 2005 Phys. Rev. Lett. 95 200404
Google Scholar
[29] Bao W, Chem L L, Lim F Y 2006 J. Comput. Phys. 219 836
Google Scholar
[30] Bao W, Wang H 2006 J. Comput. Phys. 217 612
Google Scholar
[31] Fu F F, Kong L H, Wang L, Yuan X U, Zeng Z 2018 Chin. J. Comput. Phys. 35 657
[32] Reeves M T, Anderson B P, Bradley A S 2012 Phys. Rev. A 86 053621
Google Scholar
[33] Sadler L E, Higbie J M, Leslie S R, Vengalattore M, Stamper-Kurn D M 2006 Nature 443 7109
-
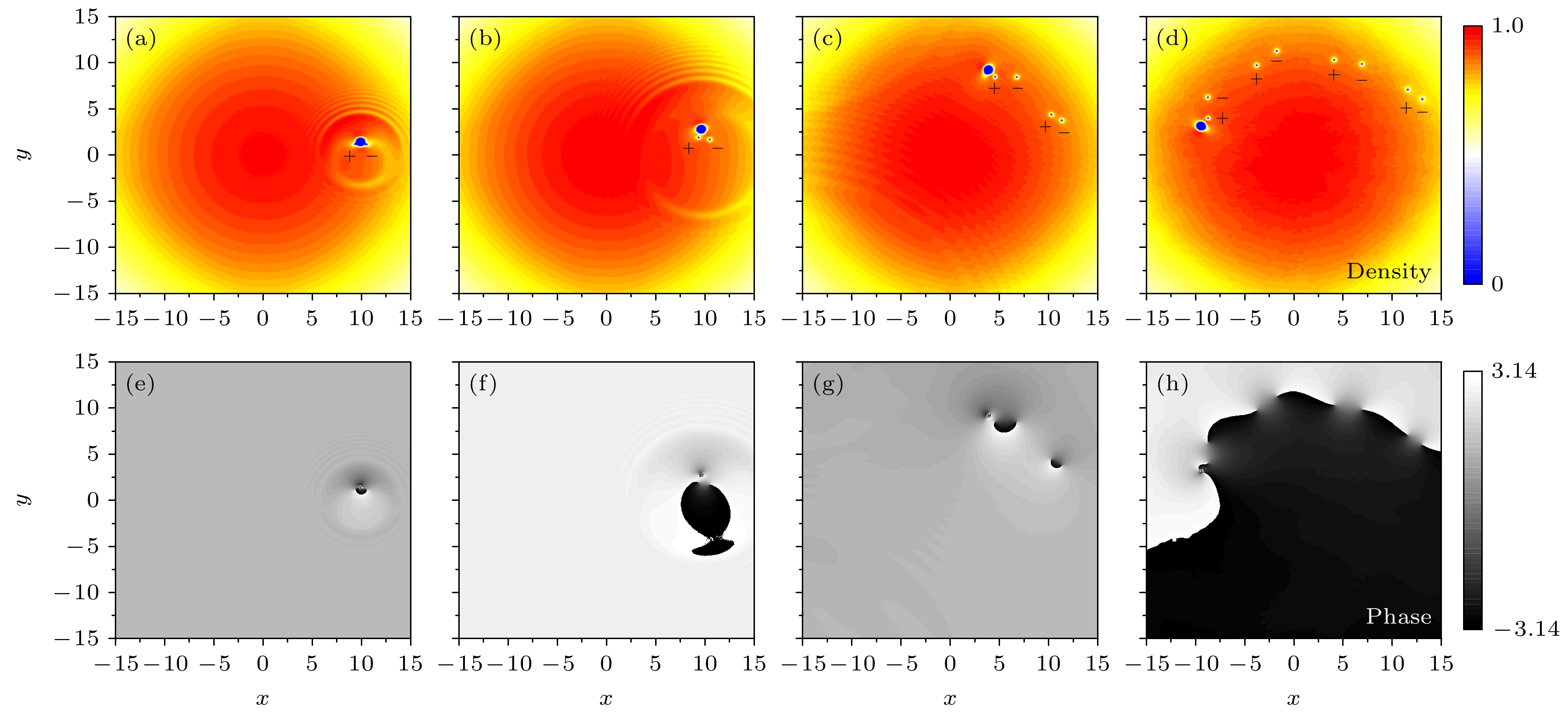
图 1 高斯势以不同速度
$ \upsilon $ 圆周运动时偶极BEC的密度分布,$ d = 1.8{a_0} $ (a)$ \upsilon = 0.6\sqrt {{{\hbar {\omega _0}} \mathord{\left/ {\vphantom {{\hbar {\omega _0}} m}} \right. } m}} $ ; (b)$ \upsilon = 0.8\sqrt {{{\hbar {\omega _0}} \mathord{\left/ {\vphantom {{\hbar {\omega _0}} m}} \right. } m}} $ ; (c)$ \upsilon = 0.9\sqrt {{{\hbar {\omega _0}} \mathord{\left/ {\vphantom {{\hbar {\omega _0}} m}} \right. } m}} $ ; (d)$ \upsilon = 1.1\sqrt {{{\hbar {\omega _0}} \mathord{\left/ {\vphantom {{\hbar {\omega _0}} m}} \right. } m}} $ Fig. 1. Density distribution of dipolar BEC condensate which is circular stirred by Gaussian potential with different velovity
$ \upsilon $ ,$ d = 1.8{a_0} $ : (a)$ \upsilon = 0.6\sqrt {{{\hbar {\omega _0}} \mathord{\left/ {\vphantom {{\hbar {\omega _0}} m}} \right. } m}} $ ; (b)$ \upsilon = 0.8\sqrt {{{\hbar {\omega _0}} \mathord{\left/ {\vphantom {{\hbar {\omega _0}} m}} \right. } m}} $ ; (c)$ \upsilon = 0.9\sqrt {{{\hbar {\omega _0}} \mathord{\left/ {\vphantom {{\hbar {\omega _0}} m}} \right. } m}} $ ; (d)$ \upsilon = 1.1\sqrt {{{\hbar {\omega _0}} \mathord{\left/ {\vphantom {{\hbar {\omega _0}} m}} \right. } m}} $ .
图 2 涡旋偶极子激发演化过程 (a)—(d)为图1(b)参数下时间
$ t = $ 30, 60, 250, 600时高斯势尾流密度分布, 观察区域为$ 15{a_0} \times 15{a_0} $ , 符号+, –分别表示点涡旋逆时针与顺时针旋转; (e)—(h)为对应时刻相图Fig. 2. Evolution of the vortex dipole emission: (a)–(d) Display density distributions of the wake after Gaussian potential at
$ t = $ 30, 60, 250, 600 for the parameters in Fig. 1(b), the field of view is$ 15{a_0} \times 15{a_0} $ , the symbols + and – denote counterclockwise and clockwise circulations of point vortices; (e)–(h) depict phase profiles corresponding to Figs. (a)–(d).
图 3 BvK涡街演化过程 (a)—(f)为图1(c)参数下时间
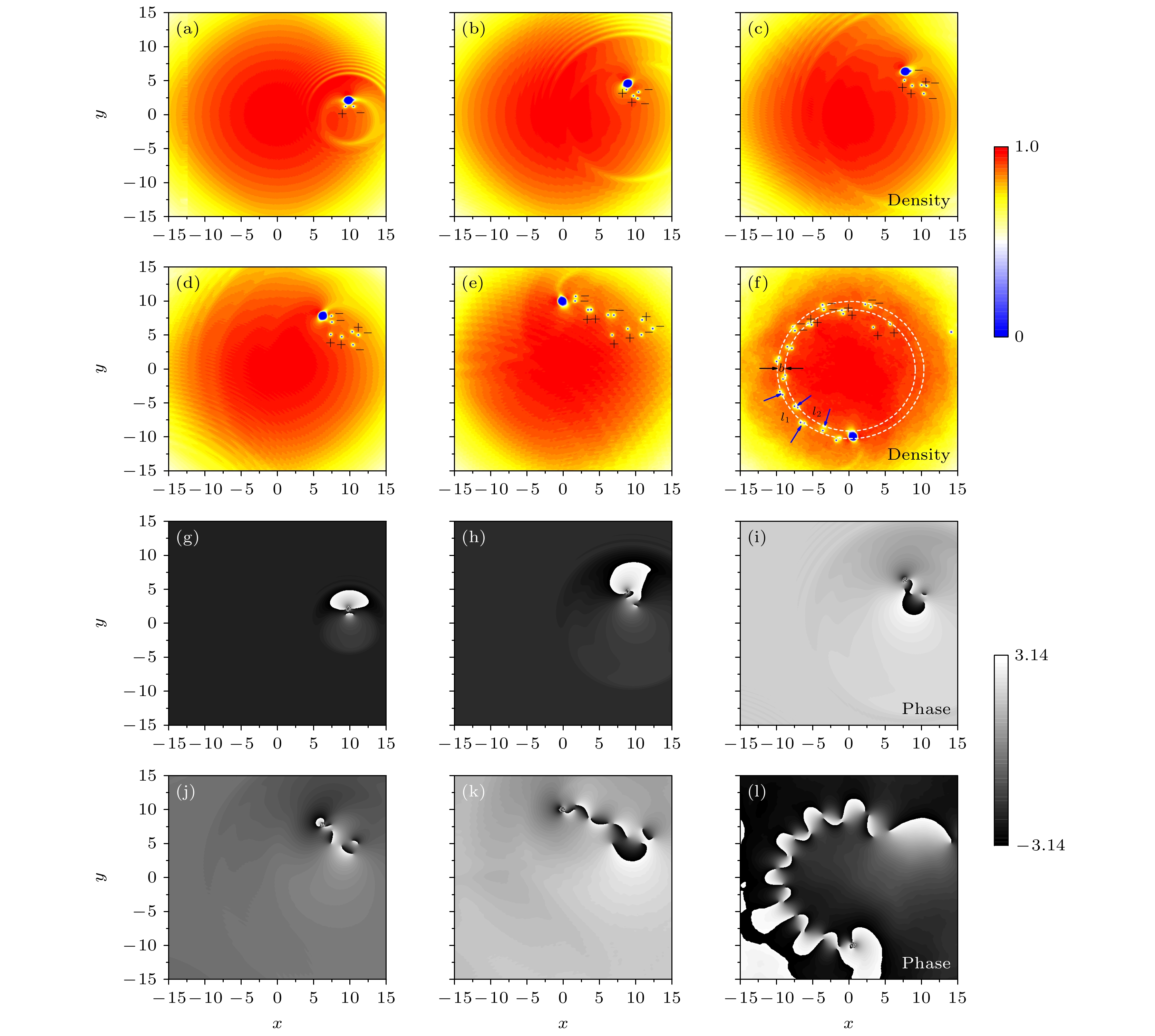
$ t = $ 40, 90, 130, 170, 300, 900时高斯势尾流密度分布, 观察区域为$ 15{a_0} \times 15{a_0} $ , (f)中白色虚线圆环分别表示内外两列涡旋对阵列稳定出现的位置; (g)—(l)为对应时刻相图Fig. 3. Evolution of the BvK vortex street: (a)–(f) Display density distributions of the wake after Gaussian potential at
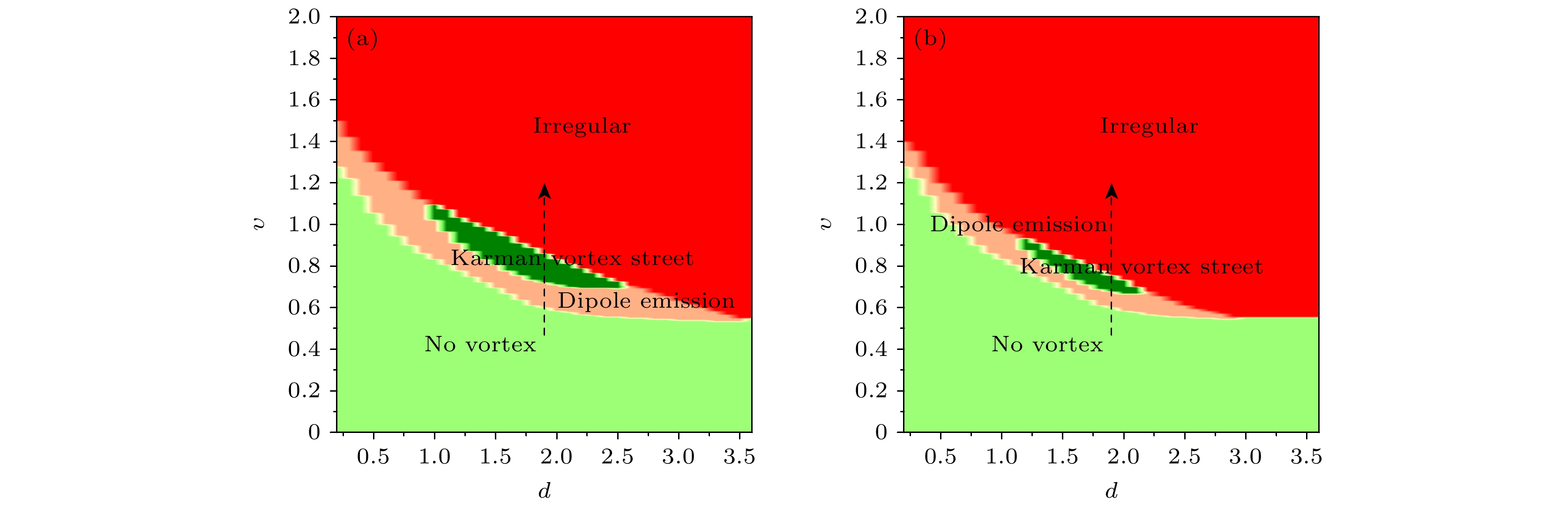
$ t = $ 40, 90, 130, 170, 300, 900 for the parameters in Fig. 1(c), the field of view is$ 15{a_0} \times 15{a_0} $ , the white dotted ring in (f) represent the position where the inner and outer vortex pair arrays appear stably; (g)–(l) depict phase profiles corresponding to Figs. (a)–(f).
图 4 不同偶极相互作用下BEC各种激发模式的参数区间 (a) g = 100,
$ {a_{{\text{dd}}}} $ = 20; (b) g = 100,$ {a_{{\text{dd}}}} $ = 40. 黑色虚线箭头表示图1中速度$ \upsilon $ 的变化Fig. 4. Parameter regimes of different vortex emission in Dipole BEC under different dipole interactions: (a) g = 100,
$ {a_{{\text{dd}}}} $ = 20; (b) g = 100,$ {a_{{\text{dd}}}} $ = 40. The black dotted arrows indicate the change of$ \upsilon $ used in Fig. 1.
图 5 高斯势所受拖拽力随时间的变化, 蓝色实线, 红色虚线分别表示拖拽力的切向和法向分量, (a)—(c)各参数分别与图1(b)—(d)对应
Fig. 5. Evolution of the normalized drag force acting on the Gaussian potential. The solid blue lines and dotted red lines show the tangential and normal components of the drag force. The parameters used in (a)–(c) are the same as those in Fig.1(b)–(d), respectively.
-
[1] Kim I, Wu X L 2015 Phys. Rev. E 92 043011
Google Scholar
[2] Crowdy D G, Krishnamurthy V S 2017 Phys. Rev. Fluids 2 114701
Google Scholar
[3] Iima M 2019 Phys. Rev. E 99 062203
Google Scholar
[4] Ponta F L Aref H 2004 Phys. Rev. Lett. 93 084501
Google Scholar
[5] Wille R 1960 Adv. Appl. Mech. 6 273
[6] Williamson C H K 1996 Annu. Rev. Fluid. Mech. 28 477
Google Scholar
[7] Thoraval M J, Takehara K, Etoh T G, Popinet S, Ray P, Josserand C, Zaleski S, Thoroddsen S T 2012 Phys. Rev. Lett. 108 264506
Google Scholar
[8] Reeves M T, Billam T P, Anderson B P, Bradley A S 2015 Phys. Rev. Lett. 114 155302
Google Scholar
[9] Fujimoto K, Tsubota M 2010 Phys. Rev. A 82 043611
Google Scholar
[10] Fujimoto K, Tsubota M 2011 Phys. Rev. A 83 053609
Google Scholar
[11] Sasaki K, Suzuki N, Saito H 2010 Phys. Rev. Lett. 104 150404
Google Scholar
[12] Sasaki K, Suzuki N, Saito H 2011 Phys. Rev. A 83 033602
Google Scholar
[13] Stagg G W, Parker N G, Barenghi C F 2014 J. Phys. B At. Mol. Opt. Phys. 47 095304
Google Scholar
[14] Stagg G W, Allen A J, Barenghi C F, Parker N G 2015 J. Phys. Conf. Ser. 594 012044
Google Scholar
[15] Kwon W J, Moon G, Choi J, Seo S W, Shin Y 2014 Phys. Rev. A 90 063627
Google Scholar
[16] Kwon W J, Moon G, Seo S W, Shin Y 2015 Phys. Rev. A 91 053615
Google Scholar
[17] Kwon W J, Seo S W, Shin Y 2015 Phys. Rev. A 92 033613
Google Scholar
[18] Kwon W J, Kim J H, Seo S W, Shin Y 2016 Phys. Rev. Lett. 117 245301
Google Scholar
[19] Wang D S, Song S W, Xiong B, Liu W M 2011 Phys. Rev. A 84 053607
Google Scholar
[20] Wang L X, Dong B, Chen G P, Han W, Zhang S G, Shi Y R, Zhang X F 2016 Phys. Lett. A 380 435
Google Scholar
[21] Cai Y Y, Matthias R, Lei Z, Bao W Z 2010 Phys. Rev. A 82 043623
Google Scholar
[22] Yi S and You L 2000 Phys. Rev. A 61 041604
Google Scholar
[23] Xi Z H, Zhao Y Z, Shi Y R 2021 Phys. A 572 125866
Google Scholar
[24] Marinescu M andYou L 1998 Phys. Rev. Lett. 81 4596
Google Scholar
[25] Deb B and You L 2001 Phys. Rev. A 64 022717
Google Scholar
[26] Nath R, Pedri P, Santos L 2009 Phys. Rev. Lett. 102 050401
Google Scholar
[27] Giovanazzi S, Gorlitz A, Pfau T, 2002 Phys. Rev. Lett. 89 130401
Google Scholar
[28] Pedri P, Santos L 2005 Phys. Rev. Lett. 95 200404
Google Scholar
[29] Bao W, Chem L L, Lim F Y 2006 J. Comput. Phys. 219 836
Google Scholar
[30] Bao W, Wang H 2006 J. Comput. Phys. 217 612
Google Scholar
[31] Fu F F, Kong L H, Wang L, Yuan X U, Zeng Z 2018 Chin. J. Comput. Phys. 35 657
[32] Reeves M T, Anderson B P, Bradley A S 2012 Phys. Rev. A 86 053621
Google Scholar
[33] Sadler L E, Higbie J M, Leslie S R, Vengalattore M, Stamper-Kurn D M 2006 Nature 443 7109
-
[1] 邵凯花, 席忠红, 席保龙, 涂朴, 王青青, 马金萍, 赵茜, 石玉仁. 双组分玻色-爱因斯坦凝聚体中PT对称势下的异步量子Kármán涡街. , 2024, 73(11): 110501. doi: 10.7498/aps.73.20232003 [2] 于术娟, 刘竹琴, 李雁鹏. 对称分子 ${\text{H}}_{\text{2}}^{\text{ + }}$ 在强短波激光场中高次谐波椭偏率性质的研究. , 2023, 72(4): 043101. doi: 10.7498/aps.72.20221946[3] 席忠红, 杨雪滢, 唐娜, 宋琳, 李晓霖, 石玉仁. 偶极玻色-爱因斯坦凝聚体在类方势阱中的Bénard-von Kármán涡街. , 2018, 67(23): 230501. doi: 10.7498/aps.67.20181604 [4] 曹万强, 刘培朝, 陈勇, 潘瑞琨, 祁亚军. 铁电体中偶极子的滞后对剩余极化的影响. , 2016, 65(13): 137701. doi: 10.7498/aps.65.137701 [5] 李雁鹏, 于术娟, 陈彦军. 不同取向角下CO2分子波长依赖的垂直谐波效率. , 2015, 64(18): 183102. doi: 10.7498/aps.64.183102 [6] 陈科, 尤云祥, 胡天群. 圆管潜射流生成偶极子涡特性实验. , 2013, 62(19): 194702. doi: 10.7498/aps.62.194702 [7] 王文元, 杨阳, 蒙红娟, 马莹, 祁鹏堂, 马云云, 段文山. Fermi超流气体在unitarity区域和Bose-Einstein 凝聚区域的自俘获现象研究. , 2012, 61(10): 100301. doi: 10.7498/aps.61.100301 [8] 葛德彪, 魏兵. 互易定理计算分层半空间上方任意取向偶极子的远区场. , 2012, 61(5): 050301. doi: 10.7498/aps.61.050301 [9] 高曾辉, 何德, 吕百达. 光涡旋偶极子经半屏衍射后的演化. , 2011, 60(7): 074209. doi: 10.7498/aps.60.074209 [10] 陈科, 尤云祥, 胡天群, 朱敏慧, 王小青. 分层流体中移动动量源生成准二维偶极子涡街特性实验. , 2011, 60(2): 024702. doi: 10.7498/aps.60.024702 [11] 徐岩, 樊炜, 陈兵, 李照鑫. S=1旋量Bose-Einstein凝聚中制备双模最大纠缠态方案. , 2011, 60(6): 060305. doi: 10.7498/aps.60.060305 [12] 严冬, 宋立军. 周期脉冲撞击的两分量Bose-Einstein凝聚系统的单粒子相干和对纠缠. , 2010, 59(10): 6832-6836. doi: 10.7498/aps.59.6832 [13] 栗生长, 段文山. 两分量Bose-Einstein凝聚体的非线性Ramsey干涉. , 2009, 58(7): 4396-4401. doi: 10.7498/aps.58.4396 [14] 吴重庆, 赵 爽. 电偶极子源定位问题的研究. , 2007, 56(9): 5180-5184. doi: 10.7498/aps.56.5180 [15] 王龙海, 于 军, 王耘波, 彭 刚, 刘 锋, 高峻雄. 基于静态电滞回线的铁电电容模型. , 2005, 54(2): 949-954. doi: 10.7498/aps.54.949 [16] 姜泽辉, 许素娟, 陈 唯, 门守强, 陆坤权. 像偶极子法计算导体颗粒簇团的偶极矩. , 2000, 49(8): 1457-1463. doi: 10.7498/aps.49.1457 [17] 谭维翰, 闫珂柱. 解有排斥相互作用中性原子的Bose-Einstein凝聚的一般方法. , 1999, 48(11): 1983-1991. doi: 10.7498/aps.48.1983 [18] 戴启润, 赵树松. Bose-Einstein关联与Q-vKv(Q)分布. , 1995, 44(8): 1203-1209. doi: 10.7498/aps.44.1203 [19] 杨正举. 应变晶体的弹性偶极子模型. , 1983, 32(11): 1416-1425. doi: 10.7498/aps.32.1416 [20] 张恩虬. 关于热电子发射理论的评述(Ⅱ)——单原子层和偶极子理论. , 1974, 23(5): 53-63. doi: 10.7498/aps.23.53
下载:
计量
- 文章访问数: 3061
- PDF下载量: 60
- 被引次数: 0
