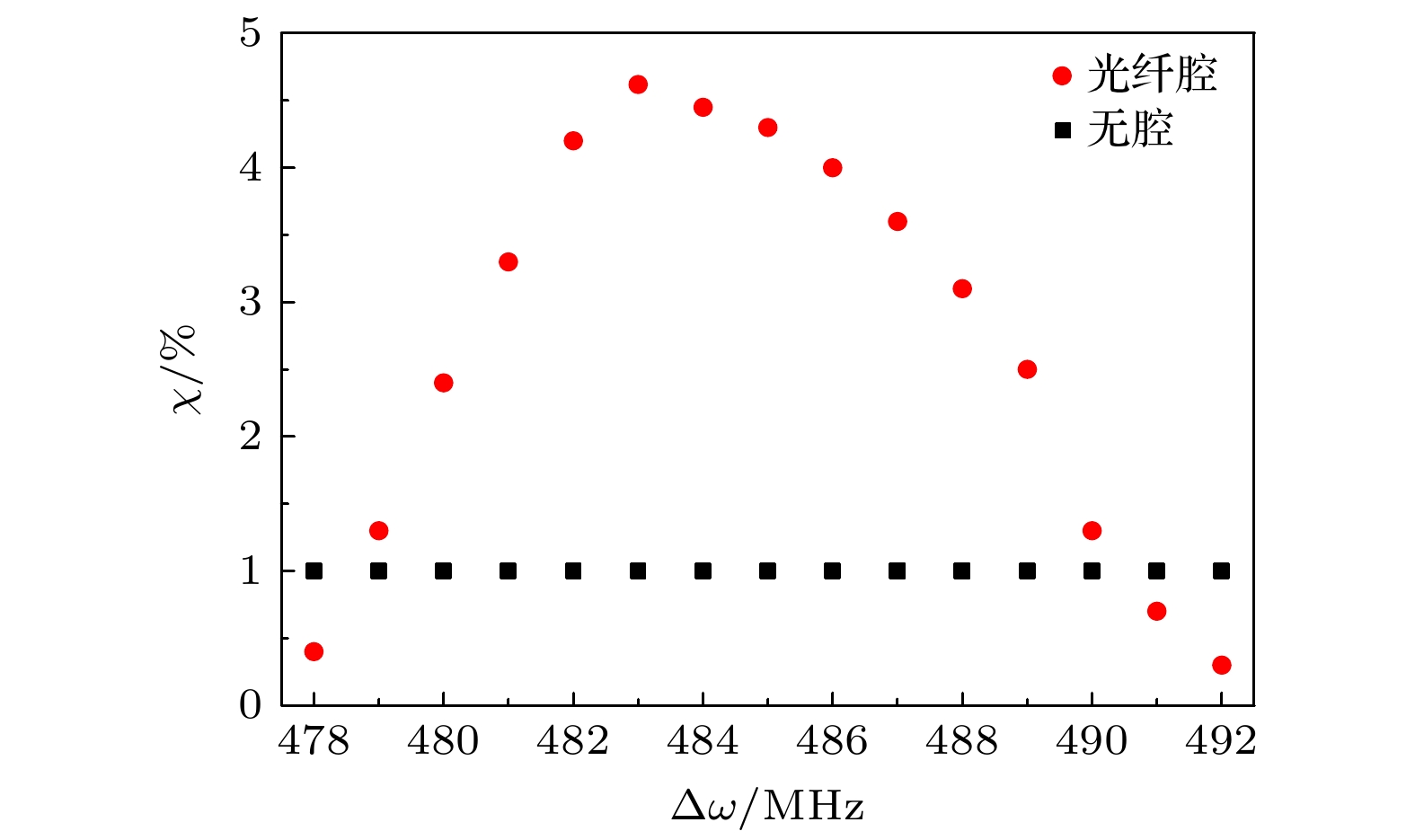
-
利用原子系综中的Duan-Lukin-Cirac-Zoller (DLCZ)过程可产生光与原子记忆(自旋波)量子纠缠, 该纠缠可作为量子中继的重要元件. 随着量子信息研究的深入发展, 人们对量子信息存储其灵活多样性、可控性等方面提出更高的要求. 本文在冷原子系综中演示了一种基于DLCZ过程的光纤腔增强且高保真度的光学存储方案, 即将87Rb原子系综放于设计的光纤腔中, 通过光纤腔增强“写出”和“读出”光子与原子系综的耦合实现自旋波量子信息的有效恢复, 同时具有较高的保真度. 观察到有腔且锁定的情况下斯托克斯光子产生概率比无腔时增加4.6倍, 原子自旋波读出效率增加1.6倍, 实验实现22%的读出效率并具有92%的量子态保真度, 该读出效率对应一个40%的本质读出效率. 这种高度可恢复、高量子态保真度的原子-光子纠缠源, 可为未来长距离量子通信及广域大规模量子网络构建的实现提供另一种有效的途径.
-
关键词:
- Duan-Lukin-Cirac-Zoller方案 /
- 光纤腔 /
- 腔增强存储 /
- 高保真度
Entanglement between a photon and an atomic memory is an important tool for quantum repeater research. By using the Duan-Lukin-Cirac-Zoller (DLCZ) process in the atomic ensemble, quantum entanglement between a photon and an atomic spin-wave memory is produced. With the further development of quantum information, it is necessary to put forward higher requirements for the diversity and controllability of quantum memory. In this work, we experimentally demonstrate an optical memory in cold atomic ensemble with enhanced fiber-cavity and high-fidelity optical memory for the first time. We design a fiber cavity to enhance the coupling strength between light and atomic ensemble and then improve the optical retrieval efficiency. Unfortunately, the use of fiber cavity may lead to the decrease of fidelity. Therefore, it is vital to realize high fidelity in the enhanced fiber-cavity optical memory. The cavity has a round-trip length of 1.5 m and a free spectral range of 190 MHz. The finesse (F) of the cavity with the cold atoms in the DLCZ condition is measured to be$ \sim $ 18. In cavity-enhanced DLCZ scheme, we use a fiber cavity instead of a stationary cavity. If a stationary cavity is used, the signal light will be reflected by the end mirror of the cavity and then pass back through the atoms. The storage of the backward signal light will generate a short-wavelength spin wave and then lead to a rapid decoherence of the memory. When cavity is locked by using the PDH frequency locking technique, we observe that the production probability of the Stokes photons is increased by 4.6 times higher than that without cavity and retrieval efficiency of atomic spin wave is increased by 1.6 times that without cavity due to the optical cavity enhancement effect. The presented cavity-enhanced storage shows that the retrieval efficiency is$ \sim $ 22%, corresponding to an intrinsic retrieval efficiency of$ \sim $ 40%, at the same time the fidelity of the quantum state is$ \sim $ 92%. The accomplishment of this project will provide another effective way of realizing long-distance quantum communication and large-scale quantum network construction.-
Keywords:
- Duan-Lukin-Cirac-Zoller protocol /
- iber cavity /
- cavity-enhanced optical memory /
- high fidelity
[1] Kimble H J 2008 Nature 453 1023
Google Scholar
[2] Wehner S, Elkouss D, Hanson R 2018 Science 362 eaam9288
Google Scholar
[3] Duan L M, Lukin M D, Cirac J I, Zoller P 2001 Nature 414 413
Google Scholar
[4] Sangouard N, Simon C, de Riedmatten H, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[5] Simon C 2017 Nature Photon. 11 678
Google Scholar
[6] Matsukevich D N, Chaneliere T, Bhattacharya M, Lan S Y, Jenkins S D, Kennedy T A B, Kuzmich A 2005 Phys. Rev. Lett. 95 040405
Google Scholar
[7] de Riedmatten H, Laurat J, Chou C W, Schomburg E W, Felinto D, Kimble H J 2006 Phys. Rev. Lett. 97 113603
Google Scholar
[8] Chen S, Chen Y A, Zhao B, Yuan Z S, Schmiedmayer J, Pan J W 2007 Phys. Rev. Lett. 99 180505
Google Scholar
[9] Ding D S, Zhang W, Zhou Z Y, Shi S, Shi B S, Guo G C 2015 Nature Photon. 9 332
Google Scholar
[10] Wu Y L, Tian L, Xu Z X, Ge W, Chen L R, Li S J, Yuan H X, Wen Y F, Wang H, Xie C D, Peng K C 2016 Phys. Rev. A 93 052327
Google Scholar
[11] Zhao B, Chen Z B, Chen Y A, Schmiedmayer J, Pan J W, 2007 Phys. Rev. Lett. 98 240502
Google Scholar
[12] Chen Z B, Zhao B, Chen Y A, Schmiedmayer J, Pan J W 2007 Phys. Rev. A 76 022329
Google Scholar
[13] Bussieres F, Sangouard N, Afzelius M, de Riedmatten H, Simon C, Tittel W 2013 J. Mod. Opt. 60 1519
Google Scholar
[14] Jiang L, Taylor J M, Lukin M D 2007 Phys. Rev. A 76 012301
Google Scholar
[15] Vernaz-Gris P, Huang K, Cao M, Sheremet A S, Laurat J 2018 Nat. Commun. 9 363
Google Scholar
[16] Wang Y, Li J, Zhang S, Su K, Zhou Y, Liao K, Du S, Yan H, Zhu S L 2019 Nature Photon. 13 346
Google Scholar
[17] Yang S J, Wang X J, Bao X H, Pan J W 2016 Nature Photon. 10 381
Google Scholar
[18] Bao X H, Reingruber A, Dietrich P, Rui J, Duck A, Strassel T, Li L, Liu N L, Zhao B, Pan J W 2012 Nature Phys. 8 517
Google Scholar
[19] Yang S J, Wang X J, Li J, Rui J, Bao X H, J W Pan 2015 Phys. Rev. Lett. 114 210501
Google Scholar
[20] Hsiao Y F, Tsai P J, Chen H S, Lin S X, Hung C C, Lee C H, Chen Y H, Chen Y F, Yu I A, Chen Y C 2018 Phys. Rev. Lett. 120 183602
Google Scholar
[21] Afzelius M, Simon C 2010 Phys. Rev. A 82 022310
Google Scholar
[22] Sabooni M, Li Q, Kröll S, Rippe L 2013 Phys. Rev. Lett. 110 133604
Google Scholar
[23] Jobez P, Usmani I, Timoney N, Laplane C, Gisin N, Afzelius M 2014 New J. Phys. 16 083005
Google Scholar
[24] Heller L, Farrera P, Heinze G, de Riedmatten H 2020 Phys. Rev. Lett. 124 210504
Google Scholar
[25] 袁亮, 温亚飞, 李雅, 刘超, 李淑静, 徐忠孝, 王海 2021 70 070302
Google Scholar
Yuan L, Wen Y F, Li Y, Liu C, Li S J, Xu Z X, Wang H 2021 Acta Phys. Sin. 70 070302
Google Scholar
[26] Wen Y F, Zhou P, Xu Z X, Yuan L, Wang M J, Wang S Z, Chen L R, Wang H 2020 Opt. Express 28 360
Google Scholar
[27] Nikolett N, Donald W, Shinya K, Scott P, Takao A 2020 Phys. Rev. Appl. 13 064010
Google Scholar
[28] Zeeb S, Noh C, Parkins A S, Carmichael H J 2015 Phys. Rev. A 91 023829
Google Scholar
[29] Huang H, Lehmann K K 2007 Opt. Express 15 8745
Google Scholar
[30] 周继阳, 李强, 许金时, 李传锋, 郭光灿 2022 71 060303
Google Scholar
Zhou J Y, Li Q, Xu J S, Li C F, Guo G G 2022 Acta Phys. Sin. 71 060303
Google Scholar
[31] Wen Y F, Zhou P, Xu Z X, Yuan L, Zhang H Y, Wang S Z, Tian L, Li S J, Wang H 2019 Phys. Rev. A 100 012342
Google Scholar
[32] Tian L, Xu Z X, Chen L R, Ge W, Yuan H X, Wen Y F, Wang S Z, Li S J, Wang H 2017 Phys. Rev. Lett. 119 130505
Google Scholar
[33] White A G, James D F V, Eberhard P H, Kwiat P G 1999 Phys. Rev. Lett. 83 3103
Google Scholar
[34] James D F V, Kwiat P G, Munro W J, White A G 2001 Phys. Rev. A 64 052312
Google Scholar
-
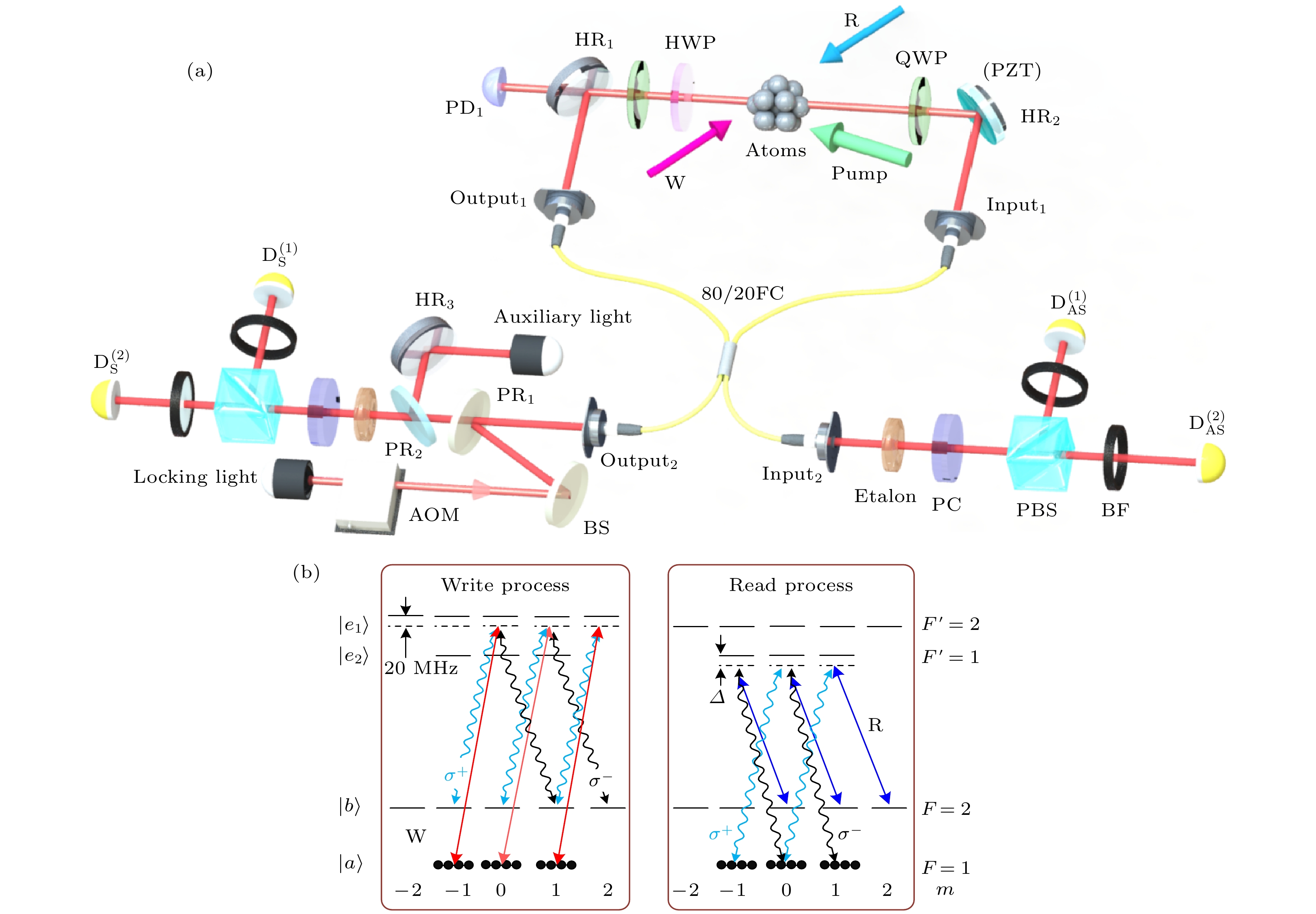
图 1 (a) 实验装置图; (b) 87Rb原子实验能级图(PBS, 偏振分束棱镜; D(PD1), 单光子探测器(探测器); HWP, 1/2波片; QWP, 1/4波片; Etalon, F-P标准具滤波器; HR1—HR3, 高反射镜; BF, 窄带滤波片; BS, 非偏振分束镜; PR, 部分反射镜; 80/20 FC, 分光比80∶20光纤耦合器; AOM, 声光调制器; PC, 相位补偿器;
$ {\sigma ^ + } $ ($ {\sigma ^ - } $ )为右旋(左旋)圆偏振的出射光子; W(R)为写(读)光场)Fig. 1. (a) Experimental setup; (b) experimental energy levels of 87Rb atomic (PBS, polarization beam splitter; D(PD1), single photon detector (detector); HWP, half wave plate; QWP, quarter wave plate; Etalon, F-P Etalon; HR1—HR3, highly reflecting mirrors; BF, bandpass filter; BS, nonpolarizing beamsplitter; PR, partially reflecting mirror; 80/20 FC, 80∶20 fiber coupler; AOM, acousto optic modulator; PC, phase compensators;
$ {\sigma ^ + } $ ($ {\sigma ^ - } $ ) represents right (left) polarization of emitted photon; W(R) represents writing (reading) field).
图 3 激发率随锁腔光失谐变化
Fig. 3. Excitation probability as the function of the detuning of locking light beam.
图 4 读出效率随存储时间的变化测量
Fig. 4. Measurement of retrieval efficiency as a function of the storage time.
图 5 χ = 1%, 有无光纤腔时Bell参数随存储时间变化
Fig. 5. Measured Bell parameter with and without the cavity as a function of storage time for χ = 1%.
图 6 利用最大似然近似方法重构双光子偏振纠缠态密度矩阵的实部与虚部(
${{\chi }} = 1{\text{%}} $ )Fig. 6. Real and imaginary parts of the reconstructed density matrices of the two-photon entangled state (
${{\chi }} = 1{\text{%}} $ ). -
[1] Kimble H J 2008 Nature 453 1023
Google Scholar
[2] Wehner S, Elkouss D, Hanson R 2018 Science 362 eaam9288
Google Scholar
[3] Duan L M, Lukin M D, Cirac J I, Zoller P 2001 Nature 414 413
Google Scholar
[4] Sangouard N, Simon C, de Riedmatten H, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[5] Simon C 2017 Nature Photon. 11 678
Google Scholar
[6] Matsukevich D N, Chaneliere T, Bhattacharya M, Lan S Y, Jenkins S D, Kennedy T A B, Kuzmich A 2005 Phys. Rev. Lett. 95 040405
Google Scholar
[7] de Riedmatten H, Laurat J, Chou C W, Schomburg E W, Felinto D, Kimble H J 2006 Phys. Rev. Lett. 97 113603
Google Scholar
[8] Chen S, Chen Y A, Zhao B, Yuan Z S, Schmiedmayer J, Pan J W 2007 Phys. Rev. Lett. 99 180505
Google Scholar
[9] Ding D S, Zhang W, Zhou Z Y, Shi S, Shi B S, Guo G C 2015 Nature Photon. 9 332
Google Scholar
[10] Wu Y L, Tian L, Xu Z X, Ge W, Chen L R, Li S J, Yuan H X, Wen Y F, Wang H, Xie C D, Peng K C 2016 Phys. Rev. A 93 052327
Google Scholar
[11] Zhao B, Chen Z B, Chen Y A, Schmiedmayer J, Pan J W, 2007 Phys. Rev. Lett. 98 240502
Google Scholar
[12] Chen Z B, Zhao B, Chen Y A, Schmiedmayer J, Pan J W 2007 Phys. Rev. A 76 022329
Google Scholar
[13] Bussieres F, Sangouard N, Afzelius M, de Riedmatten H, Simon C, Tittel W 2013 J. Mod. Opt. 60 1519
Google Scholar
[14] Jiang L, Taylor J M, Lukin M D 2007 Phys. Rev. A 76 012301
Google Scholar
[15] Vernaz-Gris P, Huang K, Cao M, Sheremet A S, Laurat J 2018 Nat. Commun. 9 363
Google Scholar
[16] Wang Y, Li J, Zhang S, Su K, Zhou Y, Liao K, Du S, Yan H, Zhu S L 2019 Nature Photon. 13 346
Google Scholar
[17] Yang S J, Wang X J, Bao X H, Pan J W 2016 Nature Photon. 10 381
Google Scholar
[18] Bao X H, Reingruber A, Dietrich P, Rui J, Duck A, Strassel T, Li L, Liu N L, Zhao B, Pan J W 2012 Nature Phys. 8 517
Google Scholar
[19] Yang S J, Wang X J, Li J, Rui J, Bao X H, J W Pan 2015 Phys. Rev. Lett. 114 210501
Google Scholar
[20] Hsiao Y F, Tsai P J, Chen H S, Lin S X, Hung C C, Lee C H, Chen Y H, Chen Y F, Yu I A, Chen Y C 2018 Phys. Rev. Lett. 120 183602
Google Scholar
[21] Afzelius M, Simon C 2010 Phys. Rev. A 82 022310
Google Scholar
[22] Sabooni M, Li Q, Kröll S, Rippe L 2013 Phys. Rev. Lett. 110 133604
Google Scholar
[23] Jobez P, Usmani I, Timoney N, Laplane C, Gisin N, Afzelius M 2014 New J. Phys. 16 083005
Google Scholar
[24] Heller L, Farrera P, Heinze G, de Riedmatten H 2020 Phys. Rev. Lett. 124 210504
Google Scholar
[25] 袁亮, 温亚飞, 李雅, 刘超, 李淑静, 徐忠孝, 王海 2021 70 070302
Google Scholar
Yuan L, Wen Y F, Li Y, Liu C, Li S J, Xu Z X, Wang H 2021 Acta Phys. Sin. 70 070302
Google Scholar
[26] Wen Y F, Zhou P, Xu Z X, Yuan L, Wang M J, Wang S Z, Chen L R, Wang H 2020 Opt. Express 28 360
Google Scholar
[27] Nikolett N, Donald W, Shinya K, Scott P, Takao A 2020 Phys. Rev. Appl. 13 064010
Google Scholar
[28] Zeeb S, Noh C, Parkins A S, Carmichael H J 2015 Phys. Rev. A 91 023829
Google Scholar
[29] Huang H, Lehmann K K 2007 Opt. Express 15 8745
Google Scholar
[30] 周继阳, 李强, 许金时, 李传锋, 郭光灿 2022 71 060303
Google Scholar
Zhou J Y, Li Q, Xu J S, Li C F, Guo G G 2022 Acta Phys. Sin. 71 060303
Google Scholar
[31] Wen Y F, Zhou P, Xu Z X, Yuan L, Zhang H Y, Wang S Z, Tian L, Li S J, Wang H 2019 Phys. Rev. A 100 012342
Google Scholar
[32] Tian L, Xu Z X, Chen L R, Ge W, Yuan H X, Wen Y F, Wang S Z, Li S J, Wang H 2017 Phys. Rev. Lett. 119 130505
Google Scholar
[33] White A G, James D F V, Eberhard P H, Kwiat P G 1999 Phys. Rev. Lett. 83 3103
Google Scholar
[34] James D F V, Kwiat P G, Munro W J, White A G 2001 Phys. Rev. A 64 052312
Google Scholar
下载:
计量
- 文章访问数: 3858
- PDF下载量: 130
- 被引次数: 0
