一维异质结构的瞬态热整流效应

赵建宁; 魏东; 吕国正; 王子成; 刘冬欢

doi:10.7498/aps.72.20222085

摘要

瞬态条件下的热整流有广阔的实际应用背景, 本文建立了一维板状复合结构热整流器的瞬态热整流模型, 并利用有限元方法研究了不同恒定热阻、不同界面间隙、周期性温度边界条件以及材料和几何参数对瞬态热整流效果的影响规律. 研究结果表明, 界面热阻的存在可以提高系统的瞬态热整流系数, 而初始界面间隙的引入让瞬态热整流系数实现了量级的飞跃. 通过几何以及材料参数的合理设置有利于优化结构的热整流效果, 针对周期性高温边界条件, 温差和频率的变化可进一步提升复合结构的热整流系数. 本文所提出热整流机制可以指导瞬态下热整流器的优化设计.

关键词:

Abstract

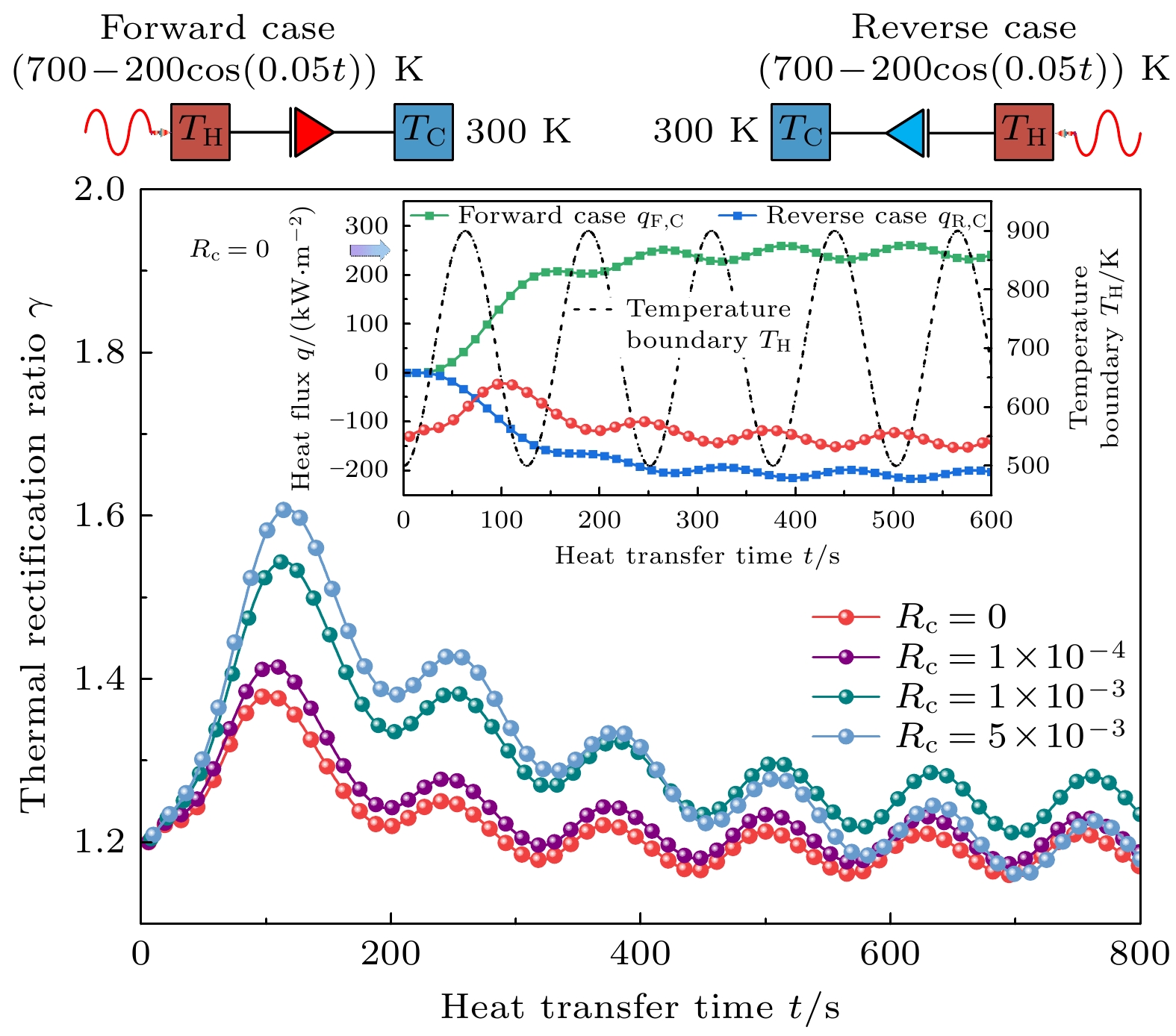
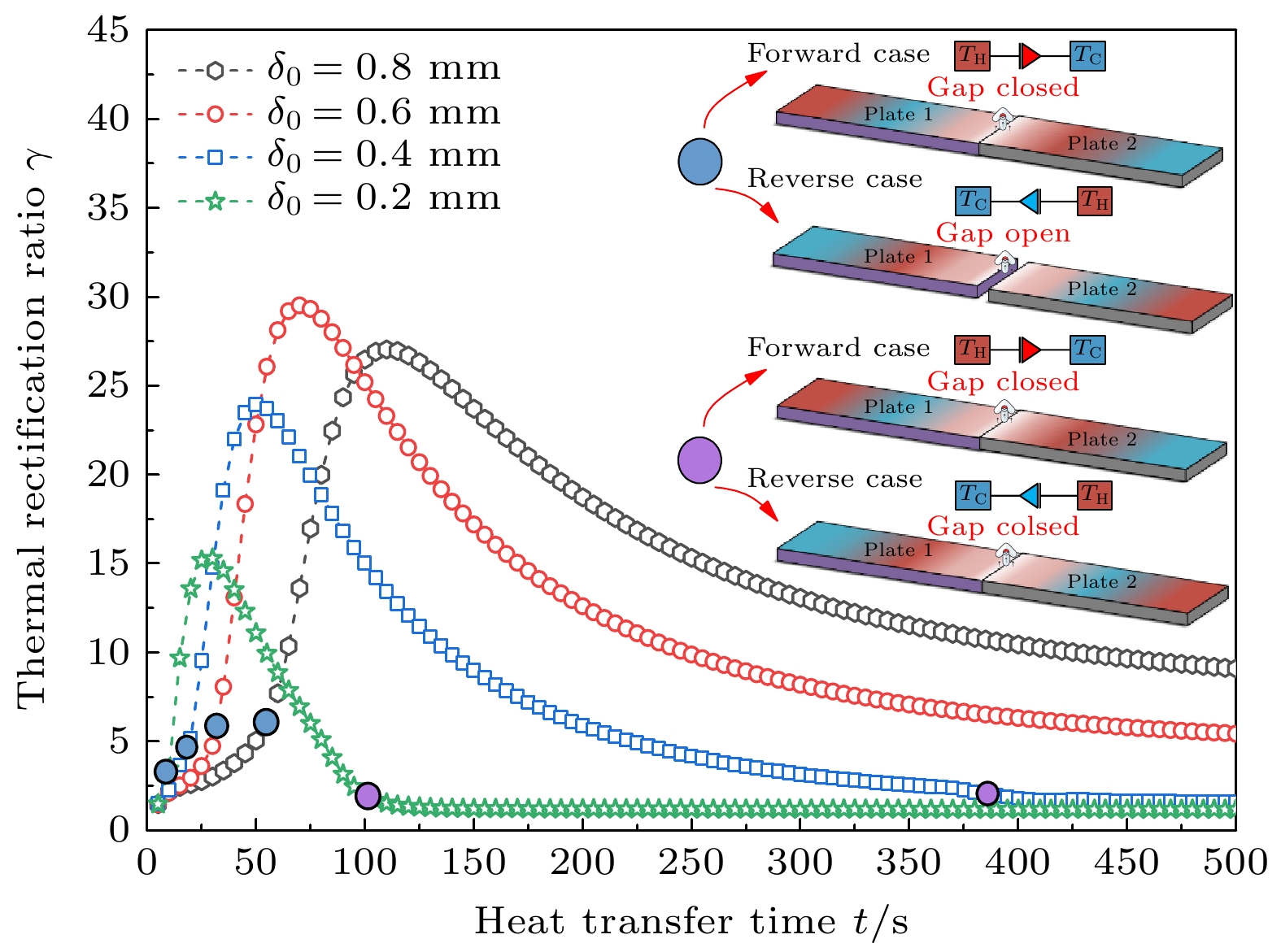
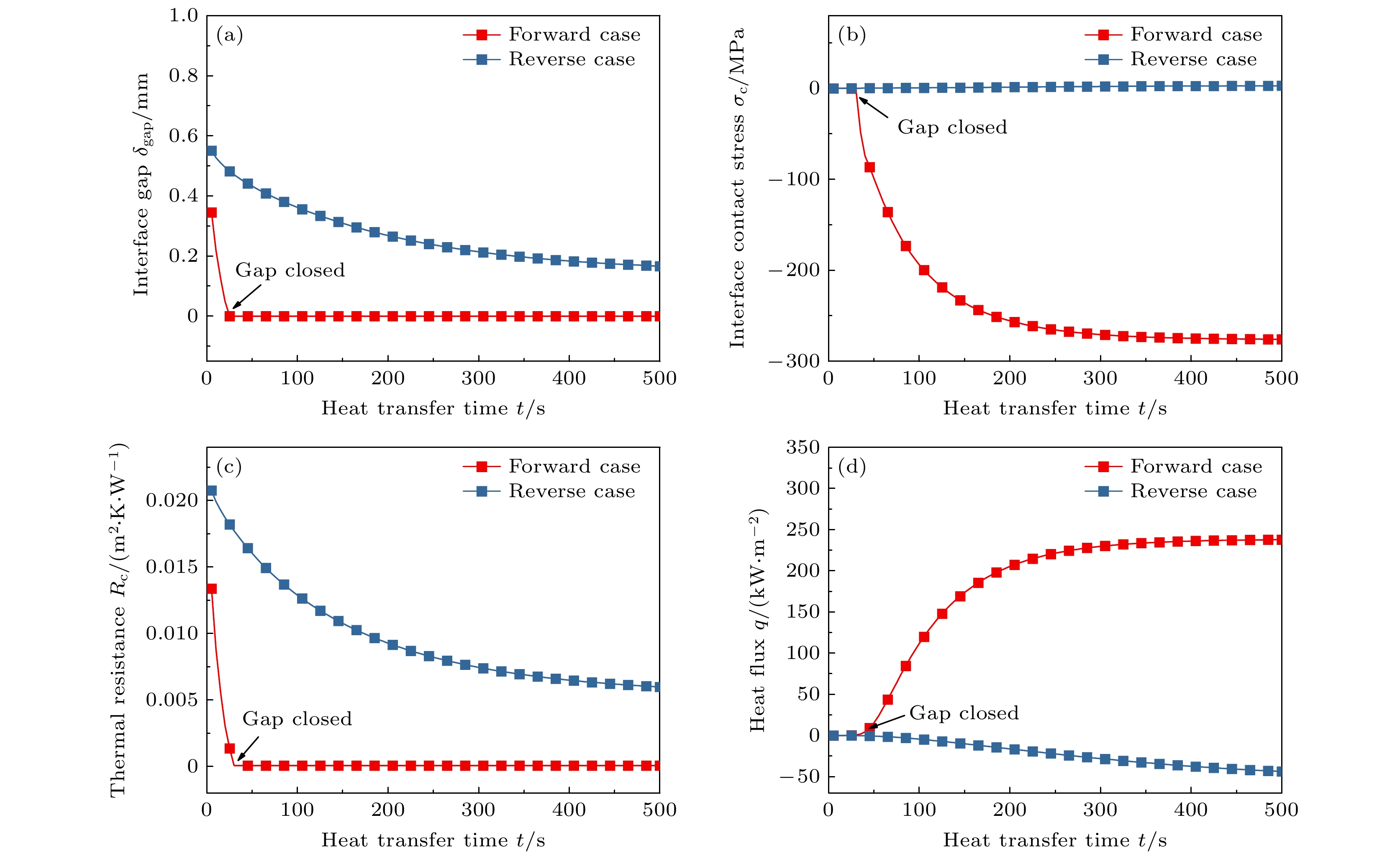
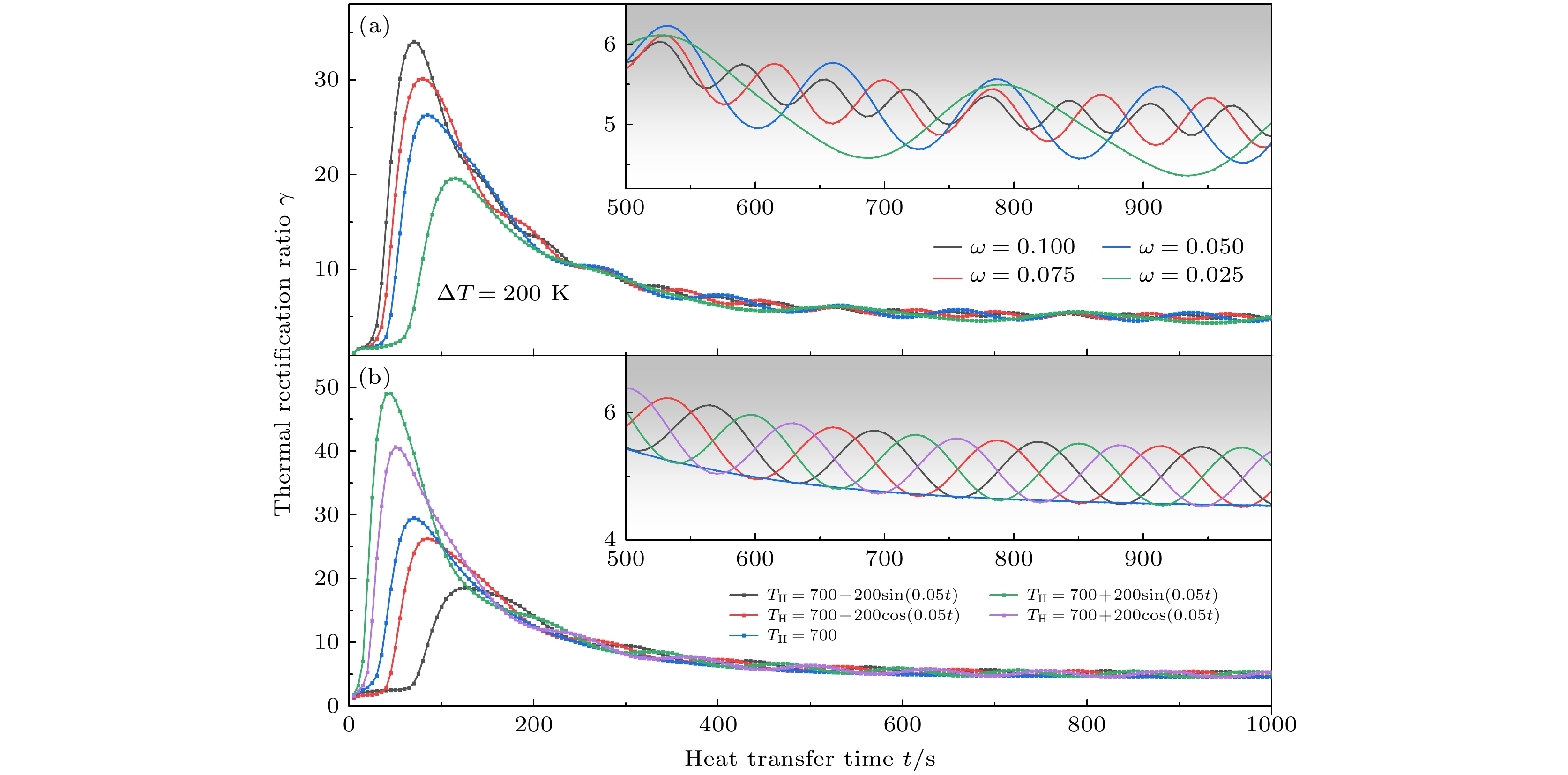
Like an electric diode, thermal diode transmits heat in a specific direction, and thermal rectification is also a fundamental phenomenon for active heat flow control. However, in practical applications, thermal rectification needs to be operated under transient conditions. In this study, transient thermal rectification ratio of a one-dimensional heterostructure is numerically investigated by using the finite element method. The effects of interface thermal resistance, interface initial gap, periodic boundary condition and geometric and material parameters on the transient thermal resistance ratio are obtained. Research indicates that the interface thermal resistance can enhance the thermal rectification effect of the system, and the introduction of the initial interface gap improves the transient thermal rectification ratio by an order of magnitude. The ability to engineer the thermal diffusivity of materials allows us to control the heat flux and improve transient thermal rectification ratio. Since interface thermal resistance can enlarge the difference in heat transfer capability between forward case and reverse case, it is reasonable to suggest that adjusting the interface thermal resistance may also enhance the thermal rectification effect, but excessive interface thermal resistance will reduce it. Under the periodic temperature boundary conditions, the larger the temperature difference in boundary fluctuation, the larger the fluctuation amplitude of the transient thermal rectification ratio is. The fluctuation frequency of thermal rectification changes with the periodic boundary frequency, which also affects the amplitude of the fluctuation. Furthermore, by adjusting the initial interface gap, the gap is closed during heat transfer and the interface thermal resistance is reduced in the forward case, while the interface gap is kept open in the reverse case, thereby improving the overall thermal rectification ratio by an order of magnitude. For different transient stages, the equivalent thermal conductivity can be changed by adjusting the material and geometrical properties to improve the thermal rectification ratio.Therefore, the proposed numerical approach and results can guide the optimal design of the transient thermal rectifier.

Keywords:

作者及机构信息

1.
北京科技大学数理学院, 磁光电复合材料与界面科学北京市重点实验室, 北京　100083

2.
中国空气动力研究与发展中心计算空气动力研究所, 绵阳　621000

3.
北京科技大学高等工程师学院, 北京　100083

通信作者: 刘冬欢, liudh@ustb.edu.cn

基金项目: 国家自然科学基金(批准号: 11772045)和国家数值风洞工程(批准号: NNW2019ZT2-B04)资助的课题.

Authors and contacts

1.
Beijing Key Laboratory for Magneto-Photoelectrical Composite and Interface Science, School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China

2.
Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China

3.
School of Advanced Engineering, University of Science and Technology Beijing, Beijing 100083, China

Corresponding author: Liu Dong-Huan, liudh@ustb.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11772045), and the National Numerical Wind Tunnel Project of China (Grant No. NNW2019ZT2-B04).

文章全文 : translate this paragraph

参考文献

[1]	Starr C 1936 Physics 7 15 Google Scholar
[2]	Wong M Y, Tso C Y, Ho T C, Lee H H 2021 Int. J. Heat Mass Transfer 164 120607 Google Scholar
[3]	Yang N, Xu X F, Zhang G, Li B W 2012 AIP Adv. 2 041410 Google Scholar
[4]	Li B W, Wang L, Casati G L 2004 Phys. Rev. Lett. 93 184301 Google Scholar
[5]	Zhu J, Hippalgaonkar K, Shen S, et al. 2014 Nano Lett. 14 4867 Google Scholar
[6]	Paolucci F, Marchegiani G, Strambini E, Giazotto F 2018 Phys. Rev. Appl. 10 024003 Google Scholar
[7]	Wang J, Shao C R, Li H Y, Xia G D 2022 Int. J. Heat Mass Transfer 188 122627 Google Scholar
[8]	Sarkar S, Nefzaoui E, Basset P, Bourouina T 2021 J. Quant. Spectrosc. Radiat. Transfer 266 107573 Google Scholar
[9]	Leon-Gil J A, Martinez-Flores J J, Alvarez-Quintana J 2018 J. Mater. Sci. 54 3211 Google Scholar
[10]	Go D B, Sen M 2010 J. Heat Transfer 132 124502 Google Scholar
[11]	Peyrard M 2006 Europhys. Lett. 76 49 Google Scholar
[12]	Dames C 2009 J. Heat Transfer 131 061301 Google Scholar
[13]	Kobayashi W, Teraoka Y, Terasaki I 2009 Appl. Phys. Lett. 95 171905 Google Scholar
[14]	Yang Y, Chen H Y, Wang H, Li N B, Zhang L F 2018 Phys. Rev. E 98 042131 Google Scholar
[15]	Majdi T, Pal S, Puri I K 2017 Int. J. Therm. Sci. 117 260 Google Scholar
[16]	Shih T M, Gao Z J, Guo Z Q, Merlitz H, Pagni P J, Chen Z 2015 Sci. Rep. 5 12677 Google Scholar
[17]	邵春瑞, 李海洋, 王军, 夏国栋 2021 70 236501 Google Scholar Shao C R, Li H Y, Wang J, Xia G D 2021 Acta Phys. Sin. 70 236501 Google Scholar
[18]	Sawaki D, Kobayashi W, Moritomo Y, Terasaki I 2011 Appl. Phys. Lett. 98 081915 Google Scholar
[19]	Tian H, Xie D, Yang Y, Ren T L, Zhang G, Wang Y F, Zhou C J, Peng P G, Wang L G, Liu L T 2012 Sci. Rep. 2 523 Google Scholar
[20]	Sadat H, Le Dez V 2016 Mech. Res. Commun. 76 48 Google Scholar
[21]	Carlomagno I, Cimmelli V A, Jou D 2020 Mech. Res. Commun. 103 103472 Google Scholar
[22]	赵建宁, 刘冬欢, 魏东, 尚新春 2020 69 056501 Google Scholar Zhao J N, Liu D H, Wei D, Shang X C 2020 Acta Phys. Sin. 69 056501 Google Scholar
[23]	朱玉鑫, 王珏, 罗爽, 王军, 夏国栋 2016 中国科学:技术科学 46 175 Google Scholar Zhu Y X, Wang J, Luo S, Wang J, Xia G D 2016 Sci. China Ser. E 46 175 Google Scholar
[24]	Chumak K, Martynyak R 2012 Int. J. Heat Mass Transfer 55 5603 Google Scholar
[25]	Sayer R A 2016 Heat Transfer Res. 47 733 Google Scholar
[26]	Carlomagno I, Cimmelli V A, Jou D 2021 J. Therm. Stresses 44 919 Google Scholar
[27]	Carlomagno I, Cimmelli V A, Jou D 2020 Phys. Lett. A 384 126905 Google Scholar
[28]	Zhao J N, Wei D, Gao A Q, Dong H L, Bao Y B, Jiang Y M, Liu D H 2020 Appl. Therm. Eng. 176 115410 Google Scholar
[29]	Zhao J N, Wei D, Dong Y Y, Zhang D, Liu D H 2022 Int. J. Heat Mass Transfer 194 123024 Google Scholar
[30]	单小东, 王沫然 2014 工程热 35 1401 Google Scholar Shan X D, Wang M R 2014 J. Eng. Thermophys. 35 1401 Google Scholar
[31]	温家乐, 徐志成, 古宇, 郑冬琴, 钟伟荣 2015 64 216501 Google Scholar Wen J L, Xu Z C, Gu Y, Zheng D Q, Zhong W R 2015 Acta Phys. Sin. 64 216501 Google Scholar
[32]	李威, 冯妍卉, 唐晶晶, 张欣欣 2013 62 076106 Google Scholar Li W, Feng Y H, Tang J J, Zhang X X 2013 Acta Phys. Sin. 62 076106 Google Scholar
[33]	鞠生宏, 梁新刚 2013 62 026101 Google Scholar Ju S H, Liang X G 2013 Acta Phys. Sin. 62 026101 Google Scholar
[34]	Herrera F A, Luo T F, Go D B 2017 J. Heat Transfer 139 091301 Google Scholar
[35]	Klinar K, Rojo M M, Kutnjak Z, Kitanovski A 2020 J. Appl. Phys. 127 234101 Google Scholar
[36]	Ordonez-Miranda J, Guo Y Y, Alvarado-Gil J J, Volz S, Nomura M 2021 Phys. Rev. Appl. 16 L041002 Google Scholar
[37]	Zhang G, Cottrill A L, Koman V B, Liu A T, Mahajan S G, Piephoff D E, Strano M S 2020 Appl. Energy 280 115881 Google Scholar
[38]	Shimokusu T J, Zhu Q, Rivera N, Wehmeyer G 2022 Int. J. Heat Mass Transfer 182 122035 Google Scholar
[39]	Barber J R, Zhang R 1988 Int. J. Mech. Sci. 30 691 Google Scholar
[40]	Touloukian Y S, Powell R W, Ho C Y, Klemens P G 1970 Thermophysical Properties of Mmatter-the Tprc Data Series (United States: Purdue University)

施引文献

图 1 复合结构热整流器模型　(a) 正向温度边界; (b) 反向温度边界

Fig. 1. Composite structure thermal rectifier model: (a) Forward case; (b) reverse case.

下载: 全尺寸图片幻灯片

图 2 不同的界面传热形式

Fig. 2. Different forms of interface heat transfer.

下载: 全尺寸图片幻灯片

图 3 不同界面热阻下的瞬态热整流系数

Fig. 3. Transient thermal rectification ratio with different interface thermal resistances.

下载: 全尺寸图片幻灯片

图 4 周期性变温边界条件下界面热阻对瞬态热整流系数的影响

Fig. 4. Effect of interface thermal resistance on transient thermal rectification ratio with periodical temperature boundary conditions.

下载: 全尺寸图片幻灯片

图 5 不同初始界面间隙下的瞬态热整流系数

Fig. 5. Transient thermal rectification ratio with different initial interface gaps.

下载: 全尺寸图片幻灯片

图 6 初始界面间隙为0.6 mm时热整流器关键参数的瞬态响应　(a) 界面间隙; (b) 界面接触应力; (c) 界面热阻; (d) 低温端热流

Fig. 6. Transient response of key parameters in thermal rectifier with 0.6 mm initial interface gap : (a) Interface gap; (b) interface contact stress; (c) interface thermal resistance; (d) heat flux at cold side.

下载: 全尺寸图片幻灯片

图 7 不同初始界面间隙下热整流系数的瞬态响应

Fig. 7. Transient response of thermal rectification ratio at different initial interface gaps.

下载: 全尺寸图片幻灯片

图 8 不同周期性条件参数$ \Delta T $下的瞬态热整流系数

Fig. 8. Transient thermal rectification ratio with different periodical condition parameters $ \Delta T $.

下载: 全尺寸图片幻灯片

图 9 不同周期性条件参数$ \omega $和高温边界形式下的瞬态热整流系数

Fig. 9. Transient thermal rectification ratio with different periodical condition parameters $ \omega $ and high temperature boundary forms

下载: 全尺寸图片幻灯片

图 10 不同几何和材料参数对瞬态热整流系数的影响

Fig. 10. Effect of geometry parameter and material pair on the transient thermal rectification ratio.

下载: 全尺寸图片幻灯片

map

[1]	Starr C 1936 Physics 7 15 Google Scholar
[2]	Wong M Y, Tso C Y, Ho T C, Lee H H 2021 Int. J. Heat Mass Transfer 164 120607 Google Scholar
[3]	Yang N, Xu X F, Zhang G, Li B W 2012 AIP Adv. 2 041410 Google Scholar
[4]	Li B W, Wang L, Casati G L 2004 Phys. Rev. Lett. 93 184301 Google Scholar
[5]	Zhu J, Hippalgaonkar K, Shen S, et al. 2014 Nano Lett. 14 4867 Google Scholar
[6]	Paolucci F, Marchegiani G, Strambini E, Giazotto F 2018 Phys. Rev. Appl. 10 024003 Google Scholar
[7]	Wang J, Shao C R, Li H Y, Xia G D 2022 Int. J. Heat Mass Transfer 188 122627 Google Scholar
[8]	Sarkar S, Nefzaoui E, Basset P, Bourouina T 2021 J. Quant. Spectrosc. Radiat. Transfer 266 107573 Google Scholar
[9]	Leon-Gil J A, Martinez-Flores J J, Alvarez-Quintana J 2018 J. Mater. Sci. 54 3211 Google Scholar
[10]	Go D B, Sen M 2010 J. Heat Transfer 132 124502 Google Scholar
[11]	Peyrard M 2006 Europhys. Lett. 76 49 Google Scholar
[12]	Dames C 2009 J. Heat Transfer 131 061301 Google Scholar
[13]	Kobayashi W, Teraoka Y, Terasaki I 2009 Appl. Phys. Lett. 95 171905 Google Scholar
[14]	Yang Y, Chen H Y, Wang H, Li N B, Zhang L F 2018 Phys. Rev. E 98 042131 Google Scholar
[15]	Majdi T, Pal S, Puri I K 2017 Int. J. Therm. Sci. 117 260 Google Scholar
[16]	Shih T M, Gao Z J, Guo Z Q, Merlitz H, Pagni P J, Chen Z 2015 Sci. Rep. 5 12677 Google Scholar
[17]	邵春瑞, 李海洋, 王军, 夏国栋 2021 70 236501 Google Scholar Shao C R, Li H Y, Wang J, Xia G D 2021 Acta Phys. Sin. 70 236501 Google Scholar
[18]	Sawaki D, Kobayashi W, Moritomo Y, Terasaki I 2011 Appl. Phys. Lett. 98 081915 Google Scholar
[19]	Tian H, Xie D, Yang Y, Ren T L, Zhang G, Wang Y F, Zhou C J, Peng P G, Wang L G, Liu L T 2012 Sci. Rep. 2 523 Google Scholar
[20]	Sadat H, Le Dez V 2016 Mech. Res. Commun. 76 48 Google Scholar
[21]	Carlomagno I, Cimmelli V A, Jou D 2020 Mech. Res. Commun. 103 103472 Google Scholar
[22]	赵建宁, 刘冬欢, 魏东, 尚新春 2020 69 056501 Google Scholar Zhao J N, Liu D H, Wei D, Shang X C 2020 Acta Phys. Sin. 69 056501 Google Scholar
[23]	朱玉鑫, 王珏, 罗爽, 王军, 夏国栋 2016 中国科学:技术科学 46 175 Google Scholar Zhu Y X, Wang J, Luo S, Wang J, Xia G D 2016 Sci. China Ser. E 46 175 Google Scholar
[24]	Chumak K, Martynyak R 2012 Int. J. Heat Mass Transfer 55 5603 Google Scholar
[25]	Sayer R A 2016 Heat Transfer Res. 47 733 Google Scholar
[26]	Carlomagno I, Cimmelli V A, Jou D 2021 J. Therm. Stresses 44 919 Google Scholar
[27]	Carlomagno I, Cimmelli V A, Jou D 2020 Phys. Lett. A 384 126905 Google Scholar
[28]	Zhao J N, Wei D, Gao A Q, Dong H L, Bao Y B, Jiang Y M, Liu D H 2020 Appl. Therm. Eng. 176 115410 Google Scholar
[29]	Zhao J N, Wei D, Dong Y Y, Zhang D, Liu D H 2022 Int. J. Heat Mass Transfer 194 123024 Google Scholar
[30]	单小东, 王沫然 2014 工程热 35 1401 Google Scholar Shan X D, Wang M R 2014 J. Eng. Thermophys. 35 1401 Google Scholar
[31]	温家乐, 徐志成, 古宇, 郑冬琴, 钟伟荣 2015 64 216501 Google Scholar Wen J L, Xu Z C, Gu Y, Zheng D Q, Zhong W R 2015 Acta Phys. Sin. 64 216501 Google Scholar
[32]	李威, 冯妍卉, 唐晶晶, 张欣欣 2013 62 076106 Google Scholar Li W, Feng Y H, Tang J J, Zhang X X 2013 Acta Phys. Sin. 62 076106 Google Scholar
[33]	鞠生宏, 梁新刚 2013 62 026101 Google Scholar Ju S H, Liang X G 2013 Acta Phys. Sin. 62 026101 Google Scholar
[34]	Herrera F A, Luo T F, Go D B 2017 J. Heat Transfer 139 091301 Google Scholar
[35]	Klinar K, Rojo M M, Kutnjak Z, Kitanovski A 2020 J. Appl. Phys. 127 234101 Google Scholar
[36]	Ordonez-Miranda J, Guo Y Y, Alvarado-Gil J J, Volz S, Nomura M 2021 Phys. Rev. Appl. 16 L041002 Google Scholar
[37]	Zhang G, Cottrill A L, Koman V B, Liu A T, Mahajan S G, Piephoff D E, Strano M S 2020 Appl. Energy 280 115881 Google Scholar
[38]	Shimokusu T J, Zhu Q, Rivera N, Wehmeyer G 2022 Int. J. Heat Mass Transfer 182 122035 Google Scholar
[39]	Barber J R, Zhang R 1988 Int. J. Mech. Sci. 30 691 Google Scholar
[40]	Touloukian Y S, Powell R W, Ho C Y, Klemens P G 1970 Thermophysical Properties of Mmatter-the Tprc Data Series (United States: Purdue University)

[1]	肖忆瑶, 何佳豪, 陈南锟, 王超, 宋宁宁. 基于负载Fe₃O₄纳米微球的大尺寸单层二维Ti₃C₂T_x微波吸收性能. , 2023, 72(21): 217501. doi: 10.7498/aps.72.20231200
[2]	宗志成, 潘东楷, 邓世琛, 万骁, 杨哩娜, 马登科, 杨诺. 混合失配模型预测金属/半导体界面热导. , 2023, 72(3): 034401. doi: 10.7498/aps.72.20221981
[3]	邵春瑞, 李海洋, 王军, 夏国栋. 多孔结构体材料热整流效应. , 2021, 70(23): 236501. doi: 10.7498/aps.70.20211285
[4]	付柏山, 廖奕, 周俊. 稀释制冷机及其中的热交换问题. , 2021, 70(23): 230202. doi: 10.7498/aps.70.20211760
[5]	张博宇, 周佳凯, 任程超, 苏祥林, 任慧志, 赵颖, 张晓丹, 侯国付. 硅异质结太阳电池中钝化层和发射层的优化设计. , 2021, 70(18): 188401. doi: 10.7498/aps.70.20210674
[6]	刘康, 孙华锐. 基于拉曼热测量技术的铜基复合物法兰GaN基晶体管的热阻分析. , 2020, 69(2): 028501. doi: 10.7498/aps.69.20190921
[7]	赵建宁, 刘冬欢, 魏东, 尚新春. 考虑界面接触热阻的一维复合结构的热整流机理. , 2020, 69(5): 056501. doi: 10.7498/aps.69.20191409
[8]	吴祥水, 汤雯婷, 徐象繁. 二维材料热传导研究进展. , 2020, 69(19): 196602. doi: 10.7498/aps.69.20200709
[9]	梅涛, 陈占秀, 杨历, 朱洪漫, 苗瑞灿. 非对称纳米通道内界面热阻的分子动力学研究. , 2020, 69(22): 224701. doi: 10.7498/aps.69.20200491
[10]	张龙艳, 徐进良, 雷俊鹏. 尺寸效应对微通道内固液界面温度边界的影响. , 2019, 68(2): 020201. doi: 10.7498/aps.68.20181876
[11]	李满, 戴志高, 应见见, 肖湘衡, 岳亚楠. 基于稳态电热拉曼技术的碳纳米管纤维导热系数测量及传热研究. , 2015, 64(12): 126501. doi: 10.7498/aps.64.126501
[12]	高凤菊. 弯曲Cu纳米线相干X射线衍射图的计算. , 2015, 64(13): 138102. doi: 10.7498/aps.64.138102
[13]	鞠生宏, 梁新刚. 带孔硅纳米薄膜热整流及声子散射特性研究. , 2013, 62(2): 026101. doi: 10.7498/aps.62.026101
[14]	葛宋, 陈民. 接触角与液固界面热阻关系的分子动力学模拟. , 2013, 62(11): 110204. doi: 10.7498/aps.62.110204
[15]	张茂平, 钟伟荣, 艾保全. 非对称双链分子结构的热整流效应. , 2011, 60(6): 060511. doi: 10.7498/aps.60.060511
[16]	王军, 李京颍, 郑志刚. 热整流效应的消失与翻转现象. , 2010, 59(1): 476-481. doi: 10.7498/aps.59.476
[17]	孙明昭, 张淳民, 宋晓平. 新型八边形谐振环金属线复合周期结构左手材料奇异性质研究. , 2010, 59(8): 5444-5449. doi: 10.7498/aps.59.5444
[18]	韩勇, 刘燕文, 丁耀根, 刘濮鲲. 螺旋线慢波结构中界面热阻率的研究. , 2009, 58(3): 1806-1811. doi: 10.7498/aps.58.1806
[19]	孟利军, 肖化平, 唐超, 张凯旺, 钟建新. 碳纳米管-硅纳米线复合结构的形成和热稳定性. , 2009, 58(11): 7781-7786. doi: 10.7498/aps.58.7781
[20]	陆宏, 杨昆, 徐建东, 李淳飞, 洪晶. 偶边界条件下的热致暗空间光孤子. , 1998, 47(3): 428-431. doi: 10.7498/aps.47.428

计量

文章访问数: 3857
PDF下载量: 81
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

一维异质结构的瞬态热整流效应