-
主动流动控制是降低流动噪声的新型途径, 近年来吸引了研究者的广泛关注. 利用二维格林函数, 推导得到了忽略四极子影响的声比拟方程的二维时域解. 在此基础之上, 基于格子Boltzmann方法为核心的流场求解器以及声比拟方程为核心的声场求解器, 在低雷诺数(Re = 100)下, 开展了合成射流频率和相位差对圆柱绕流近壁流场和声辐射远场影响的数值模拟研究. 结果表明, 在利用合成射流减小圆柱阻力时, 出现了两种频率锁定状态, 且远场辐射噪声会发生明显变化. 提高射流频率或减小相位差会增强射流的自噪声, 导致远场辐射声压进一步增大, 并使得指向性由偶极子类型转变为单极子类型. 在各个控制参数组合下, 远场的总辐射噪声增加, 与未施加控制时相比声功率增加了4到18 dB, 同时, 阻力方向的噪声始终增强. 本研究可为探索低辐射噪声的合成射流控制策略提供参考数据.
-
关键词:
- 格子Boltzmann方法 /
- 浸没边界方法 /
- 主动流动控制 /
- 流噪声
This article focuses on the effect of active control via synthetic jets (SJs) on sound generated by a two-dimensional circular cylinder by using the acoustic analogy method. The cylinder is immersed in a uniform upstream flow, where the corresponding Reynolds number is 100 and the Mach number is 0.1. A pair of SJs is placed near the cylinder’s separation point issuing periodically varying forcing, with different combinations of forcing frequency and phase difference. The lattice Boltzmann method (LBM) is coupled with the multi-direct forcing immersed boundary method to solve the near-field flow dynamics. The mechanism of the sound generation lies in the fact that pressure pluses are induced by the periodic vortex shedding from the cylinder’s surface, i.e. dipoles. In the case with active flow control, extra monopoles are generated by the unsteady flow rate resulting from the SJs' periodic blow/suction. The interaction between monopoles and dipoles is confirmed to have a big influence on the acoustic field. The acoustic analogy method is used in various cases with a wide range of control parameters, because it has a considerably lower computational cost than the direct simulation method. Taking into account the effect of the monopole, the acoustic analogy method is developed for solving two-dimensional sound field by substituting the Green’s function. Results indicate that the primary lock-on and the secondary lock-on occur in the case of specified control parameters. The frequency of vortex shedding is related to the SJs’ frequency, deviating from the unforced frequency. Owing to the noise induced by flow, the frequency and phase difference of the SJs also have significant influence on sound field. The far-field noise is enlarged although the SJs reduce drag, due to the induced extra monopole, as well as the strengthened hydrodynamic fluctuation. Further increasing SJs’ frequency or reducing the phase difference will enlarge the far-field noise and make the directivity transformed from dipole to monopole, since the SJs’ self-noise is stronger. Moreover, it is found that the acoustic power increases approximately 4–18 dB compared with the unforced circular cylinder and the drag dipole is strengthened in all combinations of control parameters. This study deepens the understanding of the effect of SJs on sound field, and provides a reference for future studying the control strategies of suppressing noise generated from bluff bodies.-
Keywords:
- lattice Boltzmann method /
- immersed boundary method /
- active flow control /
- flow-induced noise
[1] Inoue O, Hatakeyama N 2002 J. Fluid Mech. 471 285
Google Scholar
[2] 钟思阳, 黄迅 2018 空气动力学学报 36 363
Zhong S Y, Huang X 2018 Acta Aerodyn. Sin. 36 363
[3] 杨茵, 陈迎春, 李栋 2017 空气动力学学报 35 220
Yang Yin, Chen Y C, Li D 2017 Acta Aerodyn. Sin. 35 220
[4] Ren F, Jean R, Tang H 2021 Phys. Fluids 33 037121
Google Scholar
[5] Wang C L, Tang H, Yu S C M, Duan F 2016 Phys. Fluids 28 053601
Google Scholar
[6] Wang C L, Tang H, Yu S C M, Duan F 2017 Phys. Fluids 29 083602
Google Scholar
[7] Wang C L, Tang H, Duan F, Yu S C M 2016 J. Fluids Struct. 60 160
Google Scholar
[8] Wang C L, Tang H, Yu S C M, Duan F 2017 Phys. Rev. Fluids 2 104701
Google Scholar
[9] 陈蒋力, 陈少强, 任峰, 胡海豹 2022 71 084701
Google Scholar
Chen J L, Chen S Q, Ren F, Hu H B 2022 Acta Phys. Sin. 71 084701
Google Scholar
[10] Ren F, Wang C L, Tang H 2021 Phys. Fluids 33 093601
Google Scholar
[11] Du L, Sun X F 2019 J. Fluids Struct. 84 421
Google Scholar
[12] Huang X, Zhang X, Li Y 2010 J. Sound Vib. 329 2477
Google Scholar
[13] Ma R X, Liu Z S, Zhang G H, Doolan C J, Moreau D J 2019 Aerosp. Sci. Technol. 94 105370
Google Scholar
[14] Ma R X, Liu Z S, Zhang G H, Doolan C J, Moreau D J 2020 Aerosp. Sci. Technol. 106 106137
Google Scholar
[15] Guo Y P 2008 J. Sound Vib. 311 843
Google Scholar
[16] Inoue O, Mori M, Hatakeyama N 2003 Phys. Fluids 15 1424
Google Scholar
[17] Ganta N, Mahato B, Bhumkar Y G 2019 Phys. Fluids 31 026104
Google Scholar
[18] Thomas F O, Kozlov A, Corke T C 2008 AIAA J. 46 1921
Google Scholar
[19] Leonidas S, Chris L, Ghader G 2017 J. Fluids Struct. 69 293
Google Scholar
[20] Angland D, Zhang X, Goodyer M 2012 AIAA J. 50 1670
Google Scholar
[21] Abbasi S, Souri M 2020 Int. J. Appl. Mech. 12 2050036
Google Scholar
[22] Wang M, Freund J B, Lele S K 2006 Annu. Rev. Fluid. Mech. 38 483
Google Scholar
[23] Guo Y P 2000 J. Fluid Mech. 403 201
Google Scholar
[24] He X Y, Luo L S 1997 J. Stat. Phys. 88 927
Google Scholar
[25] d'Humieres D, Ginzburg I, Krafczyk M, Lallemand P, Luo L S 2002 Philos. Trans. R. Soc. London, Ser. A 360 437
Google Scholar
[26] Guo Z L, Zheng C G 2008 Int. J. Comput. Fluid Dyn. 22 465
Google Scholar
[27] Peskin C S 2002 Acta Numer. 11 479
Google Scholar
[28] Wang Z L, Fan J R, Luo K 2008 Int. J. Multiphase Flow 34 283
Google Scholar
[29] Guo Z L, Zheng C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
[30] Ziegler D P 1993 J. Stat. Phys. 71 1171
Google Scholar
[31] 戈德斯坦 著 (闫再友 译) 2014 气动声学 (北京: 国防工业出版社) 第97页
Goldstein M E (translated by Yan Z Y) 2014 Aeroacoustics (Beijing: National Defence Industry Press) p97 (in Chinese)
[32] Russell David, Wang Z J 2003 J. Comput. Phys. 191 177
Google Scholar
[33] Liu C, Zheng X, Sung C H 1998 J. Comput. Phys. 139 35
Google Scholar
[34] Chen X P, Ren H 2015 Int. J. Numer. Meth. Fluids 79 183
Google Scholar
[35] Williamson C H K, Brown G L 1998 J. Fluids Struct. 12 1073
Google Scholar
[36] Zhou J, Adrian R J, Balachandar S, Kendall T M 1999 J. Fluid Mech. 387 353
Google Scholar
[37] Margnat F 2015 Comput. Fluids 109 13
Google Scholar
-
图 1 基于合成射流的圆柱主动控制示意图
Fig. 1. Schematic of the active control of a circular cylinder using synthetic jets.
图 3 利用流-声混合方法求解得到的瞬时声辐射场
Fig. 3. Instantaneous pressure field computed via the hybrid flow-acoustics solver.
图 4 测点(70D0, 0)位置瞬时声压对比图
Fig. 4. Comparisons of temporally varying sound pressure at monitor point (70D0, 0).
图 6 典型控制参数下流场云图 (a) 未施加控制时; (b)
$f_{\rm{sj }}^*=1$ , Δϕ = π; (c)$f_{\rm{sj }}^*=2 $ , Δϕ = π; (d)$f_{\rm{sj }}^* =2.1$ , Δϕ = 0.5πFig. 6. Instantaneous vorticity contours: (a) Unforced case; (b)
$f_{\rm{sj }}^* =1$ , Δϕ = π; (c)$f_{\rm{sj }}^* =2 $ , Δϕ = π; (d)$f_{\rm{sj }}^* =2.1$ , Δϕ = 0.5π.
图 7 CL-CD相图 (a)未施加控制时; (b)
$f_{\rm{sj }}^* =1$ , Δϕ = π; (c)$f_{\rm{sj }}^* =2$ , Δϕ = π; (d)$f_{\rm{sj }}^* =2.1$ , Δϕ = 0.5πFig. 7. Phase diagrams of CL-CD: (a) Unforced case; (b)
$f_{\rm{sj }}^* =1$ , Δϕ = π; (c)$f_{\rm{sj }}^*=2 $ , Δϕ = π; (d)$f_{\rm{sj }}^* =2.1$ , Δϕ = 0.5π.
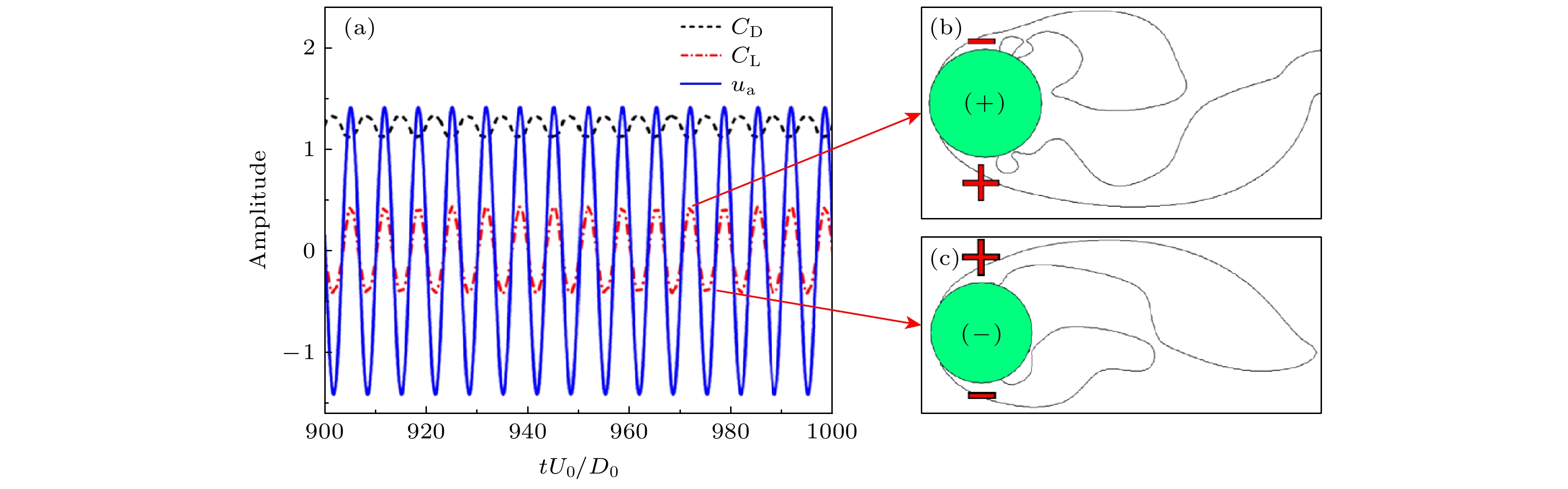
图 8 不同控制参数下流体动力参数的时频域特性 (a) 未施加控制时; (b)
$f_{\rm{sj }}^* =1$ , Δϕ = π; (c)$f_{\rm{sj }}^*=2 $ , Δϕ = π; (d)$f_{\rm{sj }}^* =2.1$ , Δϕ = 0.5πFig. 8. Time history and frequency spectra of the cylinder’s force coefficients: (a) Unforced case; (b)
$f_{\rm{sj }}^* =1$ , Δϕ = π; (c)$f_{\rm{sj }}^* =2$ , Δϕ = π; (d)$f_{\rm{sj }}^*=2.1 $ , Δϕ = 0.5π.
图 9 不同控制参数下圆柱的平均阻力系数
Fig. 9. Time-averaged drag coefficients under a range of control parameters.
图 10
$f_{\rm{sj }}^* =0.9$ 时, 不同相位差Δϕ在r' = 75D0范围声辐射指向性Fig. 10. Directivity of the pressure p'rms measured at r' = 75D0 with different Δϕ when fsj* = 0.9.
图 11
$f_{\rm{sj }}^* =0.9$ , Δϕ = 0.5π时 (a) 圆柱升阻力与上下射流瞬时速度和随时间变化曲线; (b), (c) 对应时刻声源相互作用示意图Fig. 11. (a) Instantaneous lift coefficient, drag coefficient and ua, and (b), (c) Interaction between monopole and dipole when
$f_{\rm{sj }}^* =0.9$ , Δϕ = 0.5π.
图 12
$f_{\rm{sj }}^* =1.1$ 时, 不同相位差Δϕ在r' = 75D0范围声辐射指向性Fig. 12. Directivity of the pressure p'rms measured at r' = 75D0 with different Δϕ when
$f_{\rm{sj }}^* $ = 1.1.
图 13
$f_{\rm{sj }}^* =2.1$ 时, 不同相位差Δϕ在r' = 75D0范围声辐射指向性Fig. 13. Directivity of the pressure p'rms measured at r' = 75D0 for different Δϕ when
$f_{\rm{sj }}^* =2.1 $ .
图 14 Δϕ = 0.5π时, 不同射流频率
$f_{\rm{sj }}^*$ 在r' = 75D0范围声辐射指向性Fig. 14. Directivity of the pressure p'rms measured at r' = 75D0 with different
$ f_{\rm{sj }}^* $ when Δϕ = 0.5π.
图 15 不同控制参数下圆柱辐射噪声的声功率级
Fig. 15. Acoustic power level measured at r' = 75D0 under a range of control parameters.
表 1 主动控制的参数范围
Table 1. Parameter range of the synthetic jet based active control.
参数范围 射流频率 $ f_{\rm sj}^* $ 0.8—1.2, 1.5, 1.9—2.1, 2.9—3.1 相位差 Δϕ 0, 0.25π, 0.5π, 0.75π, π 
下载: 导出CSV
-
[1] Inoue O, Hatakeyama N 2002 J. Fluid Mech. 471 285
Google Scholar
[2] 钟思阳, 黄迅 2018 空气动力学学报 36 363
Zhong S Y, Huang X 2018 Acta Aerodyn. Sin. 36 363
[3] 杨茵, 陈迎春, 李栋 2017 空气动力学学报 35 220
Yang Yin, Chen Y C, Li D 2017 Acta Aerodyn. Sin. 35 220
[4] Ren F, Jean R, Tang H 2021 Phys. Fluids 33 037121
Google Scholar
[5] Wang C L, Tang H, Yu S C M, Duan F 2016 Phys. Fluids 28 053601
Google Scholar
[6] Wang C L, Tang H, Yu S C M, Duan F 2017 Phys. Fluids 29 083602
Google Scholar
[7] Wang C L, Tang H, Duan F, Yu S C M 2016 J. Fluids Struct. 60 160
Google Scholar
[8] Wang C L, Tang H, Yu S C M, Duan F 2017 Phys. Rev. Fluids 2 104701
Google Scholar
[9] 陈蒋力, 陈少强, 任峰, 胡海豹 2022 71 084701
Google Scholar
Chen J L, Chen S Q, Ren F, Hu H B 2022 Acta Phys. Sin. 71 084701
Google Scholar
[10] Ren F, Wang C L, Tang H 2021 Phys. Fluids 33 093601
Google Scholar
[11] Du L, Sun X F 2019 J. Fluids Struct. 84 421
Google Scholar
[12] Huang X, Zhang X, Li Y 2010 J. Sound Vib. 329 2477
Google Scholar
[13] Ma R X, Liu Z S, Zhang G H, Doolan C J, Moreau D J 2019 Aerosp. Sci. Technol. 94 105370
Google Scholar
[14] Ma R X, Liu Z S, Zhang G H, Doolan C J, Moreau D J 2020 Aerosp. Sci. Technol. 106 106137
Google Scholar
[15] Guo Y P 2008 J. Sound Vib. 311 843
Google Scholar
[16] Inoue O, Mori M, Hatakeyama N 2003 Phys. Fluids 15 1424
Google Scholar
[17] Ganta N, Mahato B, Bhumkar Y G 2019 Phys. Fluids 31 026104
Google Scholar
[18] Thomas F O, Kozlov A, Corke T C 2008 AIAA J. 46 1921
Google Scholar
[19] Leonidas S, Chris L, Ghader G 2017 J. Fluids Struct. 69 293
Google Scholar
[20] Angland D, Zhang X, Goodyer M 2012 AIAA J. 50 1670
Google Scholar
[21] Abbasi S, Souri M 2020 Int. J. Appl. Mech. 12 2050036
Google Scholar
[22] Wang M, Freund J B, Lele S K 2006 Annu. Rev. Fluid. Mech. 38 483
Google Scholar
[23] Guo Y P 2000 J. Fluid Mech. 403 201
Google Scholar
[24] He X Y, Luo L S 1997 J. Stat. Phys. 88 927
Google Scholar
[25] d'Humieres D, Ginzburg I, Krafczyk M, Lallemand P, Luo L S 2002 Philos. Trans. R. Soc. London, Ser. A 360 437
Google Scholar
[26] Guo Z L, Zheng C G 2008 Int. J. Comput. Fluid Dyn. 22 465
Google Scholar
[27] Peskin C S 2002 Acta Numer. 11 479
Google Scholar
[28] Wang Z L, Fan J R, Luo K 2008 Int. J. Multiphase Flow 34 283
Google Scholar
[29] Guo Z L, Zheng C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
[30] Ziegler D P 1993 J. Stat. Phys. 71 1171
Google Scholar
[31] 戈德斯坦 著 (闫再友 译) 2014 气动声学 (北京: 国防工业出版社) 第97页
Goldstein M E (translated by Yan Z Y) 2014 Aeroacoustics (Beijing: National Defence Industry Press) p97 (in Chinese)
[32] Russell David, Wang Z J 2003 J. Comput. Phys. 191 177
Google Scholar
[33] Liu C, Zheng X, Sung C H 1998 J. Comput. Phys. 139 35
Google Scholar
[34] Chen X P, Ren H 2015 Int. J. Numer. Meth. Fluids 79 183
Google Scholar
[35] Williamson C H K, Brown G L 1998 J. Fluids Struct. 12 1073
Google Scholar
[36] Zhou J, Adrian R J, Balachandar S, Kendall T M 1999 J. Fluid Mech. 387 353
Google Scholar
[37] Margnat F 2015 Comput. Fluids 109 13
Google Scholar
下载:
计量
- 文章访问数: 3703
- PDF下载量: 76
- 被引次数: 0
